Journal of Modern Physics
Vol.5 No.3(2014), Article ID:43127,5 pages DOI:10.4236/jmp.2014.53019
Computational Study on Melting Process Using Smoothed Particle Hydrodynamics
1Department of Physics, Faculty Mathematics and Natural Sciences, Institut Teknologi Bandung, Bandung, Indonesia
2Department of Computational Science, Faculty Mathematics and Natural Sciences, Institut Teknologi Bandung, Bandung, IndonesiaEmail: supri@fi.itb.ac.id
Copyright © 2014 Suprijadi et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Suprijadi et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 22, 2013; revised November 23, 2013; accepted December 18, 2013
Keywords: Fluid Dynamic; Heat Transfer; Smoothed Particle Hydrodynamics
ABSTRACT
Recently, smoothed particle hydrodynamics (SPH) method has become popular in computational fluid dynamic and heat transfer simulation. The simplicity offered by this method made some complex system in physics such as moving interface in multiphase flow, heat conductivity jumping in multiple material boundaries and many geometrical difficulties become relative easy to calculate. We will treat a relative easy example of melting process to test the method in solving fluid motion equation coupled by heat transfer process. The main heat transfer processes are caused by solid-liquid (medium to medium) heat diffusion and convection. System interaction with ambient temperature can be modeled by gas surrounding fluid-solid system. For the ambient temperature, we proposed surface particle heat transfer governed by convectional heat flux. Using local particle number density value as surface detection method, we applied cooling and heating to surface particle on the melting ice cube and water system. The simulation result is also verified by experiment.
1. Introduction
Nowadays, computational fluid dynamics and heat transfer have become powerful tools for solving industrial and scientific problem. Typically the model arising in problem involves coupled systems of partial differential equation. For example, non-isothermal heat exchange and phase change simulation. To simulate flow with phase change, we need to solve at least fluid motion equation couple with heat equation.
One of the relative new methods for solving partial differential equation appearing in fluid dynamics is smoothed particle hydrodynamics (SPH) method. This method is based on Lagrangian frame equation of motion. It gains popularity after some authors [1,2] use the method to solve several astrophysical problems.
Our previous study on SPH methods is used for studying the dam break phenomena and its effect on a building and solid bar [3]. In this paper, SPH method is developed for supporting solid particles in use for 3D dambreak effect simulation. Solid particle have been treated as a group of rigid particles with translational and rotational motion. The same method will also be applied in this paper for solid motion of 2D ice fraction.
Phase change of material plays an important role in material properties, and understanding the phase transition and phase change of material is mandatory to control the properties. For example, temperature effect on Silicon can be used to control dislocation wake [4], and the other reporting on iron behavior, the temperature of solidification and melting process affects its hardness [5]. The process of solidification and melting is not understood well in atomic level.
In previous work, the simulation of phase change from solid to liquid can be simulated nicely using SPH method with some modifications in heat equation. The modified scheme for Laplace operator proposed by [6] is based on finite difference approximation and gives second order in accuracy. This modification is needed because it lacks stability of standard method.
However heat transfer only occurs between solid and liquid, it means that solid-liquid system is in thermally insulated system. Improvement is needed to enable the interaction with ambient temperature. One of the ideas is to put gas phase filling the remaining domain of the solid liquid system, so there will be heat exchange between the solid-liquid system and “environment” by mechanism of convection and conduction. The idea is realistic but contains some problems if we want to solve this problem using particle method. On the other hand, to clarify the result with experiment, we design an experiment based on infrared (IR) digital camera with resolution of 0.1˚C using a special apparatus.
In this paper, we study on melting process of ice in different ambient temperatures using SPH methods for the simulation. To clarify the result, we do experiment by combination of special apparatus and infra-red camera. The possibility of different temperature effect will be discussed too.
2. Simulation
2.1. Governing Equations
Motion of fluid can be described by Navier-Stokes Equations. In Lagrangian frame, the Navier-Stokes Equation takes form:
 (1)
(1)
 (2)
(2)
where ρ, p, v and g are density, pressure, velocity and body force (e.g. gravity). Θ is refers to viscous term.
With SPH method, incompressible fluid modeled by slightly compressible fluid where pressure can be directly calculated as function of density
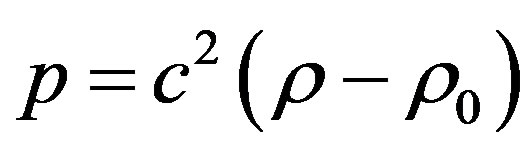 (3)
(3)
here c and ρ0 are speed of sound and initial pressure respectively as proposed in [5].
Heat transfer in material is governed by heat energy equation:
 (4)
(4)
where cp is specific heat, T is temperature and κ is coefficient of conductivity.
Equations (1), (2), (4) are solved numerically using SPH scheme, while Equation (3) is used directly to calculate pressure field.
An open non isothermal system can interact with the environment by heat transfer described by law of cooling.
The rate of change of heat energy to the system is proportional to temperature difference between fluid and environment T − Tenv and area of the contact section. Here the free surface area represents contact section with the environment [7]. The heat flow into/from the free surface can be written as:
 (5)
(5)
2.2. Numerical Scheme
SPH scheme is used to discretize the governing Equation are based on integral of interpolation:

The value of function f1 as function of position r can be calculated by integration of entire space. W is weighting kernel function with smoothing parameter h. This continuous form can be approximate by summation form for numerical work as
 (6)
(6)
To approximate the value of some physical quantity fa by its all surrounding neighbours fb at the system boundaries. The gradient of fa is
 (7)
(7)
Using formulation (7) the governing Equations (1) and (2) now take forms, for complete derivation see [7].
 (8)
(8)
Πab denote artificial viscosity for stabilization of the scheme.
The discretization of heat Equation is done by modified SPH scheme proposed by [3,4]
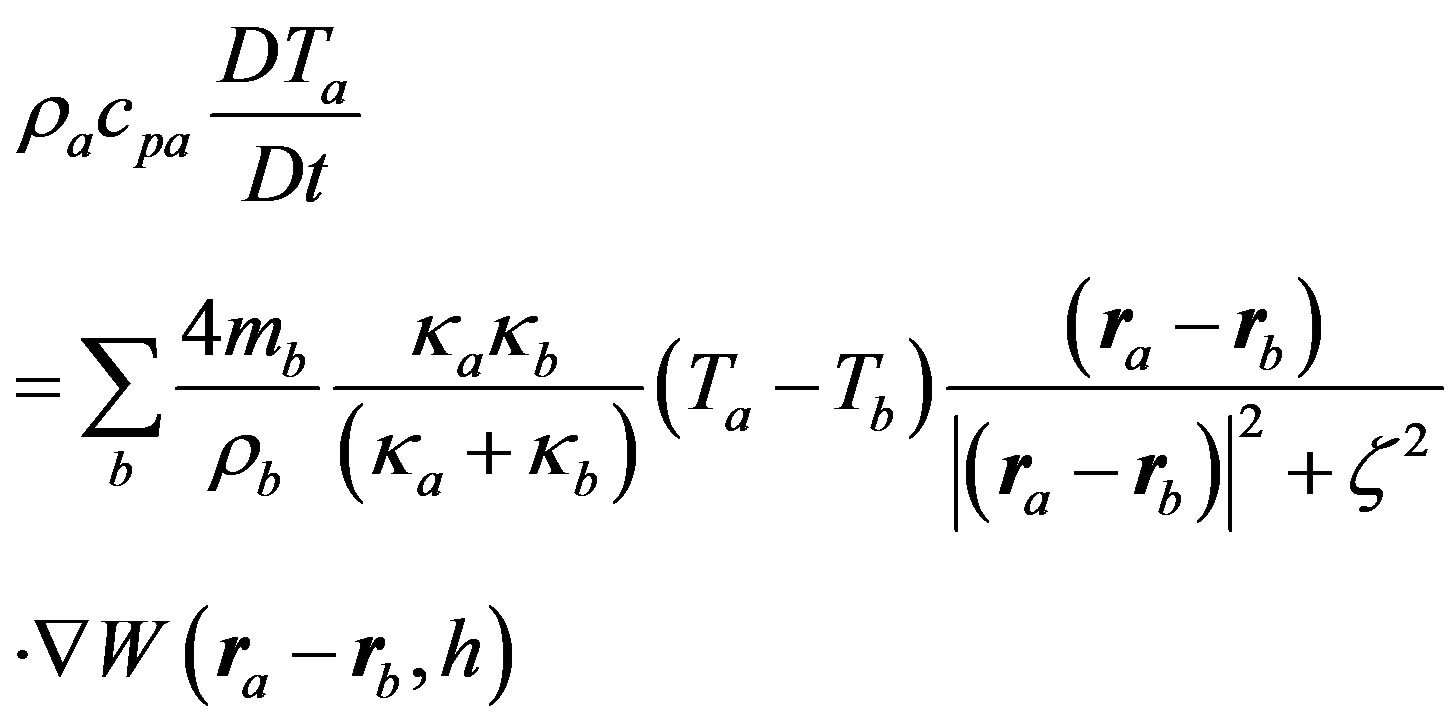 (9)
(9)
while the kernel used in this simulation is based on cubic spline kernel [7].
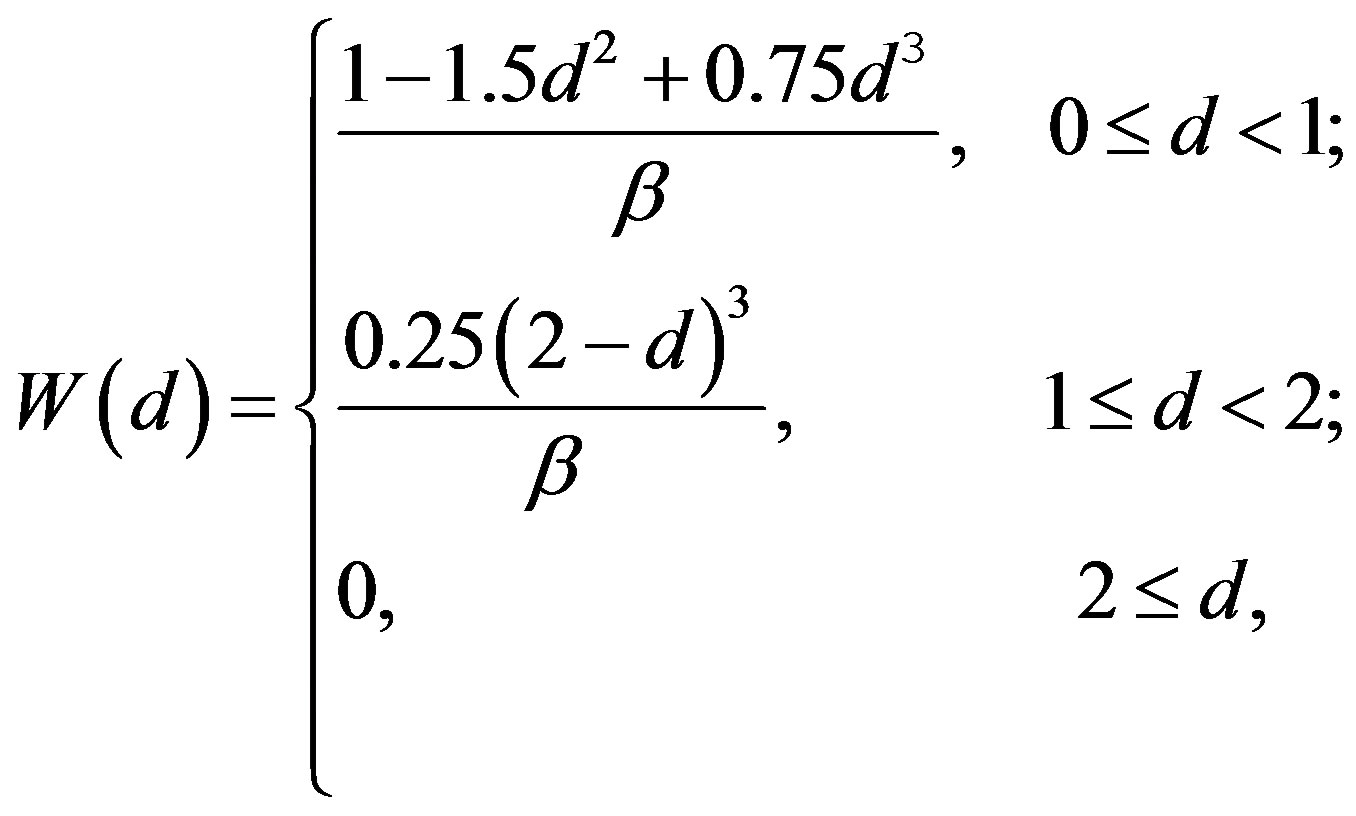
where  and β = 0.7πh2. Equations (7), (8) and (9) now are ordinary differential equation which could be solved by numerical integration. Meanwhile motion of solid body is describe by Newton Equation of motion
and β = 0.7πh2. Equations (7), (8) and (9) now are ordinary differential equation which could be solved by numerical integration. Meanwhile motion of solid body is describe by Newton Equation of motion
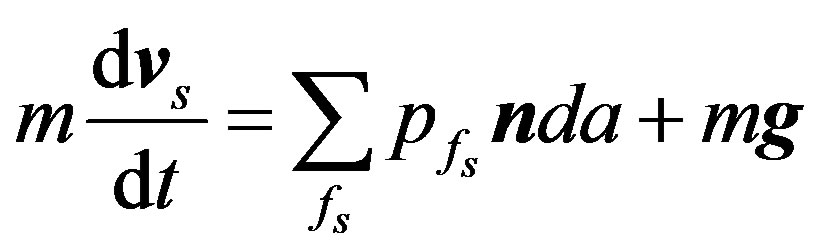 (10)
(10)
for translational motion and
 (11)
(11)
for rotational motion.
In Equation (10) vs denoted translational velocity of solid, m is mass of solid, g is gravity force and in Equation (10) and (11)  is pressure of fluid nearest to the solid, da is cross sectional area of contact force, n is normal vector to solid surface. I and
is pressure of fluid nearest to the solid, da is cross sectional area of contact force, n is normal vector to solid surface. I and  denoted moment of inertia and lever arm of torque respectively.
denoted moment of inertia and lever arm of torque respectively.
To apply Equation (5) we need to perform detection of particle at the edge this problem can be solved by calculating particle number density of fluid-solid system as illustrated in Figure 1.
To compute particle number density, an SPH scheme available:
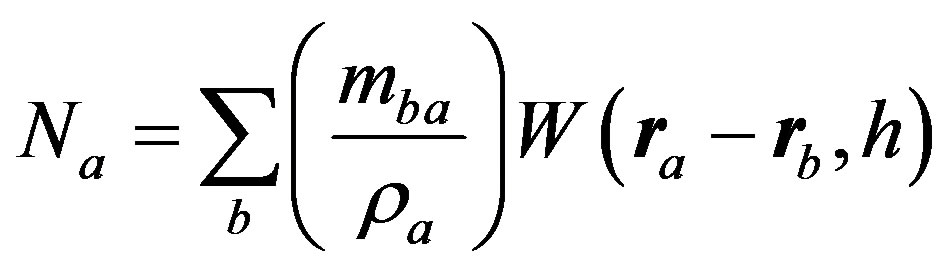
Birds, et al. [8] use condition Na < 0.84Nmax for particles to be classified as free surface particle.
3. Experimental Setup
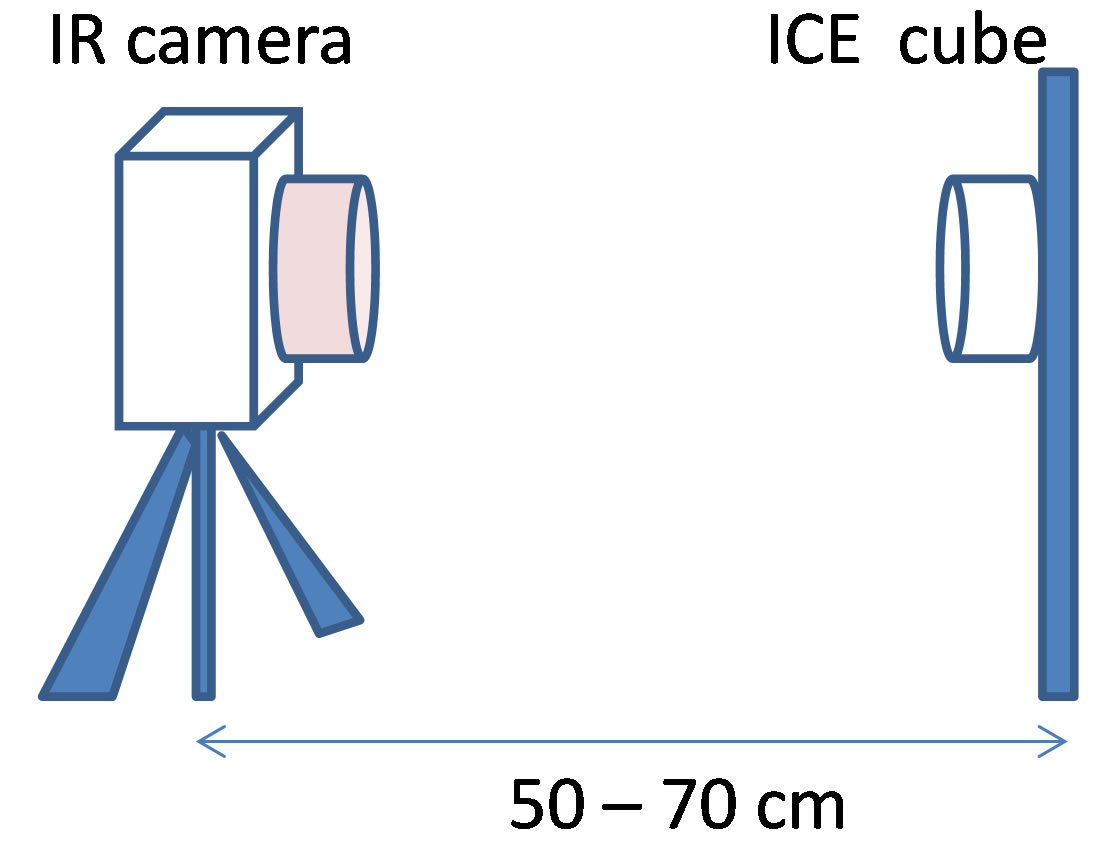
The simulation method is clarify by an experiment on ice melting in room temperature, the experiment apparatus can be seen in schematic as in Figure 2. An ice cube with dimension of 20 × 20 × 20 mm3 was used. The ice

Figure 1. Free surface detection using local particle density number.
 (a)
(a) (b)
(b)
Figure 2. Experimental schematic to observe the phase change transition on ice-water system. (a) Whole schematic; (b) Front view of ice-water system in a cup, the picture took by an infra-red camera with 2Mpixel resolution.
was put on 10˚C (282 K) of cold water, and put in a thick enough of cup and the system was covered by a 15 μm thin sheet of plastic transparence. This thickness is used to make sure that the temperature can be measure by an infra-red digital camera, and directly the same temperature with ice or water inside the cup.
Using IR-camera, we can see very clearly temperature different between ice (dark color) and water (light color) while the ambient temperature was setted higher than water (no color). Using this method, the melting process can observe directly. The camera will record whole melting process, in Figure 2(b), can be seen in the beginning (t = 0 s).
4. Result and Discussion
4.1. Simulation on Melting Process
The simulations were run at QC-cluster in Department of Physics—ITB, the melting process simulation screenshot as seen in Figure 3 shows the effect of heat transferred into ice cube by surrounding waters and ambient temperature. In this simulation, we use 400 particles, 16% is ice particles and the other is water. The different temperature was setting in 10 K. The ice start melting after 0.2 second, and the ice will move around surrounding water.
The ice cube can move freely in translation or rotation, with this movement, more interaction between ice and water will happen and heat transfer from water or ambient air more active. As the result more ice particle will be change to water. Figure 3, shows this phenomena, in (c) and (d) more ice particle change to water particle.
To confirm the model and simulation with natural melting phenomena, we made three different temperature simulation as can be read in Table 1. The results show increasing of temperature difference between ice and
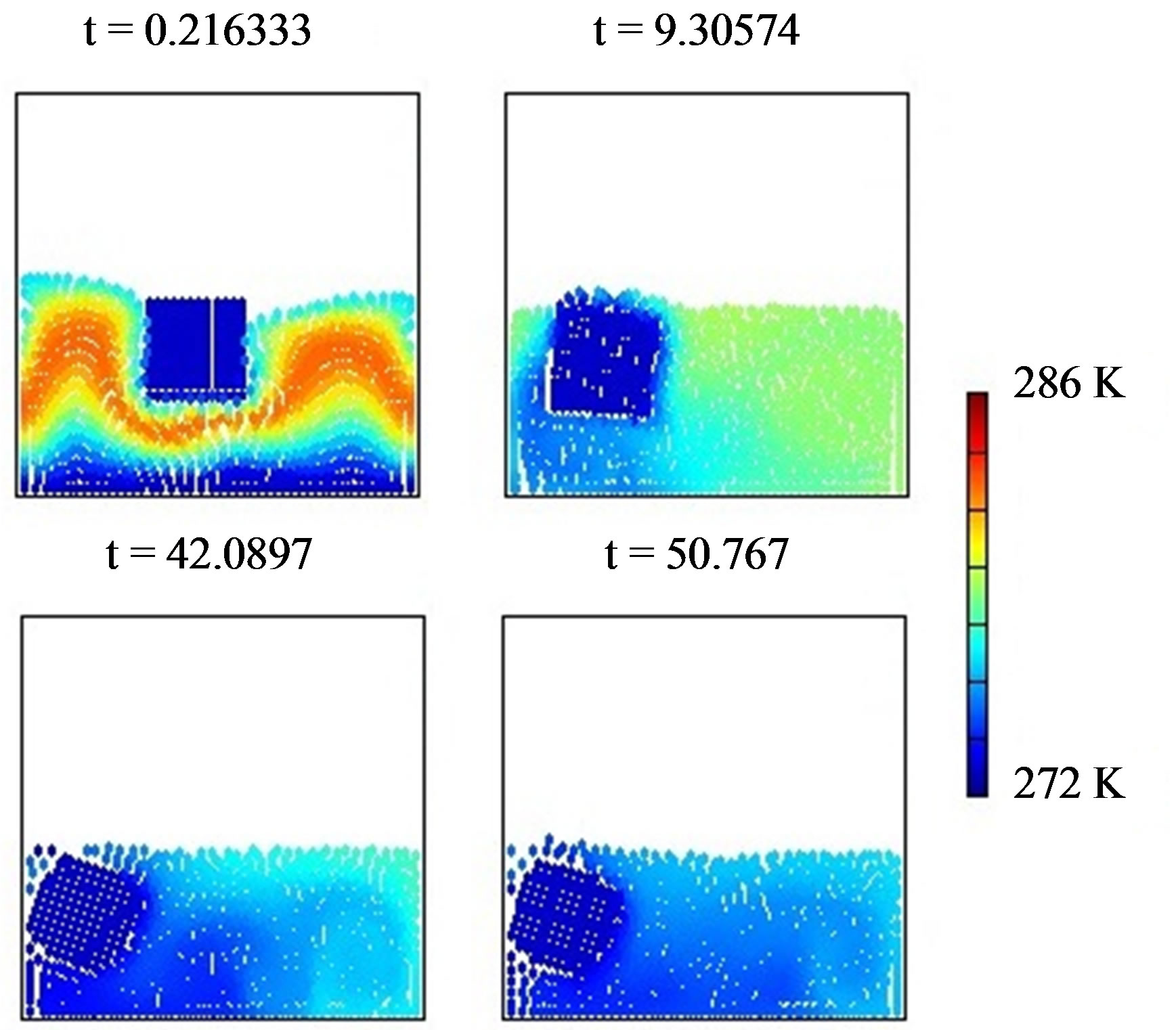
Figure 3. Simulated temperature distribution of ice cube in free surface open system with temperature difference 10 K between water and ice.
water, the ice more faster melting, as can be found in our daily observation.
Study on temperature difference effect is important to see the possibility of global warming. Bintanja et al. [9] reported that the global warming on Artic and Antartic make increasing sea level significant in late 5 years. In the Arctic, observations reveal that sea-ice area, extent and volume have been declining rapidly during the past decades, with the trend in extent being −5.3% per decade since 1985 and has reached as much as −27% per decade since 1995. Our simple simulation on difference temperature gives a good agreement to this phenomenon.
4.2. Experimental Results
Figure 4 shows sequence of an ice melting in experiments apparatus. The dark color has lower temperature, as can be seen the ice has darkest color and ambient air has lighter color.

Table 1. Effect of temperature difference on ice melting.
 (a)
(a) (b)
(b)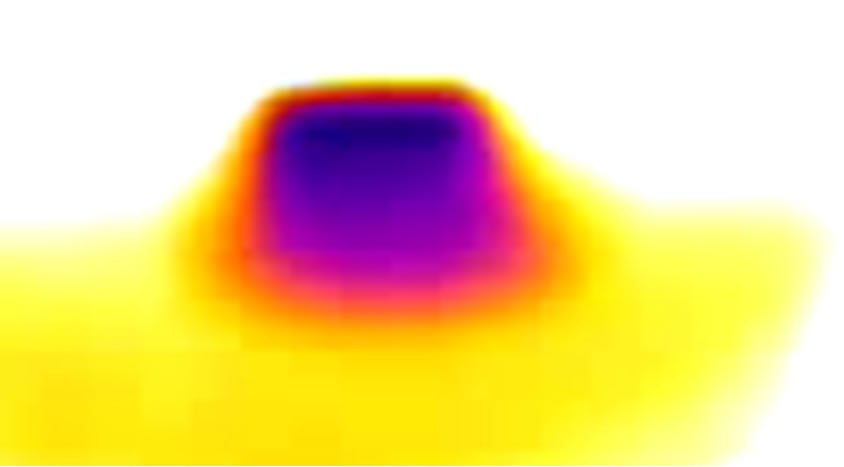 (c)
(c) (d)
(d)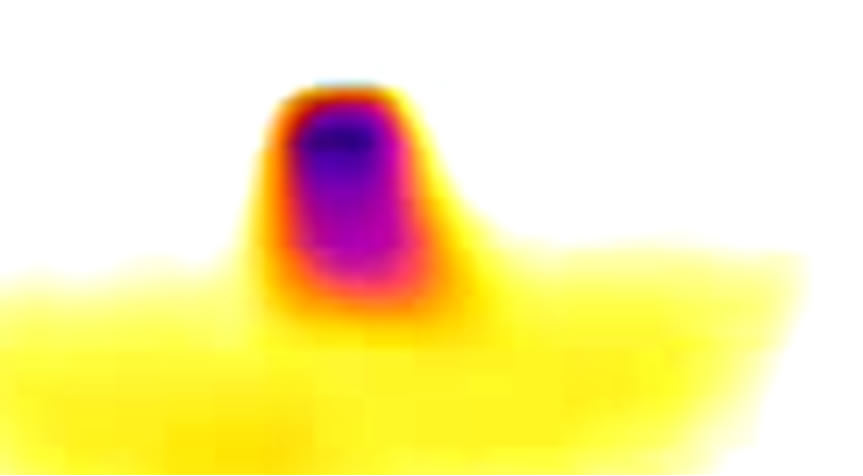 (e)
(e)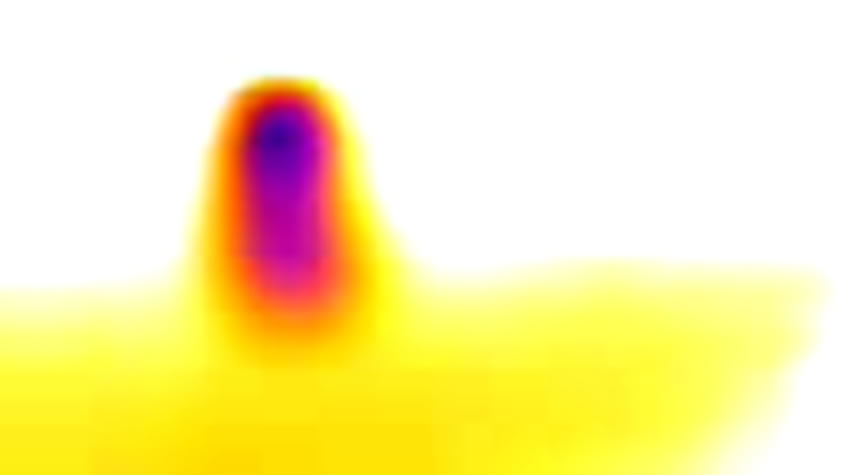 (f)
(f)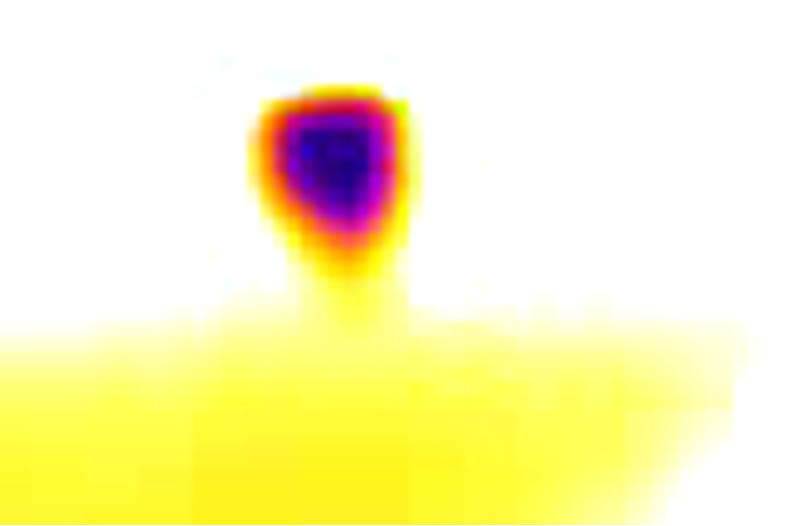 (g)
(g) (h)
(h)
Figure 4. Melting process of a cube ice in cold water. The melting starting from ice surfaces and, melting rapidly after melting rapidly after 4 minutes. (a) t = 0 minute; (b) t = 3 minutes; (c) t = 7 minutes; (d) t = 10 minutes; (e) t = 13 minutes; (f) t = 15 minutes; (g) t = 17 minutes; (h) t = 20 minutes.
The melting of ice is not in linear form, as can be seen in Figure 5. Vertical axis shows the percentage of ice remains compared to original size of ice, while horizontal axis is time in seconds. The melting process can be seen with decreasing of ice part.
The melting process is relative slow until approximately 220 seconds in exponential form, and faster after that. Starting from that point, the ice melting in linear form until all ice melted. The simulation and experiment data show this process clearly.
5. Conclusion
Smoothed particle hydrodynamics (SPH) were applied to understand the melting process in particle size in ice-water system. The validation and comparative study with experiment result show that the melting process is

Figure 5. The melting process by time (percentage of ice). Solid line is simulation result verified by experimental result at 283 K ambient temperature.
slow in the beginning and rapidly after a few seconds in linear form.
Acknowledgements
A part of this research was funding by Research and Innovation Program of Research Group ITB, grant No: 243/I.1.C01/PL/2013.
REFERENCES
- R. A. Gingold and J. J. Monaghan, Monthly Notices of the Royal Astronomical Society, Vol. 181, 1977, pp. 375-389.
- L. B. Lucy, The Astronomical Journal, Vol. 82, 1977, pp. 1013-1024. http://dx.doi.org/10.1086/112164
- Suprijadi, F. Faizal, C. F. Naa and A. Trisnawan, Recent Development on Computational Science, Vol. 4, 2013, pp. 150-154.
- Suprijadi and H. Saka, Philosophical Magazine Letters, Vol. 78, 1998, pp.435-441.
- P. W. Cleary and J. Monaghan, Journal of Computational Physics, Vol. 148, 1999, pp. 227-264. http://dx.doi.org/10.1006/jcph.1998.6118
- P. W. Cleary, Applied Mathematical Modelling, Vol. 22, 1998, pp. 981-993. http://dx.doi.org/10.1016/S0307-904X(98)10031-8
- M. Desbrun and M. P. Cani, Computer Animation and Simulation, Vol. 96, 1996, pp. 61-76. http://dx.doi.org/10.1007/978-3-7091-7486-9_5
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, “Interphase Transport in Non Isothermal System,” In: Transport Phenomena, John Wiley and Son, New York, 2002, pp. 422-450.
- R. Bintanja, G. J. van Oldenborgh, S. S. Drijfhout, B. Wouters and C. A. Katsman, Nature Geoscience, Published Online, 2013.

