Journal of Modern Physics
Vol.4 No.11(2013), Article ID:39866,5 pages DOI:10.4236/jmp.2013.411179
Application of Homotopy Perturbation Method and Parameter Expanding Method to Fractional Van der Pol Damped Nonlinear Oscillator
1Department of Mathematics, Faculty of Science, Taif University, Taif, KSA
2Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt
Email: nofal_ta@yahoo.com, *gamalm2010@yahoo.com
Copyright © 2013 Taher A. Nofal et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 27, 2013; revised August 29, 2013; accepted September 25, 2013
Keywords: Nonlinear Oscillators; Homotopy Perturbation Method; Parameter Expanding Method; Fractional Van der Pol Damped Nonlinear Oscillator
ABSTRACT
In this study, homotopy perturbation method and parameter expanding method are applied to the motion equations of two nonlinear oscillators. Our results show that both the (HPM) and (PEM) yield the same results for the nonlinear problems. In comparison with the exact solution, the results show that these methods are very convenient for solving nonlinear equations and also can be used for strong nonlinear oscillators.
1. Introduction
The study of nonlinear oscillators has been important in the development of the theory of dynamical systems. The Van der Pol oscillator can be regarded as describing a mass-spring-damper system with a nonlinear positiondependent damping coefficient or, equivalently, an RLC electrical circuit with a negative nonlinear resistor, and has been used to develop models in many applications, such as electronics, biology or acoustics. It represents a nonlinear system with an interesting behavior that arises naturally in several applications. Very recently, various kinds of analytical and numerical methods have been used to solve the problems of nonlinear oscillators, such as Frequency-amplitude formulation [1-3], Energy balance method [4-6], Variational iteration method [7,8], Homotopy perturbation method [9-12] and Parameter expanding method [13-15].
In recent years, the application of the homotopy perturbation method in nonlinear problems has been developed by scientists and engineers, because this method continuously deforms the difficult problem under study into a simple problem which is easy to solve. The homotopy perturbation method was proposed first by He in 1998 and was further developed and improved by him [10,13,16]. Homotopy is an important part of differential topology. The homotopy perturbation method is, in fact, a coupling of the traditional perturbation method and homotopy in topology [17]. The essential idea of this method is to introduce a homotopy parameter, say p, which takes the values from 0 to 1. When p = 0, the system of equations usually reduces to a sufficiently simplified form, which normally admits a rather simple solution. At p = 1, the problem takes the original form and the final stage of deformation gives the desired solution. Since most phenomena in our world are essentially nonlinear and are described by nonlinear equations, it is very difficult to solve nonlinear problems, and in general, it is often more difficult to get an analytic approximation than a numerical one for a given nonlinear problem.
Parameter expanding method proposed by He [18] is the most effective and convenient method for handing nonlinear problems [13]. In this method, the solution and unknown frequency of oscillation are expanding in a series by a bookkeeping parameter.
This paper applies (HPM) and (PEM) to fractional Van der Pol damped nonlinear oscillator. Comparison of the period of oscillation and the exact solution shows that both methods are very effective and convenient and quite accurate to nonlinear engineering problems.
2. Applications
In order to show the accuracy of homotopy perturbation method (HPM) and parameter expanding method (PEM) for solving nonlinear equations and to compare it with exact solutions, we will consider the following examples.
2.1. Example 1: The Classical Fractional Van der Pol Oscillator
The classical fractional Van der Pol damped nonlinear oscillator can be represented by the following nonlinear equation [19-21].
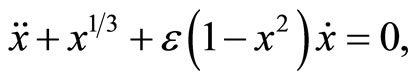 (1)
(1)
with the initial conditions:
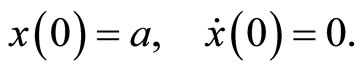 (2)
(2)
2.1.1. Application of Homotopy Perturbation Method (HPM)
The following homotopy can be constructed
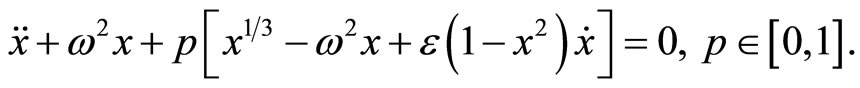 (3)
(3)
As in He’s homotopy perturbation method [9,10,16], it is obvious that when p = 0 Equation (3) becomes the linearized equation, 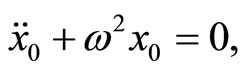 for p = 1 Equation (3) then becomes the original problem. Assume that the periodic solution to Equation (3) may be written as a power series in p:
for p = 1 Equation (3) then becomes the original problem. Assume that the periodic solution to Equation (3) may be written as a power series in p:
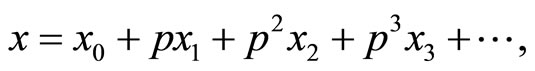 (4)
(4)
Setting p = 1, leads to the approximate solution of the problem:
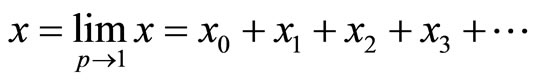 (5)
(5)
Substituting Equation (4) into Equation (3) and equating the terms with the identical powers of p,
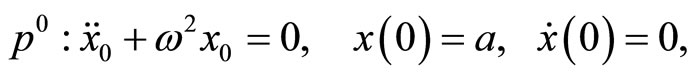 (6)
(6)
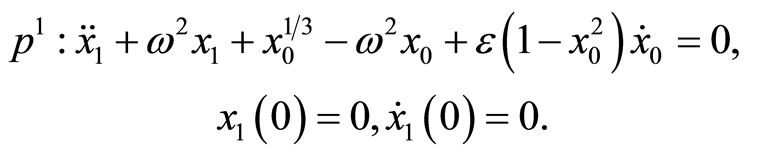 (7)
(7)
Solving Equation (6), we have
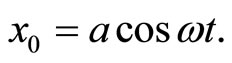 (8)
(8)
The Fourier series for 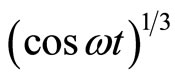 has been calculated [22] and is given by.
has been calculated [22] and is given by.
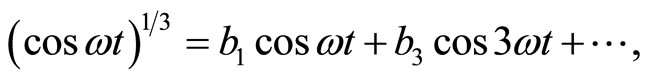 (9)
(9)
where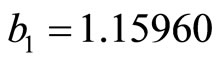 ,
, 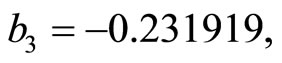
Substituting Equation (8) into Equation (7) leads to
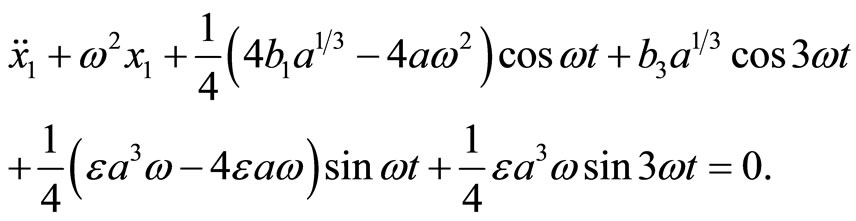 (10)
(10)
Eliminating the secular term, we have
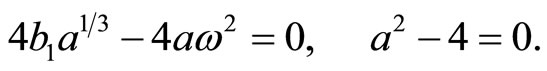 (11)
(11)
From the above equation, we can easily find that
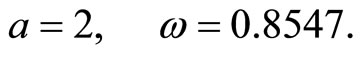 (12)
(12)
which is same with that obtained by iteration procedure (see Equation (40) in Ref [19] and Equation (23) in Ref [20]). Hence, the approximate periodic solution can be readily obtained:
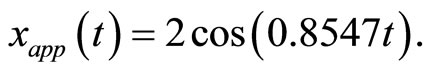 (13)
(13)
2.1.2. Application of Parameter Expanding Method (PEM)
We rewrite Equation (1) in the form
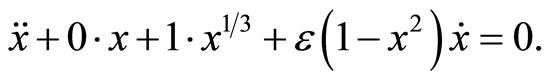 (14)
(14)
To solve Equation (1) by parameter expanding method we expand the solution of the problem and coefficients 0 and 1 in the left side of Equation (14) in series of 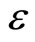 as follows
as follows
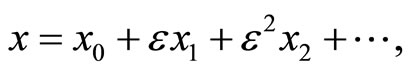 (15)
(15)
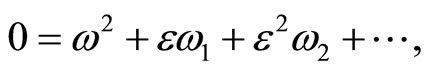 (16)
(16)
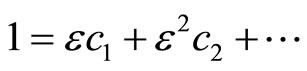 (17)
(17)
Substituting Equations (15)-(17) into Equation (14), and processing as the standard perturbation method, we have
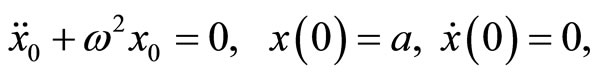 (18)
(18)
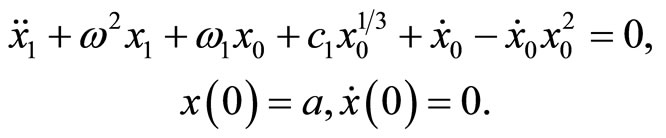 (19)
(19)
The solution of Equation (18) can be easily obtained
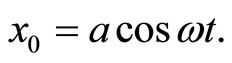 (20)
(20)
Substituting the result into Equation (19) yields
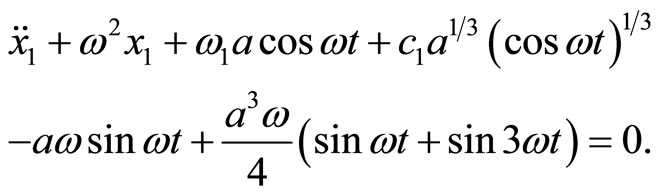 (21)
(21)
Using the relation (9) Equation (21) can be rewritten as
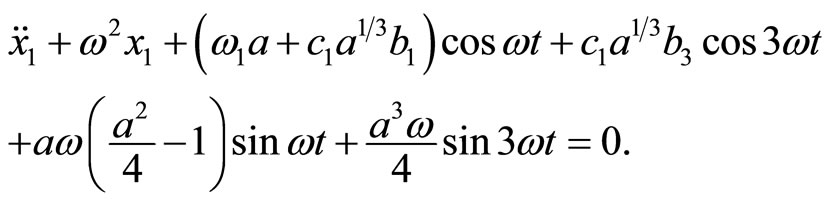 (22)
(22)
No secular terms requires
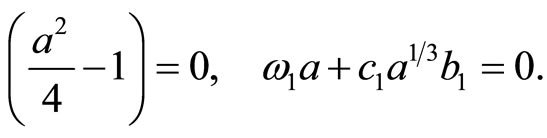 (23)
(23)
If the first order approximation is enough, then setting 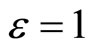 in Equations (15)-(17) yields
in Equations (15)-(17) yields
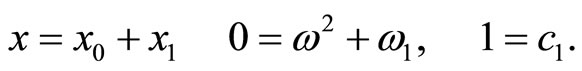 (24)
(24)
From relation (23) and (24) we have
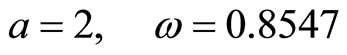 (25)
(25)
which is the same with that obtained by iteration procedure in [19,20] (see Equation (40) in Ref [19] and Equation (23) in Ref [20])
Hence, the approximate periodic solution can be readily obtained:
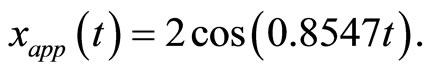 (26)
(26)
To illustrate and verify the accuracy of this method, we may compare the approximate periodic solution  and the exact periodic solution. For reference, the exact solution
and the exact periodic solution. For reference, the exact solution 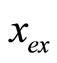 for the classical fractional Van der Pol damped nonlinear oscillator is as follows [23]:
for the classical fractional Van der Pol damped nonlinear oscillator is as follows [23]:
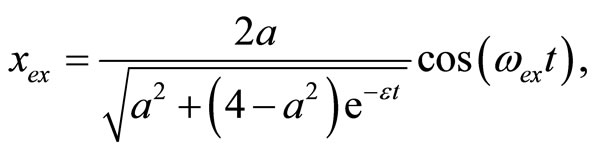 (27)
(27)
where
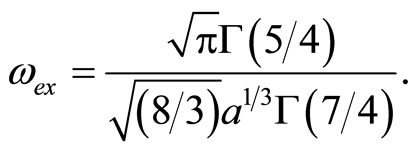 (28)
(28)
In Figure 1, we presented the variety of comparisons between approximate and exact solution for Equation (1). For 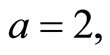
 It can be observed that Equation (26) provides excellent approximation to the exact periodic solution in Equation (27).
It can be observed that Equation (26) provides excellent approximation to the exact periodic solution in Equation (27).
2.2. Example 2: The Special Case of the Fractional Van der Pol Equation or Rayleigh Equation
The special case of the fractional Van der Pol damped nonlinear oscillator or the Rayleigh equation can be represented by [21,24,25].
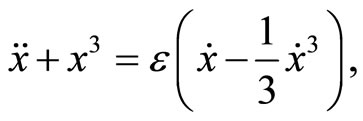 (29)
(29)
with the initial conditions:
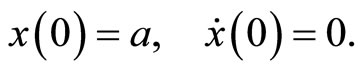 (30)
(30)
2.2.1. Application of Homotopy Perturbation Method (HPM)
We can establish the following homotopy
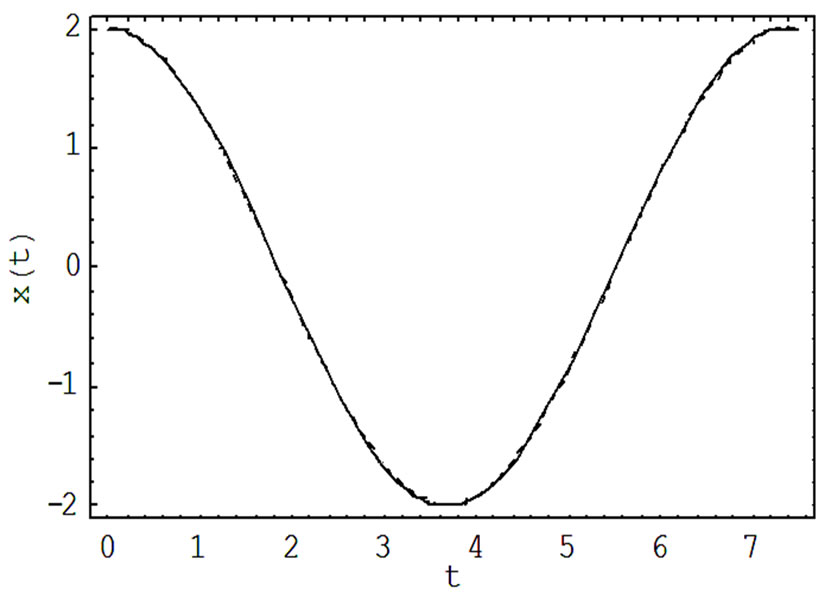
Figure 1 Comparison of the analytical solutions (-) with the exact solution (···) for a = 2; w = 0.8547.
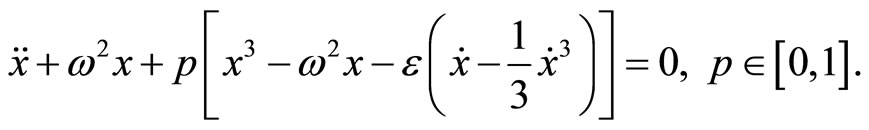 (31)
(31)
Similarly, when p = 0, Equation (31) becomes a linear equation; for p = 1, Equation (31) then becomes the original problem. Applying the perturbation technique, the solution of Equation (31) can be expressed as a power series in p:
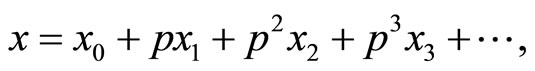 (32)
(32)
Setting p = 1, leads to the approximate solution of the problem:
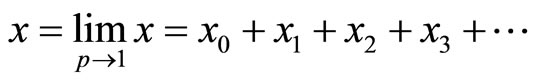 (33)
(33)
Substituting Equation (32) into Equation (31) and equating the terms with the identical powers of p,
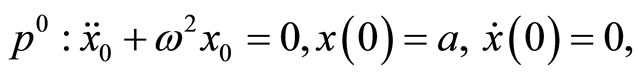 (34)
(34)
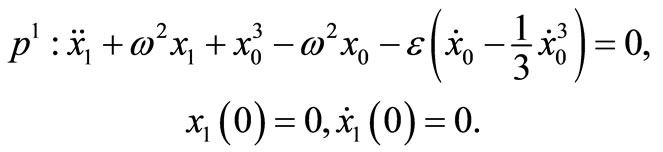 (35)
(35)
The solution for 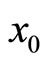 is
is
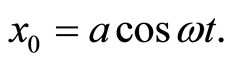 (36)
(36)
Substituting Equation (36) into Equation (35) leads to
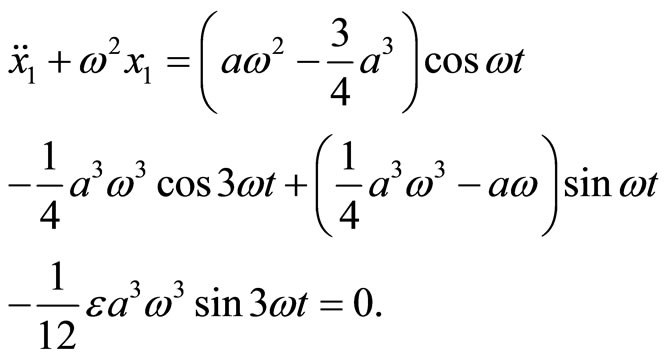 (37)
(37)
No secular terms requires
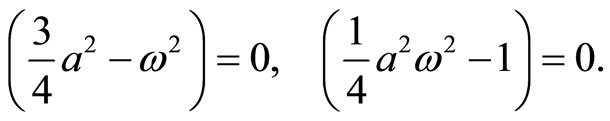 (38)
(38)
From the above equation, we can easily find that
 (39)
(39)
Hence, the approximate periodic solution can be readily obtained:
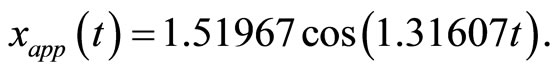 (40)
(40)
2.2.2. Application of Parameter Expanding Method (PEM)
We rewrite Equation (29) in the form
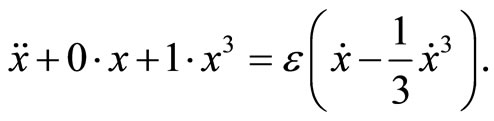 (41)
(41)
Substituting Equations (15)-(17) into Equation (41), collecting the same power of  and equating each coefficient of
and equating each coefficient of  to zero, we obtain
to zero, we obtain
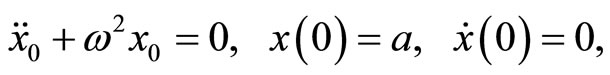 (42)
(42)
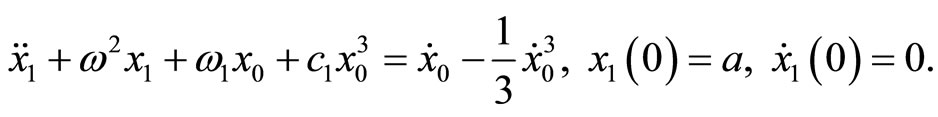 (43)
(43)
Solving Equation (42), we have
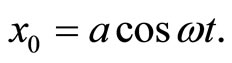 (44)
(44)
Substituting 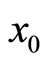 into Equation (43) results in
into Equation (43) results in
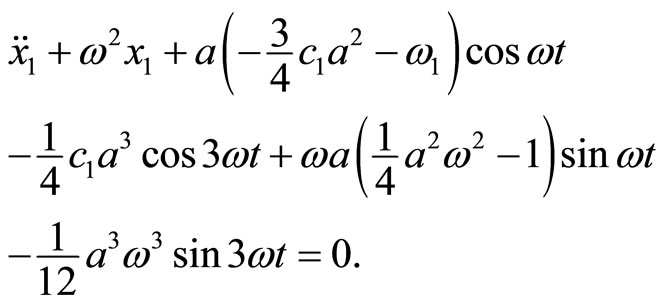 (45)
(45)
Eliminating the secular terms needs
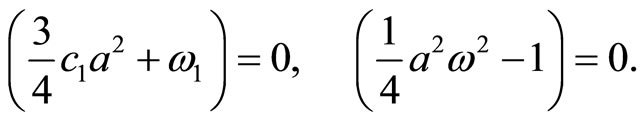 (46)
(46)
If the first order approximation is enough, then setting 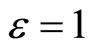 in Equations (15)-(17) yields
in Equations (15)-(17) yields
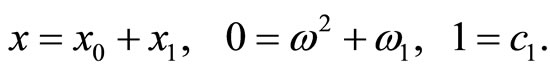 (47)
(47)
From relation (46) and (47) we have
 (48)
(48)
Hence, the approximate periodic solution can be readily obtained:
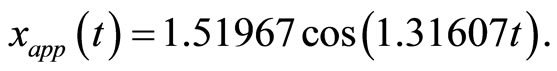 (49)
(49)
To write the exact periodic solution 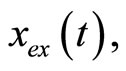 we used its values from [23], and for approximate values we used Equation (49). In fact the exact periodic solution it can be obtained from the following complicated relation that is given in [23].
we used its values from [23], and for approximate values we used Equation (49). In fact the exact periodic solution it can be obtained from the following complicated relation that is given in [23].
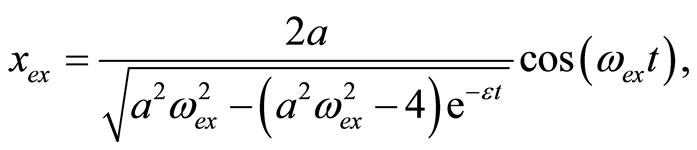 (50)
(50)
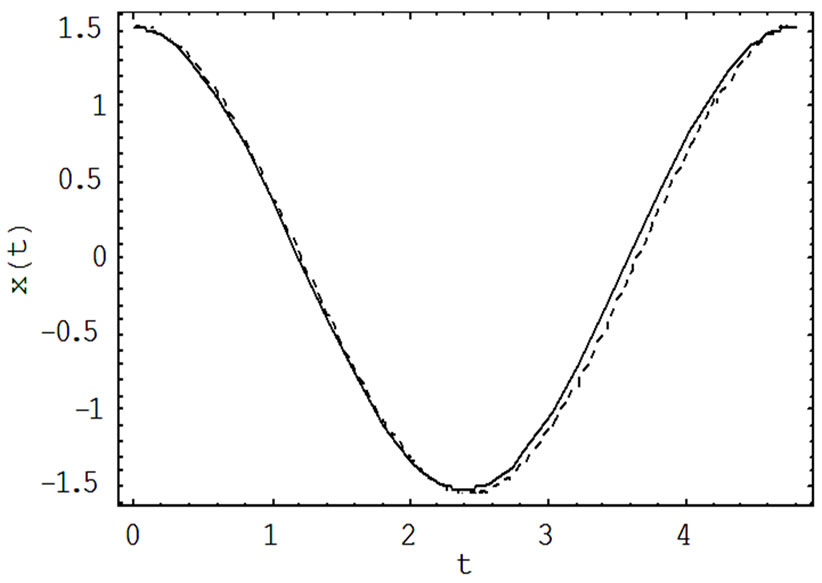
Figure 2. Comparison of the analytical solutions (-) with the exact solution (···) for a = 1.51967; w = 1.31607.
where
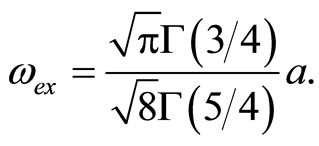 (51)
(51)
To compare with the exact period, Figure 2 shows the comparison between the approximate periodic solution  obtained from formula (49) and the exact periodic solution
obtained from formula (49) and the exact periodic solution 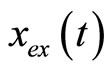 obtained from formula (50) see [23]. It can be seen from Figure 2 that the approximate periodic solution is nearly identical with that given by the exact periodic solution.
obtained from formula (50) see [23]. It can be seen from Figure 2 that the approximate periodic solution is nearly identical with that given by the exact periodic solution.
3. Conclusion
In this paper, we give a comparative study between Homotopy perturbation method (HPM) and Parameter expanding method (PEM) to obtain the approximate periodic solutions to fractional Van der Pol damped nonlinear oscillators. Illustrative examples reveal that these methods are very effective and convenient for solving nonlinear differential equations. Comparisons are also made between the exact solution and the results of the Homotopy perturbation method and Parameter expanding method in order to prove the precision of the results obtained from both methods mentioned.
REFERENCES
- J. H. He, European Journal of Physics, Vol. 29, 2008, pp. 19-22. http://dx.doi.org/10.1088/0143-0807/29/4/L02
- J. H. He, International Journal of Nonlinear Science and Numerical Simulation, Vol. 9, 2008, pp. 211-212. http://dx.doi.org/10.1515/IJNSNS.2008.9.2.211
- A. G. Davodi, D. D. Gangi, R. Azami and H. Babazadeh, Modern Physics Letters B, Vol. 23, 2009, pp. 3427-3436. http://dx.doi.org/10.1142/S0217984909021466
- I. Mehdipour, D. D. Ganji and M. Mozaffari, Current Applied Physics, Vol. 10, 2010, pp. 104-112. http://dx.doi.org/10.1016/j.cap.2009.05.016
- D. Younesian, H. Askari, Z. Saadatnia and M. Kalami Yazdi, Computers and Mathematics with Applications, Vol. 59, 2010, pp. 3222-3228. http://dx.doi.org/10.1016/j.camwa.2010.03.013
- H. Askari, M. Kalami Yazdi and Z. Saadatnia, Nonlinear Science Letters A, Vol. 1, 2010, pp. 425-430.
- J. H. He, G. C. Wu and F. Austin, Nonlinear Science Letters A, Vol. 1, 2010, pp. 1-30.
- N. Herisanu and V. Marinca, Nonlinear Science Letters A, Vol. 1, 2010, pp. 183-192.
- J. H. He, International Journal of Modern Physics B, Vol. 20, 2006, pp. 2561-2568. http://dx.doi.org/10.1142/S0217979206034819
- J. H. He, International Journal of Non-Linear Mechanics, Vol. 35, 2000, pp. 37-43.
- J. H. He, Chaos, Solitons and Fractals, Vol. 26, 2005, pp. 695-700. http://dx.doi.org/10.1016/j.chaos.2005.03.006
- D. D. Ganji, Physics Letters A, Vol. 355, 2006, pp. 337- 341. http://dx.doi.org/10.1016/j.physleta.2006.02.056
- J. H. He, International Journal of Modern Physics B, Vol. 20, 2006, pp. 1141-1199. http://dx.doi.org/10.1142/S0217979206033796
- L. Xu, Journal of Computational and Applied Mathematics, Vol. 207, 2007, pp. 148-154. http://dx.doi.org/10.1016/j.cam.2006.07.020
- L. Xu, Journal of Sound and Vibration, Vol. 302, 2007, pp. 178-184. http://dx.doi.org/10.1016/j.jsv.2006.11.011
- J. H. He, Computer Methods in Applied Mechanics and Engineering, Vol. 178, 1999, pp. 257-262. http://dx.doi.org/10.1016/S0045-7825(99)00018-3
- J. H. H Journal of Sound and Vibration, Vol. 229, 2000, pp. 1257-1263. http://dx.doi.org/10.1006/jsvi.1999.2509
- J. H. He, International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 2, 2001, pp. 257-264. http://dx.doi.org/10.1515/IJNSNS.2001.2.3.257
- R. E. Mickens, Journal of Sound and Vibration, Vol. 292, 2006, pp. 964-968. http://dx.doi.org/10.1016/j.jsv.2005.08.020
- T. Ozis and A. Yildirm, Journal of Sound and Vibration, Vol. 306, 2007, pp. 372-376. http://dx.doi.org/10.1016/j.jsv.2007.05.021
- D. D. Ganji, M. Esmaeilpour and S. Soleimani, International Journal of Computer Mathematics, Vol. 9, 2010, pp. 2014-2023.
- I. S. Gradshteyn and I. S. Ryzhik, “Table of Integrals, Series and Products,” Academic Press, New York, 1980.
- C. W. Lim and S. K. Lai, International Journal of Mechanical Sciences, Vol. 48, 2006, pp. 483-892. http://dx.doi.org/10.1016/j.ijmecsci.2005.12.009
- J. J. Stoker, “Nonlinear Vibrations in Mechanical and Electrical Systems,” Wiley, New York, 1992.
- D. W. Jordan and P. Smith, “Nonlinear Ordinary Differential Equations: An Introduction to Dynamical Systems,” Oxford University Press, New York, 1999.
NOTES
*Corresponding author.

