Journal of Modern Physics
Vol. 4 No. 10 (2013) , Article ID: 38867 , 12 pages DOI:10.4236/jmp.2013.410168
Noncommutative Phase Space and the Two Dimensional Quantum Dipole in Background Electric and Magnetic Fields
Unité de Recherche en Physique Théorique (URPT), Institut de Mathématiques et de Sciences Physiques (IMSP), Porto-Novo, Bénin
Email: anselme.dossa@imsp-uac.org, gabriel.avossevou@imsp-uac.org, avossevou@yahoo.fr
Copyright © 2013 Anselme F. Dossa, Gabriel Y. H. Avossevou. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 24, 2013; revised August 26, 2013; accepted September 29, 2013
Keywords: Noncommutative (NC) Phase Space; Quantum Dipole;  Symmetry; Similarity Transformation
Symmetry; Similarity Transformation
ABSTRACT
The two dimensional quantum dipole springs in background uniform electric and magnetic fields are first studied in the conventional commutative coordinate space, leading to rigorous results. Then, the model is studied in the framework of the noncommutative (NC) phase space. The NC Hamiltonian and angular momentum do not commute any more in this space. By the means of the 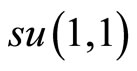 symmetry and the similarity transformation, exact solutions are obtained for both the NC angular momentum and the NC Hamiltonian.
symmetry and the similarity transformation, exact solutions are obtained for both the NC angular momentum and the NC Hamiltonian.
1. Introduction
The discovery of new fundamental interactions and the development of quantum field theory have opened the way to many research works. Then the Standard Model has become the best theory that fits our actual understanding of particle physics. However, many reasons bring us to think that it is not the end of the story. Moreover, these last decades have given birth to some new theories addressing some of the still unresolved enigmas of the nature. One of them is the hypothesis that fundamental structure of spacetime should be entirely revised, considering for instances that it is based on a NC geometry.
In recent years, there have been increasing interests in studying physical aspects of quantum theory on NC space-time, NC space as well as on NC phase space. NC physical effects have thus aroused great interest and related theories have been studied extensively (see for example [1-7]). The motivation for this kind of theory is that in the low energy effective theory of D-brane with a background magnetic field and an extreme situation such as in the string scale or at very high energy levels, not only the space noncommutativity may appear, but also the effects of momentum noncommutativity can be significant, which is called NC phase space. Hence, a lot of specific problems have been investigated on the theory of NC spaces such as the quantum Hall effects [8,9], the harmonic oscillator [10-12], the Fock-Darwin system [13], the coherent states [14], the classical-quantum relation-ship [15], the motion of the spin-1/2 particle under a uniform magnetic field [16], the Dirac equation with a magnetic field in  D [17] and with the time-dependent linear potential [18], etc. The main approach is based on the Weyl-Moyal correspondence which amounts to replacing the usual product by a star product in NC space [19]. Each of these NC theories is defined by a NC algebra where the spectrum of the NC quantum Hamiltonian is worked out. In reference [7], the analog of the Landau problem applied to dipoles in NC spaces is studied. In their paper, the authors studied the analog of Landau quantization, for a neutral polarized particle in the presence of homogeneous electric and magnetic external fields in the context of the NC quantum mechanics, where the Landau energy spectrum and the eigenfunctions of the NC space and NC phase space coordinates have been obtained. In reference [20] which is an extension of the model developed in [21], a supersymmetric description of an analog of our model without the electric field is provided in the commuting cordinates space and the energy spectrum, as well as the spectrum of the angular momentum and the supercharge are determined. Furthermore, to the best of our knowledge, the explicit expressions of spectra for both the quantum Hamiltonian and the angular momentum in NC phase space have not been reported in the literature so far.
D [17] and with the time-dependent linear potential [18], etc. The main approach is based on the Weyl-Moyal correspondence which amounts to replacing the usual product by a star product in NC space [19]. Each of these NC theories is defined by a NC algebra where the spectrum of the NC quantum Hamiltonian is worked out. In reference [7], the analog of the Landau problem applied to dipoles in NC spaces is studied. In their paper, the authors studied the analog of Landau quantization, for a neutral polarized particle in the presence of homogeneous electric and magnetic external fields in the context of the NC quantum mechanics, where the Landau energy spectrum and the eigenfunctions of the NC space and NC phase space coordinates have been obtained. In reference [20] which is an extension of the model developed in [21], a supersymmetric description of an analog of our model without the electric field is provided in the commuting cordinates space and the energy spectrum, as well as the spectrum of the angular momentum and the supercharge are determined. Furthermore, to the best of our knowledge, the explicit expressions of spectra for both the quantum Hamiltonian and the angular momentum in NC phase space have not been reported in the literature so far.
In this paper, we extend and study in the NC phase space with an uniform background magnetic field, the model describing a system of two nonrelativistic charged particles of identical mass, of opposite charges and linked by a spring through an harmonic potential1. This extension constists of considering an electric field in addition to the magnetic field and a confining potential. The considered model may be viewed as a dipole observed from a network of charged particles. Through the developments given hereafter, we note that the Hamiltonian and the angular momentum do not commute in NC phase space. Our approach which combines algebraic and analytical technics, using group theory tools, allows to diagonalyze these observables.
The outline of the paper is as follows. In Section 2, we solve the two dimensional quantum dipole coupled to external background electric and magnetic fields in the ordinary commuting coordinates space. This lights the way for us in Section 3, where we deal with the study of the system in NC phase space. In Section 4, we present an algebraic framework to show that the corresponding NC quantum Hamiltonian and NC angular momentum possesse a hidden 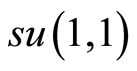 algebraic structure and we obtain the exact eigenvalues and eigenfunctions of these operators by means of the similarity transformation. Section 5 is devoted to the conclusion.
algebraic structure and we obtain the exact eigenvalues and eigenfunctions of these operators by means of the similarity transformation. Section 5 is devoted to the conclusion.
2. Quantum Dipole in the Ordinary Commuting Coordinates Space
Consider a system consisting of two nonrelativistic charged particles of identical mass 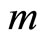 but of opposite electric charges
but of opposite electric charges 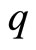 and
and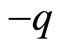 , moving in the two-dimensional Euclidean space, coupled to some background gauge fields
, moving in the two-dimensional Euclidean space, coupled to some background gauge fields 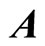 and
and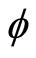 . The magnetic field
. The magnetic field  is chosen to be static, homogeneous and perpendicular to the plane, while the electric field
is chosen to be static, homogeneous and perpendicular to the plane, while the electric field 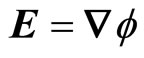 lies in that plane. Their positions—with respect to some inertial frame-are represented by two vectors
lies in that plane. Their positions—with respect to some inertial frame-are represented by two vectors  and
and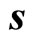 , respectively. These two particles interact with one another through an attractive harmonic force of constant spring. Furthermore, this model is generalized2 by confining the center of mass of the system in an harmonic potential.
, respectively. These two particles interact with one another through an attractive harmonic force of constant spring. Furthermore, this model is generalized2 by confining the center of mass of the system in an harmonic potential.
The system may be described by the following Lagrangian
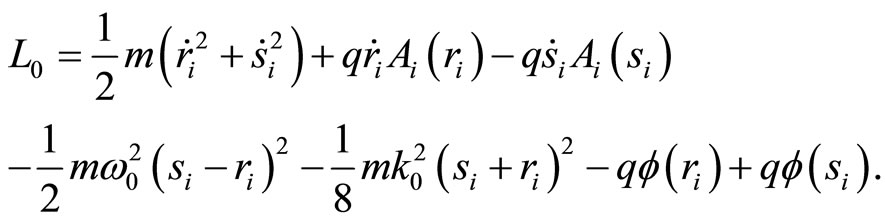 (1)
(1)
In order to keep the rotational covariance of the system explicit, the circular gauge will be used for the vector potential
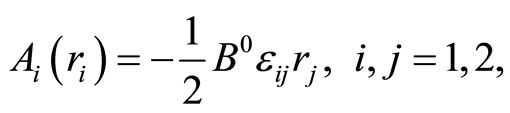 (2)
(2)
while, the scalar potential is
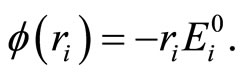 (3)
(3)
Let’s introduce now the following change of variables,
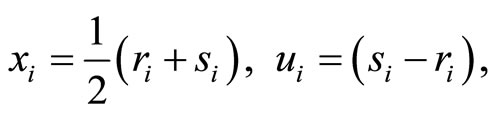 (4)
(4)
where 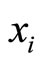 thus being the position vector of the centerof-mass of this two-body problem, while
thus being the position vector of the centerof-mass of this two-body problem, while 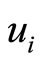 represents the relative position of the particles.
represents the relative position of the particles.
The Lagrangian may be expressed as follows
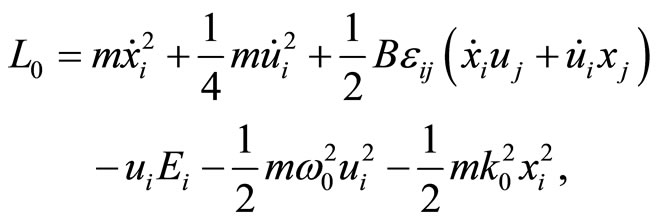 (5)
(5)
where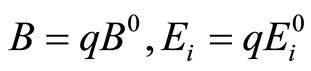 .
.
The Euler-Lagrange equations of motion for the system are,
 (6)
(6)
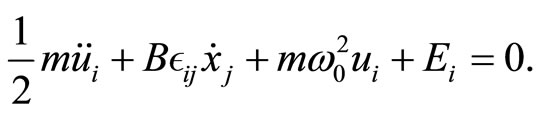 (7)
(7)
2.1. Hamiltonian Formulation
By the means of the “auxiliary” variables 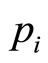 and
and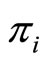 , the Lagrange function may also be written as follows,
, the Lagrange function may also be written as follows,
 (8)
(8)
where
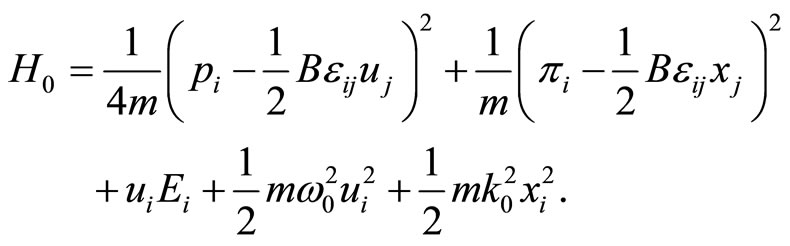 (9)
(9)
Indeed when solving for the equations of motion for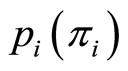 , these are seen to correspond to the conjugate momenta of
, these are seen to correspond to the conjugate momenta of 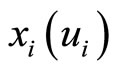 and then one recovers the original Lagrange function. Proceeding like that the action is already in first-order Hamiltonian form, both for the
and then one recovers the original Lagrange function. Proceeding like that the action is already in first-order Hamiltonian form, both for the 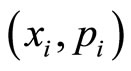 sector as well as for the
sector as well as for the  sector. Poisson brackets are then readily read off the Lagrangian in first-order form, while
sector. Poisson brackets are then readily read off the Lagrangian in first-order form, while 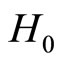 is its Hamiltonian. Thus the Dirac quantization algorithm is left implicit and one finds the following Poisson/Dirac brackets,
is its Hamiltonian. Thus the Dirac quantization algorithm is left implicit and one finds the following Poisson/Dirac brackets,
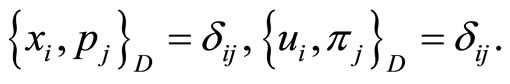 (10)
(10)
Quantisation of the system is then straightforward from these Poisson brackets and the above Hamiltonian through the correspondence principle, in an obvious manner.
2.2. The Quantum Dynamics
We now promote each degree of freedom to an operator acting on a Hilbert space to be defined. Following the canonical quantization procedure, we define the commutation relations as 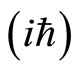 times the Dirac bracket of the classical quantities:
times the Dirac bracket of the classical quantities:
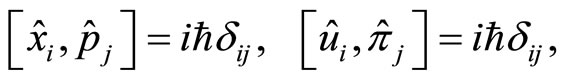 (11)
(11)
where 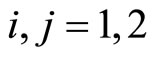 and all the operators are their own hermitian conjugate. The quantum Hamiltonian is given by,
and all the operators are their own hermitian conjugate. The quantum Hamiltonian is given by,
 (12)
(12)
When wanting to complete with the electric field coupling the square defined by the harmonic potential, one is led indeed to the following change of variables [22], which is a canonical transformation in phase space,
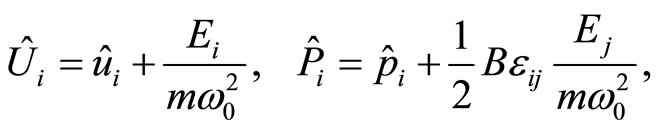 (13)
(13)
such that,
 (14)
(14)
We get
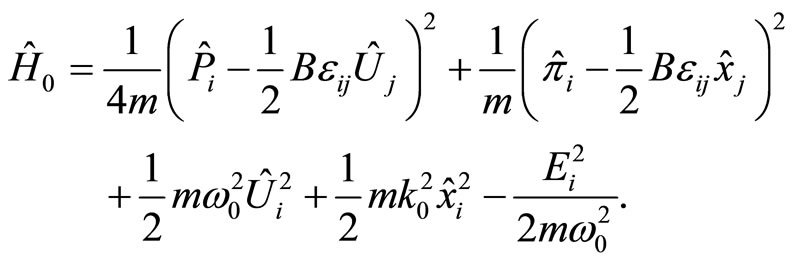 (15)
(15)
Note that these changes of variable are ill-defined if one wants to set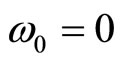 . The reason for this is the following: In the presence of a magnetic and an electric field with no other confining force, the magnetic center moves at a constant velocity, and one needs to apply a Galilei boost; quantum states are no longer all normalisable. In order to avoid that singularity, when wanting to remove the harmonic confining potential, first one needs to turn off the electric field
. The reason for this is the following: In the presence of a magnetic and an electric field with no other confining force, the magnetic center moves at a constant velocity, and one needs to apply a Galilei boost; quantum states are no longer all normalisable. In order to avoid that singularity, when wanting to remove the harmonic confining potential, first one needs to turn off the electric field 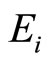 lying in the plane, and only then set
lying in the plane, and only then set 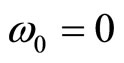 [22].
[22].
From the physics point of view, clearly the system is invariant under constant translations in time, and constant rotations in space. Consequently, there must exist conserved quantities generating the corresponding infinitesimal transformations, to which specific quantum operators also correspond which then generate these transformations for quantum states and operators. It may be shown that the generator for time translations is the quantum Hamiltonian, equation (15), while the generator for the rotations in the plane is given by,
 (16)
(16)
From here on, the solution of the quantum Hamiltonian (15) follows a standard path. Let us introduce the following quantities [20]:
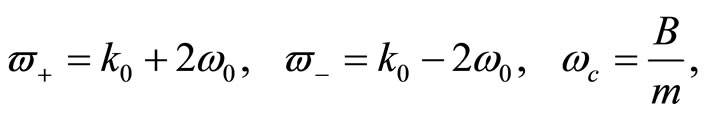 (17)
(17)
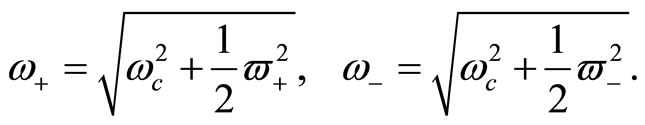 (18)
(18)
 (19)
(19)
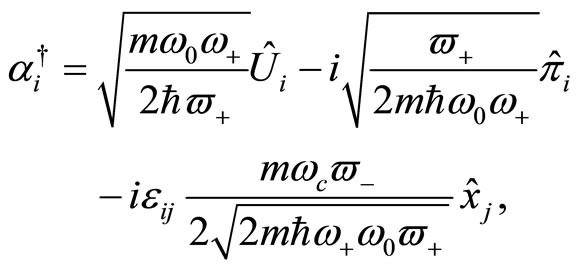 (20)
(20)
 (21)
(21)
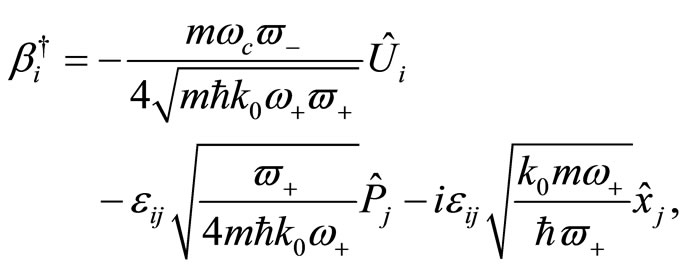 (22)
(22)
with
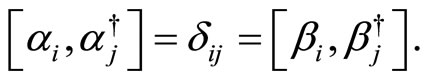 (23)
(23)
Consequently, the quantum Hamiltonian and the angular momentum may be expressed as follows
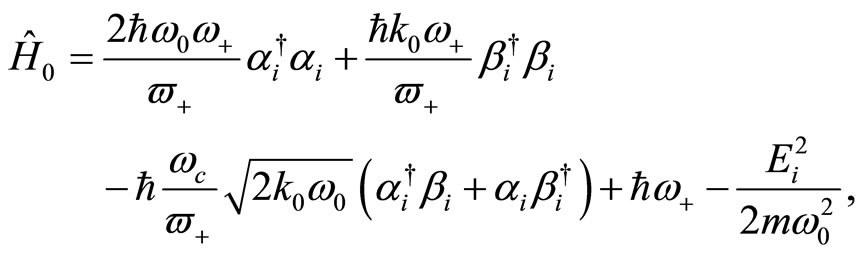 (24)
(24)
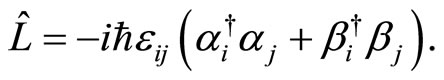 (25)
(25)
We may now apply a second change of variables to remove the remaining non-diagonal terms in the Hamiltonian. It is straightforward to check that the previous commutation relations do not change under the following change of variables:
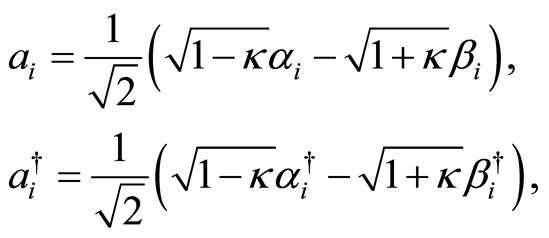 (26)
(26)
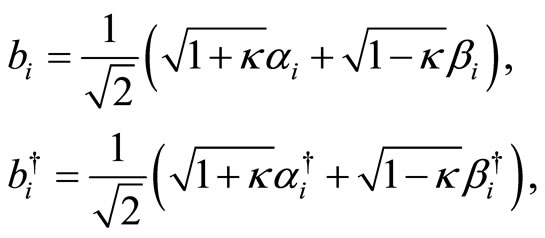 (27)
(27)
where
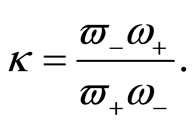 (28)
(28)
We then find,
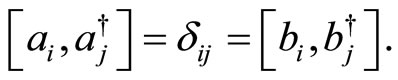 (29)
(29)
The quantum Hamiltonian and the angular momentum become
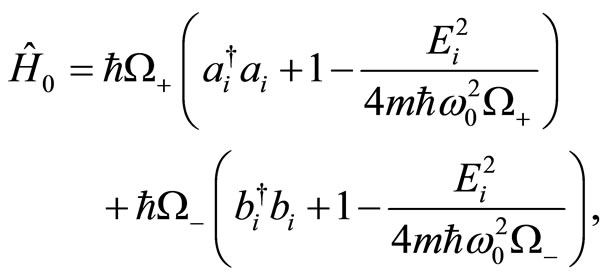 (30)
(30)
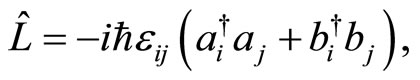 (31)
(31)
with
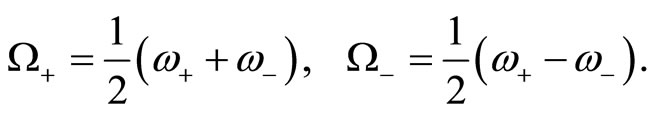 (32)
(32)
The angular momentum operator mixes the two chiral sectors that were held decoupled in the Hamiltonian. It is therefore natural that a last change of variable that mixes them is needed to diagonalize the operator . Let us introduce the following chiral Fock algebra operators,
. Let us introduce the following chiral Fock algebra operators,
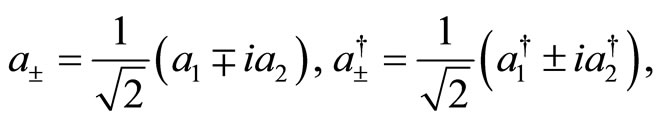 (33)
(33)
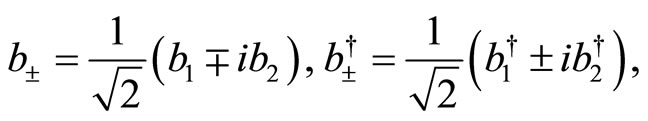 (34)
(34)
with
 (35)
(35)
Note that all these expressions may be inverted to express the original quantities 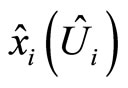 and
and 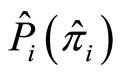 in terms of
in terms of  and
and .
.
After a direct substitution, one finds
 (36)
(36)
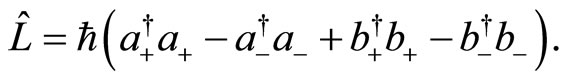 (37)
(37)
We have constructed convenient creation and annihilation operators which span bosonic Fock algebras, and diagonalize the main observables of the system, namely the Hamiltonian and the angular momentum. To complete the description of the quantum system, we now have to find a representation of these operators. We therefore have to construct the Hilbert space of the physical states, and associate to each operator a linear transformation on that space, such that the commutation relations hold. We will then be able to determine the energy spectrum of quantum Hamiltonian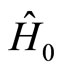 , as well as the spectrum of the angular momentum
, as well as the spectrum of the angular momentum .
.
Indeed, the orthonormalised chiral Fock states basis with as normalised Fock vacuum a state
 (38)
(38)
such that
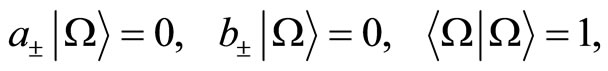 (39)
(39)
is constructed by
 (40)
(40)
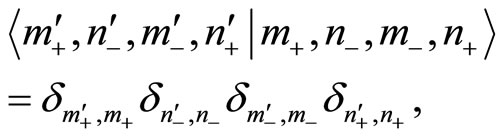 (41)
(41)
with the property:
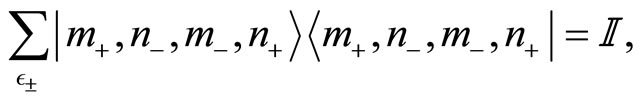 (42)
(42)
the notation  standing for
standing for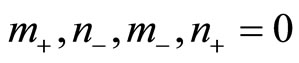 . This complete set of states is a basis which diagonalises the commuting operators
. This complete set of states is a basis which diagonalises the commuting operators 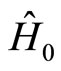 and
and 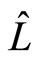
 (43)
(43)
 (44)
(44)
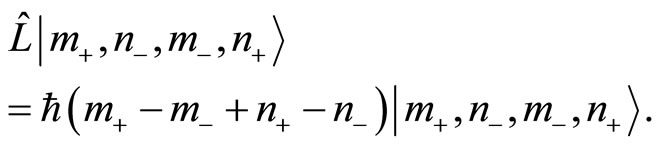 (45)
(45)
If we remove the harmonic well-which boils down to set 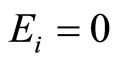 and next
and next 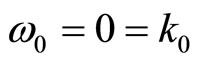 --, then we get
--, then we get
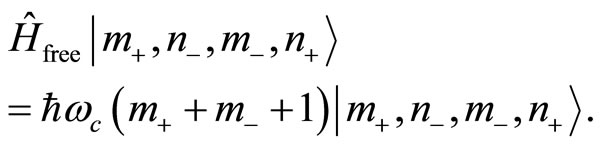 (46)
(46)
Note that in setting
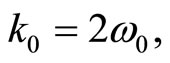 (47)
(47)
which is a condition that relates the harmonic potentials frequencies, we get the following spectrum,

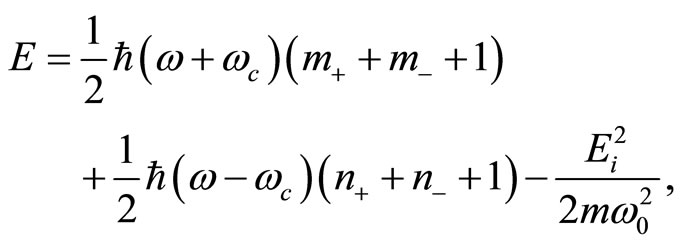 (48)
(48)
where
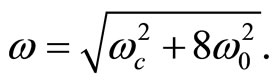 (49)
(49)
3. Quantum Dipole in NC Phase Space
The physics of two nonrelativistic charged particles of identical mass , of opposite electric charges
, of opposite electric charges 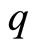 and
and 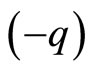 and respective positions
and respective positions 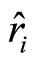 and
and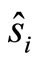 , in crossed, background electric and magnetic fields coupled with a confining harmonic potential and connecting by a spring, is described by the following quantum Hamiltonian
, in crossed, background electric and magnetic fields coupled with a confining harmonic potential and connecting by a spring, is described by the following quantum Hamiltonian
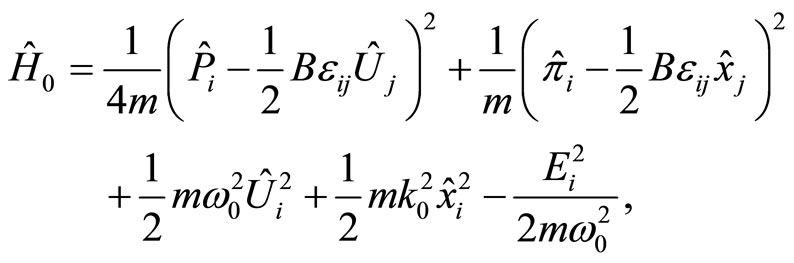 (50)
(50)
where
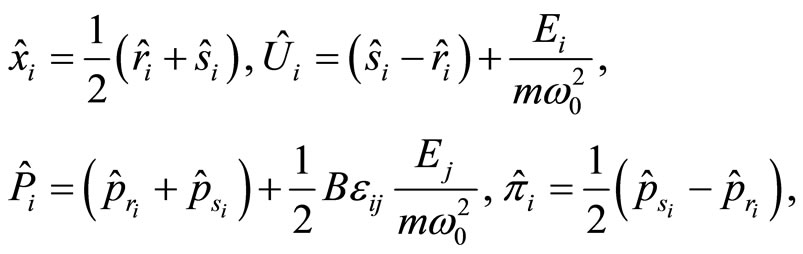 (51)
(51)
 and
and 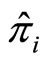 are the relative coordinate operators, the center of mass coordinate operators, the total momentum operators and the relative momentum operators, respectively.
are the relative coordinate operators, the center of mass coordinate operators, the total momentum operators and the relative momentum operators, respectively.
These operators verify the following set of commutation relations, with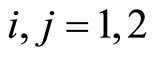 ,
,
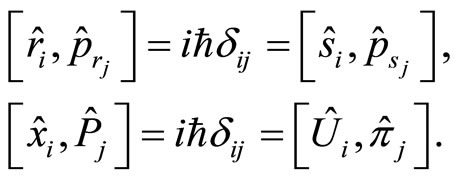 (52)
(52)
Let us denote the operators of coordinates and momenta in NC phase space as  and
and 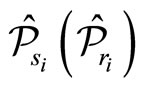 respectively, then the
respectively, then the 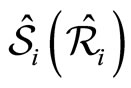 and
and 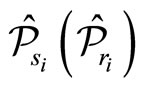 in the twodimensional NC phase space satisfy the following commutation relations [23]
in the twodimensional NC phase space satisfy the following commutation relations [23]
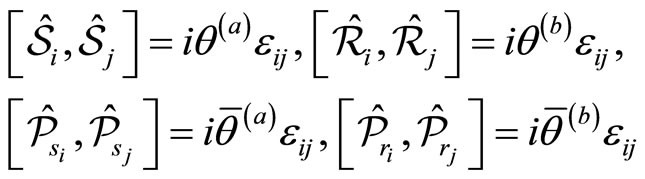 (53)
(53)
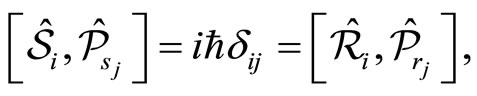 (54)
(54)
where 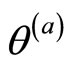 and
and  are the real-valued noncommutativity terms of the space coordinates, while
are the real-valued noncommutativity terms of the space coordinates, while 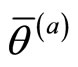 and
and 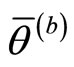 are the real-valued noncommutativity terms of the momenta,
are the real-valued noncommutativity terms of the momenta, 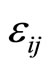 being an anti-symmetric matrix. Furthermore, the two particles have opposite charges, and each of them is supposed to have the same noncommutativity but with opposite sign
being an anti-symmetric matrix. Furthermore, the two particles have opposite charges, and each of them is supposed to have the same noncommutativity but with opposite sign
 (55)
(55)
Consequently, the relative coordinate operators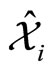 , the center of mass coordinate operators
, the center of mass coordinate operators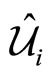 , the total momentum operators
, the total momentum operators  and the relative momentum operators
and the relative momentum operators 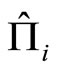 in the NC phase space satisfy the following commutation relations
in the NC phase space satisfy the following commutation relations
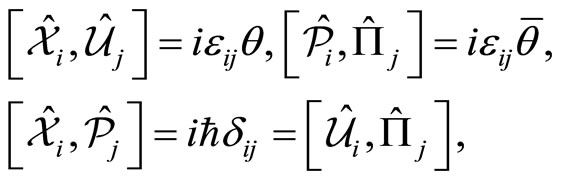 (56)
(56)
while all other commutators vanish. According to this recipe, the above quantum Hamiltonian and the angular momentum act on an arbitrary function 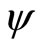 as follows
as follows
 (57)
(57)
where the star product  is the Moyal-Weyl product defined in [24,25].
is the Moyal-Weyl product defined in [24,25]. 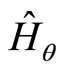 and
and 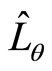 are the NC versions of the quantum Hamiltonian
are the NC versions of the quantum Hamiltonian  and of the angular momentum
and of the angular momentum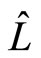 , given by
, given by
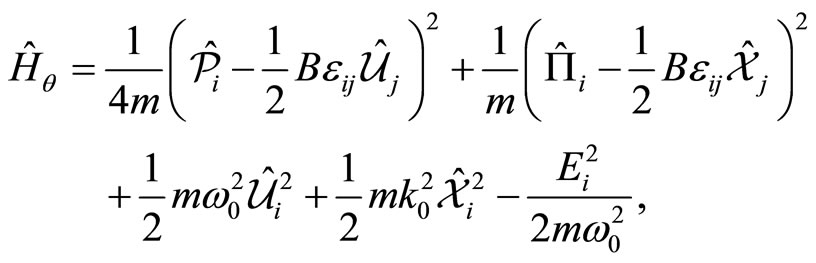 (58)
(58)
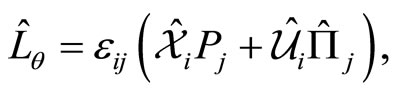 (59)
(59)
respectivily.
From the relations (56), we have the following expressions [26-28],
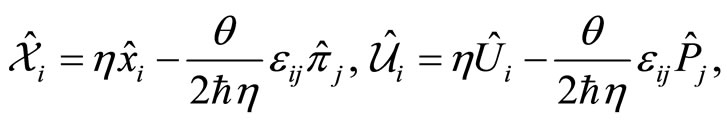 (60)
(60)
 (61)
(61)
where  is a scaling constant related to the noncommutativity of phase space:
is a scaling constant related to the noncommutativity of phase space:
 (62)
(62)
when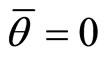 , we obtain
, we obtain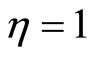 , where the space-space is noncommuting [24], while momentum-momentum is commuting [29,30].
, where the space-space is noncommuting [24], while momentum-momentum is commuting [29,30].
The constant uniform NC electric and magnetic fields Ei and Fij are given by
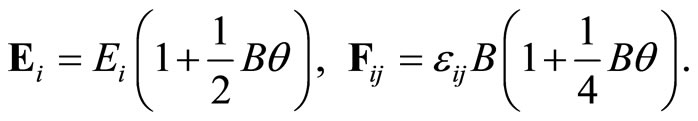 (63)
(63)
The quantum Hamiltonian written in equation (58) becomes in the NC phase space,
 (64)
(64)
where3

 (65)
(65)
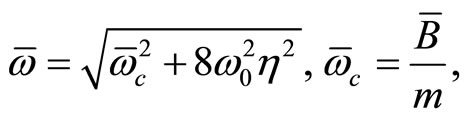
 (66)
(66)
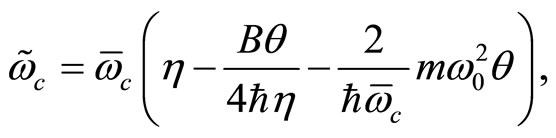 (67)
(67)
while the quantum angular momentum Equation (52) is given by
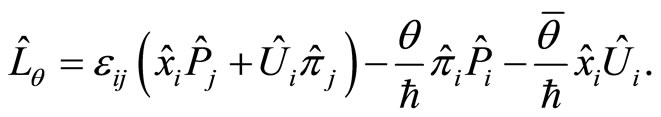 (68)
(68)
For convenience, in a NC phase space, we define the annihilation and creation operators as
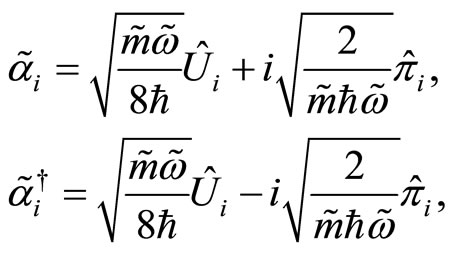 (69)
(69)
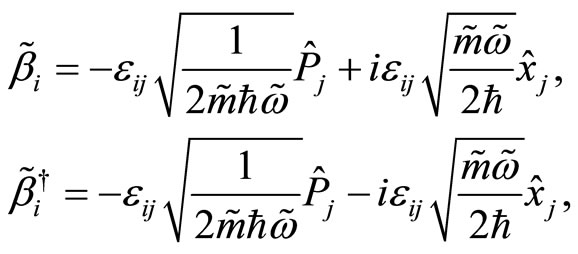 (70)
(70)
satisfying the well-known algebra
 (71)
(71)
Therefore, the quantum Hamiltonian and the angular momentum may be written as follows,
 (72)
(72)
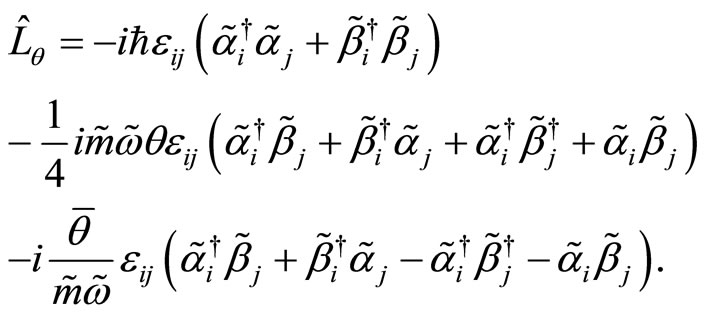 (73)
(73)
Let us now apply a second change of variables to remove the remaining non-diagonal terms in the Hamilnian. It is straightforward to check that the previous comtation relations do not change under the following change of variables:
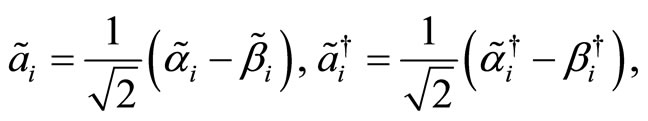 (74)
(74)
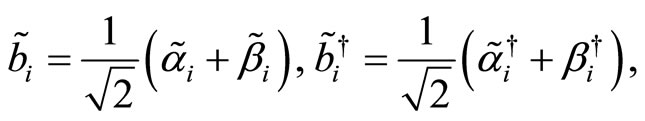 (75)
(75)
with
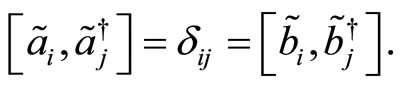 (76)
(76)
Next,
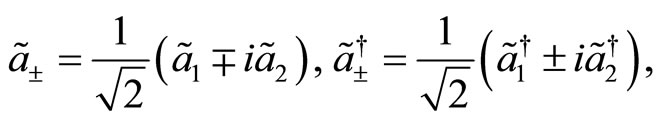 (77)
(77)
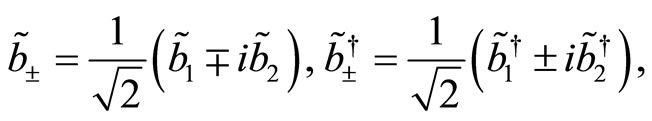 (78)
(78)
with
 (79)
(79)
Therefore, the quantum Hamiltonian takes the following form
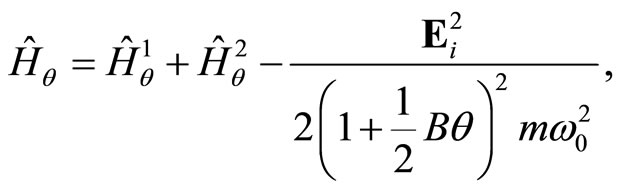 (80)
(80)
with
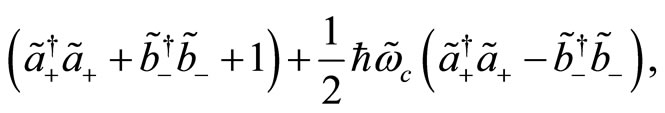
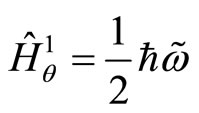 (81)
(81)
and
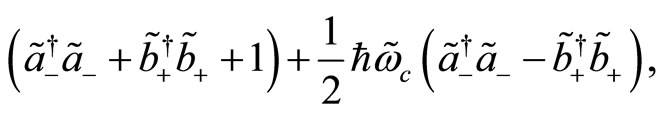
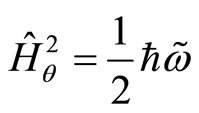 (82)
(82)
while, the quantum angular momentum is issued by
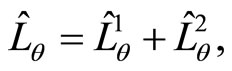 (83)
(83)
with
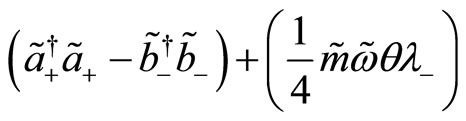
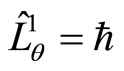
 (84)
(84)
and

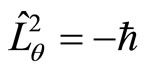
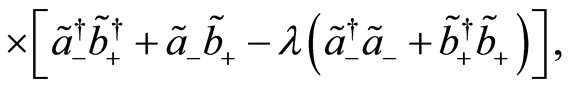 (85)
(85)
where
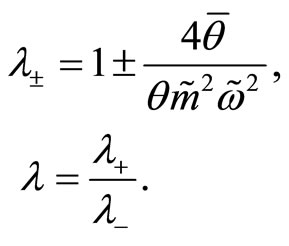 (86)
(86)
We note that, in commutating space, the quantum Hamiltonian 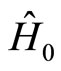 and the quantum angular momentum
and the quantum angular momentum 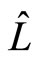 are commuting. But in NC phase space, they do not commute any more. The commutator of the
are commuting. But in NC phase space, they do not commute any more. The commutator of the  and
and  is written as follows
is written as follows
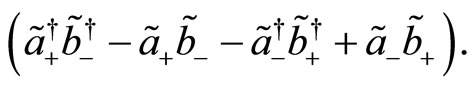
 (87)
(87)
The next section is devoted to the determination of the spectrum of these main observables.
4. Eigenvalues and Eigenstates
In this section, we construct the algebra and symmetry transformation that will help us to diagonalize skillfully the NC phase space Hamiltonian and the NC angular momentum of the model. Namely, the Fock basis which diagonalizes the Hamiltonian is introduced. Then, the 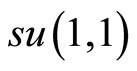 algebra is used and by means of the similarity transformation, the spectrum of the NC angular momentum is determined.
algebra is used and by means of the similarity transformation, the spectrum of the NC angular momentum is determined.
4.1. Fock Space
The chiral Fock states basis is a natural choice in the way of the quantization for our model. This basis is spanned by the vectors
 (88)
(88)
with
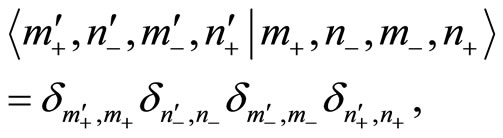 (89)
(89)
 (90)
(90)
These states diagonalise the NC quantum Hamiltonian , but not the NC angular momentum
, but not the NC angular momentum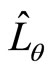 :
:
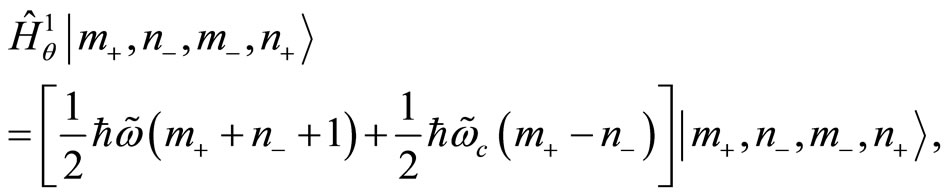 (91)
(91)
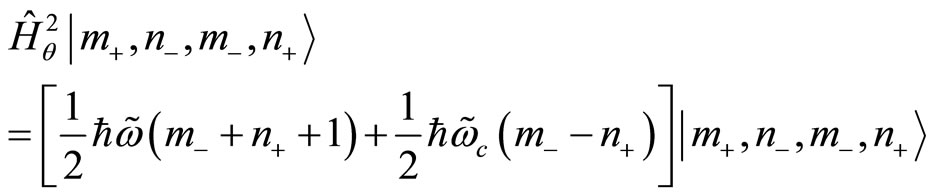 (92)
(92)
 (93)
(93)
 (94)
(94)
Additional considerations are thus necessary to solve the NC angular momentum.
4.2. 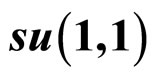 Realizations
Realizations
It is well known that if a system is characterized by boson operators, then the simplest way to find the corresponding symmetry algebra is to construct the boson realizations of this algebra. In this section we introduce some basic boson realizations of 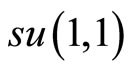 that we need to solve the quantum Hamiltonian (80) and the angular momentum (83).
that we need to solve the quantum Hamiltonian (80) and the angular momentum (83).
The Lie algebra  possesses interesting realizations of bosons and is more appropriate to solve numerous physical problems. Using the set of boson operators (77) and (78) we introduce the operators
possesses interesting realizations of bosons and is more appropriate to solve numerous physical problems. Using the set of boson operators (77) and (78) we introduce the operators
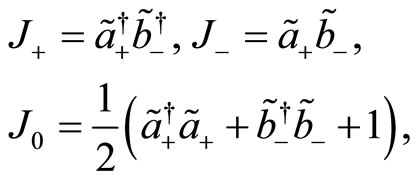 (95)
(95)
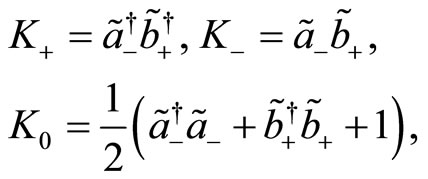 (96)
(96)
satisfying the commutation relations
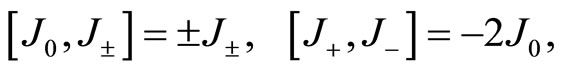 (97)
(97)
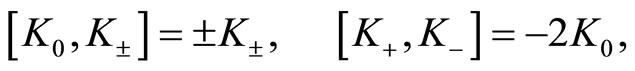 (98)
(98)
all the others being vanishing.
The number operators which commute with the generators of the 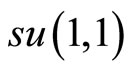 algebra are issued by
algebra are issued by
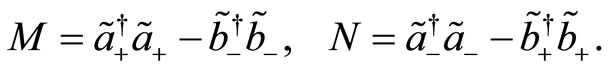 (99)
(99)
The Casimir operators corresponding to this realization are issued by
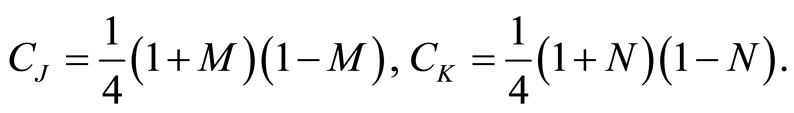 (100)
(100)
Therefore, if the eigenvalue of the operators 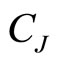 and
and  are
are  and
and 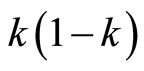 respectively, then
respectively, then 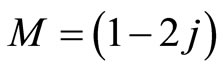 and
and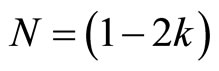 . Consequently, the action of the realizations (95) and (96) on the states
. Consequently, the action of the realizations (95) and (96) on the states , leads to an infinite dimensional unitary irreducible representation so-called positive representation
, leads to an infinite dimensional unitary irreducible representation so-called positive representation 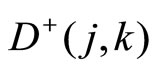 and corresponds to any
and corresponds to any . Therefore, the action of the operators on the basis states
. Therefore, the action of the operators on the basis states 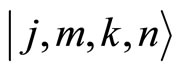 is issued by
is issued by
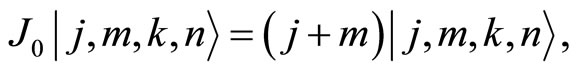 (101
(101
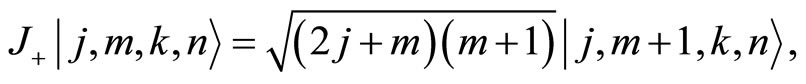 (102)
(102)
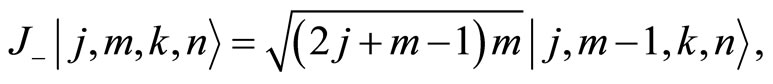 (103)
(103)
and
 (104)
(104)
 (105)
(105)
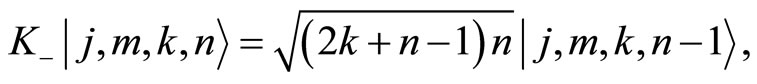 (106)
(106)
and finally
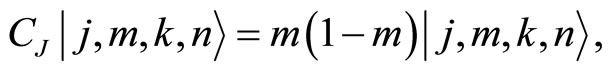 (107)
(107)
 (108)
(108)
The quantum Hamiltonians 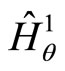 and
and 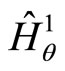 may be expressed in terms of generators of the
may be expressed in terms of generators of the 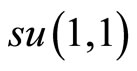 algebra,
algebra,
 (109)
(109)
Likewise, the angular momentums 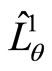 and
and 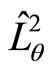 may also be expressed as follows:
may also be expressed as follows:
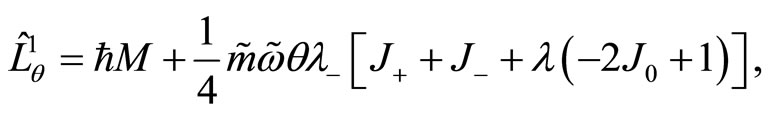 (110)
(110)
and
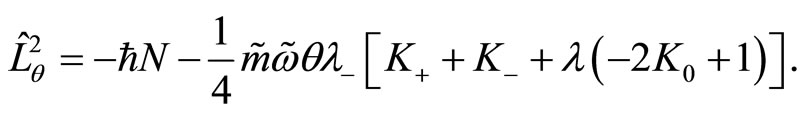 (111)
(111)
Obviously, the NC Hamiltonian remains diagonal in the  basis and the eingenvalue equations are written as follows,
basis and the eingenvalue equations are written as follows,
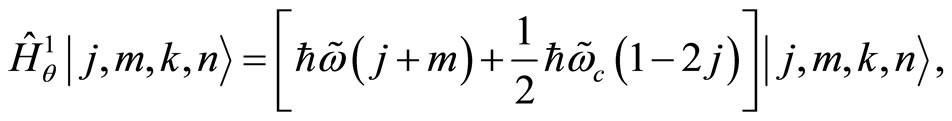 (112)
(112)
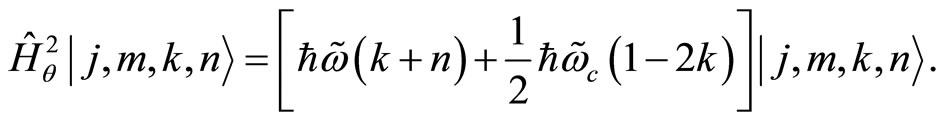 (113)
(113)
At the opposite, the NC angular momentum is not yet diagonal in this basis:
 (114)
(114)
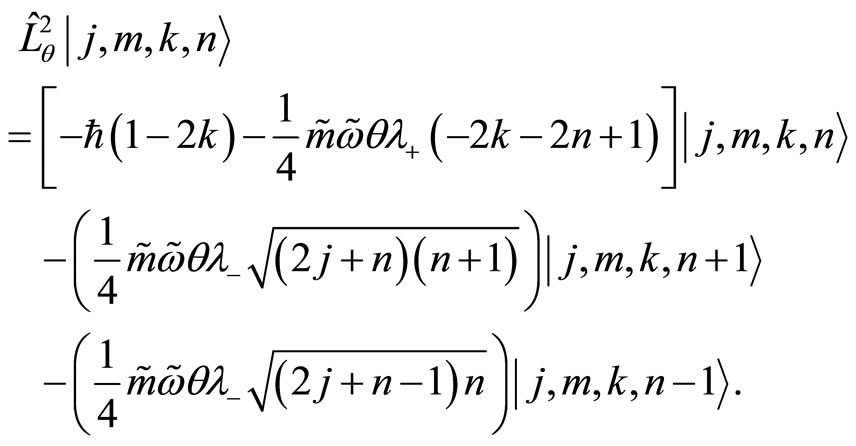 (115)
(115)
Note that the Fock states  are equivalent to the
are equivalent to the 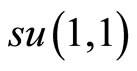 states
states 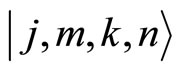 for
for
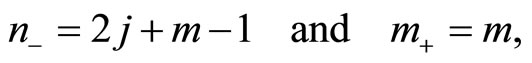 (116)
(116)
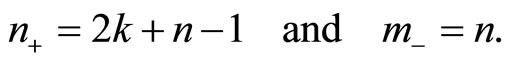 (117)
(117)
So far the 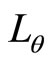 -spectrum remains to be determined. The next section aims at solving this question by means of a similarity transformation that gives rise to analytical results.
-spectrum remains to be determined. The next section aims at solving this question by means of a similarity transformation that gives rise to analytical results.
4.3. Similarity Transformation
To get the analytical solution from the present problem, let us introduce the following similarity transformation [31] induced by the operators
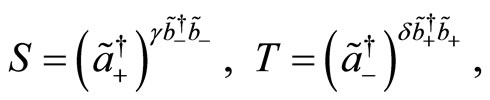 (118)
(118)
where 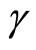 and
and 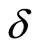 are constants.
are constants.
Since the operators 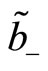 and
and 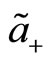 commute, the transformation of the
commute, the transformation of the 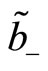 and
and 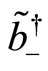 under
under 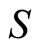 may be obtained in setting
may be obtained in setting
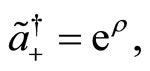 (119)
(119)
with the following relations
 (120)
(120)
One finds

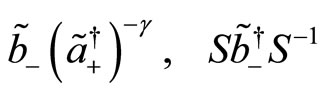
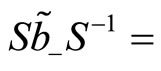 (121)
(121)
The transformations of 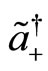 and
and 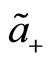 are written as follows
are written as follows
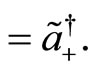
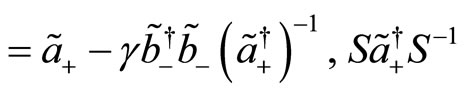
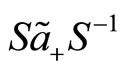 (122)
(122)
Likewise, the operators transform under 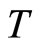 as follows:
as follows:
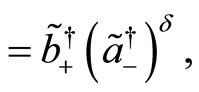
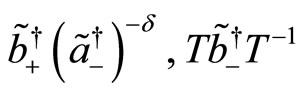
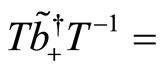 (123)
(123)

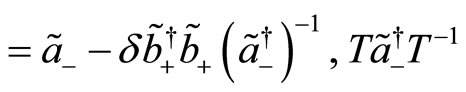
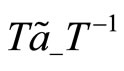 (124)
(124)
Consequently, the algebra  under the transformations
under the transformations 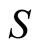 and
and 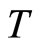 is closed for
is closed for . Then, one finds the following results
. Then, one finds the following results
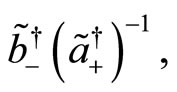
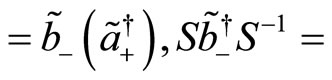

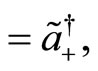


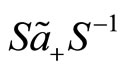 (125)
(125)

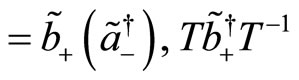
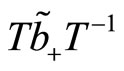
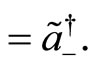
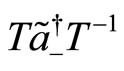
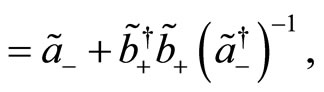
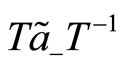 (126)
(126)
By the means of the transformed operators (125) and (126), the generators of the algebra 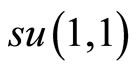 take the following form
take the following form
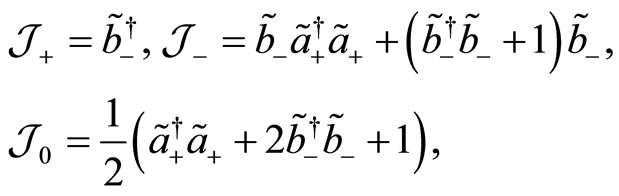 (127)
(127)
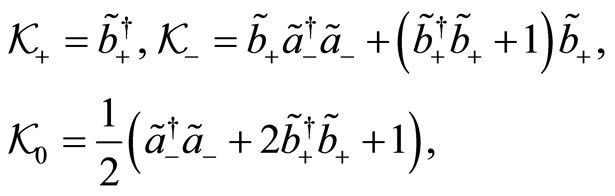 (128)
(128)
and satisfy the commutation relations
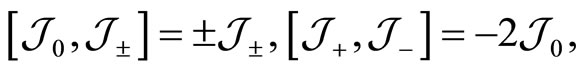 (129)
(129)
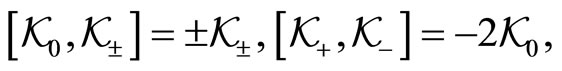 (130)
(130)
all the others are vanishing.
The transformed number operators which commute with the generators of the 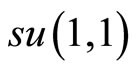 algebra are issued by
algebra are issued by
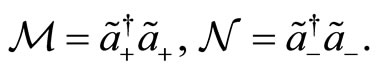 (131)
(131)
If the representations are characterized by fixed numbers  and
and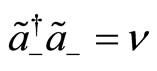 , with
, with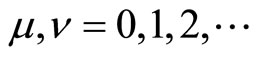 , then the transformed
, then the transformed 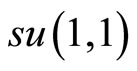 generators may be expressed in term of one boson operator. One finds
generators may be expressed in term of one boson operator. One finds
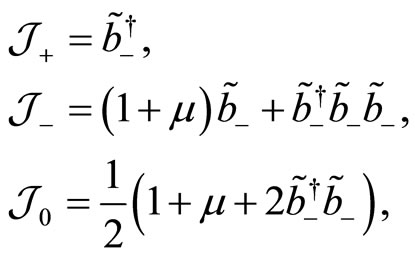 (132)
(132)
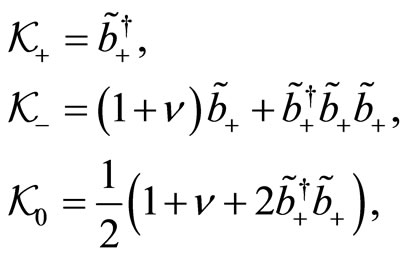 (133)
(133)
satisfying the commutation relations (129) and (130). These generators play an important role in the formulation of the exact solutions for the angular momentum. To achieve this goal, let us define the following differential representions of these generators in terms of the bosonic variables in the Bargmann-Fock space (see [32]),
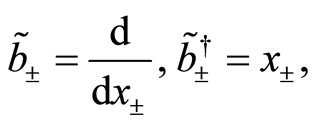 (134)
(134)
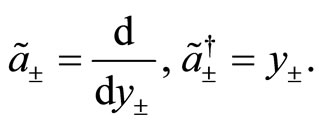 (135)
(135)
Consequently, we get
 (136)
(136)
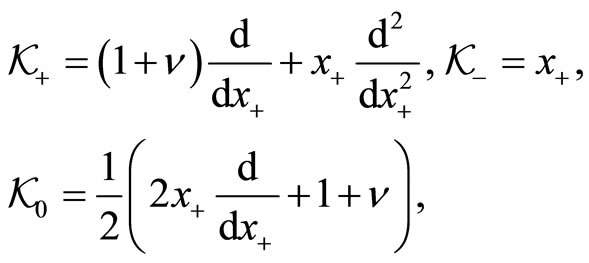 (137)
(137)
 (138)
(138)
Therefore, the transformed NC quantum Hamiltonians 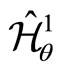 and
and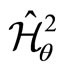 , and the transformed NC angular momenta
, and the transformed NC angular momenta 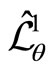 and
and 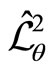 are respectively given by,
are respectively given by,
 (139)
(139)
 (140)
(140)
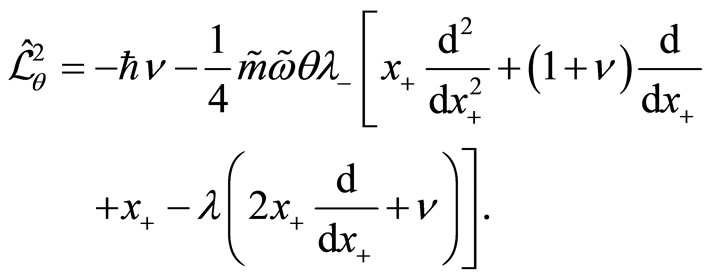 (141)
(141)
The eigenvalue equations for the operators 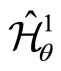 and
and  can be written as follows
can be written as follows
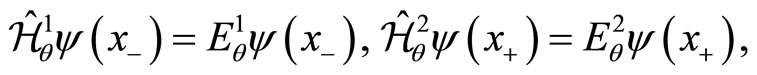 (142)
(142)
providing the corresponding eigenvalues and eigenstates,

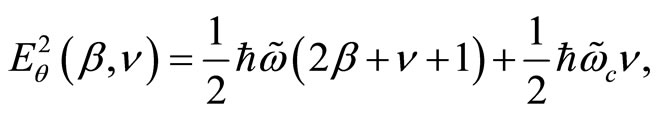 (143)
(143)
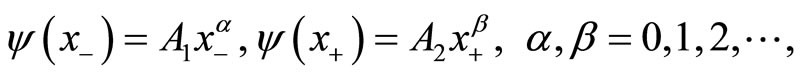 (144)
(144)
where 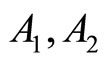 are the normalization constants. Concerning the NC angular momenta
are the normalization constants. Concerning the NC angular momenta 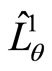 and
and , the eigenvalue equations are given by
, the eigenvalue equations are given by
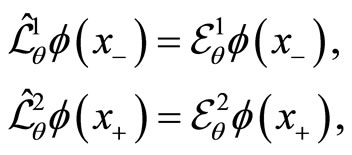 (145)
(145)
providing the eigenstates and eigenvalues [33],
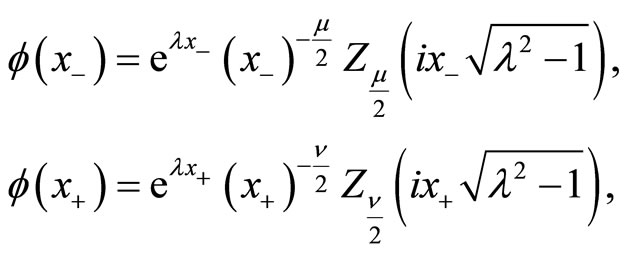 (146)
(146)
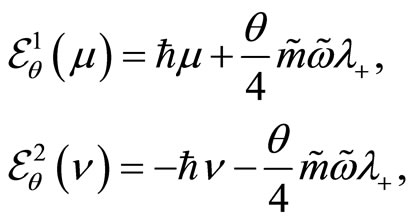 (147)
(147)
respectively. Here
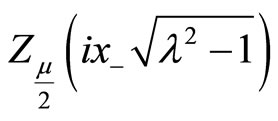 and
and 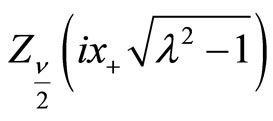
are the Bessel functions satisfying the following differential equations
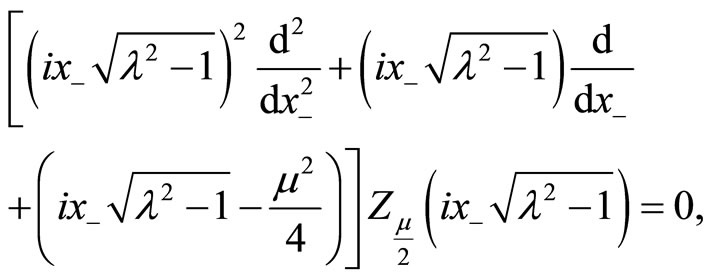 (148)
(148)
 (149)
(149)
The general solutions of (148) and (149) are given by
 (150)
(150)
and
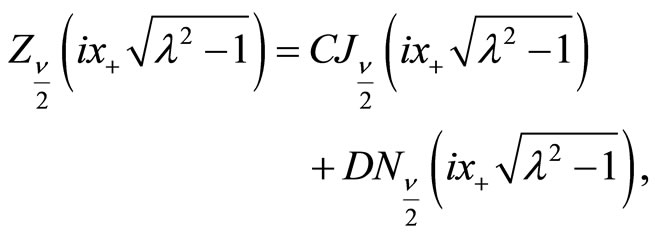 (151)
(151)
where
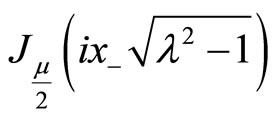 and
and 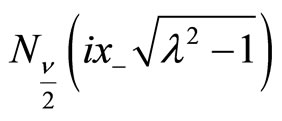
are the Bessel and Neumann functions of order 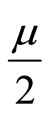 respectively, and
respectively, and 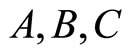 and
and 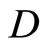 are constants to be determined via application of the boundary conditions. Since the solution must be finite at
are constants to be determined via application of the boundary conditions. Since the solution must be finite at , and
, and
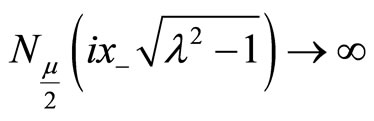 as
as the coefficient of
the coefficient of

must be vanished, implying , leaving
, leaving
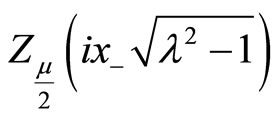
to be expressed as follows
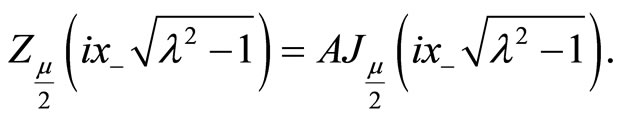 (152)
(152)
By using similar arguments to those given above, we set  and write
and write
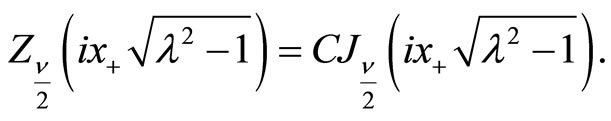 (153)
(153)
Consequently, we find
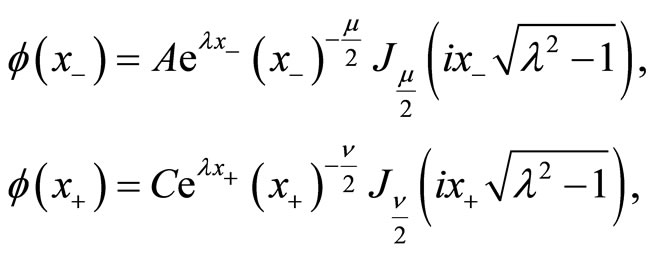 (154)
(154)
where 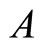 and
and 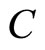 are the normalization constants.
are the normalization constants.
In comparison with the algebraic method developed in Section (4.2), we can see that 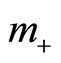 and
and 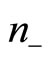 are related to
are related to 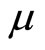 and
and  by the following relations,
by the following relations,
 (155)
(155)
while 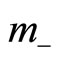 and
and 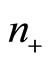 are related to
are related to 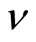 and
and  as follows,
as follows,
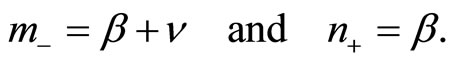 (156)
(156)
Finally, the spectrum of the system is given by
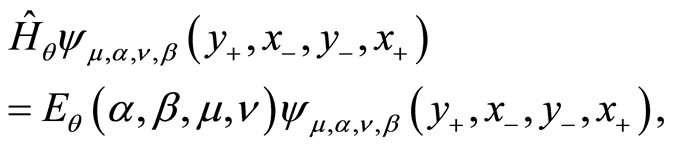 (157)
(157)
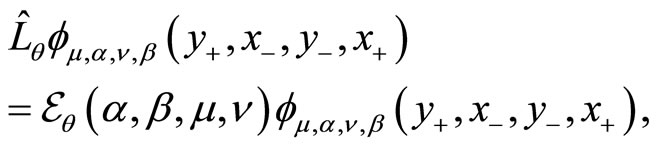 (158)
(158)
with
 (159)
(159)
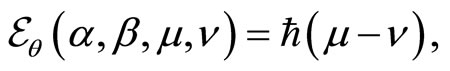 (160)
(160)
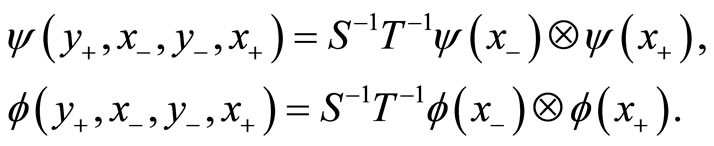 (161)
(161)
From the expression (62), we obtain that when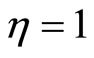 ,
, 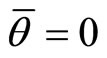 , so
, so 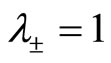 and
and , which corresponds to NC space where only momentum-momentum is commuting,
, which corresponds to NC space where only momentum-momentum is commuting,
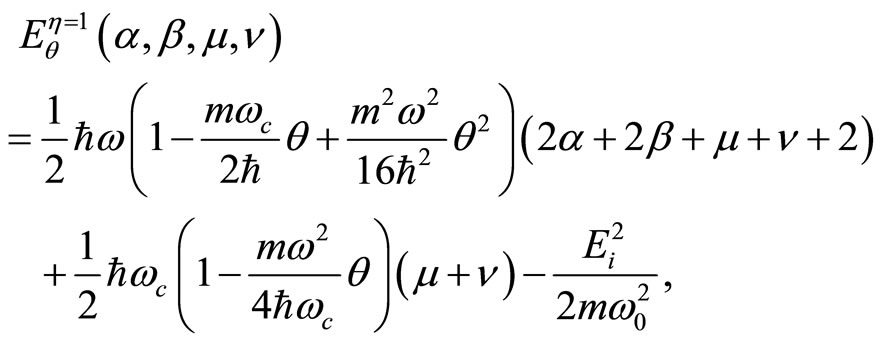
(162)
 (163)
(163)
If 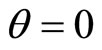 and
and , then the results return to those of the quantum dipole in the commutation space
, then the results return to those of the quantum dipole in the commutation space
 (164)
(164)
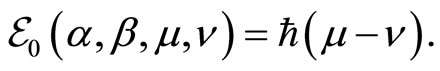 (165)
(165)
The energy shift caused by the noncommutativity of both space-space and momentum-momentum can be given as follows
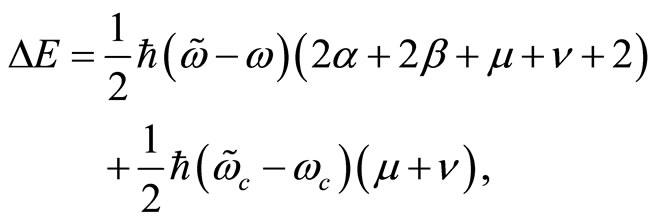 (166)
(166)
which can be rewritten as follows,
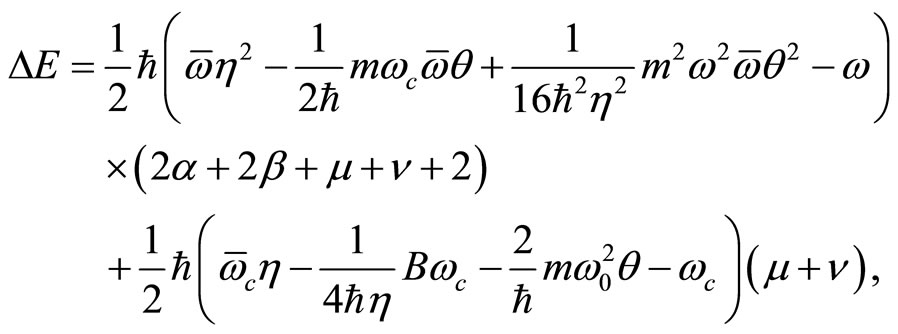 (167)
(167)
while the angular momentum does not present the shift term caused by the noncommutativity of both spacespace and momentum-momentum
 (168)
(168)
Finally, we note that our method allows to solve rigorously the angular momentum in noncommuting phase space eventhough this operator does not commute with the NC phase space quantum Hamiltonian.
5. Conclusions
In this paper, we have studied a generalization of the two dimensional quantum dipole coupled to external uniform electric and magnetic background fields. We started in studying the model in the ordinary commutating variables space. The Hamiltonian and the angular momentum operators are diagonalized in the standard Fock space basis. Then, the quantum dipole is studied in the NC phase space. We have found that the NC quantum Hamiltonian and angular momentum do not form a complete set of commuting observables since the specification of their two eigenvalues do not specify uniquely a state of the considered basis of states, here the Fock basis. Subsequently, the eigenstates and the corresponding eigenvalues of the NC quantum Hamiltonian and angular momentum have been derived through algebraic and analytical methods. Specifically, the analytical solutions have been made possible by means of the similarity transformation of the 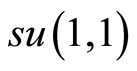 algebra identified through the system.
algebra identified through the system.
Note interestingly that when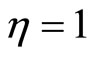 , we have
, we have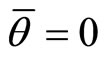 , which corresponds to the case where only the spacespace is noncommuting, while when
, which corresponds to the case where only the spacespace is noncommuting, while when  and
and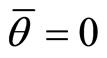 , the results return to those of the quantum dipole coupled to external electric and magnetic background fields in commuting space. We have obtained explicitly the energy shift due to the description of the model in NC phase space. At the opposite, the NC phase space angular momentum doesn't have such a shift term. Our study shows that the alternative choice that constitutes the NC phase space is compatible with this model. Furthermore, we have shown that with a careful observation of the hidden symmetries, it is possible to diagonalize an observable, in this case the angular momentum. This shows, if necessary, the importance of the theory of groups. In prospect, we envisage to study the thermodynamic properties of this model.
, the results return to those of the quantum dipole coupled to external electric and magnetic background fields in commuting space. We have obtained explicitly the energy shift due to the description of the model in NC phase space. At the opposite, the NC phase space angular momentum doesn't have such a shift term. Our study shows that the alternative choice that constitutes the NC phase space is compatible with this model. Furthermore, we have shown that with a careful observation of the hidden symmetries, it is possible to diagonalize an observable, in this case the angular momentum. This shows, if necessary, the importance of the theory of groups. In prospect, we envisage to study the thermodynamic properties of this model.
REFERENCES
- D. Bahns, S. Doplicher, K. Fredenhagen and G. Piacitelli, Physical Review Letters D, Vol. 71, 2005, pp. 1-12.
- S. Doplicher, K. Fredenhagen and J. E. Roberts, Communications in Mathematical Physics, Vol. 172, 1995, pp. 187-220. http://dx.doi.org/10.1007/BF02104515
- H. Grosse and M. Wohlgenannt, The European Physical Journal, Vol. 52, 2007, pp. 435-450. http://dx.doi.org/10.1140/epjc/s10052-007-0369-5
- Y. Habara, Prog.Theor. Phys, 107, 2002, pp. 211-230. http://dx.doi.org/10.1143/PTP.107.211
- L. Jonke and S. Meljanac, The European Physical Journal C, Vol. 29, 2003, pp. 433-439. http://dx.doi.org/10.1140/epjc/s2003-01205-6
- K. Li and J. Wang, The European Physical Journal C, Vol. 50, 2007, pp. 1007-1011. http://dx.doi.org/10.1140/epjc/s10052-007-0256-0
- L. R. Ribeiro, E. Passos, C. Furtado and J. R. Nascimento, The European Physical Journal C, Vol. 56, 2008, pp. 597-606. arXiv: hep-th/0711.1773
- S. Dulat and K. Li, The European Physical Journal C, Vol. 60, 2009, p. 162.
- B. Basu and S. Ghosh, Physics Letters A, Vik, 346, 2005, p. 133.
- F. G. Scholtz, L. Gouba, A. Hafrer, et al., Journal of PhysicsA, Vol. 42, 2009, Article ID: 175303. http://dx.doi.org/10.1088/1751-8113/42/17/175303
- A. Jellal, M. Schreiber and E. H. E. Kinani, International Journal of Modern Physics A, Vol. 20, 2005, p. 1515.
- B. G. Joseph, G. Sunandan and G. S. Frederik, “Harmonic oscillator in a Background Magnetic Field in Noncommutative Quantum Phase-Space,” ICMPA-MPA, 2009.
- X.-M. Yu and K. Li, Chinese Physics Letters, Vol. 25, 2008, p. 1980.
- J. B. Geloun and F. G. Scholtz, Journal of Mathematical Physics, Vol. 50, 2009, Article ID: 043505. http://dx.doi.org/10.1063/1.3105926.3
- F. S. Bemfica and H. O. B. Girotti, Journal of Physics A, Vol. 38, 2008, p. 227.
- Y. Yuan, K. Li, J. H. Wang, et al., Chinese Physics C (HEP and P), Vol. 34, 2010, p. 543. http://dx.doi.org/10.1088/1674-1137/34/5/005
- M.-L. Liang, Y.-B. Zhang, R.-L. Yang and F.-L. Zhang, Chinese Physics C, Vol. 37, 2013, Article ID: 063106. http://dx.doi.org/10.1088/1674-1137/37/6/063106
- X. L. Jiang, C. Long and S. Qin, Journal of Modern Physics, Vol. 4, 2013, pp. 940-944.
- K. Li and S. Dulat, Chin. Phys. C, Vol. 34, 2010.
- A. Jago, “Noncommutative Geometry and Supersymmetry in a Generalization of the Bigatti-Susskind System,” Master Thesis, Université Catholique de Louvain, Louvain-La-Neuve, 2011.
- D. Bigatti and L. Susskind, Physical Review D, Vol. 62, 2000, Article ID: 066004. http://dx.doi.org/10.1103/PhysRevD.62.066004
- J. Govaerts, M. N. Hounkonnou and H. V. Mweenec, “Variations on the Planar Landau Problem: Canonical Transformations, A Purely Linear Potential and the Half-Plane 2009”. e-print arXiv: 0909.2659v1
- A. E. F. Djemaï and H. Smaïl, International Academic Publishers, Vol. 41, 2004, pp. 937-844.
- K. Li, J. H. Wang and C. Y. Chen, Modern Physics Letters A, Vol. 20, 2005, p. 2165.
- P. Polychronakos, Physics Letters B, Vol. 505, 2001, p. 267. L. Mezincescu, 2000. arXiv:hep-th/0007046
- R. Jackiw, Nuclear Physics B—Proceedings Supplements, Vol. 108, 2002, pp. 30-36.
- A. Connes, “Noncommutative Geometry,” Academic Press San Diego, 1994.
- N. Seiberg and E. Witten, Journal of High Energy Physics, Vol. 9, 1999, Article ID: 032.
- J. Gamboa, M. Loewe, F. Méndez and J. C. Rojas, Modern Physics Letters A, Vol. 16, 2001, p. 2075, E-Preprint arXiv:hep-th/0104224
- K. Li, X.-H. Cao and D.-Y. Wang, Chinese Physics, Vol. 15, 2006, pp. 2236-2239. http://dx.doi.org/10.1088/1009-1963/15/10/008
- H. Tütüncüler and R. Koç, Turkish Journal of Physics, Vol. 28, 2004, pp. 145-153.
- R. Koç, O. Özer, H. Tütüncüler and R. G. Yldrm, The European Physical Journal B, Vol. 59, 2007, pp. 375- 383. http://dx.doi.org/10.1140/epjb/e2007-00294-0
- I. S. Gradshteyn and I. M. Ryzhik, “Table of Integrals, Series, and Products,” 6th Edition, Academic Press, Waltham, 2000.
NOTES
1This description leads to the term “quantum dipole spring” that we call simply “quantum dipole” in the title of the paper.
2For the sake of this problem and the next, the Coulomb interaction between these two charges is ignored.
3The condition (47) is used.

