Journal of Modern Physics
Vol.4 No.6A(2013), Article ID:33579,3 pages DOI:10.4236/jmp.2013.46A004
A Numerical Study of the Effect of Disorder on Optical Conductivity in Inhomogeneous Superconductors
Department of Physics, Beijing Normal University, Beijing, China
Email: yunsong@bnu.edu.cn
Copyright © 2013 Long He et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 20, 2013; revised April 22, 2013; accepted May 20, 2013
Keywords: Inhomogeneous Superconductor; Disorder Effect; Anderson Localization; Kernel Polynomial Method; Lanczos Method
ABSTRACT
We present the effect of disorder on the optical conductivity of two-dimensional inhomogeneous superconductors by applying the kernel polynomial method to solve the Bogoliubov-de Gennes equations. By means of the lattice size scaling of the generalized inverse participation ratio, we find that the localization length of the quasiparticle decreases significantly with the increase of the disorder strength. Meanwhile, the weak disorder can readily restrain the Drude weight, while the superconducting gap has the tendency to suppress the low-energy optical conductivity. We also employ the Lanczos exact diagonalization method to study the competition between the on-site repulsive interactions and disorder. It is shown that the screening effect of repulsive interactions significantly enhances the Drude weight in the normal phase.
1. Introduction
The strong electron correlations are widely accepted as the key to solve the fundamentally important problems of the high-temperature superconductors [1]. Apart from the electron-electron interactions, the effect of disorder is also an essential ingredient of high temperature superconductors, since a certain extent of structure and chemical inhomogeneity will inevitably exist in the experimental samples, bringing about significant influence on both the excitations of the normal state and the superconducting gap (SG) [2,3]. To present the effect of disorder in the inhomogeneous superconductors, the self-consistent field method based on the Bogoliubov-de Gennes (BdG) equations has been widely used [4-7].
In this paper, we study an effective tight-binding model of the inhomogeneous superconductor on a square lattice [5]
 (1)
(1)
where 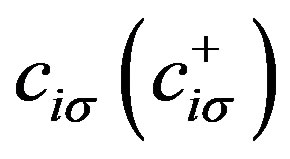 are the electronic annihilation (creation) operators at sites
are the electronic annihilation (creation) operators at sites  with spin
with spin  (
( or
or ),
), 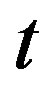 denote the hopping integrals between nearest neighbor (NN) sites,
denote the hopping integrals between nearest neighbor (NN) sites,  present the on-site disorder energies. The superconducting order parameters,
present the on-site disorder energies. The superconducting order parameters, 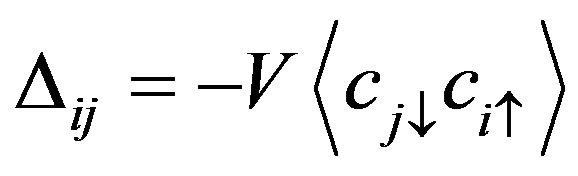 [8], can be obtained by
[8], can be obtained by
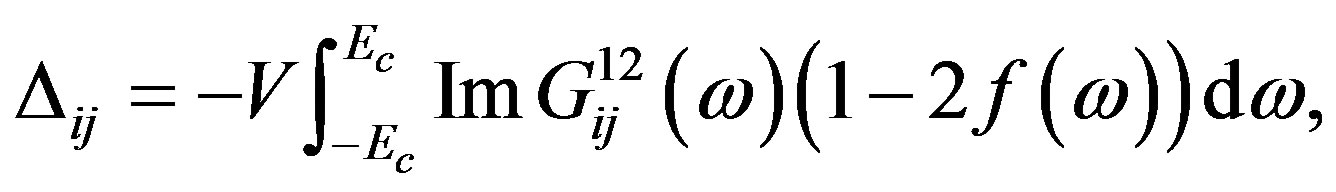 (2)
(2)
where 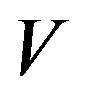 represent the NN attractive interactions,
represent the NN attractive interactions,  is the Fermi-Dirac distribution function, and
is the Fermi-Dirac distribution function, and 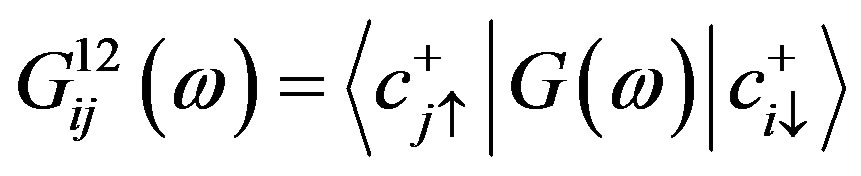 indicate the off-diagonal Green’s function of NN sites
indicate the off-diagonal Green’s function of NN sites  and
and .
.
We introduce the kernel polynomial method (KPM) [9] to expend the off-diagonal single particle Green’s function  into a series of Chebyshev polynomials of order
into a series of Chebyshev polynomials of order  [8,9],
[8,9],
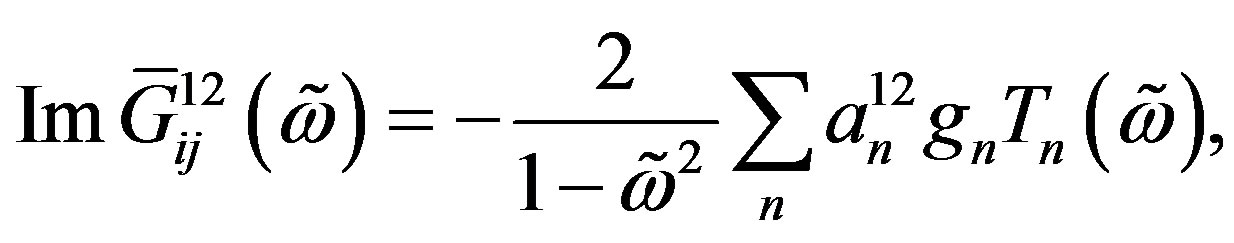 (3)
(3)
With
 (4)
(4)
where 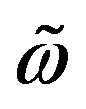 represent the scaled energies within the interval [–1, 1], and
represent the scaled energies within the interval [–1, 1], and  denote the Chebyshev polynomials of the first kind, and we introduce the Lorentz kernel
denote the Chebyshev polynomials of the first kind, and we introduce the Lorentz kernel to overcome the Gibbs oscillation.
to overcome the Gibbs oscillation.
We define the on-site disorder energies  as random variables distributed uniformly between
as random variables distributed uniformly between 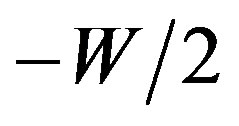 and
and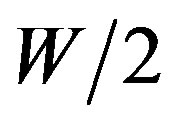 , where
, where 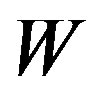 can be regarded as the strength of disorder. In Figure 1, we present the disorder effects on
can be regarded as the strength of disorder. In Figure 1, we present the disorder effects on . To our surprise, we also find that disorder can strongly enhance the superconducting order in some small local regions. The strong superconducting local regions emerge near the sites with smaller disorder potentials, while the non-superconducting local regions occur at the hills of the disorder potentials, where the local density of states are very weak. When
. To our surprise, we also find that disorder can strongly enhance the superconducting order in some small local regions. The strong superconducting local regions emerge near the sites with smaller disorder potentials, while the non-superconducting local regions occur at the hills of the disorder potentials, where the local density of states are very weak. When 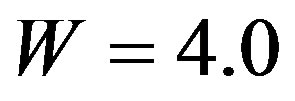 and
and , we observe very strong fluctuations of
, we observe very strong fluctuations of 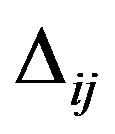 with the maximum value
with the maximum value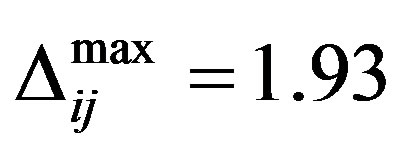 , which is quite larger than
, which is quite larger than 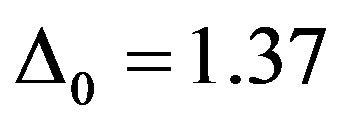 of the homogeneous case. Here the energies are unit of
of the homogeneous case. Here the energies are unit of . Our findings are in good agreement with the results obtained in the inhomogeneous s-wave superconductors, where some isolated superconducting islands are found to survive strong disorder [10].
. Our findings are in good agreement with the results obtained in the inhomogeneous s-wave superconductors, where some isolated superconducting islands are found to survive strong disorder [10].
Neglecting the intervalley scatterings, the interactions can introduce metal-insulator transition (MIT) in the two dimensional (2D) electron systems with a large number of degenerated valleys [11]. Therefore, it is a crucial problem to study the delocalization effect of interactions in 2D systems with disorder. We introduce a new approach [12] to do lattice size scaling of the generalized inverse participation ration (RIPR) [13], which is defined as
 (5)
(5)
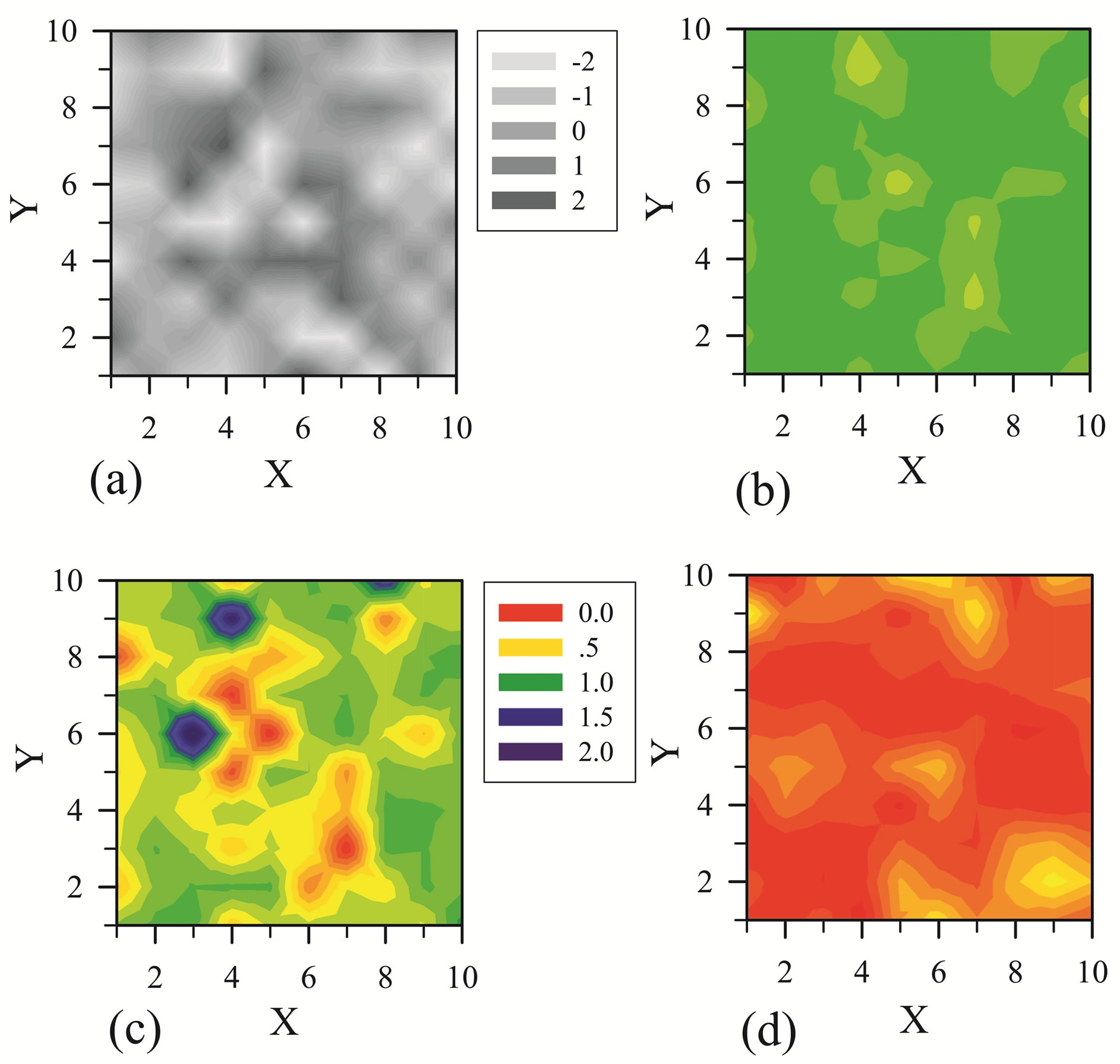
Figure 1. (a) The disorder configuration of a square lattice with N = 100 sites, and the corresponding distributions of the inhomogeneous superconducting gap 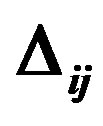 for the cases with W = 2 (b), 4 (c) and 8 (d). Some other parameters are t = 1.0, V = 2.0, M = 2000, and λ = 10.0.
for the cases with W = 2 (b), 4 (c) and 8 (d). Some other parameters are t = 1.0, V = 2.0, M = 2000, and λ = 10.0.
where 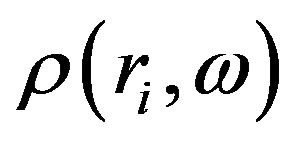 denote the local density of states (LDOS) at sites
denote the local density of states (LDOS) at sites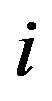 . We find that the dependence of
. We find that the dependence of 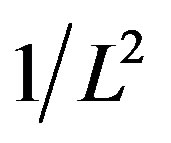 is a good approximation for the lattice size scaling of GIPR of the 2D inhomogeneous systems. As shown in Figure 2,
is a good approximation for the lattice size scaling of GIPR of the 2D inhomogeneous systems. As shown in Figure 2,  of 2D inhomogeneous superconductors also has very good linear relationship with
of 2D inhomogeneous superconductors also has very good linear relationship with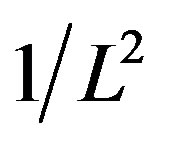 , where
, where 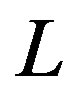 represent the size of a square lattice. In addition, it is shown that the intercept on the limitation of
represent the size of a square lattice. In addition, it is shown that the intercept on the limitation of 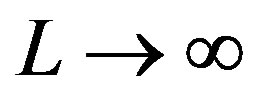 of a localized state increases significantly with the increasing of the disorder strength
of a localized state increases significantly with the increasing of the disorder strength . Since the localization lengths of quasiparticles are proportion to the the inverse of the square root of the above intercept. Therefore the localization length of quasiparticle decreases with the increase of disorder strength
. Since the localization lengths of quasiparticles are proportion to the the inverse of the square root of the above intercept. Therefore the localization length of quasiparticle decreases with the increase of disorder strength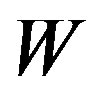 .
.
The optical conductivity can be calculated by [9]
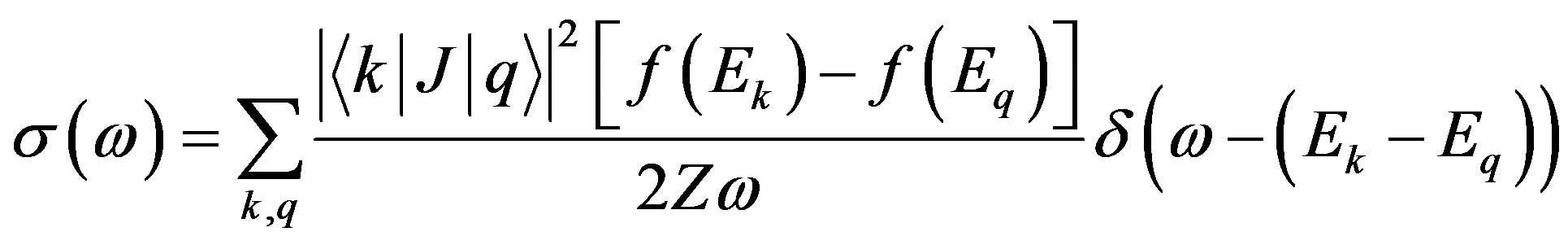 (6)
(6)
where , and
, and  is the coordination number. In Figure 3(a), we present the effect of disorder on the optical conductivity of the inhomogeneous superconductors with different attractive interactions
is the coordination number. In Figure 3(a), we present the effect of disorder on the optical conductivity of the inhomogeneous superconductors with different attractive interactions . We find that the density of optical conductivity in the low-energy region suppressed by the enhancement of superconducting order parameters. In addition, the Drude weight increases slightly with the increase of
. We find that the density of optical conductivity in the low-energy region suppressed by the enhancement of superconducting order parameters. In addition, the Drude weight increases slightly with the increase of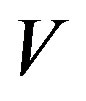 , suggesting the delocalization effect of
, suggesting the delocalization effect of , which is in agreement with the prediction drawn from the scaling of GIPR. It is obvious that, in the superconducting phase, the localization effect of disorder is weakened by the off-diagonal superconducting order.
, which is in agreement with the prediction drawn from the scaling of GIPR. It is obvious that, in the superconducting phase, the localization effect of disorder is weakened by the off-diagonal superconducting order.
To study the competition between the on-site repulsive interactions and disorder, we employ the Lanczos method [14] to investigate the Hubbard model with box distributed Anderson disorder, which is also called Anderson-Hubbard model with Hamiltonian,
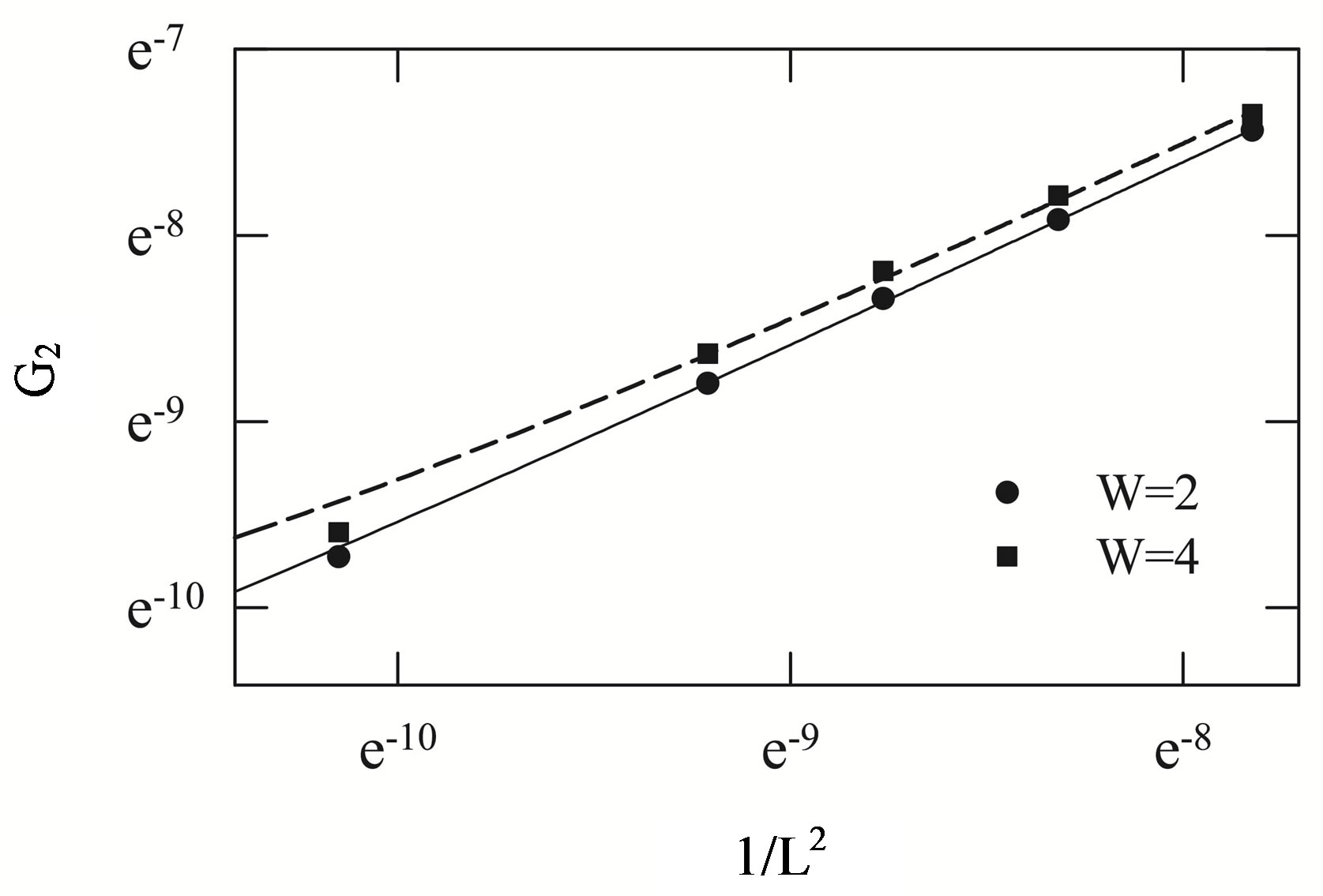
Figure 2. The lattice size scaling of the generalized inverse participation ratio  for the quasiparticles with energy
for the quasiparticles with energy 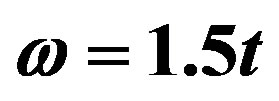 in the conditions with attractive interactions
in the conditions with attractive interactions 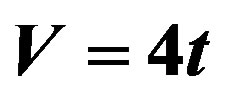 and different disorder strength W.
and different disorder strength W.
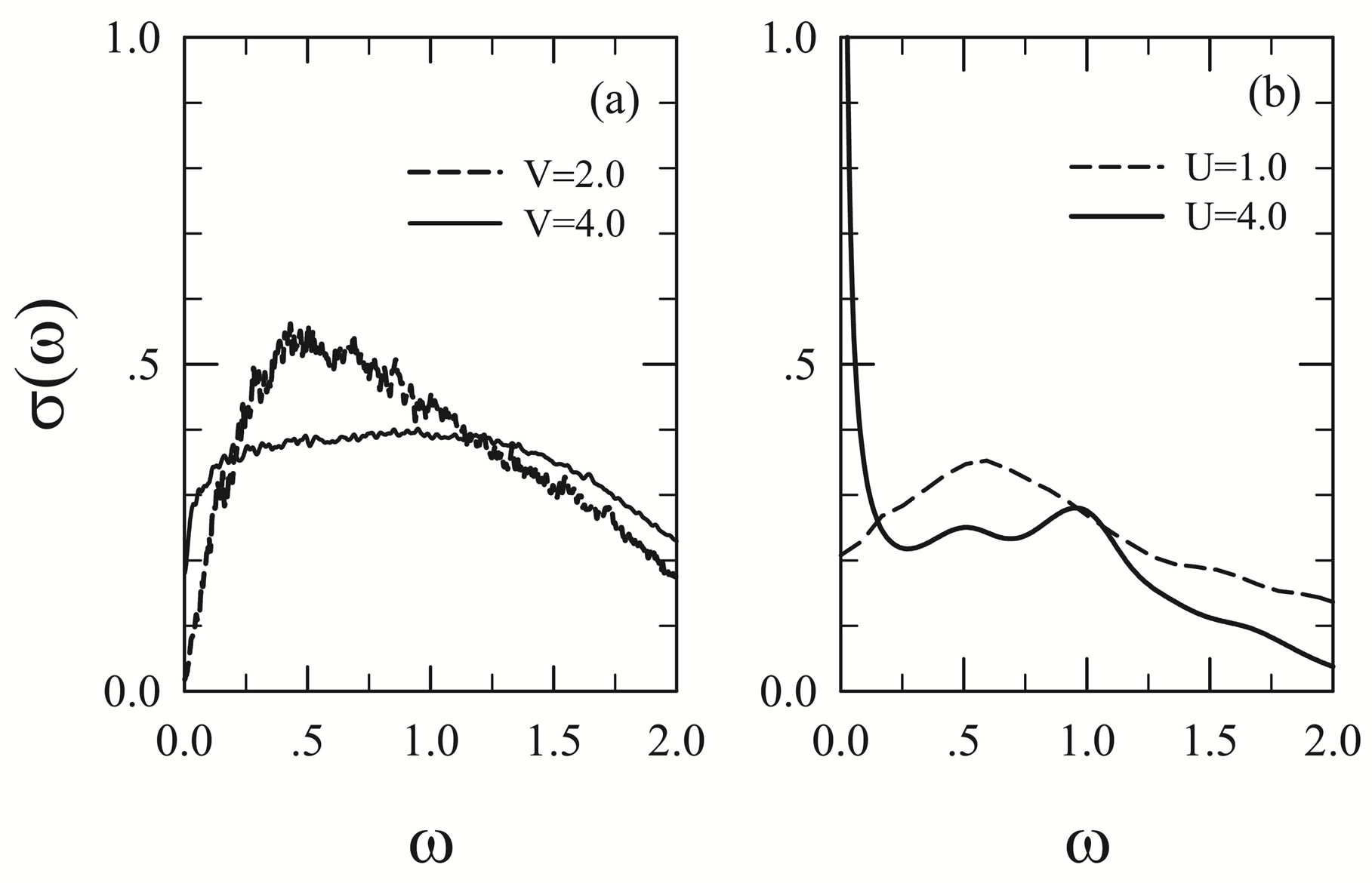
Figure 3. The optical conductivity obtained by (a) the kernel polynomial method for the mean-field superconducting model with N = 200, M = 2000 and W = 4.0, and by (b) the Lanczos diagonalization method for the Anderson-Hubbard model at half-filling with N = 8 and W = 4.0. Energies are in unit of t.
 (7)
(7)
where 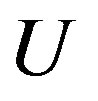 is the on-site repulsive interactions. We fix the disorder strength
is the on-site repulsive interactions. We fix the disorder strength  to study the effect of the on-site repulsive interactions on the optical conductivity. As shown in Figure 3(b), the Drude weight increases significantly when the on-site interactions increase from
to study the effect of the on-site repulsive interactions on the optical conductivity. As shown in Figure 3(b), the Drude weight increases significantly when the on-site interactions increase from 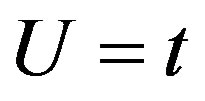 to
to . As discussed in reference [15], the delocalization effect comes from the screening effect of the on-site interaction on the disorder potential.
. As discussed in reference [15], the delocalization effect comes from the screening effect of the on-site interaction on the disorder potential.
In summary, the localization effect of disorder has been investigated by applying the scaling of generalized inverse participation ratio. We find that the off-diagonal superconducting order has the delocalization effect, while the on-site repulsive interactions can suppress significantly the localization of quasiparticles by screening strongly the disorder potential. The foregoing solutions can be demonstrated by observing the evolution of Drude weight.
2. Acknowledgements
The work was supported by the NSFC of China, under Grant No. 10974018 and 11174036, and the National Basic Research Program of China (Grant Nos. 2011CBA 00108).
REFERENCES
- P. A. Lee, Reports on Progress in Physics, Vol. 71, 2008, Article ID: 012501. doi:10.1088/0034-4885/71/1/012501
- A. N. Pasupathy, A. Pushp, K. K. Gomes, C. V. Parker, J. S. Wen, Z. J. Xu, et al., Science, Vol. 320, 2008, pp. 196-201. doi:10.1126/science.1154700
- K. Chatterjee, M. C. Boyer, W. D. Wise, T. Kondo, T. Takeuchi, H. Ikuta and E. W. Hudson, Nature Physics, Vol. 4, 2008, pp. 108-111. doi:10.1038/nphys835
- P. G. de Gennes, “Superconductivity of Metals and Alloys,” Addison-Wesley, Boston, 1989.
- W. A. Atkinson, P. J. Hirschfeld and A. H. MacDonald, Physical Review Letters, Vol. 85, 2000, pp. 3922-3925. doi:10.1103/PhysRevLett.85.3922
- A. Garg, M. Randeria and N. Trivedi, Nature Physics, Vol. 4, 2008, pp. 762-765. doi:10.1038/nphys1026
- H. Alloul, J. Bobroff, M. Gabay and P. J. Hirschfeld, Reviews of Modern Physics, Vol. 81, 2009, pp. 45-108.
- L. Covaci, F. M. Peeters and M. Berciu, Physical Review Letters, Vol. 105, 2010, Article ID: 167006. doi:10.1103/PhysRevLett.105.167006
- A. Weiße, G. Wellein, A. Alvermann and H. Fehske, Reviews of Modern Physics, Vol. 78, 2006, pp. 275-306. doi: 10.1103/RevModPhys.78.275
- A. Ghosal, M. Randeria and N. Trivedi, Physical Review B, Vol. 65, 2001, Article ID: 014501. doi:10.1103/PhysRevB.65.014501
- A. Punnoose and A. M. Finkel’stein, Science, Vol. 14, 2005, pp. 289-291. doi:10.1126/science.1115660
- Y. Song, H. K. Song and S. P. Feng, Journal of Physics: Condensed Matter, Vol. 23, 2011, Article ID: 205501. doi:10.1088/0953-8984/23/20/205501
- N. C. Murphy, R. Wortis and W. A. Atkinson, Physical Review B, Vol. 83, 2011, Article ID: 184206. doi:10.1103/PhysRevB.83.184206
- E. Dagotto, Reviews of Modern Physics, Vol. 66, 1994, pp. 763-840. doi:10.1103/RevModPhys.66.763
- Y. Song, S. Bulut, R. Wortis and W. A. Atkinson, Journal of Physics: Condensed Matter, Vol. 21, 2011, Article ID: 385601. doi:10.1088/0953-8984/21/38/385601

