Journal of Modern Physics
Vol.4 No.5(2013), Article ID:31416,5 pages DOI:10.4236/jmp.2013.45082
Dilepton Emission at Temperature Dependent Baryonic Quark-Gluon Plasma
Department of Physics and Astrophysics, University of Delhi, Delhi, India
Email: sssingh@physics.du.ac.in, yogesh.du81@gmail.com
Copyright © 2013 Shougaijam Somorendro Singh, Yogesh Kumar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 20, 2012; revised February 3, 2013; accepted March 5, 2013
Keywords: Dilepton; Quark-Gluon Plasma
ABSTRACT
Dilepton emission is calculated from quark-gluon plasma (QGP) with the consideration of temperature dependent chemical potential (TDCP). The model is considered to be quasi-model and hence take the dynamical quark mass as a finite value dependence on temperature. The temperature in quark mass enhances in the growth of dilepton emission rates. The emission rate of dilepton spectrum is shown in the intermediate mass region (IMR) of 1.0 - 4.0 GeV and its rate is observed to be a strong increasing function of the temperature dependent chemical potential for quark and anti-quark annihilation.
1. Introduction
The ongoing experiments like ultra-relativistic heavy-ion collision at BNL and the large hadron collider at CERN have focused on the search of the QCD phase structure and the formation of mini big bang. The experiments at BNL and CERN will provide the best platform to study the creation and evolution of such mini big bang called Quark-Gluon Plasma (QGP), which is perhaps believed to be formed in the expansion of the early universe [1,2]. Since we believe that the matter existed only for a few microseconds after the big-bang, its direct detection is very difficult even in these experiments. There are indirect possibilities for detection like strangeness enhancement [3],  suppression [4] and radiation of dileptons and photons [5-7] etc. Among these indirect probes, dileptons and photons are considered to be the most promising signals for its detection of QGP formation created in relativistic heavy-ion collision (RHIC). It is due to the fact that the dilepton driving out of the collisions among the quarks, anti-quarks and gluons bring the whole information about the existence of the plasma fireball and tell the properties of the fireball to the detector. They interact through electromagnetic force due to the large mean free path in their production. In order to see the production of dilepton for the signal of QGP formation, we look at the process of annihilation of quark and antiquark and they produce virtual photons which subsequently decay into dileptons such as
suppression [4] and radiation of dileptons and photons [5-7] etc. Among these indirect probes, dileptons and photons are considered to be the most promising signals for its detection of QGP formation created in relativistic heavy-ion collision (RHIC). It is due to the fact that the dilepton driving out of the collisions among the quarks, anti-quarks and gluons bring the whole information about the existence of the plasma fireball and tell the properties of the fireball to the detector. They interact through electromagnetic force due to the large mean free path in their production. In order to see the production of dilepton for the signal of QGP formation, we look at the process of annihilation of quark and antiquark and they produce virtual photons which subsequently decay into dileptons such as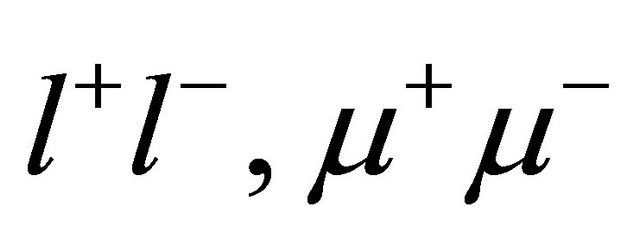 .
.
Many theoretical and experimental researchers have calculated dilepton and photon emissions at finite temperature and at quark chemical potential. The experiments at AGS and SPS energies [8-11] have reported the presence of significant amount of baryon chemical potential and even at RHIC energies  there has been the detection of such baryon chemical potential. These information indicate [12,13] that the colliding heavy ions may not be fully transparent in the centrality region of the colliding particles and the region may have significant amount of dense nuclear matter. The work of Hammon and coworkers [14] support these arguments of existing the chemical potential and predict the initial non-equilibrium QGP produced at RHIC energies, indicating that the system has finite baryon density or chemical potential. So, in the theoretical study, dilepton emissions in finite baryonic chemical potential have been calculated through various distribution functions and perhaps, the work of Dumitru et al. [15] gives the first signal of dilepton emission at finite baryonic chemical potential with Fermi distribution functions. Then this work is further studied by many others using quark and gluon fugacities in jüttner distribution function. It shows promising results calculated from the non-equilibrium quarkgluon plasma [16]. The recent work of Majumder et al. [17] has indicated the emission of dileptons from QGP at the RHIC energies at finite baryon density. Bass et al. [18] idea of parton rescattering and fragmentation leads to a substantial increase in the net-baryon density at midrapidity region. Besides these works, we have reports of other authors on dilepton production at low mass region [19-21]. These works suggest the importance of chemical potential in the dilepton calculation. To produce such emission, we consider a QGP system in which the equilibrium thermodynamic of system is a function of temperature T and chemical potential
there has been the detection of such baryon chemical potential. These information indicate [12,13] that the colliding heavy ions may not be fully transparent in the centrality region of the colliding particles and the region may have significant amount of dense nuclear matter. The work of Hammon and coworkers [14] support these arguments of existing the chemical potential and predict the initial non-equilibrium QGP produced at RHIC energies, indicating that the system has finite baryon density or chemical potential. So, in the theoretical study, dilepton emissions in finite baryonic chemical potential have been calculated through various distribution functions and perhaps, the work of Dumitru et al. [15] gives the first signal of dilepton emission at finite baryonic chemical potential with Fermi distribution functions. Then this work is further studied by many others using quark and gluon fugacities in jüttner distribution function. It shows promising results calculated from the non-equilibrium quarkgluon plasma [16]. The recent work of Majumder et al. [17] has indicated the emission of dileptons from QGP at the RHIC energies at finite baryon density. Bass et al. [18] idea of parton rescattering and fragmentation leads to a substantial increase in the net-baryon density at midrapidity region. Besides these works, we have reports of other authors on dilepton production at low mass region [19-21]. These works suggest the importance of chemical potential in the dilepton calculation. To produce such emission, we consider a QGP system in which the equilibrium thermodynamic of system is a function of temperature T and chemical potential 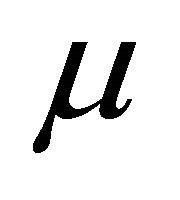 and the potential itself as function of temperature.
and the potential itself as function of temperature.
In this brief article, we choose the baryonic chemical potential which is considered to be temperature dependent chemical potential (TDCP) and the value has a change on the quark and anti-quark distribution functions. We take the value of the chemical potential in the scale of QCD parameter of dense nuclear matter. The chemical potential considered is obtained through [22]:
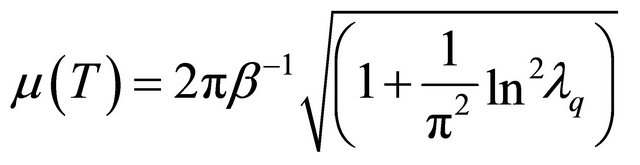 (1)
(1)
where 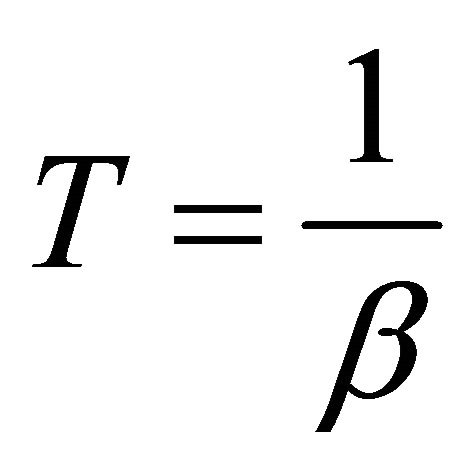 taken in the scale of QCD and
taken in the scale of QCD and
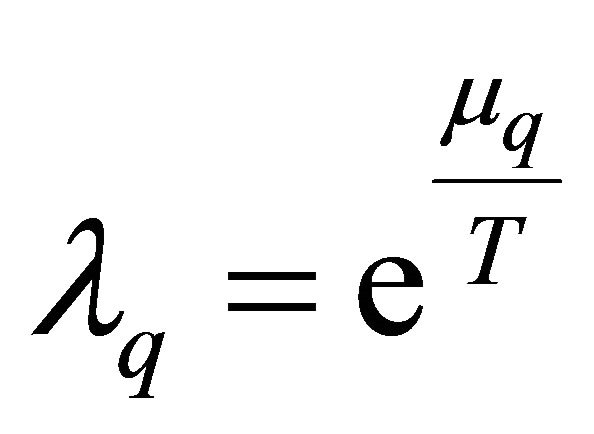 is quark fugacity. However, we consider the massless dynamical quark as a finite value and it is called thermal dependent quark mass (TDQM) obtained through temperature of the system. The finite value of the quark mass is defined as [23-25]
is quark fugacity. However, we consider the massless dynamical quark as a finite value and it is called thermal dependent quark mass (TDQM) obtained through temperature of the system. The finite value of the quark mass is defined as [23-25]
 (2)
(2)
with the QCD parameter 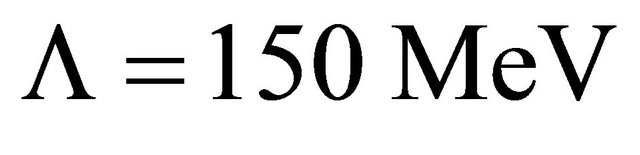 and normalizing
and normalizing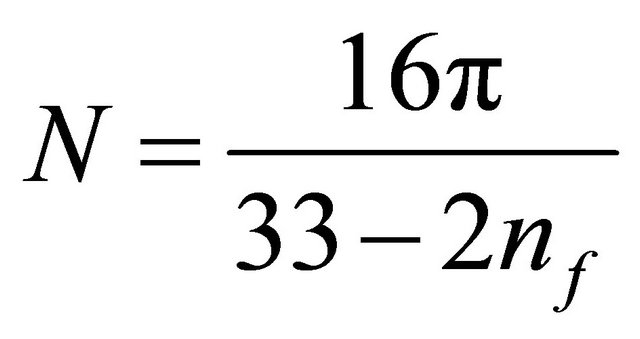 .
. 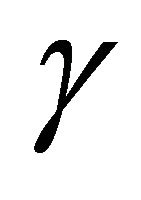 is a parametrization factor which is like the Reynold’s number to take care of the hydrodynamical aspects of the hot QGP flow. Its value is determined in the most effective way of the flow parameter of quarks
is a parametrization factor which is like the Reynold’s number to take care of the hydrodynamical aspects of the hot QGP flow. Its value is determined in the most effective way of the flow parameter of quarks 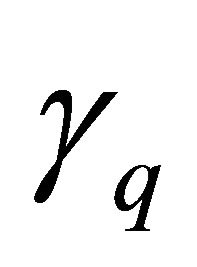 and gluons
and gluons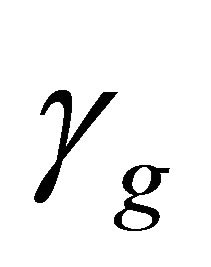 . It is expressed as
. It is expressed as
 (3)
(3)
with the value of 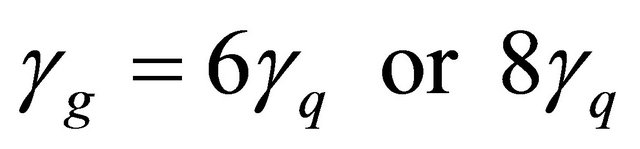 and
and 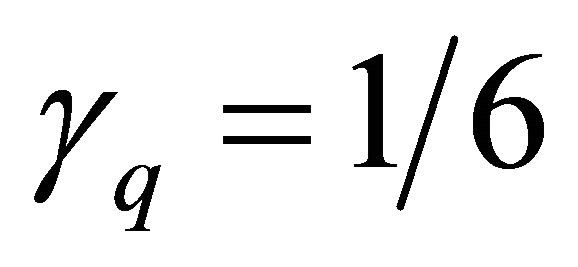 [24- 26].
[24- 26].
Using all such parameters, we calculate dilepton emission at the TDCP from system of QGP and see its emission rate in comparison to our earlier results and also the results of He and Dutta.
The paper is organized as follows: In Section II we look at the dilepton emission and integrated yields at temperature dependent chemical potential (TDCP). In Section III we present our results and in Section IV, we give our conclusion.
2. Dilepton Emission at TDCP from QGP
The calculation of dilepton emission at finite temperature and at finite baryon chemical potential have been done by many authors. These calculations are performed on the basis of the expected results coming out from the heavy-ion collision experiments. The experiments expect more productions of lepton than of other particles produced. The possible sources of dilepton are from the annihilation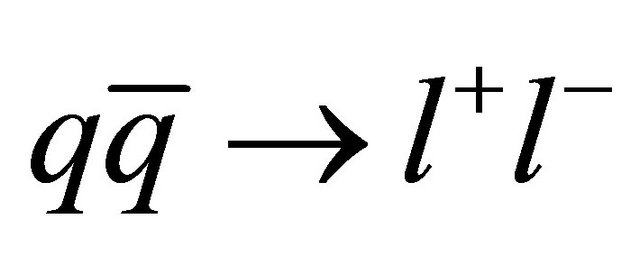 , Compton like scattering,
, Compton like scattering,
 and
and  fusion processes. Among the processes, Drell-Yan reaction is mostly used for thermal emission of dilepton pairs [27] and the Compton scattering such as
fusion processes. Among the processes, Drell-Yan reaction is mostly used for thermal emission of dilepton pairs [27] and the Compton scattering such as 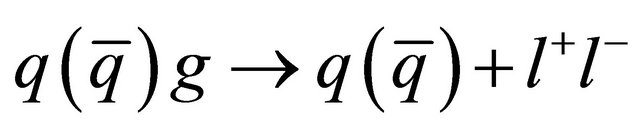 follows after Drell-Yan reaction. In this article, we exclusively engage in quark-antiquark annihilation such as
follows after Drell-Yan reaction. In this article, we exclusively engage in quark-antiquark annihilation such as
 reaction for the dilepton emission. This is due to fact that the collision produces larger amount of lepton pair in comparison to the other collision processes. In the process, we consider only the dominant production of dilepton in the intermediate mass region neglecting the dilepton spectra from the low mass region. This is fact that the contribution of dilepton through the decay of mesons in the system is negligence. So the dilepton emission rate produced
reaction for the dilepton emission. This is due to fact that the collision produces larger amount of lepton pair in comparison to the other collision processes. In the process, we consider only the dominant production of dilepton in the intermediate mass region neglecting the dilepton spectra from the low mass region. This is fact that the contribution of dilepton through the decay of mesons in the system is negligence. So the dilepton emission rate produced 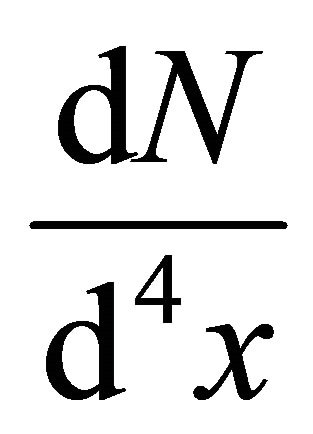 is given by [28,29]:
is given by [28,29]:
 (4)
(4)
where,
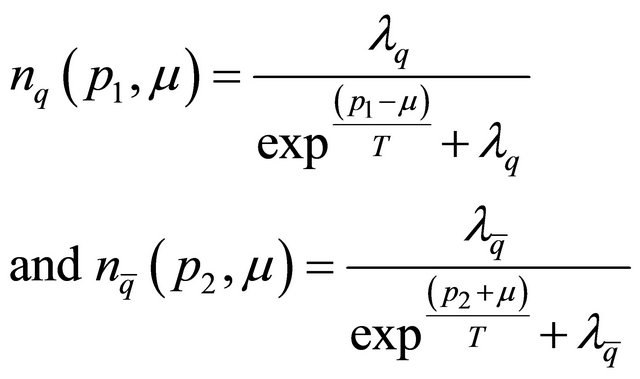 (5)
(5)
are modified Fermi-Dirac distribution functions for quarks and anti-quarks [30-34] with their corresponding parton fugacities . For gluon, the modified BoseEinstein distribution function is:
. For gluon, the modified BoseEinstein distribution function is:
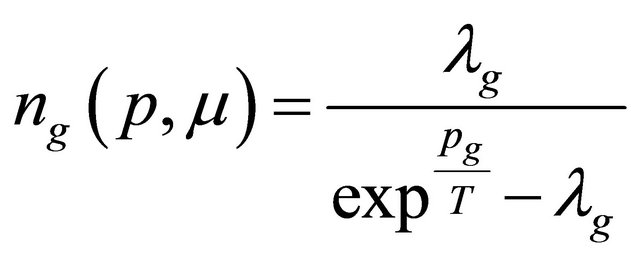 (6)
(6)
with parton gluon fugacity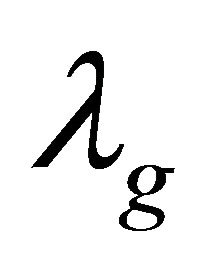 . The function for gluon can be used in the collision of
. The function for gluon can be used in the collision of 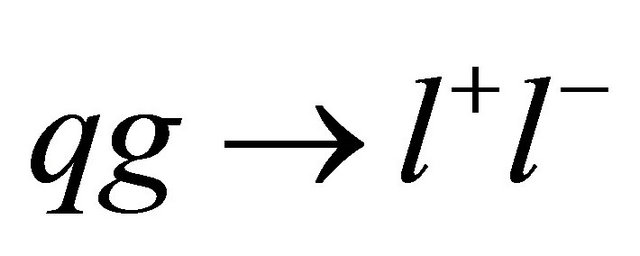 or
or 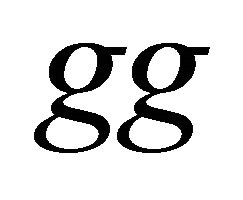 fusion reaction.
fusion reaction. 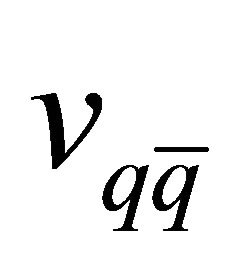 is the relative velocity of annihilating quark pair and
is the relative velocity of annihilating quark pair and 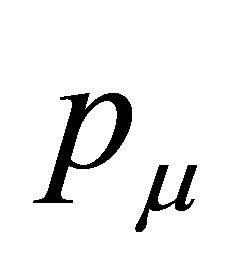 is lepton pair four momentum (
is lepton pair four momentum (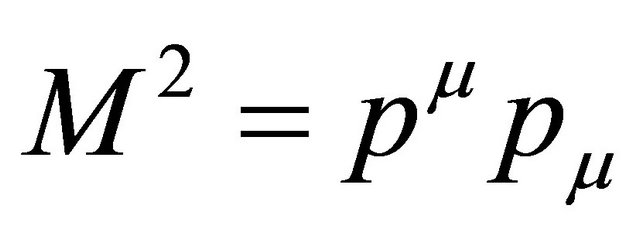 invariant lepton pair mass).
invariant lepton pair mass).  is the electromagnetic annihilation cross section. Substituting the distribution functions for quark and anti-quark in the Equation (4) using (5), and integrate over
is the electromagnetic annihilation cross section. Substituting the distribution functions for quark and anti-quark in the Equation (4) using (5), and integrate over  and
and 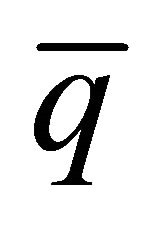 momentum, we obtain dilepton emission rate at TDCP as:
momentum, we obtain dilepton emission rate at TDCP as:
 (7)
(7)
In the above solution,  which is known as the modified Bessel’s function and volume element is
which is known as the modified Bessel’s function and volume element is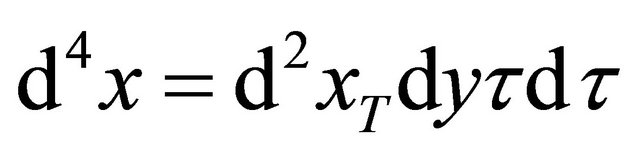 . We expand longitudinally the above expression and finally we have emission rate as:
. We expand longitudinally the above expression and finally we have emission rate as:
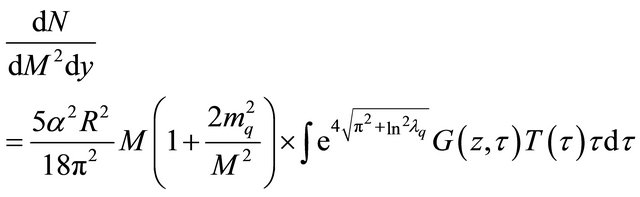 (8)
(8)
where, 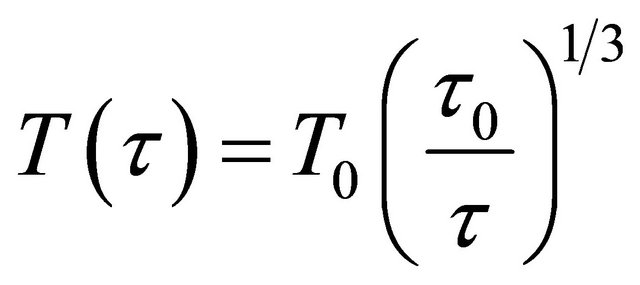 and
and 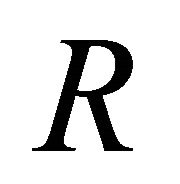 is droplet size of the QGP. Similarly, the dilepton emission using these modified distribution functions is calculated by He and Dutta and they calculate the production rate at zero and finite value of chemical potential.
is droplet size of the QGP. Similarly, the dilepton emission using these modified distribution functions is calculated by He and Dutta and they calculate the production rate at zero and finite value of chemical potential.
3. Results
In Figure 1, we show dilepton emission rate for various values of initial temperature 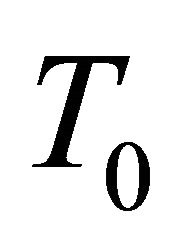 and at transition temperature Tc = 0.17 GeV without the chemical potential and compared the results with other theoretical calculations of dilepton emission at
and at transition temperature Tc = 0.17 GeV without the chemical potential and compared the results with other theoretical calculations of dilepton emission at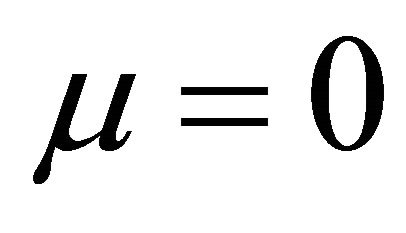 . The results are same over the range of lepton pair mass
. The results are same over the range of lepton pair mass 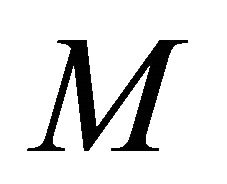 [25,30-34]. In the Figure 2, we show the comparison of emission rates of dilepton at the temperature dependent chemical potential and at finite chemical potential [25,30-34]. The emission rate increases with the increase of temperature dependent chemical potential at the transition temperature Tc = 0.17 GeV over the finite chemical potential. The emission rate is much higher at the temperature dependent chemical potential than the emission at finite chemical potential.
[25,30-34]. In the Figure 2, we show the comparison of emission rates of dilepton at the temperature dependent chemical potential and at finite chemical potential [25,30-34]. The emission rate increases with the increase of temperature dependent chemical potential at the transition temperature Tc = 0.17 GeV over the finite chemical potential. The emission rate is much higher at the temperature dependent chemical potential than the emission at finite chemical potential.
Now, if we look dilepton yields with the change of the lepton pair mass in the figures of dilepton production, we obtain a uniform fall in the production rate of dilepton with increase in lepton pair mass M upto 3 GeV. It indicates that at higher lepton pair mass more suppression

Figure 1. The dilepton emission rate,  , at transition temperature Tc = 0.17 GeV and at zero chemical potential for different initial temperatures and its compared curve.
, at transition temperature Tc = 0.17 GeV and at zero chemical potential for different initial temperatures and its compared curve.

Figure 2. The dilepton emission rate, 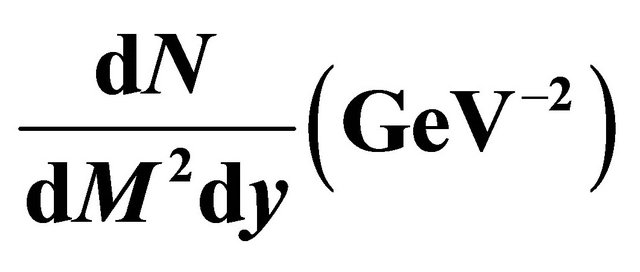 , at transition temperature Tc = 0.17 GeV for the different values of μ with different initial temperatures and its compared curves.
, at transition temperature Tc = 0.17 GeV for the different values of μ with different initial temperatures and its compared curves.
is obtained in comparison to the low mass region.
We look again at dilepton integrated yields with the evolution time of the QGP droplet. The dilepton integrated yield is exponentially increasing with the evolution time and after a certain time, it becomes almost constant for these different values of chemical potential. The plots are shown in the Figures 3-4 for the chemical potential with their corresponding initial temperatures at

Figure 3. The dilepton integrated yields,  , at transition temperature Tc = 0.17 GeV and at zero chemical potential (μ = 0) with different initial temperatures and its compared curves.
, at transition temperature Tc = 0.17 GeV and at zero chemical potential (μ = 0) with different initial temperatures and its compared curves.
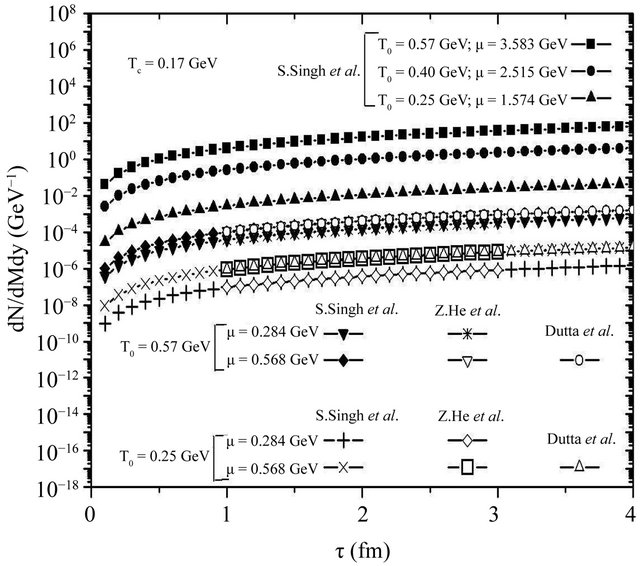
Figure 4. The dilepton integrated yield, 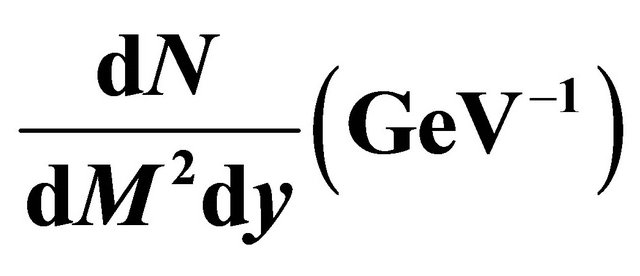 , at transition temperature Tc = 0.17 GeV for the different values of μ with different initial temperatures and its compared curves.
, at transition temperature Tc = 0.17 GeV for the different values of μ with different initial temperatures and its compared curves.
transition temperature Tc = 0.17 GeV. Figure 3 shows the integrated yields at transition temperature Tc = 0.17 GeV without the finite value of chemical potential and again compared the results with other results [25,30-34]. They are same at this zero chemical potential. In Figure 4, we plot the integrated yield for the temperature dependent chemical potential and finite chemical potential at the transition temperature Tc = 0.17 GeV. The integrated yield is very large as compared to the results of the earlier work of integrated yield at finite value of chemical potential [25,30-34]. This is due to the fact that both temperature and chemical potential enhance in the interaction of the particles of the system and yields more dileptons.
4. Conclusions
This paper has twofold purposes. First we introduce the quasi-model and hence we take quark mass as temperature dependent finite value. Second we calculate the dilepton emission rate and integrated yield at TDCP incorporating this finite quark mass. Due to the TDCP, the dilepton emission rate and integrated yield are much higher in comparison to the other results at finite value chemical potential and at zero chemical potential. It means that QGP phase where the temperature and chemical potential coexist together, the interactions among the constituent particles are more and dileptons are happened to emit more due to the collision among them. So the model with the temperature dependent chemical potential (TDCP) can produce much larger amounts of dilepton over the finite and zero chemical potential. The model produces overall improvement over results of finite baryonic chemical potential and zero chemical potential calculated by others.
5. Acknowledgements
We are very thankful to R. Ramanathan for his constructive suggestions and discussions. The author (YK) would like to thank the Department for research facility and highly obliged to express his gratitude to Rajiv Gandhi Fellowship, UGC, New Delhi for the financial support.
REFERENCES
- F. Karch, E. Laermann, A. Peikert, Ch. Schmidt and S. Stickan, Nuclear Physics B (Proceeding Supplement), Vol. 94, 2001, pp. 411-414. doi:10.1016/S0920-5632(01)00988-4
- T. Renk, R. Schneider and W. Weise, Physics Review C, Vol. 66, 2002, Article ID: 014902. doi:10.1103/PhysRevC.66.014902
- J. Rafelski and B. Müller, Physics Review Letter, Vol. 48, 1948, pp. 1066-1069. doi:10.1103/PhysRevLett.48.1066
- T. Matsui and H. Satz, Physics Letter B, Vol. 178, 1986, pp. 416-422. doi:10.1016/0370-2693(86)91404-8
- E. Shuryak, Physics Report, Vol. 80, 1980, pp. 71-158. doi:10.1016/0370-1573(80)90105-2
- K. Kajantie, J. Kapusta, L. McLerran and A. Mekjian, Physics Review D, Vol. 34, 1986, pp. 2746-2754. doi:10.1103/PhysRevD.34.2746
- D. K. Srivastava and B. Sinha, Physics Review Letter, Vol. 73, 1994, pp. 2421-2424. doi:10.1103/PhysRevLett.73.2421
- S. Nagamiya, Nuclear Physics A, Vol. 544, 1992, p. 5. doi:10.1016/0375-9474(92)90562-X
- W. Busza, Nuclear Physics A, Vol. 418, 1984, p. 635.
- O. Hansen, Proceeding of the 20th International Workshop on Gross Production of Nuclei and Nuclear Excitations, Hirschegg, 1992.
- G. Gustafson, Proceeding of the Workshop on Relativistic Heavy-Ion Physics at Present and Future Accelerators, Budapest, 1992.
- H. J. Möhring and J. Ranft, Zeitschrift für Physik C, Vol. 52, 1991, pp. 643-653. doi:10.1007/BF01562339
- Hammon, et al., Physics Review C, Vol. 61, 1999, Article ID: 014901. doi:10.1103/PhysRevC.61.014901
- A. Dumitru, D. H. Rischke, Th. Schonfeld, L. Winckelmann, H. Stöcker and W. Greiner, Physics Review Letter, Vol. 70, 1993, pp. 2860-2863. doi:10.1103/PhysRevLett.70.2860
- M. Strickland, Physics Letter B, Vol. 331, 1994, pp. 245- 250. doi:10.1016/0370-2693(94)91045-6
- A. Majumder, et al., Physics Review D, Vol. 63, 2001, Article ID: 114008. doi:10.1103/PhysRevD.63.114008
- S. A. Bass, Physics Review Letter, Vol. 91, 2003, Article ID: 052302. doi:10.1103/PhysRevLett.91.052302
- R. Rapp, Physics Review C, Vol. 63, 2001, Article ID: 054907. doi:10.1103/PhysRevC.63.054907
- K. Dusling and I. Zahed, Physics Review C, Vol. 82, 2010, Article ID: 054909. doi:10.1103/PhysRevC.82.054909
- J. Cleymans, J. Finghberg and K. Redlich, Physics Review D, Vol. 35, 1987, pp. 2153-2165. doi:10.1103/PhysRevD.35.2153
- S. Hamieh, J. Letessier and J. Rafelski, Physics Review C, Vol. 62, 2000, Article ID: 064901. doi:10.1103/PhysRevC.62.064901
- R. Ramanathan, et al., Physics Review C, Vol. 70, 2004, Article ID: 027903. doi:10.1103/PhysRevC.70.027903
- R. Ramanathan, K. K. Gupta, A. K. Jha and S. S. Singh, Pramana Journal of Physics, Vol. 68, 2007, p. 757.
- S. S. Singh, D. K. Gosain, Y. Kumar and A. K. Jha, Pramana Journal of Physics, Vol. 57, 2010, p. 27.
- Y. Kumar and S. S. Singh, Canadian Journal of Physics, Vol. 90, 2012, pp. 955-961. doi:10.1139/p2012-089
- G. D. Yen and M. I. Gorenstein, Physics Review C, Vol. 59, 1999, p. 2788.
- A. Peshier, B. Kämpfer, O. P. Pavlenko and G. Soff, Physics Letter B, Vol. 337, 1994, p. 235.
- P. V. Ruuskanen, “Quark-Gluon Plasma,” World Scientific, Singapore City, 1991.
- C. Gale and J. I. Kapusta, Canadian Journal of Physics, Vol. 67, 1989, p. 1200.
- T. S. Biro, E. V. Doorn, B. Müller, et al., Physics Review C, Vol. 48, 1993, pp. 1275-1284. doi:10.1103/PhysRevC.48.1275
- Z. He, et al., Nuclear Physics A, Vol. 724, 2003, pp. 477- 489. doi:10.1016/S0375-9474(03)01516-1
- Z. He, et al., Physics Review C, Vol. 68, 2003, Article ID: 024902. doi:10.1103/PhysRevC.68.024902
- Z. He, et al., Physics Review C, Vol. 80, 2009, Article ID: 014908.
- D. Dutta, et al., Physics Review C, Vol. 60, 1999, Article ID: 014905. doi:10.1103/PhysRevC.60.014905

