Journal of Modern Physics
Vol.4 No.3(2013), Article ID:28571,6 pages DOI:10.4236/jmp.2013.43043
Entropy Change of Non-Spinning Black Holes w.r.t. the Radius of Event Horizon in AGN
1Department of Physics, Marwari College, Tilka Manjhi Bhagalpur University, Bhagalpur, India
2Department of Physics, Tilka Manjhi Bhagalpur University, Bhagalpur, India
3Department of Physics, T. N. B. College, Tilka Manjhi Bhagalpur University, Bhagalpur, India
4Department of Physics, A. K. Gopalan College, Sultanganj, India
Email: dipomahto@hotmail.com
Received December 11, 2012; revised January 19, 2013; accepted January 27, 2013
Keywords: Radius of Event-Horizon; AGN; Entropy
ABSTRACT
In this research paper, we have used the formula for the change in entropy of Non-spinning black holes with respect to the change in the radius of event horizon (Mahto et al. 2012) and entropy of black holes (Hawking 1973 & Mahto et al. 2012) to calculate their values in Active Galactic Nuclei (AGN) which shows that the variation of change in entropy of black holes with respect to the radius of the event horizon/entropy of black holes with increasing the values of the radius of the event horizon of different test Non-spinning black holes are like a wave-pattern.
1. Introduction
The important property of entropy is that the total change in entropy is zero in a reversible process. The entropy is an intrinsic property of a given system and is a function of the energy and the volume [1]. In 1971, Stephen Hawking showed under general conditions that the total area of the event horizon of any collection of classical black holes can never decrease, even if they collide and merge [2] which means that 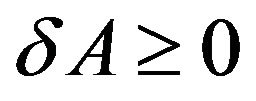 (second law of black hole mechanics). In 1973, Bekenstein suggested that a physical identification does hold between the laws of thermodynamics and the laws of black hole mechanics [3] and proposed that a black hole should have an entropy, and that it should be proportional to its horizon area [4] leading that
(second law of black hole mechanics). In 1973, Bekenstein suggested that a physical identification does hold between the laws of thermodynamics and the laws of black hole mechanics [3] and proposed that a black hole should have an entropy, and that it should be proportional to its horizon area [4] leading that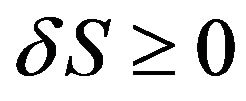 . In 1973, Bekenstein and Hawking gave a formula
. In 1973, Bekenstein and Hawking gave a formula  for calculation of entropy of a black hole, where A, G, ћ, k and c denoting Area of a black hole, Newton’s gravity constant, the Plank-Dirac constant
for calculation of entropy of a black hole, where A, G, ћ, k and c denoting Area of a black hole, Newton’s gravity constant, the Plank-Dirac constant , Boltzmann’s constant and the speed of light respectively [5]. The general formula for the entropy due to Bekenstein and Hawking provides a deep connection between quantum mechanics, general relativity and thermodynamics. In 1995, Strominger and Vafa showed that counting the microstates of a specific super symmetric black hole in string theory reproduced the Bekenstein-Hawking entropy [6]. Since then, similar results have been reported for different black holes both in string theory and in other approaches to quantum gravity like loop quantum gravity [7]. In 2011, Dipo Mahto et al. derived two formulae for the change in entropy of Non-spinning black holes
, Boltzmann’s constant and the speed of light respectively [5]. The general formula for the entropy due to Bekenstein and Hawking provides a deep connection between quantum mechanics, general relativity and thermodynamics. In 1995, Strominger and Vafa showed that counting the microstates of a specific super symmetric black hole in string theory reproduced the Bekenstein-Hawking entropy [6]. Since then, similar results have been reported for different black holes both in string theory and in other approaches to quantum gravity like loop quantum gravity [7]. In 2011, Dipo Mahto et al. derived two formulae for the change in entropy of Non-spinning black holes
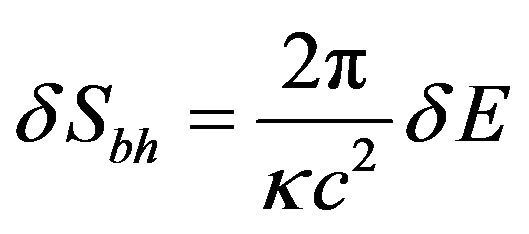
and
 applying first law of black hole mechanics to Einstein’s mass-energy equivalence relation
applying first law of black hole mechanics to Einstein’s mass-energy equivalence relation , where
, where 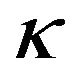 is the surface gravity and other parameters have their usual meaning [8]. In 2012, Dipo Mahto et al. derived a formula for the change in entropy of Non-spinning black holes with respect to the radius of event horizon and extended to derive the entropy of black holes in XRBs [9].
is the surface gravity and other parameters have their usual meaning [8]. In 2012, Dipo Mahto et al. derived a formula for the change in entropy of Non-spinning black holes with respect to the radius of event horizon and extended to derive the entropy of black holes in XRBs [9].
In the present research work, we have used the formula for change in entropy of Non-spinning black holes with respect to the change in the radius of event horizon [9] and entropy of black holes [9,10] to calculate their values in Active Galactic Nuclei (AGN) which shows that the variation of change in entropy of black holes with respect to the radius of the event horizon/entropy of black holes with increasing the values of the radius of the event horizon of different test Non-spinning black holes are like a wave-pattern.
2. Discussion
2.1. Black Hole
A black hole is a solution of Einstein’s gravitational field equations in the absence of matter that describes the space time around a gravitationally collapsed star. Its gravitational pull is so strong that even light cannot escape from it [1]. Karl Schwarzschild had found a spherically symmetric, static and exact solution of the full nonlinear Einstein’s field equation without any presence of matter about few months after the publication of final form of Einstein’s field equation [11]. This solution had a peculiar behaviour at what is now called the Schwarzschild radius, where it became singular meaning that some of the terms in the Einstein’s equation became infinite. The nature of this surface was not quite understood at time. Oppenheimer and his co-authors interpreted the singularity at the boundary of the Schwarzschild radius as indicating that this was the boundary of a bubble in which time is stopped. This is a valid point of view for external observers, but not for in falling observers. Because of this property, the collapsed stars were called “Frozen stars”, and an outside observer would see the surface of the star frozen in time at the instant where its collapse takes it inside the Schwarzschild radius [12].
2.2. Equation for Entropy and Entropy Change
The change in entropy of the Non-spinning black holes with respect to the change in the radius of event horizon is given by the following equation [9].
 (1)
(1)
or
 (2)
(2)
or
 (3)
(3)
or
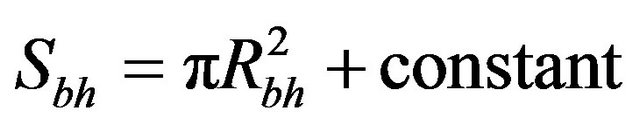 (4)
(4)
Assuming that a small black hole has zero entropy, the integration constant is zero. For the justification for the constant of integration in Equation (4), equal to almost zero, many reasons are mentioned in the research paper [9].
Hence,
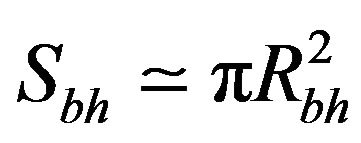 (5)
(5)
or
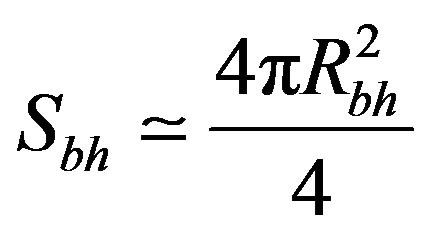
or
 (6)
(6)
where , for spherically symmetric and stationary or Schwarzschild black hole. Equation (6) indicates that the entropy of black holes with units
, for spherically symmetric and stationary or Schwarzschild black hole. Equation (6) indicates that the entropy of black holes with units
 .
.
The relation (6) is almost the same to the entropy of black holes as explained for the case of vacuum general relativity [8,13]. The term 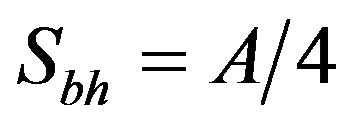 represents the physical entropy of a black hole. The term
represents the physical entropy of a black hole. The term 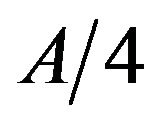 in general relatively plays the mathematical role of entropy by identifying the quantum dynamical degrees of a black hole [8].
in general relatively plays the mathematical role of entropy by identifying the quantum dynamical degrees of a black hole [8].
2.3. Data in Support of Mass of BHs in AGN
There are two categories of Black holes classified on the basis of their masses clearly very distinct from each other, with very different masses M ~5 - 20  for stellarmass Black holes in X-ray binaries and M ~106 - 109.5
for stellarmass Black holes in X-ray binaries and M ~106 - 109.5 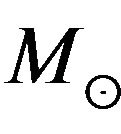 for super massive black holes in Active Galactic Nuclei [9,14]. The most viable scenario for modeling of active galactic nuclei includes a super massive black hole with the mass 106 - 109
for super massive black holes in Active Galactic Nuclei [9,14]. The most viable scenario for modeling of active galactic nuclei includes a super massive black hole with the mass 106 - 109  accreting the galaxian matter from its vicinity [15]. Our understanding of the fundamental processes operating in AGN is far from that in all cases, the ultimate source of power is accretion-via some form of an accretion disk-on to black holes with masses ranging from ~106 - 109
accreting the galaxian matter from its vicinity [15]. Our understanding of the fundamental processes operating in AGN is far from that in all cases, the ultimate source of power is accretion-via some form of an accretion disk-on to black holes with masses ranging from ~106 - 109 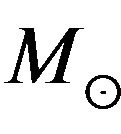 [15]. At the distance of the Virgo cluster, 15 Mpc, the sphere of influence of a
[15]. At the distance of the Virgo cluster, 15 Mpc, the sphere of influence of a  super-massive black holes (SBH) would shrink to a projected radius of 0”.07, not only well beyond the reach of any ground based telescope, beyond even HST capabilities [16]. Using a simultaneous multiorbital solution, Ghez, A. M. et al. derived a best fit central mass of
super-massive black holes (SBH) would shrink to a projected radius of 0”.07, not only well beyond the reach of any ground based telescope, beyond even HST capabilities [16]. Using a simultaneous multiorbital solution, Ghez, A. M. et al. derived a best fit central mass of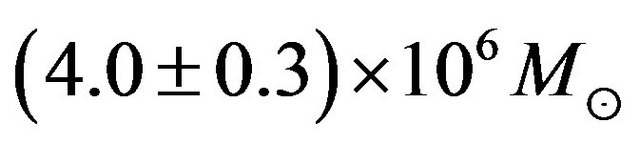 . The implied central mass density of
. The implied central mass density of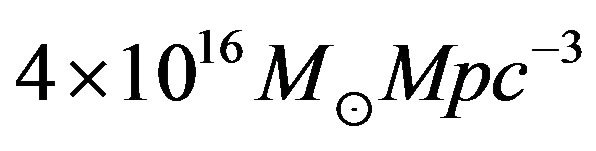 , provides virtually incontrovertible evidence that the mass is indeed in the form of singularity [17]. Assuming an isotropic, spherically symmetric system, Sargent et al. detected a central dark mass
, provides virtually incontrovertible evidence that the mass is indeed in the form of singularity [17]. Assuming an isotropic, spherically symmetric system, Sargent et al. detected a central dark mass  within the inner 110 pc of M87 [18]. Assuming the disk is Keplerian, Greenhill and Gwinn estimated the mass enclosed within 0.65 pc to be
within the inner 110 pc of M87 [18]. Assuming the disk is Keplerian, Greenhill and Gwinn estimated the mass enclosed within 0.65 pc to be  Although the NGC 1068 observations provide only partial evidence for the presence of a massive black hole, they do give us perhaps the clearest picture of the centre of an AGN [16].
Although the NGC 1068 observations provide only partial evidence for the presence of a massive black hole, they do give us perhaps the clearest picture of the centre of an AGN [16].
Greenhill et al. used VLBA observations to resolve the maser clouds in to two distinct morphological and kinematical components. Some of the clouds trace warped accretion disk extending from 0.1 pc to 0.4 pc from the centre of this galaxy, with a peak rotational speed of 260 km/s. A second population of clouds defines a wide-angle bipolar outflow up to 1 pc from the centre. The clouds belonging to the disk follow a Keplerian rotation curve rather closely implying a central mass of 
 , corresponding to a mass density of
, corresponding to a mass density of 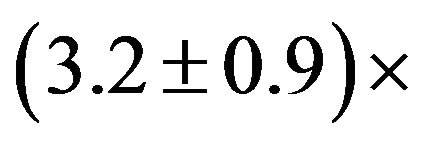
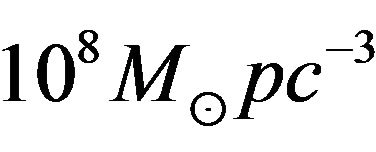 [19]. A kinematical study of NGC4261 followed in 1996, claiming a
[19]. A kinematical study of NGC4261 followed in 1996, claiming a  [20]. In NGC 4041, acquiescent Shc spiral, Marconi et al. (2003) remark that the systematic blue shift of the disk relative to systemic velocity might be evidence that the disk is kinematically decoupled. They conclude that only an upper limit, of
[20]. In NGC 4041, acquiescent Shc spiral, Marconi et al. (2003) remark that the systematic blue shift of the disk relative to systemic velocity might be evidence that the disk is kinematically decoupled. They conclude that only an upper limit, of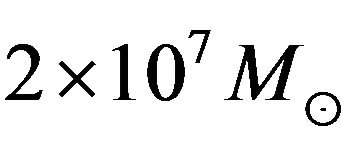 , can be put on the central mass. Cappellari et al. (2002) conclude that non-gravitational motions might indeed be present in the case of IC 1459, for which the ionized gas shows no indication of rotation in the inner 1”. IC 1459 is the only galaxy for which a SBH mass estimate exists based both on gas and stellar kinematics. Three-integral models applied to the stellar kinematics produce,
, can be put on the central mass. Cappellari et al. (2002) conclude that non-gravitational motions might indeed be present in the case of IC 1459, for which the ionized gas shows no indication of rotation in the inner 1”. IC 1459 is the only galaxy for which a SBH mass estimate exists based both on gas and stellar kinematics. Three-integral models applied to the stellar kinematics produce,  , while the gas kinematics produces estimates between a few × 108 and 109
, while the gas kinematics produces estimates between a few × 108 and 109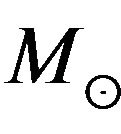 , depending on the assumptions made regarding nature of the gas velocity dispersion [16].
, depending on the assumptions made regarding nature of the gas velocity dispersion [16].
The virial hypothesis has recently received strong observational support from the work of Peterson and Wanndel (2002) and Onken and Peterson (2002). If the motion of the gas is gravitational, using the lags derived from different emission lines in the same AGN must lead to the same mass measurement. NGC 5548 was the first galaxy for which this was indeed verified. The highest ionization lines are observed to have the shortest time lag, so that the virial product remains constant. The implied central mass is equal to . The same has now been observed in three additional galaxies, NGC 7469, NGC 3783, and 3c390.3; in all cases, the time lag and measured line width obey a virial relationship [16].
. The same has now been observed in three additional galaxies, NGC 7469, NGC 3783, and 3c390.3; in all cases, the time lag and measured line width obey a virial relationship [16].
With the important exception of the Balbus-Hawley (1998) instability, the major developments in recent years have been observational or at least strongly motivated by observations. Masses of “central dark object” have been estimated in about forty cases, using stellar dynamics, emission lines of orbiting gas and, most accurately, using water masers. They range from 
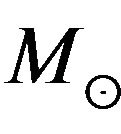 to
to 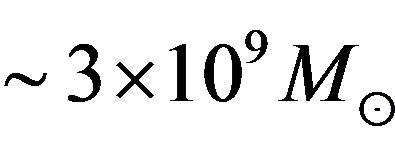 and, in many cases, the compactness is sufficient to rule out star clusters with confidence [21]. Most detected SBHs are in the
and, in many cases, the compactness is sufficient to rule out star clusters with confidence [21]. Most detected SBHs are in the 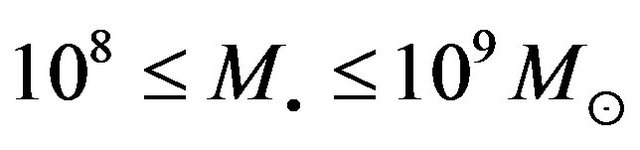 range, there are no detections below 106
range, there are no detections below 106 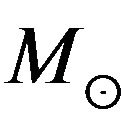 (the “building block” range) or above 1010
(the “building block” range) or above 1010 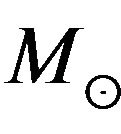 (the brightest quasar range), and even the
(the brightest quasar range), and even the  range is very poorly sampled [16].
range is very poorly sampled [16].
On the basis of the data mentioned above regarding the mass of black holes in AGN in terms of solar masses, we have calculated the change in entropy of black holes with respect to the change in radius of event horizon 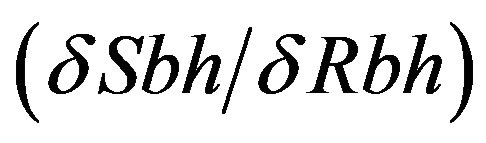 , using Equation (1) and entropy of black holes using Equation (5) for different test Non-spinning black holes listed in the Table 1.
, using Equation (1) and entropy of black holes using Equation (5) for different test Non-spinning black holes listed in the Table 1.
3. Result and Discussion
In present work, we have used the formula for the change in entropy of Non-spinning black holes with respect to the change in radius of event horizon 
and entropy of black holes  to calculate their values for different Non-spinning black holes existing in Active Galactic Nuclei (AGN) and the graphs have been plotted between:
to calculate their values for different Non-spinning black holes existing in Active Galactic Nuclei (AGN) and the graphs have been plotted between:
1) the radius of event horizon  of different BHs and their corresponding values of change in entropy w.r.t. change in radius of event of horizon in AGN using logarithmic scale (Figure 1).
of different BHs and their corresponding values of change in entropy w.r.t. change in radius of event of horizon in AGN using logarithmic scale (Figure 1).
2) the radius of event horizon of different BHs and their corresponding entropy in AGN using logarithmic scale (Figure 2).
When logarithmic scale is used to plot the graph in the case of Active galactic nuclei (AGN), a peculiar nature of graph is obtained for each case of 1) and 2). The nature of graph is neither in straight line nor in a complete curved line. The nature of the graph is approximately similar to the transverse wave showing that the variation in change of entropy of black holes with respect to the radius of the event horizon/entropy of black holes with increasing the values of the radius of the event horizon of different test Non-spinning black holes are almost the same to a wave-pattern in Active Galactic Nuclei (AGN).
From the observation of the Figures 1 and 2, it is clear that when the some points for the mass of black holes like (106, 107, 108, 109 & 109.5), (2 × 106, 2 × 107, 2 × 108, 2 × 109 & 2 × 109.5), (3 × 106, 3 × 107, 3 × 108, 3 × 109 & 3 × 109.5) and so on with their corresponding radius of event horizon are joined separately in both graphs, then straight line can be obtained for each sets of black holes mentioned above. Thus these sets give will give parallel lines. Hence the black holes existing on the same line should have the same character.
From the observation of the Table 1, it is clear that the entropy change/entropy of the non-spinning increases with increasing the radius of the event horizon of the different test black holes showing that 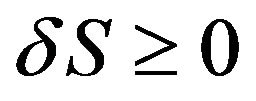 (second law of thermodynamics).
(second law of thermodynamics).
4. Conclusions
In the study of present research work, we can draw the following conclusions:
1) The graphs in Figures 1 and 2 shows that the variation of change in entropy of black holes with respect to the radius of the event horizon/entropy of black holes with increasing the values of the radius of the event horizon is almost the same to wave pattern in AGN.
2) The change in entropy of black holes with respect to the radius of the event horizon/entropy of black holes with increasing the values of the radius of the event horizon of different test black holes is non-uniform in AGN.
Table 1. Change in entropy w.r.t. change in radius of event horizon and entropy of BHs in AGN.
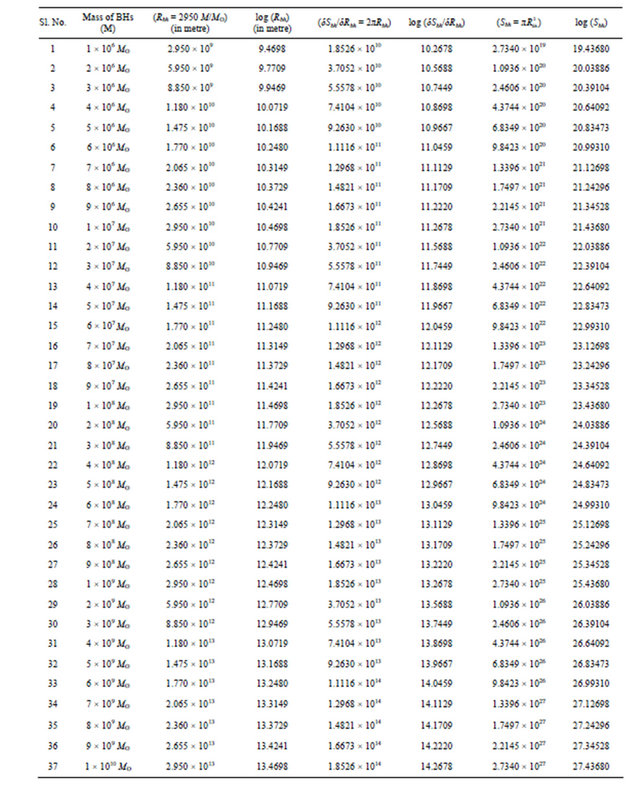
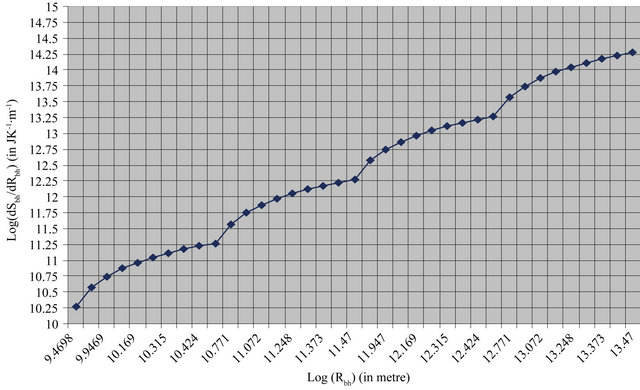
Figure 1. The graph plotted the radius of event horizon (Rbh) of different BHs and their corresponding values of change in entropy w.r.t. change in Rbh in AGN using logarithmic scale.
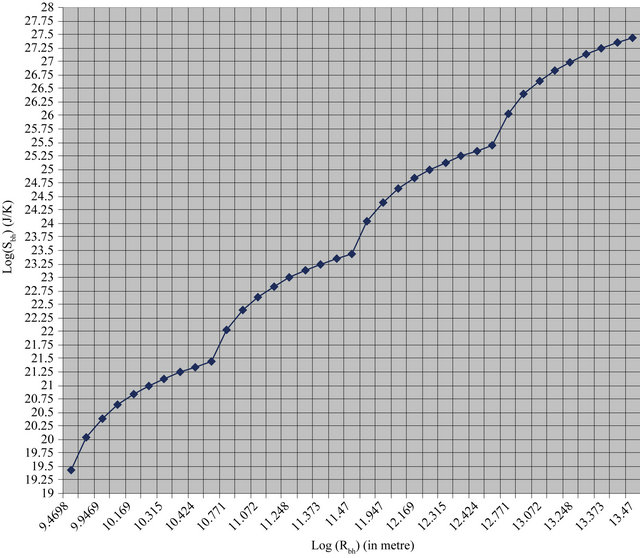
Figure 2. The graph plotted the radius of event horizon of different BHs and their corresponding entropy in AGN using logarithmic scale.
3) The calculated values of change in entropy showing that 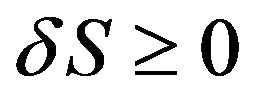 for each black hole candidates either existing in AGN. This result agrees with the second law of Thermodynamics.
for each black hole candidates either existing in AGN. This result agrees with the second law of Thermodynamics.
4) The Non-spinning black holes having mass of the same order should have the same character in AGN.
5. Acknowledgements
The authors acknowledge to Dr. G. K. Jha, Prof. & Former Head, Univ. Deptt. of Physics, L. N. M. U, Darbhanga, Dr. Kamal Prasad, Associate Professor, Univ. Deptt. of Physics, T. M. B. U Bhagalpur and Dr. Neeraj Pant, Associate Professor, Deptt. of Mathematics, N. D. A. Khadhakwasala, Pune for their fruitful discussions.
REFERENCES
- A. Dabholkar, “Black Hole Entropy in String the Ory—A Window in to the Quantum Structure of Gravity,” Current Science, Vol. 89, No. 12, 2005.
- S. W. Hawking, “A Brief History of Time,” Bantam Books, New York, 1998.
- J. Transchen, “An Introduction to Black Hole Evaporation,” 2000. arXiv:gr-qc/0010055V1
- R. M. Wald, “The Thermodynamics of Black Hole,” 1999. arXiv:gr-qc\9912119v2[gr-qc]
- J. D. Bekenstein, “Bekenstein-Hawking Entropy,” Scholarpedia, Vol. 3, No. 10, 2008, p. 7375.
- A. Strominger and C. Vafa, “Microscopic Origin of the Bekenstin-Hawking Entropy,” Physics Letters B, Vol. 379, No. 1-4, 1996, pp. 99-104. doi:10.1016/0370-2693(96)00345-0
- S. Carlips, “Black Hole Thermodynamics and Statistical mechanics,” Vol. 769, 2009, p. 89. doi:10.1007/978-3-540-88460-6
- D. Mahto, K. Kumari, R. K. Sah and K. M. Singh, “Study of Non-Spinning Black Holes with Reference to the Change in Energy and Entropy,” Astrophysics and Space Science, Vol. 337, No. 2, 2012, pp. 685-691. doi:10.1007/s10509-011-0883-7
- D. Mahto, V. Prakash, U. Prasad, B. K.Singh and K. M. Singh, “Change in Entropy of Non-Spinning Black Holes w.r.t. the Radius of Event Horizon in XRBs,” Astrophysics and Space Science, Vol. 343, No. 1, 2012, pp. 153- 159. doi:10.1007/s10509-012-1219-y
- S. W. Hawking, “Black Hole Explosions,” Nature, Vol. 248, 1974, pp. 30-31. doi:10.1038/248030a0
- K. Schwarzschild, “Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie,” Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik, 1916, p. 189.
- R. Ruffini and J. A. Wheeler, “Introducing the Black Hole,” Physics Today, Vol. 24, No. 12, 1971, p. 30. doi:10.1063/1.3022513
- R. M. Wald, “The Thermodynamics of Black Holes,” Living Reviews in Relativity, Vol. 4, 2001, p. 6.
- R. Narayan, “Black Holes in Astrophysics,” 2005. arXiv:gr-qc/0506078v1
- G. Madejski, “Black Holes in Active Galactic Nuclei,” SLAC-PUB-9702, 2003.
- L. Ferrarese and H. Ford, “Super Massive Black Holes in Galactic Nuclei: Past Present & Future Research,” Space Science Reviews, Vol. 116, No. 3-4, 2005, pp. 523-624. doi:10.1007/s11214-005-3947-6
- A. M. Ghez, et al., “The First Measurement of Spectral Lines in a Short-Period Star Bound to the Galaxy’s Central Black Hole: A Paradox of Youth,” The Astrophysical Journal, Vol. 586, No. 2, 2003, p. L127. doi:10.1086/374804
- W. L. W. Sargent, et al., “Dynamical Evidence for a Central Mass Concentration in the Galaxy M87,” The Astrophysical Journal, Vol. 221, 1978, p. 731. doi:10.1086/156077
- L. Greenhill, et al., “The Discovery of H2O Maser Emission in Seven Active Galactic Nuclei and at High Velocities in the Circinus Galaxy,” The Astrophysical Journal, Vol. 582, 2003, p. L11. doi:10.1086/367602
- L. Ferrarese, H. C. Ford and W. Jaffe, “Evidence for a Massive Black Hole in the Active Galaxy NGC 4261 from Hubble Space Telescope Images and Spectra,” The Astrophysical Journal, Vol. 470, 1996, p. 444. doi:10.1086/177876
- R. D. Blandford, “Recent Results on Active Galactic Nuclei,” Astrophysics and Space Science, Vol. 261, No. 1-4, 1999, pp. 245-252. doi:10.1023/A:1002093710287

