ABSTRACT

Based on the equation of motion in nonequilibrium Green function formalism, the matching conditions for the distribution functions of Boltzmann equation at interfaces of metallic multilayers are investigated in the nonequlibrium transport procedure. We also explore the matching conditions when the current-induced spin accumulation is accounted for, the contribution of coulomb interaction due to accumulated electrons is included. In order to study the matching conditions in the position space, we generalize the tunneling Hamiltonian to the formalism in position space, the matching conditions in this case is then obtained, which is convenient for us to match the usual distribution function of Boltzmann equation.

1. Introduction

In the past few years, a number of theoretical studies had been carried out in the Boltzmann equation approach on the spin-polarized transport of electrons tunneling through a magnetic multiplayer [1-5], the spin dependent transport is found to exhibit the interesting giant magnetoresistance effect and the current-induced switching of magnetic layers. The usual way in the Boltzmann equation approach is to solve the distribution function in each layer and connect them between layers by use of the matching conditions, which has been well used to investigate the transport problem of collinear magnetic multilayers [3,6,7]. The matching conditions in the noncollinear case are also explored by introducing an artifice to account for correlations between states in different layers [8,9]. However, these matching conditions for the distribution functions at the interface of two layers are only given out in the equilibrium case or in the steady state, how to extend them to the nonequilibrium transport procedure is still an open question. Actually, it is worthwhile to study the matching conditions out of equilibrium, because most of spin-dependent transport procedure occurs in the nonequilibrium situation. Also, the current-induced spin accumulation will happen in the nonequilibrium case, the coulomb interaction among the accumulated electrons will have their contributions to the matching condition, which had been illustrated in the steady state [10].

In this paper, we try to obtain the matching conditions out of equilibrium in the nonequilibrium Green function formalism. The lesser Green functions in different layers are related by their equations of motion, which can lead to the matching conditions for the distribution function of Boltzmann equation after Wigner transformation. Meanwhile, if we consider the coulomb interaction among accumulated electron in the tunneling Hamiltonian, it’s contribution to the matching conditions can also be obtained. Finally, the matching conditions are also expressed in the usual position space.

2. Green’s Functions and Wigner Distribution Functions

Consider a Ferromagnet/Insulator (Semiconductor)/Ferromagnet (FM/I(S)/FM) tunneling structure with the Hamiltonian given by [1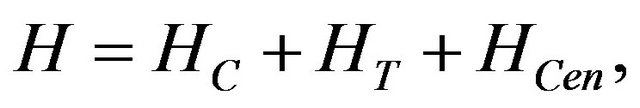1],

(1)

where the contact (ferromagnet) Hamiltonian is

,

is the creation (annihilation) operator of an electron of lead 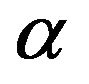with momentum 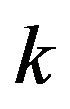and spin, 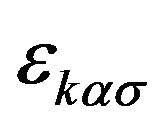is the single particle energy,

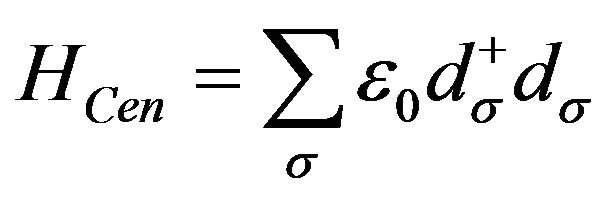
is the Hamiltonian of central region, creates (destroys) an electron with spin in central region, 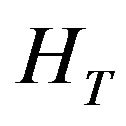is the tunneling coupling between contacts and the central region,

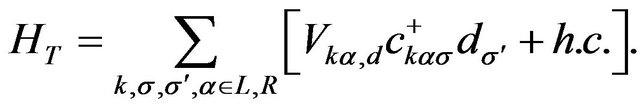
It is well known that the Green function in the contact is defined as

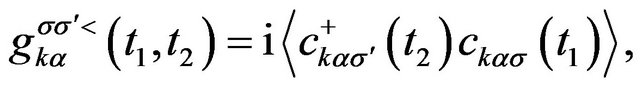(2)

which satisfies the following equation of motion,

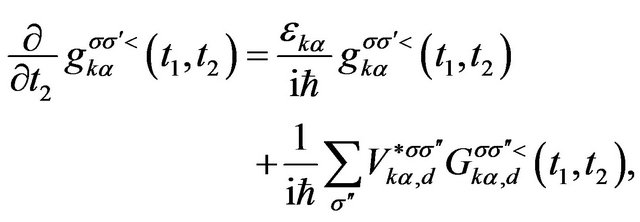(3)

where the Green function

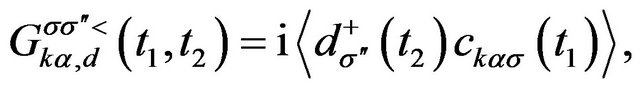
which is determined by it’s equation of motion

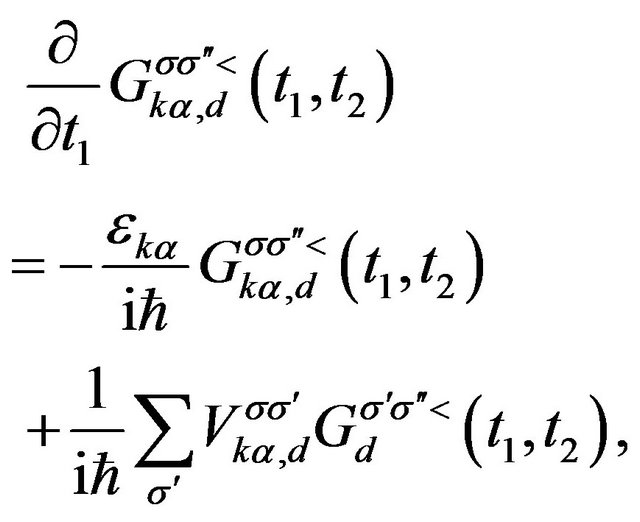(4)

where 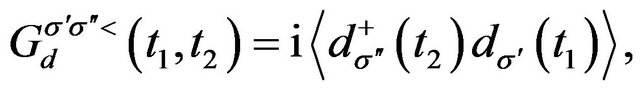is the Green function of central region. After Fourier transformation to the variable 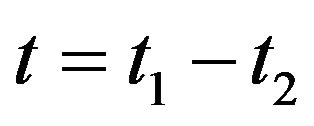on both sides of Equation (4), it will turn to

(5)

with solution

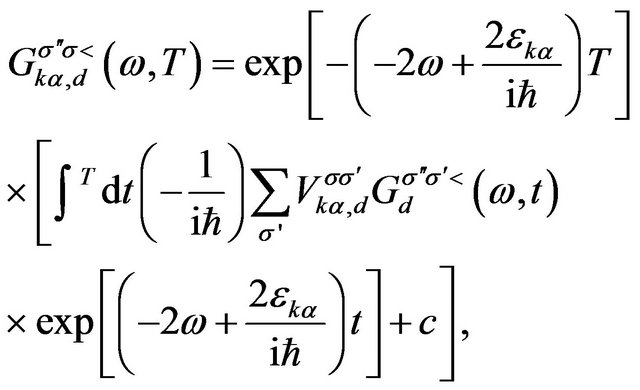(6)

where 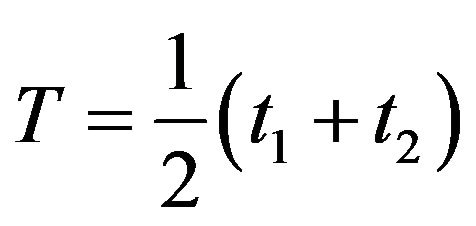is the center of mass variable and

is a constant which can be determined by the initial condition. Similarly, performing the same Fourier transformation to Equation (3), then substituting Equation (6) into it, we have

(7)

This equation relates the Green function of contacts with the Green function of central region.

Usually, the Wigner distribution function of quantum Boltzmann equation in contact and central region are defined as

(8)

and

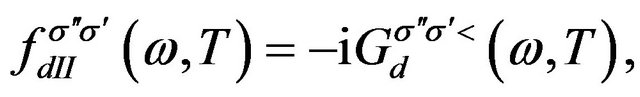(9)

respectively. Then from Equation (7), the distribution function of contact and the distribution function 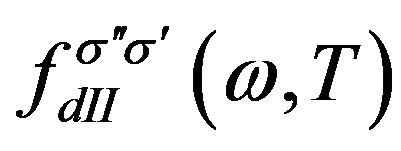of central region can be connected together, it is

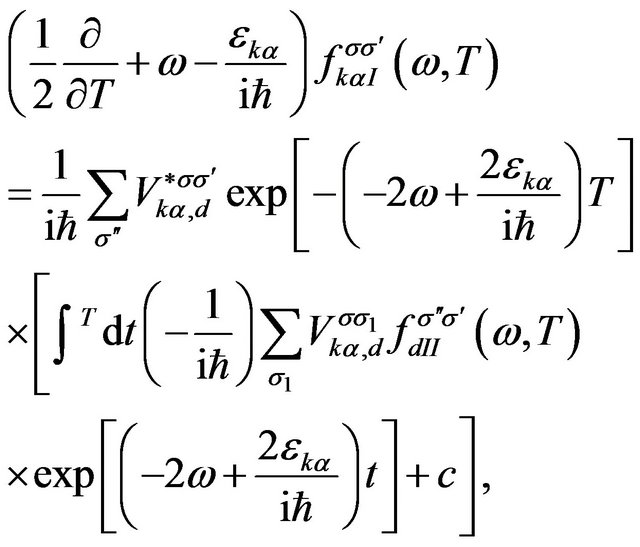(10)

which is exactly the matching condition between contact and central region in the nonequilibrium case. This complicated integro-differential condition about time 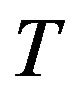is in essence the equation of motion for the lesser Green function, so far we have arrived one of our results.

3. Matching Conditions

The above matching conditions (10) and the Hamiltonian (1) are given in the second quantization formalism. However, the usual matching conditions we use to connect the distribution function of Boltzmann equation in different layers is expressed in the position formalism. It is necessary to explore the matching conditions out of equilibrium in position space. For this purpose, we introduce the Hamiltonian of tunneling structure as

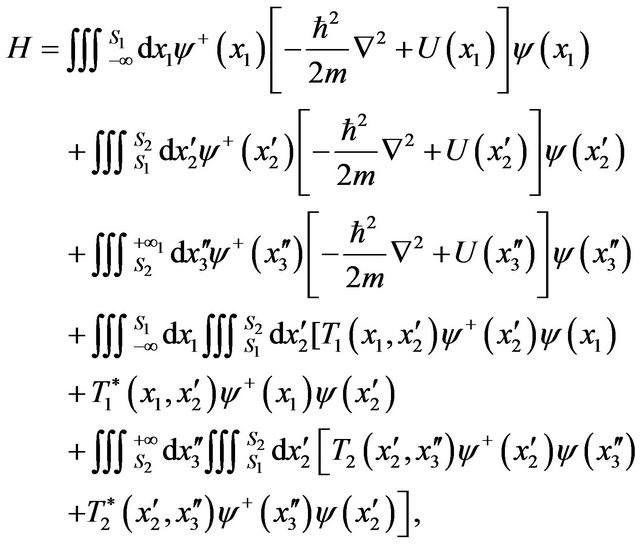
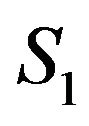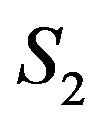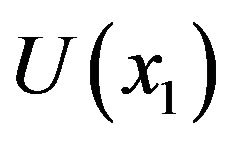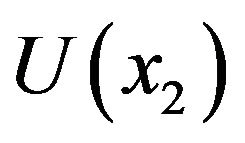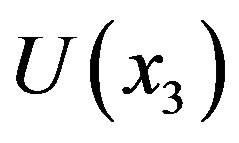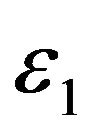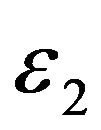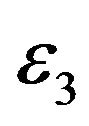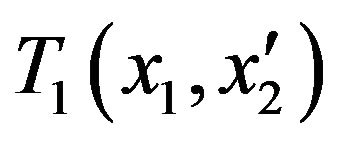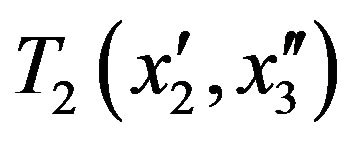where is the interface between the left contact and central region, is the interface between the central region and the right contact, , and are the potentials in the left contact, in the central region and in the right contact, the single particle energy corresponding to them are denoted as, and, respectively. and are the coupling coefficient between the contacts and the central region. In this case, we can define the lesser Green function in the contact as

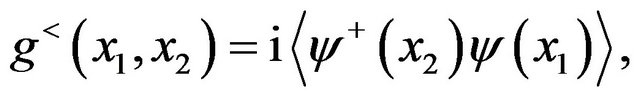(19)

which satisfies the following equation of motion

(20)

where the Green function 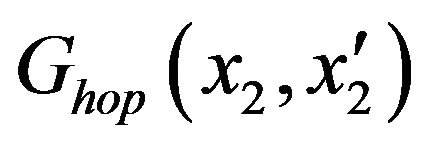is defined as

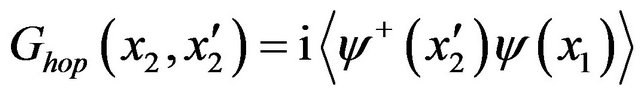. From this definition, we can get it’s equation of motion by use of the Hamiltonian in position space, it is

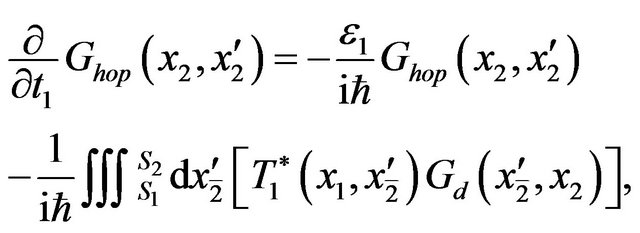(21)

where is the lesser Green function in the central region,

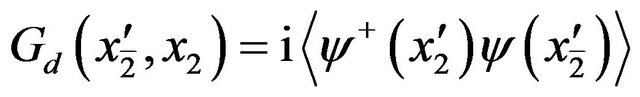(22)

Usually, the Wigner distribution function in the Boltzmann equation is defined as the Fourier transformation of the lesser Green function [12-14].

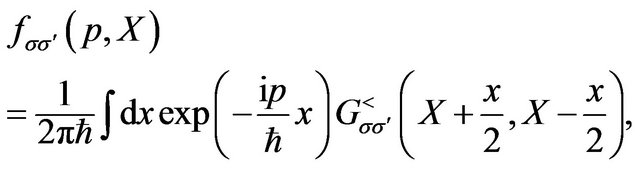(23)

where 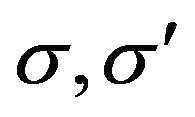denote the spin indices, 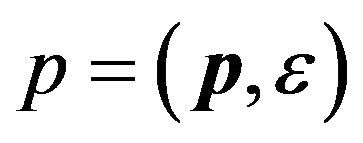is the four dimensional momentum, 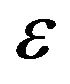is the energy,

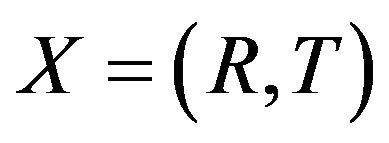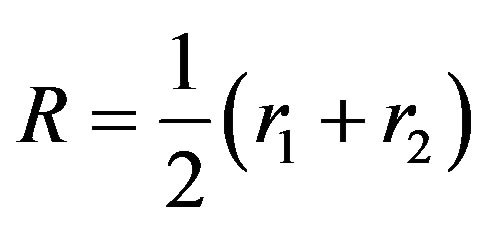where, is the center of mass variable, the variable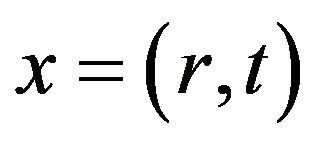, which represents the differences between two position and time variables entering these functions, and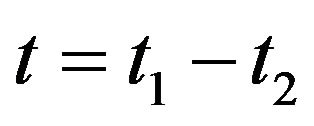. Performing the above Fourier transformation to both sides of Equation (20), we have

(23)

where 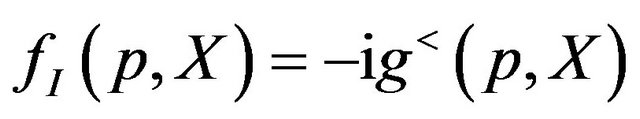is the distribution function in the contact, and 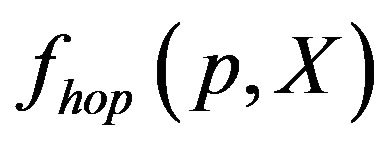is defined as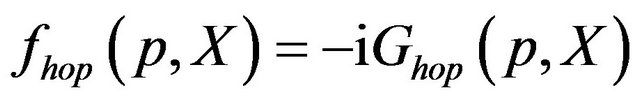. We have adopted the gradient approximation in the Fourier transformation of the second term in the above equation [12-14]. In order to express 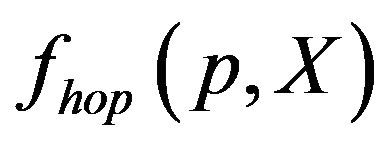in terms of the distribution function of contact region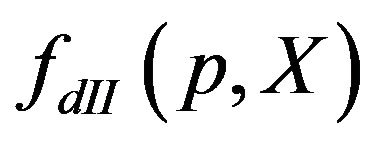, we write out the equation of motion for the Green function 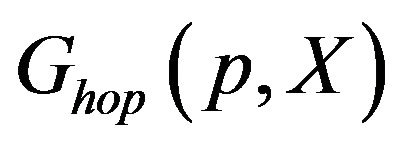as

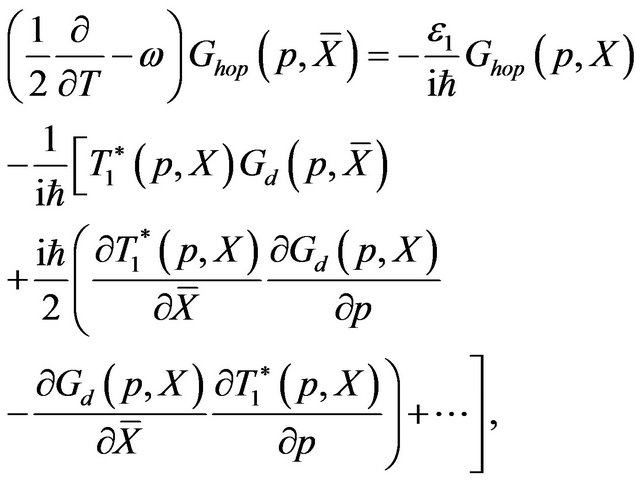(24)

where. The above equation is just the Fourier transformation of Equation (21). The variable 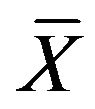has relation with the variable 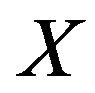as

,

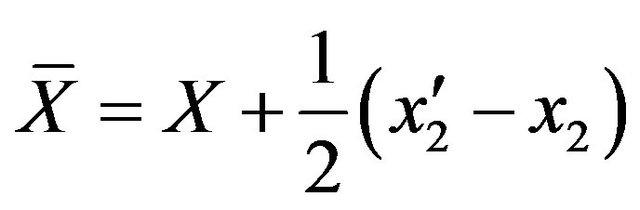is the position of electron before jumping from contact to central region, it is in the contact. is the position after jumping, which is in the central region. As we know, the jumping usually occurs as the electrons are near the interface, so, then we can approximate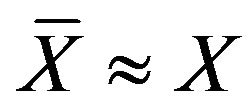. In this approximation, Equation (24) has solution

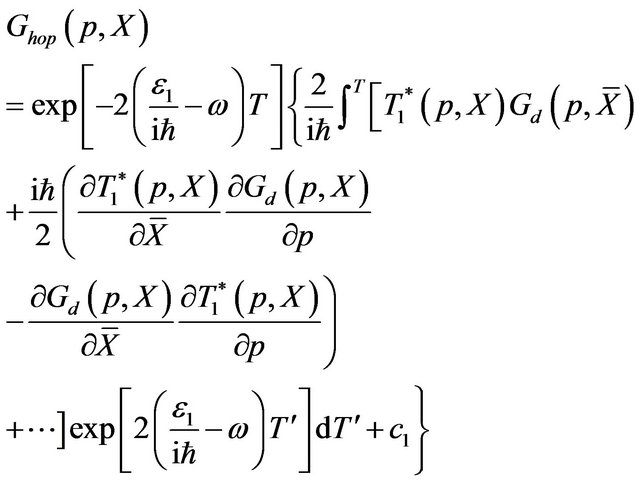(25)

where 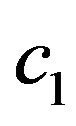is a constant which can be determined by the initial condition. Substituting expression (25) into Equation (23), we finally obtain the matching condition out of equilibrium in the position space, which connects the distribution function 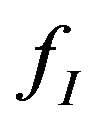in the contact with the distribution function 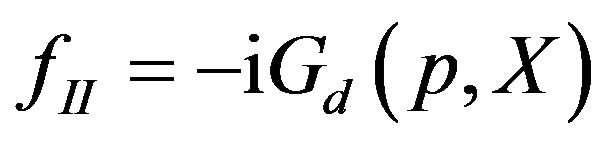in the central region. Certainly, this matching condition is very complicated, it has simple expression in the steady state or in the equilibrium case.

4. Conclusion

In summary, we have obtained the matching condition out of equilibrium for the distribution function of Boltzmann equation in different layers, which is based on the equation of motion method within the framework of nonequilibrium Green function formalism. The contribution of coulomb interaction among the accumulated electrons to the matching condition is also discussed, we compare it with the results in Reference [10]. Our research is in fact a microscopic model to illuminate the results in Reference [10]. The usual matching condition in position space formalism are finally expressed by means of a Hamiltonian chosen in the position formalism.

5. Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grant No. 10404037 and 11274378. This research was done while Z. C. Wang was a visiting scholar at New York University; he expresses his gratitude to Prof. P. M. Levy for his invaluable help and thanks the Physics Department for their hospitality during his stay.

REFERENCES

Appendix

Current Driven Accumulation

As we know, the current-induced spin accumulation will happen in the nonequilibrium case, it is necessary to consider the coulomb interaction among accumulated electrons in the Hamiltonian if we want to account for the spin accumulation in the matching conditions. The Hamiltonian in this case is similar to Exp. (1) but with the 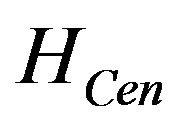replaced by [11]

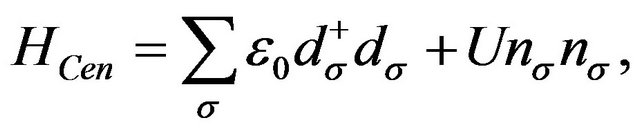(11)

where 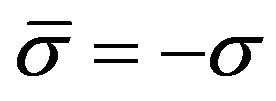and 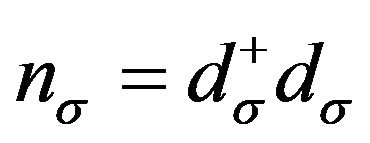is the occupation number of the spin-state, describe the coulomb interaction among accumulated electrons. In the Hartree-Fock approximation, the distribution function 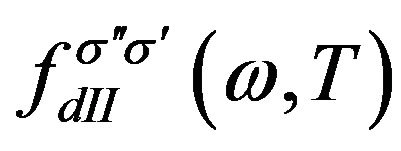of the central region in Equation (10) satisfies the following equation of motion

(12)

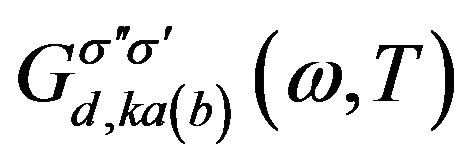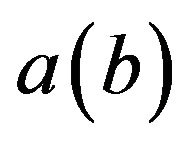where is the Fourier transformation of Green function at contact. The last term in the right hand side of Equation (12) indicates the contribution of coulomb interaction of accumulated electrons to the matching condition (10) when we include the interaction in the Hamiltonian (11). In order to demonstrate this clearly, we concentrate on the study of a steady state, in which

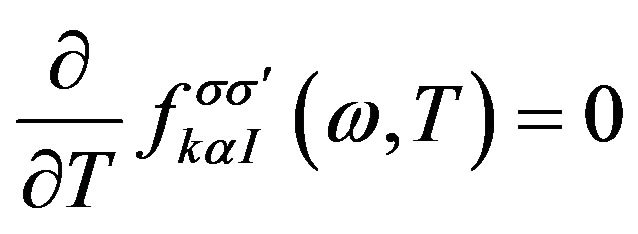, and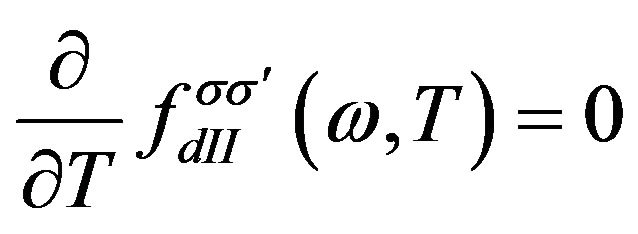, the matching condition (10) will reduce to

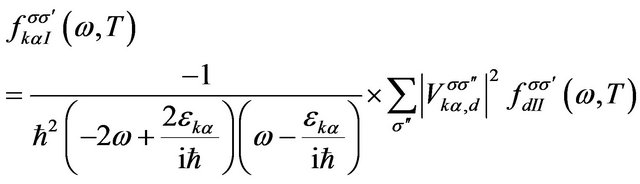(13)

which is similar to the matching conditions of steady state in previous work. Suppose the distribution function in equilibrium case is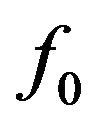, because of the coulomb interaction due to the accumulated electrons, the distribution function in the steady state will deviate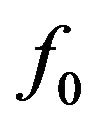, that is

(14)

where 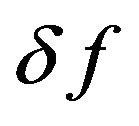is the deviation away from the equilibrium distribution function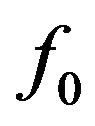. According to Equation (13), the deviation in the steady state satisfy the following equation

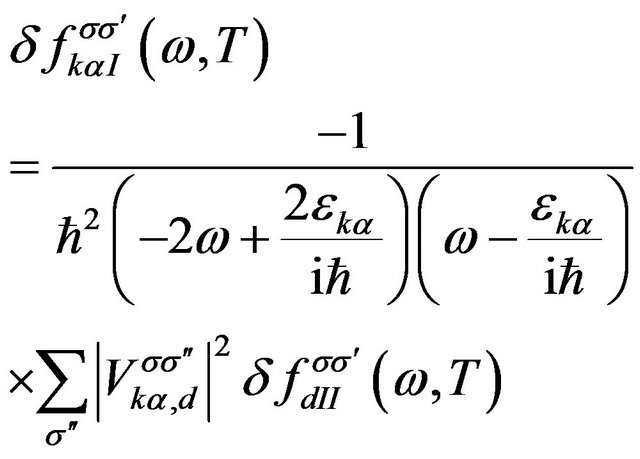(15)

where the deviation of the distribution function in the central region 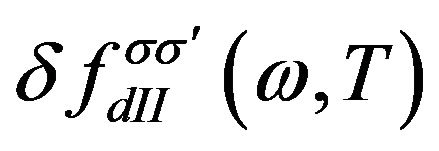can be obtained from the equation of motion (12) when we adopt the steady condition, it is

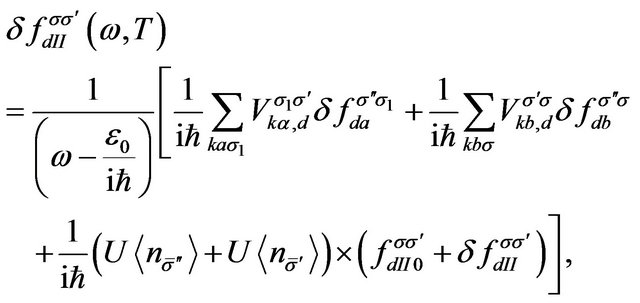(16)

where

and

.

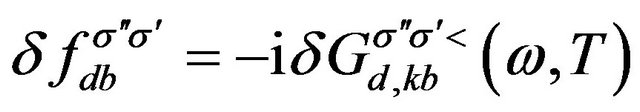Substituting the above expression into Equation (15), we have

(17)

This equation is helpful for us to compare with the results shown in Reference [10]. In Reference [10], the contribution of coulomb interaction due to accumulated electrons to the matching conditions was investigated in the steady state, the deviation of distribution function is given by

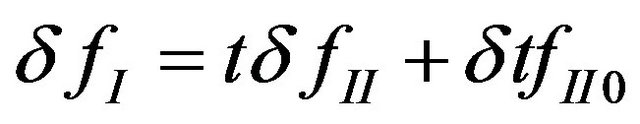(18)

where is the scattering matrix which relate the distribution function of the contact 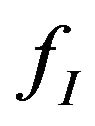and the distribution function of the central region in the equilibrium case, 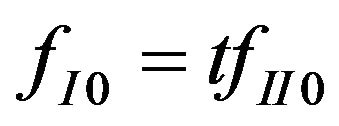, Equation (18) indicates that the deviation of 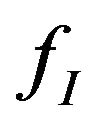in the contact contain two parts, the first part is contributed by the deviation of in the central region, the second is by the change of scattering matrix which is induced by the coulomb interaction among accumulated electrons. Comparing Equation (18) with Equation (17), we can find that the first part corresponds to the first term in Equation (17) which is involved with the deviation of distribution functions, while the second part corresponds to the second term in Equation (17), the coulomb interaction among the accumulated electrons plays a important role in it. In fact, a microscopic model had been proposed to illuminate the results in Reference [10].