ABSTRACT

Modified Newtonian Dynamics (MOND) is one of the successful theories to explain the dark matter problem in galaxies. However, the data from clusters and the cosmic microwave background (CMB) indicate some dark matter should exist in larger scales. In addition, recent dynamical studies of clusters show that the effect of dark energy should not be ignored in cluster scale. In this article, I will demonstrate how dark energy affects the cluster mass calculation by using MOND. Also, I will show that the calculated cluster mass is consistent with the total matter to baryonic matter ratio obtained by the CMB data.

1. Introduction

The dark matter problem is one of the key issues in modern astrophysics. The existence of cold dark matter (CDM) particles is the generally accepted model to tackle the darkmatter problem. However, no such particles have been detected directly. In addition, the CDM model also encounter many well-known unresolved issues such as the cusp problem [1,2], the missing satellite problem [3] and more recently the observation of the tidal dwarf galaxies [4]. Another alternative theory uses the Modified Newtonian Dynamics (MOND) as the weak accelerationlimit of Einstein’s general relativity to explain the dark matter problem [5-7]. It is consistent with a wide range of observational data including the rotation curves of galaxies and the Tully-Fisher relation [6]. However, the recent data from gravitational lensing and hot gas in clusters challenge the original idea of MOND without any dark matter (classical MOND) [7-9]. Sanders (1999) studied 93 X-ray emitting clusters and pointed out that the cluster dark matter problem cannot be solved by MOND alone. Some 2 eV active neutrinos are needed to account for the missing mass in clusters [10]. Later, studies of gravitational lensing and hot gas in clusters show that the existence of 2 eV neutrinos is still not enough to explain the missing mass in clusters. Therefore, some more massive dark matter particles (e.g. sterile neutrinos) is required to account for the missing mass [9,11,12]. It can be shown that the equilibrium configuration of these sterile neutrinos is consistent with the missing mass in clusters [13]. On the other hand, the data from the Cosmic Microwave Background (CMB) indicate a large amount of dark matter is needed to explain the CMB spectral shape [14]. Angus (2009) shows that the existence of ∼11 eV neutrinos is consistent with the CMB data and the analytic results of the Miniboone experiment [15]. Therefore, the mainstream of the discussion in MOND recently is not opposing the existence of dark matter, but the existence of CDM [16].

It has recently been recognized that dark energy exists in our universe. Angus (2009) shows that if MOND theory is needed to satisfy the fitting in CMB spectrum, a large amount of dark energy is required. Therefore, both CDM and MOND theories should consider the effect of dark energy. The local dynamic effects of dark energy were first reported by Chernin, Teerikorpi and Baryshev (2003) [17]. Later, Bisnovatyi-Kogan and Chernin (2012) show that the dark energy may affect the clusters at a few Mpc scale by Newtonian dynamics [18]. In the MOND regime, the calculated cluster mass is smaller than the one calculated by the Newtonian dynamics [6]. Therefore, the effect of the dark energy in clusters under the MOND theory will be larger. In this article, I will demonstrate how dark energy affects the cluster mass calculation by using MOND. Also, I will show that the calculated cluster mass is consistent with the total matter to baryonic matter ratio obtained by the CMB data.

2. MOND with Dark Energy in Clusters

The effective gravitational acceleration in MOND is given by [5,6]

(1)

when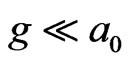, where g_n is the Newtonian gravity and a₀ = 1.2 × 10⁻⁸ cm·s⁻². If we assume that the hot gas with uniform temperature T in cluster is a pressure supported system, we have [6]

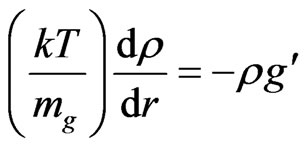(2)

where m_g is the mass of a gas particle, is the density profile of the hot gas and g′ is the total gravity of the system. The global dark energy density is 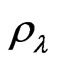= 7 × 10⁻³⁰ g·cm⁻³ [18]. This dark energy density contributes to the antigravity in the system. Since there are no MOND effects before recombination, no MOND effects should influence the CMB [7]. Therefore, the amount of dark energy should be the same for Newtonian and MOND limit. The major difference is the effect of the dark energy in MOND limit may be smaller than that in the Newtonian limit. Therefore, the anti-gravity in the MOND regime is

(3)

Since the total gravity can be written as, by using Equations (1)-(3), we have

(4)

where M is the total mass of the cluster. By using the gas model in clusters for large r, [19]. Therefore, from the above equation, we get

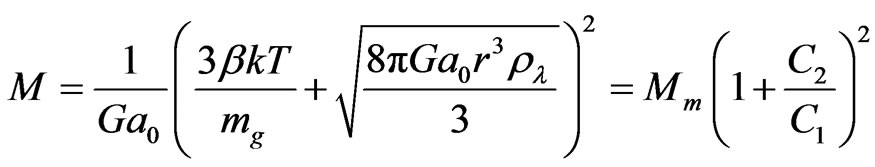(5)

where M_m ≈ 6 × 10¹² M_⊙(T/1 keV)² is the total cluster mass without dark energy in classical MOND [10], 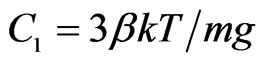and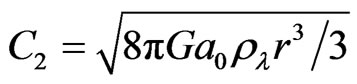. For a typical cluster, β = 0.66, T = 5 × 10⁷ K and r = 1.5 Mpc, C₂/C₁ ≈ 0.17. Therefore, the total cluster mass is 1.17² ≈ 1.4 times larger than the one calculated by the classical MOND. For larger clusters, the effect of dark energy will be much more significant. Therefore, the cluster mass probed from the hot gas by MOND is underestimated if we do not consider the dark energy. It means that more dark matter should exist in clusters.

In fact, observational data shows that the mass of hot gas can be fitted empirically by [20]

(6)

where M_g is the total mass of hot gas in a cluster. Therefore, the predicted cluster mass by the classical MOND is 3.5 times larger than the observed baryonic mass (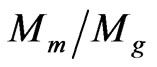≈ 3.5) [10]. Sanders (2007); Angus, Famaey and Buote (2008) propose that the existence of active or sterile neutrinos in clusters may account for the missing mass. Angus (2009) obtains a good fit to the CMB spectrum by assuming all non-baryonic matter is composed by the acitve and sterile neutrinos. The fitted cosmological density parameters of baryons and matter are Ω_bh² = 0.0024 and Ω_mh² = 0.117 respectively [7]. Therefore, we have 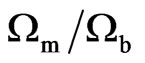≈ 5. This ratio is indeed larger than the ratio predicted by the classical MOND. Nevertheless, if we include the effect of dark energy by using the Equation (5) for a typical cluster, the ratio becomes 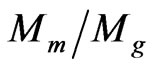= 1.17² 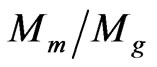≈ 4.8, which is very closed to the ratio obtained by the cosmological density parameters. Therefore, the calculated ratio of total matter to baryonic matter in clusters by using MOND matches the result of the CMB if we include the effect of dark energy.

3. Discussion and Conclusions

In this article, we consider the effect of dark energy in clusters. In the MOND regime, the contribution of the anti-gravity effect by dark energy density is significant to the total cluster mass calculation. The total cluster mass for a typical cluster can be 40% larger than the one calculated by the classical MOND. It represents a larger amount of dark matter should exist in clusters. Therefore, the existence of 2 eV active neutrinos in clusters is not enough to account for the missing mass. Since more massive active neutrinos (>2 eV) may violate the experimental bounds [10], the existence of sterile neutrinos are required for the explanation in MOND. On the other hand, the calculated total mass to baryonic mass ratio is consistent with the cosmological data from the CMB spectrum if we include the effect of dark energy.

Since the CDM scenario encounters many fundamental problems including the cusp and the missing satellite problem, the MOND together with the existence of sterile neutrino hot dark matter (HDM) is the only theory which can retain in the recent challenges. Since neutrinos contain mass, there should exist right-handed neutrinos which may indeed be the massive sterile neutrinos [21]. The existence of eV order sterile neutrinos can explain the missing mass in the clusters and our universe [7]. Also it can explain the recent analysis of the Miniboone experiment and get a good fit in the CMB spectrum [7, 15]. The free stremaing scale of the eVorder sterile neutrinos is λ∼Mpc [10], which can form structure in clusters and contribute to the total mass in clusters. Since the free streaming scale is larger than the size of a typical galaxy, no hot dark matter can form detectable structure within galaxies. As a result, the classical MOND alone is able to explain the rotation curves of galaxies without the help of HDM.

To conclude, the existence of dark energy can affect the calculated cluster mass by MOND significantly. Also, the MOND + HDM scenario may be one of the best theories to explain the dark matter problem in the future.

REFERENCES