Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21673,5 pages DOI:10.4236/jmp.2012.38090
The Quantum Oscillatory Modulated Potential—Part II
——The Stability of the Hydrogen Atom
Instituto de Física, Universidade Federal de Goiás, Goi^ania, Brasil
Email: wwolney@yahoo.com.br
Received April 25, 2012; revised May 24, 2012; accepted June 15, 2012
Keywords: Quantum Oscillator; Hydrogen Atom; Electron
ABSTRACT
The purpose of this work is to show the stability of the hydrogen atom with useing the Quantum Oscillatory Modulated Potential and the Heisenberg equations of motion, postulating that the electron in the hydrogen atom is behaving as a quantum harmonic oscillator. With the electron confined between two potential barriers, created by the new potential function, we are considering that at absolute temperature the power absorbed or emitted by the electron per unit of time can be used to determine the zero point energy of the oscillator. Assuming that electron is only exchanging energy with the nucleus of the atom we are making use of the operators of creation and annihilation of a photon to explain how the energy between the proton and the electron can be exchanged to keep the atom a stable system.
1. Introduction
In 1913, the Dane physicist Niels Bohr, to assure the stability of the atoms as a nuclear planetary model, such as proposed two years earlier, by the New Zealand physicist Ernest Rutherford, postulated the quantization of the angular momentum of the electrons when revolving the nuclei of the atoms. About twelve years later the Bohr theory was supplanted by the quantum mechanics, a new theory, independently formulated by Erwin Schroedinger and Werner Heisenberg [1,2]. Both theories have wider applications to more complex atomic systems. In the Schroedinger theory, the concept of orbit for the electron was ignored and its position around the nucleus was formulated in terms of probability density. In the application of the new quantum theory for the hydrogen atom, the question of the stability of the atom was set aside. However, we need to taken into consideration that an electron bound to the nucleus of the atom is always under the action of a central force field [3]. Therefore, whatever be its movement in the vicinity of the nucleus of the atoms, in someway, it needs to be accelerated and, according to the Classical Law of the Electrodynamics, losing energy by radiation [4]. Since the atoms are stable systems, this does not occur and the question of the stability of the atoms needs to be explained.
In this work we are proposing to solve the problem of the stability of the atoms, making use of the Quantum Oscillatory Modulated Potential1—QOMP. This potential was formulated to explain in different mathematical bases and concepts the interaction between the proton and the electron in the hydrogen atom. The new potential is represented by the formula
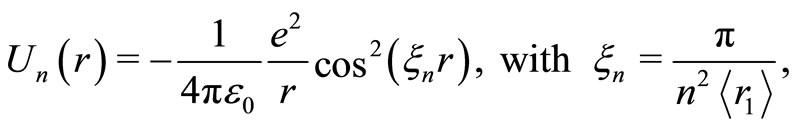 (1)
(1)
where the 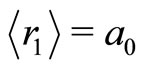 is the Bohr radius for the hydrogen atom. The potential
is the Bohr radius for the hydrogen atom. The potential  is quantized, oscillatory and presents potential wells and barriers, partially modulated by the Coulomb potential. As gradient of the new potential, the interaction force between the proton and the electron takes the form
is quantized, oscillatory and presents potential wells and barriers, partially modulated by the Coulomb potential. As gradient of the new potential, the interaction force between the proton and the electron takes the form
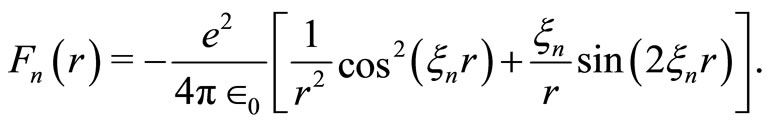 (2)
(2)
These forces have the form of wave packets around the nucleus of the atom. The Figure 1 shows the graphic of this interaction force between the proton and the electron in the hydrogen atom in its ground state. It displays positive and negative peaks and is null at the position more likely to be occupied by the electron. Let us observe that with the Coulomb potential, the interaction force between the proton and the electron is always attractive and never becomes null, except at infinite distance from the nucleus of the atom. With the use of the QOMP, it is shown that the interaction force at the equilibrium position 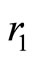 is null and the electron cannot be orbiting the nucleus of the atom as predicted by Bohr theory. Then, the most plausible movement of the electron is the radial, what makes the angular momentum of the electron be null. Thus, in its ground state, the electron must behaves like a harmonic oscillator, bouncing back and forth radially, confined by two potential barriers, making the electron to be accelerated towards the equilibrium position and, consequently, losing energy by radiation [4,5]. In the next section we will use the concept of the quantum harmonic oscillator to investigate the behavior of the oscillating electron inside the first quantum well produced by the new potential.
is null and the electron cannot be orbiting the nucleus of the atom as predicted by Bohr theory. Then, the most plausible movement of the electron is the radial, what makes the angular momentum of the electron be null. Thus, in its ground state, the electron must behaves like a harmonic oscillator, bouncing back and forth radially, confined by two potential barriers, making the electron to be accelerated towards the equilibrium position and, consequently, losing energy by radiation [4,5]. In the next section we will use the concept of the quantum harmonic oscillator to investigate the behavior of the oscillating electron inside the first quantum well produced by the new potential.
2. The Hydrogen Atom as a Quantum Harmonic Oscillator
Let us assume that the departure of first potential well from the potential of a harmonic oscillator is small. The origin of the quantum harmonic oscillator potential is taken at the bottom of the first potential well, at the position 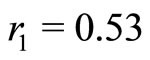 Å and nearly
Å and nearly 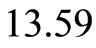 eV bellow the energy of the electron in the ground state. See Figure 2. Symbolically the movement of the electron inside the quantum well is represented by arrows as shown in the same figure. The Hamiltonian for the quantum harmonic oscillator may be written as [2]
eV bellow the energy of the electron in the ground state. See Figure 2. Symbolically the movement of the electron inside the quantum well is represented by arrows as shown in the same figure. The Hamiltonian for the quantum harmonic oscillator may be written as [2]
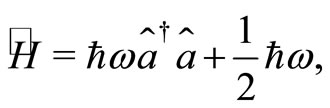 (3)
(3)
where 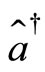 and
and 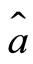 are, respectively, the operators of creation and annihilation of a photon (a quantum unit of energy
are, respectively, the operators of creation and annihilation of a photon (a quantum unit of energy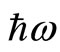 ). The term
). The term 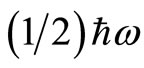 in the Hamiltonian operator represents the zero point energy, it is the minimum energy of the quantum harmonic oscillator. The operators for position
in the Hamiltonian operator represents the zero point energy, it is the minimum energy of the quantum harmonic oscillator. The operators for position  and momentum
and momentum  of the electron may be expressed in terms of the operators
of the electron may be expressed in terms of the operators 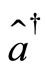 and
and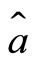 , written as
, written as
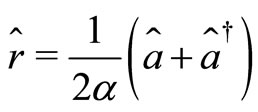 (4)
(4)
 (5)
(5)
where 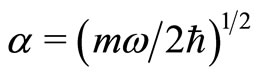 and
and 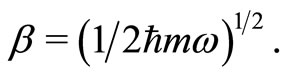 These operators when applied to the eingenstates
These operators when applied to the eingenstates  of the quantum harmonic oscillator, produce the following well known relations
of the quantum harmonic oscillator, produce the following well known relations
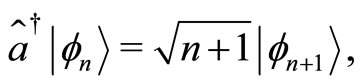 (6)
(6)
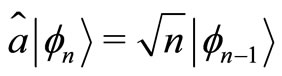 , (7)
, (7)
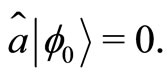 (8)
(8)
The eingenstates 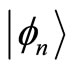 of the quantum harmonic oscillator are orthonormal. That is, they obey the condition
of the quantum harmonic oscillator are orthonormal. That is, they obey the condition
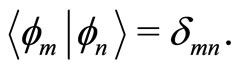
Moreover, 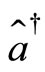 and
and 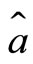 are not commuting operators, they satisfy the relation
are not commuting operators, they satisfy the relation
 (9)
(9)
what means that the kets 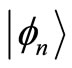 are not eigenstates of these two operators. That is, they cannot act simultaneously on the eingstates of the harmonic oscillator. As simple harmonic oscillator the binding energy of the electron in the atom in its ground state
are not eigenstates of these two operators. That is, they cannot act simultaneously on the eingstates of the harmonic oscillator. As simple harmonic oscillator the binding energy of the electron in the atom in its ground state 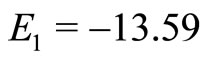 eV and can be totally kinetic at equilibrium position
eV and can be totally kinetic at equilibrium position  or totally potential at the classical turning points
or totally potential at the classical turning points 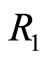 and
and 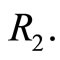 See Figure 2. According to Equations (3) and (8) the zero
See Figure 2. According to Equations (3) and (8) the zero
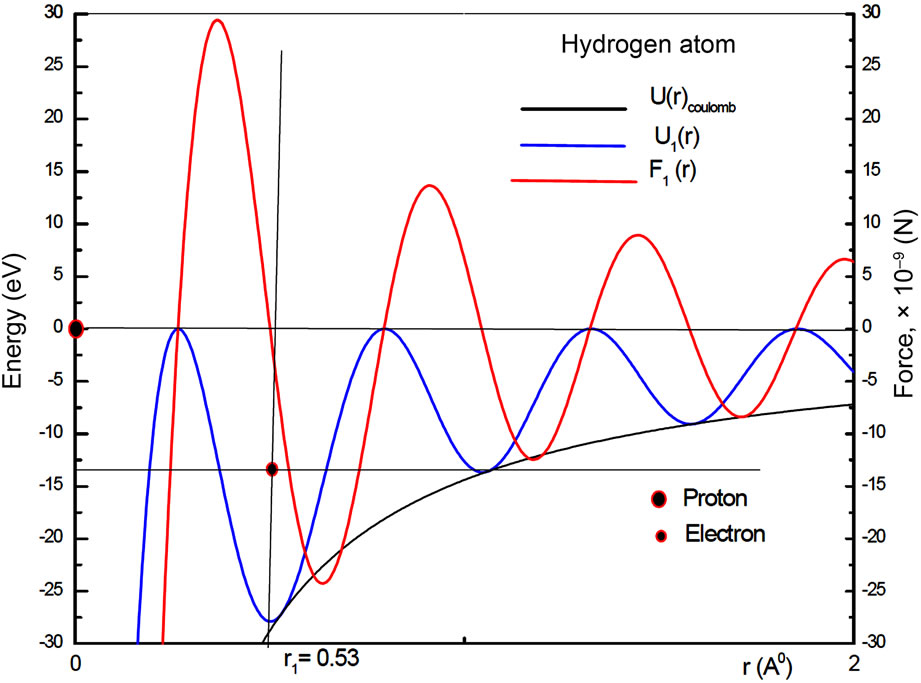
Figure 1. The coulomb potential U(r)Coul., the quantum oscillatory modulated potential U1(r) and electric oscillatory force F2(r) for the hydrogen atom in its ground state. The vertical line represents the position where the oscillatory force is null.

Figure 2. In the ground state of the hydrogen atom, the electron is oscillating, bouncing back and forth like a quantum harmonic oscillator. The positions R1 and R2 represent classical turning points.
point energy of the harmonic oscillator is given by the expectation value [2,6]
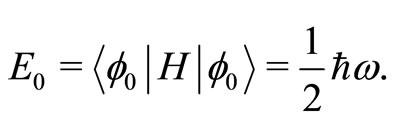 (10)
(10)
To determine the angular frequency  in Equation (10) and, consequently the zero point energy of the quantum harmonic oscillator, we will make the assumption, that in the ground state of the hydrogen atom, the amount of energy absorbed or emitted by the electron per unit of time, at absolute temperature,
in Equation (10) and, consequently the zero point energy of the quantum harmonic oscillator, we will make the assumption, that in the ground state of the hydrogen atom, the amount of energy absorbed or emitted by the electron per unit of time, at absolute temperature, 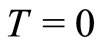 , can be expressed by a formula obtained by Silva and França [7,8] with the use of the stochastic electrodynamics. The power absorbed by the electron may be expressed by
, can be expressed by a formula obtained by Silva and França [7,8] with the use of the stochastic electrodynamics. The power absorbed by the electron may be expressed by
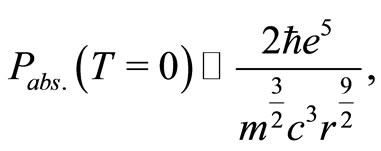 (11)
(11)
where 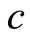 is the velocity of light. However, differently of Silva and França, that for deduction of Equation (11), assumed that the electron is orbiting the nucleus of the atom, as in Bohr theory, we are arguing that the electron is oscillating radially in the first potential well, with average distance equal to the radius of Bohr,
is the velocity of light. However, differently of Silva and França, that for deduction of Equation (11), assumed that the electron is orbiting the nucleus of the atom, as in Bohr theory, we are arguing that the electron is oscillating radially in the first potential well, with average distance equal to the radius of Bohr, 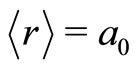 , as predicted by the QOMP.
, as predicted by the QOMP.
For the hydrogen atom, in its ground state, we are assuming that at absolute temperature, electron is only be able to exchange energy with the nucleus of the atom, with which it is interacting. This image is the analogue to two masses M and m, with  tied at the end of a spring, oscillating with an angular frequency
tied at the end of a spring, oscillating with an angular frequency  and exchanging energy between them. With the use of Equation (11), we can write,
and exchanging energy between them. With the use of Equation (11), we can write,
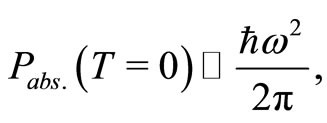 (12)
(12)
where  is the lowest angular frequency corresponding to the zero point energy of the quantum harmonic oscillator. From Equation (12) we have
is the lowest angular frequency corresponding to the zero point energy of the quantum harmonic oscillator. From Equation (12) we have
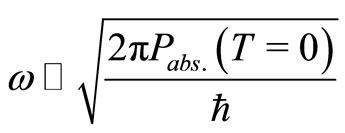 . (13)
. (13)
Considering that, at absolute temperature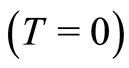 , the most probable position for the electron is
, the most probable position for the electron is 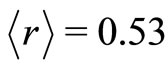 Å, from Equations (11) and (13) we can estimate the value of the angular frequency of the quantum harmonic oscillator in its lowest state. The predicted value is
Å, from Equations (11) and (13) we can estimate the value of the angular frequency of the quantum harmonic oscillator in its lowest state. The predicted value is 
 . Thus, the amount of energy absorbed or emitted by the electron when moving between two adjacent quantum states
. Thus, the amount of energy absorbed or emitted by the electron when moving between two adjacent quantum states 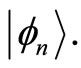 and
and 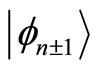 is
is 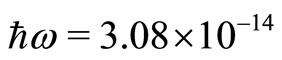 eV. A photon with energy of this magnitude would be very difficult to be experimentally observed. The zero point energy of the quantum oscillator is
eV. A photon with energy of this magnitude would be very difficult to be experimentally observed. The zero point energy of the quantum oscillator is  eV, sometimes called the vacuum state energy. With the electron oscillating between the classical turning points
eV, sometimes called the vacuum state energy. With the electron oscillating between the classical turning points 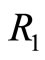 and
and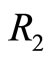 , corresponds to the quantum harmonic oscillator be in an excited state
, corresponds to the quantum harmonic oscillator be in an excited state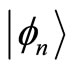 , with energy
, with energy 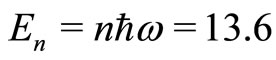 eV. Thus, the number of eigenstates
eV. Thus, the number of eigenstates 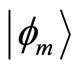 existing between the energy
existing between the energy 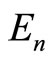 and
and 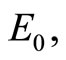 the lowest energy level is
the lowest energy level is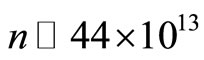 . This very large number of eigenstates is a consequence of the very small magnitude of quantum unit of energy exchanged between the proton and the electron in the atom, in each quantum transition. In the next section we will consider the time evolution of the electron in the hydrogen atom.
. This very large number of eigenstates is a consequence of the very small magnitude of quantum unit of energy exchanged between the proton and the electron in the atom, in each quantum transition. In the next section we will consider the time evolution of the electron in the hydrogen atom.
3. The Time Evolution of the Electron in the Hydrogen Atom
The time evolution of the electron as a quantum harmonic oscillator can be investigate with the use the Heinsenberg equations of motion for the operators  and
and 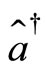 given by [2]
given by [2]
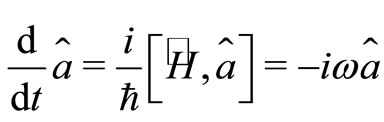 (14)
(14)
 (15)
(15)
whose solution may written as
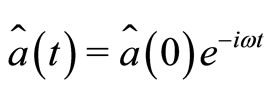 (16)
(16)
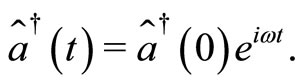 (17)
(17)
Thus, the operators of position 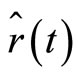 and momentum
and momentum 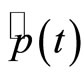 , given by Equations (4) and (5) take the form
, given by Equations (4) and (5) take the form
 (18)
(18)
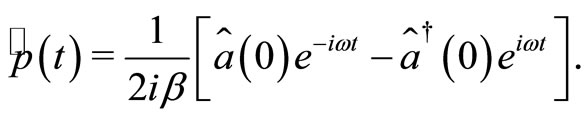 (19)
(19)
We need to observe that the expectation values of 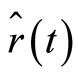 and
and 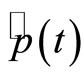 will not oscillate with angular frequency
will not oscillate with angular frequency , because for any well defined energy eigenstates, characterized by
, because for any well defined energy eigenstates, characterized by 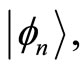 the expectation values
the expectation values 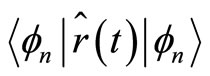 and
and  vanish. In order to see more clearly the action of the operators
vanish. In order to see more clearly the action of the operators  and
and , let us consider a linear combination of two adjacent energy eigenstates of the oscillator, written as
, let us consider a linear combination of two adjacent energy eigenstates of the oscillator, written as
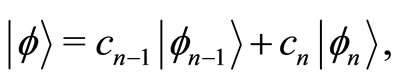 (20)
(20)
where 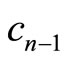 and
and 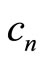 are complex numbers [9]. With the use of Equaitons (8), (9), (18) and (19), we obtain the time dependence for the expectation values of the operators
are complex numbers [9]. With the use of Equaitons (8), (9), (18) and (19), we obtain the time dependence for the expectation values of the operators 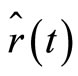 and
and 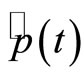 written as
written as
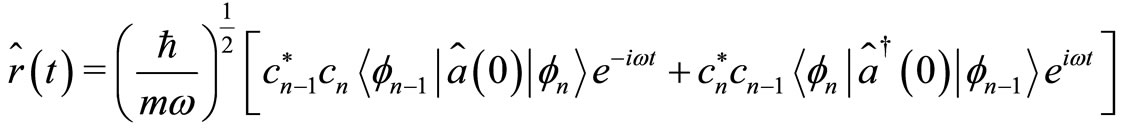 (21)
(21)
 (22)
(22)
where, according to Equations (6) and (7), the first braket in Equation (21) represents the probability amplitude for a transition from the eigenstate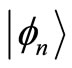 , with energy
, with energy  to the eigenstate
to the eigenstate 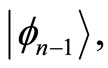 and energy
and energy 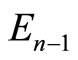 with the annihilation of a photon. The second braket represents the probability amplitude for a transition from the eigenstate
with the annihilation of a photon. The second braket represents the probability amplitude for a transition from the eigenstate 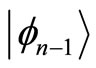 with energy
with energy  to the eigenstate
to the eigenstate  with energy
with energy 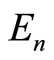 creating a photon with the same energy. The same interpretation is given to Equation (22). These two equations tell us that for an isolated atom, the electron is exchanging energy with the particle with which it is interacting, the nucleus of the atom, losing and receiving a quantum unit of energy
creating a photon with the same energy. The same interpretation is given to Equation (22). These two equations tell us that for an isolated atom, the electron is exchanging energy with the particle with which it is interacting, the nucleus of the atom, losing and receiving a quantum unit of energy  with magnitude as calculated previously. The constant exchange of energy between the proton and electron explain the stability of the atom. Besides its small energy magnitude of the photon, the exchange of energy between the two particles cannot be observed because it is an internal affair of the atom. According to the interpretation given above, the time required for the electron to make one cycle oscillation between the classical turning points
with magnitude as calculated previously. The constant exchange of energy between the proton and electron explain the stability of the atom. Besides its small energy magnitude of the photon, the exchange of energy between the two particles cannot be observed because it is an internal affair of the atom. According to the interpretation given above, the time required for the electron to make one cycle oscillation between the classical turning points  and
and 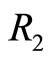 is 4 times larger than the time required for the electron to span n eigenstates
is 4 times larger than the time required for the electron to span n eigenstates 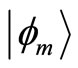 between highest and the lowest energy levels allowed for the quantum oscillator, emitting and receiving a quantum unit of energy
between highest and the lowest energy levels allowed for the quantum oscillator, emitting and receiving a quantum unit of energy 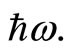
Another way to see the time evolution of the electron in one cycle of oscillation as described above, is to make use of the Equations (4) and (5), to obtain [9]
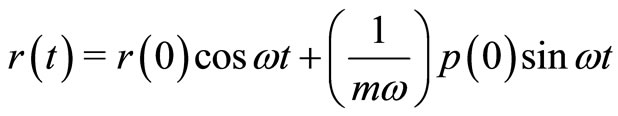 (23)
(23)
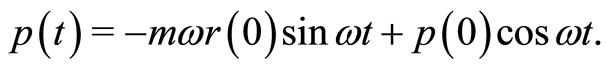 (24)
(24)
These two equations present a close resemblance to the classical equations for a simple harmonic oscillator. We can see that the operators 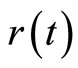 and
and 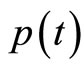 oscillate just like their classic analogues where, in a cycle of oscillation, the energy of the electron is exchanged between the kinetic energy
oscillate just like their classic analogues where, in a cycle of oscillation, the energy of the electron is exchanged between the kinetic energy 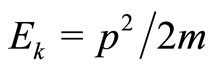 and the potential energy
and the potential energy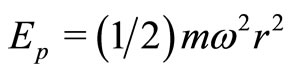 , according to the sequence
, according to the sequence 
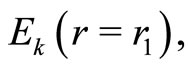 making one complete cycle of oscillation. Thus, according to this model, we argue that the mechanism responsible for the stability of the atom is the exchange of energy between the electron and the proton, mathematically represented by the action of the operators of creation
making one complete cycle of oscillation. Thus, according to this model, we argue that the mechanism responsible for the stability of the atom is the exchange of energy between the electron and the proton, mathematically represented by the action of the operators of creation 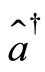 and the operator o annihilation
and the operator o annihilation 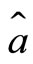 acting on the eigenstates, creating and annihilating a photon of energy
acting on the eigenstates, creating and annihilating a photon of energy 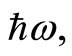 in such a way that the loss of energy by the atom is zero. Base on the Quantum Oscillatory Modulated Potential, for the first time, as far as we know, we have an idea of the energy magnitude of the empty space (the so-called vacuum state energy), and how the electron and the proton in the hydrogen atom are exchanging energy, to keep the atom a stable system.
in such a way that the loss of energy by the atom is zero. Base on the Quantum Oscillatory Modulated Potential, for the first time, as far as we know, we have an idea of the energy magnitude of the empty space (the so-called vacuum state energy), and how the electron and the proton in the hydrogen atom are exchanging energy, to keep the atom a stable system.
4. Conclusion
The use of Quantum Oscillatory Modulate Potential for describing the interaction between the proton and the electron in the hydrogen atom, lead us to conclude that inside potential well created around the nucleus of the atom, the electron behaves approximately as a quantum harmonic oscillator, oscillating radially bouncing back and forth, confined by two potential barriers. Assuming that in the ground state of the atom, the amount of energy absorbed or emitted by the electron per unit of time, at absolute temperature, 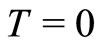 , can be calculated by a formula obtained with the base in the stochastic electrodynamics, it was possible to determine the zero point energy of the of the oscillator, and consequently, the quantum unit of energy, a photon of very small magnitude, that the electron is exchanging with the nucleus of the atom during one cycle of oscillation. We are concluding that the constant exchange of energy between the proton and the electron through the emission and absorption of photon, mathematically represented by the action of the operators of creation and annihilation, is the mechanism responsible for the stability of the atoms and consequently, for its own existence.
, can be calculated by a formula obtained with the base in the stochastic electrodynamics, it was possible to determine the zero point energy of the of the oscillator, and consequently, the quantum unit of energy, a photon of very small magnitude, that the electron is exchanging with the nucleus of the atom during one cycle of oscillation. We are concluding that the constant exchange of energy between the proton and the electron through the emission and absorption of photon, mathematically represented by the action of the operators of creation and annihilation, is the mechanism responsible for the stability of the atoms and consequently, for its own existence.
REFERENCES
- D. A. McQuarrie, “Quantum Chemistry,” Universe Science Books, Margate, 1983.
- W. W. Filho, “Mecânica Quântica,” Editora da Universidade Federal de Goiás, Goiânia, 2002.
- J. S. Towsend, “A Modern Approach to Quantum Mechanics,” McGraw Hill International Edition, 1992.
- W. Hauser, “Introduction to the Principles of Electromagnetism,” Addison Wesley Publishing Company Inc., Boston, 1986.
- P. A. Tipler, “Modern Physics,” Worh Publishers Inc., New York, 1977.
- R. M. Eisberg, “Fundamentals of Modern Physics,” John Wesley & Sons Inc., New York, 1961.
- R. da Silva and H. Prança, “A Estabilidade do Átomo de Hidrogênio Segundo a Eletrodinâmica Estocástica,” Revista Brasileira de Ensino de Física, Vol. 24, No. 1, 2002, pp. 1-13.
- E. Merzbacher, “Quantum Mechanics,” John Willey & Sons Inc., New York, 1976.
- J. J. Sakurai, “Modern Quantum Mechanics,” The Benjamin Cummings, Publishing Company Inc., Menlo Park, 1985.
NOTES
1This potential was formulated in first part of the series of work.

