Journal of Modern Physics
Vol.3 No.6(2012), Article ID:20097,20 pages DOI:10.4236/jmp.2012.36062
The Definition of Universal Momentum Operator of Quantum Mechanics and the Essence of Micro-Particle’s Spin
——To Reveal the Real Reason That the Bell Inequality Is Not Supported by Experiments
Institute of Innovative Physics in Fuzhou, Department of Physics, Fuzhou University, Fuzhou, China
Email: ycwlyjs@yeah.net, yupingpingyu@yahoo.com
Received March 21, 2012; revised April 12, 2012; accepted April 25, 2012
Keywords: Quantum mechanics; Universal momentum operator; Universal angle momentum operator; Hermitian operator; Self-adjoint operator; Spin; Bell inequality; Hidden variables
ABSTRACT
The definition of momentum operator in quantum mechanics has some foundational problems and needs to be improved. For example, the results are different in general by using momentum operator and kinetic operator to calculate microparticle’s kinetic energy. In the curved coordinate systems, momentum operators can not be defined properly. When momentum operator is acted on non-eigen wave functions in coordinate space, the resulting non-eigen values are complex numbers in general. In this case, momentum operator is not the Hermitian operator again. The average values of momentum operator are complex numbers unless they are zero. The same problems exist for angle momentum operator. Universal momentum operator is proposed in this paper. Based on it, all problems above can be solved well. The logical foundation of quantum mechanics becomes more complete and the EPY momentum paradox can be eliminated thoroughly. By considering the fact that there exist a difference between the theoretical value and the real value of momentum, the concepts of auxiliary momentum and auxiliary angle momentum are introduced. The relation between auxiliary angle momentum and spin is deduced and the essence of micro-particle’s spin is revealed. In this way, the fact that spin gyro-magnetic ratio is two times of orbit gyro-magnetic ratio, as well as why the electrons of ground state without obit angle momentum do not fall into atomic nuclear can be explained well. The real reason that the Bell inequality is not supported by experiments is revealed, which has nothing to do with whether or not hidden variables exist, as well as whether or not locality is violated in microcosmic processes.
1. Introduction
Since quantum mechanics was established, its correctness has been well verified. But there exists serious controversy on its physical significance. Many people believe that quantum mechanics has not been well explained up to now days. However, the mathematical structure of quantum mechanics is commonly considered complete and perfect. It seems difficult to add additional things to it. Is it true? It is pointed out in this paper that the definition of momentum operator of quantum mechanics has several problems so that it should be improved.
In this paper, we first prove that using kinetic energy operator and momentum operator to calculate microparticle’s kinetic energies, the results are different. That is to say, kinetic energy operator and momentum Operator are not one to one correspondence. Secondly, in the curved coordinate system, momentum operator can not be defined well though we can define kinetic energy operator well. That is to say, except in the rectangular coordinates, the definition of momentum operator is still an unsolved problem in quantum mechanics.
With operators of quantum mechanics acting on the eigen functions, we obtain real eigen values. However, if operators act on the non-eigen functions, the results are complex numbers in general. We call theses complex numbers as non-eigen values. For non-eigen functions, the operators of quantum mechanics are not the Hermitian operators. In general, the average values of operators on non-eigen functions are complex number, unless they are zero.
Because the non-eigen values of complex numbers are meaningless in physics, the non-eigen functions have to be developed into the sum of the eigen functions of operators or the superposition of wave functions. The eigen function of momentum operator is the wave function of free particle. Hence, a very fundamental question is raised. We have to consider a non-free particle, for example an electron in the ground state of hydrogen, as the sum of infinite numbers of free electrons with different momentums. This result is difficult in constructing a physical image, thought it is legal in mathematics. Besides, it violates the Pauli’s exclusion principle. It is difficult for us to use it re-establishing energy levels and spectrum structure of hydrogen atoms.
Besides, some operators of quantum mechanics have no proper eigen functions, for example, angle momentum operator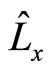 ,
, 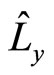 and
and 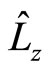 in rectangular coordinate system. We can not develop arbitrary functions into the sum of their eigen functions. By acting them on arbitrary functions directly, we always obtain complex numbers. Can we say they are meaningless?
in rectangular coordinate system. We can not develop arbitrary functions into the sum of their eigen functions. By acting them on arbitrary functions directly, we always obtain complex numbers. Can we say they are meaningless?
The descriptions of quantum mechanics are independent on representations. In momentum representation, the positions of momentum operator and coordinate can be exchanged with each other. It is proved that when the non-eigen wave functions in coordinate space are transformed in momentum space for description, the problems of complex non-eigen value and complex average value of coordinate operator occurs, though the problem of complex non-eigen value of momentum operator disappear.
In addition, there exists a famous problem of the EYP momentum paradox in quantum mechanics [1-3]. Because it can not be solved well, someone even thought that the logical foundation of quantum mechanics was inconsistent.
Because angle momentum operator is the vector product of coordinate operator and momentum operator, the problem also exists in the definition of angle momentum operator. For example, we can not define angle momentum operator in curved coordinate system well at present. The physical image and essence of micro-particle’s spin is still unclear at present.
Therefore, the momentum operator of quantum mechanics can not represent the real momentums of microparticles. It needs to be improved. The concept of universal momentum operator is proposed to solve theses problems in this paper.
Using universal momentum operator and kinetic operator to calculate the kinetic energy, we can explain the problem of inconsistency as mentioned before. In curved coordinate system, we can define momentum operator rationally. When universal momentum operator is acted on arbitrary non-eigen wave functions, the non-eigen values are real numbers. In coordinate space, the average value of universal momentum is real number. The EYP momentum paradox can also be resolved thoroughly.
After universal momentum operator is defined, we can define universal angle momentum operator. Because there is a difference between calculated value and real momentum value, the concepts of auxiliary momentum and auxiliary angle momentum are introduced. The relation between auxiliary angle momentum and spin is revealed. It is proved that spin is related to the supplemental angle momentum of micro-particle which orbit angel momentum operator can not describe. The fact that spin gyromagnetic ratio is two times of orbit gyro-magnetic ratio, as well as why the electron of ground state do not fall into atomic nuclear without orbit angle momentum can be explained well.
By the clarification of spin’s essence, we can understand real reason why the Bell inequality is not supported by experiments. The misunderstanding of spin’s projection leads to the Bell inequality. No any real angle momentum can have same projections at different directions in real physical space. The formula 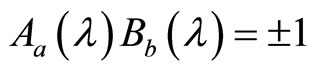 does not hold in the deduction process of the Bell inequality. The result that the Bell inequality is not supported by experiments has nothing to do with whether or not hidden variables exist.
does not hold in the deduction process of the Bell inequality. The result that the Bell inequality is not supported by experiments has nothing to do with whether or not hidden variables exist.
2. The Necessity and Possibility to Introduce Universal Momentum Operator in Quantum Mechanics
2.1. Inconsistency in Calculating Kinetic Energy Using Momentum and Kinetic Operators
The Hermitian operators are used to represent physical quantities in quantum mechanics. The result of Hermitian operator acting on eigen function is a real constant. Momentum operator and its eigen function are
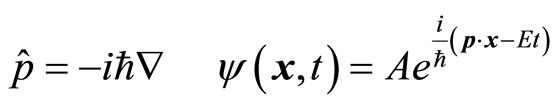 (1)
(1)
We have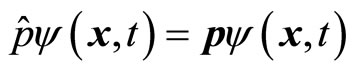 . The momentum
. The momentum  is a constant. However, more common situation is that wave functions are not the eigin functions of operators. In this case, we have
is a constant. However, more common situation is that wave functions are not the eigin functions of operators. In this case, we have
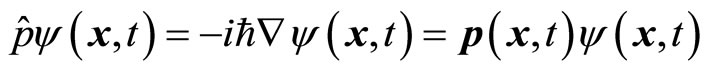 (2)
(2)
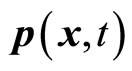 is a constant and we call it as the non-eigen value of momentum operator. If
is a constant and we call it as the non-eigen value of momentum operator. If 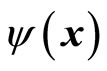 describes a single particle, according to definition,
describes a single particle, according to definition, 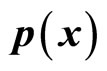 should represent the momentum of particle. Because momentum is the function of coordinate, is it consistent with the uncertainty relation? Or is the function form of
should represent the momentum of particle. Because momentum is the function of coordinate, is it consistent with the uncertainty relation? Or is the function form of 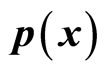 meaningful? This problem involves the understanding of real meaning of the uncertainty relation. We will discuss it in the end of this section.
meaningful? This problem involves the understanding of real meaning of the uncertainty relation. We will discuss it in the end of this section.
Because (2) is only a calculation formula of mathematics and the definitions of operator and wave function are alright, we should consider it is effective. We prove in this section that the results are different by using momentum operator and kinetic energy operator to calculate the kinetic energies of micro-particles. Taking ground state wave functions of hydrogen atom 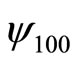 and linear harmonic oscillator
and linear harmonic oscillator 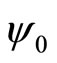 as examples, we have
as examples, we have
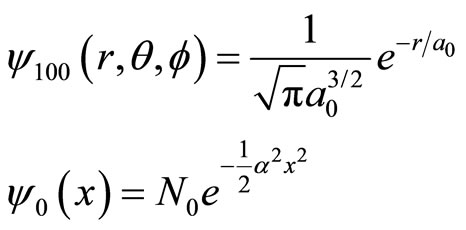 (3)
(3)
Here 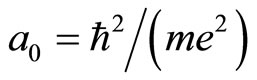 and
and 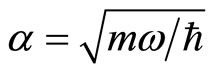 in which
in which 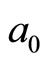 is the Bohr first orbit radius of hydrogen atom and
is the Bohr first orbit radius of hydrogen atom and 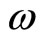 is the angle frequency of harmonic oscillator. When momentum operator is acted on
is the angle frequency of harmonic oscillator. When momentum operator is acted on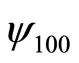 , we get
, we get
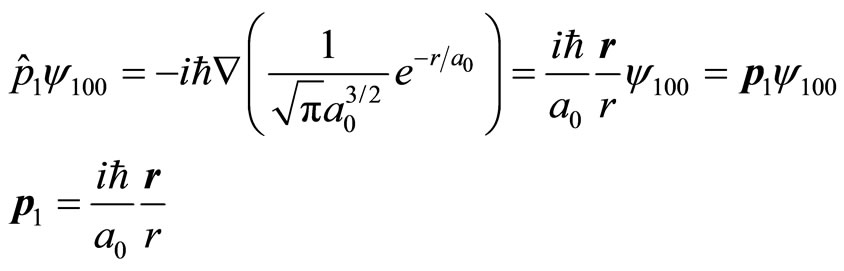 (4)
(4)
It is obvious that 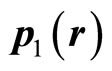 can not be the momentum of electron in ground state hydrogen atom. Despite
can not be the momentum of electron in ground state hydrogen atom. Despite 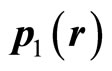 is an imaginary number, if it is electron’s momentum, the kinetic energy should be
is an imaginary number, if it is electron’s momentum, the kinetic energy should be
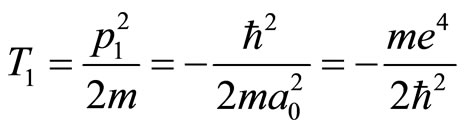 (5)
(5)
It indicates that kinetic energy is a negative number. Of cause, this is impossible. If kinetic operator is acted on the wave function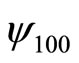 , we obtain
, we obtain
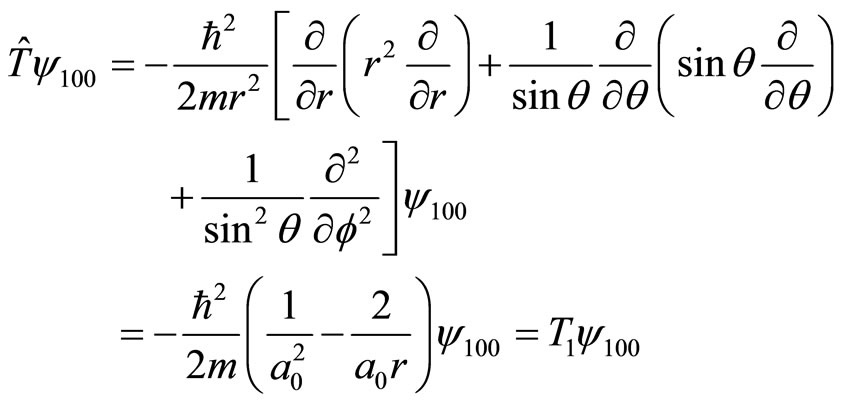 (6)
(6)
Therefore, the kinetic energy of electron in ground state hydrogen atom is
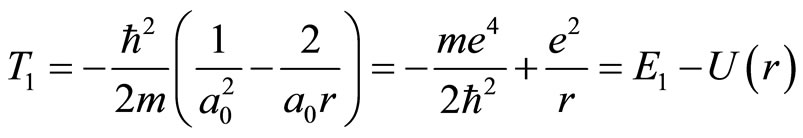 (7)
(7)
(7) is obviously different from (5). (7) is just the formula of energy conservation, in which 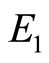 is the total energy of ground state electron and
is the total energy of ground state electron and 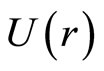 is potential energy. According to (5), we have
is potential energy. According to (5), we have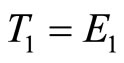 , i.e., electron’s kinetic is equal to its total energy, so (5) is wrong.
, i.e., electron’s kinetic is equal to its total energy, so (5) is wrong.
If momentum operator is acted on the wave function 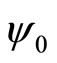 of linear harmonic oscillator, we obtain
of linear harmonic oscillator, we obtain
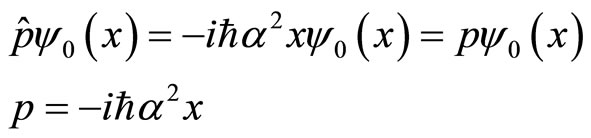 (8)
(8)
Momentum 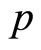 is also an imaginary number. Based on it, particle’s kinetic energy is
is also an imaginary number. Based on it, particle’s kinetic energy is
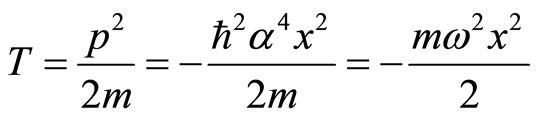 (9)
(9)
It means that particle’s kinetic energy is a negative number which can not be true. Acting kinetic operator on it, we have
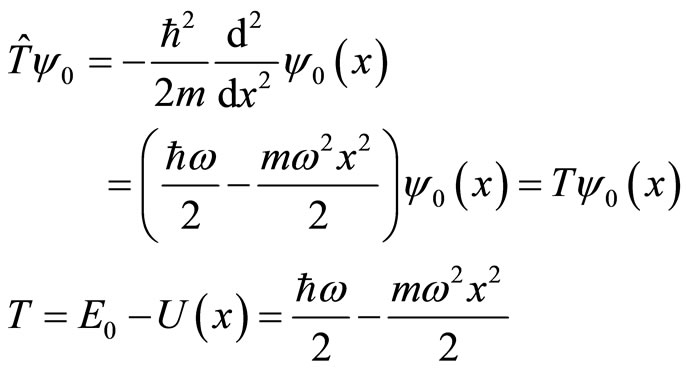 (10)
(10)
Here 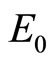 is the energy of ground state harmonic oscillator and
is the energy of ground state harmonic oscillator and 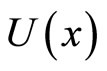 is potential energy. It is obvious that the calculating results of two methods are different. According to (9), we have
is potential energy. It is obvious that the calculating results of two methods are different. According to (9), we have 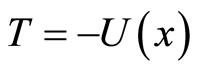 which is certainly wrong. In fact, this problem exists commonly in quantum mechanics. Kinetic operator and momentum operator do not have one-to-one correspondence, so that we can not determine the non-eigen values of momentum operator uniquely. Because kinetic operator is aright, we have to improve momentum operator to make it consistent with kinetic operator.
which is certainly wrong. In fact, this problem exists commonly in quantum mechanics. Kinetic operator and momentum operator do not have one-to-one correspondence, so that we can not determine the non-eigen values of momentum operator uniquely. Because kinetic operator is aright, we have to improve momentum operator to make it consistent with kinetic operator.
2.2. The Difficulty to Define Momentum Operator in Curved Coordinate System
In the current quantum mechanics, the definition of momentum operator in curved coordinate system is an unsolved problem [4]. Several definitions were proposed, but none of them is proper. If we claim that three partial quantities of momentum operator are commutative each other, the definition should be
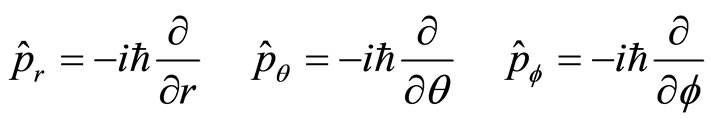 (11)
(11)
However, it is easy to prove that 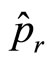 and
and 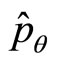 are not the Hermitian operators. Their non-eigen values are imaginary numbers in general. Most fatal is that we can not construct correct kinetic operator based on (11). In classical mechanics, the Hamiltonian of free particles in spherical coordinate system is
are not the Hermitian operators. Their non-eigen values are imaginary numbers in general. Most fatal is that we can not construct correct kinetic operator based on (11). In classical mechanics, the Hamiltonian of free particles in spherical coordinate system is
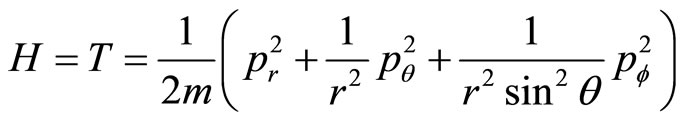 (12)
(12)
According to the correspondence principle between classical mechanics and quantum mechanics, by considering the definition (11), the kinetic operator of quantum mechanics is
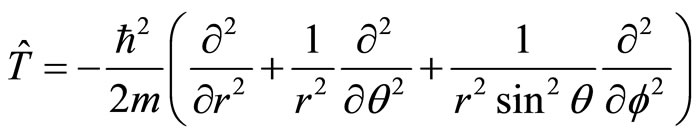 (13)
(13)
However, the kinetic operator of quantum mechanics in spherical reference system is actually
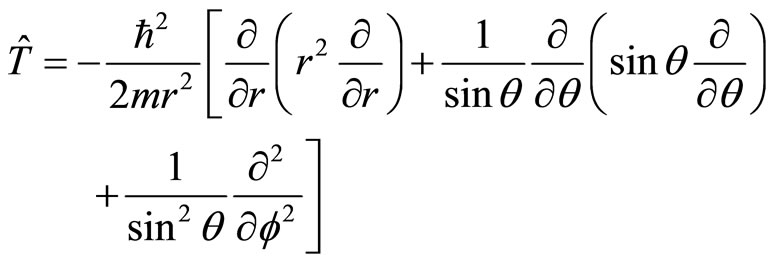 (14)
(14)
(13) and (14) are obviously different. Another definition of momentum operator is [5]
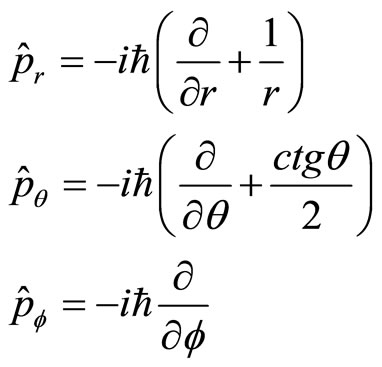 (15)
(15)
Substitute (15) in (12), we get
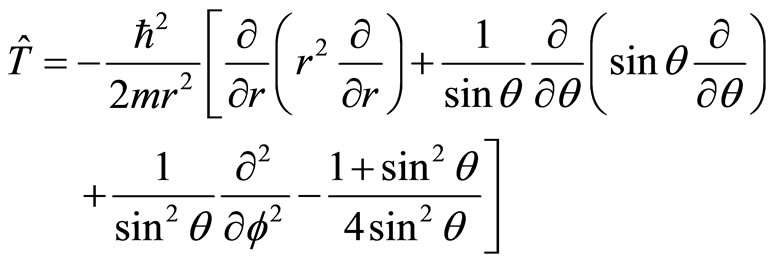 (16)
(16)
We see that (16) has one item more than (14), so (15) is improper too.
The covariant differential operator  in differential geometry was also suggested to define momentum operator in the curved coordinate reference system [6]. The action forms of operator
in differential geometry was also suggested to define momentum operator in the curved coordinate reference system [6]. The action forms of operator  on scalar
on scalar 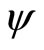 and vector
and vector 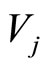 are individually
are individually
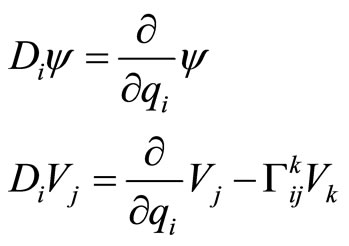 (17)
(17)
By considering the metric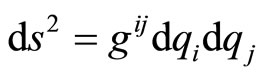 , we have
, we have
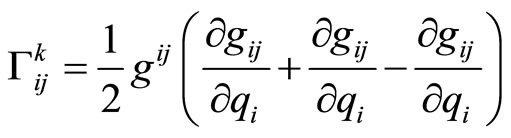 (18)
(18)
According to this definition, the kinetic operator in curved coordinate reference system can be written as
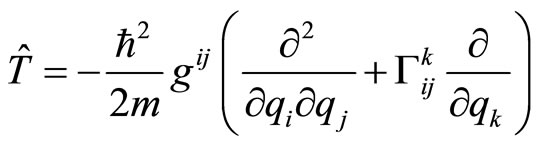 (19)
(19)
In spherical coordinate reference system, (19) is just (14). But this result was also criticized to have inconsistent for scalar and vector fields [7]. Meanwhile, according to (17), the result of 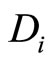 acting on scalar field is (15). Therefore, the non-eigen values and average values of operators
acting on scalar field is (15). Therefore, the non-eigen values and average values of operators  and
and 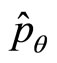 may still be complex numbers. All problems existing in the Descartes coordinate system would appear in the spherical coordinate system.
may still be complex numbers. All problems existing in the Descartes coordinate system would appear in the spherical coordinate system.
2.3. The Problems of Complex Number Non-Eigen Values of Momentum Operator
The Hermitian operators are used to describe physical quantities in quantum mechanics. The eigen values of the Hermitian operators are real numbers. But the premise is that the operators should be acted on eigen wave functions. However, we have seen many situations in quantum mechanics that wave functions are not the eigen functions of operators. For example, only the wave function of free particle is the eigen function of momentum operator. All other non-free particle’s functions are not the eigen function of momentum operator. In the coordinate space, when momentum operator is acted on noneigen functions, the obtained result, called as non-eigen values, are complex numbers in general. The average values of momentum operator in coordinate space are also complex numbers. These results are irrational and can not be accepted in physics, unless the average values are zero.
Let both 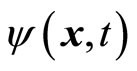 and
and 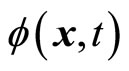 be arbitrary wave functions in coordinate spaces, according to the definition of quantum mechanics, if
be arbitrary wave functions in coordinate spaces, according to the definition of quantum mechanics, if 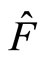 satisfies following relation
satisfies following relation
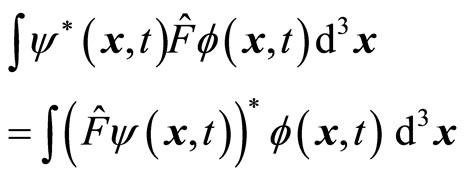 (20)
(20)
we call it the Hermitian operator. The eigen equation of the Hermitian operator is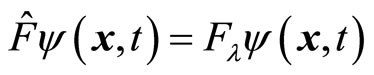 . It is easy to prove that the eigen value
. It is easy to prove that the eigen value 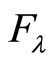 is a real constant We have
is a real constant We have
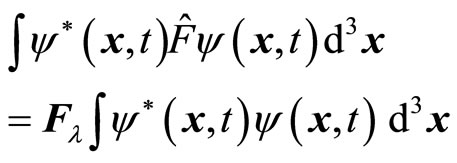 (21)
(21)
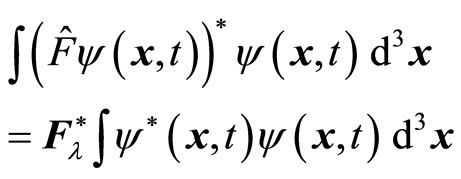 (22)
(22)
By considering (20), we get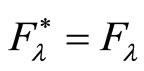 , i.e.,
, i.e., 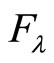 is a real number. In this case, the average value
is a real number. In this case, the average value 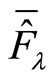 of operator is also a real number. We have
of operator is also a real number. We have
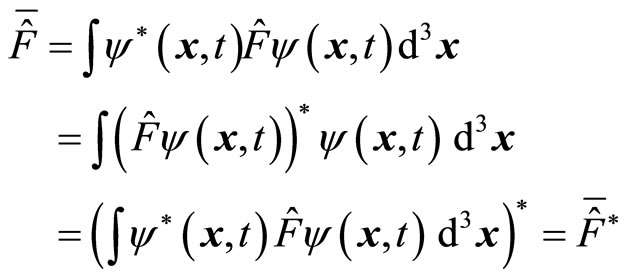 (23)
(23)
Suppose the action result of operator on the non-eigen function is
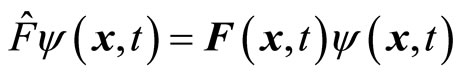 (24)
(24)
We call it as the non-eigen equation of operator 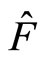 and
and 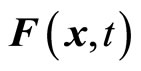 as the non-eigen value of operator. It is easy to prove that if wave function is not eigen function of operator, non-eigen value
as the non-eigen value of operator. It is easy to prove that if wave function is not eigen function of operator, non-eigen value 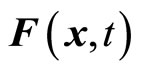 may be a complex number. In this case, operator will no longer be Hermitian. We have
may be a complex number. In this case, operator will no longer be Hermitian. We have
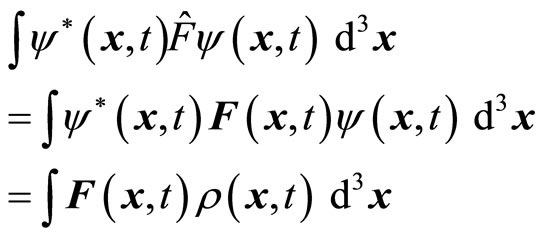 (25)
(25)
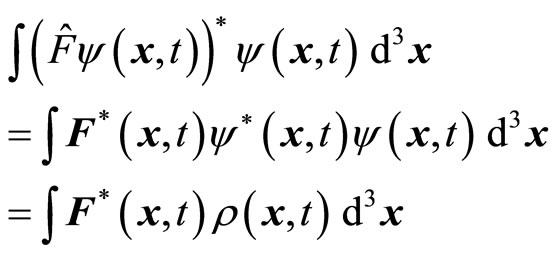 (26)
(26)
In which the probability density 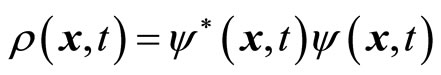 is a real number. Obviously, if
is a real number. Obviously, if 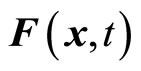 is a complex number, (25) and (26) are not equal to each other, so that (20) can not be satisfied. So
is a complex number, (25) and (26) are not equal to each other, so that (20) can not be satisfied. So 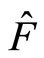 is not the Hermitian operator. Because
is not the Hermitian operator. Because 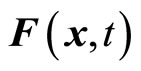 is a complex number, the average value
is a complex number, the average value
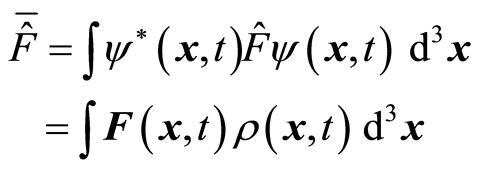 (27)
(27)
is also a complex number too. Because the average value of operator in quantum mechanics is measurable quantity, complex average value is meaningless in physics, unless it is equal to zero.
Let’s discuss the average values of momentum operator in momentum space. The wave functions 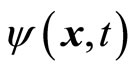 in coordinate space and
in coordinate space and 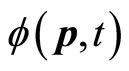 in momentum space satisfies following Fourier transformation
in momentum space satisfies following Fourier transformation
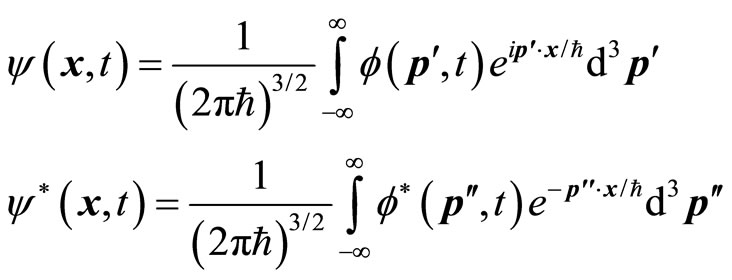 (28)
(28)
The Fourier transformation and its inverse transformation of non-eigen value of operator are
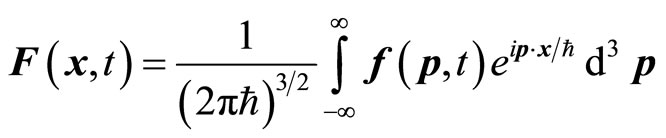 (29)
(29)
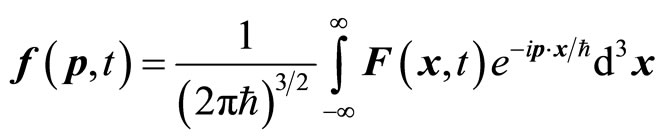 (30)
(30)
Substitute formulas above in (27), we obtain the average value of operator on non-eigen function in momentum space.
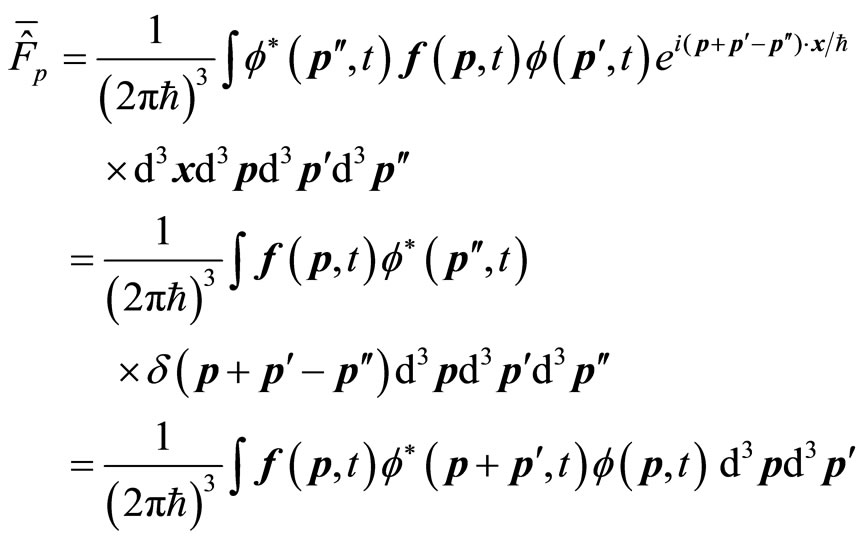 (31)
(31)
If  is a complex number,
is a complex number,  is also a complex number too. Therefore, similar to the situation in coordinate space, the average values of momentum operator in momentum space is also a complex number which is meaningless in physics.
is also a complex number too. Therefore, similar to the situation in coordinate space, the average values of momentum operator in momentum space is also a complex number which is meaningless in physics.
2.4. The Problems of Complex Values of Coordinate Operator in Momentum Space
On the other hand, the positions of coordinate and momentum exchanges each other when we describe physical processes in momentum space. It is proved below that in momentum space, the problem of imaginary non-eigen value of momentum operator disappears, but the problem of imaginary non-eigen value of coordinate operator emerges. In momentum space, coordinate operator becomes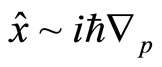 . When it is acted on the wave function in momentum space, we have
. When it is acted on the wave function in momentum space, we have
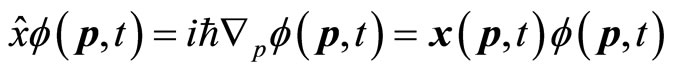 (32)
(32)
Similar to non-eigen value of momentum operator in coordinate space, 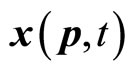 is a complex number in general. So the average value of coordinate operator in momentum space is a complex number. We have
is a complex number in general. So the average value of coordinate operator in momentum space is a complex number. We have
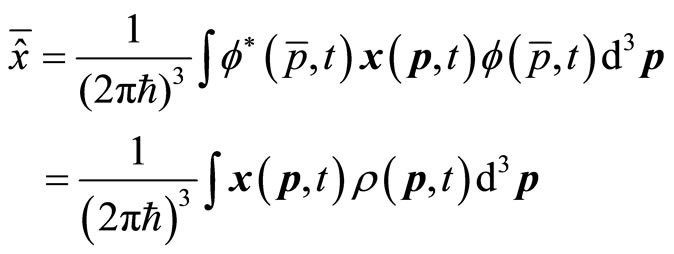 (33)
(33)
Here 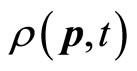 is a real number. However, in coordinate space, the average value of coordinate operator is a real number. The problem of imaginary average value is transformed from coordinate space to momentum space. The problem exists still, unless (33) is equal to zero.
is a real number. However, in coordinate space, the average value of coordinate operator is a real number. The problem of imaginary average value is transformed from coordinate space to momentum space. The problem exists still, unless (33) is equal to zero.
All of these problems indicate that the definition of momentum operator in quantum mechanics should be revised. The revised momentum operator should have real non-eigen values. The average values of momentum operator and coordinate operator should be real numbers no matter whether in coordinate representation or in momentum representation. Using momentum operator and kinetic operator to calculate the kinetic energies of micro-particles, the results should be consistent. If they are not, we should have reasonable explanation. Only when these are done, we can say that the definition of momentum operator is complete.
As mentioned before, when the non-eigen values of operator are complex numbers, the operator is not the Hermitian operator any more. In fact, someone had seen this problem and demanded that the operators in quantum mechanics should be self-adjoint operators [8]. In fact, in his famous book “the principles of quantum mechanics”, Dirac only used real operator, instead of the Hermitian operator. From the angle of mathematics, the relation between the self-adjoint operator and the Hermitian operator is subtle. We do not discuss it in this paper. From the angle of physics, self-adjoint operator can be considered as one which has the complete set of eigen functions [9], so that its eigen values are certainly real numbers. But the Hermitian operator has no such restriction. The problem is that this restriction condition would greatly effects the universality of operator and can not be satisfied actually. For example, for all non-particle’s wave functions, momentum operator is not the one with selfadjoint. However, we can prove that although we can not make momentum operators self-adjoint, we can make its non-eigen functions to be real by redefinition.
It is proved below that though we can not make momentum operators is self-adjoint one, we can introduce universal momentum operators to make their non-eigen values be real numbers.
2.5. The Problems Caused by Non-Commutation of Operators in Quantum Mechanics
As well know that momentum operator and coordinate do not commutate with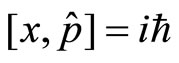 . Let
. Let 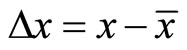 and
and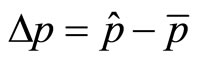 , in which
, in which 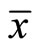 and
and 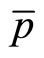 are the averages of coordinate and momentum, we have so-called uncertainty relation:
are the averages of coordinate and momentum, we have so-called uncertainty relation:
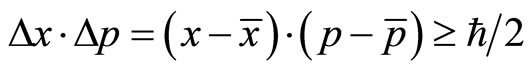 (34)
(34)
According to current understanding, (34) means that coordinates and momentums of micro-particle can not be determined simultaneously. If it is true, the function relation 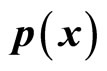 is meaningless.
is meaningless.
However, 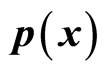 in (2) is only the result of mathematical calculation. Because the definitions of operator and wave function have no problems, how can we consider the result meaningless? According to (2), as long as we know the concrete form of wave function, we know the momentum. It is unnecessary for us to measure momentum. How can we think that the coordinate and momentum of micro-particle can not be determined simultaneously? We need to discuss the real meaning of the uncertainty relation in brief.
in (2) is only the result of mathematical calculation. Because the definitions of operator and wave function have no problems, how can we consider the result meaningless? According to (2), as long as we know the concrete form of wave function, we know the momentum. It is unnecessary for us to measure momentum. How can we think that the coordinate and momentum of micro-particle can not be determined simultaneously? We need to discuss the real meaning of the uncertainty relation in brief.
Firstly, the wave function 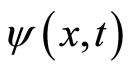 describes the probability of a particle appears at the point
describes the probability of a particle appears at the point  at moment
at moment . Therefore,
. Therefore, 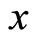 is the accurate value of particle’s coordinate in theory. It is not the value of measurement, for measurements always have error. Therefore,
is the accurate value of particle’s coordinate in theory. It is not the value of measurement, for measurements always have error. Therefore, 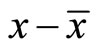 is the difference between particle’s theoretical coordinate and average coordinate. It is not the measurements error of coordinate. In fact, it is actually the fluctuation of coordinate about average value as that defined in classical statistics physics. Similarly,
is the difference between particle’s theoretical coordinate and average coordinate. It is not the measurements error of coordinate. In fact, it is actually the fluctuation of coordinate about average value as that defined in classical statistics physics. Similarly, 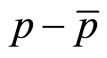 is also the difference between particle’s accurate momentum and average momentum, or the fluctuation of momentum about the average value. It is not the measurements error of momentum. According to classical theory, fluctuation is also uncertainty. But this uncertainty is due to statistics, having nothing to do with measurement. In this meaning, (34) is not the uncertainty relation for a single particle recognized in the current quantum mechanics.
is also the difference between particle’s accurate momentum and average momentum, or the fluctuation of momentum about the average value. It is not the measurements error of momentum. According to classical theory, fluctuation is also uncertainty. But this uncertainty is due to statistics, having nothing to do with measurement. In this meaning, (34) is not the uncertainty relation for a single particle recognized in the current quantum mechanics.
Secondly, the strict uncertain relation in quantum mechanics is
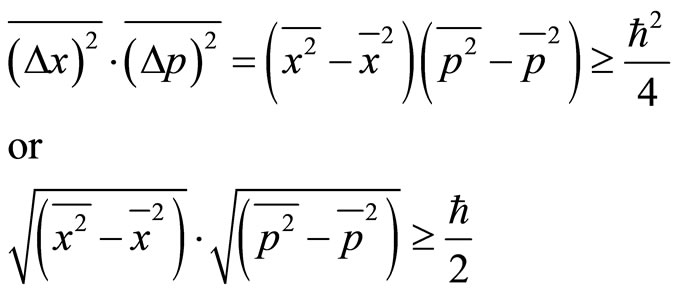 (35)
(35)
In the formula (35), 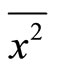 ,
, 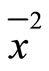 ,
, 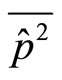 and
and 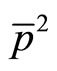 are the average values, not the values for a single event. Therefore, (35) represents the product of mean square errors of coordinates and momentums. It is the result of statistical average over a large number’s of events. For a single event, we may have
are the average values, not the values for a single event. Therefore, (35) represents the product of mean square errors of coordinates and momentums. It is the result of statistical average over a large number’s of events. For a single event, we may have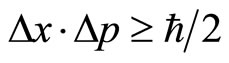 ,
, 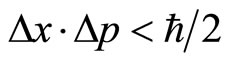 and
and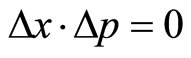 . Merely, their statistical average satisfies (35).
. Merely, their statistical average satisfies (35).
In fact, because (35) only contains average values, does not contain 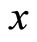 and
and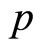 , its forms and meaning is completely different from (34). In the current quantum mechanics, (35) is simplified into (34), then the uncertainty relation is declared. This is improper. It is also the misunderstanding to consider the uncertainty relation as the foundational principle of quantum mechanics for (35) is only the deduced result of quantum mechanics.
, its forms and meaning is completely different from (34). In the current quantum mechanics, (35) is simplified into (34), then the uncertainty relation is declared. This is improper. It is also the misunderstanding to consider the uncertainty relation as the foundational principle of quantum mechanics for (35) is only the deduced result of quantum mechanics.
On the other hand, according to quantum mechanics, time and micro-particle’s coordinates can be determined simultaneously. The definition of velocity is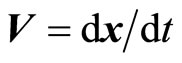 . As long as we determine particle’s coordinates at different moments, we can determine particle’s velocity and momentum
. As long as we determine particle’s coordinates at different moments, we can determine particle’s velocity and momentum 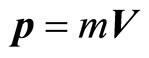 by calculation without doing measurements. The more accurate the measurement of particle’s coordinate, the more accurate the particle’s velocity and momentum. In this meaning, where is the uncertain relation?
by calculation without doing measurements. The more accurate the measurement of particle’s coordinate, the more accurate the particle’s velocity and momentum. In this meaning, where is the uncertain relation?
This kind of paradox exists commonly in quantum mechanics and the problem is more serious than what we have imagined. Let’s discuss the commutation relation between coordinate and kinetic energy operator. The kinetic energy operator is
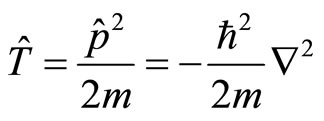 (36)
(36)
Acting on the wave function of a single non-free particle, we obtain
 (37)
(37)
It is easy to prove that  and
and  are commutative with
are commutative with
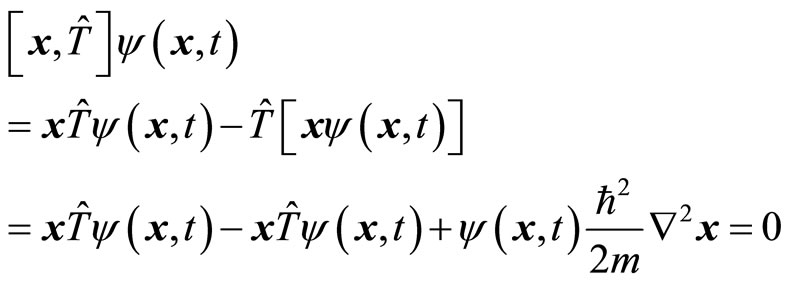 (38)
(38)
According to the understanding of quantum mechanics, the kinetic energy and coordinate of micro-particle can be determined simultaneously, so it is meaningful to write micro-particle’s kinetic energy as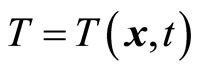 . According to (36), we can naturally obtain particle’s momentum
. According to (36), we can naturally obtain particle’s momentum 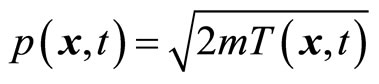 after its kinetic energy is known. In fact, the kinetic operator and momentum operator are commutative with
after its kinetic energy is known. In fact, the kinetic operator and momentum operator are commutative with
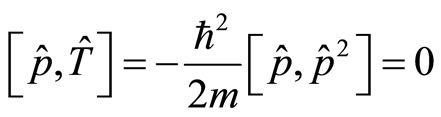 (39)
(39)
So kinetic energy and momentum can be determined simultaneously. Because micro-particle’s kinetic energy is the function of coordinates, if coordinates are known, we can determine its kinetic energy. After that, we can determine its momentum. That is to say, we can determine particle’s momentum by determining its coordinate.
We consider particle’s energy operator again. Acting the operator on the non-eigen wave function of a single particle, we get:
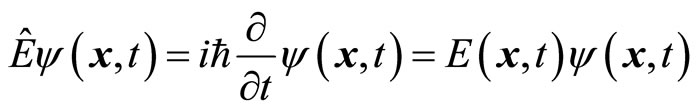 (40)
(40)
It is easy to see that 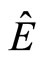 commutates with
commutates with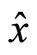 ,
, 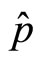 and
and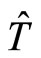 , so particle’s energy, kinetic and potential energy can be determined simultaneously. For a particle in stationary state, we have certain energy
, so particle’s energy, kinetic and potential energy can be determined simultaneously. For a particle in stationary state, we have certain energy
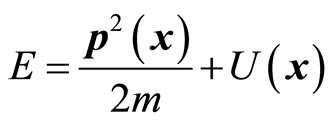 (41)
(41)
Here 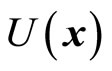 is potential energy. As long as particle’s coordinates are known, we know its kinetic energy, potential energy and momentum without direct measurements. However, on the other hand, because kinetic energy operator and potential operator do not commutate in general, we have
is potential energy. As long as particle’s coordinates are known, we know its kinetic energy, potential energy and momentum without direct measurements. However, on the other hand, because kinetic energy operator and potential operator do not commutate in general, we have
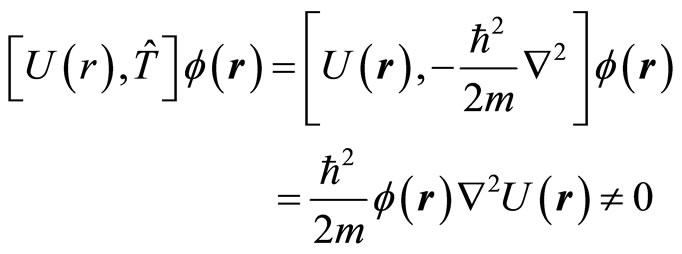 (42)
(42)
For example, for hydrogen atom, we have 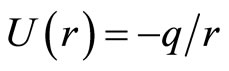 and get
and get 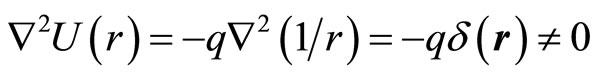 .
.
According to the current understanding, electron’s kinetic energy and potential energy could not be determined simultaneously (this is so-called quantum tunnel effect), (41) becomes meaningless. However, (41) is also deduced based the principle of quantum mechanics, how can we say it is meaningless? If it is true, how can we have the fine structure of hydrogen atom spectrum? In fact, (41) is the formula of energy conservation. If it does not hold, all theories and experiments of quantum mechanics become meaningless!
In essence, quantum mechanics is a statistical theory which involves a large number of micro-processes. Quantum measurement process always involves a large number of micro-particles. Once statistical average is considered, many problems do no exist any more. Our current understanding on quantum mechanics may have same foundational error. The standard explanation of quantum mechanics should have some essential changes.
We will discuss the real meaning of the uncertainty relation and the explanation of quantum mechanics further in another paper. In this paper, we mainly discuss the definition of universal momentum operator. We do not consider the restriction of the uncertainty relation again and think that it is meaningful to act operators on non-eigen wave functions directly. In operator equation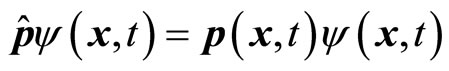 , p(x,t) represent microparticle’s momentum at time
, p(x,t) represent microparticle’s momentum at time  and position
and position .
.
2.6. The Fourier’s Series of Non-Eigen Wave Functions of Momentum Operator
According to quantum mechanics, if the wave functions are not the eigen functions of operators, they should be developed into the eigen functions of operators. The eigen function of momentum operator is that of free particle. For the stationary state wave functions of non-free particles, we have
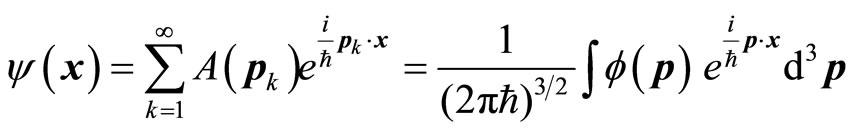 (43)
(43)
This is actually the Fourier’s transformation of wave function which is legal in mathematics. It can be considered as the principle of superposition principle of wave function in quantum mechanics.
If 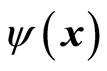 describe a single particles, for example, an electron in the ground state of hydrogen atom, it represents the momentum distribution of an electron in hydrogen atom [10]. But it does not mean that a non-free electron is equivalent to infinite number of free electrons with different momentums and energies. This is impossible in physics. In fact, there are only two electrons with opposite spins in the ground states of hydrogen. If (43) describes the hydrogen atom of ground state, it violates the Pauli’s exclusion principle. It is impossible for us to use so many free electrons with different energies to construct hydrogen atom’s energy levels and the spectrum structures.
describe a single particles, for example, an electron in the ground state of hydrogen atom, it represents the momentum distribution of an electron in hydrogen atom [10]. But it does not mean that a non-free electron is equivalent to infinite number of free electrons with different momentums and energies. This is impossible in physics. In fact, there are only two electrons with opposite spins in the ground states of hydrogen. If (43) describes the hydrogen atom of ground state, it violates the Pauli’s exclusion principle. It is impossible for us to use so many free electrons with different energies to construct hydrogen atom’s energy levels and the spectrum structures.
The reason we write the wave function of a single particle in the form of (43) is due to the definition of momentum operator which is only effective to free particles. It is ineffective when it is acted on the wave functions of non-free particles due to complex non-eigen values. If we can find proper momentum operator to describer non-free particle’s momentums, it is unnecessary for us always to write the wave function of a single non-free particles in the superposition form of free particle’s wave functions. In fact, the eigen function of kinetic energy operator is also the wave function of free particle. We do not need to write arbitrary wave function as the form of (43) for kinetic operator. The reason is just that when kinetic operator is acted on arbitrary wave functions, the results are always real numbers.
In fact, for some operators of quantum mechanics, we can not find proper eigen functions, for example, angle momentum operator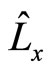 ,
, 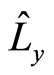 and
and 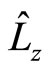 in the rectangular coordinate system. Because they have no proper eigen functions, we can not developed arbitrary functions into the sum of their eigen functions. Acted them on arbitrary functions directly, we always obtain complex numbers. Can we say they are meaningless? The universal momentum and angle momentum operators proposed in this paper can solve these problems well.
in the rectangular coordinate system. Because they have no proper eigen functions, we can not developed arbitrary functions into the sum of their eigen functions. Acted them on arbitrary functions directly, we always obtain complex numbers. Can we say they are meaningless? The universal momentum and angle momentum operators proposed in this paper can solve these problems well.
3. The Definition of Universal Momentum Operator
3.1. The Definition of Universal Momentum Operator in Coordinate Space
In order to make all non-eigen values of momentum operator be real numbers, we need to redefine the momentum operator of quantum mechanics. In the Cartesian coordinate reference system, we write the partial quantities of universal momentum operator as
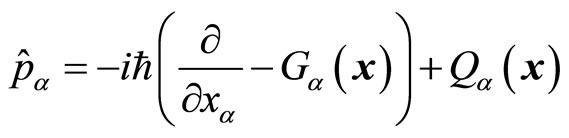 (44)
(44)
In which 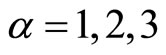 is the index of partial quantities,
is the index of partial quantities, 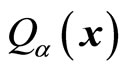 is real number with its form to be decided.
is real number with its form to be decided. 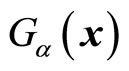 is complex number in general to satisfy following relation
is complex number in general to satisfy following relation
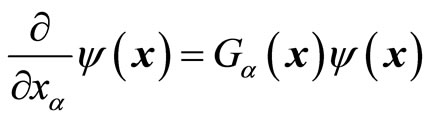 (45)
(45)
For the purpose of universality, the functions here can be both the stationary state 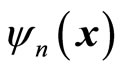 and the superposetion state of
and the superposetion state of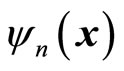 . If we want to connect
. If we want to connect 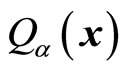 with particle’s momentum, it should be stationary state
with particle’s momentum, it should be stationary state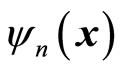 . By solving the motion equation of quantum mechanics, we can obtain the concrete forms of wave functions, so we can determinate the forms of
. By solving the motion equation of quantum mechanics, we can obtain the concrete forms of wave functions, so we can determinate the forms of 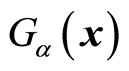 based on (44). By acting universal momentum operator on common wave functions and considering (45), we obtain the non eigne equation and the non-eigen values of real numbers
based on (44). By acting universal momentum operator on common wave functions and considering (45), we obtain the non eigne equation and the non-eigen values of real numbers
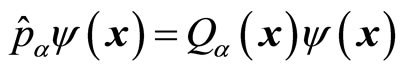 (46)
(46)
The average values of universal momentum operator are also real numbers
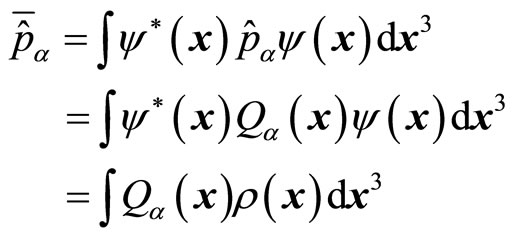 (47)
(47)
If 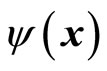 is the eigen function of momentum operator, we take
is the eigen function of momentum operator, we take
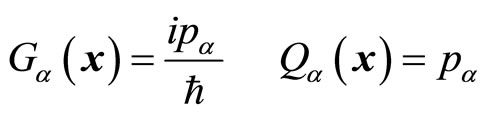 (48)
(48)
(44) becomes the current definition of the Hermitian operator. We now discuss the concrete forms of 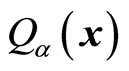 below. According to (44), the kinetic operator of microparticles is
below. According to (44), the kinetic operator of microparticles is
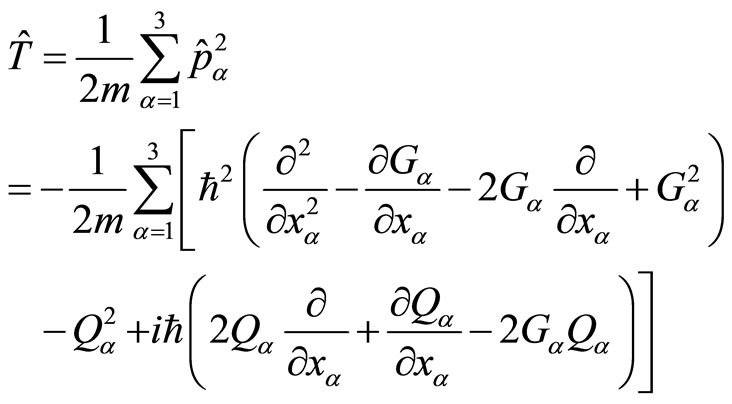 (49)
(49)
However, practical kinetic operator should be actually
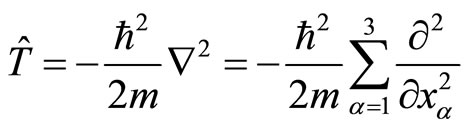 (50)
(50)
By comparing (49) with (50) and considering (45), we get
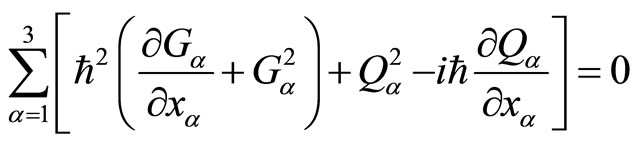 (51)
(51)
Because 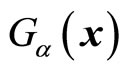 is known complex number, we separate it into imaginary and real parts and write it as
is known complex number, we separate it into imaginary and real parts and write it as
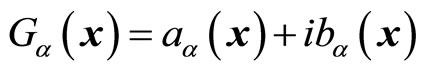 (52)
(52)
Substituting it in (51), and dividing the equation into imaginary and real parts again, we obtain two formulas
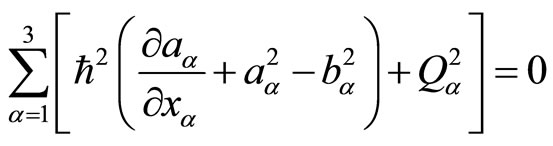 (53)
(53)
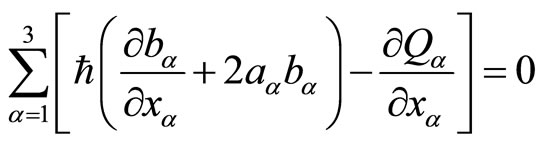 (54)
(54)
There are three 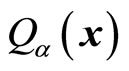 needs to be determined, but we only have two equations (53) and (54). Therefore, one of them can be arbitrary. Let
needs to be determined, but we only have two equations (53) and (54). Therefore, one of them can be arbitrary. Let 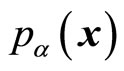 be the partial momentum of particle, we can decide its value by acting kinetic operator on stationary state wave function and have
be the partial momentum of particle, we can decide its value by acting kinetic operator on stationary state wave function and have
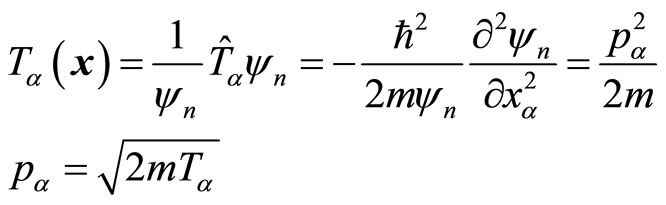 (55)
(55)
Let 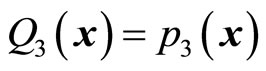 and substitute it in (53) and (54), we can determine
and substitute it in (53) and (54), we can determine 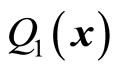 and
and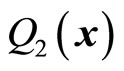 . In general,
. In general, 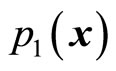 and
and 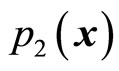 are different from
are different from 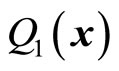 and
and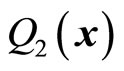 . We assume
. We assume
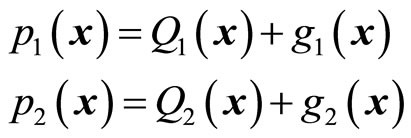 (56)
(56)
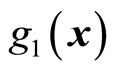 and
and 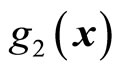 are known due to the fact that
are known due to the fact that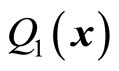 ,
, 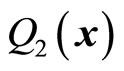 ,
, 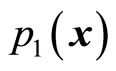 and
and 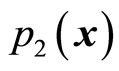 are known. In this way, we determine the concrete form of universal momentum operator (44) and explain why the results are not the same when we use kinetic operator and momentum operator to calculate the kinetic energy of microparticles. By consider (55), we have
are known. In this way, we determine the concrete form of universal momentum operator (44) and explain why the results are not the same when we use kinetic operator and momentum operator to calculate the kinetic energy of microparticles. By consider (55), we have
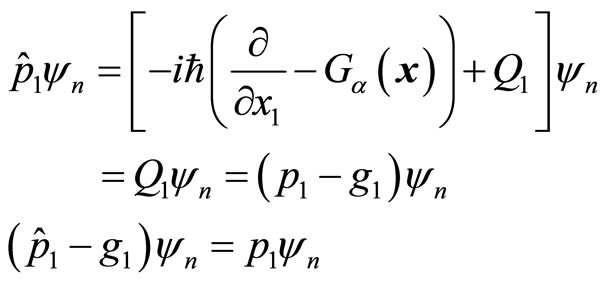 (57)
(57)
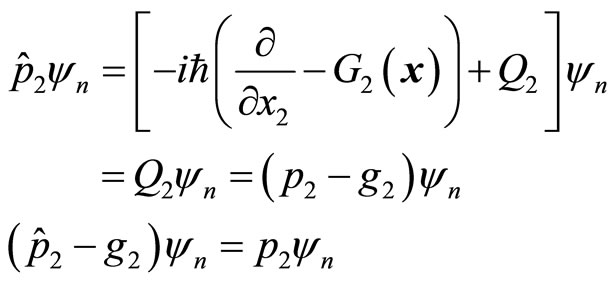 (58)
(58)
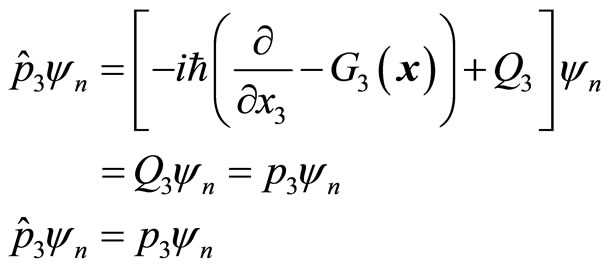 (59)
(59)
In this way, all non-eigen values of universal momentum operator are real numbers, but two of them are not real momentums of micro-particles. Using universal momentum operator and kinetic operator to calculate particle’s kinetic energy, the results may be different. It is due to that three partial quantities of universal momentum operator do not commute with each other.
If micro-particles moves in two dimensional spaces, both 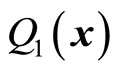 and
and 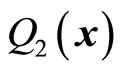 are determined just by two equations (53) and (54). Meanwhile,
are determined just by two equations (53) and (54). Meanwhile, 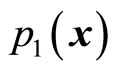 and
and 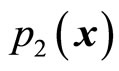 are determined by kinetic operators. The relations between them are still shown in (56). If particles move in one dimensional space, only one
are determined by kinetic operators. The relations between them are still shown in (56). If particles move in one dimensional space, only one 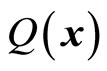 needs to be determined, but we still have two equations (53) and (54) as follows
needs to be determined, but we still have two equations (53) and (54) as follows
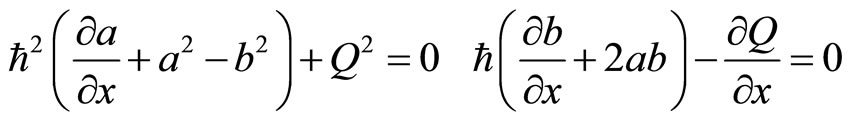 (60)
(60)
Therefore, 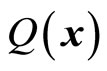 is not unique, unless two equations are compatible. From both equations, we obtain
is not unique, unless two equations are compatible. From both equations, we obtain
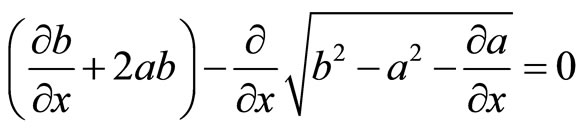 (61)
(61)
The formula has infinite solutions. The simplest one is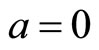 , so we have
, so we have 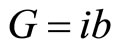 and
and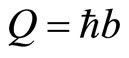 . That is to say,
. That is to say, 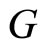 is a purely imaginary number. In the case, universal momentum operator is
is a purely imaginary number. In the case, universal momentum operator is
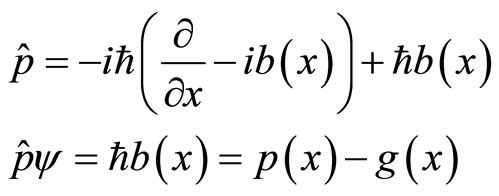 (62)
(62)
So in general situations, we can not define proper momentum operator in one dimensional space in quantum mechanics, though we can define proper kinetic operator.
According this kind of definition, universal momentum operator is not the Hermitian operator again. However, as discussed before, the restriction of Hermitian operator is neither necessary nor possible for non-eigen functions. Most important is that the non-eigen values and average values of operator should be real numbers. Only in this way, the descriptions of physical processes can be consistent in different representations. The universal momentum operator can do it.
Although the deductions above are based on the wave function of single particle, we can also do it for multiparticle’s functions. We do not discuss it here. According to (44), the commutation relations between coordinate and momentum operators are unchanged with
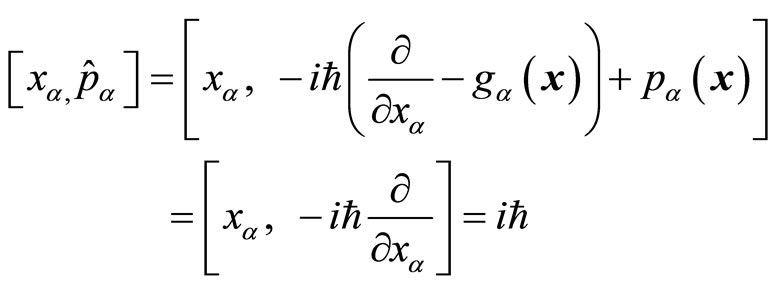 (63)
(63)
As discussed before, the non-commutation of operators does not mean the uncertain of physical quantities simultaneously.
3.2. The Average Values of Universal Momentum Operator
The average value of universal momentum operator is a real number. According to (57)-(59), we have
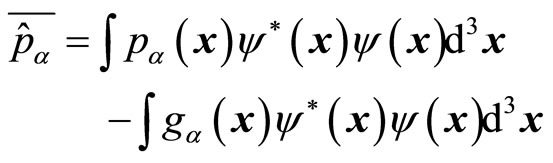 (64)
(64)
The first item on the right side of equal sign is the real average of particle’s momentum. By transforming into momentum space, we have
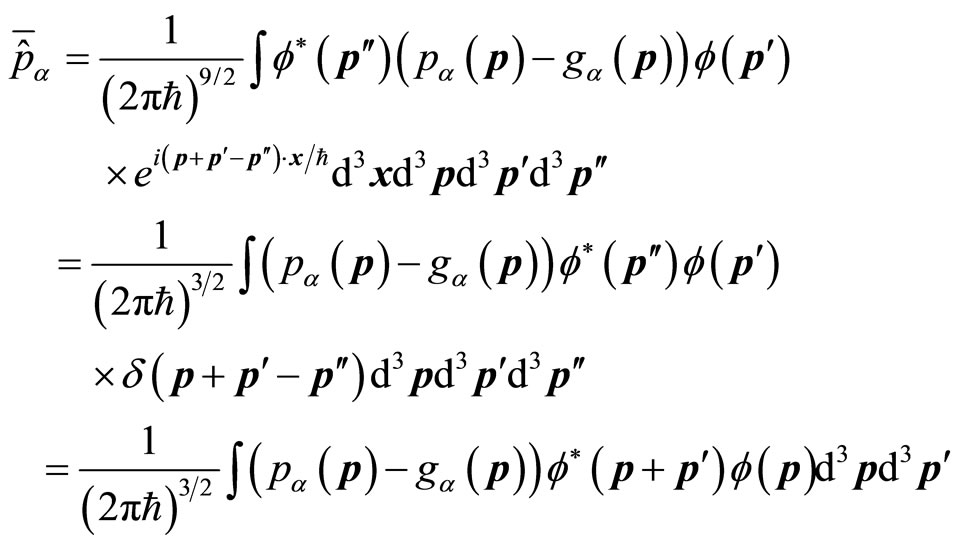 (65)
(65)
The result is similar to (41).
3.3. The Definition of Universal Coordinate Operator in Momentum Space
As mentioned above, the average value of coordinate operator in momentum space is a complex number. So the coordinate operator in momentum space should also be revised. Similar to (44), we define the universal coordinate operator 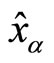 and momentum operator
and momentum operator 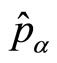 in momentum space as
in momentum space as
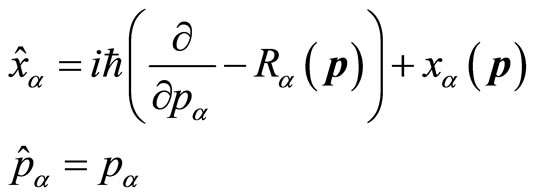 (66)
(66)
Here 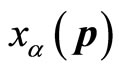 is a real number and
is a real number and 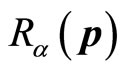 is a complex number in general to satisfy following equation
is a complex number in general to satisfy following equation
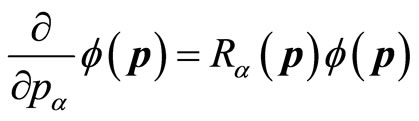 (67)
(67)
Here 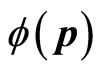 is the wave function in momentum space. The relation between
is the wave function in momentum space. The relation between 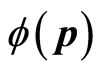 and
and 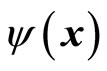 is the Fourier transform with
is the Fourier transform with
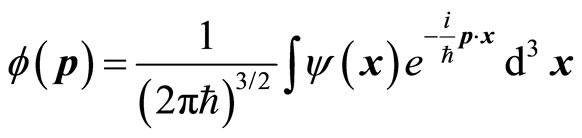 (68)
(68)
We can determine 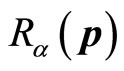 based on (67). Thus, we have
based on (67). Thus, we have
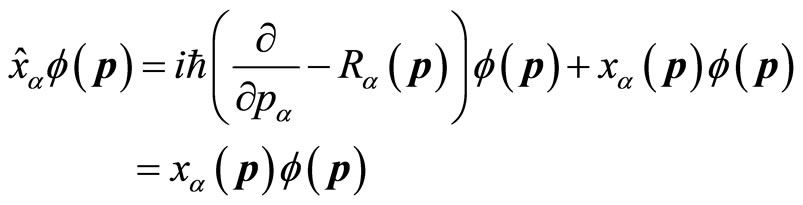 (69)
(69)
Therefore, the results that universal coordinate operators are acted on the non-eigen wave functions are real numbers. The average values of universal coordinate operators over non-eigen functions are also real numbers. We have
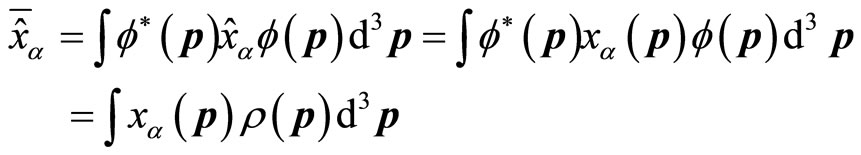 (70)
(70)
The Fourier transform of 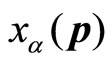 is
is
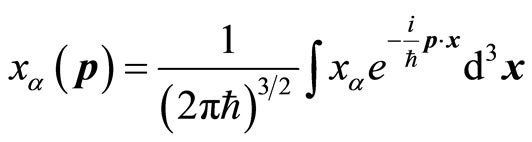 (71)
(71)
By considering (68) and (71), we transform (70) into coordinate space for description and obtain
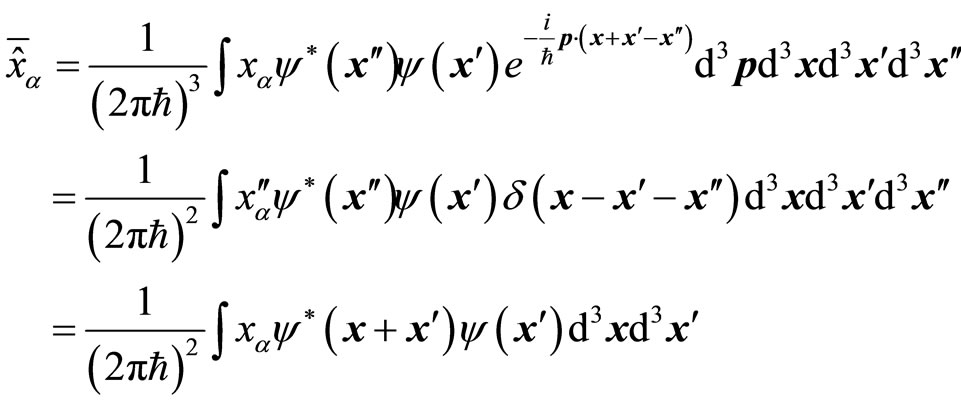 (72)
(72)
The result is similar (41) and (65).
3.4. The Definition of Universal Momentum Operator in Spherical Coordinate System
Based on the definition of universal momentum in the Descartes coordinate system, we can define universal momentum operator in spherical coordinate system. Similar to (44), we define
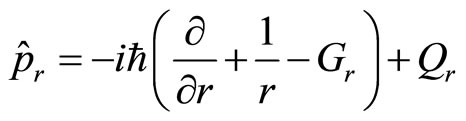 (73)
(73)
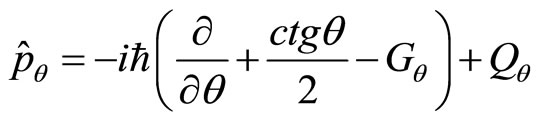 (74)
(74)
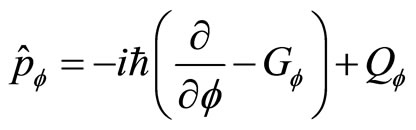 (75)
(75)
Here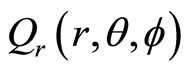 ,
, 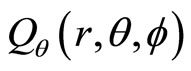 and
and 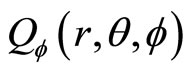 are real numbers, and
are real numbers, and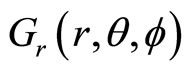 ,
, 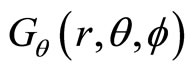 and
and
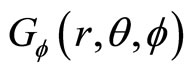 are complex numbers which satisfy following relations
are complex numbers which satisfy following relations
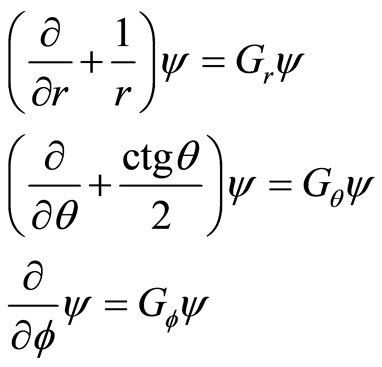 (76)
(76)
By acting (71)-(73) on general non-eigen wave functions, we get non-eigen values of real numbers with
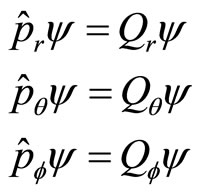 (77)
(77)
Now let’s determine the concrete forms of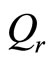 ,
, 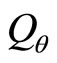 and
and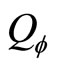 . Substitute (73)-(75) into (12), we get
. Substitute (73)-(75) into (12), we get
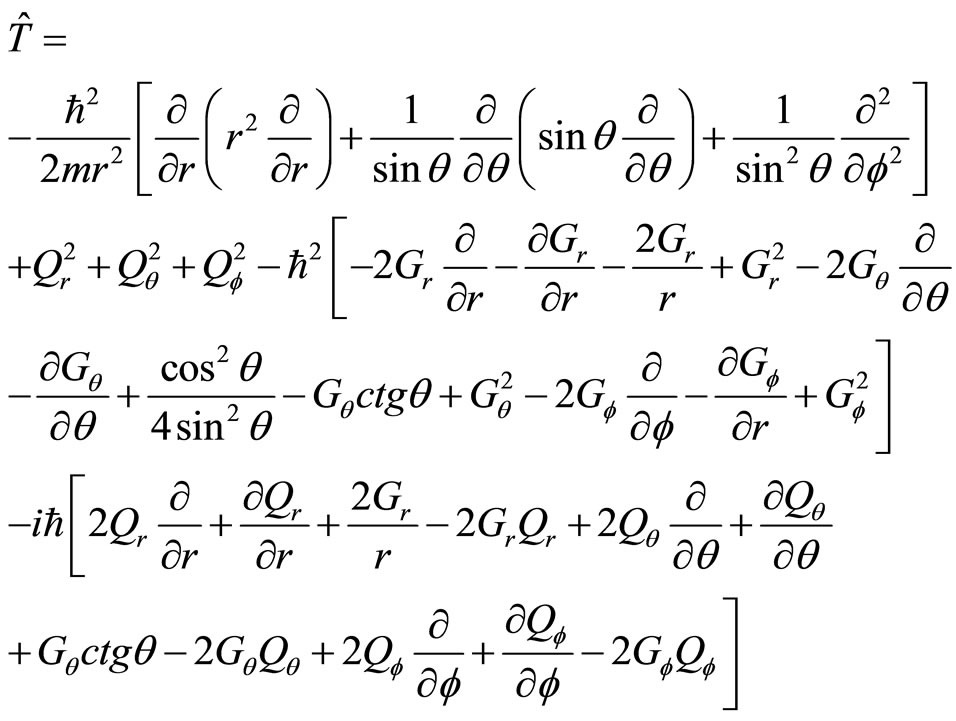 (78)
(78)
By considering (13) and (76), we get
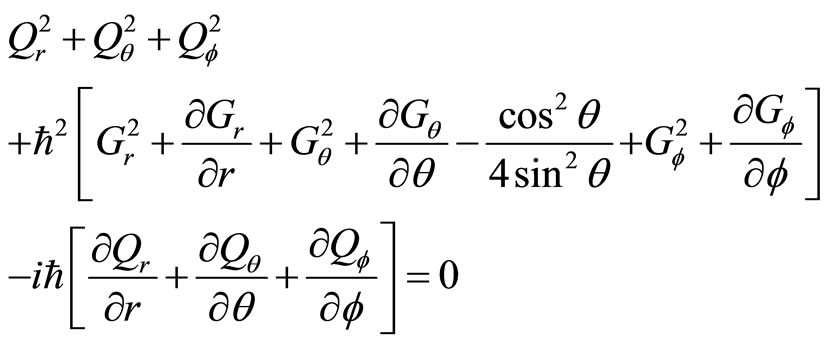 (79)
(79)
We take
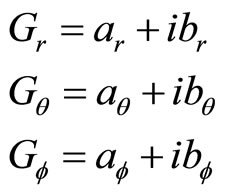 (80)
(80)
By substituting (80) into (79) and dividing it into imaginary part and real part, we have
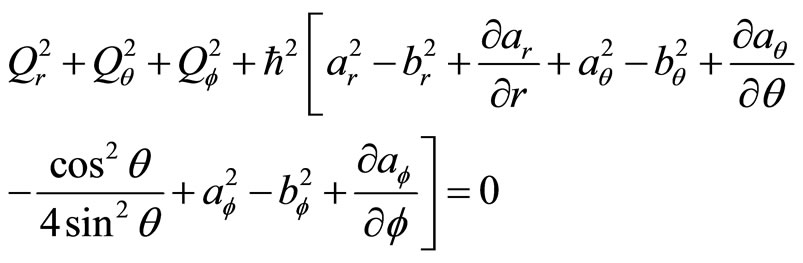 (81)
(81)
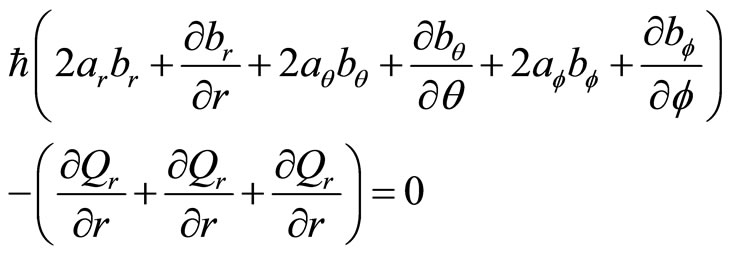 (82)
(82)
We have three 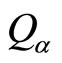 but only have two equations (81) and (82), so we
but only have two equations (81) and (82), so we 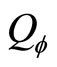 can be chosen arbitrary. By solving the motion question of quantum mechanics, we know the form of wave functions. Let
can be chosen arbitrary. By solving the motion question of quantum mechanics, we know the form of wave functions. Let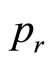 ,
,  and
and 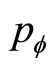 are the partial momentum of a particle. Their forms can be determined by following formulas
are the partial momentum of a particle. Their forms can be determined by following formulas
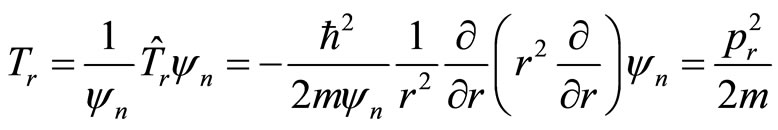 (83)
(83)
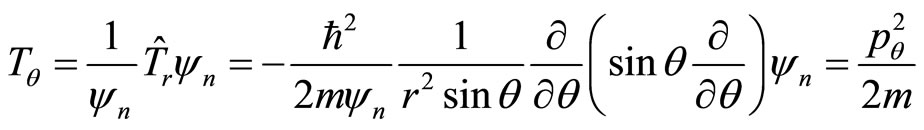 (84)
(84)
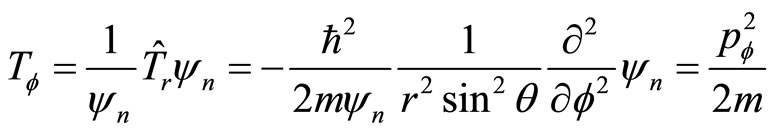 (85)
(85)
Let 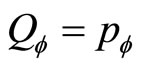 and substitute it in (81) and (82), we can determine
and substitute it in (81) and (82), we can determine 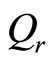 and
and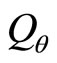 . In general,
. In general, 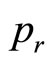 and
and 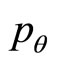 are different from
are different from 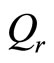 and
and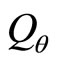 . We let
. We let
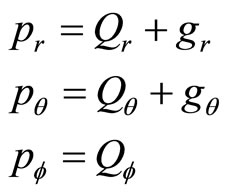 (86)
(86)
Because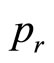 ,
, 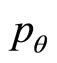 ,
, 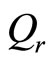 and
and 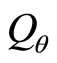 are known,
are known, 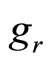 and
and 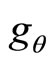 are known too. So (63) can be written as
are known too. So (63) can be written as
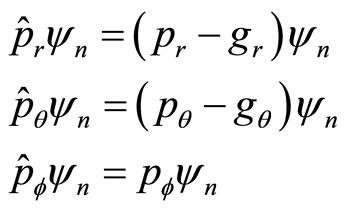 (87)
(87)
The non-eigen values of universal momentum operator 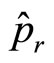 and
and 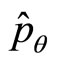 do not represent real momentums of micro-particle too. In this way, we define universal momentum operator in spherical coordinate system. By the same method, we can define universal momentum operator in other curved coordinate systems.
do not represent real momentums of micro-particle too. In this way, we define universal momentum operator in spherical coordinate system. By the same method, we can define universal momentum operator in other curved coordinate systems.
4. The Definition of Universal Angle Momentum Operator and the Essence of Micro-Particle’s Spin
4.1. The Definition of Universal Angle Momentum Operator
In quantum mechanics, angle momentum operator is related to momentum operator with relation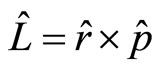 . If we think that micro-particle’s momentums are unobservable so that its values are unimportant, the angle momentum of micro-particles are related to atomic magnetic moment and the magnetic moments are measurable directly. It is obvious that when angle momentum operators act on general wave function, their non-eigen values and average values may be complex numbers too. The angel momentum operators in the Descartes coordinate system is
. If we think that micro-particle’s momentums are unobservable so that its values are unimportant, the angle momentum of micro-particles are related to atomic magnetic moment and the magnetic moments are measurable directly. It is obvious that when angle momentum operators act on general wave function, their non-eigen values and average values may be complex numbers too. The angel momentum operators in the Descartes coordinate system is
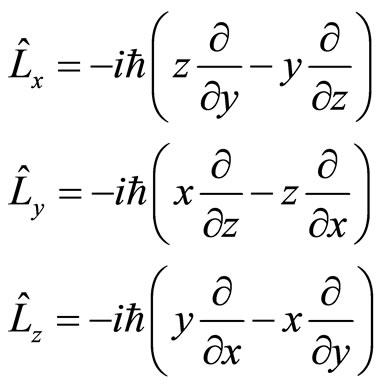 (88)
(88)
By introducing spherical coordinate, (88) can also be written as
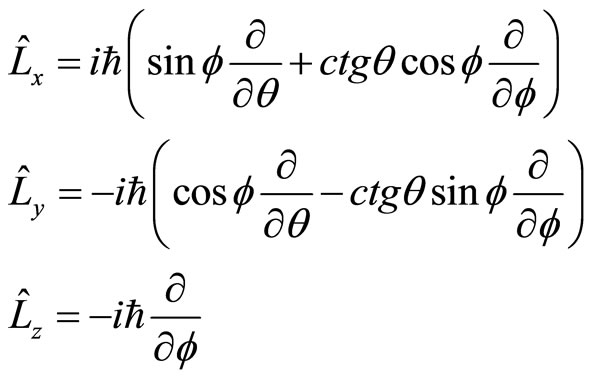 (89)
(89)
In which 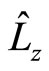 is the eigen operator of stationary wave function
is the eigen operator of stationary wave function  of hydrogen atom with eigen values
of hydrogen atom with eigen values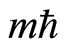 , but
, but 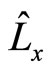 and
and 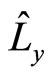 are not. Their non-eigen values and average values are complex numbers in general. The square of angle momentum operators is the eigen operator of angle momentum, we have
are not. Their non-eigen values and average values are complex numbers in general. The square of angle momentum operators is the eigen operator of angle momentum, we have
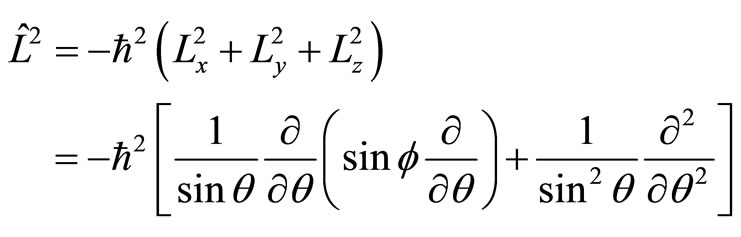 (90)
(90)
Acting 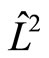 on
on , we get real eigen values
, we get real eigen values 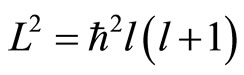 . In order to make the non-eigen values of
. In order to make the non-eigen values of 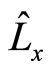 and
and 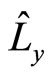 real numbers, we should refine they. Based on (44), universal angle operators are
real numbers, we should refine they. Based on (44), universal angle operators are
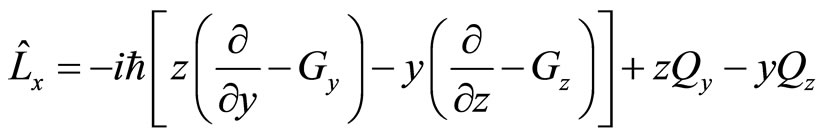 (91)
(91)
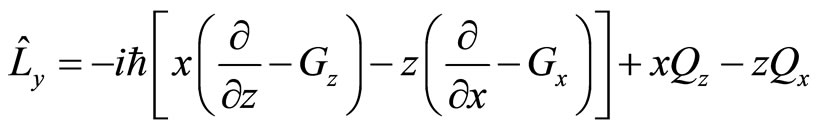 (92)
(92)
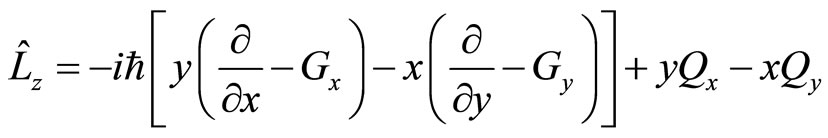 (93)
(93)
Here 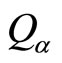 is determined by (53) and (54) with
is determined by (53) and (54) with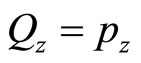 . By acting universal angle operators on common noneigen wave function, we get
. By acting universal angle operators on common noneigen wave function, we get
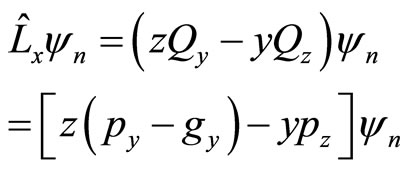 (94)
(94)
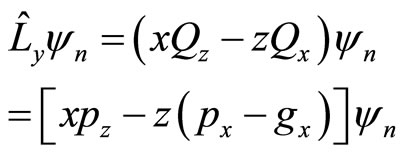 (95)
(95)
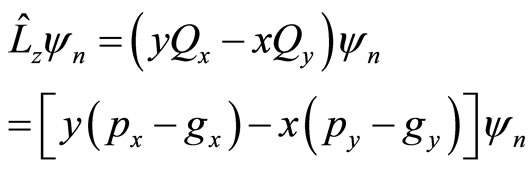 (96)
(96)
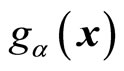 and
and 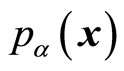 are also determined by (55) and (56). In this way, the non-eigen values and average values of universal angle momentum operators are real umbers. We do not discuss the forms of universal angle momentum operators in curved coordinate reference systems here.
are also determined by (55) and (56). In this way, the non-eigen values and average values of universal angle momentum operators are real umbers. We do not discuss the forms of universal angle momentum operators in curved coordinate reference systems here.
4.2. Auxiliary Momentum and Auxiliary Angle Momentum
We use the square of momentum operator 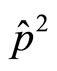 to construct the motion equation of quantum mechanics but use
to construct the motion equation of quantum mechanics but use  to construct angle momentum, in quantum mechanics. So the kinetic energy
to construct angle momentum, in quantum mechanics. So the kinetic energy 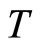 and angle momentum
and angle momentum 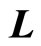 are not one-to-one correspondent. In fact, according to quantum mechanics, the kinetic energy of electron in ground state hydrogen atom is not zero but its angle momentum is zero. This state can not exist stationary. The angle momentum should exist for electron moving around atomic nuclear, otherwise electron would fall into nuclear. By considering the error between calculated values of momentum using momentum operator and real values, auxiliary momentum and auxiliary angle momentum are introduced. By establishing relation between auxiliary angle momentum and spin, the essence of micro-particle’s spin can be revealed.
are not one-to-one correspondent. In fact, according to quantum mechanics, the kinetic energy of electron in ground state hydrogen atom is not zero but its angle momentum is zero. This state can not exist stationary. The angle momentum should exist for electron moving around atomic nuclear, otherwise electron would fall into nuclear. By considering the error between calculated values of momentum using momentum operator and real values, auxiliary momentum and auxiliary angle momentum are introduced. By establishing relation between auxiliary angle momentum and spin, the essence of micro-particle’s spin can be revealed.
Let 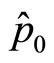 represents universal momentum operator,
represents universal momentum operator, 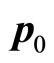 represents its value with
represents its value with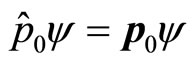 . It has been proved before that
. It has been proved before that 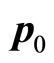 is still not real momentum of microparticle. Let
is still not real momentum of microparticle. Let 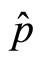 represent real momentum operator and
represent real momentum operator and 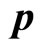 represent real momentum with
represent real momentum with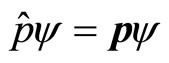 .
. 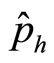 represent auxiliary momentum operator and
represent auxiliary momentum operator and 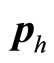 represents auxiliary momentum with
represents auxiliary momentum with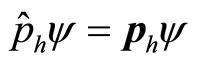 . Their relation is
. Their relation is
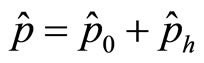 (97)
(97)
Let
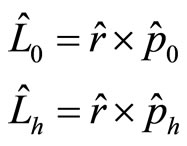 (98)
(98)
Here 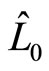 is angle momentum operator in current quantum mechanics and
is angle momentum operator in current quantum mechanics and 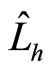 is supplemental momentum operator. The real angle momentum operator
is supplemental momentum operator. The real angle momentum operator 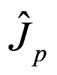 is
is
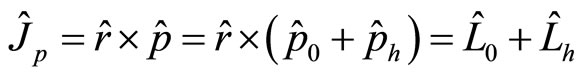 (99)
(99)
The relations among them are shown in Figure 1. Auxiliary angle momentum 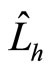 is related to spin
is related to spin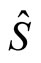 . We discuss their relation below and prove that spin is related to the partial angle momentum of micro-particle which current momentum operator can not describe. By establishing the relation between them, the essence of spin can be explained well.
. We discuss their relation below and prove that spin is related to the partial angle momentum of micro-particle which current momentum operator can not describe. By establishing the relation between them, the essence of spin can be explained well.
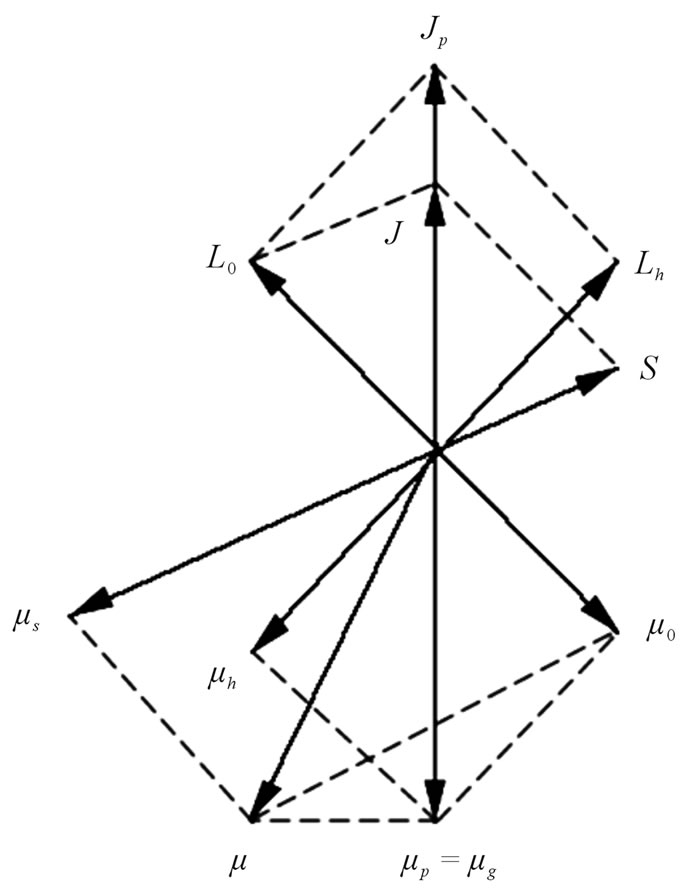
Figure 1. Auxiliary angle momentum, spin and magnetic moment.
4.3. The Essence of Micro-Particle’s Spin
In order to explain the fine structure of light spectrum, we assume that electron has a spin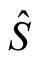 . The projections of spin can only take two values
. The projections of spin can only take two values 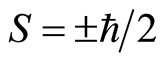 at arbitrary direction in space. Spin seems an angle momentum but not real. Sometimes, we consider spin as that electron rotates around itself symmetry axis. But the calculation shows that if it is true, the tangential speed of electron’s surface would be 137 times more than light’s speed [11]. It is difficult to understand the concept of micro-particle’s spin from the point of view of classical mechanics. Although quantum mechanics has been fully developed, the essence of spin is still an enigma at present day.
at arbitrary direction in space. Spin seems an angle momentum but not real. Sometimes, we consider spin as that electron rotates around itself symmetry axis. But the calculation shows that if it is true, the tangential speed of electron’s surface would be 137 times more than light’s speed [11]. It is difficult to understand the concept of micro-particle’s spin from the point of view of classical mechanics. Although quantum mechanics has been fully developed, the essence of spin is still an enigma at present day.
In quantum mechanics, spin is considered as angle momentum actually. However, angle momentum is a kind of vector. So it is an unreasonable thing for spin vector to only take two projection values 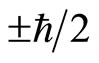 at arbitrary direction in space. In real physical space, such vector can not exist. The projection of a vector with mode 1 at any
at arbitrary direction in space. In real physical space, such vector can not exist. The projection of a vector with mode 1 at any  direction can only be
direction can only be 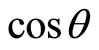 with values
with values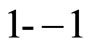 . Because spin is always coupled with magnetic field, the correct understanding should be that if we take
. Because spin is always coupled with magnetic field, the correct understanding should be that if we take 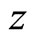 axis as the direction of magnetic field, the projections of spin at
axis as the direction of magnetic field, the projections of spin at 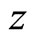 axis direction take two values
axis direction take two values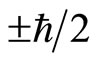 . At other directions, spin’s projection should be related to
. At other directions, spin’s projection should be related to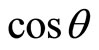 . We will see below that it is just due to the hypothesis that the projections of spin can only take two values, the Bell inequality can not be correct.
. We will see below that it is just due to the hypothesis that the projections of spin can only take two values, the Bell inequality can not be correct.
According to current quantum mechanics, magnetic moment caused by spin in magnetic field is
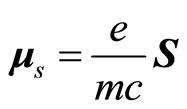 (100)
(100)
Magnetic moment caused by angle momentum 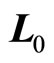 is
is
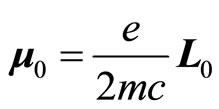 (101)
(101)
In atomic physics, the ratio that atomic magnetic moment divided by angle momentum is called as orbit gyro-magnetic ratio. According to (101), we have the ratio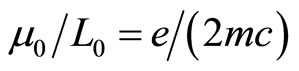 . However, according to (100), we have
. However, according to (100), we have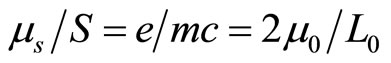 . So spin gyro-magnetic ratio is two times of orbit gyro-magnetic ratio. It indicates that spin is not normal angle momentum. Let
. So spin gyro-magnetic ratio is two times of orbit gyro-magnetic ratio. It indicates that spin is not normal angle momentum. Let 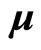 represent total magnetic moment of charged particle in magnetic field, as shown in Figure 1, magnetic moment
represent total magnetic moment of charged particle in magnetic field, as shown in Figure 1, magnetic moment 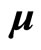 precesses around total angle momentum
precesses around total angle momentum , so
, so 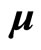 is considered as an immeasurable quantity in current theory. What can be measured directly is the partial quantity
is considered as an immeasurable quantity in current theory. What can be measured directly is the partial quantity 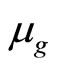 of
of 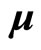 at the direction of angle momentum
at the direction of angle momentum . We have
. We have
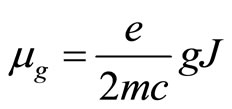 (102)
(102)
Here 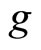 is the Lande factor. Let
is the Lande factor. Let 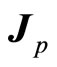 represent new total angle momentum after auxiliary angle momentum is considered, suppose that the relation between
represent new total angle momentum after auxiliary angle momentum is considered, suppose that the relation between 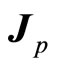 and
and  is
is
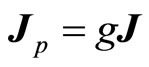 (103)
(103)
The formula above gives the Lande factor a new physical meaning. In this way, magnetic moment of particle becomes
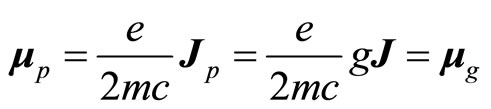 (104)
(104)
By introducing new total angle momentum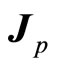 , the direction of magnetic moment is the same as
, the direction of magnetic moment is the same as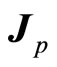 . We do not need the assumption that
. We do not need the assumption that 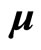 precesses around angle total momentum
precesses around angle total momentum 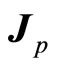 again. In experiments, particle’s angle momentum can not be observed directly. What can be done is magnetic moment. We obtain angle momentum through measurement of magnetic moment actually. So introducing new total angle momentum does not cause inconsistent. Inversely, angle momentum theory of micro-particle becomes more rational.
again. In experiments, particle’s angle momentum can not be observed directly. What can be done is magnetic moment. We obtain angle momentum through measurement of magnetic moment actually. So introducing new total angle momentum does not cause inconsistent. Inversely, angle momentum theory of micro-particle becomes more rational.
The relation between auxiliary angle momentum and spin is discussed below. Because the motions of objects are restrained on a plane in center force fields, we suppose that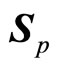 ,
,  ,
, 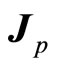 ,
, 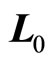 and
and 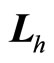 are located on a plane. As shown in Figure 1, we have following relations
are located on a plane. As shown in Figure 1, we have following relations
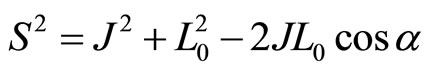 (105)
(105)
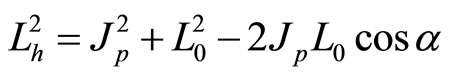 (106)
(106)
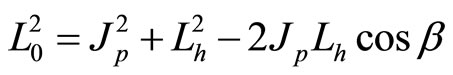 (107)
(107)
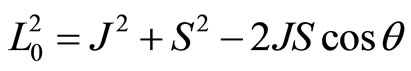 (108)
(108)
From (103), (105) and (106), we get
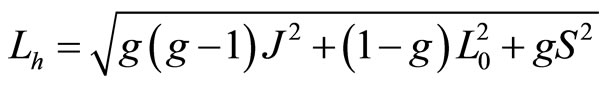 (109)
(109)
From (107) and (108), we obtain
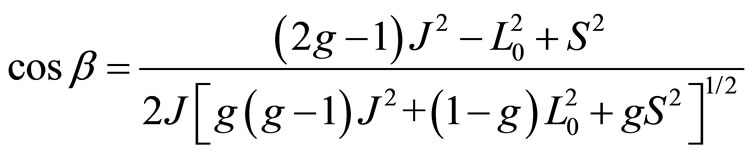 (110)
(110)
We know the values of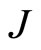 ,
, 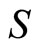 and
and 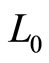 from quantum mechanics. The Lande factor
from quantum mechanics. The Lande factor 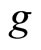 can be obtained from experiment. So
can be obtained from experiment. So  and
and 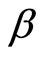 can be determined based on (109) and (110). For example, when
can be determined based on (109) and (110). For example, when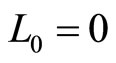 ,
, 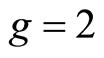 and
and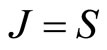 , we have
, we have 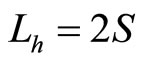 and
and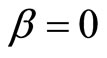 . In this case,
. In this case, 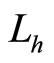 is just the angle momentum of electron in ground state hydrogen atom. That is to say, for ground state hydrogen atom with
is just the angle momentum of electron in ground state hydrogen atom. That is to say, for ground state hydrogen atom with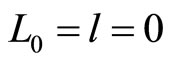 , it is just angle momentum
, it is just angle momentum 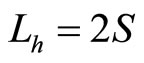 which ensures electron’s stable motion around atomic nuclear without falling into it. In this case, the magnetic moment caused by auxiliary angle momentum is
which ensures electron’s stable motion around atomic nuclear without falling into it. In this case, the magnetic moment caused by auxiliary angle momentum is
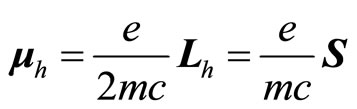 (111)
(111)
In this way, we explain that spin gyro-magnetic ratio is two times of orbit gyro-magnetic ratio. It indicates that 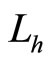 is real angle momentum, in stead of spin. We should consider
is real angle momentum, in stead of spin. We should consider 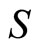 as a kind of quantum number. Based on it, we can obtain real angle momentums of micro-particles. As shown in Figure 1, we have relation
as a kind of quantum number. Based on it, we can obtain real angle momentums of micro-particles. As shown in Figure 1, we have relation
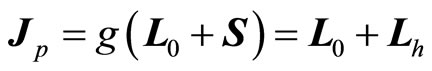 (112)
(112)
In fact, in quantum mechanics, we use the Pauli equations to describe the Zeeman effects of spectrum splits in magnetic fields. The equations are
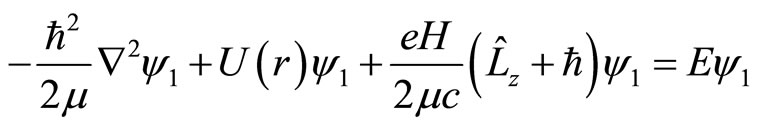 (113)
(113)
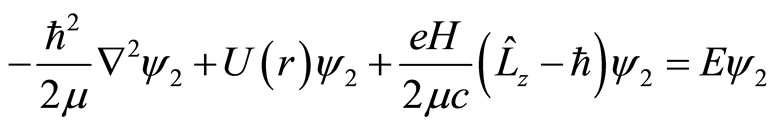 (114)
(114)
In the formulas, we have  and
and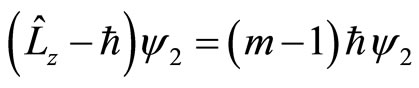 . It means that the partial quantity of angle momentums at
. It means that the partial quantity of angle momentums at 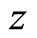 axis direction is
axis direction is 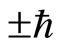 actually. The reason to write the projection of spin at any direction of space as
actually. The reason to write the projection of spin at any direction of space as 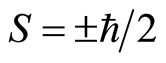 is only for of mathematical convenience. Speaking correctly, we should consider
is only for of mathematical convenience. Speaking correctly, we should consider 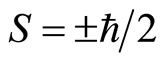 as a kind of quantum number based on it we can obtain correct angle momentums of micro-particles.
as a kind of quantum number based on it we can obtain correct angle momentums of micro-particles.
In general situations , the angle momentum of micro-particles becomes complex. For example, for the states
, the angle momentum of micro-particles becomes complex. For example, for the states ,
,  and
and 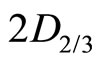 of hydrogen atom, according to (109) and (110), we obtain
of hydrogen atom, according to (109) and (110), we obtain
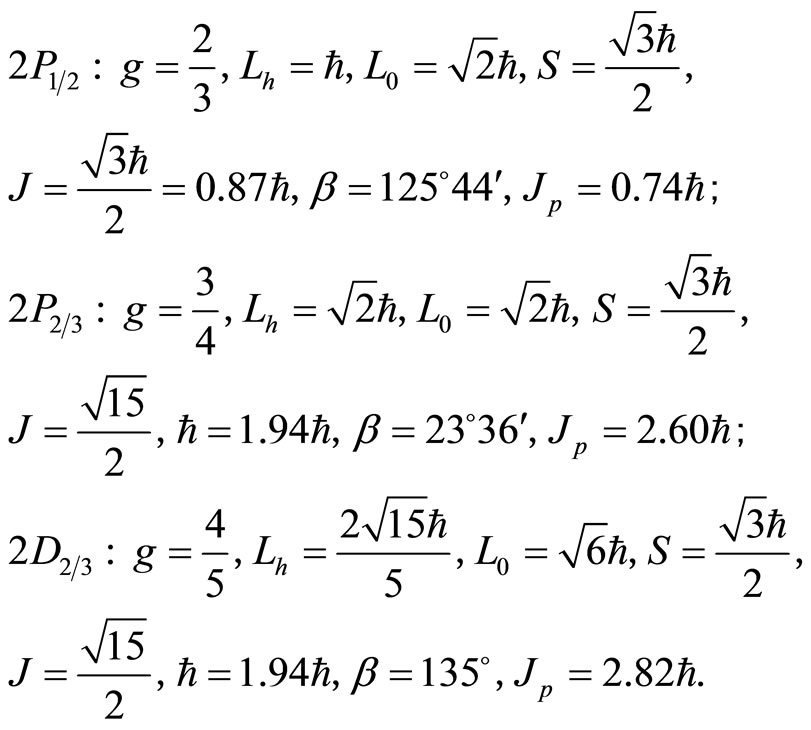 (115)
(115)
In this way, we reveal the essence of micro-particle’s spin. Spin is not real angle momentum though it related to angle momentum. Due to the incompleteness of angle momentum operator in quantum mechanics, we introduce the concept of spin. The quantities of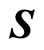 ,
, 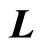 and
and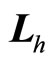 , are only useful tools. By means of these, we can construct real angle momentum
, are only useful tools. By means of these, we can construct real angle momentum 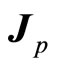 of micro-particles. Auxiliary angle momentum
of micro-particles. Auxiliary angle momentum 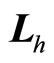 does not appear automatically in quantum mechanics. By means of it, the relation between real total angle momentum
does not appear automatically in quantum mechanics. By means of it, the relation between real total angle momentum 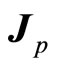 and magnetic moment
and magnetic moment 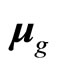 becomes normal. We do not need to assume that magnetic moment precesses around
becomes normal. We do not need to assume that magnetic moment precesses around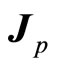 . We have only a real angle momentum
. We have only a real angle momentum 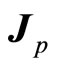 for microparticle.
for microparticle.
5. The Real Reason That Bell Inequality Is Not Supported by Experiments
5.1. The Deduction of the Bell Inequality
Based on the clarification of spin’s essence, we can explain why the Bell inequality is not supported by experiments. It is due to the misunderstanding of the spin’s projections of micro-particles.
Let’s first describe the deduction process of the Bell inequality briefly [12]. Suppose there is a system composed of two particles with opposites spin 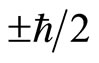 individually, so the total spin of system is zero. Spin operator is
individually, so the total spin of system is zero. Spin operator is 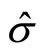 and we take
and we take 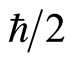 as unite. Let
as unite. Let  represent the spin’s measurement value of particle 1 at
represent the spin’s measurement value of particle 1 at  direction,
direction, 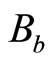 represent the spin’s measurement value of particle 2 at
represent the spin’s measurement value of particle 2 at 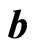 direction. The average value
direction. The average value 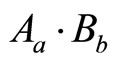 of association operator
of association operator 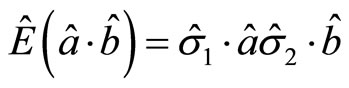 is
is
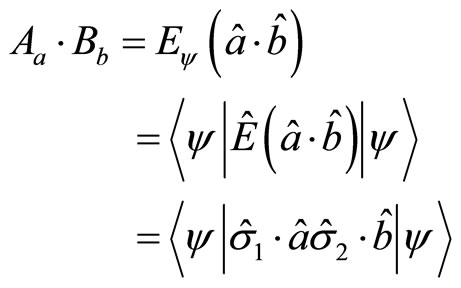 (116)
(116)
The wave function of the system is
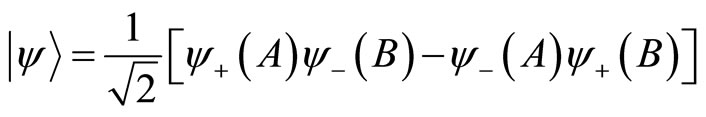 (117)
(117)
By substituting (117) in (116), the calculating result of quantum mechanics is
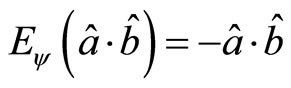 (118)
(118)
When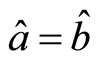 , we have
, we have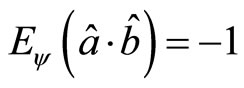 . Suppose that there exists hidden variable
. Suppose that there exists hidden variable 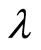 which makes deterministic motion possible for micro-particle. The ensemble distribution function of hidden variable is
which makes deterministic motion possible for micro-particle. The ensemble distribution function of hidden variable is 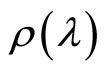 which is normalized with
which is normalized with
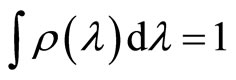 (119)
(119)
The average value of association operator on the ensemble function of hidden variable is
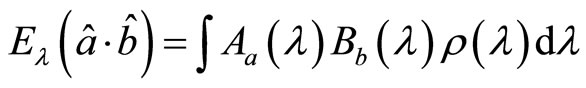 (120)
(120)
If theory is localized one without interaction at distance, the measurement about particle 1 only depends on 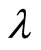 and
and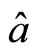 , having nothing to do with
, having nothing to do with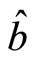 . Meanwhile, the measurement about particle 2 also depends on
. Meanwhile, the measurement about particle 2 also depends on 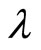 and
and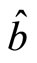 , having nothing to do with
, having nothing to do with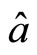 . So for arbitrary
. So for arbitrary 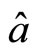 and
and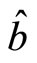 , we have
, we have
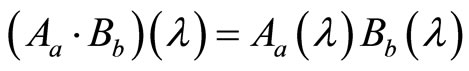 (121)
(121)
Because two particles have opposites spins, when 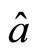 and
and 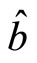 are at the same directions, according to (118), we have
are at the same directions, according to (118), we have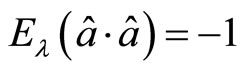 . It means
. It means
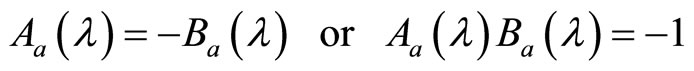 (122)
(122)
Let  be another direction vector, because of
be another direction vector, because of 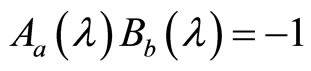 , we have
, we have
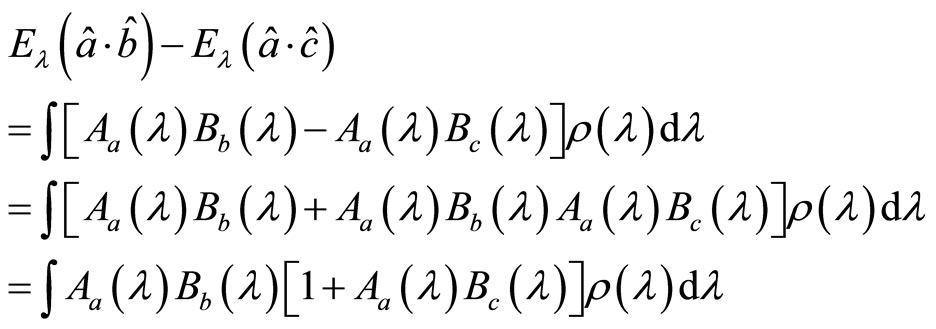 (123)
(123)
Because of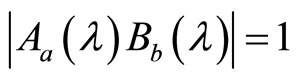 , from (123) we get
, from (123) we get
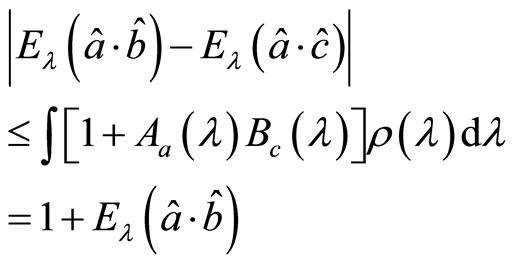 (124)
(124)
Let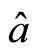 ,
, 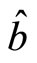 and
and 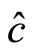 are vectors on the same surface. The angles between
are vectors on the same surface. The angles between 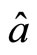 and
and 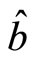 is
is , between
, between 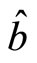 and
and 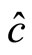 is also
is also , between
, between 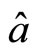 and
and 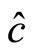 is
is . According to quantum mechanics we have
. According to quantum mechanics we have
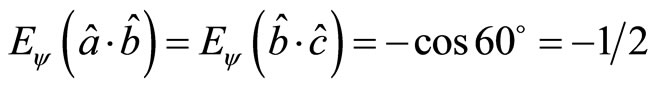 ,.
,.
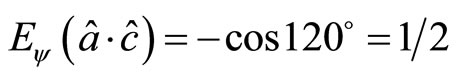 .
.
Let 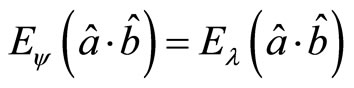 and substitute it into (124), however, we get absurd result
and substitute it into (124), however, we get absurd result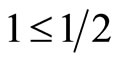 . It means that (124) can not coincide with the result of quantum mechanics (118). Since the Bell inequality is advanced, many experiments are completed. Most of them support quantum mechanics, not support the Bell inequality. So physicists do not think that hidden variables exist. The determined descriptions of micro-particles are considered impossible.
. It means that (124) can not coincide with the result of quantum mechanics (118). Since the Bell inequality is advanced, many experiments are completed. Most of them support quantum mechanics, not support the Bell inequality. So physicists do not think that hidden variables exist. The determined descriptions of micro-particles are considered impossible.
5.2. The Real Reason That the Bell Inequality Is Not Supported by Experiments
After the Bell inequality was established, a lots of experiments were completed. Most of them support quantum mechanics does not support the Bell inequality. So according to current point of view, hidden variables do not exist and the deterministic descriptions of microparticles are considered impossible.
Based on discussion above, we can say that real reasons to make the Bell inequality impossible is the misunderstanding of spin’s projection. According to current understanding, the projections of spin at arbitrary directions are always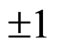 . However, this kind of vector can not exist in physical space. Suppose vector
. However, this kind of vector can not exist in physical space. Suppose vector 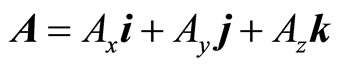 with mode
with mode , if the projection of
, if the projection of  at direction
at direction  is
is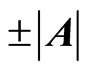 , the projections at directions
, the projections at directions 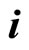 and
and 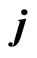 can only be zero. No any physical vector can have same projections at different directions in real space.
can only be zero. No any physical vector can have same projections at different directions in real space.
In fact, spin is always coupled with magnetic field when we construct the interaction Hamiltonian. The correct understanding of spin is that if we chose z axis as the direction of magnetic field, the projection of spin at z axis direction of is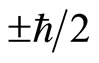 . That is to say, the projection of spin at the direction of magnetic field is
. That is to say, the projection of spin at the direction of magnetic field is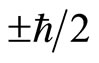 , rather than at arbitrary direction! Speaking strictly, in quantum mechanics, spin is coupled with magnetic field in the value of
, rather than at arbitrary direction! Speaking strictly, in quantum mechanics, spin is coupled with magnetic field in the value of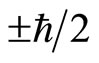 . If the direction of magnetic field is certain, the coupling between spin and magnetic field is certain. At other directions, we can not observe the physical affections of spin. In fact, in current quantum mechanics, matrix operators are used to describe spin with
. If the direction of magnetic field is certain, the coupling between spin and magnetic field is certain. At other directions, we can not observe the physical affections of spin. In fact, in current quantum mechanics, matrix operators are used to describe spin with
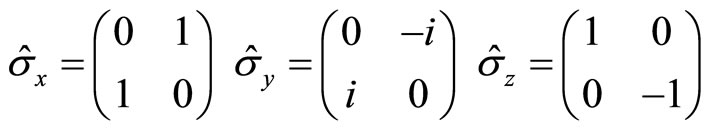 (125)
(125)
By acting them on spin wave functions 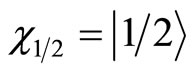 and
and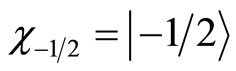 , we have
, we have
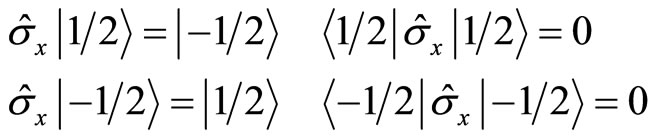 (126)
(126)
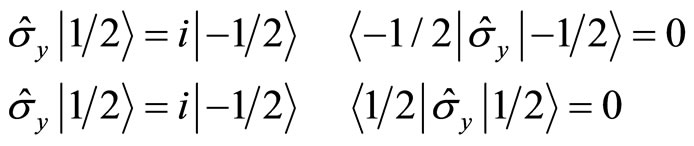 (127)
(127)
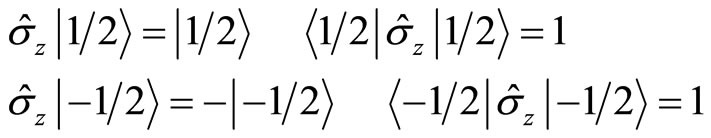 (128)
(128)
Therefore, only (128) is the eigen equation of spin operator 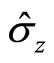 with eigen values
with eigen values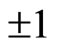 .
. 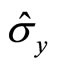 and
and 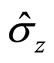 are not the eigen operators of
are not the eigen operators of 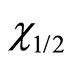 and
and 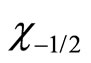 and do not have certain eigen values. So we can not think particle’s spins have same projection values
and do not have certain eigen values. So we can not think particle’s spins have same projection values 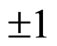 at arbitrary directions. Because the square of spin operator is
at arbitrary directions. Because the square of spin operator is
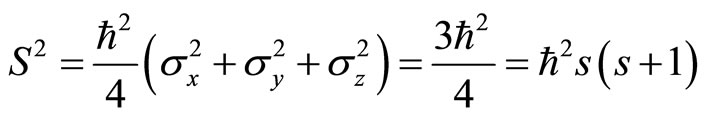 (129)
(129)
so the value of spin is actually
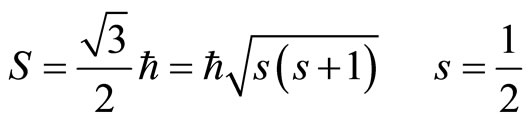 (130)
(130)
It is more proper to consider 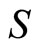 and
and 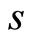 as a kind of quantum number, in stead of spin angle momentum itself. In light of mathematics strictly, as a practical physical quantity, the projection of spin operator at
as a kind of quantum number, in stead of spin angle momentum itself. In light of mathematics strictly, as a practical physical quantity, the projection of spin operator at 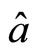 direction is
direction is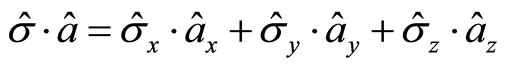 . The projection at z direction should be
. The projection at z direction should be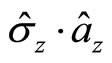 . According to quantum mechanics, we have
. According to quantum mechanics, we have
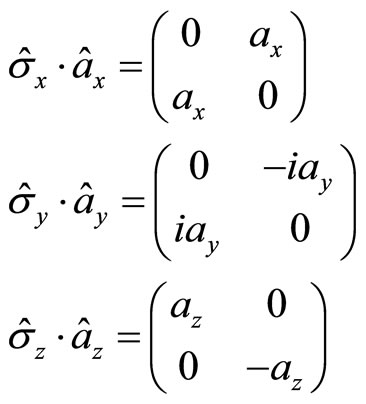 (131)
(131)
Here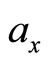 ,
, 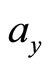 and
and 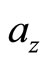 are the projections of unit vector
are the projections of unit vector 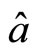 at
at ,
, 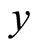 and
and 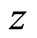 axis directions. We have
axis directions. We have
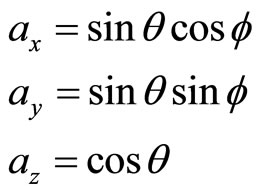 (132)
(132)
So the formula (131) means that the projections of spin operator at arbitrary direction take the values between , rather than
, rather than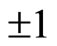 . When calculating the average values of
. When calculating the average values of 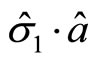 about the wave function of a single particle, we have
about the wave function of a single particle, we have
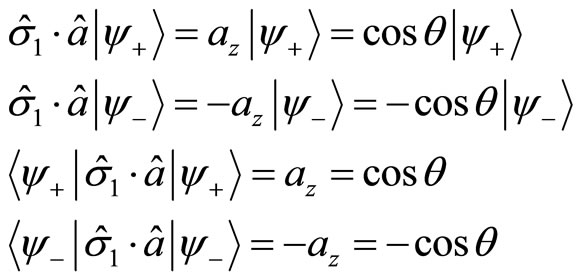 (133)
(133)
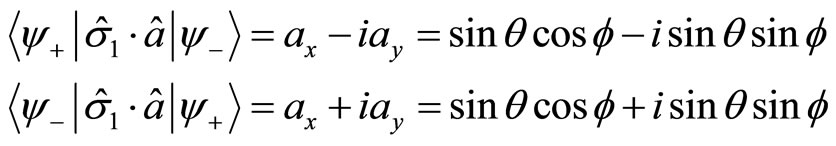 (134)
(134)
Based on (133) and (134), we get (118). However, in the deduction of the Bell inequality, we let 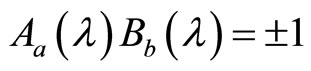 . It means that the projection of electron’s spin at arbitrary direction can only take
. It means that the projection of electron’s spin at arbitrary direction can only take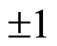 . This result is different from (131)-(134) and can not be realized in real physical space. So it is inevitable that the Bell inequality can not be supposed by experiments. The Bell inequality is a misunderstanding of mathematics, having nothing to do with hidden hypotheses. It neither coincides with quantum mechanics, nor coincides with classical mechanics and any logic of mathematics and physics.
. This result is different from (131)-(134) and can not be realized in real physical space. So it is inevitable that the Bell inequality can not be supposed by experiments. The Bell inequality is a misunderstanding of mathematics, having nothing to do with hidden hypotheses. It neither coincides with quantum mechanics, nor coincides with classical mechanics and any logic of mathematics and physics.
In fact, according to this paper, spin is not real physiccal quantity which can be determined directly. What can be done in experiments is magnetic moment. Magnetic moment is related with angle momentum directly. According to (112), the projection of auxiliary angle momentum at α direction is
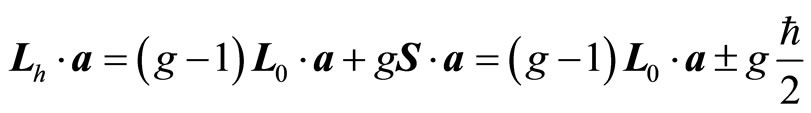 (135)
(135)
The eigen values of 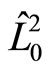 is
is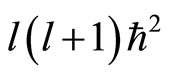 . Suppose that the angle between
. Suppose that the angle between 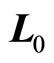 and
and 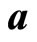 is
is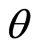 , (135) becomes
, (135) becomes
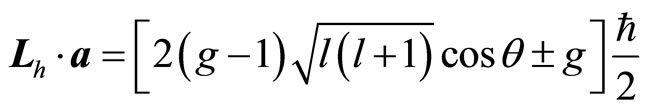 (136)
(136)
Take 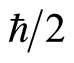 as unit, let
as unit, let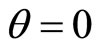 , for the electron at
, for the electron at 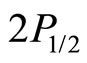 state, we have
state, we have 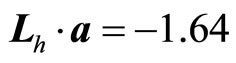 or
or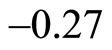 . For the electron at
. For the electron at state, we have
state, we have 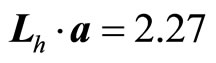 or
or 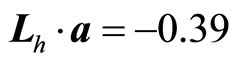 . For the electron at
. For the electron at 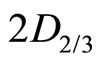 state, we have
state, we have 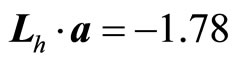 or
or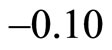 . For the ground electron with
. For the ground electron with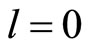 , we have
, we have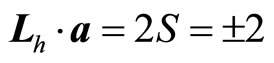 , so
, so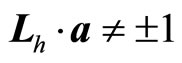 . Let
. Let 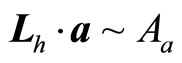 and
and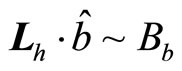 , we have
, we have 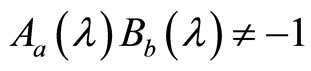 in general.
in general.
In fact, E. P. Wigner had posed a proof of the Bell inequality which did not depend on hidden variables [13]. But it still based on the hypothesis that the projections of spin at arbitrary direction of space were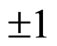 . From this result we see again that the deduction of Bell inequality has nothing to do with hidden variables. The violation of the Bell inequality also has nothing to do with whether or not hidden variables exist.
. From this result we see again that the deduction of Bell inequality has nothing to do with hidden variables. The violation of the Bell inequality also has nothing to do with whether or not hidden variables exist.
5.3. The Polarization Correlation of Photon and the Bell Inequality
Most experiments for the verification of Bell inequality are related to polarization correlation of photons [14]. In the deduction of Bell inequality for these processes, photon’s polarization values are considered to be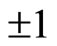 . When a photon passes through a polarize, its polarization value is considered to be
. When a photon passes through a polarize, its polarization value is considered to be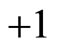 . When a photon does not pass, its polarization value is considered to be –1 [15]. The deduced Bell inequality can not be supported by experiments. The reason is the same as the projections of spin. In fact, light’s polarization is macro-concept. It is meaningless to talk about polarization about a single photon. We can only discuss light’s polarization from the macro-viewpoint of statistical average.
. When a photon does not pass, its polarization value is considered to be –1 [15]. The deduced Bell inequality can not be supported by experiments. The reason is the same as the projections of spin. In fact, light’s polarization is macro-concept. It is meaningless to talk about polarization about a single photon. We can only discuss light’s polarization from the macro-viewpoint of statistical average.
We know in classical optics that the polarization direction of light is defined as the vibration direction of electromagnetic field. When a beam of polarization light passes through polarizer, the vibration direction of electromagnetic field is changed. For example, when a beam of polarization light passes through calcite, it becomes two lights named e light and o light. Their vibration directions are different from original one. If we must define the concept of polarization for a single photon, we can only consider its polarization direction as the direction of electromagnetic field. When a photon pass through a polarizer with an angle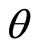 , the vibration direction of electromagnetic field turns an angle
, the vibration direction of electromagnetic field turns an angle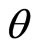 . In this case, we should think that photon’s polarization becomes
. In this case, we should think that photon’s polarization becomes . That is to say, even in classical optics, for photons which pass through polarizer, their polarization is considered as
. That is to say, even in classical optics, for photons which pass through polarizer, their polarization is considered as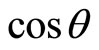 , in stead of
, in stead of 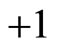 in general. For photons which are reflected without passing through polarizer, their polarization values depend on the angle of reflection, in stead of
in general. For photons which are reflected without passing through polarizer, their polarization values depend on the angle of reflection, in stead of 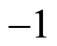 in general. In fact, in quantum mechanics, when calculating polarization correlation of photons, we use some formulas similar to (126)-(128) which are related to the direction angle
in general. In fact, in quantum mechanics, when calculating polarization correlation of photons, we use some formulas similar to (126)-(128) which are related to the direction angle 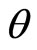 of polarization. It is impossible for photons always to have polarization values
of polarization. It is impossible for photons always to have polarization values 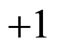 or
or 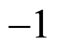 under arbitrary situation.
under arbitrary situation.
Because photon’s polarization values are always taken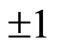 , the mistake is the same as made for particle’s spin when we deduct the Bell inequality of photon’s polarizations correlation. It is also inevitable that this kind of Bell inequality can not be supported by experiments. Therefore, the violation of Bell inequality of photon’s polarizations correlation also has nothing to do with hidden variables.
, the mistake is the same as made for particle’s spin when we deduct the Bell inequality of photon’s polarizations correlation. It is also inevitable that this kind of Bell inequality can not be supported by experiments. Therefore, the violation of Bell inequality of photon’s polarizations correlation also has nothing to do with hidden variables.
6. The Elimination of EPY Momentum Paradox in Quantum Mechanics
The momentum paradox of Einstein-Pauli-Yukawa is a confusing problem in quantum mechanics. Based on the definition of universal momentum operator in this paper, we can eliminate it. Let’s first repeat this problem. We discuss a micro-particle’s motion in the infinite potential trap of one dimension with form
 (137)
(137)
By solving the motion equation of quantum mechanics, we obtain particle’s energy
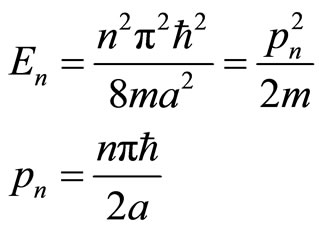 (138)
(138)
Here 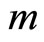 is particle’s mass. In the region
is particle’s mass. In the region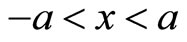 , wave function is
, wave function is
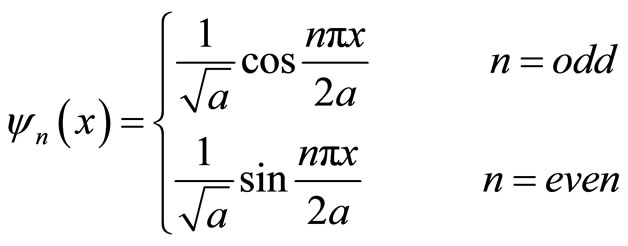 (139)
(139)
In the region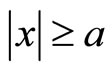 ,
,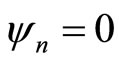 . The wave function of ground state can be written as
. The wave function of ground state can be written as
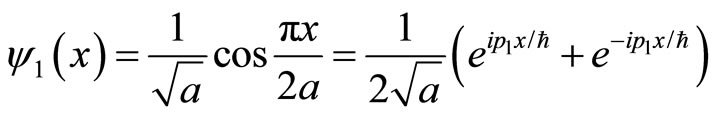 (140)
(140)
By acting momentum operator 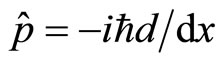 on (140), we obtain two egein values
on (140), we obtain two egein values . The result indicates that the wave function can be considered as the overlap of two wave functions with different momentums
. The result indicates that the wave function can be considered as the overlap of two wave functions with different momentums  . So Einstein, Pauli and Yukawa thought that the particles in the ground state has only two independent momentum
. So Einstein, Pauli and Yukawa thought that the particles in the ground state has only two independent momentum 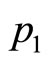 and
and 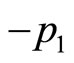 with probability
with probability 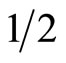 individually.
individually.
On the other hand, by substituting (140) in (68), the wave function in momentum space is
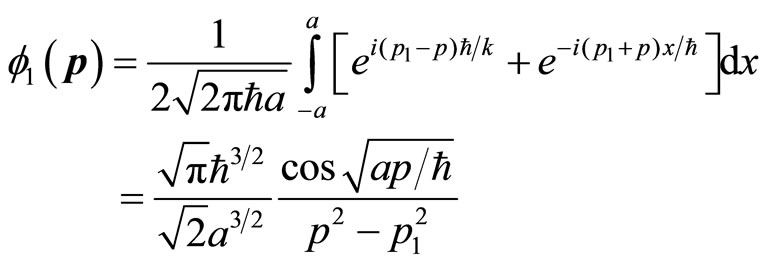 (141)
(141)
The possibility distribution of momentum is
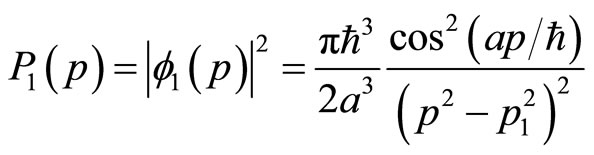 (142)
(142)
It is not the distribution of two momentums 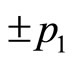 with probability
with probability  individually. This is the so-called EPY momentum paradox is caused. Because this paradox can not be solved up to now days, some persons even thought that the logical foundation of quantum mechanics was inconsistent [16].
individually. This is the so-called EPY momentum paradox is caused. Because this paradox can not be solved up to now days, some persons even thought that the logical foundation of quantum mechanics was inconsistent [16].
The problem is that according to discussion above, we can not define rational momentum operator for quantum mechanics in the situation of one dimension. If we act current momentum operator on wave functions (139) or (140), the obtained non-eigen value is an imaginary number. We have
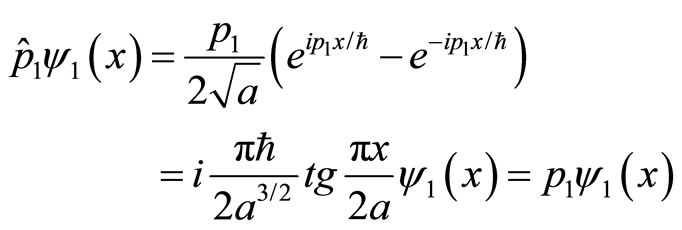 (143)
(143)
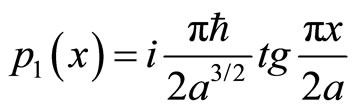 (144)
(144)
According to discussion before, we can not find a proper momentum operator for micro-particle which moves in one dimensional space. That is to say, in one dimensional infinite trap, particle’s momentums can not be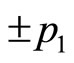 .
.
Some one proposed the explanation of boundary condition trying to eliminate EPY paradox [6]. According to this explanation, when (139) is written in the form of (140), 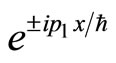 is the normalized wave function in a box, rather than the wave function of free particle in the region without boundary. The restriction of boundary condition would produce a great influence on the nature of wave functions. If
is the normalized wave function in a box, rather than the wave function of free particle in the region without boundary. The restriction of boundary condition would produce a great influence on the nature of wave functions. If 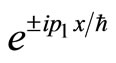 are the wave functions with infinite boundary, after they are transformed in momentum space, the wave functions should be the
are the wave functions with infinite boundary, after they are transformed in momentum space, the wave functions should be the 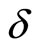 function with
function with
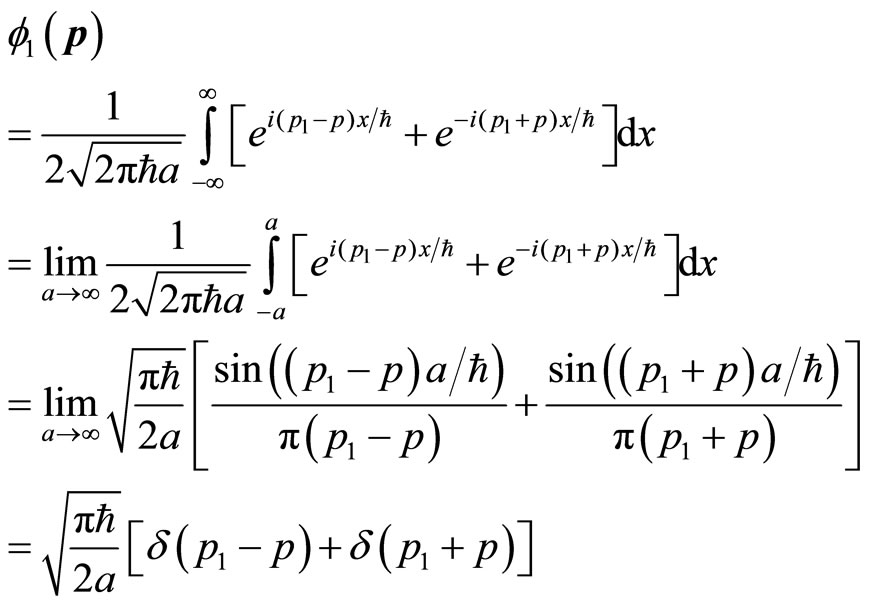 (145)
(145)
It represents two momentums which is the same with the result in coordinate space. But if particles are located in infinite trap with the restriction of boundary condition, (145) can not hold.
This kind of explanation has its reason but has not touch the essence. Because (138) is the wave function in coordinate space, the definition of momentum operator of quantum mechanics is unrelated to boundary condition, no matter whether boundary conditions are finite or infinite, the actions of momentum operator on wave function are effect and certain. In fact, the boundary conditions have been considered when we solve the motion equation of quantum mechanics. That is to say, the influence of boundary condition has been contained in the wave functions. So it is unnecessary for us to consider boundary condition. When we act momentum operator on wave function, the result we get is what it should be. By acting 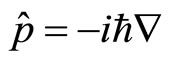 on wave function (140), we can only get
on wave function (140), we can only get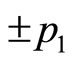 . It indicates that we only have two discrete momentums. The EPY momentum paradox has not eliminated really by considering boundary condition.
. It indicates that we only have two discrete momentums. The EPY momentum paradox has not eliminated really by considering boundary condition.
According this paper, though (140) represents the wave function in coordinate space, the momentum operator is not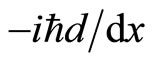 , so particle’s momentum is not
, so particle’s momentum is not 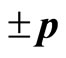 in infinite trap. Because the Fourier transform of (68) is a pure mathematical one, its result is undisputed. Therefore, the momentum distribution (142) is correct. We see again that thought we can have rational definition of kinetic energy operator, we may not find proper momentum operator to match with kinetic energy operator sometimes.
in infinite trap. Because the Fourier transform of (68) is a pure mathematical one, its result is undisputed. Therefore, the momentum distribution (142) is correct. We see again that thought we can have rational definition of kinetic energy operator, we may not find proper momentum operator to match with kinetic energy operator sometimes.
7. Conclusions
According to current quantum mechanics, when the operator is acted on non-eigen function, non-eiegn values and average values of momentum operator are complex numbers in general. In theses cases, momentum operator is no longer the Hermitian operator. Though we can make the average values real numbers in momentum representation, it leads to inconsistency of coordinate space and momentum space. Using momentum operator and kinetic operator to calculate momentum of micro-particles, the results may be different. It means that kinetic operator and momentum operator of quantum mechanics are not one-to-one correspondence. Besides momentum operator, other operators in quantum mechanics, just as angle momentum operator, also have the same problems. These problems have not caused the attention of physicists at present day. Because these problems involve the rationality of logical foundation of quantum mechanics, we should treat them seriously.
By introducing the concept of universal momentum operator, all of these problems can be solved well. Under the premises of ensuring kinetic operator to be invariable, non-eigen values and average values of universal momentum operator are real numbers. In this way, the description of physical processes can be equivalent really in coordinate representation and momentum representation. For eigen wave function, universal momentum operator restores to the current Hermitian operator. For general situations, universal operator is not the Hermitian operator because it is unnecessary. The most important thing in physics is that the average values of operator should be real numbers. Using universal momentum operator and kinetic operator to calculate micro-particle’s kinetic energy, the results are still different, but we can get consistent result through proper method. Only in this way, we can reach logical consistency for quantum mechanics. The problems of momentum operator’s definition in the curved coordinate reference systems can be solved well.
Therefore, we need to introduce the concept of auxiliary momentum and auxiliary angle momentum. The relation between auxiliary angle momentum and spin is deduced and the essence of micro-particle’s spin is revealed. Spin is related to auxiliary angle momentum of micro-particle which angle momentum operator can not describe. We understand real reason why the Bell inequality is not supported by experiments. It is due to the misunderstanding of spin’s projections and photon’s polarizations. No any real angle momentum can have same projections at different directions in real physical space. The violation of the Bell inequality has nothing to do with whether or not the hidden variables exist actually. In this way, the EPY momentum paradox can also be eliminated thoroughly. The logical foundation of quantum mechanics becomes more perfect.
REFERENCES
- A. Einstein, “Science Paper Presented to Max Born, on His Retirement from the Tait Chair of Natural Philosopby in the University of Edinburgh,” 1953.
- W. Pauli, “Pauli Lecture on Physics,” MIT Press, Cambridge, 1973.
- H. Yukawa, “Quantum Mechanics,” 2nd Edition, YanBo, Bookshop, Tokyo, 1978.
- X. l. Ge, “Quantization of Canonical Coordinates,” 2001.
- Y. b. Zhang, “Momentum Operator and Kinetic Operator in Curved Coordinates,” 1988.
- Z. Xu, “Discuss on Canonical Operators,” 1991.
- C. b. Liang, “Quantization of Classical Systems,” Journal of Beijing Normal University, Vol. l, 1994, p. 67.
- H. Guang, “Foundation of Quantum Mechanics,” 1996.
- J. M. Domingos and M. H. Caldeira, “Self-Adjiontness of Momentum Operators in Generalized Coordinates,” Foundation of Physics, Vol. 14, No. 2, 1984, pp. 147-154. doi:10.1007/BF00729971
- M. Vos and I. McCarthy, “Electron-Momentum Spectroscopy and the Measurement of Orbits,” American Journal of Physics, Vol. 65, No. 6, 1997, p. 544. doi:10.1119/1.18586
- Y. d. Zhang, “Quantum Mechnics,”, 2008.
- J. S. Bell, “On the Problem of Hidden Variables in Quantum Mechanics,” Reviews of Modern Physics, Vol. 38, No. 3, 1966, pp. 447-452.
- E. P. Wigner, “Survival and the Bomb; Methods of Civil Defense,” American Journal of Physics, Vol. 38, No. 11, 1970, p. 1367. doi:10.1119/1.1976129
- J. F. Clauser, M. A. Horne, A. Shimony and R. A. Holt, “Proposed Experiment to Test Local Hidden-Variable Theories,” Physical Review Letters, Vol. 23, No. 15, 1969, pp. 880-884. doi:10.1103/PhysRevLett.23.880
- S. J. Freedman and J. F. Clauser, “Experimental Test of Local Hidden-Variable Theories,” Physical Review Letters, Vol. 28, No. 14, 1973, pp. 938-941. doi:10.1103/PhysRevLett.28.938
- Z. y. Tao, “An Question on the Foundation of Quantum Mechanics,” Academic Journal of Photons, Vol. 26, 1997, p. 769.

