Journal of Modern Physics
Vol.3 No.4(2012), Article ID:25413,6 pages DOI:10.4236/jmp.2012.34045
The Investigation and Study of Hydrogen Atom in Spherical Cavity Using B-Spline Basis Functions: A Mathematical Approach
Institute for Advanced Studies, Tehran, Iran
Email: *mohammadalighorbani1983@yahoo.com
Received January 11, 2012; revised February 27, 2012; accepted March 10, 2012
Keywords: Hydrogen Atom; Spherical Cavity; B-Spline Basis Functions; Quantum Systems; Nanoscience; Variational Method; Wave Functions; B-Splines’ Properties
ABSTRACT
The importance of studying the confined quantum systems as one of the most basic subjects in nanoscience is undeniable. The hydrogen atom confined in the spherical cavity is considered as one of the most important systems. In this paper, the energy spectrum of the hydrogen atom confined in the center of impermeable spherical cavity is computed through the variational method, and B-splines are utilized as the basis functions. These basis functions are able to produce the test wave functions with appropriate boundary conditions. High flexibility and localizability are the most significant B-splines’ properties. Furthermore, these functions are numerically stable, and able to accurately perform a substantial number of calculations. The proportion of changes in energy levels to changes in cavity’s dimensions is investigated. Considering the obtained results suggests this method’s high accuracy and performance.
1. Introduction
When an atom is confined in a space being proportional to its dimensions, it shows different properties than the state it is free. These differences include changes in atomic orbitals, energy levels, how filling electron shells, linear and non-linear polarizability, photoionization/photon absorption, and hyperfine structure [1]. It is evident that the investigation of these changes has attracted the interest of many researchers in physics and chemistry.
In the year 1937, when Michels et al. were studying the impact of pressure on the hydrogen atom [2], they came up with the idea of simplifying the solution to problem through using atom-in-cage model that has been really beneficial. This simple model’s important role in the investigation of confined systems was revealed in various scientific fields thereafter.
Over the past decade, the confined quantum systems have attracted a great deal of attention. In this regard, the cases such as quantum wells, quantum wires, and quantum dots in the solid-state physics are well known. Considering the dimensions and behaviors the nanocrystals have and exhibit, they are considered as the actual sample of confined quantum systems. In the atomic physics, the good examples of confined quantum systems include the atoms imprisoned in the zeolite trap, the atoms trapped in the fullerene cages, and the nanobubbles formed around external particles in the liquid-helium medium under high pressure in the nuclear reactor wall [3,4]. The cage model has also been employed to design the internal parts of giant planets such as Jupiter and Saturn [5]. The structure of hydrogen atom is simpler than the other atoms. Thanks to its simple structure, it has been constantly considered as the first choice in the most of fundamental studies conducted on elements. With regards to the study of confined quantum systems, considering the simplicity of confined hydrogen atom and its various applications, many studies on this atom have been hitherto carried out [6]. The model of hydrogen atom confined in the spherical cavity is being widely applied to the semiconductor physics. This model is able to desirably describe the donor behavior of hydrogen (such as confined in the quantum dot). To solve this problem, an accurate variational method is shown using the B-spline basis sets. The energy spectrum for different-sized cavities is investigated. A very good convergence is observed in the results owing to B-splines’ special features. During all the calculations, the atomic units are used as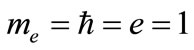 .
.
In this paper, first, the B-spline functions are introduced; then, the method of solving the problem is described; finally, the results are provided, evaluated, and analyzed.
2. The B-Splines Functions
In recent years, one of the advances in the atomic and molecular computational physics has been the utilization of B-spline basis set to calculate the dynamics and structure of atoms and molecules. The B-splines are a special kind of piecewise polynominal functions which were officially introduced by Shoenberg in 1946 for the first time. In the early 1970s, Shore presented the first applications of B-spline functions in the atomic physics. In 1986, Johnson et al. successfully applied the B-splines to the computation of secondor higher-order corrections to study the heavy atoms’ properties. From then onwards, the B-splines have been widely used to investigate various properties of atoms and molecules [7,8]. Over the past few years, the applications of B-spline functions in the quantum, solid mechanics, molecular, atomic, and nuclear physics have been highly developed. These functions have been widely employed to solve the atomicand molecular-photoionization problems [9-23].
The B-splines are square integrable basis functions defined in a limited space (usually called box). These functions’ significant properties include high localizability, flexibility, and numerical stability. Other B-splines’ properties are that they are sufficiently complete with a relatively small number of basis functions, and their linear dependence can be neglected even for a large number of bases. The B-spline basis sets’ completeness is an ideal feature particularly for describing the continuous states and the problems in which all the spectrum is required [7].
A B-spline  with the order
with the order  and a set of points
and a set of points  known as the strand node is defined through the below recurrence relation:
known as the strand node is defined through the below recurrence relation:
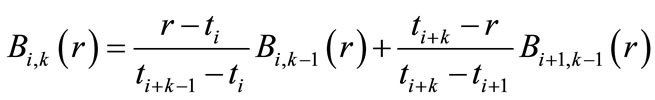 (1)
(1)
 (2)
(2)
where 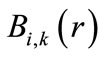 is a piecewise polynomial of the degree
is a piecewise polynomial of the degree 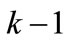 that is non-zero only in the interval
that is non-zero only in the interval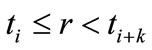 . This indicates the B-splines’ high localizability. The distance between nodes is not required to be equal; the form of
. This indicates the B-splines’ high localizability. The distance between nodes is not required to be equal; the form of 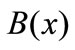 changes smoothly through changing nodes. The nodes are points that are uniformly, non-uniformly, or non-decreasingly distributed over a special interval along the axis r:
changes smoothly through changing nodes. The nodes are points that are uniformly, non-uniformly, or non-decreasingly distributed over a special interval along the axis r:
 (3)
(3)
where N is the number of B-spline basis functions.
One of the B-splines’ advantages is that we have considerable freedom to shear nodes. The distance between nodes can be different; or even, they can overlap each other (the multiplicity nodes). Certainly, if each node overlaps its own adjacent node, the spline function’s degree of continuity will decrease by one unit in that point. The multiple-nodes technique is utilized to establish the boundary conditions.
3. The Solution Method
The state in which an immobile nucleus sits in the center of a sphere with the radius R is considered. The electron can be anywhere inside the sphere, and move freely; but, it never exits through the surface of sphere. It means that the electron wave function is zero outside the sphere. Due to imposing limitation on the system, the confining potential of spherical cage is difficultly applied to the system as the following form:
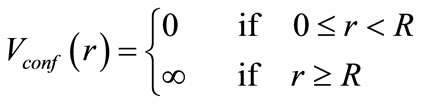 (4)
(4)
An energy eigenstate 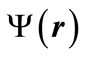 with the energy E, which is a single-electron atom’s delineator, is a solution of the below Schrödinger equation:
with the energy E, which is a single-electron atom’s delineator, is a solution of the below Schrödinger equation:
 (5)
(5)
Considering the problem’s symmetry, it is common to isolate the radial variable, and find a solution to the Schrödinger equation as the following form:
 (6)
(6)
In this equation, the wave function’s angular part has not changed compared with the free-atom wave function. The radial function 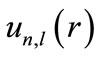 is the solution to the below reduced Schrödinger equation:
is the solution to the below reduced Schrödinger equation:
 (7)
(7)
The variational method is exploited to solve this equation. For this purpose, first,  is expanded in the space of B-spline basis sets:
is expanded in the space of B-spline basis sets:
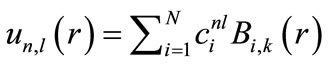 (8)
(8)
where 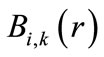 is the ith B-spline of the degree k. N denotes the number of B-spline basis functions utilized to expand the radial wave function. Through the variational method, the Schrödinger radial wave function is as follows:
is the ith B-spline of the degree k. N denotes the number of B-spline basis functions utilized to expand the radial wave function. Through the variational method, the Schrödinger radial wave function is as follows:
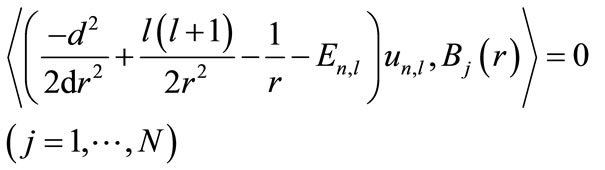 (9)
(9)
The above equation establishes the bases’ orthogonality condition. For a constant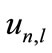 , this equation must be established for all the test functions
, this equation must be established for all the test functions . The normality constraint of the wave function is insured by the Lagrangian multiplier
. The normality constraint of the wave function is insured by the Lagrangian multiplier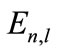 . The integral form of Equation (9) is as follows:
. The integral form of Equation (9) is as follows:
As the Equation (10).
To obtain the Equation (10), the integration by parts is employed. In fact, Equation (10) is a generalized eigenvalue equation as the below form:
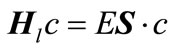 (11)
(11)
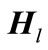 and
and  are the Hamiltonian matrix and overlap matrix, respectively. The Hamiltonian’s index l indicates that the Hamiltonian is written for a specific l. The formation of overlap matrix originates from the fact that the B-splines do not comprise a normal orthogonal set of basis functions. The eigenvalues and Hamiltonian eigenvectors are achieved through solving the eigenvalue function [4,7,24].
are the Hamiltonian matrix and overlap matrix, respectively. The Hamiltonian’s index l indicates that the Hamiltonian is written for a specific l. The formation of overlap matrix originates from the fact that the B-splines do not comprise a normal orthogonal set of basis functions. The eigenvalues and Hamiltonian eigenvectors are achieved through solving the eigenvalue function [4,7,24].
4. Results and Discussion
The seventh-order B-spline basis functions with nodal distribution are used:
 (12)
(12)
where  symbolizes nodes, m and k denote respectively the total number of nodes and the order of B-spline functions. As can be observed, there is a multiplicity of nodal k on the boundaries, and the other nodes are uniformly distributed.
symbolizes nodes, m and k denote respectively the total number of nodes and the order of B-spline functions. As can be observed, there is a multiplicity of nodal k on the boundaries, and the other nodes are uniformly distributed.
The numerical-solution program is written in FORTRAN, and the subprograms of ARPACK and LAPACK libraries are exploited to compute the matrixes. Despite complex calculations, the required period of time to run the program is a few seconds. This is derived from the advantageous features of B-spline functions.
In Table 1, the convergence process of energy eigenvalues for the spherical cage with the radius 1 a.u. is studied. As is obvious, the eigenvalues have an excellent convergence. This matter indicates the completeness of B-spline basis sets.
Tables 2 and 3 provide the energy values for the ground state, and some first excited states for different radii. Currently, the most accurate existing results for the energy eigenvalues of hydrogen atom in the center of spherical cavity pertain to the work conducted by Aquino et al. [25]. Hence, the obtained results are compared with their results as much as possible. In these two tables, the numbers in parentheses are the Aquino et al.’s results. As can be seen, our results are appropriately consistent with their results.
In Table 4, the energy values for four different radii with various quantum numbers of n and l are recorded. It is observed that as the atom is confined more, the energy eigenvalues tend towards larger numbers. This matter demonstrates the first impact of limitation on the energy levels. In the large radii about 10 B, the energy eigenvalues uniformly tend to the energy eigenvalues of free hydrogen atom; actually, in these radii, the hydrogen atom does not sense limited. This case can be clearly seen in Figure 1. The changes in the energy of three states of 1s, 2s, and 2p in proportion to the increase in the confinement radius are illustrated in this figure. As can be observed, the energy levels are relatively high for smaller radii (more severe limitation). As the limitation declines, the values of energy levels tend to constant numbers that actually equal the energy levels of free hydrogen atom.
The second impact of this cage is that it increases the distance between consecutive energy levels of atom in comparison to its free state. In Table 5, this effect can be
 (10)
(10)
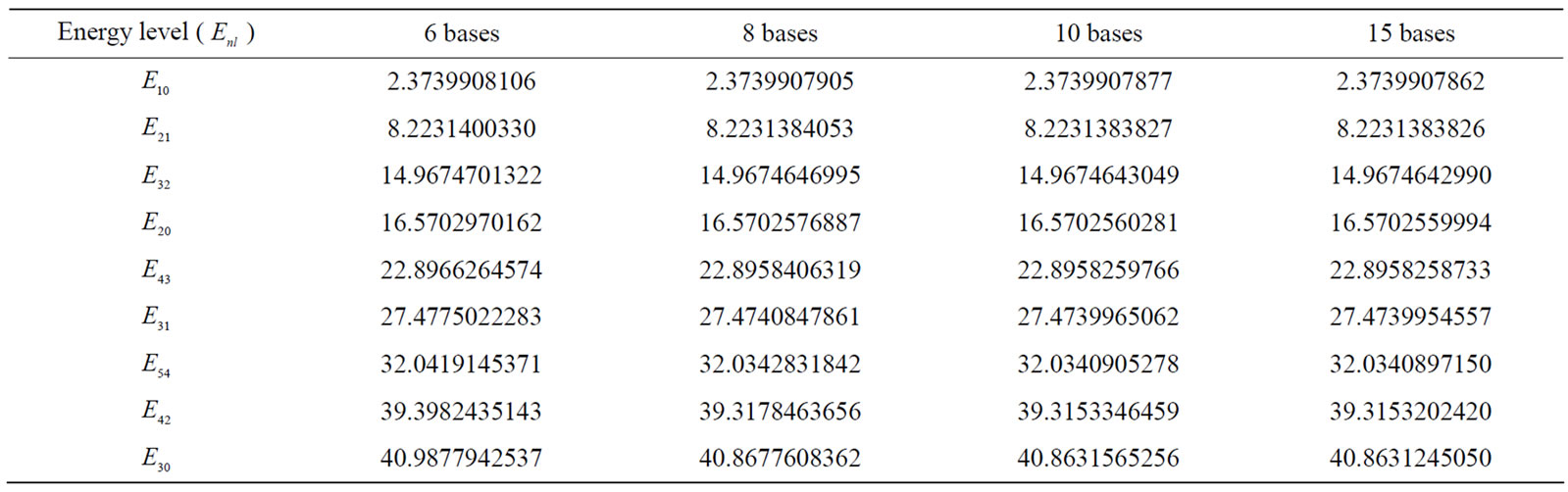
Table 1. The convergence process of energy eigenvalues for the spherical cavity with the radius of 1 B.
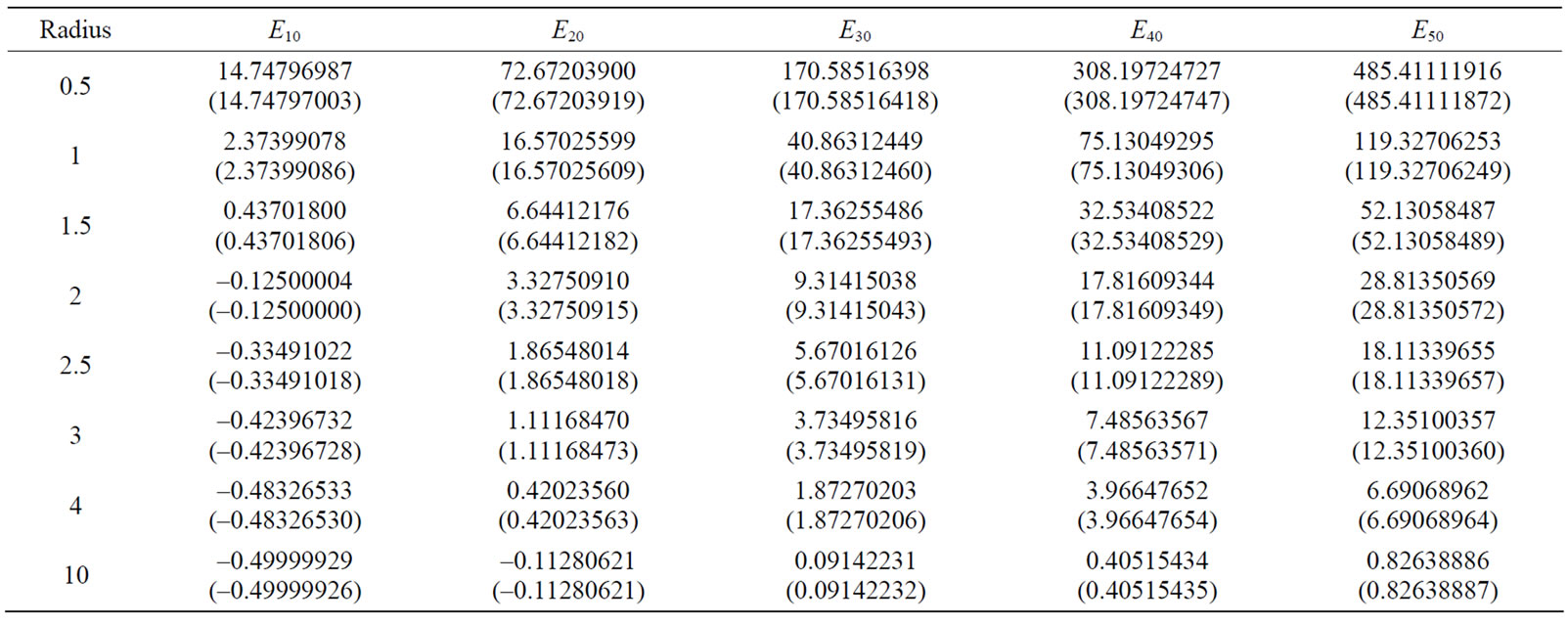
Table 2. The obtained results for the lowest energy levels with l = 0, for different radii. The numbers in parentheses are achieved by Aquino et al.

Table 3. The obtained results for the lowest energy levels with l = 1, for different radii. The numbers in parentheses are achieved by Aquino et al.

Table 4. The values of energy levels for four different radii.
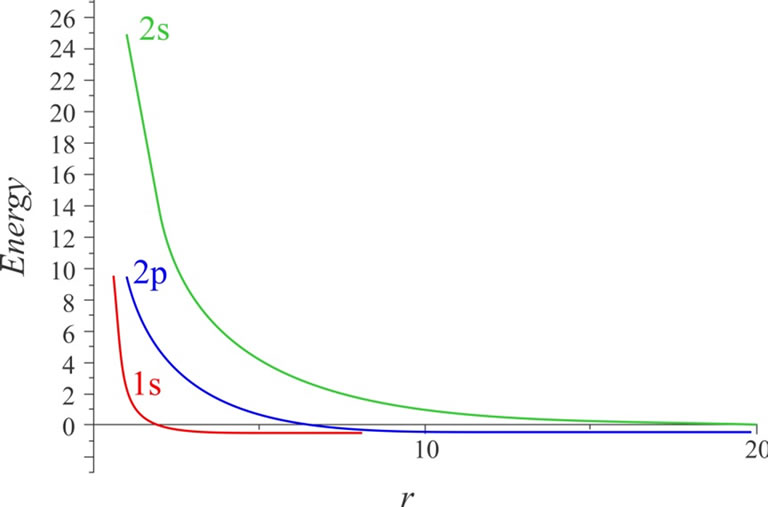
Figure 1. The changes in the energy for the states of 1s, 2s, and 2p according to the cavity’s radius.
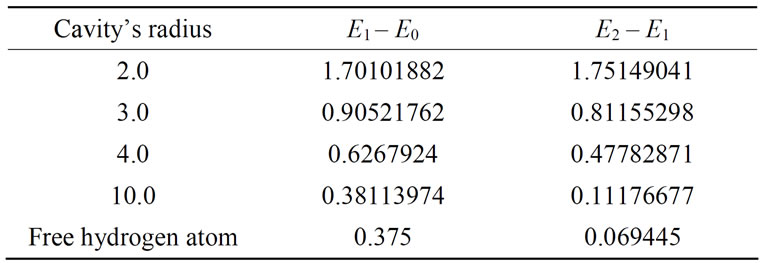
Table 5. The changes in the energy of two consecutive levels in relation to the increase in radius.
observed for the three lowest levels. Moreover, placing the hydrogen atom into the cage causes a loss of degeneracy of energy levels having the same level numbers and different angular momenta; reducing the sphere’s radius, the difference between these levels increases. This case is indicated in Tables 6 and 7 [26].
5. Conclusions
In this paper, through exploiting an effective variational method, the Schrödinger equation is solved for the hydrogen atom confined in the center of a spherical cavity; the various effects of limitation on the atom are studied; the energy eigenvalues are accurately and cost-effectively obtained; the correctness of results and the utilized method’s importance are properly approved using the convergence tests and comparing with the existing results.
Finally, it should be noted that considering the B-spline bases’ high abilities, the method proposed in this paper can be employed to solve various quantum-physics problems. This method is applied to solve problems in which the cavity has a specific confined potential, the impurity is outside the center of cavity, or the cavity is nonspherical.
6. Acknowledgements
The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely
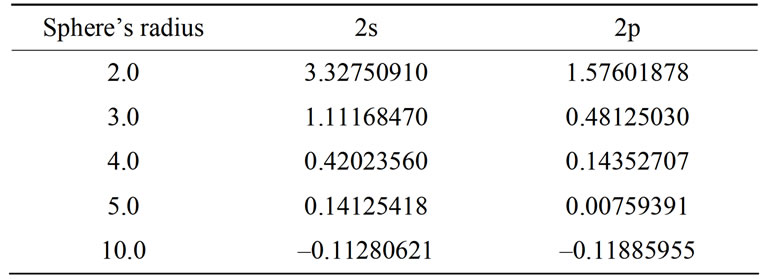
Table 6. The detachment of the first excited level into two levels.
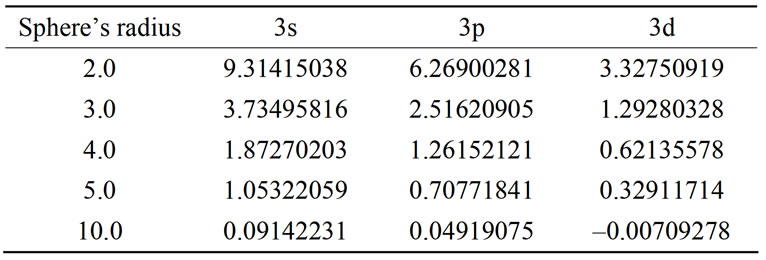
Table 7. The detachment of the second excited level into three levels.
thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.
REFERENCES
- V. K. Dolmatov, A. S. Baltenkov, J.-P. Connerade and S. T. Manson, “Structure and Photoionization of Confined Atoms,” Radiation Physics and Chemistry, Vol. 70, No. 1-3, 2004, pp. 417-433. doi:10.1016/j.radphyschem.2003.12.024
- A. Michels, J. Deboer and A. Bijl, “Remarks Concerning Molecural Interaction and Their Influence on the Polarisability,” Physica, Vol. 4, 1937, pp. 981-994. doi:10.1016/S0031-8914(37)80196-2
- S. Kang, Q. Liu, H. Y. Meng and T. Y. Shi, “Hydrogen Atom in Ellipsoidal Cavity,” Physics Letters A, Vol. 360, No. 4-5, 2007, pp. 608-614. doi:10.1016/j.physleta.2006.08.055
- S. H. Patil, “Hydrogen Atom Confined to an Ellipsoid,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 34, No. 6, 2001, p. 1049. doi:10.1088/0953-4075/34/6/306
- T. Guillot, “A Comparison of the Interiors of Jupiter and Saturn,” Planetary and Space Science, Vol. 47, No. 10-11, 1999, pp. 1183-11200. doi:10.1016/S0032-0633(99)00043-4
- T. Y. Shi, H. X. Qiao and B. W. Li, “Variational Calculations for a Hydrogen Atom Confined Off-Centre in an Impenetrable Spherical Box Using B-Splines,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 33, No. 9, 2000, p. L349. doi:10.1088/0953-4075/33/9/106
- H. Bachau, E. Cormier, P. Decleva, J. E. Hansen and F. Martín, “Applications of B-Splines in Atomic and Molecular Physics,” Reports on Progress in Physics, Vol. 64, No. 12, 2001, p. 1815. doi:10.1088/00344885/64/12/205.
- W. R. Johnson and J. Sapirstein, “Computation of Second-Order Many-Body Corrections in Relativistic Atomic Systems,” Physical Review Letters, Vol. 57, No. 9, 1986, pp. 1126-1129. doi:10.1103/PhysRevLett.57.1126
- D. A. Horner, S. Miyabe, T. N. Rescigno, C. W. McCurdy, F. Morales and F. Martín, “Classical Two-Slit Interference Effects in Double Photoionization of Molecular Hydrogen at High Energies,” Physical Review Letters, Vol. 101, No. 18, 2008, pp. 183002-183005. doi:10.1103/PhysRevLett.101.183002
- D. A. Horner, C. W. McCurdy and T. N. Rescigno, “Triple Differential Cross Sections and Nuclear Recoil in Two-Photon Double Ionization of Helium,” Physical Review A, Vol. 78, No. 4, 2008, Article ID 04341. doi:10.1103/PhysRevA.78.043416
- A. Palacios, T. N. Rescigno and C. W. McCurdy, “Cross Sections for Short-Pulse Single and Double Ionization of Helium,” Physical Review A, Vol. 77, No. 3, 2008, Article ID 032716.
- F. L. Yip, C. W. McCurdy and T. N. Rescigno, “Hybrid Gaussian-Discrete-Variable Representation Approach to Molecular Continuum Processes: Application to Photoionization of Diatomic Li2+,” Physical Review A, Vol. 78, No. 2, 2008, Article ID 023405. doi:10.1103/PhysRevA.78.023405
- P. L. Bartlett, A. T. Stelbovics, T. N. Rescigno and C. W. McCurdy, “Application of Exterior Complex Scaling to Positron-Hydrogen Collisions including Rearrangement,” Physical Review A, Vol. 77, No. 3, 2008, Article ID 032710. doi:10.1103/PhysRevA.77.032710
- D. A. Horner, W. Vanroose, T. N. Rescigno, F. Martin and C. W. McCurdy, “The Role of Nuclear Motion in the Photo-Double Ionization of Molecular Hydrogen,” Lawrence Berkeley National Laboratory, Paper LBNL- 61189, 2008.
- J. C. Morrison and C. Bottcher, “Spline Collocation Methods for Calculating Orbital Energies,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 26, No. 22, 1993, pp. 3999-4006. doi:10.1088/0953-4075/26/22/007.
- W. R. Johnson, S. A. Blundell and J. Sapirstein, “Finite Basis Sets for the Dirac Equation Constructed from B Splines,” Physical Review A, Vol. 37, No. 2, 1988, pp. 307-315. doi:10.1103/PhysRevA.37.307
- W. R. Johnson, S. A. Blundell and J. Sapirstein, “ManyBody Perturbation-Theory Calculations of Energy Levels along the Lithium Isoelectronic Sequence,” Physical Review A, Vol. 37, No. 8, 1988, pp. 2764-2777. doi:10.1103/PhysRevA.37.2764
- W. R. Johnson, S. A. Blundell and J. Sapirstein, “ManyBody Perturbation-Theory Calculations of Energy Levels along the Sodium Isoelectronic Sequence,” Physical Review A, Vol. 38, No. 6, 1988, pp. 2699-2706. doi:10.1103/PhysRevA.38.2699
- W. R. Johnson, S. A. Blundell, Z. W. Liu and J. Sapirstein, “Correlation Effects in the Parity-Noncomserving 6s→7s Transition in Cesium,” Physical Review A, Vol. 37, 1988, pp. 1395-1400. doi:10.1103/PhysRevA.37.1395
- S. A. Blundell, W. R. Johnson and J. Sapirstein, “HigherOrder Many-Body Perturbation-Theory Calculations of Energy Levels in Cesium,” Physical Review A, Vol. 38, No. 10, 1988, pp. 4961-4966. doi:10.1103/PhysRevA.38.4961
- T. K. Fang and T. N. Chang, “Photoionization from Excited Mg Atoms,” Physical Review A, Vol. 61, No. 5, 2000, Article ID 052716. doi:10.1103/PhysRevA.61.052716
- T. K. Fang and T. N. Chang, “B-Spline-Based MultichanNel K-Matrix Method for Atomic Photoionization,” Physical Review A, Vol. 61, No. 6, 2000, Article ID 062704. doi:10.1103/PhysRevA.61.062704
- C. W. McCurdy and F. Martin, “Implementation of Exterior Complex Scaling in B-Splines to Solve Atomic and Molecular Collision Problems,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 37, No. 4, 2004, p. 917. doi:10.1088/0953-4075/37/4/017
- B. Nine, O. Haif-Khaif and A. Zerarka, “The Eigenenergies of the Wave Function through the Non-Variational Galerkin-B-Spline Approach,” Applied Mathematics and Computation, Vol. 178, No. 2, 2006, pp. 486-492. doi:10.1016/j.amc.2005.11.067
- N. Aquino, G. Campoy and H. E. Montgomery Jr., “Highly Accurate Solutions for the Confined Hydrogen Atom,” International Journal of Quantum Chemistry, Vol. 107, No. 7, 2007, pp. 1548-1558. doi:10.1002/qua.21313
- S. Goldman and C. Joslin, “Spectroscopic Properties of an Isotropically Compressed Hydrogen Atom,” Journal of Physical Chemistry, Vol. 96, No. 14, 1992, pp. 6021- 6027. doi:10.1021/j100193a069
NOTES
*Corresponding author.

