Journal of Modern Physics
Vol.3 No.1(2012), Article ID:17101,9 pages DOI:10.4236/jmp.2012.31004
l-Mixing Collision in Presence of Microwave Field
1Department of Physics and Astrophysics, University of Delhi, Delhi, India
2Department of Physics, Swami Shraddhanand College, University of Delhi, Delhi, India
Email: *brijender.dahiya@gmail.com
Received October 11, 2011; revised November 19, 2011; accepted December 10, 2011
Keywords: l-mixing; Floquet technique; Cross section
ABSTRACT
We have studied excitation of multilevel Na-Rydberg atom due to collision with proton in the presence of variable laser field. The interaction of laser field and Na-Rydberg atom is explored using non perturbative Floquet technique. The transition probability is calculated at different laser frequencies (GHz), projectile velocities and impact-parameter. We have also calculated total cross-section for near resonant energy transfer collision of proton with Na-Rydberg atom at different frequencies.
1. Introduction
Rydberg atom [1,2] is an excited atom with one or more electrons that have high principle quantum number. These atoms have a number of peculiar properties, like, large dipole moment, large size, including an exaggerated response to electric field and magnetic fields, longdecay periods and electron wave function that approximate, under some conditions, classical orbits of electrons about the nucleus. Collision of Rydberg atom with rare gas atoms or charged particles have been intensively studied theoretically and experimentally and still the subject of great interest [3-9]. One reason for selecting the alkali metal atom is that, they are relatively easy to access experimentally as well as theoretically, which opens up the possibility for detailed comparisons. Experimental and theoretical studies of inelastic collisions between charged particles and atoms/molecules play an important role under wide variety of physical situations, such as in the interpretation of variety of atmospheric and astrophysical data including the distribution of ions and atom in the upper atmosphere. In the last two decades, the use of laser technology and computational methods involving selective excitation methods has renewed interest in this field. In fact, computational process and aligned or oriented Rydberg atomic states allow us to insight into the dynamics of collisional excitation in a better way. Inelastic collisions of ion with Rydberg atoms demonstrate that nearly all states of an excited target are strongly coupled by the laserfield [10-12]. The dynamics of a Rydberg electron driven by such time-dependent field is complex, a large number of energetically accessible states that are coupled by the laser field during collisional process. The relatively small electric fields present in such situations distort the highly excited Rydberg states. The l changing transitions l → l' occurs within the same shell “n” of Rydberg atom due to time dependent electric field generated by the passing charged particle and shift of n → n' occurs due to the present laser field. Thus, state to state transitions by the collision process in the presence of laser field involve not only dipole allowed transitions but dipole forbidden transitions also. It is, therefore, of great interest to study the effect of small electric field due to collision on transitions of different states of Na-Rydberg atom in the presence of laser field. We have taken the frequency of the laser field in the GHz range. One fundamental collision process, that is not well understood, is inelastic collision transition from one Rydberg state to another Rydberg state; these collisional events involve not only dipoleallowed transitions of states but dipole-forbidden transitions as well. Work on state changing collisions in sodium nl targets has revealed distinctly different behavior at low and high impact velocity. A study of collisions between electrons and 30s state has been published by Rolfes et al. [13]. In the present paper, ion atom collision is studied using Floquet analysis of time dependent Schrödinger equation in the impact parameter approach. For the computation of Rydberg states, we require a careful choice of Rydberg wave function, which can be computed with the help of radial wave function of Picart et al. [14]. The principal quantum number (n) varies from 26 → 35, and angular quantum number (l) varies from 0 → 9. We have used the concept of single channel quantum defects theory (QDT), which assumes the constant values of quantum defects for s, p, d, f, g, h, i, j, k, l states. Here, we have calculated the transition probabilities of all the states for different parameters i.e. laser frequency, impact parameter and ion velocity. Keeping in view, the importance of cross-section results for various properties and phenomenon, we have also calculated the total crosssection for dipole allowed as well as for dipole forbidden transitions for proton impact with Na-Rydberg atom in the presence of microwave field. The excitation of alkali Rydberg states from their nl ground states has been a popular subject for theoretical and experimental study. The experimental study of excitation of sodium by H+, H2+, H3+, He+, Ne+ has been reported by Irby et al. [15]. Theoretical treatment of the collisional excitation or stark mixing of Rydberg states has been reported in [16-18] and excitation of Rydberg states by electromagnetic field has been reported in [19,20]. But, collisional excitation in the presence of electromagnetic field has been scarce.The paper is organized as follow: In Section 2, we have described the theoretical tools of interaction of proton with Rydberg atom in the presence of microwave field. In Section 3, wediscuss computational details. The results thus obtained are presented in Section 4. Conclusion and a prognosis for future work in the direction of collision aided problem are drawn in Section 5.
2. Theory
We consider the collision between the proton and the Na Rydberg atom which is assumed to be at rest in the presence of microwave field. The microwave field is treated classically as a spatially homogeneous electric field, linearly polarized and single mode, represented by
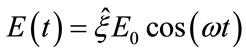 (1)
(1)
where 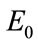 and
and 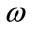 are respectively amplitude and frequency of the microwave field.
are respectively amplitude and frequency of the microwave field. 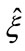 is the linear polarization vector. The time-dependent Schrödinger equation for the above ion-atom system is given by:
is the linear polarization vector. The time-dependent Schrödinger equation for the above ion-atom system is given by:
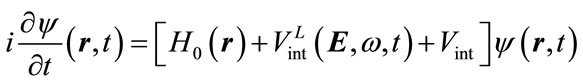 (2)
(2)
The energy operator H0 is unperturbed Hamiltonian, satisfies the equation:
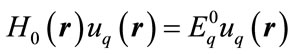 (3)
(3)
where 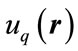 are the unperturbed eigen functions corresponding to energies
are the unperturbed eigen functions corresponding to energies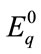 . The energy operator of the interaction of atom with the electromagnetic field is given by:
. The energy operator of the interaction of atom with the electromagnetic field is given by:
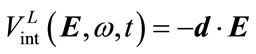 (4)
(4)
describes the coupling of atom with the microwave field, where d, is the radiative transition moment and E, is the laser field. Vint describes the interaction potential between the projectile ion and the Rydberg atom. At large distances ion and the atom interaction is negligible and hence Vint → 0, equation (2) reduces to the Schrödinger equation of isolated atom in the presence of electromagnetic field i.e.
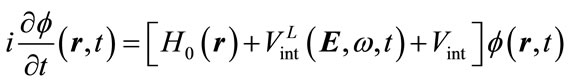 (5)
(5)
where, 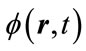 are the dressed states of the atom in the presence of microwave field. The total wave function of the system
are the dressed states of the atom in the presence of microwave field. The total wave function of the system  in terms of dressed state of atom in the presence of laser field can be expanded as:
in terms of dressed state of atom in the presence of laser field can be expanded as:
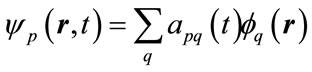 (6)
(6)
Here “q” stands for the all the quantum states of the system. Substituting equation (6) into equation (2) and using the orthogonality condition for the dressed states. We obtain the following set of coupled differential equation:
 (7)
(7)
where
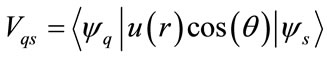 (8)
(8)
denote the radiative transition matrix elements for the atom interacting with the microwave field. The above coupled differential equation can be written in matrix notation, like
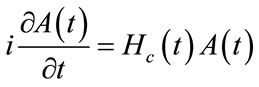 (9)
(9)
where  is the time dependent periodic matrix with periodicity
is the time dependent periodic matrix with periodicity . It is well known that the conventional method fails at resonance frequency as well as high intensities. Hence we have used the non-perturbative Floquet theorem for the solution of such problem [21]. The general solution of (9) as asserted by Floquet theorem in matrix notation is of the form:
. It is well known that the conventional method fails at resonance frequency as well as high intensities. Hence we have used the non-perturbative Floquet theorem for the solution of such problem [21]. The general solution of (9) as asserted by Floquet theorem in matrix notation is of the form:
 (10)
(10)
where  and λ is the diagonal quasi energy matrix or Floquet characteristics exponent. Following [21], the Fourier expansion of
and λ is the diagonal quasi energy matrix or Floquet characteristics exponent. Following [21], the Fourier expansion of 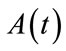 and
and 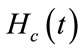 are given as:
are given as:
 (11)
(11)
 (12)
(12)
where 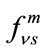 and
and  are the mth Fourier amplitude of
are the mth Fourier amplitude of 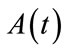 and
and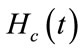 , respectively corresponding to particular value of m. Where “m”, correspond to photon number, the indices “ν” and “s” range over the dimension Nnl. Where Nnl is the total number of atom states included in the study. The Fourier components
, respectively corresponding to particular value of m. Where “m”, correspond to photon number, the indices “ν” and “s” range over the dimension Nnl. Where Nnl is the total number of atom states included in the study. The Fourier components 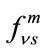 and characteristic values can be obtained by substituting (11) and (12) in (9) [20]. The eigenvalue problem is
and characteristic values can be obtained by substituting (11) and (12) in (9) [20]. The eigenvalue problem is
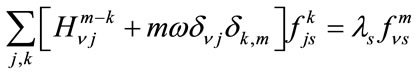 (13)
(13)
The first multiplier (within the bracket) on the left hand side represents the Floquet Hamiltonian HF matrix. The HF matrix is diagonalized to obtain the eigenvalues of the Floquet matrix 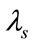 and corresponding eigenvectors
and corresponding eigenvectors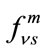 . The transition probability from initial state to the final state, in the presence of microwave field for the time duration “t”, can be calculated by using the eigenvalues (
. The transition probability from initial state to the final state, in the presence of microwave field for the time duration “t”, can be calculated by using the eigenvalues (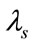 ) and the corresponding eigenvector (
) and the corresponding eigenvector (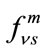 ) in equation (13) and is given [22] as
) in equation (13) and is given [22] as
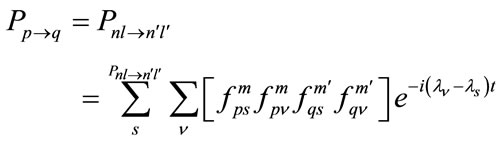 (14)
(14)
For continuous coherent operation of the laser for a infinitely long duration, the time averaged transition probability from initial state  to final state
to final state 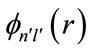 is
is
 (15)
(15)
where summation is over all the eigenvalues of the concerned Floquet matrix. The time averaged transition probability characterizes the optical transition. The experimental spectra in microwave field obtained by Stoneman et al. [23] is explained theoretically by Rao et al. [20] using Floquet theory.
3. Computational Method
By considering back equation (5), we can expand the total wave function of the system in terms of dressed states.
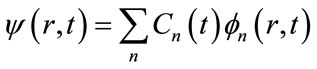 (16)
(16)
where the subscript n runs over all dressed states. The microwave field couples only the dipole allowed transition that is ∆l = ±1. Substituting equation (16) in equation (5), and using the orthogonality condition, we get the set of first order coupled differential equations:
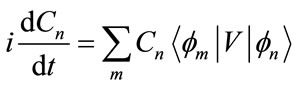 (17)
(17)
The accurate computation of the wave function requires a careful choice of the radial part, therefore it is of vital importance to determine the correct value of the radial element [24]. We have calculated the radial matrix elements rigorously for all the hundred levels, including both dipole allowed and dipole forbidden transitions. In matrix form we can write the coupled differential equation (17) as:
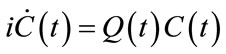 (18)
(18)
where  is a column matrix and
is a column matrix and  is a coupling matrix defined by:
is a coupling matrix defined by:
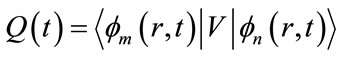 (19)
(19)
The above equations can be solved numerically for the time-dependent coefficients 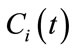 for a particular set of initial condition, using the standard diagonalization technique used by [25-28], the coupled equation (18), can be solved at
for a particular set of initial condition, using the standard diagonalization technique used by [25-28], the coupled equation (18), can be solved at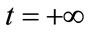 . We define
. We define
 (20)
(20)
where U, is a unitary operator and MD is a digonalized matrix obtained by unitary transformation.
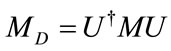 (21)
(21)
The probability for transition from state i to final state f is given by
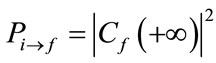 (22)
(22)
This probability can be integrated with respect to the impact parameter to find out the total cross-section.
4. Results and Discussion
Here we have considered the collision of Na-Rydberg atom in the presence of varying microwave field in GHz. We present a model of l-changing reactions in ion collisions with Na-Rydberg atom. The dressed state of NaRydberg atom are calculated using the Floquet theory as discussed in Section 2. Floquet theory is an accurate non-perturbative method to convert the time-dependent Schrödinger equation into infinite time-independent Floquet matrix, HF. Floquet analysis is now frequently used for the study of Rydberg state evolution in the oscillatory fields. Our approach to inelastic collision bears only a formal resemblance to the theory of field induced transition among Rydberg levels. In constructing the Floquet Hamiltonian HF (the term in the bracket of equation (13)), we require to calculate the radiative transition matrix elements between the adjacent levels. The HFmatrix is diagonalized to obtain the eigenvalues of the Floquetmatrix (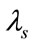 ) and corresponding eigenvectors (
) and corresponding eigenvectors (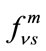 ). Once the dressed states are known, one can solve the close coupling equation by diagonalization techniques, which gives transition amplitude. Finally using the equation (22), we calculated the total cross-section. SI units are used throughout the paper otherwise mentioned. In figure 1, we present the variation of transition probabilities without collision as the function of the microwave frequency at laser intensity I = 1 W/cm2. Here, we have shown the transition probabilities for all the available levels (i.e. from 26s - 35l levels). The red curve shows the survival probability of the ground state (here 26s). Various peaks in the figure correspond to the transition to a particular level. Whenever there is a resonance between two levels a sharp peak shows the transition. Due to the photonic transition, there are various peaks, as shown in the figure 1. At low frequency, for a range of 0 → 50 GHz, we get a bunch of transitions of various levels. This bunch occurs as the energy levels of different states are near to each other thus slight change in the frequency causes transition to different level. In figure 1, resonance conditions for different levels can be observed, such as, at point a single photon transition between 26s - 26p having resonance at 209.65 GHz, at point b two photon transition between 26s - 26d having resonance at 270.66 GHz, at point c three photon transition between 26s - 26f having resonance at 183.06 GHz. Similarly, points d and e show the resonance conditions for 27d and 27f level transitions respectively. The point f shows resonance for three different levels 28d, 28f and 28g at frequencies 55.21, 53.09 and 50.79 GHz respectively. Thus, for higher levels a small frequency shift satisfies a different level resonance condition due to multiphoton transition. Although, we have calculated the variation of eigenvalues as a function of laser frequency for the range 0 → 300 GHz.
). Once the dressed states are known, one can solve the close coupling equation by diagonalization techniques, which gives transition amplitude. Finally using the equation (22), we calculated the total cross-section. SI units are used throughout the paper otherwise mentioned. In figure 1, we present the variation of transition probabilities without collision as the function of the microwave frequency at laser intensity I = 1 W/cm2. Here, we have shown the transition probabilities for all the available levels (i.e. from 26s - 35l levels). The red curve shows the survival probability of the ground state (here 26s). Various peaks in the figure correspond to the transition to a particular level. Whenever there is a resonance between two levels a sharp peak shows the transition. Due to the photonic transition, there are various peaks, as shown in the figure 1. At low frequency, for a range of 0 → 50 GHz, we get a bunch of transitions of various levels. This bunch occurs as the energy levels of different states are near to each other thus slight change in the frequency causes transition to different level. In figure 1, resonance conditions for different levels can be observed, such as, at point a single photon transition between 26s - 26p having resonance at 209.65 GHz, at point b two photon transition between 26s - 26d having resonance at 270.66 GHz, at point c three photon transition between 26s - 26f having resonance at 183.06 GHz. Similarly, points d and e show the resonance conditions for 27d and 27f level transitions respectively. The point f shows resonance for three different levels 28d, 28f and 28g at frequencies 55.21, 53.09 and 50.79 GHz respectively. Thus, for higher levels a small frequency shift satisfies a different level resonance condition due to multiphoton transition. Although, we have calculated the variation of eigenvalues as a function of laser frequency for the range 0 → 300 GHz.
In Figure 2, we present the variation of eigenvalue with the laser frequency for a range of 0 → 50 GHz only. The anticrossing between two levels corresponds to the transition between those levels at that particular frequency. The minimum separation determines the resonance position. This figure also explains the bunch of transition probabilities for frequencies less than 50 GHz as shown in figure 1. Furthermore, in the inset, we have tried to show the anticrossings of levels for a frequency range 25 → 30 GHz in a magnified way. Collision changes the picture of induced transition, for example, the transition from the 26s - 27(s, d, f) are not allowed, these are dipole forbidden transition. But the collision induces that particular transition which was otherwise forbidden. Thus collision will wholesome changes the picture of transition probability.
Figure 3 shows how the transition probabilities are modified by the collision process. Panel a → i, represent transition probabilities for different n values, where different l levels are marked in the figure 3 by s, p, d, f, g, h, i, j, k and l. The variation of transition probability with frequency is taken at intensity 0.1 W/cm2 and the velocity of incident projectile is v = 0.01 au (1 au = 2.18769 × 106 ms−1) with an impact parameter “b” as 400.0 au (1 au = 0.0529 nm). In figure 3(a), when the frequency is 27.88 GHz survival probabilityof state 26s dips to 0.44
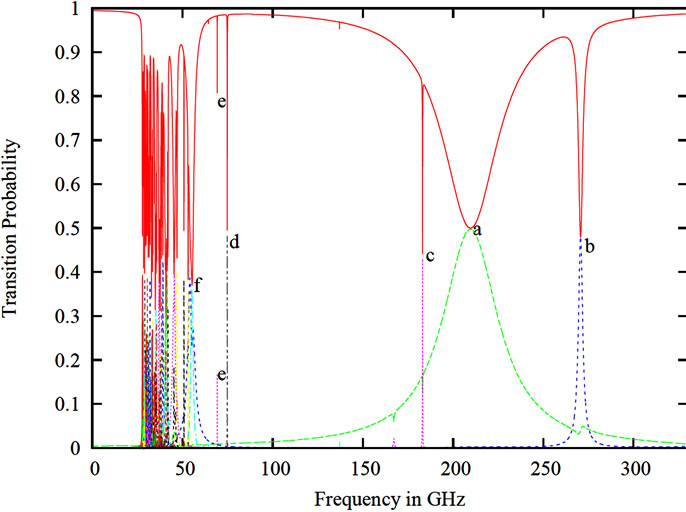
Figure 1. Transition probability as a function of laser frequency (in GHz) without collision. The laser intensity is 1.0 W/cm2. The red curve shows the ground state.
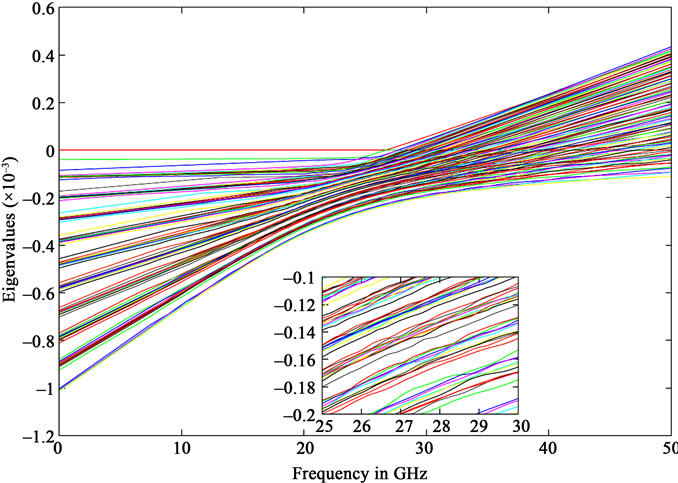
Figure 2. Eigenvalues as a function of laser frequency in GHz without collision. The laser intensity is 1.0 W/cm2. Here we have taken all possible levels, so it is very difficult to clarify various levels due to limitations in the availability of colors.
and after that become almost independent of frequency. Also, the transition probability of state 26d (dipole forbidden) becomes almost independent of frequency after 35.0 GHz. Figure 3(b), for n = 27, the transition probability triggered to maximum value to 0.43, and after that it become almost constant. Figure 3(c), for n = 28, at low frequency region, there is sharp rise in the transition probability of the particular state indicating a resonance for that state, and after that it decreases and attain a constant value and similar variation is shown by the other states.
Figure 4 shows the transition probabilities as a function of laser frequency in GHz with the collision for a lower impact parameter. Panel a → i, represent transition probabilities for different n values, where different l levels are marked in the figure 4 by s, p, d, f, g, h, i, j, k and l. The variation of transition probability with frequency is
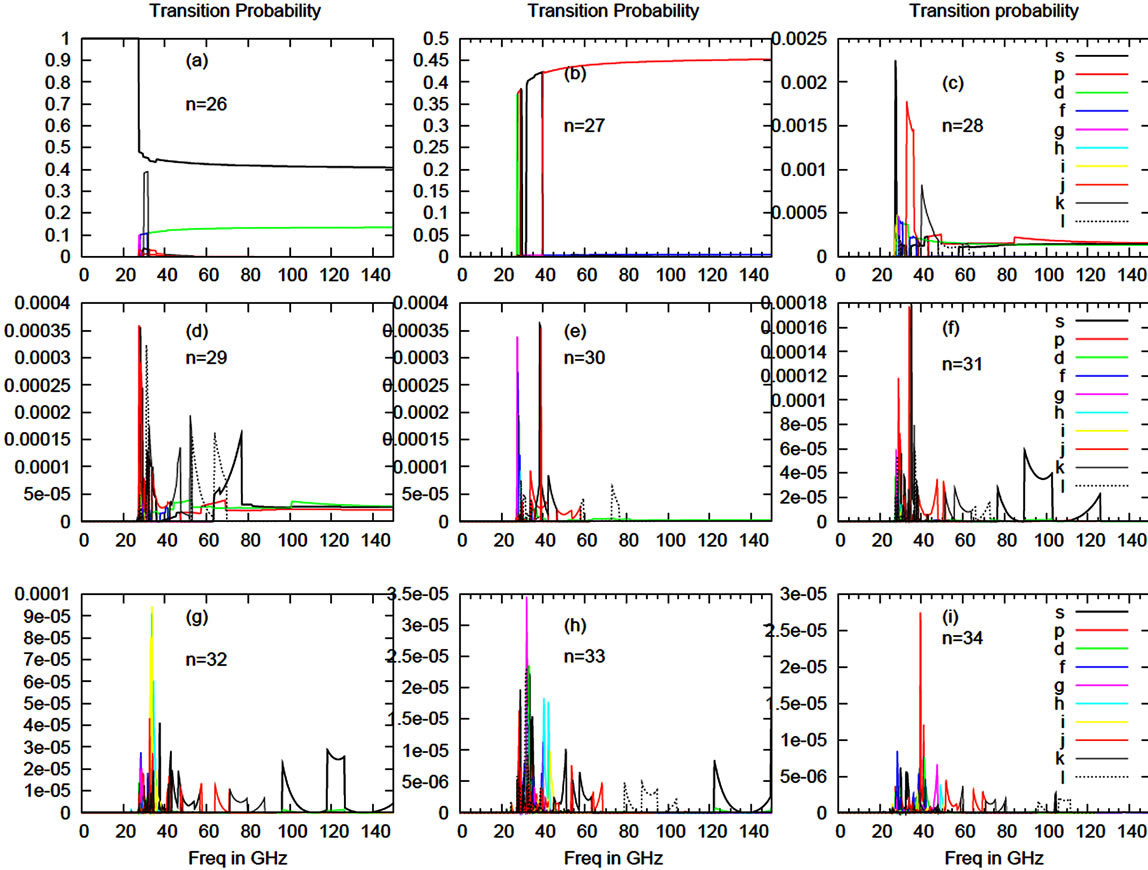
Figure 3. Transition probability as a function of laser frequency with collision. Here, impact parameter is 400 au and velocity of the proton is 0.01 au. The laser intensity is 0.1 W/cm2.
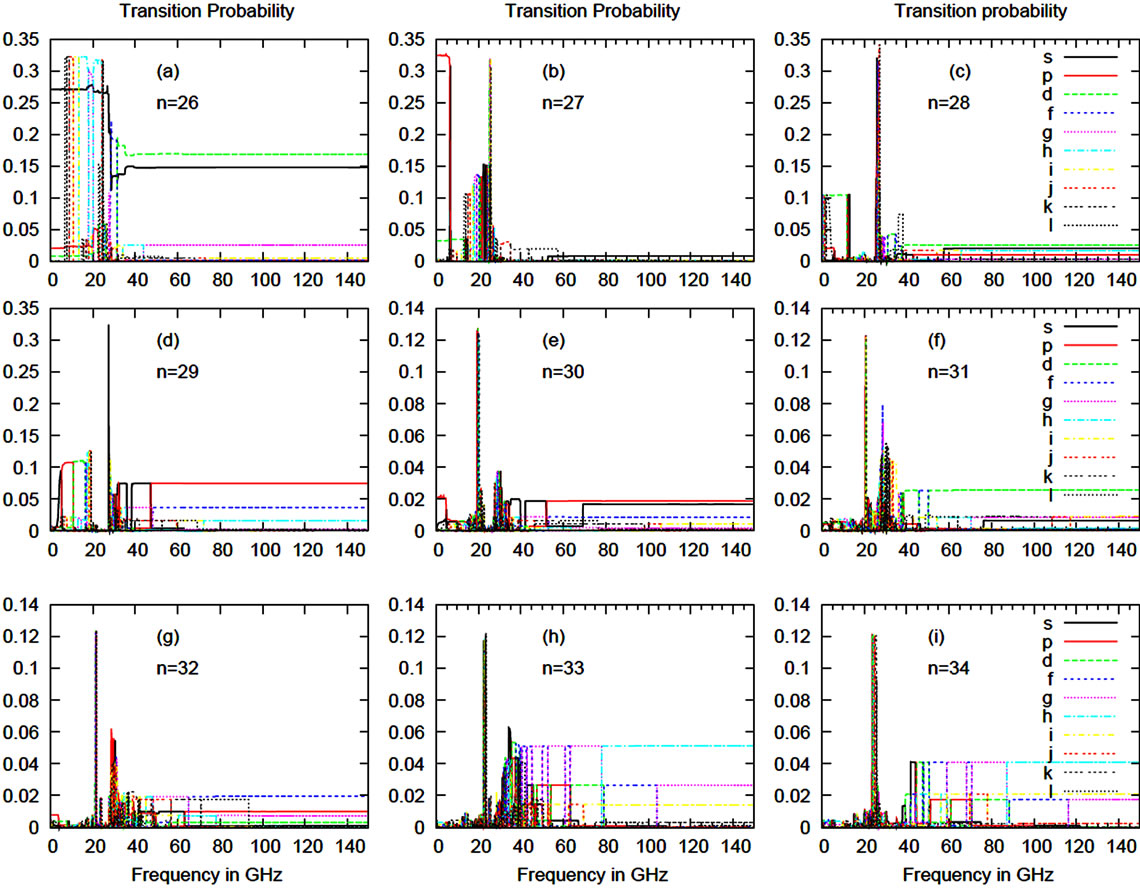
Figure 4. Transition probability as a function of laser frequency with collision. Here, impact parameter is 100 au and velocity of the proton is 0.01 au. The laser intensity is 0.01 W/cm2.
taken at intensity 0.01 W/cm2 and the velocity of incident projectile is v = 0.01 au with an impact parameter “b” as 100.0 au. We can compare the results obtained in Figure 3 and figure 4. Although, the intensity of laser field is reduced, but due to a smaller value of impact parameter, the probabilities are completely changed. Now, even for zero frequency, we have some value of 26p, 26d and 27p due to the collisional field associated with the system. In figure 4(a), when the frequency is 40.0 GHz survival probability of state 26s dips to 0.15 and after that become almost independent of frequency. Also, the transition probability of state 26d (dipole forbidden) becomes almost independent of frequency after 40.0 GHz. Figure 4, for n = 28, the transition probability triggered to maximum value to 0.34. Figure 4, also shows the transition probability of every level is higher for n > 27. Also, the transition probability of different l states of n = 29 are greater than transition probability of corresponding l states of n = 30. Similar behavior is observed for n = 31 & 32 and n = 33 & 34.
In figure 5, we have presented the variation of transition probability with velocity of projectileat off-resonance frequency (54.56 GHz) and the impact parameter is 100 au. Panel a → i, represent transition probabilities for different n values, where different l levels are marked in the Figure 5 by s, p, d, f, g, h, i, j, k and l. We have shown the transition probability for different values of n (i.e. n = 26 → 34). Different levels of different n dominates for various values of velocity, such as, in panel (a) 26d level dominates for the entire range of velocity and in panel (b), for n = 27, transition probability of 27p dominates over 27d for low values of velocity whereas 27d dominates over 27p for higher velocities. Also, as shown in panel (c) 28l shows the maximum probability for intermediate velocity and so on.
In figure 6, we present the variation of transition probability as a function of impact parameter “b”, where frequency of microwave field is 50.96 GHz and incident particle velocity v = 0.001 au. As shown in the figure, the transition probabilities of different n states are restricted to lower values of impact parameter as value of n increases. For n > 28, we do not get any transition probabilities beyond a value of b > 100 au. The behavior of transition probability variation is a general feature of the collision problem and can be explained on the basis of multichannel coupling effect. The interaction between the atom and Na-Rydberg atom is weak at large value of impact parameter compared to when the value of the impact parameter is small, and due to this transition probability is negligible for large values of impact parameter. Also transition probability of PL(27p) is much greater in magnitude than PL(34p), at the same intensity.
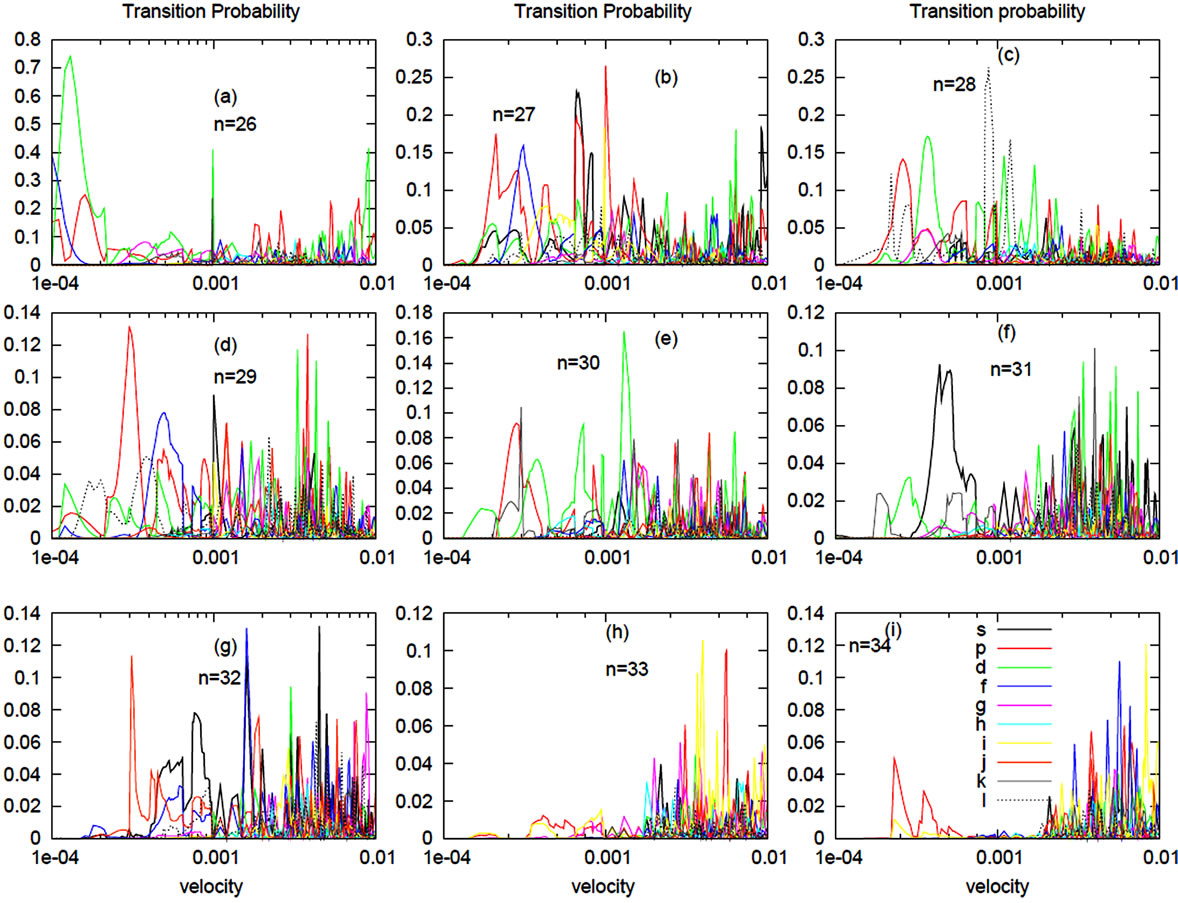
Figure 5. Transition probability with change in velocity of the projectile. Here, the impact parameter is 100 au, laser intensity is 0.1 W/cm2 and frequency is 54.56 GHz.
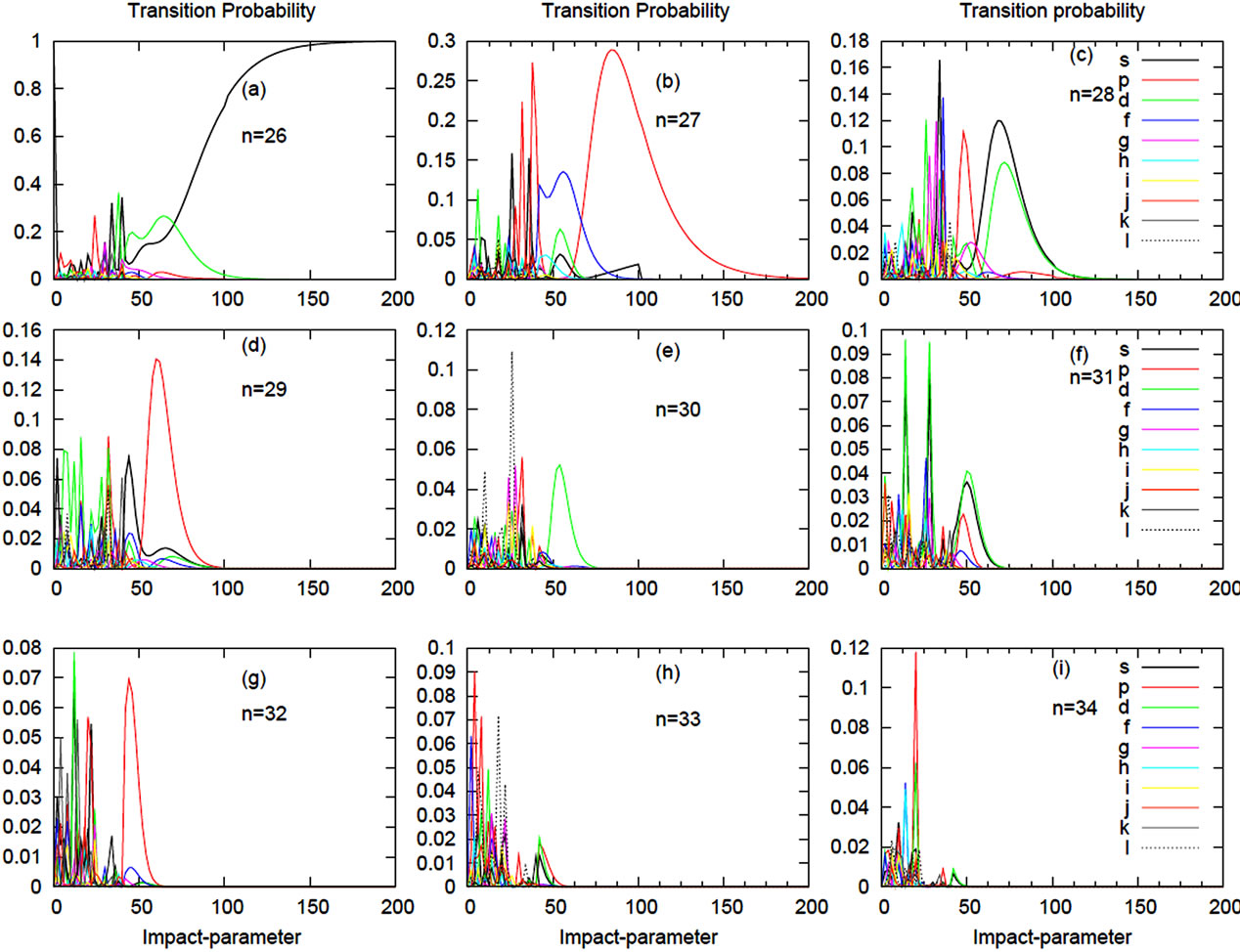
Figure 6. Transition probability with change in impact parameter. Here the frequency of laser is 225.45 GHz and velocity of proton (p) is 0.001 au.
In figure 7, the cross-section of the collisional excitation of Na-Rydberg atom has been shown as a function of field frequency. Here the velocity of projectile is 0.01 au. Figure 7 describe the variation of cross section for the transition 26s - 26p at an intensity I = 0.1 W/cm2. It is shown in figure 7, there is a sharp decrease in the crosssection at 90 GHz, indicating theresonance for any other state. Also, a sharp peak at 135 GHz indicates the resonance between 26s and 26p. Cross-section is triggered to maximum value of 7769 au2 at 135 GHz and then it attain almost constant value after 145 GHz. Decrease in the value of cross-section of any state indicates that there is increase in the cross-section for some other level due to l-mixing in the presence of collision as sharp decrease here indicates for the resonance condition of any other level.
Figure 8 shows the variation in the cross-section for the state 26s - 35s (which is dipole forbidden transition) as a function of field frequency. The velocity of projectile is 0.01 au. Here the intensity of the field is 0.1 W/cm2. This particular transition is although not field coupled but the field frequency and intensity modifies the crosssection to significant level. As the projectile approaches the target the field generated by the interaction of proton and atom modifies the states and we get significant results for dipole forbidden states also. As here shown in figure 8, this cross section is due to l-mixing modified by collision. It is found that the cross-section is significant only for particular values of frequencies and not for all. For these particular frequencies resonance occurs with the collisional field.
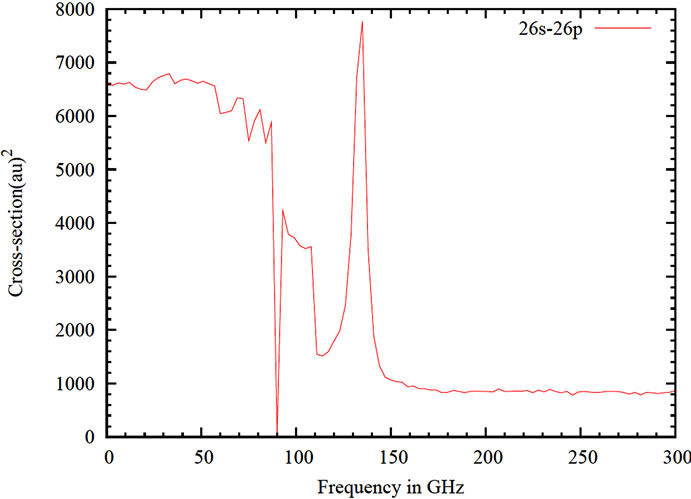
Figure 7. Cross-section with change in frequency for state 26s - 26p.

Figure 8. Coss-section with change in frequency for state 26s - 35s, which is dipole forbidden transition.
5. Summary and Conclusion
We have described a combination of Floquet approach for the radiation part and the close-coupling diagonalization technique for the collision part for the study of collisional aided radiative excitation of dressed atomic state in the presence of the laser field. The effect of collision on the radiative excitation process is discussed in detail by changing various collision parameters, for example, the collision velocity, impact parameter etc. We have shown that the laser can enhance the transition probabilities when the frequency is quite near the resonance of the atomic state. We also calculated total cross-section for dipole allowed as well as dipole forbidden transition for proton impact with Na-Rydberg atom in the presence of the microwave field and our results fairly match with various experimental and theoretical results, for example, in case of 30s → 30p transition our results for E0 → 0 closely matches with those of [15]. Finally our method is quite general and can be extended to other (ion-atom), (atom-atom) collisions in the presence of laser beam with an arbitrary interaction potential. Also, there is no doubt that the unusual properties of the Rydberg atoms will open the new lines of research in collision physics.
6. Acknowledgements
UA acknowledges the help from University Grants Commission (UGC) for financial support. VP is thankful to DST for financial support.
REFERENCES
- T. F. Gallaghar, “Rydberg Atoms Cambridge Monographs on Atomic, Molecular and Chemical Physic,” 3rd Edition, Cambridge University Press, Cambridge, 1994.
- T. F. Gallaghar, “Rydberg Atoms,” Reports on Progress in Physics, Vol. 51, No. 2, 1988, pp. 143-188. doi:10.1088/0034-4885/51/2/001
- M. I. Chibisov, “Coulomb Rydberg Electron l-Mixing in Collisions with Atomic Ions,” Journal of Experimental and Theoretical Physics, Vol. 105, No. 5, 2007, pp. 927- 952. doi:10.1134/S1063776107110076
- G. Benenti, G. Casati and D. L. Shepelyansky, “100-Photon Microwave Ionization of Rydberg Atoms in a Static Electric Field,” Physical Review A, Vol. 57, No. 3, 1998, pp. 1987-1991. doi:10.1103/PhysRevA.57.1987
- K. A. Safinya, J. F. Delpech, F. Gounand, W. Sandner and T. F. Gallagher, “Resonant Rydberg-Atom-RydbergAtom Collisions,” Physical Review Letters, Vol. 47, No. 6, 1981, pp. 405-408. doi:10.1103/PhysRevLett.47.405
- P. M. Fu, T. J. Scholz, J. M. Hettema and T. F. Gallagher, “Ionization of Rydberg Atoms by a Circularly Polarized Microwave Field,” Physical Review Letters, Vol. 64, No. 5, 1990, pp. 511-514. doi:10.1103/PhysRevLett.64.511
- C. H. Cheng, C. Y. Lee and T. F. Gallagher, “Production of Circular Rydberg States with Circularly Polarized Microwave Fields,” Physical Review Letters, Vol. 73, No. 23, 1994, pp. 3078-3081. doi:10.1103/PhysRevLett.73.3078
- P. M. Koch and K. A. H. van Leeuwen, “The Importance of Resonances in Microwave ‘Ionization’ of Excited Hydrogen Atoms,” Physics Reports, Vol. 255, No. 5-6, 1995, pp. 289-403. doi:10.1016/0370-1573(94)00093-I
- D. L. Dorofeev and B. A. Zon, “Mixing of Rydberg States Induced by Interaction with Moving Ion,” Journal of Chemical Physics, Vol. 106, No. 23, 1997, pp. 9609- 9617. doi:10.1063/1.473859
- R. G. Rolfes, L. G. Gray and K. B. MacAdam, “Collisions of Na+ Ions with Na Rydberg Atoms in Electricfields: Depopulation Cross Sections and Final-State Distributions from 36s and 30p Initial States,” Journal of Physics B, Vol. 25, No. 10, 1992, pp. 2319-2342. doi:10.1088/0953-4075/25/10/013
- D. B. Smith, R. G. Rolfes and K. B. MacAdam, “lChanging Depopulation of Na s and p Rydberg States by Ion Impact,” Physical Review A, Vol. 37, No. 7, 1988, pp. 2378-2385. doi:10.1103/PhysRevA.37.2378
- K. B. MacAdam, R. G. Rolfes and D. A. Crosby, “l Change in Sodium Rydberg Atoms Induced by Ion Collisions near the Matching Velocity,” Physical Review A, Vol. 24, No. 3, 1981, pp. 1286-1298. doi:10.1103/PhysRevA.24.1286
- R. G. Rolfes, L. G. Gray, O. P. Makarov and K. B. MacAdam, “Electron-Collision-Induced Dipole Transitions in Na Rydberg Atoms: 30s - 30p and 30s - 29p Absolute Cross Sections,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 26, No. 14, 1993, pp. 2191- 2200. doi:10.1088/0953-4075/26/14/018
- J. Picart, A. R. Edmonds and N. T. Minh, “Extrapolation to High Principal Quantum Numbers of Radial Integrals in the Coulomb Approximation,” Journal of Physics B, Vol. 11, No. 21, 1978, pp. L651-L654. doi:10.1088/0022-3700/11/21/001
- V. D. Irby, R. G. Rolfes, O. P. Makarov, K. B. MacAdam and M. I. Syrkin, “Absolute Cross Sections for the Dipole-Allowed Transitions 30s - 30p and 29d - 30p Incollisions between Charged Particles and Na Rydberg Atoms,” Physical Review A, Vol. 52, No. 5, 1995, pp. 3809- 3815. doi:10.1103/PhysRevA.52.3809
- R. J. Bell and B. G. Skinner, “Excitation of the 1s - 2p Transition in Hydrogen and the 3s - 3p Transition in Sodium by Nuclei,” Proceedings of the Physical Society, Vol. 80, No. 2, 1962, pp. 404-412. doi:10.1088/0370-1328/80/2/307
- M. J. Cavagnero, “Floquet Analysis of Inelastic Collisions of Ions with Rydberg Atoms,” Physical Review A, Vol. 52, No. 4, 1995, pp. 2865-2875. doi:10.1103/PhysRevA.52.2865
- G. S. Balaraman and M. R. Flannery, “Stark Mixing by Ion-Rydberg Atom (Molecule) Collisions,” International Journal of Mass Spectrometry, Vol. 280, No. 1-3, 2009, pp. 179-183. doi:10.1016/j.ijms.2008.08.017
- C. E. Theodosiou, “Excitation of the Na 3p Level by Light Ions,” Physical Review A, Vol. 36, No. 5, 1987, pp. 2067-2071. doi:10.1103/PhysRevA.36.2067
- J. Rao, B. Li and K. T. Taylor, “A New Floquet-Based Method for Calculation of Multiphoton Transition Transition Probabilities of Non-Hydrogenic Atoms in Strong Microwave Fields,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 32, No. 7, 1999, pp. L145-L154. doi:10.1088/0953-4075/32/7/001
- J. H. Shirley, “Solution of the Schrödinger Equation with a Hamiltonian Periodic in Time,” Physical Review, Vol. 138, No. 4B, 1965, pp. B979-B987. doi:10.1103/PhysRev.138.B979
- J. V. Moloney and F. H. Faisal, “Computation of Multiphoton IR Spectra of Small Molecules: Application CO,” Journal of Physics B, Vol. 12, No. 17, 1999, pp. 2829-2840. doi:10.1088/0022-3700/12/17/013
- R. C. Stoneman, D. S. Thompson and T. F. Gallgher, “Microwave Multiphoton Transitions between Rydberg States of Potassium,” Physical Review A, Vol. 37, No. 5, 1988, pp. 1527-1540. doi:10.1103/PhysRevA.37.1527
- K. Batra, V. Prasad and M. Mohan, “Collisional Excitation of Na-Rydberg Atoms,” The European Physical Journal D, Vol. 20, No. 2, 2002, pp. 191-198. doi:10.1140/epjd/e2002-00134-y
- M. Mohan and V. Prasad, “Laser-Assisted Vibrational Excitations during Ion-Molecule Collisions,” Journal of Physics B, Vol. 24, No. 3, 1991, pp. L81-L88. doi:10.1088/0953-4075/24/3/008
- V. Prasad and M. Mohan, “Vibrational Excitation of SH Radical Due to Proton Impact in the Presence of a Laser Beam,” Chemical Physics Letters, Vol. 187, No. 1-2, 1991, pp. 161-165.
- V. Prasad and K. Yamashita, “Effect of Laser Field Ellipticity on Therovibrational Excitations of a Diatomic Molecule,” Chemical Physics Letters, Vol. 426, No. 1-3, 2006, pp. 8-12. doi:10.1016/j.cplett.2006.04.120
- J. Callaway and E. Bauer, “Inelastic Collisions of Slow Atoms,” Physical Review, Vol. 140, No. 4A, 1995, pp. A1072-A1084. doi:10.1103/PhysRev.140.A1072
NOTES
*Corresponding author.

