Journal of Modern Physics
Vol. 2 No. 8 (2011) , Article ID: 7084 , 11 pages DOI:10.4236/jmp.2011.28093
Neutrino Masses in Supersymmetric Economical 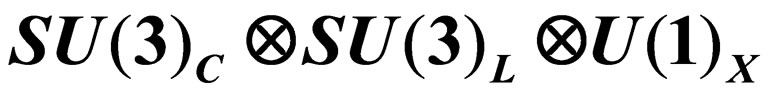 Model
Model
1Institute of Physics, VAST, Hanoi, Vietnam
2Universidade Federal do Rio Grande, Instituto de Matemática, Campus Carreiros, Rio Grande, Brazil
E-mail: dthuong@iop.vast.ac.vn
Received March 15, 2011; revised April 20, 2011; accepted May 5, 2011
Keywords: 11.30.Er, 14.60.Pq, 14.60.-z, 12.60.Jv
ABSTRACT
The R-symmetry formalism is applied for the supersymmetric economical 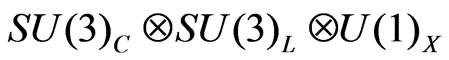 (3-3-1) model. The generalization of the minimal supersymmetric standard model relation among R-parity, spin and matter parity is derived, and discrete symmetries for the proton stability in this model are imposed. We show that in such a case it is able to give leptons masses at just the tree level. A simple mechanism for the mass generation of the neutrinos is explored. With the new R-parity, the neutral fermions get mass matrix with two distinct sectors: one light which is identified with neutrino mass matrix, another heavy one which is identified with neutralinos one. The similar situation exists in the charged fermion sector. Some phenomenological consequences such as proton stability, neutrinoless double beta decays are discussed.
(3-3-1) model. The generalization of the minimal supersymmetric standard model relation among R-parity, spin and matter parity is derived, and discrete symmetries for the proton stability in this model are imposed. We show that in such a case it is able to give leptons masses at just the tree level. A simple mechanism for the mass generation of the neutrinos is explored. With the new R-parity, the neutral fermions get mass matrix with two distinct sectors: one light which is identified with neutrino mass matrix, another heavy one which is identified with neutralinos one. The similar situation exists in the charged fermion sector. Some phenomenological consequences such as proton stability, neutrinoless double beta decays are discussed.
1. Introduction
Although the Standard Model (SM) gives very good results in explaining the observed properties of the charged fermions, it is unlikely to be the ultimate theory. It maintains the masslessness of the neutrinos to all orders in perturbation theory, and even after non-pertubative effects are included. The recent groundbreaking discovery of nonzero neutrino masses and oscillations [1] has put massive neutrinos as one of evidences on physics beyond the SM.
The Super-Kamiokande experiments on the atmospheric neutrino oscillations have indicated to the difference of the squared masses and the mixing angle with fair accuracy [2,3]
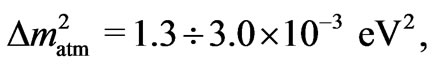 (1)
(1)
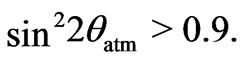 (2)
(2)
while, those from the combined fit of the solar and reactor neutrino data point to
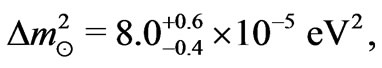 (3)
(3)
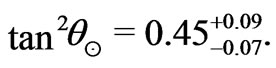 (4)
(4)
Since the data provide only the information about the differences in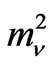 , the neutrino mass pattern can be either almost degenerate or hierarchical. Among the hierarchical possibilities, there are two types of normal and inverted hierarchies. In the literature, most of the cases explore normal hierarchical one in each. In this paper, we will mention on a supersymmetric model which naturally gives rise to three pseudo-Dirac neutrinos with an inverted hierarchical mass pattern.
, the neutrino mass pattern can be either almost degenerate or hierarchical. Among the hierarchical possibilities, there are two types of normal and inverted hierarchies. In the literature, most of the cases explore normal hierarchical one in each. In this paper, we will mention on a supersymmetric model which naturally gives rise to three pseudo-Dirac neutrinos with an inverted hierarchical mass pattern.
The gauge symmetry of the SM as well as those of many extensional models by themselves fix only the gauge bosons. The fermions and Higgs contents have to be chosen somewhat arbitrarily. In the SM, these choices are made in such a way that the neutrinos are massless as mentioned. However, there are other choices based on the SM symmetry that neutrinos become massive. We know these from the popular seesaw [4-14] and radiative [7-11] models. Particularly, the models based on the 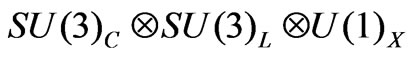 gauge unification group [12-23], called 3-3-1 models, give more stricter fermion contents. Indeed, only three fermion generations are acquired as a result of the anomaly cancelation and the condition of QCD asymptotic freedom. The arbitrariness in this case are only behind which SM singlets put in the bottoms of the lepton triplets? In some scenarios, exotic leptons may exist in the singlets. Result of this is quite similar the case of the SM neutrinos. As a fact, the mechanisms of the Zee’s type [7-11] for neutrino masses arise which been explored in Ref. [24].
gauge unification group [12-23], called 3-3-1 models, give more stricter fermion contents. Indeed, only three fermion generations are acquired as a result of the anomaly cancelation and the condition of QCD asymptotic freedom. The arbitrariness in this case are only behind which SM singlets put in the bottoms of the lepton triplets? In some scenarios, exotic leptons may exist in the singlets. Result of this is quite similar the case of the SM neutrinos. As a fact, the mechanisms of the Zee’s type [7-11] for neutrino masses arise which been explored in Ref. [24].
Forbidding the exotic leptons, there are two main versions of the 3-3-1 models as far as minimal lepton sectors is concerned. In one of them [12-14] the three known left-handed lepton components for each generation are associated to three 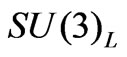 triplets as
triplets as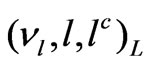 , in which
, in which 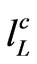 is related to the right-handed isospin singlet of the charged lepton
is related to the right-handed isospin singlet of the charged lepton 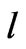 in the SM. No extra leptons are needed and therefore it calls that a minimal 3-3-1 model. In the variant model [15-18] three
in the SM. No extra leptons are needed and therefore it calls that a minimal 3-3-1 model. In the variant model [15-18] three 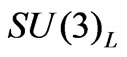 lepton triplets are of the form
lepton triplets are of the form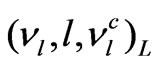 , where
, where 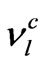 is related to the right-handed component of the neutrino field
is related to the right-handed component of the neutrino field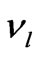 , thus called a model with the right-handed neutrinos. This kind of the 3-3-1 models requires only a more economical Higgs sector for breaking the gauge symmetry and generating the fermion masses. It is interesting to note that two Higgs triplets of this model have the same
, thus called a model with the right-handed neutrinos. This kind of the 3-3-1 models requires only a more economical Higgs sector for breaking the gauge symmetry and generating the fermion masses. It is interesting to note that two Higgs triplets of this model have the same  charges with two neutral components at their top and bottom. Allowing these neutral components vacuum expectation values (VEVs) we can reduce number of Higgs triplets to be two. Therefore we have a resulting 3-3-1 model with two Higgs triplets [27-28]. As a result, the dynamical symmetry breaking also affects lepton number. Hence it follows that the lepton number is also broken spontaneously at a high scale of energy. Note that the mentioned model contains very important advantage, namely, there is no new parameter, but it contains very simple Higgs sector, therefore the significant number of free parameters is reduced. To mark the minimal content of the Higgs sector, this version that includes righthanded neutrinos is going to be called the economical 3-3-1 model.
charges with two neutral components at their top and bottom. Allowing these neutral components vacuum expectation values (VEVs) we can reduce number of Higgs triplets to be two. Therefore we have a resulting 3-3-1 model with two Higgs triplets [27-28]. As a result, the dynamical symmetry breaking also affects lepton number. Hence it follows that the lepton number is also broken spontaneously at a high scale of energy. Note that the mentioned model contains very important advantage, namely, there is no new parameter, but it contains very simple Higgs sector, therefore the significant number of free parameters is reduced. To mark the minimal content of the Higgs sector, this version that includes righthanded neutrinos is going to be called the economical 3-3-1 model.
Among the new gauge bosons in this model, the neutral non-Hermitian bilepton field 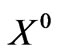 may give promising signature in accelerator experiments and may be also the source of neutrino oscillations [25-26]. In the current paper, the neutrinos of the 3-3-1 model with righthanded neutrinos is a subject for extended study.
may give promising signature in accelerator experiments and may be also the source of neutrino oscillations [25-26]. In the current paper, the neutrinos of the 3-3-1 model with righthanded neutrinos is a subject for extended study.
The 3-3-1 model with right-handed neutrinos gives the tree level neutrino mass spectrum with three Dirac fermions, one massless and two degenerate in mass [29]. This is clearly not realistic under the experimental data. However, this pattern may be severely changed by quantum effects and gives rise to an inverted hierarchy mass pattern. This is a specific feature of the 3-3-1 model with right-handed neutrinos which was considered in Ref. [29] (see also [30]), but such effects exist in the very high level of the loop corrections.
The outline of this work is as follows. In Section 2 we define the R-charge in our model in order to get similar results as in the Minimal Supersymmetric Standard Model (MSSM). While in Section 3 we impose another discrete symmetry that allow neutrino masses but forbid the proton decay and the neutron-antineutron oscillation. In Section 4 we calculate the fermion masses in our model, then we present some phenomenological discussion of this model. Our conclusions are found in the last section. In Appendix, we present the mass matrix elements of the neutral fermions.
2. Discrete R-Parity in the Supersymmetric Economical 3-3-1 Model (SUSYECO331)
In the supersymmetric 3-3-1 model with right-handed neutrinos (SUSY331RN) [31-32], the R-parity was already studied and we have shown that if R-symmetry is broken, the simple mechanism for the neutrinos mass can be constructed [33]. This mechanism produces the neutrinos mass which is in agreement with the experimental data.
The supersymmetric extension of the economical 3-3-1 model (SUSYECO331) was presented in [34]. The fermionic content of SUSYECO331 is the following: the left-handed fermions are in the triplets/antitriplets under the 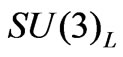 group, namely, the usual leptons are the triplets
group, namely, the usual leptons are the triplets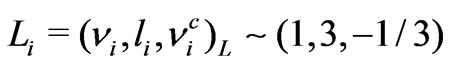 ,
,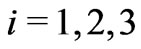 ; while in the quark sector, we have two families in the antitriplets
; while in the quark sector, we have two families in the antitriplets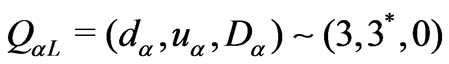 ,
, 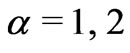 , and one family in the triplet
, and one family in the triplet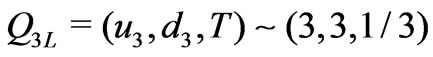 . The right-handed components are in the singlets under the
. The right-handed components are in the singlets under the 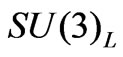 group:
group: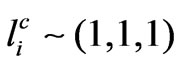 ,
, 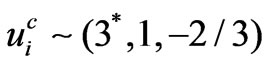 ,
, 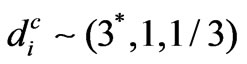 , which are similar to those in the SM. In addition, the exotic quarks transform as
, which are similar to those in the SM. In addition, the exotic quarks transform as 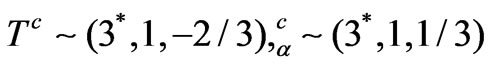 .
.
The scalar content is minimally formed by two Higgs triplets:
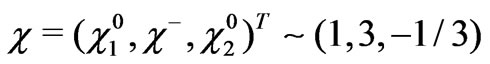
and 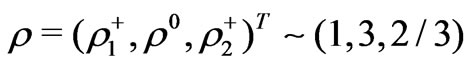 .
.
In order to cancel chiral anomalies in the SUSYECO331 model, we have to introduce the followings scalar Higgs triplets
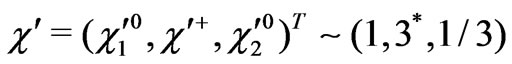
and 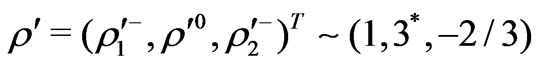 .
.
In this model, the VEVs are defined by
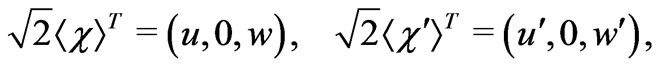 (5)
(5)
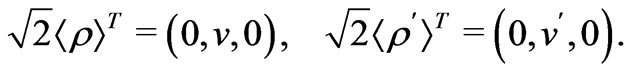 (6)
(6)
The VEVs 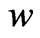 and
and 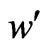 are responsible for the first step of the symmetry breaking, while
are responsible for the first step of the symmetry breaking, while 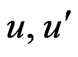 and
and 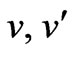 are responsible for the second one. Therefore, they have to satisfy the constraints:
are responsible for the second one. Therefore, they have to satisfy the constraints:
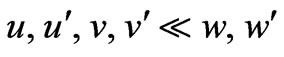 (7)
(7)
The complete set of fields and the full lagrangian of SUSYECO331 are given in Ref. [34]. The most general superpotential is given by:
 (8)
(8)
where
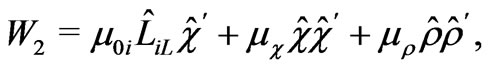 (9)
(9)
and
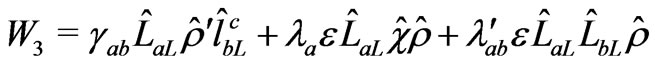
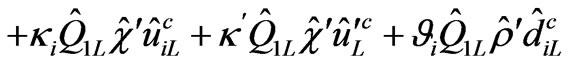
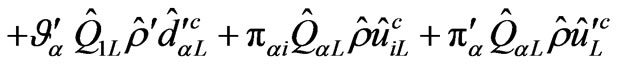
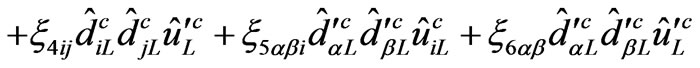
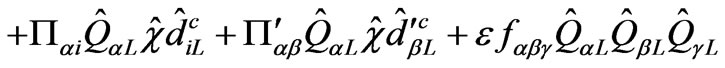
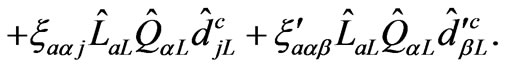 (10)
(10)
The coefficients  and
and 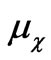 have mass dimension and can be complex variables [35], while all coefficients in
have mass dimension and can be complex variables [35], while all coefficients in 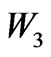 are dimensionless, and
are dimensionless, and .
.
Let us impose the R-parity as the same as that of the minimal supersymmetric standard model. In this case, we have to choose the following R-charges
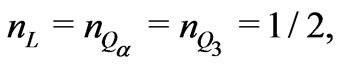
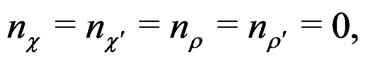
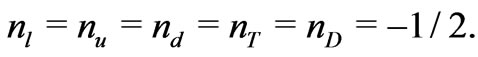 (11)
(11)
The superpotential satisfying the above R-parity conservation is written as
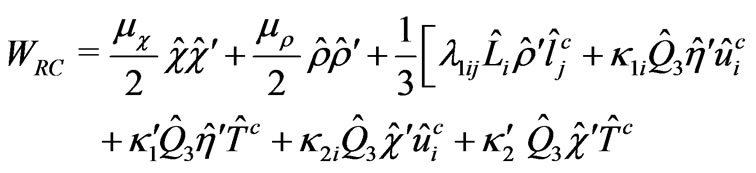
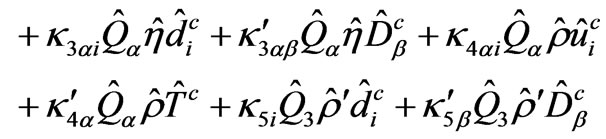
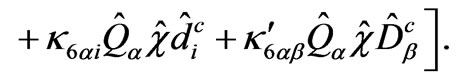 (12)
(12)
with this superpotential, we have shown that [34] the boson, Higgs sectors and the fermion one gain masses.
Thus, the R-parity in this model, as in the SUSY331RN, can be re-expressed via the spin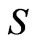 , new charges L and β in terms of [33]
, new charges L and β in terms of [33]
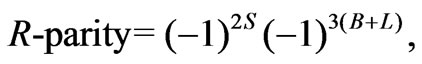 (13)
(13)
where the charges B and L for the multiplets are defined as follows [29]
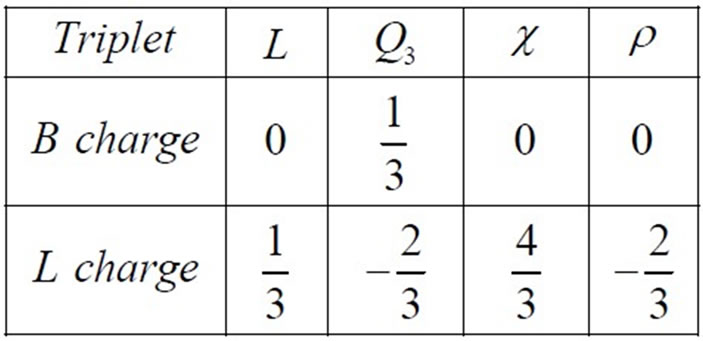 (14)
(14)
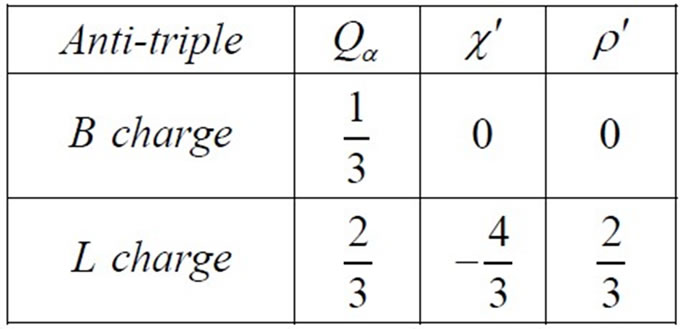 (15)
(15)
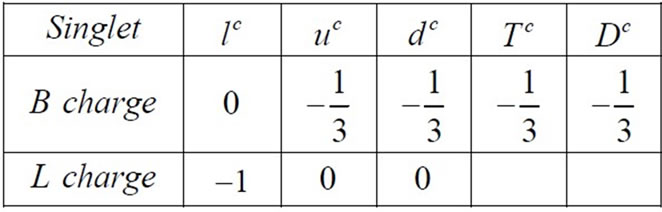 (16)
(16)
From the superpotential given in Equation (12), it is easy to see that the charged leptons gain mass through the term
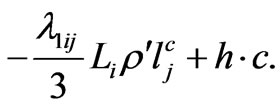 (17)
(17)
Their mass matrix, see Equation (6), is given by
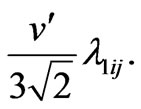 (18)
(18)
Note that there is only VEV of 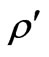 given the charged leptons masses.
given the charged leptons masses.
Unfortunately, as in the MSSM case, due to conservation of the R-parity defined in Equation (11), there are no term which gives neutrinos masses. However, looking at the superpotential of this model given in Equation (10), we see that there is a term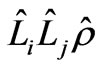 , which generates the following
, which generates the following
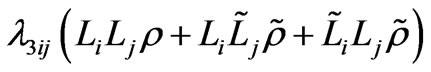 (19)
(19)
The first term in (19) generates the following neutrino mass matrix
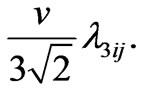 (20)
(20)
As shown in Ref. [34], the mass pattern of this sector is 0, 0, 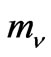 ,
, 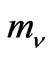 ,
, 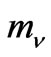 ,
,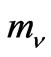 . Note that in this case, we have two massless neutrinos. Unfortunately, as in the nonsymmetric version, the quantum corrections at one loop level cannot generate the realistic mass spectrum to the neutrinos. To get the realistic neutrino masses, one have to introduce new physics scale or inflaton with mass around the GUT scale [37-38].
. Note that in this case, we have two massless neutrinos. Unfortunately, as in the nonsymmetric version, the quantum corrections at one loop level cannot generate the realistic mass spectrum to the neutrinos. To get the realistic neutrino masses, one have to introduce new physics scale or inflaton with mass around the GUT scale [37-38].
In this article, we will explore a new mass mechanism to generate neutrino masses at tree level for all neutrinos and study the flavor violating processes, such as neutrinoless double beta decay, which do not exist in our previous work.
3. The Discrete Symmetry for Proton Stability and Neutrino Masses in SUSYECO331
In this section to get neutrino mass and impose flavor violating processes, we chose the new R charge as follows
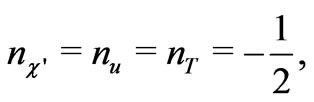
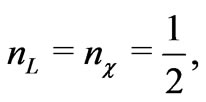
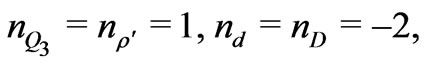
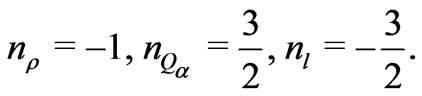 (21)
(21)
This R-charge is different from those presented in Ref. [34]. We will show that in this case, there exist some new phenomena, which are previously not allowed.
The terms under this symmetry are obtained by
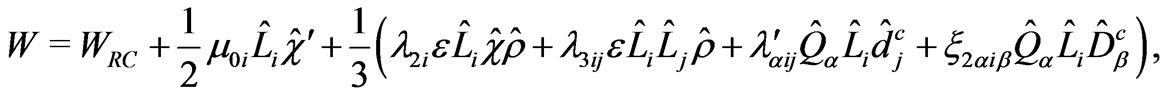 (22)
(22)
where 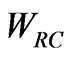 is defined in Equation (12). The superpotential given in (22) will not only allow some interesting flavor violating processes but also will simultaneously give the nucleons a stability. As we will show in next section, this superpotential will also generate masses to all neutrinos in the model.
is defined in Equation (12). The superpotential given in (22) will not only allow some interesting flavor violating processes but also will simultaneously give the nucleons a stability. As we will show in next section, this superpotential will also generate masses to all neutrinos in the model.
4. Fermion Masses
The superpotential (22) provides us the mixing between the leptons and higgsinos as
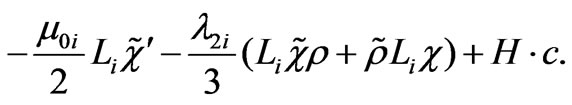 (23)
(23)
With the above terms, we get the mass matrices for the neutral and charged fermions. Diagonalizing these matrices we obtain the physical masses for the fermions. Firstly, let us study the neutral fermions masses.
4.1. Masses of the Neutral Fermions
In the basis 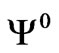 of the form
of the form
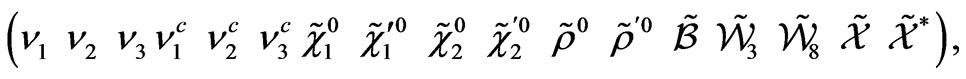
the mass Lagrangian can be written as follows
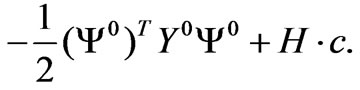 (24)
(24)
Here 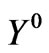 is symmetric matrix with the nonzero elements given in Appendix, where the mass eigenstates are given by
is symmetric matrix with the nonzero elements given in Appendix, where the mass eigenstates are given by
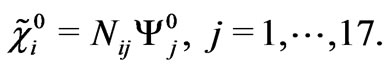 (25)
(25)
The mass matrix of the neutral fermions consists of three parts: a) the first part  is the
is the 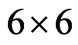 mass matrix of the neutrinos which belongs to the SUSYECO331; b) the second part
mass matrix of the neutrinos which belongs to the SUSYECO331; b) the second part 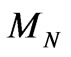 is the 11 × 11 mass matrix of the neutralinos, which exists only in the presented supersymmetric version, has been analyzed in [36]; c) the last part
is the 11 × 11 mass matrix of the neutralinos, which exists only in the presented supersymmetric version, has been analyzed in [36]; c) the last part 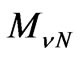 arises due to mixing among the neutrinos and the neutral higgsinos. Thus, the mass matrix for the neutral fermions is signified as follows
arises due to mixing among the neutrinos and the neutral higgsinos. Thus, the mass matrix for the neutral fermions is signified as follows
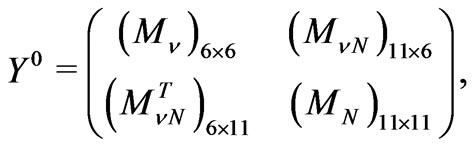 (26)
(26)
where matrices 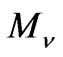 and
and 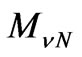 are presented in Equations (52) and (54).
are presented in Equations (52) and (54).
Let us keep the mass constraints from astrophysics and cosmology [39] as well as being consistent with all the earlier analysis [40], the parameters in the mass matrix 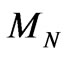 can be chosen as a typical example:
can be chosen as a typical example:
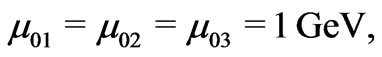
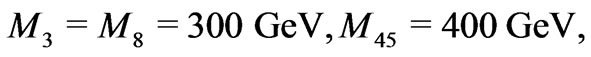
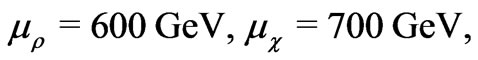
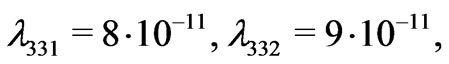
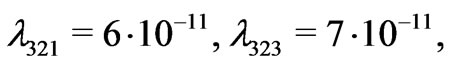
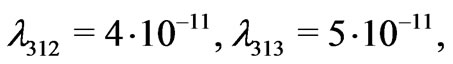
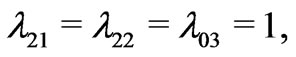 (27)
(27)
Here in this model, the Higgs bosons’ VEVs are fixed as follows
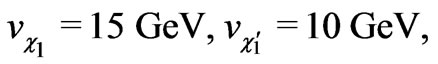
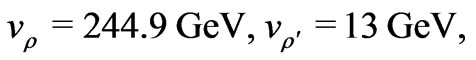
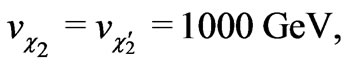 (28)
(28)
and the value of g is given in Ref. [39].
Using the values given in Equations (27) and (28), the eigenvalues of fermion mass matrix are obtained as
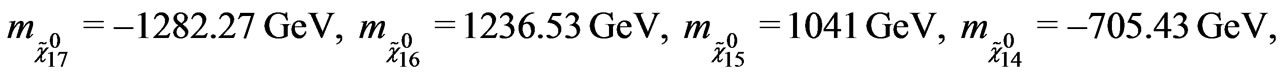
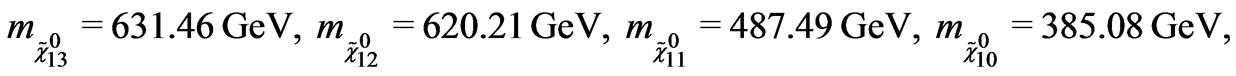
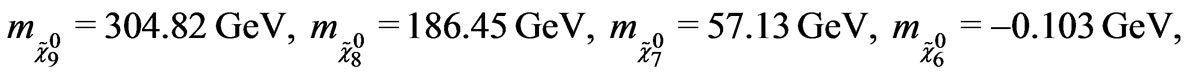
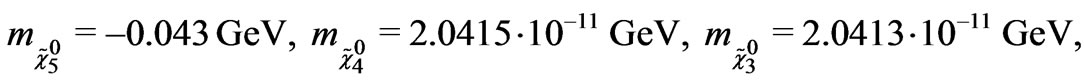
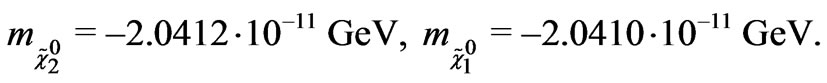 (29)
(29)
In the Equation (29), there are some negative eigenvalues. In order to obtain the positive mass, the eigenstates need to be redefined by the chiral rotations.
Equation (29) shows that we have two very distinct sector, one contains the light neutral fermions that we will associate with the usual neutrinos in the SM and the other one contains the heavy neutralinos. The lightest neutralino mass equals to 57 GeV and it is consistent with limits on inelastic dark matter from ZEPLIN-III [41].
Using the values given in Equations (27) and (28), the eigenvalues of the mass matrix 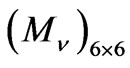 are obtained as
are obtained as
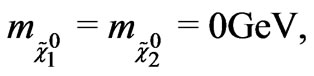
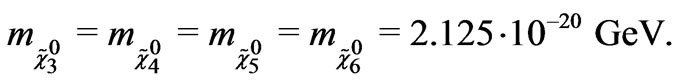 (30)
(30)
These values are smaller than that of the new mechanism given in (29). On the other hand, the eigenvalues of the matrix 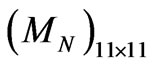 are obtained by putting the numerical given in Equations (27) and (28) as follows
are obtained by putting the numerical given in Equations (27) and (28) as follows
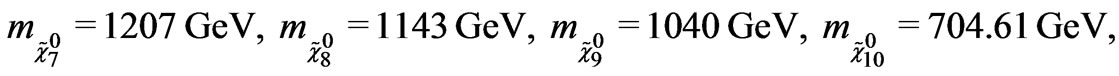
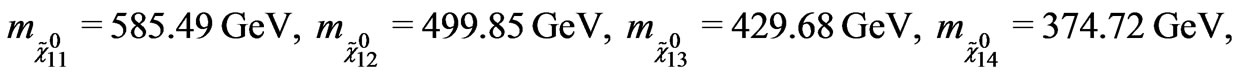
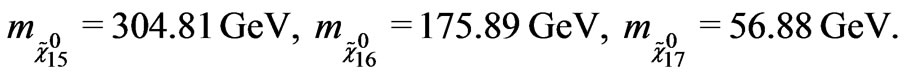 (31)
(31)
These results can be understood as follows: Because of the interference matrix 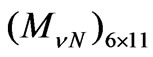 between the neutrino mass matrix and the neutralino mass matrix, all neutrinos gain mass at the tree level. This change of the neutrino mass spectrum is suitable to experiment data. Thus the neutrino mass spectrum in the model under consideration depends on the choice of
between the neutrino mass matrix and the neutralino mass matrix, all neutrinos gain mass at the tree level. This change of the neutrino mass spectrum is suitable to experiment data. Thus the neutrino mass spectrum in the model under consideration depends on the choice of  -parity. Now we deal with the charged fermions.
-parity. Now we deal with the charged fermions.
4.2. Masses of the Charged Fermions
To write mass matrix of the charged fermions, we will choose the following bases
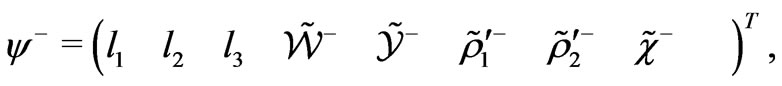
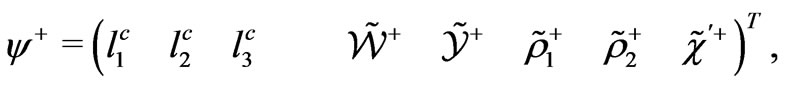 (32)
(32)
and define
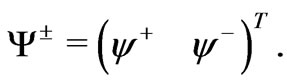 (33)
(33)
with these definitions, the mass term is written in the form
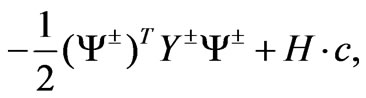 (34)
(34)
where
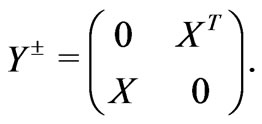 (35)
(35)
Here the 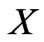 matrix is given by
matrix is given by
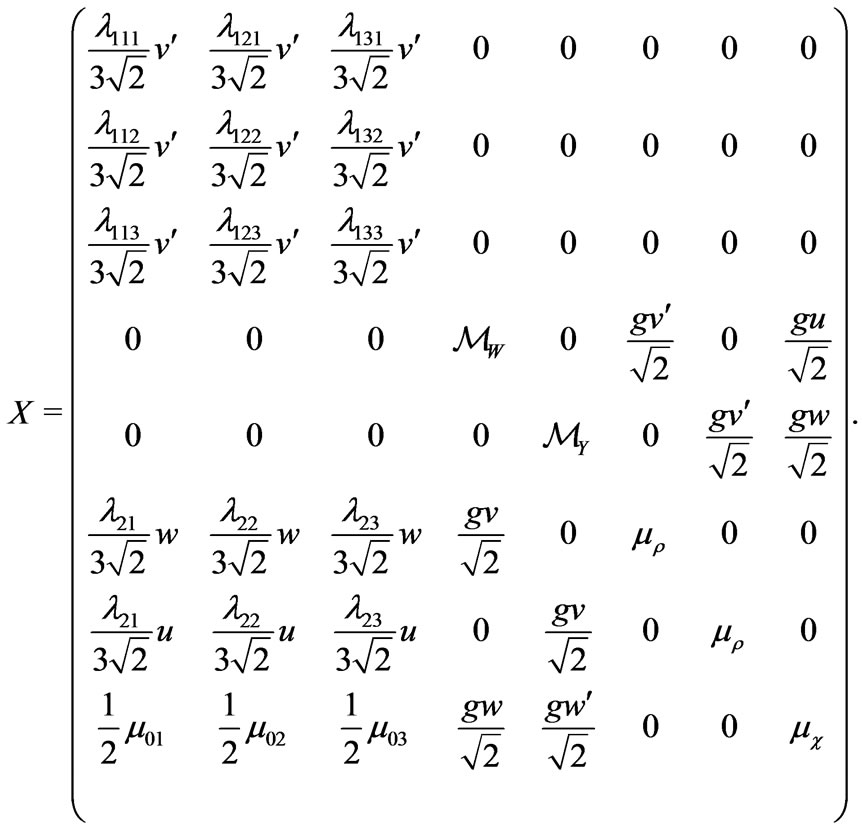
The chargino mass matrix 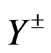 is diagonalized by using two unitary matrices,
is diagonalized by using two unitary matrices, 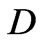 and
and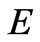 , defined by
, defined by
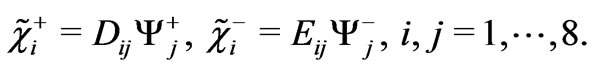 (36)
(36)
The characteristic equation for the matrix 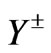 is
is
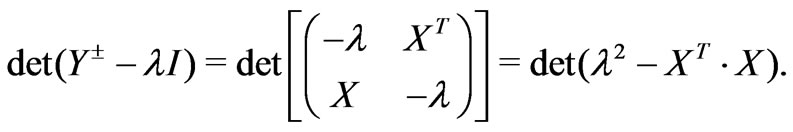 (37)
(37)
Since 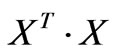 is a symmetric matrix,
is a symmetric matrix, 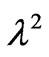 must be real and positive because
must be real and positive because 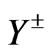 is also symmetric. In order to obtain eigenvalues, one only have to calculate
is also symmetric. In order to obtain eigenvalues, one only have to calculate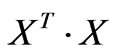 . The diagonal mass matrix can be written as
. The diagonal mass matrix can be written as
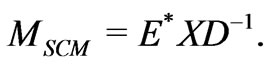 (38)
(38)
To determine E and D, it is useful the following observation
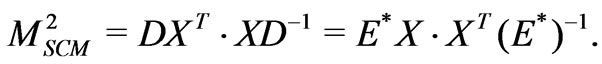 (39)
(39)
It means that D diagonalizes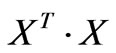 , while
, while 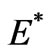 diagonalizes
diagonalizes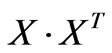 . In this case we can define the following Dirac spinors:
. In this case we can define the following Dirac spinors:
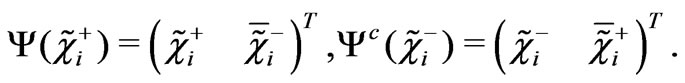 (40)
(40)
where 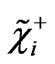 is the particle and
is the particle and 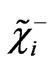 is the anti-particle [42].
is the anti-particle [42].
Using the values given in Equations (27) and (28), the eigenvalues of the charged fermion matrix given at Equation (36) are obtained as
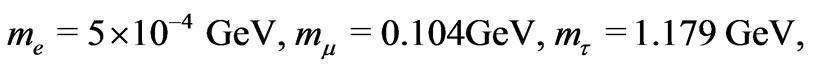
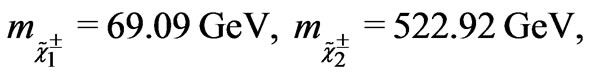
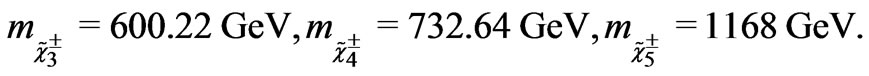 (41)
(41)
It is easily to see that the mass matrix is divided in two sectors: one heavy which is identified as the charginos and has been studied in our previous work [34]. Another one light which is identified as the usual leptons.
On the other hand, if we take the mass matrix from our work and using the same values to the parameters we get masses of the charged leptons:
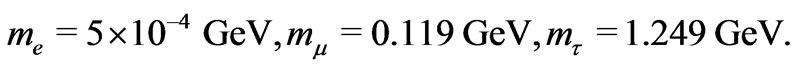 (42)
(42)
Now using the mass matrix to the charginos given in [18] we get
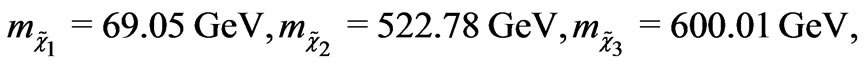
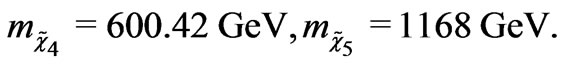 (43)
(43)
In this case, the new elements put down masses of the muon and tauon and at the same time remove the mass degeneracy between 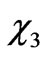 and
and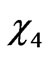 . Anyway we can see that the mass matrix in the charged fermion sector is basically divided in two sectors: one giving masses of the usual known leptons and another one giving masses of the new charginos.
. Anyway we can see that the mass matrix in the charged fermion sector is basically divided in two sectors: one giving masses of the usual known leptons and another one giving masses of the new charginos.
5. Nucleon Decay in the SUSYECO331
Let us remind that in the MSSM [35,43-47], the R-parity violating terms in superpotential are given by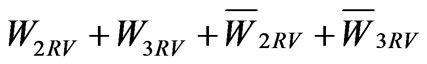 , where
, where
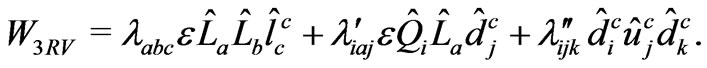
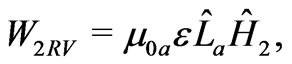 (44)
(44)
Here we have suppressed 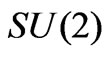 indices,
indices, 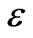 is the antisymmetric
is the antisymmetric 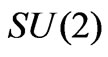 tensor. Above, and below in the following, the subindices
tensor. Above, and below in the following, the subindices 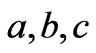 run over the lepton generations
run over the lepton generations 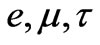 but a superscript
but a superscript 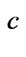 indicates charge conjugation;
indicates charge conjugation; 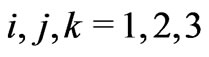 denote quark generations.
denote quark generations.
Note that the 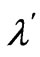 -coupling in the MSSM is similar to the
-coupling in the MSSM is similar to the 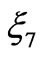 -coupling in the most general form of the superpotential in the SUSYECO331, which is given in Equation (10), and the coupling
-coupling in the most general form of the superpotential in the SUSYECO331, which is given in Equation (10), and the coupling 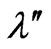 is similar to the coupling
is similar to the coupling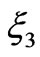 .
.
From Equation (44), we can obtain the B-violating Yukawa couplings as follows
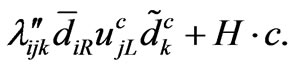 (45)
(45)
The interactions among lepton, quark and squark are given by
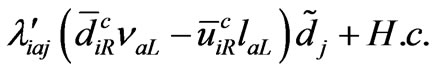 (46)
(46)
Taking into account Equations (45) and (46), we can draw two Feynmann diagrams describing the proton decay, which are shown in the Figures 1 and 2. The Figure 1 describes the proton decay into charged leptons. At the lowest approximation, there is no mixing in the quark, neutrino and squark sectors. It means that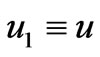 ,
, 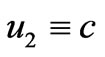 and
and 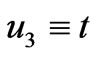 and so on. The proton could decay into
and so on. The proton could decay into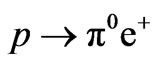 ,
, 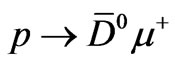 and
and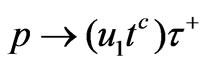 , but the last two modes are forbidden kinematically.
, but the last two modes are forbidden kinematically.
The analysis presented above shows that the proton can decay only in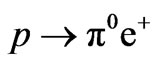 . On dimensional grounds, we estimate
. On dimensional grounds, we estimate
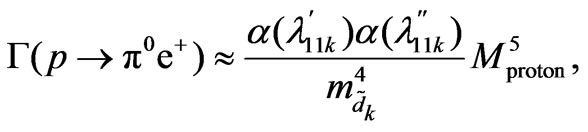 (47)
(47)
where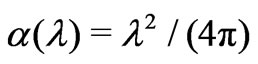 . Giving
. Giving 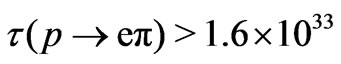 years [20] and taking
years [20] and taking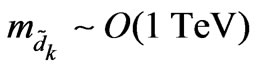 , we obtain
, we obtain
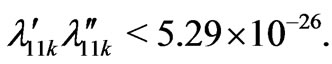 (48)
(48)
It is consistent with the limits presented in [48]. For a more detailed calculation see [49,50]. Other decay modes,
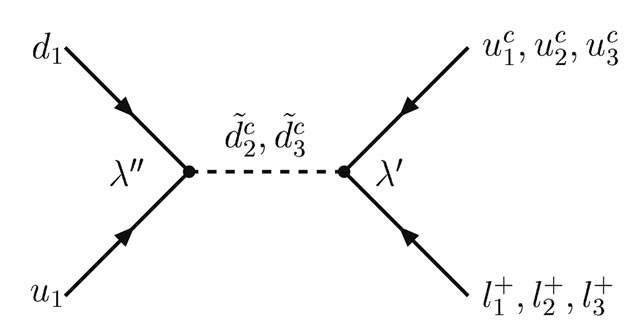
Figure 1. Proton decay into charged leptons in the MSSM and in SUSYECO331 (with  and
and ).
).
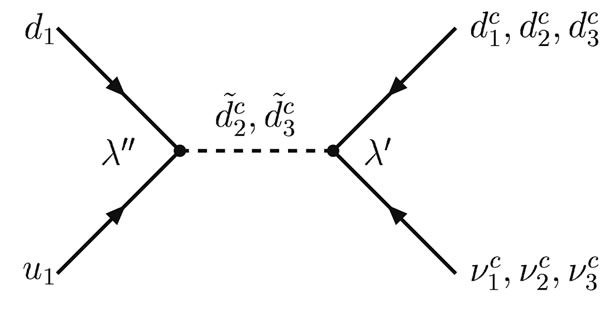
Figure 2. Proton decay into antineutrinos in the MSSM and in SUSYECO331 (with  and
and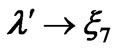 ).
).
where the proton decay into antineutrino, have been considered in [51]. The mentioned decay modes are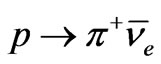 ,
, 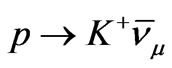 ,
, 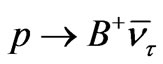 1. In these cases, we get the same numerical results as presented in Equation (48).
1. In these cases, we get the same numerical results as presented in Equation (48).
The bound presented in Equation (48) is so strict. So the natural explanation only is that at least one of the couplings has to be zero. In order to avoid that the simplest way is to impose the R-symmetry. This leads to avoid the proton decay.
In our superpotential given at Equation (22), we allow only interactions that violate L-number. Therefore the proton is stable at tree-level. However it is not only forbidden the dangerous processes of proton decay but also forbidden the neutron-antineutron oscillation. This oscillation was studied in detail in [52-55].
In [45-46], in the framework of the supersymmetric 3-3-1 model with right handed neutrinos, the R-parity violating interaction was applied for instability of the nucleon. The result is consistent with that of the present article (noting that in Ref. [45-46], the authors have taken a lower limit of the proton lifetime equal to 1032 y).
6. Neutrinoless Double Beta Decay in SUSYECO331
Neutrinoless double beta (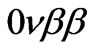 ) decay is a sensitive probe of physics beyond the standard model, see Figure 3, since it violates lepton number [56-62]. This experimental result casts stringent constraints on new physics. Particularly, for the conventional mechanism of
) decay is a sensitive probe of physics beyond the standard model, see Figure 3, since it violates lepton number [56-62]. This experimental result casts stringent constraints on new physics. Particularly, for the conventional mechanism of 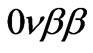 -
-
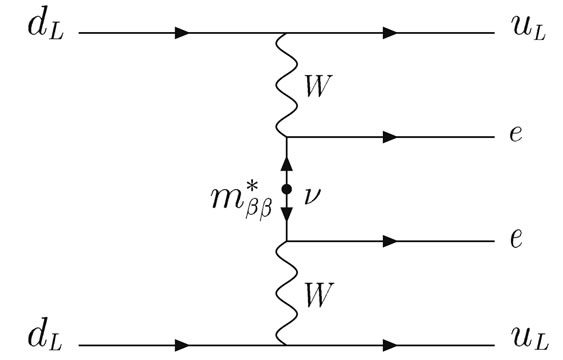
Figure 3. Neutrinoless double beta decay in SM with massive neutrinos.
decay with massive Majorana neutrino exchange between decaying nucleons it implies an upper bound on the neutrino mass below 1 eV.
The neutrinoless double nuclear beta decay reaction, 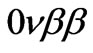 , takes place by the nucleon level process,
, takes place by the nucleon level process,
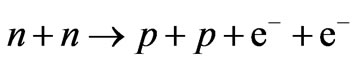 , initiated through the lepton number violating subprocess,
, initiated through the lepton number violating subprocess,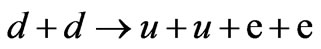 . These rare reactions bear close similarities in the lepton number conserving double beta decay reactions,
. These rare reactions bear close similarities in the lepton number conserving double beta decay reactions,
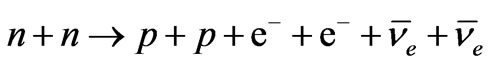 . The relevant experimental situation corresponds to a parent nucleus whose beta decay channel,
. The relevant experimental situation corresponds to a parent nucleus whose beta decay channel, 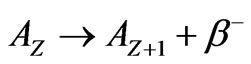 , is energetically closed, but which is allowed to decay to the daughter nucleus,
, is energetically closed, but which is allowed to decay to the daughter nucleus, 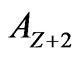 , via the two-step beta decay process involving virtual transitions to the neighboring nucleus,
, via the two-step beta decay process involving virtual transitions to the neighboring nucleus, . The double beta decay processes probe the nuclear structure through the nuclear ground state matrix elements of two-current correlation functions. Only the regular double beta reactions have been experimentally observed so far, while active searches are currently pursued for the
. The double beta decay processes probe the nuclear structure through the nuclear ground state matrix elements of two-current correlation functions. Only the regular double beta reactions have been experimentally observed so far, while active searches are currently pursued for the 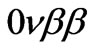 reactions, which offer sensitive probes of new physics.
reactions, which offer sensitive probes of new physics.
The experimental measurements of the double beta decay nuclear reactions,
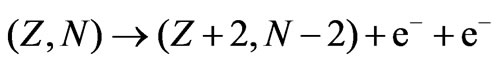 are performed for even-even heavy nuclei, with a representative sample of the nuclear transitions given by,
are performed for even-even heavy nuclei, with a representative sample of the nuclear transitions given by,
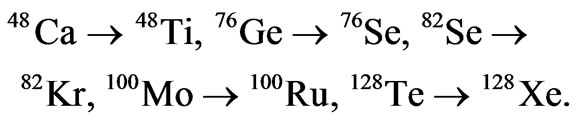
The experimental setups using geochemical (Se, Zr, Te nuclei) or radiochemical (U, Pu) techniques and employ dedicated detectors with Ge semiconductor material, cryogenic, scintillation, or beta ray tracking. The most stringent experimental limits are those obtained by the Moscow-Heidelberg collaboration [60,61], with the corresponding experimental limits for the 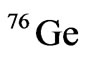 nucleus
nucleus 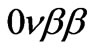 half-life given by,
half-life given by, 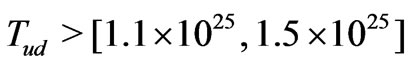 yrespectively. The future projects aim at a half-life sensitivity of order,
yrespectively. The future projects aim at a half-life sensitivity of order, 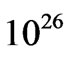 y. A summary of the available experimental information along with a review of the fu-
y. A summary of the available experimental information along with a review of the fu-
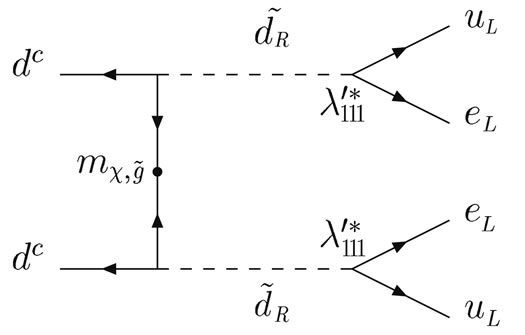
Figure 4. Neutrinoless double beta ( ) decay in the MSSM with massive neutrinos and in SUSYECO331 (with
) decay in the MSSM with massive neutrinos and in SUSYECO331 (with ).
).
ture experimental projects can be found in Ref. [62].
The supersymmetric mechanism of  decay was first proposed by Mohapatra [63] and later studied in more details in Refs. [64,65]. In Ref. [66] it was shown that the gluino exchange contribution to
decay was first proposed by Mohapatra [63] and later studied in more details in Refs. [64,65]. In Ref. [66] it was shown that the gluino exchange contribution to 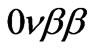 -decay leads to a very stringent limit on the first generation
-decay leads to a very stringent limit on the first generation 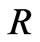 parity violation-Yukawa coupling
parity violation-Yukawa coupling 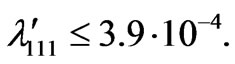 Recently, Babu and Mohapatra [67] found another contribution comparable in size with the gluino exchange. It allows one to set stringent limits on combinations of the intergeneration R parity violation-Yukawa couplings such as
Recently, Babu and Mohapatra [67] found another contribution comparable in size with the gluino exchange. It allows one to set stringent limits on combinations of the intergeneration R parity violation-Yukawa couplings such as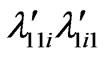 , where
, where 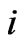 denotes generations, see Fiure 4.
denotes generations, see Fiure 4.
The constraints on the parameters of the minimal supersymmetric standard model with explicit R―parity violation deduced [67,68] from the 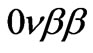 half―life limit are more stringent than those from other low― energy processes and from the largest high energy accelerators. The limits are
half―life limit are more stringent than those from other low― energy processes and from the largest high energy accelerators. The limits are
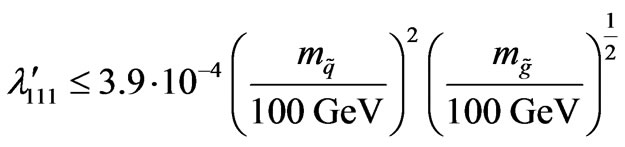 (49)
(49)
with 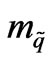 and
and 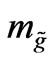 denoting squark and gluino masses, respectively, and with the assumption
denoting squark and gluino masses, respectively, and with the assumption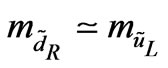 . This result is important for the discussion of new physics in the connection with the high―Q2 events seen at HERA.
. This result is important for the discussion of new physics in the connection with the high―Q2 events seen at HERA.
We find further [66]
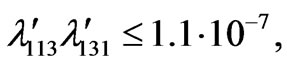 (50)
(50)
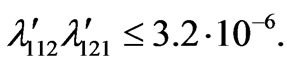 (51)
(51)
The analyses presented in the MSSM to the neutrinoless double beta decay are still hold in the SUSYECO331 model, because the 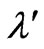 is allowed in our superpotential as shown at Equation (22).
is allowed in our superpotential as shown at Equation (22).
7. Conclusions
In this paper we have presented new R-symmetry for the supersymmetric economical 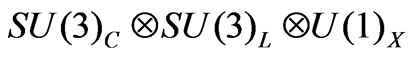 mode and studied neutrino mass by implication for the obtained R-parity. The neutrino mass spectrum is affected by the chosen R-parity. By imposing the R-parity, namely:
mode and studied neutrino mass by implication for the obtained R-parity. The neutrino mass spectrum is affected by the chosen R-parity. By imposing the R-parity, namely: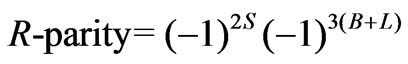 , the neutrino mass spectrum at the tree level contains two massless.
, the neutrino mass spectrum at the tree level contains two massless.
We remind that in the non-supersymmetric economical 3-3-1 model, to give neutrinos a correct mass pattern, we have to introduce new mass scale around the GUT scale. The same situation happens in the supersymmetric version and the above puzzle can be solved with the help of the inflaton having mass in the range of the GUT scale. In this paper, we have showed that by the chosen R parity and the set of parameters, the pseudoDirac neutrino mass is available.
We have found that the other R-parity given in (21) leads to the interference between the neutrino and neutralino mass matrices. Because of this interference mass matrix, all neutrino gain mass only just at the tree level and the interference mass matrix does not much affect on the neutralino mass spectrum. In the charged lepton sector, with the new R-parity, there is also an interference mass matrix between the usual leptons and charginos. By taking the numerical, we show that the charged sector is basically divided in two distinct sectors: one giving the usual known leptons and the other ones given the new charginos. If we ignore the interference charged lepton mass matrix, the chargino mass spectrum is degenerated. This degenerated mass spectrum is removed by imposing the new R-parity.
The new R-parity not only provides a simple mechanism for the mass generation of the neutrinos but also gives some lepton flavor violating interactions at the tree level. This will play some important phenomenology in our model such as the proton’s stability, forbiddance of the neutron-antineutron oscillation and neutrinoless double beta decay.
8. Acknowledgments
M. C. R. is grateful to Conselho Nacional de Desenvolvimento Cient fico e Tecnológico (CNPq) under the processes 309564/2006-9 for supporting his work, he also would like to thank Vietnam Academy of Science and Technology for the nice hospitality, warm atmosphere during his stay at Institute of Physics to do this work. This work was supported in part by the National Foundation for Science and Technology Development (NAFOSTED) under grant No: 103.01.16.09.
REFERENCES
- S. F. SuperK, et al., “Solar B-8 and Hep Neutrino Measurements from 1258 Days of Super-Kamiokande Data,” Physical Review Letters, Vol. 86, No. 25, 2001, pp. 5651- 5655. doi:10.1103/PhysRevLett.86.5651
- T. Araki, et al., “Measurement of Neutrino Oscillation with KamLAND: Evidence of Spectral Distortion,” Physical Review Letters, Vol. 94, No. 8, 2005, pp. 081801- 1-081801-5.
- SNO Collaboration, B. Aharmim, et al., “Electron Energy Spectra, Uxes, and Daynight Asymmetries of B-8 Solar Neutrinos from Measurements with NaCl Dissolved in the Heavy-Water Detector at the Sudbury Neutrino Observatory,” Physical Review C, Vol. 72, No. 5, 2005, pp 055502-1-055502-47. doi:10.1103/PhysRevC.72.055502
- M. Gell-Mann, P. Ramond and R. Slansky, In: D. Freedman and P. van Nieuwenhuizen, Ed., Super-Gravity, Proceedings of the Work-Shop, North-Holland, Amsterdam, 1979,
- J. Schechter and J. W. F. Valle, “Neutrino Masses in SU(2) × U(1) Theories,” Physical Review D, Vol. 22, No. 9, 1980, pp. 2227-2235. doi:10.1103/PhysRevD.22.2227
- J. Schechter and J. W. F. Valle, “Neutrino Decay and Spontaneous Violation of Lepton Number,” Physical Review D, Vol. 25, No. 3, 1982, pp. 774-783.
- A. Zee, “A Theory of Lepton Number Violation, Neutrino Majorana Mass, and Oscillation,” Physical Review B, Vol. 93, No. 4, 1980, pp. 389-393. doi:10.1016/0370-2693(80)90349-4
- A. Zee, “Quantum Numbers of Majorana Neutrino Masses,” Nuclear Physics B, Vol. 264, 1986, pp. 99-110. doi:10.1016/0550-3213(86)90475-X
- K. S. Babu, “Model of ‘Calculable’ Majorana Neutrino Masses,” Physical Review Letters, Vol. 203, No. 1-2, 1988, pp. 132-136. doi:10.1016/0370-2693(88)91584-5
- K. S. Babu and E. Ma, “Natural Hierarchy of Radiatively Induced Majorana Neutrino Masses,” Physical Review Letters, Vol. 61, No. 6, 1988, pp. 674-677. doi:10.1103/PhysRevLett.61.674
- D. Chang, W.-Y. Keung and P. B. Pal, “Spontaneous Lepton Number Breaking at Electroweak Scale,” Physical Review Letters, Vol. 61, No. 21, 1988, pp. 2420-2423. doi:10.1103/PhysRevLett.61.2420
- F. Pisano and V. Pleitez, “An SU(3) × U(1) Model for Electroweak Interactions,” Physical Review D, Vol. 46, 1992, pp. 410-417. doi:10.1103/PhysRevD.46.410
- P. H. Frampton, “Chiral Dilepton Model and the Avor Question,” Physical Review Letters, Vol. 69, No. 20, 1992, pp. 2889-2891. doi:10.1103/PhysRevLett.69.2889
- R. Foot, O. F. Hernandez, F. Pisano and V. Pleitez, “Lepton masses in an SU(3)L × U(1)N gauge model,” Physical Review D, Vol. 47, No. 9, 1993, pp. 4158-4161. doi:10.1103/PhysRevD.47.4158
- M. Singer, J. W. F. Valle and J. Schechter, “Canonical Neutral Current Predictions from the Weak Electromagnetic Guage Group SU(3) × U(1),” Physical Review D, Vol. 22, No. 3, 1980, pp. 738-743. doi:10.1103/PhysRevD.22.738
- R. Foot, H. N. Long and T. A. Tran, “SU(3)L × U(1)N and SU(4)L × U(1)N Gauge Models with Right-Handed Neutrinos,” Physical Review D, Vol. 50, No. 1, 1994, pp. 34-38. doi:10.1103/PhysRevD.50.R34
- J. C. Montero, F. Pisano and V. Pleitez, “Neutral Currents and GIM Mechanism in SU(3)L × U(1)N Models for Electroweak Interactions,” Physical Review D, Vol. 47, No. 7, 1993, pp. 2918-2929. doi:10.1103/PhysRevD.47.2918
- H. N. Long, “SU(3)C × SU(3)N × U(1)N Model with RightHanded Neutrinos,” Physical Review D, Vol. 53, No. 1, 1996, pp. 437-445. doi:10.1103/PhysRevD.53.437
- F. Pisano, “A Simple Solution for the Flavor Question,” Modern Physics Letters A, Vol. 11, No. 32-33, 1996, pp. 2639-2647. doi:10.1142/S0217732396002630
- C. A. de S. Pires and O. P. Ravinez, “Charge Quantization in a Chiral Bilepton Gauge Model,” Physical Review D, Vol. 58, 1998, pp. 035008-1-035008-5.
- J. C. Montero, C. A. de S. Pires and V. Pleitez, “Neutrino Masses through a Type II Seesaw Mechanism at TeV Scale,” Physical Review B, Vol. 502, 2001, pp. 167-170.
- A. G. Dias and V. Pleitez, “Stabilizing the Invisible Axion in 3-3-1 Models,” Physical Review D, Vol. 69, No. 7, 2004, pp. 077702-1-077702-4. doi:10.1103/PhysRevD.69.077702
- A. G. Dias and A. Dor, “Neutrino Decay and Neutrinoless Double Beta Decay in a 3-3-1 Model,” Physical Review D, Vol. 72, No. 3, 2005, pp. 035006-1-035006-8. doi:10.1103/PhysRevD.72.035006
- T. Kitabayashi and M. Yasuµe, “Two Loop Radiative Neutrino Mechanism in an SU(3)L × U(1)N Gauge Model,” Physical Review D, Vol. 63, No. 9, 2001, pp. 095006-1-095006-6.
- H. N. Long and T. Inami, “S, T, U Parameters in SU(3)C × SU(3)L × U(1) Model with Right-Handed Neutrinos,” Physical Review D, Vol. 61, No. 7, 2000, pp. 075002- 1-075002-9. doi:10.1103/PhysRevD.61.075002
- P. Van Dong, H. N. Long and D. V. Soa, “Higgs-Gauge Boson Interactions in the Economical 3-3-1 Model,” Physical Review D, Vol. 73, No. 7, 2006, pp. 075005-1- 075005-15. doi:10.1103/PhysRevD.73.075005
- P. V. Dong, H. N. Long, D. T. Nhung and D. V. Soa, “SU(3)C × SU(3)L × U(1)X Model with Two Higgs Triplets,” Physical Review D, Vol. 73, No. 3, 2006, pp. 035004-1-035004-11. doi:10.1103/PhysRevD.73.035004
- P. V. Dong and H. N. Long, “The Economical SU(3)C × SU(3)L × U(1)X Model,” Advanced High Energy Physics, Vol. 2008, 2008, pp. 739492-739567.
- D. Chang and H. N. Long, “Interesting Radiative Patterns of Neutrino Mass in an SU(3)C × SU(3)L × U(1)X Model with Right-Handed Neutrinos,” Physical Review D, Vol. 73, No. 5, 2006, pp. 053006-1-053006-17. doi:10.1103/PhysRevD.73.053006
- A. G. Dias, C. A. de S. Pires and P. S. Rodrigues da Silva, “Naturally Light Right-Handed Neutrinos in a 3-3-1 Model,” Physical Letters B, Vol. 628, No. 1-2, 2005, 85- 92. doi:10.1016/j.physletb.2005.09.028
- J. C. Montero, V. Pleitez and M. C. Rodriguez, “Supersymmetric 3-3-1 Model with Right-Handed Neutrinos,” Physical Review D, Vol. 70, No. 7, 2004, pp. 075004-1- 075004-8. doi:10.1103/PhysRevD.70.075004
- D. T. Huong, M. C. Rodriguez and H. N. Long, “Scalar Sector of Supersymmetric Su(3)C × Su(3)L × U(1)N Model with Right-Handed Neutrinos,”.
- P. V. Dong, D. T. Huong, M. C. Rodriguez and H. N. Long, “Neutrino Masses in the Supersymmetric SU(3)C × SU(3)L × U(1)X Model with Right-Handed Neutrinos,” The European Physical Journal C, Vol. 48, No. 1, 2006, pp. 229-241. doi:10.1140/epjc/s10052-006-0010-z
- P. V. Dong, D. T. Huong, M. C. Rodriguez and H. N. Long, “Supersymmetric Economical 3-3-1 Model,” Nuclear Physics B, Vol. 772, No. 1-2, 2007, pp. 150-174. doi:10.1016/j.nuclphysb.2007.03.003
- H. E. Haber and G. L. Kane, “The Search for Supersymmetry: Probing Physics beyond the Standard Model,” Physics Reports, Vol. 117, No. 2-4, 1985, pp. 75-263. doi:10.1016/0370-1573(85)90051-1
- D. T. Huong and H. N. Long, “Neutralinos and Charginos in Supersymmetric Economical 3-3-1 Model,” JHEP07, Vol. 2008, 2008, pp. 049-1-049-17.
- P. V. Dong, H. N. Long and D. V. Soa, “Neutrino Masses in the Economical 3-3-1 Model,” Physical Review D, Vol. 75, No. 7, 2007, pp. 073006-1-073006-13. doi:10.1103/PhysRevD.75.073006
- D. T. Huong and H. N. Long, “Non-thermal Leptogenesis in Supersymmetric 3-3-1 Model with in Ationary Scenario,” Journal of Physics G: Nuclear and Particle Physics, Vol. 38, No. 1, Article ID: 015202.
- W. M. Yao, et al., “Review of Particle Physics,” Journal of Physics G: Nuclear and Particle Physics, Vol. 33, No. 1, 2006, 1-1232. doi:10.1088/0954-3899/33/1/001
- J. C. Montero, V. Pleitez and M. C. Rodriguez, “Lepton Masses in a Supersymmetric 3-3-1 Model,” Physical Review D, Vol. 65, No. 9, 2002, pp. 095008-1-095008-11. doi:10.1103/PhysRevD.65.095008
- D. Yu. Akimov, et al., “Limits on Inelastic Dark Matter from ZEPLIN-III,” Vol. 692, No. 3, 2010, pp. 180-183.
- M. Capdequi-Peyranµere and M. C. Rodriguez, “Charginos and Neutralinos Production at 3-3-1 Supersymmetric Model in e-e Scattering,” Physical Review D, Vol. 65, No. 3, 2002, pp. 035001-1-035001-16.
- P. Fayet, “Supergauge Invariant Extension of the Higgs Mechanism and a Model for the Electron and Its Neutrino,” Nuclear Physics B, Vol. 90, 1975, pp. 104-124. doi:10.1016/0550-3213(75)90636-7
- P. Fayet, “Supersymmetry and Weak, Electromagnetic and Strong Interactions,” Physical Review B, Vol. 64, No. 2, 1976, pp. 159-162.
- P. Fayet, “Spontaneously Broken Supersymmetric Theories of Weak, Electromagnetic and Strong Interactions,” Physical Review B, Vol. 69, No. 4, 1977, pp. 489-494. doi:10.1016/0370-2693(77)90852-8
- P. Fayet, In: A. Perlmutter and L. F. Scott, Eds., New Frontiers in High-Energy Physics, Proceedings Orbis Scientiae, Coral Gables, 1978, p. 413.
- M. C. Rodriguez, “History of Supersymmetric Extensions of the Standard Model,” International Journal of Modern Physics A, Vol. 25, No. 6, 2010, pp. 1091-1121. doi:10.1142/S0217751X10048950
- H. Dreiner, “An Introduction to Explicit R-Parity Violation,” Pramana, Vol. 51, No. 1-2, pp. 123-133.
- J. L. Goity and Marc Sher, “Bounds on Delta B = 1 Couplings in the Supersymmetric Standard Model,” Physical Review B, Vol. 346, No. 1-2, 1995, pp. 69-74.
- I. Hinchliffe and T. Kaeding, “Band L-Violating Couplings in the Minimal Supersymmetric Standard Model,” Physical Review D, Vol. 47, No. 1, 1993, pp. 279-284. doi:10.1103/PhysRevD.47.279
- A. Yu. Smirnov and F. Vissani, “Upper Bound on All Products of R-Parity Violating Couplings Lambda-Prime and Lambda-Prime-Prime from Proton Decay,” Physical Review B, Vol. 380, No. 3-4, 1996, pp. 317-323. doi:10.1016/0370-2693(96)00495-9
- M. Dress, R. M. Godbole and P. Royr, “Theory and Phenomenology of Sparticles,” 1st Edition, World Scientific Publishing Co., Singapore City, 2004.
- H. Baer and X. Tata, “Weak Scale Supersymmetry: From Superfields to Scattering Events,” 1st Edition, Cambridge University Press, Cambridge, 2006.
- R. Barbier, et al., “R-Parity Violating Supersymmetry,” Physics Reports, Vol. 420, No. 1-6, 2005, pp. 1-195. doi:10.1016/j.physrep.2005.08.006
- G. Moreau, “Phenomenological Study of R-Parity Symmetry Violating Interactions in Supersymmetric Theories,” In French, arXiv: hep-ph/0012156.
- HEIDELBERG-MOSCOW Collaboration, A. Balysh, et al., “SubeV Limit for the Neutrino Mass from Ge-76 Double Beta Decay by the Heidelberg―Moscow Experiment,” Physical Review B, Vol. 356, 1995, p. 450.
- H. V. Klapdor-Kleingrothaus, “Double Beta Decay and Neutrino Mass: The Heidelberg-Moscow Experiment,” Progress in Particle and Nuclear Physics, Vol. 32, 1994, pp. 261-280. doi:10.1016/0146-6410(94)90024-8
- H. V. Klapdor-Kleingrothaus, “Double-Beta Decay And Related Topics: Proceedings of the International Workshop Held at European Centre for Theoretical Studies (ECT): Trento, Italy, April 24-May 5, 1995,” 1995, World Scientific, Singapore.
- L. Baudis, et al., “The Heidelberg—Moscow Experiment: Improved Sensitivity for Ge-76 Neutrinoless Double Beta Decay,” Physical Review B, Vol. 407, No. 3-4, 1997, pp. 219-224. doi:10.1016/S0370-2693(97)00756-9
- [61] H. V. Klapdor-Kleingrothaus, A. Dietz, H. L. Harney and I. V. Krivosheina, “Evidence for Neutrinoless Double Beta Decay,” Modern Physics Letters A, Vol. 16, No. 37, 2001, pp. 2409-2420. doi:10.1142/S0217732301005825
- [62] M. GÄunther, et al., “Heidelberg—Moscow Beta-Beta Experiment with Ge-76: Full Setup with ve Detectors,” Physical Review D, Vol. 55, 1996, pp. 54-67.
- [63] R. N. Mohapatra, “New Contributions to Neutrinoless Double Beta Decay in Super-Symmetric Theories,” Physical Review D, Vol. 34, No. 11, 1986, pp. 3457-3461. doi:10.1103/PhysRevD.34.3457
- [64] J. D. Vergados, “Neutrinoless Double Beta Decay without Majorana Neutrinos in Supersymmetric Theories,” Physical Review B, Vol. 184, No. 1, 1987, pp. 55-62. doi:10.1016/0370-2693(87)90487-4
- [65] M. Hirsch, H. V. Klapdor-Kleingrothaus and S. G. Kovalenko, “New Supersymmetric Contributions to Neutrinoless Double Beta Decay,” Physical Review B, Vol. 352, No. 1-2, 1995, pp. 1-7.
- [66] M. Hirsch, H. V. Klapdor-Kleingrothaus and S. G. Kovalenko, “New Constraints On R-Parity Broken Supersymmetry from Neutrinoless Double Beta Decay,” Physical Review Letters, Vol. 75, No. 1, 1995, pp. 17-20. doi:10.1103/PhysRevLett.75.17
- [67] K. S. Babu and R. N. Mohapatra, “New Vector―Scalar Contributions to Neutrinoless Double Beta Decay and Constraints on R-Parity Violation,” Physical Review Letters, Vol. 75, No. 12, 1995, pp. 2276-2279. doi:10.1103/PhysRevLett.75.2276
- [68] M. Hirsch, H. V. Klapdor-Kleingrothaus and S. G. Kovalenko, “On the SUSY Accompanied Neutrino Exchange Mechanism of Neutrinoless Double Beta Decay,” Physical Review B, Vol. 372, No. 3-4, 1996, pp. 181-186.
- [69] M. Hirsch, H. V. Klapdor-Kleingrothaus and S. G. Kovalenko, “Supersymmetry and Neutrinoless Double Beta Decay,” Physical Review D, Vol. 53, No. 3, 1996, pp. 1329-1348. doi:10.1103/PhysRevD.53.1329
Appendix
Elements of Neutrino Mass Matrix in SUSYECO331
The elements of 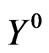 presented in Equation (24) is given by Equation (26) where
presented in Equation (24) is given by Equation (26) where
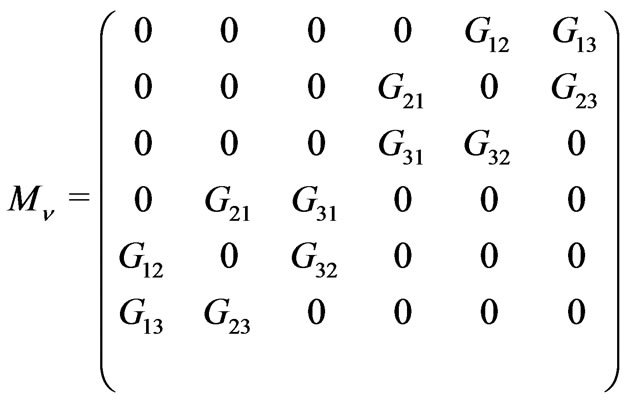 (52)
(52)
and
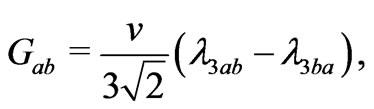 (53)
(53)
while
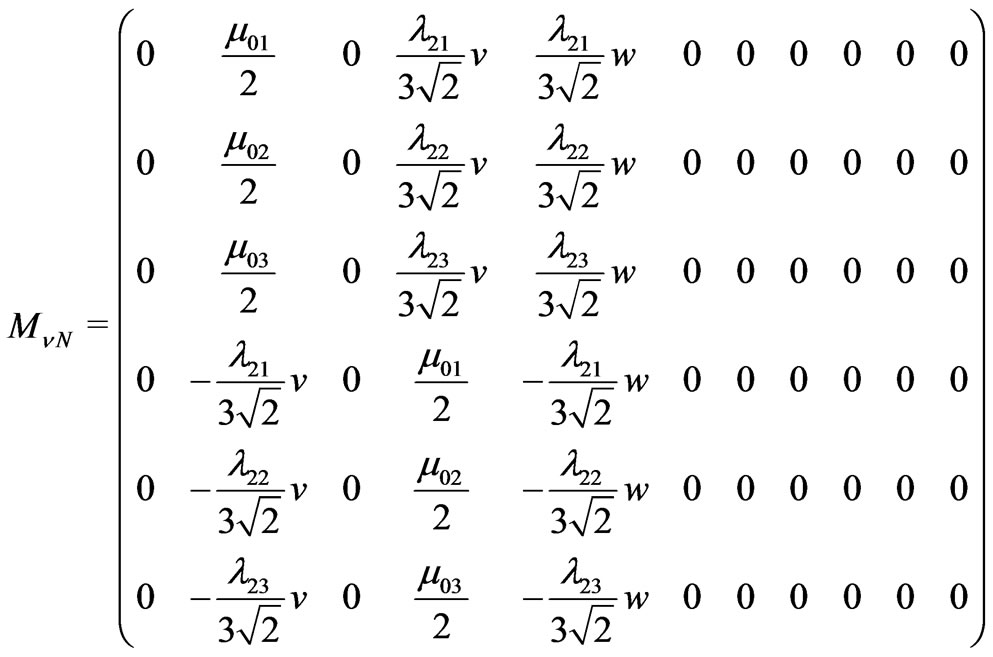 (54)
(54)
and  is presented in [18].
is presented in [18].
NOTES
1Again, we are bare mixing in the quarks, neutrinos and squarks sectors.

