Journal of Modern Physics
Vol.2 No.10(2011), Article ID:8049,5 pages DOI:10.4236/jmp.2011.210138
Electromotive Force Generation with Hydrogen Release by Salt Water Flow under a Transverse Magnetic Field
Dipartimento di Matematica e Informatica (DMI), Università degli Studi di Salerno, Fisciano, Italy
E-mail: rdeluca@unisa.it
Received January 7, 2011; revised May 6, 2011; accepted June 10, 2011
Keywords: Renewable Energies, Hydrogen Production, Faraday Voltage
ABSTRACT
By considering an electrolyte solution in motion in a duct under a transverse magnetic field, we notice that a so called Faraday voltage arises because of the Lorentz force acting on anions and cations in the fluid. When salt water is considered, hydrogen production takes place at one of the electrodes if an electric current, generated by Faraday voltage, flows in an external circuit. The maximum amount of hydrogen production rate is calculated by basic electrochemical concepts.
1. Introduction
Aqueous ionic solutions and conducting metals show some similarities in their electrical transport properties. One of the simplest phenomenological laws of classical electrodynamics is Ohm’s law of conduction [1], namely
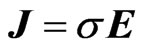 (1)
(1)
where ![]() is the current density flowing under the effect of the electric field
is the current density flowing under the effect of the electric field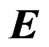 , and s is the electrical conductivity of the material. A similar relation can be found in electrolyte solutions. In the latter case, the partial conductivities can be expressed in terms of the mobility mP of cations and mN of anions, so that:
, and s is the electrical conductivity of the material. A similar relation can be found in electrolyte solutions. In the latter case, the partial conductivities can be expressed in terms of the mobility mP of cations and mN of anions, so that:
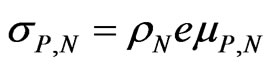 (2)
(2)
where 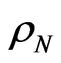 is the volume density of both types of ions and e is the electron charge. Mobility, on its turn, is defined as the proportionality constant linking the ions velocity
is the volume density of both types of ions and e is the electron charge. Mobility, on its turn, is defined as the proportionality constant linking the ions velocity  and the electric field
and the electric field , according to the following:
, according to the following: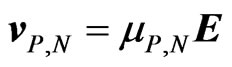 . We recall that the total conductivity s is given by
. We recall that the total conductivity s is given by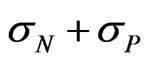 .
.
It is well known that Lorentz force acts on charged particles moving in the presence of a magnetic field. Let us then consider anions and cations in an electrolyte solution flowing in a duct with velocity , where
, where 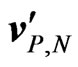 is the velocity of the particles measured with respect to a reference frame moving with the aqueous solution. In the presence of a constant magnetic field
is the velocity of the particles measured with respect to a reference frame moving with the aqueous solution. In the presence of a constant magnetic field , these ions are subject to a Lorentz force given by:
, these ions are subject to a Lorentz force given by:
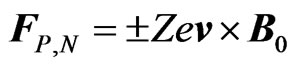 (3)
(3)
where the plus and minus signs refer to cations and anions, respectively, both assumed to have ionic charge Ze in absolute value (Z thus being their valence). Because of Lorentz force, a voltage difference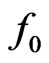 , known in the literature as Faraday voltage [2,3], appears between the electrodes A and B of Figure 1. This voltage, similarly to what observed in the Hall’s effect in metals [1], can be expressed as the product
, known in the literature as Faraday voltage [2,3], appears between the electrodes A and B of Figure 1. This voltage, similarly to what observed in the Hall’s effect in metals [1], can be expressed as the product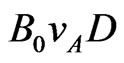 , when the electrolyte flows in a circular pipe of diameter D. Notice that in the present work boldface letters and corresponding plain text letters are used for vectors and their amplitudes, respectively. Geselowitz [4] has shown that this result is valid for any velocity profile, provided the flow is axially symmetric. It can also be shown that this result is valid, in particular, for a thin rectangular wire [5].
, when the electrolyte flows in a circular pipe of diameter D. Notice that in the present work boldface letters and corresponding plain text letters are used for vectors and their amplitudes, respectively. Geselowitz [4] has shown that this result is valid for any velocity profile, provided the flow is axially symmetric. It can also be shown that this result is valid, in particular, for a thin rectangular wire [5].
In the present work we propose an electromotive force (e.m.f.) generator consisting of a rectangular pipe with two lateral conducting plates enclosing salt water in motion under a magnetic field orthogonal to the flow velocity vector (see Figure 1). A similar system has already been proposed by Yamaguchi et al. [6] for a non-poison electro-conductive polymer and its mixture with magnetic fluid. We here also notice that, taking salt water solution as the electrolyte flowing in the rectangular pipe, hydrogen gas is formed at one of the two electrodes of the e.m.f. generator proposed. In the present work we calculate a general expression for the rate of production of hydrogen gas as a function of the flux rate of salt wa-

Figure 1. Schematic representation of the system: salt water flows through a rectangular pipe of section 4wh (2w is the width and 2h is the height) with velocity v in a volume of length L where a magnetic field B0, orthogonal to V, is present. Because of Lorentz force, the charged ions in the solution accumulate in the vicinities of the lateral conducting plates, generating, at equilibrium, a constant electric field E.
ter flowing within the rectangular pipe. Experimental work is awaited to provide validation of the proposed analysis and to suggest further development of the topic of hydrogen production by salt water.
2. Faraday Voltage
Let us consider the schematic view of the e.m.f. generator given in Figure 1. Take the magnetic field along the z-direction and the velocity  along the x-axis. Assume a velocity profile
along the x-axis. Assume a velocity profile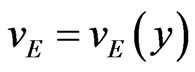 , and neglect, in the calculation of
, and neglect, in the calculation of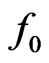 , the amplitude of the drift velocities
, the amplitude of the drift velocities 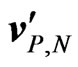 with respect to the average velocity of the fluid within the rectangular pipe
with respect to the average velocity of the fluid within the rectangular pipe . Under these hypotheses we may write the voltage drop
. Under these hypotheses we may write the voltage drop  across the two conductors as follows:
across the two conductors as follows:
 (4)
(4)
Notice that a factor of two appears in Equation (4), differently from what reported by Yamaguchi et al. [6], because of the presence of two ionic species in the electrolyte in our case. A detailed analysis of the dynamical problem is given in the Appendix, also to clarify how the low mobility coefficients for sodium and chlorine ions give drift velocities which are in amplitude much smaller than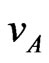 .
.
By considering the equivalent circuit in Figure 2, where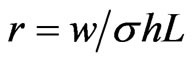 ,
, 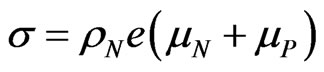 being the conductivity of the electrolyte solution, we may write:
being the conductivity of the electrolyte solution, we may write:
 (5)
(5)
where 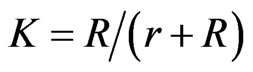 and a multiplicative factor of 4 is present when comparing the above result with that obtained by Yamaguchi et al.[6], because of Equation (4).
and a multiplicative factor of 4 is present when comparing the above result with that obtained by Yamaguchi et al.[6], because of Equation (4).
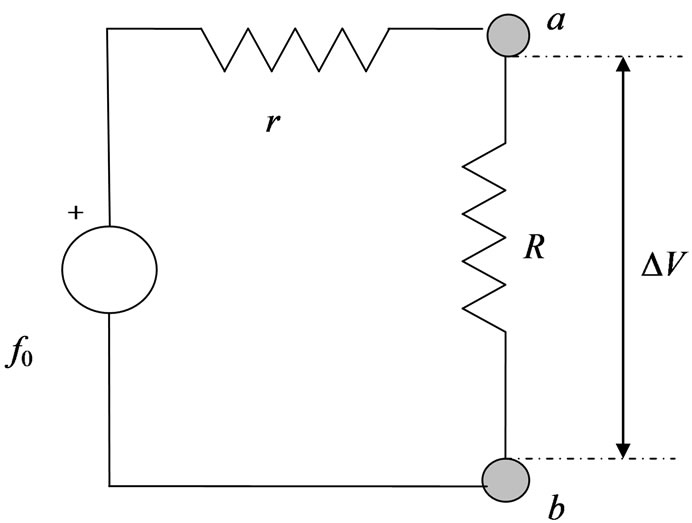
Figure 2. Equivalent circuit for an electric power generator with an open-circuit voltage f0. When the internal resistance r is connected in series with an external load R, the output voltage is ΔV. Maximum power output  is attained for
is attained for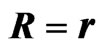 .
.
The above formula can be derived by setting 
 , where
, where 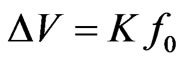 is the voltage output of the device as shown in Figure 2. In order to estimate of the maximum power output (obtained for
is the voltage output of the device as shown in Figure 2. In order to estimate of the maximum power output (obtained for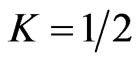 ) in terms of the average water flow rate Q, for which
) in terms of the average water flow rate Q, for which , we write
, we write
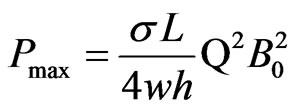 (6)
(6)
Therefore, for seawater at room temperature, by taking
 ,
, 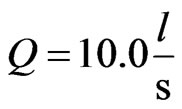 ,
, 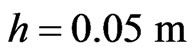 ,
, 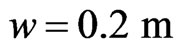 ,
,
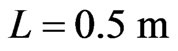 , and
, and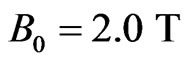 , we have
, we have 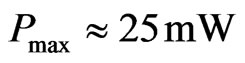 and
and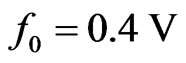 . Notice that the power output depends on the square of the average velocity
. Notice that the power output depends on the square of the average velocity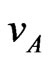 , in such a way that the device may be effective also in cases where the periodic motion of seawater could be used. The above calculation has been performed by assuming that the concentration of salt in water is sufficient to allow circulation of current in the system. However, as suggested by Wright and Van der Beken [2], and as calculated by the author [5], the average salinity of salt water is by far sufficient for current circulation in the system.
, in such a way that the device may be effective also in cases where the periodic motion of seawater could be used. The above calculation has been performed by assuming that the concentration of salt in water is sufficient to allow circulation of current in the system. However, as suggested by Wright and Van der Beken [2], and as calculated by the author [5], the average salinity of salt water is by far sufficient for current circulation in the system.
3. Hydrogen Production
In addition to the power output estimated in the previous section, we may notice that chemical reactions take place at the electrodes of the device in Figure 1. In fact, we may state that the current I can be sustained by oxidation of chlorine ions at one electrode (negatively charged), with production of chlorine gas, according to the following reaction [7]
 (7)
(7)
At the same time, reduction of water takes place at the opposite electrode according to the following additional reaction [7]
![]() (8)
(8)
The reaction in (8) implies production of sodium hydroxide and hydrogen gas at the positively charged electrode. Therefore, also confiding on the experimental evidence in ref. [2], we may argue that it is possible to device an e.m.f. generator by letting salt water run in a pipe with average velocity  under an orthogonal magnetic field
under an orthogonal magnetic field  and that, at the same time, it is also possible to produce hydrogen gas by this type of device.
and that, at the same time, it is also possible to produce hydrogen gas by this type of device.
The question is now the following: “How much hydrogen can be produced when a given amount of salt water flows inside the rectangular pipe in Figure 1?”
We start by assuming that, because of the reduction and oxidation reaction at the two electrodes, corresponding to the two lateral conducting plates of the device, it is possible to sustain a steady current flow in the system. However, the flow of electrons must be provided by a congruous number of ions moving along the pipe. Let us then also assume that only a fraction of charges in the volume  participate to the reductionoxidation processes specified in (7) and (8). When a stationary state sets in, the number of charges participating in the redox reactions must be such that a depletion of electron charges at the negative electrode is counterbalanced by the oxidation of chlorine ions, as seen in (7). Similarly, these charges must be also sufficient, in number, to compensate the excess of electrons at the other electrode by reduction of water as in (8). Contrarily to what assumed in a previous work [5], this aspect needs to be treated with great care. Indeed, the drift velocities in the y-direction
participate to the reductionoxidation processes specified in (7) and (8). When a stationary state sets in, the number of charges participating in the redox reactions must be such that a depletion of electron charges at the negative electrode is counterbalanced by the oxidation of chlorine ions, as seen in (7). Similarly, these charges must be also sufficient, in number, to compensate the excess of electrons at the other electrode by reduction of water as in (8). Contrarily to what assumed in a previous work [5], this aspect needs to be treated with great care. Indeed, the drift velocities in the y-direction  and
and 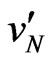 of the sodium and chlorine ions in salt water, respectively, can be seen to be much less than
of the sodium and chlorine ions in salt water, respectively, can be seen to be much less than 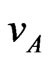 in the Appendix. In this way, in the time
in the Appendix. In this way, in the time  only a small fraction of charges of those available in the volume
only a small fraction of charges of those available in the volume 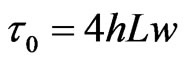 may be available for the redox reactions. In fact, if we consider the transverse current density given by (1), we may write
may be available for the redox reactions. In fact, if we consider the transverse current density given by (1), we may write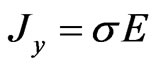 . Therefore, the available current
. Therefore, the available current  is given by
is given by
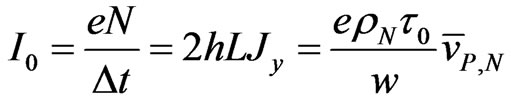 (9)
(9)
where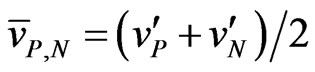 . As it appears from Equation (9), N is much less than the total number of charged ions flowing in a time
. As it appears from Equation (9), N is much less than the total number of charged ions flowing in a time  in the region of length L of the rectangular pipe. We now need to compare the expression of
in the region of length L of the rectangular pipe. We now need to compare the expression of  with the maximum current
with the maximum current  circulating in the device when an external load of resistance
circulating in the device when an external load of resistance 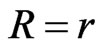 is applied to it. Therefore, since
is applied to it. Therefore, since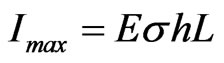 , we have
, we have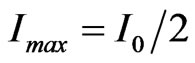 , which confirms the possibility of having ionic conduction according to the picture represented in the previous section.
, which confirms the possibility of having ionic conduction according to the picture represented in the previous section.
The number of hydrogen moles 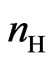 produced by the device in one second is then calculated by recognizing that one mole of H2 is obtained when two moles of electrons are involved in the reactions at the electrons, in such a way that
produced by the device in one second is then calculated by recognizing that one mole of H2 is obtained when two moles of electrons are involved in the reactions at the electrons, in such a way that
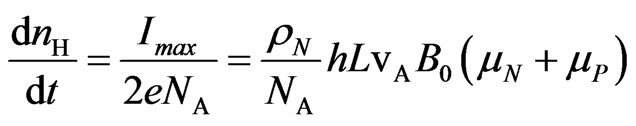 (10)
(10)
By now setting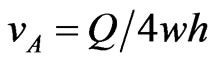 , the above expression can be recast in the following form
, the above expression can be recast in the following form
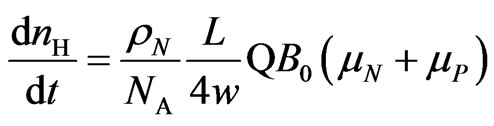 (11)
(11)
which gives the rate of hydrogen production in a salt water solution under a constant magnetic field  when the flux flow rate of the solution is
when the flux flow rate of the solution is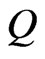 . Typical values for seawater concentrations at 25˚C can be seen to be
. Typical values for seawater concentrations at 25˚C can be seen to be
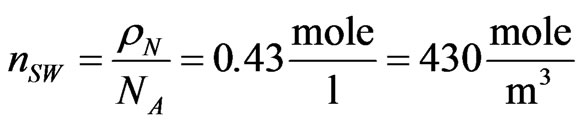 . Therefore, by taking again
. Therefore, by taking again ,
, 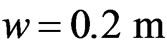 ,
, 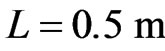 , and
, and , we have
, we have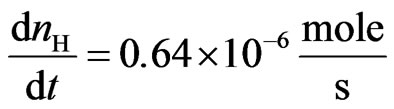 .
.
4. Conclusions
In the present work it has been shown that an electromotive force generator can be realized by letting salt water run though a rectangular pipe under the influence of a transverse magnetic field. Because of Lorentz force on the moving sodium and chlorine ions in salt water, one can shown that an equilibrium electric field can be created by the accumulation of charged ions in the vicinities of the lateral conducting plates. By considering the problem in one dimension, it can be shown that the charge distribution varies linearly from one electrode to the other, if the velocity profile of the fluid in the pipe is parabolic [5]. Furthermore, it can be argued that the electric field across the electrodes can sustain a constant electromotive force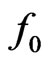 , which, on its turn, can generate an electric power output.
, which, on its turn, can generate an electric power output.
The device could be used as an alternative electric power source in situations where salt water is forced to run in large closed ducts, as it happens, for example, in some desalination plants. Experiments on small scale devices carried out by Wright and Van Der Beken [2] for a pipe with circular section do confirm the existence of a Faraday voltage across the device. In the present paper it is also predicted that, according to properties of ions in aqueous solutions, hydrogen gas can be produced at the positively charged lateral conducting plate. The rate of production of hydrogen gas is however small for not large values of salt water flow rate. Nevertheless, the present analysis can be seen as a starting point for further development of similar applications in the realm of alternative energy devices. In particular, provided experimental validation of the electro-chemical properties of the proposed system, one might envision applications where the increase in the concentration or the flow rate of salt water allows better hydrogen production rates and larger power output.
5. Acknowledgements
The author would like to thank A. Fedullo for useful discussions
REFERENCES
- C. Kittel, “Introduction to Solid State Physics,” John Whiley, New York, 1959.
- J. J. Wright and S. Van Der Beken, “The Hall Effect in a Flowing Electrolyte,” American Journal of Physics, Vol. 40, No. 2, February 1972, pp. 245-247.
- H. S. T. Driver, “Comment on the Hall Effect in a Flowing Electrolyte,” American Journal of Physics, Vol. 46, No. 12, December 1978, pp. 1275-1276.
- D. B. Geselowitz, “Comment on the Hall Effect in a Flowing Electrolyte,” American Journal of Physics, Vol. 40, No. 8, August 1972, pp. 1183-1184. doi:10.1119/1.1986792
- R. De Luca, “Lorentz Force on Sodium and Chlorine Ions in a Salt Water Solution Flow under a Transverse Magnetic Field,” European Journal of Physics, Vol. 30, No. 3, May 2009, pp. 459-466. doi:10.1088/0143-0807/30/3/004
- H. Yamaguchi, X.-R. Zhang, S. Higashi and M. Li, “Study on Power Generation Using Electro-Conductive Polymer and Its Mixture with Magnetic Fluid,” Journal of Magnetism and Magnetic Materials, Vol. 320, No. 7, 2008, pp. 1406-1411. doi:10.1016/j.jmmm.2007.12.014
- P. Mazzoldi, M. Nigro and C. Voci, “Fisica,” EdiSES, 1998.
Appendix
We would like to illustrate a simple dynamical model for ions moving in an electrolyte solution in the presence of a transverse magnetic field  (see Figure 1) and a viscous force
(see Figure 1) and a viscous force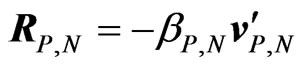 , where
, where 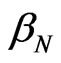 and
and 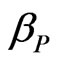 are the damping coefficient of anions and cations, respectively, and
are the damping coefficient of anions and cations, respectively, and ![]() is the velocity of the positive (P) and negative (N) ions measured with respect to a reference frame moving with the aqueous solution. By letting the solution move with velocity
is the velocity of the positive (P) and negative (N) ions measured with respect to a reference frame moving with the aqueous solution. By letting the solution move with velocity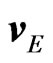 , which here we assume as constant for simplicity, the ions, due both to the Lorentz force, expressed as
, which here we assume as constant for simplicity, the ions, due both to the Lorentz force, expressed as
 (A1)
(A1)
and to the viscous force , move relatively to the solvent, considered to be an incompressible viscous fluid medium.
, move relatively to the solvent, considered to be an incompressible viscous fluid medium.
By Newton’s law of motion, neglecting gravitation and buoyancy effects, we can therefore write:
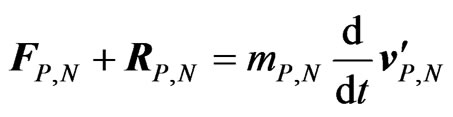 (A2)
(A2)
or
 (A3)
(A3)
where 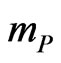 and
and 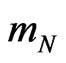 are the mass of the cations and of the ions in the solution, respectively. Notice that the only difference between the above equations of the motions for anions (N) and cations (P) is the sign in the Lorentz force. Therefore, we can first solve, for example, for
are the mass of the cations and of the ions in the solution, respectively. Notice that the only difference between the above equations of the motions for anions (N) and cations (P) is the sign in the Lorentz force. Therefore, we can first solve, for example, for 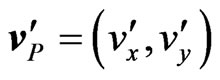 and then obtain the solution for
and then obtain the solution for  by letting
by letting 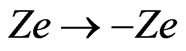 and by changing the index of the parameters from P to N. By now expressing all vectors in terms of their components and by carrying out the cross product in (A3), we may write, for cations:
and by changing the index of the parameters from P to N. By now expressing all vectors in terms of their components and by carrying out the cross product in (A3), we may write, for cations:
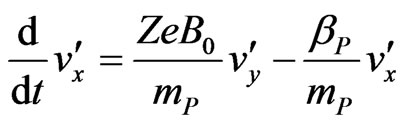 (A5)
(A5)
 (A6)
(A6)
By simple algebraic manipulations, we can decouple the above system of differential equations, writing
 (A7)
(A7)
 (A8)
(A8)
where ,
, ![]() , and
, and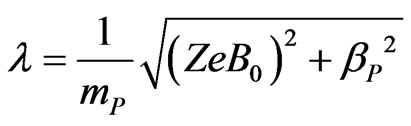 . The stationary solutions of Equations (A7) and (A8) are thus the following:
. The stationary solutions of Equations (A7) and (A8) are thus the following:
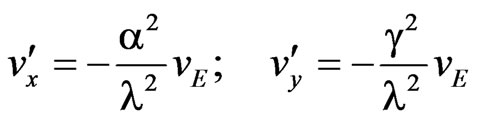 (A9)
(A9)
Therefore, the velocity ratios are:
 (A10)
(A10)
Notice that in the case of anions only the second ratio changes sign. It can be finally shown that the ratio 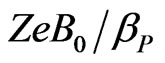 is of the order 10–7 for seawater, in such a way that
is of the order 10–7 for seawater, in such a way that , and
, and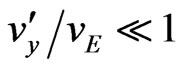 .
.

