ABSTRACT

A dominating set D in a graph G is called an injective equitable dominating set (Inj-equitable dominating set) if for every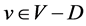, there exists 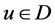such that u is adjacent to v and. The minimum cardinality of such a dominating set is denoted by 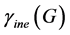and is called the Inj-equitable domination number of G. In this paper, we introduce the injective equitable domination of a graph and study its relation with other domination parameters. The minimal injective equitable dominating set, the injective equitable independence number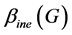, and the injective equitable domatic number 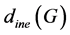are defined.

Keywords:

Domination, Injective Equitable Domination, Injective Equitable Domination Number

1. Introduction

By a graph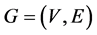, we mean a finite undirected graph with neither loops nor multiple edges. The order and the size of G are denoted by n and m respectively, the open neighborhood and the closed neighborhood 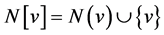. The degree of a vertex v in G is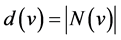. Let G and H be any two graphs with vertex sets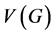, 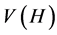and edge sets, , respectively. Then, the union 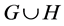is the graph whose vertex set is 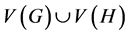and edge set is. For graph theoretic terminology, we refer to [1] and [2] .

A set D of vertices in a graph is a dominating set if every vertex in is adjacent to some vertex in D. The domination number is the mini- mum cardinality of a dominating set. An excellent treatment of the fundamentals of domination is given by Hayens et al. [3] . A survey of several advanced topics in domi- nation is given in the book edited by Haynes et al. [4] .

The injective domination of graphs has been introduced by A.Alwardi et al. [5] . For a graph G, a subset D of is called an injective dominating set (Inj-dominating set) if for every vertex there exists a vertex such that, where is the number of common neighborhood between the vertices u and v. The minimum cardinality of such dominating set is denoted by and is called the injective domination number(Inj-domination number) of G. The Inj-neighborhood of a vertex denoted by is defined as . The cardinality of is called the injective degree of the vertex u and is denoted by in G and.

A subset D of V is called equitable dominating set of G if every vertex adjacent to at least one vertex and. The minimum cardinality of such a dominating set is denoted by and is called equitable domination number of G [6] . Equitable domination has interesting applications in the context of social networks. In a network, nodes with nearly equal capacity may interact with each other in a better way.

The importance of injective and equitable domination of graphs motivated us to introduce the injective equitable domination of graphs which mixes the two concepts.

As there are a lot of applications of domination, in particular the injective and equitable domination, we are expecting that our new concept has some applications.

2. The Injective Equitable Dominating Set

Definition 1 A subset D of is called injective equitable dominating set (Inj- equitable dominating set) if for every vertex there exists a vertex such that u is adjacent to v and. The minimum cardinality of such a dominating set is denoted by and is called the Inj-equitable domination number of G. A -set of G is the minimum dominating set of G.

It is easy to see that any Inj-equitable dominating set in a graph G is also a domi- nating set, and then and if and only if.

In the following propostion the Inj-equitable domination number of some standard graphs are determined.

Proposition 1

1) For any complete graph,

2) For any path, with n vertices,

3) For any cycle on n vertices,.

4) For any complete bipartite graph, where,

5) For any wheel graph.

Definition 1 motivated us to define the inherent Inj-equitable graph of any graph G as follows:

Definition 2 Let be a graph. The inherent Inj-equitable graph of G, denoted by, is defined as the graph with vertex set and two vertices u and v are adjacent in the if and only if u and v are adjacent in G and .

Theorem 2: For any graph,

Proof. Since any Inj-equitable dominating set of is a dominating set of, then. Now, let be any -dominating set of. Then for any, there exists such that u and v are adjacent in. So,. Therefore, D is Inj-equitable dominating set of G. Then,. Hence,.

Definition 3 The Inj-equitable neighborhood of, , is defined as

The cardinality of is called the Inj-equitable degree of u and is denoted by. The maximum and minimum Inj-equitable degree of a vertex in G are denoted respectively by and. That is,

Definition 4 For any graph G, an edge is called Inj-equitable edge if and we say u is Inj-equitable adjacent to v or u is Inj-equitable dominate v.

Proposition 3 For any graph, , where is the number of Inj-equitable edges in G.

Proof. Let G be a graph and let H be the Inj-equitable graph of G. Then

, where q is the number of edges in H. Since the number of edges in

H is the number of Inj-equitable edges in G, then q equals. Also, in G

is equal to in H. Hence,.

Definition 5 Let be a graph. A vertex is called Inj-equitable isolated vertex if. The set of all Inj-equitable isolated vertices is denoted by. Hence for every Inj-equitable dominating set D, where I is the set of isolated vertices.

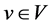
Definition 6 A graph G is called Inj-equitable totally disconnected graph if it has no Inj-equitable edge.

Theorem 4 For any graph G with n vertices,. Further, if and only if there exists at least one vertex v in G such that. if and only if G is Inj-equitable totally disconnected graph.

Proof. It is obviously that. Also, for any graph, is an injective equitable dominating set. Therefore,. Hence,.

Now, we want to prove that if and only if there exists at least one vertex v in G such that. Suppose that and is a - set. So, for all, and. Hence,.

conversely, suppose that there exists at least one vertex v in G such that . Then, is an Inj-equitable dominating set. Hence,.

To prove that if and only if G is Inj-equitable totally disconnected graph, suppose that G is Inj-equitable totally disconnected graph. So, all the vertices are Inj-equitable isolated. Hence,.

Conversely, suppose that G has at least one Inj-equitable edge, say. So,. Therefore, is an Inj-equitable dominating set, and so, contradicts that. Hence, G is Inj-equitable totally dis- connected graph.

Proposition 5 If a graph G has no Inj-equitable isolated vertices, then

In the following theorem, we present the graph for which and are equal.

Theorem 6 Let G be a graph such that any two adjacent vertices contained in a triangle or G is regular triangle-free graph. Then,.

Proof. Suppose that G is a regular triangle-free graph and D is a -set of G. Then. Let u and v be any two adjacent vertices in G. Then. Therefore,. Since G is regular,. So, . Therefore, D is an Inj-equitable domi- nating set. So that,. But. Hence, .

Let G be a graph such that any two adjacent vertices contains in a triangle. It is clear that for any,. So, . By the same way of the proof of regular triangle-free graph we can prove that.

Lemma 1 For any two graphs and,.

Proof. Let and let and be the minimum Inj-equitable domi- nating set of and, respectively, such that and. Now, it is obviously that is an Inj-equitable dominating set of. Therefore,

That is,

(1)

To prove by contradiction. Let be the minimum Inj-equitable dominating set of G such that. Let . Then there exist and, where is the mini- mum Inj-equitable dominating set of and is the minimum Inj-equitable dominating set of and either or which is a contradiction. Hence

(2)

From 1 and 2, we get

By mathematical induction, we can generalize Lemma 1 as follows:

Proposition 7 Let be a graph. Then

Theorem 8 Let G be a graph with vertices. Then if and only if, where H is Inj-equitable totally disconnected graph.

Proof. Let G be a graph with vertices and let. By Theorem 2, which implies that will be of the form. By the Definition 2, all the edges of G are not Inj-equitable edge except one edge. Therefore,.

Conversely, let where H is an Inj-equitable totally disconnected graph. By Lemma 1,.

Definition 7 An Inj-equitable dominating set D is said to be a minimal Inj-equitable dominating set if no proper subset of D is an Inj-equitable dominating set. A minimal Inj-equitable dominating set D of maximum cardinality is called -set and its cardinality, denoted by, is called upper Inj-equitable domination number.

The following theorem gives the characterization of the minimal Inj-equitable domi- nating set .

Theorem 9 An Inj-equitable dominating set D is minimal if and only if for every vertex one of the following holds:

1) u is not Inj-equitable adjacent to any vertex in D.

2) There exists a vertex such that.

Proof. Suppose that D is minimal Inj-equitable dominating set and suppose that. Then, is not Inj-equitable dominating set. Therefore, there exists a vertex which is not Inj-equitable adjacent to any vertex in. Then, either or. If, then u is not Inj-equitable adjacent to any vertex in D. If, then and not Inj-equitable adjacent to any vertex in. But V is Inj-equitable dominated by D. So, V is Inj-equitable adjacent only to vertex u in D. Hence,.

Conversely, suppose that D is an Inj-equitable dominating set and for every vertex one of the two conditions holds. We want to prove that D is minimal. Suppose D is not minimal. Then there exists a vertex such that is an Inj- equitable dominating set. Therefore, there exists such that v Inj-equitable adjacent to u. Therefore, u does not satisfy (i). Also, if is Inj-equitable domi- nating set, then every vertex is Inj-equitable adjacent to at least one vertex in. So, condition (ii) does not hold which is a contradiction. Hence, D is a minimal Inj-equitable dominating set.

Theorem 10 A graph G has a unique minimal Inj-equitable dominating set if and only if the set of all Inj-equitable isolated vertices forms an Inj-equitable dominating set.

Proof. Let G has a unique minimal Inj-equitable dominating set D and let. Since v is not an Inj-equitable isolated, is an Inj-equitable domi- nating set. Therefore, there exists a minimal Inj-equitable dominating set and, which contradicts that G has a unique minimal Inj-equitable dominating set. Hence,.

Conversely, let forms an Inj-equitable dominating set. Then it is clear that G has a unique minimal Inj-equitable dominating set.

Theorem 11 If G is a graph has no Inj-equitable isolated vertices, then the com- plement of any minimal Inj-equitable dominating set S is also an Inj-equitable dominating set.

Proof. Let S be any minimal Inj-equitable dominating set of G and is not Inj- equitable dominating set. So, there exist at least one vertex which is not Inj- equitable dominated by any vertex in. Since G has no Inj-equitable isolated vertices, the vertex u must be Inj-equitable dominated by at least one vertex in. Thus, is an Inj-equitable dominating set of G, which contradicts the mini- mality of S. Hence, is an Inj-equitable dominating set.

Theorem 12 For any graph with n vertices

Proof. Let S be a -set of G. Then for all,

Thus,

Now,

Therefore,

Hence,

Definition 8 Let. A subset S of is called an Inj-equitable in- dependent set if for any, for all. The maximum car- dinality of an Inj-equitable independent set is denoted by.

Definition 9 An Inj-equitable independent set S is called maximal if any vertex set properly containing S is not Inj-equitable independent set. The lower Inj-equitable independent number is the minimum cardinality of the maximal Inj-equitable independent set.

Theorem 13 Let S be a maximal Inj-equitable independent set. Then S is a minimal Inj-equitable dominating set.

Proof. Let S be a maximal Inj-equitable independent set. Let. If for every, then is an Inj-equitable independent set, a contradiction to the maximality of S. So, for some. Hence, S is ann Inj-equitable dominating set. Since for any, for every, either or for all. Therefore, S is minimal Inj-equitable dominating set.

Theorem 14 For any graph G,

3. Injective Equitable Domatic Number

The maximum order of a partition of a vertex set V of a graph G into dominating sets is called the domatic number of G and is denoted by [7] . In this section we pre- sent a few basic results on the Inj-equitable domatic number of a graph.

Definition 10 An Inj-equitable domatic partition of a graph G is a partition of in which each is Inj-equitable dominating set of G. The Inj-equitable domatic number is the maximum order of an Inj-equitable domatic parti- tion and is denoted by.

Example 1 For the graph G given in Figure 1, is an Inj-equitable domatic partition of maximum order. Therefore, the Inj-equitable domatic number of G is.

Proposition 15

1) For any path with,.

2) For any cycle with,

3) For any complete graph,.

4) For any complete bipartite graph, where,

Proposition 16 For any graph G, , where is the domatic number of G.

Proof. Since any partition of V into Inj-equitable dominating set is also partition of V into dominating set,.

4. Conclusions

In this paper, we introduced the Inj-equitable domination of graphs and some other related parameters like Inj-equitable independent number, uper Inj-equitable domi- nation number and domatic Inj-equitable domination number.

There are many other related parameters for future studies like connected Inj- equitable domination, total Inj-equitable domination, independent Inj-equitable domi- nation, split Inj-equitable domination and clique Inj-equitable domination.

Cite this paper

Alkenani, A.N., Alashwali, H. and Muthana, N. (2016) On the Injective Equitable Domination of Graphs. Applied Mathematics, 7, 2132-2139. http://dx.doi.org/10.4236/am.2016.717169

References