Received 12 April 2016; accepted 12 June 2016; published 15 June 2016

ABSTRACT

In this paper a new method for solving Goursat problem is introduced using Reduced Differential Transform Method (RDTM). The approximate analytical solution of the problem is calculated in the form of series with easily computable components. The comparison of the methodology presented in this paper with some other well known techniques demonstrates the effectiveness and power of the newly proposed methodology.

Keywords:

Reduced Differential Transform Method, Goursat Problem, Adomian Decomposition Method (ADM), Variational Iteration Method (VIM)

1. Introduction

In this paper, we consider the standard form of the Goursat problem [1] [2] as provided below

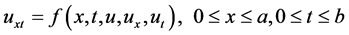(1)

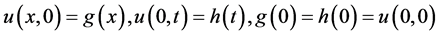(2)

This equation has been examined by several numerical methods such as Runge-Kutta method, finite difference method, finite elements method and Adomian Decomposition Method (ADM).

We will prove the applicability and effectiveness of RDTM on solving linear and non-linear Goursat problems. The main advantage of RDTM is that it can be applied directly to the problems without requiring linearization, discretization or perturbation.

2. One Dimensional Differential Transform Method

The differential transform of the function 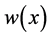is defined as follows

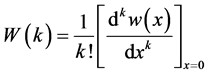(3)

where 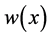is the original function and 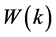is the transformed function. Here 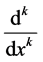means the k^th deriv-

ative with respect to x.

The differential inverse transform of 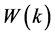is defined as

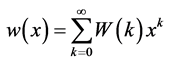(4)

Combining (3) and (4) yields

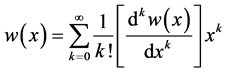(5)

From (3) and (4) it is easy to see that the concept of the differential transform is derived from Taylor series expansion [see Table 1].

3. Analysis of the Reduced Differential Transform Method

The basic definitions of reduced differential transform method are introduced below.

Definition

Assume that the function 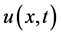is analytic and continuously differentiable with respect to time t and space x in the domain of interest, then let

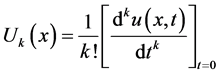(6)

Where the t-dimensional spectrum function 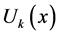is the transformed function. The differential inverse of 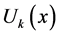is defined as follows

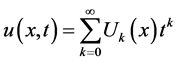(7)

Then combining Equation (6) and (7) we can write

(8)

Now, we express the Goursat problem in the standard operator form.

(9)

With the initial conditions

(10)

where

We applying RDTM of Equations (1) and (2) giving

(11)

(12)

(13)

(14)

where is transformed value of and is transformed value of.

By iterative calculations we obtain the following values of as:

(15)

From (7) we have.

(16)

One can get the exact solution of (1) by substituting (14) and (15) in (16).

With reference to the articles [4] [5] . We easy prove the transformation in the following Table 2.

4. Application and Results

In this section, we apply the method to some linear and non linear Goursat problem in order to demonstrate its efficiency.

A. The linear homogeneous Goursat problem

We first consider the linear homogeneous Goursat problem defined below

(17)

(18)

Where is a linear function of u.

Example 1: Consider the homogeneous Goursat problem

(19)

(20)

Taking RDTM of (19) and (20), we obtain

(21)

(22)

Substituting (22) into (21) and using the recurrence relation, we will reach to the results listed below.

And so on. In general, we have for substituting all into (7) yields the solution

. This result is in full agreement with the one obtained in [6] by VIM.

Example 2: Now consider the homogeneous Goursat problem

(23)

(24)

Applying RDT to (23) and (24) we obtain

(25)

(26)

Substituting (26) into (25) and using the recurrence relation we have

And so on. By substituting all into (7), the solution becomes. This results perfectly matches the results obtained in [6] by VIM.

B. The linear inhomogeneous Goursat problem:

We now consider inhomogeneous Goursat problem

where is linear function of u.

Example 3: We first consider the linear in homogeneous Goursat problem.

(27)

(28)

Taking RDM of (27) and (28) will lead to

(29)

(30)

Substituting (30) into (29) and using the recurrence relation we have

And so on. In general, we have for substituting all in (7) yields the solution

, this result is again identical to the one obtained in [6] by VIM .

Example 4: Consider the linear in homogeneous Goursat problem

(31)

(32)

Taking RDM of (31) and (32) gives rise to

(33)

(34)

Substituting (34) into (33) and using the recurrence relation we have

And so on. In general, we have except substituting all in (7) yields the solu-

tion, This result is again in full agreement with one obtained in [6] by VIM .

C. The non-linear Goursat problem:

(35)

(36)

where

is non-linear term.

Here, we apply RDTM to non-linear Goursat problem.

Example 5: We first consider the non-linear Goursat problem .

(37)

(38)

Taking RDM of (37), (38) yields

(39)

And

(40)

(41)

Substituting (41) into (40) and (39) and using the recurrence relation we have

yields the solution which is in full agreement with one obtained in [6] by VIM.

Example 6: We finally consider the non-linear Goursat problem

(42)

(43)

Taking RDM of (42) and (43) we obtain

(44)

where is the reduced transform of such that

And so on,

(45)

Substituting (45) into (44) and using the recurrence relation we have and so on.

Therefore, the solution is which is the exact solution.

5. Comparison

In this section, we use the Adomian decomposition method to obtain the solution of (1) and (2). and discuss the comparison between the reduced differential transform method and the Adomian decomposition method.

With reference to the article [7] - [9] , (1) can be rewritten In an operator form as:

(46)

where

(47)

The inverse operators and can defined as:

(48)

By applying and respectively to both sides of (46) and substituting gives

(49)

Adomian method admits the use of recursive relation

(50)

(51)

where

(52)

We applying adomian decomposition method to examples (3) and (6) to illustrate the comparison between the two method.

Following the pervious discussion and using (49) Equations (27) and (28) gives

(53)

This gives

(54)

This result is again identical to the one obtained by the RDTM example (3).

Again applying pervious discussion and using (49) Equations (42) and (43) gives

(55)

where are adomian polynomials for the nonlinear term giving by

Then the closed form solution is giving by

(56)

This result is again identical to the one obtained by RDTM in example (6).

We have carried out the comparative study between the reduced differential transform method and the Adomian decomposition method by handling the Goursat problem, Two numerical examples have shown that the reduced differential transform method is a very simple technique to handle linear and nonlinear Goursat problem than the Adomian decomposition method, and also, it is demonstrated that the reduced differential transform method solves linear and nonlinear Goursat problem without using any complicated polynomials like as the Adomian polynomials.

In addition, the obtained series solution by the reduced differential transform method converges faster than those obtained by the Adomian decomposition method. It is concluded that this simple reduced differential transform method is a powerful technique to handle linear and nonlinear initial value problems.

6. Conclusion

The Goursat problem has been analyzed using reduced differential transform method. All the illustrative examples have shown that the reduced differential transform method is powerful mathematical tool to solving Goursat problem. It is also a promising method to solve other nonlinear equations, the presented method reduces the computational difficulties existing in the other traditional methods and all the calculations can be done by simple manipulations.

Cite this paper

Sharaf Mohmoud,Mohamed Gubara, (2016) Reduced Differential Transform Method for Solving Linear and Nonlinear Goursat Problem. Applied Mathematics,07,1049-1056. doi: 10.4236/am.2016.710092

References