Received 15 March 2016; accepted 21 May 2016; published 24 May 2016

ABSTRACT

In the present paper, a three-component, stationary, multistate flow network system is studied. Detailed costs and incomes are specified. The aim is to minimize the expected total net loss with respect to the expected times the components spend in each state. This represents a novelty in that we connect the expected component times spent in each state to the minimal total net loss of the system, without first finding the component importance. This is of interest in the design phase where one may tune the components to minimize the expected total net loss. Due to the complex nature of the problem, we first study a simplified version. There the expected times spent in each state are assumed equal for each component. Then a modified version of the full model is presented. The optimization in this model is completed in two steps. First the optimization is carried out for a set of pre-chosen fixed expected life cycle lengths. Then the overall minimum is identified by varying these expectations. Both the simplified and the modified optimization problems are nonlinear. The setup used in this article is such that it can easily be modified to represent other flow network systems and cost functions. The challenge lies in the optimization of real life systems.

Keywords:

Reliability, Nonlinear Optimization, Multistate Flow Network

1. Introduction

A series of challenges concerning reliability engineering is presented in [1] . Some of these challenges are connected to the representation and modeling of complex systems, such as multistate systems, and their operational tasks, for instance maintenance optimization.

Over the past decades various measures of component importance have been studied. The use of such measures permits the reliability analyst to prioritize the system components in order to allocate resources efficiently. In [2] a new theory for measures of importance of system components is presented. Generalizations of the Birnbaum, Barlow-Proschan and Natvig measures (see [3] - [5] respectively) from the binary to the multistate case, both for unrepairable and repairable systems are covered. A numerical study of the above mentioned multistate measures of component importance is also covered in [2] . Loss of utility due to the system leaving the different sets of better states are introduced in that study. However, no detailed costs or incomes are specified. Recently, work has been done to also include costs in the determination of component importance for binary systems. In [6] and [7] the Birnbaum measure is extended to also include both failure induced and maintenance costs, while [8] and [9] introduce other cost-effective importance measures.

In maintenance optimization studies one is often interested in choosing a maintenance plan which minimizes life cycle costs, maximizes net present value or maximizes system reliability for a given system. See for instance [10] - [14] for some recent work on these subjects.

In this article we will look at one particular type of maintenance action, the complete repair. As the components reach the complete failure state, they are repaired to what we will denote the perfect functioning state. The aim is to include both costs and incomes in the study of a repairable multistate flow network system. To achieve this, we will define incomes and cost functions for the purpose of minimizing the expected total net loss over a time period with respect to the expected component times in the different states. This represents a novelty in that we connect the expected component times spent in each state to the minimal total net loss of the system, without first finding the component importances.

It would of course have been nice to optimize with respect to probability distributions instead of expectations, but this is not trivial even for a simple three-component system. However, the optimization problem considered in this article is particularly interesting in a design or re-design phase, where one may tune the components in such a way that the expected total net loss is minimized.

With the optimization problem considered in this article we are facing complex dependencies. We therefore study both a simplified version and a modified version of the optimization problem. In the simplified version we see that the optimal expected time spent in each state increases with increasing operational time for all three cost function types considered. However, the extent of the increase differs with the different basic cost function types. Due to basic investment costs this is not a trivial result. In the modified version of the optimization problem we only find approximate solutions. We observe that the different types of cost functions influence the end results significantly. For instance one of the functioning states is redundant for two of the three cost function types when the cost function parameter is increasing. For both problems we see that the minimum expected total net loss is increasing with increasing component cost per repair.

The rest of the article is organized as follows: Section 2 introduces the basic model, the three different types of cost functions and the three-component system of interest. The simplified version of the optimization problem with results is presented in Section 4. Section 5 presents the modified optimization problem with results, and concluding remarks are found in Section 6.

2. Basic Model

Let S be the set of possible system states, and, the set of possible component states. Throughout this article we will assume that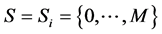. Since we are regarding the system as a flow network, the system state is the amount of flow that can be transported through the network. In the same way, the component state is the amount of flow that can be transported through each component. Let 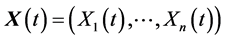be the vector of component states at time t. That is 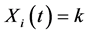if component 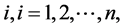is in state at time t.

A binary minimal cut set is a minimal set of components which upon failure will break the connection between the endpoints of the network. Let, , 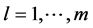be the binary minimal cut sets of the network. Then, by applying the max-flow-min-cut theorem (see [15] ), we get that the system state is given by

(1)

Thus, the system state equals the smallest total flow through the minimal cut sets of the system. Assume now that no components are in series with the rest of the system. Then there must be at least two components in every minimal cut set. If all components are in the perfect functioning state, M, the system state will be at least 2M, and therefore we must have that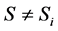. Thus, the assumption of equality between the set of system states and the set of component states, 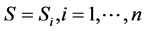, implies that at least one component is in series with the rest of the system. For this reason, we will in Sections 4 and 5 focus on the three component system given in Figure 1.

Assume that the components deteriorate by going through all states in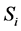, from the perfect functioning state M to the complete failure state 0, before being repaired back to M.

Let be the expected time component 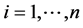spends in state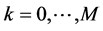, and let the vector of positive expected component times in each state be denoted.

Assume for that the basic investment costs of component i spending the expected amount of time in state are given by the cost functions for and for. These basic costs appear once in the time interval for each combination of and.

For any given functioning state, it seems natural that these basic expenses grow when the expected times become large. If however, no time is spent in a functioning state, there will not be any basic costs of keeping the component in this state. Similarly, the shorter the expected time spent in the complete failure state, the more expensive it should be. In other words, the faster a complete repair is executed, the more

expensive it should be. Therefore, we assume that the cost function is increasing and the cost function is assumed to be decreasing; moreover, both functions are assumed to be twice differentiable with. Throughout this article we assume the cost functions, and, to be of one of the following types:

Type 1: and

Type 2: and

Type 3: and,

where are constants. These cost functions are constructed by the authors according to the above mentioned criteria to represent a variation in the potential basic cost development.

In this article we only consider perfect repairs. Let denote the cost per repair from the complete failure state to the perfect functioning state of component. The total number of repairs of component in the interval is denoted for.

Let be the fixed income per unit of time when the system is in state, and assume that

This means that the income decreases, starting from the perfect functioning state, from one state to the next until the system reaches the complete failure state, where the income is non-positive. Thus, there is a loss per time unit that the system spends in the complete failure state. Such negative income might correspond to interest rate expenses connected to system building investments. The presence of such costs will increase the incentive for repairing the failed components.

The contribution from the i-th component to the total cost connected to the operation of the system in the time interval, is the total repair cost over the interval, , in addition to the basic investment costs related to component i spending the expected amount of time in state,. To get the total costs connected to the operation of the system we sum over all components.

Let denote the indicator function of the event A. Then the income at time t connected to the operation of the system is given by

To find the total income we integrate the income at time t over the time period. Hence, the total net loss connected to the operation of the system in the time interval is

Note that a negative net loss equals a positive net gain. By taking the expectation we find that the corresponding objective function is

(2)

In the remaining parts of this article, we will focus on stationary multistate systems. Component availabilities are now given by

(3)

for and. The stationary system availabilities are given by

(4)

Let denote the vector of component availabilities. When the components operate independently the stationary system availabilities, , equals for.

The expected number of repairs of component i is now given by, . The objective function, given in (2), therefore becomes

(5)

which is determined explicitly by, ,.

Thus, the optimization problem that we will consider is to minimize (5) with respect to and with different cost functions and.

3. The Three-Component System

For simplicity, the system we will focus on, is the multistate flow network system consisting of three com- ponents where component 1 is in series with the parallel structure of components 2 and 3 (see Figure 1). We will assume that all components and the system are in one of three states, that is we assume.

The structure function of the module consisting of components 2 and 3 in parallel is, whereas the structure function of the system is

(6)

since. For the system to be in the perfect functioning state, state 2, both modules, that is both component 1 and the parallel structure of components 2 and 3, must be in the perfect functioning state. For the system to be in state 1 both modules must be functioning, and at least one of the modules must be functioning at level. For the system to be in the complete failure state, at least one of the modules must be in the complete failure state. The system availabilities are hence given by

(7)

4. The Simplified Problem

Because of the complex nature of the problem presented in Section 2 we first study a simplified version of the problem. Assume the expected times spent in each state to be equal for each component. That is, we assume, for and. It is now natural to also assume for and. As a consequence, the component availabilities are equal to for all i and k. Thus, the system availabilities are equal to

As a consequence, the total income, given by the last term in the objective function (5), is constant. Let be the vector of expected component times. The simplified objective function is given by

(8)

and the corresponding optimization problem is

(9)

This is a box constrained nonlinear optimization problem. Note that the sum, in (8), is independent of and will therefore not affect the minimum.

4.1. Analysis of Convexity

Let denote the Hessian matrix related to the objective function (8). This is a matrix.

where

(10)

The objective function is convex if and only if the Hessian matrix is positive semidefinite (see for instance [16] ). In our case, the Hessian matrix is a diagonal matrix with on the diagonal. Hence, if all the diagonal elements are non-negative, i.e., then the objective function is convex and a local minimum will also be the global minimum.

4.2. The Objective Functions

4.2.1. Type 1 Cost Functions

Let the cost functions be given by and respectively. The objective function (8) is now given by

(11)

and the diagonal elements of the Hessian matrix are, for,

Thus, in this case, the objective function is convex.

Differentiating gives

For the optimal is given by

(12)

We see from (12) that the optimal is depending on and. T is the operational time period, is the cost per repair of component i and is a constant connected to the basic investment costs of component i spending the expected amount of time, , in state k. Furthermore, the optimal is independent of,. It is increasing in T, as seen by the solid line in Figure 2, increasing in, as seen in Table 1 for and as the basic investment cost parameter, , increases, the optimal decreases. This is also seen in Table 1 for. These latter results are reasonable.

4.2.2. Type 2 Cost Functions

Let for the cost functions be logarithmic and given by and. The objective function (8) becomes

(13)

The diagonal elements, (10), in the Hessian matrix are in this case given by

for. The numerator, A, is given by

This is a 5-th order polynomial in. As grows large A is dominated by the term which has negative sign. Hence, the numerator, and, are negative for large. On the other hand, when approaches 0, is positive. The objective function (13) is thus neither convex nor concave. We see that

approaches infinity when, approaches either 0 or. Therefore the objective function (13) has minimum values.

Differentiating (13) with respect to, gives the following:

The solutions to are the zeroes of the third degree polynomial in

(14)

which can be solved numerically. Every third degree polynomial has at least one real root, and since is the expected time component i spends in each state, we are only interested in positive solutions of.

4.2.3. Type 3 Cost Functions

The cost functions are in this section given by for the two functioning states, and for the complete failure state. The objective function (8) now becomes

(15)

The diagonal elements of the Hessian matrix are, for all, given by

Hence, (15) is convex and therefore it has a global minimum value.

4.3. Results

In this section the incomes per time unit are chosen to be, and. For the starting values for the numerical computations are chosen to be.

The assumption, , implies that the total income term in the objective function, (8), is constant, as has already been stated. Thus, the optimal 's only depend on the parameter values, and not on the structural placements of the components. Therefore, only results for component 1 are given in the following.

4.3.1. Effect of T

Figure 2 shows the development of the optimal expected times spent in each state (the optimal) as function of the operational time T. Note that in this case, because of the chosen parameter values, from (12) valid for cost functions of type 1, the optimal, and the optimal expected life cycle length is for all components.

In Figure 2 we see that, and hence the optimal life cycle length, increases when the operational time increases. Due to the basic investment costs this is not a trivial result. However, the extent of the increase differs with the different cost function types.

For cost functions of type 1 we see some increase in the optimal expected. This is in compliance with (12). We also see that is by far the largest for cost functions of type 2 for all T. For cost functions of type 3, on the other hand, we only observe a slight increase in the optimal as T increases.

From Figure 3 we see that the minimum expected net loss as function of the operational time T behaves differently with different types of cost functions. For cost functions of type 1 and 2, the minimum expected net loss is decreasing with increasing operational time T. For type 3 the minimum expected net loss is increasing at first before it starts to decrease. The minimum expected net loss is positive for when we use cost functions of type 3.

4.3.2. Effect of C₁

For cost functions of type 1, we see from Table 1 that the theoretical results given by (12) are equal to the computational results. For constant the theoretical and computational results are also constant, which is in accordance with (12). Even though is held constant (see Table 1 for), we see an increase

in the minimum expected net loss. The minimum expected net loss is dependent on the values of and respectively. We see that when these values increase, the net loss increases, as is obvious from (11).

For cost functions of type 2 we found in Section 2.2.2 that the optimal’s are the zeroes of the cubic

polynomial given in (14). For the parameter values in Table 2 this polynomial has one positive root, which equals the results obtained from the optimization routine. We see an increase in the optimal as increases.

Figure 4 shows the development of the minimum expected net loss as the repair costs, , of component 1 increases. We see that the minimum expected net loss is negative for cost functions of type 2. That is, we have a positive maximum expected net gain for this cost function. For the other two types of cost functions we have a positive minimum expected net loss. For all, the loss is greater for cost functions of type 3 than it is for cost functions of type 1. The corresponding optimal, and are shown in Figure 5.

From Figure 5 we see that for cost functions of type 2 it is optimal to spend longer time in each state than it is for the other two cost functions. The optimal expected time spent in each state for component 1 is increasing with increasing repair costs. This seems natural. The results for components 2 and 3 are equal because the parameter values concerning these two components are equal. From the right plot in Figure 5 we see that the increase in the repair costs of component 1 has no influence on the optimal expected time spent in each state for components 2 and 3, thus we see that the optimal are constant.

4.3.3. Effect of c₁

Figure 6 shows the minimum expected net loss as a function of the cost function parameter. The minimum expected net loss is increasing with an increasing. We see that an increase in has much larger effect on the minimum expected net loss when we use cost functions of type 3 than when we use the other two types of cost functions. This is natural since the type 3 cost functions are exponential.

The corresponding optimal are shown in Figure 7. We see that is constant., on the other hand, seems to be decreasing with increasing when we have cost functions of type 1 and 3. This behavior seems reasonable. For cost functions of type 2 we see that eventually starts to increase when increases, which seems unnatural.

5. Modifications of the Full Model Optimization Problem

The original problem, represented by the objective function (5), turned out to be quite complex even though we only considered a simple three-component system with three possible system and component states. Thus, the optimization of this problem was not straightforward. In order to overcome difficulties with starting value sensitive optimization results, we reformulated the original optimization problem in order to find an approximate solution.

Let, , be the fixed expected length of the life cycle of component i. Then, the objective function is given by

(16)

where is a vector of the expected times spent in each state for each component. We are interested in minimizing the expected total net loss (16) subject to the fixed expected length of the life cycles,. The optimization of the modified problem goes as follows:

Step 1: Choose values for. For every combination of these, the nonlinear optimization problem with both equality and inequality constraints, (17), is solved.

(17)

Step 2: Identify the overall minimum from the optimization results from step 1. The corresponding will approximately minimize the expected total net loss over the time period.

Optimization problems as the ones in step 1 may be solved using the augmented Lagrange multiplier method, for instance using the SOLNP algorithm as described in [17] . This algorithm is implemented in the Rsolnp package, see [18] , in R.

Note that minimizing the expected total net loss is equivalent to maximizing the expected total net gain, and that a negative expected total net loss is a positive expected net gain. Since we are using minimization algorithms instead of maximization algorithms, the focus has been on minimizing the total net loss rather than maximizing the total net gain.

5.1. Results

In this section lower bounds on, and are chosen to be 10^-15 for cost functions of type 1 and 2, and 0.01 for cost functions of type 3. The upper bound is chosen to be equal to the operational time T.

As in the previous section, the incomes per time unit when the system is in state, are, and respectively. The possible life cycle lengths are chosen to be , and the starting values are for and.

Component 2 and component 3 are in parallel. Their roles in the system are therefore interchangeable. Since we assume that the components’ cost functions are of the same type and that we are varying one parameter at a time, we are in the following only varying the parameters connected to component 1 and component 2. When the parameters of component 1 are varied the results for components 2 and 3 are identical. Hence, results for component 3 are then omitted.

5.1.1. Effect of T

Figure 8 shows the minimum expected net loss as a function of T. We see that with cost functions of type 1 and 2, the minimum expected net loss is negative and decreasing for the chosen values of T. This means that for these cost functions we have an increasing maximum expected net gain. The loss is smaller for cost functions of type 2 than it is for the other two types of cost functions. For cost functions of type 3 the minimum expected net loss is positive for small T.

The corresponding optimal’s, and, are given in Figure 9. It seems like the optimal’s stabilizes as T becomes large.

5.1.2. Effect of an Increasing Cost Per Repair C_i, i = 1, 2

For this, and the following sections, the operational time is set to. Figure 10 and Figure 11 shows the minimum expected net loss as a function of the repair cost of component 1 and 2 respectively. We see that the minimum expected net loss is increasing with increasing repair costs, for all three cost functions. This seems natural.

The corresponding optimal as functions of are shown in Figure 12 and for in Figure 13 for. As the repair costs of component 1, , increases, the optimal expected life cycle length for component 1 increases for cost function types 1 and 3. For cost functions of type 2 the optimal are constant. For cost functions of type 1 and type 2, it is optimal to keep

component 1 in the perfect functioning state for as long as possible. Hence, we see a large for these two cost function types. For cost functions of type 3, on the other hand, the increase in expected life cycle length is placed in state, and we see an increase in for this cost function. The extra costs connected to an increase in the expected times spent in either of the two functioning states are much larger for cost functions of type 3 than for the other two types of cost functions.

As the repair costs of component 2, , increases, we see from Figure 13 that the results for component 1 are constant. Hence, for component 1 the optimal expected time spent in each state is independent of the repair cost of component 2. We also see that an increasing repair cost results in an increasing optimal expected life cycle length for component 2 for all cost functions. For cost functions of type 1 and 2 the increase is on the expected time spent in state 2, , while the increase is on the expected repair time, , for cost functions of type 3.

Since component 1 is critical to the functioning of the system we see from Figure 12 an increase in for cost functions of type 3 as increases. Component 2 is in parallel with component 3. It is therefore possible to extend the expected repair time of this component when increases, while at the same time the expected repair times of component 3, , are kept low. This is seen in Figure 13 for cost functions of type 3.

5.1.3. Effect of an Increasing

As the cost function parameter for component 1 increases, the minimum expected net loss also increases for cost functions of type 1 and 3. The minimum expected net loss remains unchanged when cost functions of type 2 are used. See Figure 14 and Figure 15. An increase in has largest impact on the minimum expected net loss when the cost functions are of type 3, that is when we have exponential cost

functions. In state there was no increase in the minimum expected net loss with increasing, as seen in Figure 16. Figures 17-19 show the development in the optimal, as increases.

The effect of an increasing is evident in the increasing optimal for cost functions of type 3. This is seen in Figure 17, where there is also a slight increase in for cost functions of type 1. The behaviour of and differs for the three cost function types as the cost function parameter increases. In state, is close to 0 for both cost functions of type 1 and 2, while positive for for cost functions of type 3. For the optimal is high and (close to) constant for cost functions of type (1) 2. For cost functions of type 3 the optimal is lower.

An increasing has no effect on the optimal. This is seen in Figure 18.

As increases, we see from Figure 19 that the optimal expected time spent in state 2 for component 1, , is decreasing for both cost functions of type 1 and 3. As the costs of keeping at a fixed level is

increasing, it becomes less desiring to maintain this level, and we see a decrease. The decrease is faster in for cost functions of type 3. For this cost function we see an increase in with increasing that is in contrast to the results for cost functions of type 1 and 2 which are independent of the increase in and equal to 0.

5.1.4. Effect of an Increasing

An increasing has little effect on the minimal expected net loss. This is seen in Figures 20-22 where the minimal expected net loss with cost functions of type 2 seems to be constant and the result for cost functions of type 1 and 3 is increasing slightly for small before it seems to be constant.

Figures 23-25 show the optimal expected times spent in each state for each component as the cost function parameter, , increases. The optimal expected times spent in each state for component 1, remain unchanged for all types of cost functions.

For every cost function type we see from Figure 23, for component 2, an increase in and a decrease in as increases. For component 3 we have the opposite behaviour. As the costs of keeping the expected

repair times of component 2 low increases, it is optimal to spend more expected time repairing this component. At the same time, it will be more important to keep the expected repair times of component 3 low.

We see from Figure 24 that the optimal is slightly decreasing with increasing for both cost functions of type 1 and 3. is also slightly decreasing for these two cost functions, but the optimal is increasing for these cost functions. For cost functions of type 1 we see from Figure 24 that the optimal is

high (approximately 15) for, while is below 5 for all values of for cost functions of type 3. For component 3 we see that the results for cost functions of type 1 and 2 are lower than the corresponding results for cost functions of type 3 in state and above in state.

The optimal, and for increasing are shown in Figure 25. We see that the results for cost functions of type 2 are constant. Furthermore, for cost functions of type 1 and 3, component 2

has increasing and decreasing with increasing, whereas, component 3 has decreasing and increasing. This is the same behaviour as observed for increasing for these cost functions.

6. Concluding Remarks

In the present paper we have been minimizing the expected total net loss over a time period as a function of the expected component times in each state for a three-component flow network system. First the basic model was presented. The assumption of equality between the set of system states and the set of component states implied that an appropriate flow network system would have at least one component in series with the rest of the system. Hence, the three-component system given in Figure 1 was chosen as a case. With three possible system and component states and three components, the original box-constrained optimization problem had 9 variables. Due to the complexity of this problem, we first studied the simplified problem, where

and for and, and then a modification of the original problem where the

optimization was done in two steps (see Section 5). This method found an approximate solution. The indication of lack of constructive conclusions is mainly due to that we are facing complex dependencies.

The variables and for in the simplified problem, and the variables and for and in the modified full problem, were varied one at a time with three different types of cost functions.

For the simplified problem we were able to find expressions for the optimal for cost functions of type 1. For cost functions of type 1 and 3, the objective function, (8), turned out to be a convex function. With cost functions of type 2 the objective function is neither convex nor concave. The type 2 cost functions are logarithmic, and hence concave while the other two types are convex. For this cost function, we saw in Figure 7 that the optimal has a minimum as increased, which seems unnatural.

In both the simplified problem and the modified full model, the minimum expected net loss was increasing with increasing for every cost function type (as seen in Figure 4, Figure 10 and Figure 11 respectively).

As the operational time T increased we saw a decrease in the minimum expected net loss in the modified full model for all three cost functions (as seen in Figure 8). This is in contrast to the results with the simplified model when the exponential cost functions were used. Then, the minimum expected net loss increased at first, before it started to decrease (as seen in Figure 3).

For every cost function parameter, , we varied, we saw in Figures 17-19 that the optimal was constant for cost functions of type 2. The same observation of constant for cost functions of type 2 was done in Figures 23-25 where were varied. The values were also close to

zero. Hence, it was, for cost functions of type 2, optimal to spend as little time as possible in state 1 independent

of the values of the parameters. With cost functions of type 1 we observed the same, except from when was increasing where decreased from around 15 to close to 0 as increased from 0 to 2. For

stayed constant and close to 0. Thus, it seems like the functioning component state 1 is in a way redundant for cost functions of type 1 and 2. This was not the case with cost functions of type 3.

The general objective function (5) can quite easily be modified to represent the expected net loss of other network flow systems, and to include other types of cost functions. However, with larger systems, with more components and possibly more component states, the optimization problem quickly becomes large. Hence, the real challenge lies in the optimization of real life systems.

Acknowledgements

The authors thank Professor Geir Dahl for the idea on how to modify the full optimization problem and Ph.D Olav Skutlaberg for valuable feedback throughout the process.

Cite this paper

Kristina Skutlaberg,Bent Natvig, (2016) Minimization of the Expected Total Net Loss in a Stationary Multistate Flow Network System. Applied Mathematics,07,793-817. doi: 10.4236/am.2016.78071

References