Applied Mathematics
Vol.07 No.12(2016), Article ID:68984,14 pages
10.4236/am.2016.712115
A Mathematical Model of Tuberculosis with Drug Resistance Effects
Marilyn Ronoh1, Rym Jaroudi2, Patrick Fotso3, Victor Kamdoum3, Nancy Matendechere4, Josephine Wairimu1, Rose Auma1, Jonnes Lugoye5
1University of Nairobi, Nairobi, Kenya
2University of Tunis El Manar, Tunis, Tunisia
3University of Dschang, Yaounde, Cameroon
4Kenyatta University, Nairobi, Kenya
5University of Dar es Salaam, Dar es Salaam, Tanzania

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 February 2016; accepted 22 July 2016; published 25 July 2016
ABSTRACT
Despite the enormous progress in prevention and treatment, tuberculosis disease remains a leading cause of death worldwide and one of the major sources of concern is the drug resistant strain, MDR-TB (multidrug resistant tuberculosis) and XDR-TB (extensively drug resistant tuberculosis). In this work, we extend the standard SEIRS epidemiology model of tuberculosis to include MDR-TB. For that, we considered compartments of susceptible, exposed, infected, resistant to a first line of treatment and recovered humans and we modeled the natural growth, the interactions between these populations and the effects of treatments. We calculate the basic reproduction number, 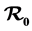 , using the next generation method. The DFE and the EE are established and their stability analysis done to show that they are locally and globally asymptotically stable. Numerical analysis for the model with and without delay is done and demonstrated that in the case of patients with both active tuberculosis and MDR tuberculosis, both strains will still persist due to lack of permanent immunity to tuberculosis while the recovered can still lose their immunity to become susceptible again.
, using the next generation method. The DFE and the EE are established and their stability analysis done to show that they are locally and globally asymptotically stable. Numerical analysis for the model with and without delay is done and demonstrated that in the case of patients with both active tuberculosis and MDR tuberculosis, both strains will still persist due to lack of permanent immunity to tuberculosis while the recovered can still lose their immunity to become susceptible again.
Keywords:
Tuberculosis, Mtb, MDR, Reproduction Number, DFE, EE, Stability

1. Introduction
Tuberculosis is an airborne disease caused by Mycobacterium tuberculosis (Mtb) bacteria [1] . It is an ancient disease with evidence of its existence being found in relics from ancient Egypt, India and China [1] . In the eighteenth century, Western Europe suffered terribly from this disease with a prevalence as high as 900 deaths per 100,000. This was largely due to poor ventilation, overcrowded housing, primitive sanitation, malnutrition among other risk factors that led to the epidemic [1] . Today, this disease ranks as the second leading cause of morbidity and mortality in the world from a single infectious agent, after the human immunodeficiency virus (HIV) [2] . Interestingly, about one-third of the world’s population is infected with Mtb with approximately nine million people developing active tuberculosis and up to nearly two million people worldwide die from the disease every year. In 2013, approximately nine million people contracted active tuberculosis and this included 1.1 million cases among people living with HIV and 550,000 children. Out of these nine million cases 1.5 million people succumbed to the disease and this included 360,000 among people who were HIV-positive, 510,000 were women out of which 180,000 were HIV-positive. Africa recorded the highest tuberculosis/HIV burden with three out of four Tuberculosis patients knowing their HIV status. Approximately 480,000 people developed multidrug-resistant (MDR) tuberculosis globally with 210,000 of those who developed MDR tuberculosis succumbing to it [2] . Figure 1 showed the global incidence of tuberculosis in 2008 [3] .
Figure 1. Global distribution of tuberculosis [3] .
In addition to posing a major health concern to low and middle income countries, tuberculosis affects economic growth negatively [4] . Psycho-social distress that communities go through is enormous. This involves thinking about the loss of their loved ones and the economic impact of taking care of the sick ones especially among the low income individuals. This impacts not only the individuals, but also the economic progress of the country. Over the last twenty five years, the mortality rate of tuberculosis has greatly decreased by forty five percent since and this is largely due to effective diagnosis and treatment [5] . However, the world is still far from defeating the disease. About 8 billion US dollars per year is needed for a full response to the global tuberculosis epidemic in low and middle income countries by the year 2015 with a funding gap of 2 billion US dollars per year. This amount excluded resources required for research and development, which was estimated to be about 2 billion US dollars yearly [2] . Clearly, this reveals that the current investment in tuberculosis falls below the low and middle income country’s needs.
(Mtb) bacteria spreads through inhaling droplets from the cough or sneeze of a person suffering from active tuberculosis. The bacteria enters the body causing an Mtb infection affecting majorly the lungs but it can also affect any other part of the body including the urinary tract, brain, lymph nodes, bones, joints and the ear. Person(s) with lowered immunity such as those with HIV, diabetes, immune disorders, end-stage renal disease, those on drugs that suppress immunity, young children, pregnant women among others are at a higher risk of contracting the disease [6] . Also people suffering from malnutrition due to lifestyle, drug abuse or poverty equally are at risk of contracting tuberculosis. Another category of people largely at risk of contracting tubercu- losis are those who work closely or live close to a person with active tuberculosis and they could include health- care workers, people living in crowded living spaces or confined places such as schools or prisons [7] .
The intensity of transmission depends on factors related to the bacteria, the human host, the environment and migration. Non-climatic factors such as environmental development and urbanization, population movement and migration affect the severity and incidence of tuberculosis. When it comes to environment and urbanization, the incidence of tuberculosis is generally lower in prime urban areas than in rural areas as there is difficulty in accessing proper medical care in rural villages compared to urban areas. However, rapid urbanization of areas within or on the outskirts of urban centers is commonly done in an uncontrolled fashion without thought or planning. The settlers are mainly migrant workers from rural villages and they tend to settle mostly in poor, overcrowded houses commonly known as slums with hardly any proper sanitation and this in turn leads to increased exposure of the population to Mtb hence a possibility of amplification of the disease to epidemic proportions through lack of effective treatment [6] . Population movements have significant implications for tuberculosis transmission as migration introduces tuberculosis problem to the areas to which the migrants migrate to. Temporary migrant workers often bring the bacteria to lower prevalence areas and local transmission can be readily established [5] .
Tuberculosis is curable provided an early diagnosis is made and one follows the proper treatment regimen which could take six months upto two years for the active tuberculosis to clear [8] . There is an emerging form of tuberculosis commonly known as multi-drug resistant (MDR) tuberculosis which is defined as tuberculosis resistant to both of the two most effective first line of antibiotic treatment of active tuberculosis i.e., isoniazid (INH) and rifampin (RIF), and it is harder and more expensive to treat [6] . It is currently a major health concern to medical workers and researchers and one can get MDR tuberculosis by either spending time with an MDR patient and breathing in the MDR tuberculosis bacteria or those with active tuberculosis not following their prescribed treatment regimen or TB medicine not being readily available to them. MDR tuberculosis is much more difficult to treat and the mortality of persons with this form of tuberculosis is far much higher if the second line of antibiotic treatment is not effected promptly [6] .
The first tuberculosis model for the transmission dynamics of tuberculosis was developed by Waaler and Anderson (1962) [9] who used a mathematical model to study the epidemiology of tuberculosis. With time other models have been developed to help prevent the risk of transmission of tuberculosis [10] . Recent global reports of multidrug resistant and extensively drug-resistant tuberculosis have renewed concerns that antibiotic resistance may undermine progress in tuberculosis control [11] . Including MDR tuberculosis in mathematical models is relatively new and there are very few models with this aspect. Agusto et al. [12] used a deterministic model with isolation where they studied the transmission dynamics of three strains of mycobacterium tuberculosis (TB), namely, the drug sensitive, multi-drug-resistance (MDR) and extensively-drug-resistance (XDR) tuberculosis strains. Their result of the global sensitivity analysis indicated that the dominant parameters are the disease progression rate, the recovery rate, the infectivity parameter, the isolation rate, the rate of cost to follow up and fraction of fast progression rates. They also found that an increase in isolation rate leads to a decrease in the total number of individuals who are cost to follow up. Trauer, Denholm and McBryde (2014) [8] used a mathematical model to simulate tuberculosis transmission in the highly endemic regions of the Asia-pacific. They found out that their model could not be calibrated to the estimated incidence rate without allowing for re-infection during latency and that even in the presence of a moderate fitness cost and a lower value of , MDR tuberculosis becomes the dominant strain at equilibrium. Improved treatment of drug susceptible tuberculosis did not result in decreased rates of MDR tuberculosis through prevention of the new resistance but rather resulted in a modest increase in a modest increase in MDR tuberculosis. Cohen and Murray (2004) [13] modelled epidemics of multi-drug resistant tuberculosis of heterogeneous fitness. Their model suggested that the threat of multidrug resistance to tuberculosis control depends on relative fitness of MDR strains and this implied that the strains is considerably less than that of drug-sensitive strains and that the emergence of resistance would not jeopardize the success of tuberculosis control efforts. Their results implied that current epidemiological measures and short- term trends in the burden of MDR tuberculosis do not provide evidence that MDR tuberculosis strains can be contained in the absence of specific efforts to limit transmission from those with MDR disease.
, MDR tuberculosis becomes the dominant strain at equilibrium. Improved treatment of drug susceptible tuberculosis did not result in decreased rates of MDR tuberculosis through prevention of the new resistance but rather resulted in a modest increase in a modest increase in MDR tuberculosis. Cohen and Murray (2004) [13] modelled epidemics of multi-drug resistant tuberculosis of heterogeneous fitness. Their model suggested that the threat of multidrug resistance to tuberculosis control depends on relative fitness of MDR strains and this implied that the strains is considerably less than that of drug-sensitive strains and that the emergence of resistance would not jeopardize the success of tuberculosis control efforts. Their results implied that current epidemiological measures and short- term trends in the burden of MDR tuberculosis do not provide evidence that MDR tuberculosis strains can be contained in the absence of specific efforts to limit transmission from those with MDR disease.
2. Model Analysis
2.1. The Model Equations
We will first extend the standard SEIRS mathematical model for the transmission of tuberculosis which will demonstrate the transmission of the Mycobacterium tuberculosis in human hosts taking into account the multi- drug resistant (MDR) tuberculosis. Most classical models developed for studying tuberculosis dynamics often ignore the resistant class and if they include them, they end up with very complicated models. We seek to pre- sent a simple model that can easily be analysed so as to properly understand the dynamics of this disease.
Humans can contract Mtb tuberculosis through contact with individuals who are infected with the disease. After which they enter the exposed (latent) phase where a proportion of this class develop active tuberculosis thus moving into the infectious class. If treatment is administered promptly, those who recover from the disease will move to the recovered class and those who delay treatment and develop MDR tuberculosis will move to the resistant class. Those who recover from MDR tuberculosis will move to the recovered class. Given that there is no permanent immunity to tuberculosis, the recovered can lose their immunity and become susceptible again. Figure 2 represents the flow of individuals into the different compartments and it has been constructed with these assumptions: recruitment is by births only, a variable population, a constant mortality rate, no permanent immunity to tuberculosis, no immediate infectivity.
Figure 2. Schematics of the compartmental model. State variables: S, susceptible human, E, exposed human with Mtb, I, Infected human with active tuberculosis, 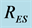 , resistant humans to first line of treatment, R, recovered humans from both active tuberculosis and MDR tuberculosis. Parameters:
, resistant humans to first line of treatment, R, recovered humans from both active tuberculosis and MDR tuberculosis. Parameters: , recruitment by births,
, recruitment by births, 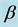 , force of infection,
, force of infection, 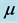 , death rate of humans,
, death rate of humans,  , disease induced deaths in humans due to active tuberculosis,
, disease induced deaths in humans due to active tuberculosis,  , disease induced deaths in humans due to MDR tuberculosis,
, disease induced deaths in humans due to MDR tuberculosis, 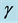 , recovery rate of infected humans from active tuberculosis,
, recovery rate of infected humans from active tuberculosis,  , recovery rate of infected humans from MDR tuberculosis,
, recovery rate of infected humans from MDR tuberculosis, 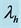 ,
, 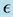 , rate at which the exposed become infectious,
, rate at which the exposed become infectious,  , rate at which the infected with active tuberculosis become resistant
, rate at which the infected with active tuberculosis become resistant
The human population is categorized into five classes such that at time 



















Table 1. Description of state variables.
Table 2. Description of parameters.
2.2. Differential Equations

2.3. Equilibrium Points
We obtain the equilibrium points for the system of differential Equation (1) above by equating each of the equations to 0 as shown below

Calculation results in two equilibrium points, one being the disease free equilibrium while the other being the endemic equilibrium.
Disease Free Equilibrium Point 
Endemic Equilibrium Point 

With:
2.4. Condition of Existence/Positivity
The system will remain positive provided this condition holds:
Substituting for x yields:
The expression obtained above then is the condition of existence.
Lemma
Let the initial data be


2.5. Calculation of the Reproduction Number
The reproduction number 

ber, 



and 








The above system can be represented in matrix form as shown below where 
of infection rates and 

Next we used a Maple Software to obtain 
We then obtain the spectral radius of




2.6. Stability Analysis
Local Stability of the DFE
In this section we will determine the stability of the disease free equilibrium points. We will establish this by linearizing the system of differential Equations (1) by obtaining its Jacobian at the disease free equilibrium

Next, we will establish the eigenvalues for the linearized system as follows:
Evaluating the determinant above yields these eigenvalues:




Thus, the disease free equilibrium is locally asymptotically stable given that all the eigenvalues
Global Stability of the Disease Free Equilibrium
The local dynamics of a general SEIRS model is determined by the reproduction number






Theorem 2.1
If


Proof
We construct the following Lasalle-Lyapunov function 




The system of ordinary differential equations given by Equation (4) can be written as
This can be written as 


If we define 

which is strictly decreasing when 

We define the set
for which 








Global Stability of the Endemic Equilibrium
Theorem 2.2
The endemic equilibrium 

Proof
To establish the global stability of the endemic equilibrium, 




where 
Taking the derivative of the lyapunov function 


where 

Choosing

Thus from Equation (9), 



only if






the endemic equilibrium. By Lasalle Invariance principle 

3. Numerical Simulation
In this section we shall explore the behavior of tuberculosis disease when introduced into a naive environment and conduct numerical simulations of an isolated system (that is, no immigration or emigration). We will pay particular attention to the infected class and the resistance class and the effect of delay in intervention. We used two types of delays: a time dependent and a constant. The model uses a yearly time step and is solved by a fourth order Runge-Kutta scheme. For each simulation, we start with 




Table 3. Parameters values.
Without delay:
Here, we assume that the treatment has the same effect for both the infected I and the resistant
To test the sensitivity of our system to the disease induced death rate 




Figure 4 shows that when 




With delay:
Now, we suppose that the treatment affects each of the individuals I and 
Figure 3. Evolution of each population without delay.
Figure 4. Evolution of



add a delay function to the last equations of system (1) as shown below

To better investigate on the drug efficiency we used a function 
Figure 5 illustrates the dynamics of the populations under the effect of constant 5 years treatment delay.
Comparing to Figure 3, the I and 
After that, we used a low delay with a short period 

Figure 5. Evolution of each population with constant delay.
Figure 6. Evolution of each population with the low time dependent delay.
Figure 7. Evolution of each population with the fast time dependent delay.
What we see in Figure 6 is the positive effect of the drugs on the resistant class as there is reduction in the resistant class and an increase in the recovered class at exactly the same time whereas Figure 7 shows that a fast time dependent gives similar results as Figure 3. This implies that the drugs have a similar effect on both I and
4. Conclusion
This study presents a simple yet more realistic deterministic model for the transmission dynamics of tuberculosis. In contrast to many tuberculosis models in literature, we include the class resistant to the first line of treatment for tuberculosis. The resistant category is of particular importance in modeling tuberculosis in low and middle income countries mostly found in Africa where public health is under developed. In particular, the number of individuals who seek medical intervention and those who actually recover from both active tuberculosis and MDR tuberculosis is worth noting. MDR parameter is used to measure the success of treatment administered to MDR patients. The recovery parameters are also used to measure the implications of failure in treating both active tuberculosis and MDR tuberculosis. Our results and simulations demonstrate that when MDR tuberculosis patients delay treatment or fail to go for treatment altogether this strain will still persist over time. Also in the case of patients with both active tuberculosis and MDR tuberculosis, we establish that both strains will still persist at some equilibrium since there is no permanent immunity to tuberculosis and the recovered can still lose their immunity and become susceptible again. Of particular concern is the relation of tuberculosis and HIV as most tuberculosis patients are aware of their HIV status. We hope a lot of efforts, resources and research will be placed for a rigorous analysis of this co-infection model so as to fully understand this problem and the inter-
ventions for possible prevention of this predicament.
Acknowledgements
We would like to start by thanking all the organizers and sponsors of the CIMPA Kenya School 2015 making special mention of Prof. Sylvain Sylva in 2011, CIMPA coordinator for Sub Saharan Africa, for granting us an opportunity to participate in this school and for financially supporting our participation which gave us the opportunity to meet great mathematicians from all parts of the world. Our special thanks go to Prof. Dorothy Musekwa, Dr. Josephine Kagunda and Dr. Nelson Owuor who inspired us through an exercise that resulted in this work. We would wish to thank Prof. Wilson Lamb, Prof. Jacek Banasiak, Prof. Luboobi, Prof. Wandera Ogana, Dr. Winnie Mutuku, Dr. Irene Wattanga, Dr. Samuel Mwalili and Prof. David Malonza who offered us great insights as we formulated this problem. Lastly, we would like to thank our fellow participants from all over the world who offered us encouragement and sincere advice to better this work. May God bless each one of you richly.
Cite this paper
Marilyn Ronoh,Rym Jaroudi,Patrick Fotso,Victor Kamdoum,Nancy Matendechere,Josephine Wairimu,Rose Auma,Jonnes Lugoye, (2016) A Mathematical Model of Tuberculosis with Drug Resistance Effects. Applied Mathematics,07,1303-1316. doi: 10.4236/am.2016.712115
References
- 1. Daniel, T.M. (2006) History of Tuberculosis. Respiratory Medicine, 100, 1862-1870.
http://dx.doi.org/10.1016/j.rmed.2006.08.006 - 2. WHO (2014) Global Tuberculosis Report. WHO Report.
- 3. CDC. National Tuberculosis Surveillance System Highlights.
http://www.cdc.gov/tb/?404;
http://www.cdc.gov:80/tb/statistics/surv/surv2008/default.htm 2008 - 4. Klein, E., Laxminarayan, R., Smith, D. and Gilligan, C. (2007) Economic Incentives and Mathematical Models of Di- sease. Environment and Development Economics, 12, 707-732.
http://dx.doi.org/10.1017/S1355770X0700383X - 5. Semenza, J., Suk, J. and Tsolova, S. (2010) Social Determinants of Infectious Diseases: A Public Health Priority. Euro Surveill, 15.
- 6. Mandal, A. (2013) Tuberculosis causes.
http://www.news-medical.net/health/Tuberculosis-Causes.aspx - 7. Zaman, K. (2010) Tuberculosis: A Global Health Problem. Journal of Health, Population and Nutrition, 28, 111-113.
http://dx.doi.org/10.3329/jhpn.v28i2.4879 - 8. Trauer, J., Denholm, J. and McBryde, E. (2014) Construction of a Mathematical Model for Tuberculosis Transmission in Highly Endemic Regions of the Asia-Pacific. Journal of Theoretical Biology, 358, 74-84.
http://dx.doi.org/10.1016/j.jtbi.2014.05.023 - 9. Waaler, H. and Anderson, S. (1962) The Use of Mathematical Models in the Study of the Epidemiology of Tuberculosis. American Journal of Public Health, 52, 1002-1013.
http://dx.doi.org/10.2105/AJPH.52.6.1002 - 10. Castillo-Chavez, C. and Feng, Z. (2009) Mathematical Models for the Disease Dynamics of Tuberculosis. Mathematical Biosciences and Engineering Sciences, 6, 209-237.
http://dx.doi.org/10.3934/mbe.2009.6.209 - 11. Young, D., Stark, J. and Kirschner, D. (2008) Systems Biology of Persistent Infection: Tuberculosis as a Case Study. Nature Reviews Microbiology, 6, 520-528.
http://dx.doi.org/10.1038/nrmicro1919 - 12. Agusto, F.B., Cook, J., Shelton, P.D. and Wickers, M.G. (2015) Mathematical Model of mdr-tb and xdr-tb with Isolation and Lost to Follow-Up. Abstract and Applied Analysis, 2015, 1-21.
http://dx.doi.org/10.1155/2015/828461 - 13. Cohen, T. and Murray, M. (2004) Modelling Epidemics of Multidrug-Resistant m. Tuberculosis of Heterogeneous Fitness. Nature Medicine, 10, 1117-1121.
http://dx.doi.org/10.1038/nm1110 - 14. Diekmann, O. and Heesterbeek, J.P.A. (2000) Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation. Wiley Series in Mathematical and Computational Biology, 1.
- 15. Ullah, R., Zaman, G. and Islam, S. (2013) Stability Analysis of a General Sir Epidemic Model. VFAST Transactions on Mathematics, 1, 16-20.



























