Received 24 November 2015; accepted 17 January 2016; published 20 January 2016

ABSTRACT

This paper gives the extension of Newton’s method, and a variety of formulas to compare the convergences for the extension of Newton’s method (Section 4). Section 5 gives the numerical calculations. Section 1 introduces the three formulas obtained from the cubic equation of a hearth by Murase (Ref. [1] ). We find that Murase’s three formulas lead to a Horner’s method (Ref. [2] ) and extension of a Newton’s method (2009) at the same time. This shows originality of Wasan (mathematics developed in Japan) in the Edo era (1603-1868). Suzuki (Ref. [3] ) estimates Murase to be a rare mathematician in not only the history of Wasan but also the history of mathematics in the world. Section 2 gives the relations between Newton’s method, Horner’s method and Murase’s three formulas. Section 3 gives a new function defined such as.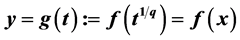

Keywords:

Recurrence Formula, Newton-Raphson’s Method (Newton’s Method), Extension of Newton’s Method

1. Murase’s Three Formulas from the Cubic Equation of a Hearth

We write this paper from two kinds of recurrence formulas of the square 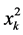and the deformation of a cubic equation written in Murase’s book (Ref. [1] ), and a hint of Tsuchikura (Ref. [4] ). It is enough for readers to know these three formulas. It is very difficult even for Japanese people to read the Murase’s book written in the Japanese ancient writing. Therefore, the readers do not need to read the book. Furthermore, the readers do not need to mind Japanese references. From now on, we explain the Murase’s three formulas as introduction. The readers can know the origin of this paper.

Murase made the cubic equation for the next problem in 1673.

There is a rectangular solid (base is a square). We put it together four and make the hearth such as Figure 1.

We claim one side of length of the square that one side is 14, and a volume becomes 192 of the hearth. Let one side of length of the square be x, then the next cubic equation is obtained.

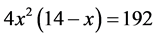(1.1)

that is

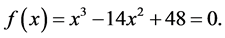(1.2)

This has three solutions of real number 2,.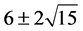

Murase derived two following recurrence formulas (1.3), (1.4) and deformed equation (1.5) from (1.2).

The first method:

(1.3)

Using on an abacus, Murase calculates to x₀ = 0 (initial value), x₁ = 1.85, x₂ = 1.97, x₃ = 1.9936, and decides a solution with 2.

The second method:

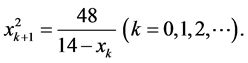(1.4)

Here he calculates to x₀ = 0, x₁ = 1.85, x₂ = 1.976, x₃ = 1.9989, x₄ = 1.9999907, and decides a solution with 2. Formula (1.4) has better precision than that (1.3), and convergence becomes fast.

The third method was nonrecurring in spite of a short sentence for many years. However, Yasuo Fujii (Seki Kowa Institute Mathematics of Yokkaichi University) succeeds in decoding in May 2009. It is the next equation.

The third method:

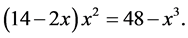(1.5)

The studies of three formulas of Murase progress by the third method have been decoded. Furthermore we obtain the next recurrence formula from (1.5).

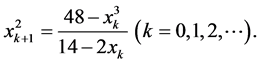(1.6)

2. Relations between Newton’s Method, Horner’s Method and the Murase’s Three Formulas

Throughout this paper, function f(x) be i (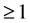) times differentiable if necessary, and f⁽ⁱ⁾(x) continuous. We start with the definition of Newton’s method.

Next Newton’s method is explained in a book of the standard numerical computation (Ref. [5] ).

The recurrence formula to approximate a root of the equation f(x) = 0

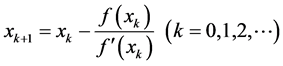(2.1)

is called Newton’s method or Newton-Raphson’s method.

Newton’s method is a method of giving the initial value x₀, calculating 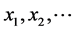one after another, and to determine for a root.

The quadratic convergence and the linearly convergence of the Newton’s method are known as followings.

Let α be a simple root for f(x) = 0, i.e.,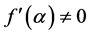. Then Newton’s method to the quadratic convergence of the following formula.

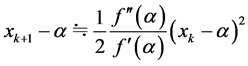(2.2)

If α is m () multiple root, then it will become the linearly convergence of the following formula.

(2.3)

Remark. Concerning choosing the initial value x₀, the number of iterations until it converges on a root changes. Moreover, it may not be converged on a root.

Example 2.1. By the transformation of variable, Murase’s equation f(x) = x³ − 14x² + 48 = 0 becomes

(2.4)

It becomes the following formula if Newton’s method is applied to.

(2.5)

This becomes the following formula by t = x².

(2.6)

This is a middle formula of (1.4) and (1.6) exactly. That is, Murase’s formulas (1.3), (1.4), and (1.5) lead to extension of a Newton’s method (2009).

Example 2.2. Applying the Horner’s method to Murase’s equation f(x) = x³ − 14x² + 48 = 0 for root 2, we get Table 1. Here, number −14, −12, −10 of the second column corresponds to the denominator for x_k = 2 of (1.3), (1.4), (1.6), respectively. Therefore, from the Table 1, we find that the Murase’s formulas (1.3), (1.4), and (1.6) lead to a Horner’s method. Furthermore, please read Ref. [2] if you want to know this deeply.

Proposition 2.3. We expand the first, second, third method of Murase, and obtain the next recurrence formula where m is a real number.

(2.7)

3. Function y = g(t) Defined by of y=f(x)

Definition 3.1. Let where q is a real number that is not 0. We define the function g(t) such as

. (3.1)

Because g(x^q) = f(x), the graph of g(x) is extended and contracted by x^q = t in the x-axis, without changing the height of f(x). Expansion and contraction come to object in and.

Lemma 3.2., are represented by as follows.

(3.2)

Proof. It is proved by the next calculations.

Theorem 3.3. The curvature of the curve y = g(x) at the point x^q is this.

These become of f(x) if q = 1 in particular.

Proof. Formula (3.5) is obtained by substituting the formulas (3.2), (3.3) for in the curvature.

4. Extension of Newton’s Method (Tsuchikura-Horiguchi’s Method)

4.1. Extension of Newton’s Method and the Convergences

In 2009, we found the extension of Newton’s method from the Murase’s three formulas as follows. Applying the Newton’s method to g(t), we have

. (4.1)

This means the intersection with the t(x)-axis of the tangent in the point of the graph of. Returning to the variable x by x^q = t, we get an extension of Newton’s method below.

Definition 4.1. For equation f(x) = 0, we call the next recurrence formulas the extension of Newton’s method or Murase-Newton’s method, Tsuchikura-Horiguchi’s method.

(4.2)

(4.2′)

Here, if q = 1, then the formulas (4.2), (4.2′) become Newton’s method.

Example 4.2. In the case of q = 2, applying the formula (4.2) to the Murase’s equation (1.2) of the hearth, we get

(4.3)

The formula (4.3) equals to (2.6).

Lemma 4.3. In the sequence {x_n}, let, and q, r anarbitrary real constant that is not 0, respectively. In this case, following formula holds for large enough integer n.

(4.4)

Proof. Applying L’Hospital’s rule to, (4.4) is obtained.

Proposition 4.4. If α is a simple root (m (>1) multiple root resp.) of f(x) = 0, then becomes the simple root (m multiple root resp.) of g(x).

Theorem 4.5. Let α (≠0) be a simple root for f(x) = 0, i.e.,. For x_k sufficiently close to α, q-th power of TH-method (Tsuchikura-Horiguchi’s method) becomes the quadratic convergence of the following formula.

(4.5)

If α is m () multiple root, then it will become linearly convergence of the following formula.

(4.6)

Proof. If is a simple root for g(t) = 0, then Newton’s method for g(t) becomes the quadratic convergence of the following formula.

(4.7)

Since

, , (4.8)

(4.7) becomes

. (4.9)

Here by the formula (4.4),

(4.10)

is obtained. Similarly formula (4.6) is obtained from (2.3).

4.2. Varieties of Formulas to Compare the Convergences for the Extension of Newton’s Method (Tsuchikura-Horiguchi’s Method)

We deform the equation f(x) = 0 to h(x) = 0. That is, two equations have the same root. r-th power of TH-method for h(x) is

, (4.11)

and if α (≠0) is a simple root, then it becomes quadratic convergence

. (4.12)

We get the following proposition by comparing the coefficients of of formula (4.5) and (4.12).

Proposition 4.6. Let the equation h(x) = 0 be deformed from f(x) = 0. Let, and α(≠0) a simple root. Then the necessary and sufficient condition for the convergence to α of q-th power of TH-method of f(x) to be equal to or faster than that r-th power of TH-method of h(x) is that the real numbers q and r satisfy the following condition.

(4.13)

Theorem 4.7. Let α (≠0) be a simple root of f(x) = 0, and. Then a necessary and sufficient condition for the convergence to α of q-th power of TH-method is equal to or faster than that Newton’s method is that q satisfies the following conditions.

(4.14)

i.e.,

(4.15)

Equal signs are the case of q = 1 and.

Proof. Compare the coefficient of of the quadratic convergence (4.5) of q-th power of TH-method and that (2.2) of Newton’s method. Then the necessary and sufficient condition is equivalent to

. (4.16)

The formula (4.14) is obtained from (4.16).

Theorem 4.8. Let α (≠0) be a simple root of f(x) = 0, and (i.e. the graph of f(x) is nearly the straight line in the neighborhood of the point α.). In this case (4.17) holds.

(4.17)

This is equivalent to the convergence to α of Newton’s method equals to or faster than that q-th power of TH- method.

Proof. By deforming the formula to, we compare it with.

(4.18)

(4.19)

We get the conclusion by this.

The following are the results related to the convex-concave of curve and the formulas for comparing convergences of TH-method.

Lemma 4.9. Let and. Then a necessary and sufficient condition for and are the same sign (opposite sign resp.) is

. (4.20)

Proof. Because

, (4.21)

according to, and become the same sign (opposite sign resp.).

We get the next theorem from Lemma 4.9, directly.

Theorem 4.10. Let α(≠0) be a simple root of f(x) = 0, and. We divide the Formula (4.14) of Theorem 4.7 into positive and negative range as follows.

(4.22)

(4.23)

If q satisfies the condition (4.23) ((4.22) resp.)), then the convex-concave of curve of g(x) in the neighborhood of and the f(x) in the neighborhood of are the same (opposite resp.).

Theorem 4.11. Let the conditions be the same as the above theorem. We give the following inequality.

(4.24)

Then the convergence to α of q-th power of TH-method is equal to or faster than Newton’s method equivalent to the formula (4.24).

Proof. By the formula

(4.25)

and (4.14) of Theorem 4.7, (4.24) is obtained.

Corollary 4.12. If then inequality (4.24) becomes

. (4.26)

The following are the results related to the curvature and the formulas for comparing the convergences of TH- method.

Theorem 4.13. Let α (≠0) be a simple root of f(x) = 0, and. Suppose that the curvature μ_q(x) of g(x) satisfies the condition

. (4.27)

Then the convergence to α of q-th power of TH-method is equal to or faster than that Newton’s method is equivalent to that (4.27) holds.

Proof. The formula

(4.28)

and (4.14) of Theorem 4.7, (4.27) is obtained.

Theorem 4.14. Let the conditions be same as the above theorem. Then formulas (4.29) and (4.30) are the equivalent.

(4.29)

(4.30)

Proof. (4.30) is obtained from (4.29).

Theorem 4.15. Let the conditions be same as Theorem 4.13. If

(4.29)

and

(4.31)

hold, then the convergence to α of q-th power of TH-method is equal to or faster than that Newton’s method.

Proof. Assertion is obtained from (4.14) of Theorem 4.7 and (4.30), (4.31).

5. Convergence Comparisons of the Numerical Calculations of Newton’s Method and Expansion of Newton’s Method (Tsuchikura-Horiguchi’s Method)

We use formula (4.2') for the numerical calculations of q-th power of TH-method for various equations such as n-th order equations (), equations of trigonometric, exponential, logarithmic function. We perform numerical calculations in the standard format in Excel of Microsoft.

Example 5.1. Numerical calculation of the p-th root.

Let A be a real number, and p a natural number. The equation for p-th root is this.

(5.1.1)

(1) The application of the formula (4.15) is p-th root of (5.1.1), and we get

(5.1.2)

In this case, formula (4.15) becomes

i.e.. (5.1.3)

Especially p-th power of TH-method for is

. (5.1.4)

Therefore, it converges to the root once for any initial value. Hence the number of iterations of formula (5.1.4) is less than that of the recurrence formula other.

(2) Speeds of convergences. The roots of are α = ±2. The interval of q of (5.1.3) is.

In the following, we examine the speed of convergence of q-th power of TH-method in case of α = 2. The results of the calculations are Table 2. We explain how to read this.

The first column represents the initial value x₀ and the absolute error, and the first row represents the real number q of. Two numbers 3 and 1.36646E−11 of intersection of two rows and two columns mean the following. Number 3 indicates the number of iterations that 0.5-th power of TH-method

(5.1.5)

to converge to a root 2. 1.36646E−11 indicates the absolute error |the value 2 of the convergence of the numerical calculation x_k+1 − root 2|.

2-th power of TH-methods converges to 2 in number of iterations 1; other TH-methods converge to that in three times. In case of x₀ = 1.9, 1.95, absolute errors of q = 1.2, 1.5, 2.5, 3 are smaller than that q = 1 (Newton’s method). Therefore degree of approximations of q = 1.2, 1.5, 2.5, 3 is better than that q = 1. Furthermore, absolute errors of q = 0.5, 3.5 are larger than that q = 1. Thus, these numerical calculations are compatible with the theory of Theorem 4.7.

(3) The application of the formula (4.27) of Theorem 4.13 for is this.

(5.1.6)

Indeed, by calculating the left and right sides of (5.1.6) for q in the Table 3 we get the numbers there.

g(x) becomes a straight line x − 4 in case of q = 2, and the curvature is 0. Therefore, the square of TH-method converges to root 2 in the number of iterations 1. For each q, the second and third columns are calculations of formula (5.1.6). The fourth column is the calculations of. Columns 5 and 6 are the calculation of the left-hand side and the right-hand side of the inequality (4.30), respectively. For each q in, the numbers of the second column and third column satisfy the condition (5.1.6).

(4) Formulas (4.29), (4.30) and (4.31). In case of q = 1.2, the formulas (4.29), (4.30) of Theorem 4.14 do not hold, respectively. Formulas (4.29), (4.31) of Theorem 4.15 hold in except for q = 1.2. However, in, formula (4.29) holds, but (4.31) does not hold.

Example 5.2. A quadratic equation

(5.2.1)

(1) The roots of (5.2.1) are α = 1, 2. Because, condition (4.15) becomes

(5.2.2)

A. In case of α = 1

(5.2.3)

Numerical calculations of TH-method, formulas (4.27), , (4.30) for α = 1.

(2A) We examine the speed of convergence of q-th power of TH-method in.

The results of the calculations are Table 4.

In case of x₀ = 1.05, 1.1, q-th (q = _3, _2, _1, 0.5) power of TH-method converges better than Newton’s method, respectively. Therefore, these are compatible with the theory of Theorem 4.7.

(3A) For and α=1, formula (4.27) of Theorem 4.13 becomes

(5.2.4)

Indeed, by calculating the left and right sides of (5.2.4) for q in the Table 5 we get the numbers there. For each q in, the numbers of the second column and third column satisfy the condition (5.2.4).

(4A) Formulas (4.29), (4.30) of Theorem 4.14 hold. Formula (4.31) of Theorem 4.15 hold for q = _0.5, 0.5, 1.

B. In case of α = 2

(5.2.5)

Numerical calculations of TH-method, formulas (4.27), , (4.30) for α = 2.

(2B) We examine the speed of convergence of q-th power of TH-method in.

The results of the calculations are Table 6.

In case of x₀ = 2.1, numerical calculations of q-th power of TH-method are compatible with the theory of Theorem 4.7.

(3B) For α = 2, formula (4.27) of Theorem 4.13 becomes

(5.2.6)

Indeed, by calculating the left and right sides of (5.2.6) for q in Table 7 formula (5.2.6) holds in.

(4B) Formulas (4.29), (4.30) of Theorem 4.14 hold except for q = _2. In this case, according to q increases, the value of the right-hand side of (4.30) increases rapidly. Formula (4.31) of Theorem 4.15 holds the equal sign only q = 1.

Example 5.3. Murase’s third degree equation (5.3.1) = (1.2).

Graph of f(x) is this (Figure 2).

The graph is drawn in Bear Graph of free software.

(1) For a root 2 of (5.3.1), condition (4.15) becomes

(5.3.2)

(2) In case of q = 0.5, 1, 1.5, 2, 2.45, 2.5, we calculate q-th power of TH-method. The results are Table 8.

In case of x₀ = 1.9, numerical calculations of q-th power of TH-method are compatible with Theorem 4.7.

(3) Formula (4.27) of Theorem 4.13 becomes

(5.3.3)

By calculating the left and right sides of (5.3.3) for q in Table 9 formula (5.3.3) holds except for 0.5 and 2.5.

(4) Formulas (4.29), (4.30) of Theorem 4.14 hold for q = 0.5, 1, 1.5. Formula (4.31) of Theorem 4.15 holds for q = 1, 1.5.

Example 5.4. A fifth degree equation

(5.4.1)

f(x) has no terms of, and a root is α = 1. Graph of f(x) is Figure 3.

Graph is the convex downward and monotonic decreases in, the convex upward and monotonic decreases in, and point (0,3) is a point of inflection.

(1) Condition (4.15) becomes

(5.4.2)

(2) In case of q = _1, 1, 3, 5, 6, 6.81, 7, we calculate q-th power of TH-method. The results are Table 10.

Notation 5(#DIV/0!) denotes that it is #DIV/0! in 5 iterations. In case of x₀ = 1.063, numerical calculations of q-th power of TH-method are compatible with Theorem 4.7. There is a noteworthy thing. In case of x₀ = 0.1, number of iterations of Newton’s method is 22 times but that 3-th power of TH-method is 5 times only.

(3) Formula (4.27) of Theorem 4.13 becomes

(5.4.3)

Indeed, by calculating the left and right sides of (5.4.3) for q = _1, 1, 3, 5, 6, 6.81, 8, 10 we get Table 11. Formula (5.4.3) holds for q = 1, 3, 5, 6, 6.81, respectively.

(4) Formulas (4.29), (4.30) of Theorem 4.14 hold for q = 1 and 3. Similarly formulas (4.29), (4.31) of Theorem 4.15 also hold for q = 1 and 3.

Example 5.5. Fifth degree equation

(5.5.1)

f(x) has no terms of, and a root of (5.5.1) is α ? 2.055967397. Graph of f(x) is Figure 4. The graph

becomes minimum at x = 0, which is parallel to the x-axis in the neighborhood. Next it increases and becomes maximum at x = 1.6. Further, it decreases monotonically from here, and intersects with root α. The graph changes intensely in this way in _1 < x < 2.5.

(1) The formula (4.15) of Theorem 4.7 becomes (5.5.2).

(5.5.2)

(The value of formula (5.5.2) for q = 16.018 is 1.999993923.)

(2) For q = _1, 1, 3, 6, 9, 12, 15, 16, 17, we calculate q-th power of TH-method. The results are Table 12.

① For x₀ = 1.85, number of iterations of Newton’s method and 3-th power of TH-method are the same 5. But absolute error of Newton’s method is slightly smaller than that 3-th power of TH-method. The theory compatible with all other cases.

② In particular for the initial value is x₀ = 1.5, the number of iterations of the 9-th power of TH-method is 4, which is extremely small than 54 times of the Newton’s method. Therefore, we examine the state of convergence of the 9-th power of TH-method.

Converting f(x) by, following formula is obtained.

(5.5.3)

The formula of the tangent of the curve of g(t) at point is the following.

(5.5.4)

For the initial value is 1.5⁹, we give in Table 13 the calculations of 9-th power of TH-method to converge to 656.3659005 (=2.055967397⁹) and the tangents. Then we give the graphs of Figure 5 g(x) and the changes of the tangents.

Straight line 1, 2 and 3 in Figure 5 indicates the tangent to the number of iterations k = 1, 2, 3, respectively. Point is a point of inflection of graph f(x). It becomes convex downward in x < 1.2, minimum at x = 0, and parallel to the x-axis in the neighborhood of x = 0. It becomes convex upward in 1.2 < x, maximum at x = 1.6. Therefore, choosing to 1.5 initial value for Newton’s method, x_k vibrate, and the number of iterations increase. Graph g(t) (g(x)) becomes minimum at t(x) = 0, but parallel parts to the t(x)-axis do not exist in the neighborhood of this point. Further it becomes convex upward in, convex downward in, intersects at with t-axis, and close to the shape of a straight line in the neighborhood. Therefore,

vibration is only once, become a monotonically increasing sequence, and the number of iterations is reduced.

(3) Formula (4.27) of Theorem 4.13 becomes

(5.5.5)

Indeed, by calculating the left and right sides of (5.5.5) for q = _1, 1, 3, 6, 9, 12, 15, 16, 17 we get Table 14. Formula (5.5.5) holds for q = 1, 3, 6, 9, 12, 15, 16.

(4) Formulas (4.29), (4.30) of Theorem 4.14 do not hold for q = 3. Theorem 4.15 holds as equality for q = 1.

Equation (5.4.1),(5.5.1) has only one term which degree is smaller than highest degree, respectively. These equations have the trend that the convergences of TH-methods are extremely fast than that Newton’s method.

Example 5.6.

(5.6)

Roots of equation (5.6) are α = mπ (m is an integer, π ? 3.141592654), and. Because of Theorem 4.8 holds, convergence of Newton’s method of q = 1 is the fastest in other q-th power of TH-method. For α = π, q = ±1, ±2, ±3, we calculate q-th power of TH-method. The results are Table 15.

Example 5.7.

(5.7.1)

A root of equation (5.7.1) is α. Because, , , this is also an example of Theorem 4.8. Particular if n ? 4 then root α of becomes multiple root. For n = 3, α = 2, equation (5.7.1) is the following.

(5.7.2)

For q = _2, _1, 1, 2, 3, we calculate q-th power of TH-method, and get Table 16.

Example 5.8.

(5.8.1)

(1) The root of (5.8.1) is ln2 ? 0.693147181, and. Applying (4.15) of Theorem 4.7, we have

(5.8.2)

(2) For q = 0.5, 1, 1.5, 2, 2.386294361, 2.5, we calculate q-th power of TH-method.

However, we calculate the absolute error as ln2 ? 0.693147181 root. The results are Table 17.

For x₀ = 0.73, 0.76, q-th power of TH-method has better approximate degree than Newton’s method in the range of (5.8.2).

(3) Formula (4.27) of Theorem 4.13 for (5.8.1) becomes

(5.8.3)

By calculating the left and right sides of (5.8.3) for q in Table 18 we get the numbers there. Formula (5.8.3) holds for q except for 0.8 and 2.4.

(4) In Table 18, formulas (4.29), (4.30) hold in the range of (5.8.2) except for q = 2.386294361. (4.31) holds in (5.8.2).

Example 5.9.

(5.9.1)

(1) The root of (5.9.1) is α = 1, and. Applying (4.15) we have

(5.9.2)

(2) The calculations for TH-method are Table 19.

For x₀ = 1.05, 1.1, 1.2, q-th (q = _1, _0.5, 0.5) power of TH-method converges better than Newton’s method, respectively.

(3) Formula (4.27) of Theorem 4.13 for (5.9.1) is this.

(5.9.3)

By calculating the left and right sides of (5.9.3) for q in Table 20 we get the numbers in its. In equality (5.9.3) holds for q except for _1.5 and 1.5.

(4) Formulas (4.29), (4.30), (4.31) hold for q = _1, _0.5, 0.5, 1.

Acknowledgements

Dr. Tamotsu Tsuchikura (1923-2015, professor emeritus of Tohoku University) and Dr. Mitsuo Morimoto (professor emeritus of Sophia University) gave hints to me. I am deeply grateful to them.

Cite this paper

ShunjiHoriguchi, (2016) The Formulas to Compare the Convergences of Newton’s Method and the Extended Newton’s Method (Tsuchikura-Horiguchi Method) and the Numerical Calculations. Applied Mathematics,07,40-60. doi: 10.4236/am.2016.71004

References