Received 13 November 2015; accepted 27 December 2015; published 30 December 2015

ABSTRACT

In this paper, we consider the existence of multiple solutions to the Kirchhoff problems with critical potential, critical exponent and a concave term. Our main tools are the Nehari manifold and mountain pass theorem.

Keywords:

Kirchhoff Problems, Critical Potential, Concave term, Nehari Manifold, Mountain Pass Theorem

1. Introduction

In this paper, we consider the multiplicity results of nontrivial solutions of the following Kirchhoff problem

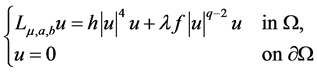(1.1)

where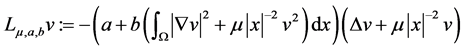, Ω is a smooth bounded domain of, ,

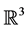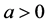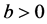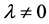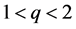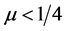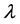, , , , is a real parameter, 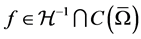with 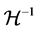is the topological dual of 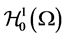satisfying suitable conditions, h is a bounded positive function on Ω.

The original one-dimensional Kirchhoff equation was introduced by Kirchhoff [1] in 1883. His model takes into account the changes in length of the strings produced by transverse vibrations.

In recent years, the existence and multiplicity of solutions to the nonlocal problem

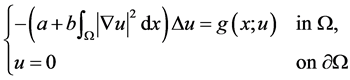(1.2)

has been studied by various researchers and many interesting and important results can be found. For instance, positive solutions could be obtained in [2] -[4] . Especially, Chen et al. [5] discussed a Kirchhoff type problem when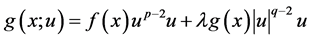, where 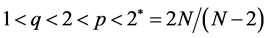if, if and with some proper conditions are sign-changing weight functions. And they have obtained the existence of two positive solutions if,.

Researchers, such as Mao and Zhang [6] , Mao and Luan [7] , found sign-changing solutions. As for in nitely many solutions, we refer readers to [8] [9] . He and Zou [10] considered the class of Kirchhoff type problem when with some conditions and proved a sequence of a.e. positive weak solutions tending to zero in.

In the case of a bounded domain of with, Tarantello [8] proved, under a suitable condition on f,

the existence of at least two solutions to (1.2) for, and.

Before formulating our results, we give some definitions and notation.

The space is equiped with the norm

wich equivalent to the norm

with. More explicitly, we have

for all, with and.

Let be the best Sobolev constant, then

(2.1)

Since our approach is variational, we define the functional on by

(2.2)

A point is a weak solution of the Equation (1.1) if it is the critical point of the functional. Generally speaking, a function u is called a solution of (1.1) if and for all it holds

Throughout this work, we consider the following assumptions:

(F) There exist and such that, for all x in.

(H)

Here, denotes the ball centered at a with radius r.

In our work, we research the critical points as the minimizers of the energy functional associated to the problem (1.1) on the constraint defined by the Nehari manifold, which are solutions of our system.

Let be positive number such that

where

Now we can state our main results.

Theorem 1. Assume that, and (F) satisfied and verifying then the problem (1.1) has at least one positive solution.

Theorem 2. In addition to the assumptions of the Theorem 1, if (H) hold and then there exists such that for all verifying the problem (1.1) has at least two positive solutions.

Theorem 3. In addition to the assumptions of the Theorem 2, assuming then the problem (1.1) has at least two positive solutions and two opposite solutions.

This paper is organized as follows. In Section 2, we give some preliminaries. Section 3 and 4 are devoted to the proofs of Theorems 1 and 2. In the last Section, we prove the Theorem 3.

2. Preliminaries

Definition 1. Let E a Banach space and.

i) is a Palais-Smale sequence at level c (in short) in E for I if

where tends to 0 as n goes at infinity.

ii) We say that I satisfies the condition if any sequence in E for I has a convergent subsequence.

Lemma 1. Let X Banach space, and verifying the Palais-Smale condition. Suppose that and that:

i) there exist, such that if then

ii) there exist such that and

let where

then c is critical value of J such that.

Nehari Manifold

It is well known that the functional is of class in and the solutions of (1.1) are the critical points of which is not bounded below on. Consider the lowing Nehari manifold

Thus, if and only if

(2.3)

Define

Then, for

(2.4)

Now, we split in three parts:

Note that contains every nontrivial solution of the problem (1.1). Moreover, we have the following results.

Lemma 2. is coercive and bounded from below on.

Proof. If, then by (2.3) and the Hölder inequality, we deduce that

Thus, is coercive and bounded from below on.

We have the following results.

Lemma 3. Suppose that is a local minimizer for on. Then, if, is a critical point of.

Proof. If is a local minimizer for on, then is a solution of the optimization problem

Hence, there exists a Lagrange multipliers such that

Thus,

But, since. Hence. This completes the proof.

Lemma 4. There exists a positive number such that, for all we have.

Proof. Let us reason by contradiction.

Suppose such that. Moreover, by the Hölder inequality and the Sobolev embedding theorem, we obtain

and

with

From (2.5) and (2.6), we obtain, which contradicts an hypothesis.

Thus. Define

For the sequel, we need the following Lemma.

Lemma 5. i) For all such that, one has.

ii) There exists such that for all, one has

Proof. i) Let. By (2.4), we have

and so

We conclude that.

ii) Let. By (2.4) and the Hölder inequality we get

Thus, for all such that, we have.

For each with, we write

Lemma 6. Let real parameters such that. For each with, there exist unique and such that, , ,

Proof. With minor modifications, we refer to [11] .

Proposition 1. (see [11] )

i) For all such that, there exists a sequence in.

ii) For all such that, there exists a a sequence in.

3. Proof of Theorem 1

Now, taking as a starting point the work of Tarantello [8] , we establish the existence of a local minimum for on.

Proposition 2. For all such that, the functional has a minimizer and it satisfies:

i)

ii) is a nontrivial solution of (1.1).

Proof. If, then by Proposition 1. i) there exists a sequence in, thus it bounded by Lemma 2. Then, there exists and we can extract a subsequence which will denoted by such that

(3.1)

Thus, by (3.1), is a weak nontrivial solution of (1.1). Now, we show that converges to strongly

in. Suppose otherwise. By the lower semi-continuity of the norm, then either and we obtain

We get a contradiction. Therefore, converge to strongly in. Moreover, we have. If not, then by Lemma 6, there are two numbers and, uniquely defined so that and. In particular, we have. Since

there exists such that. By Lemma 6, we get

which contradicts the fact that. Since and, then by Lemma 3, we may assume that is a nontrivial nonnegative solution of (1.1). By the Harnack inequality, we conclude that and, see for exanmple [12] .

4. Proof of Theorem 2

Next, we establish the existence of a local minimum for on. For this, we require the following Lemma.

Lemma 7. Assume that then for all such that, the functional has a minimizer in and it satisfies:

i)

ii) is a nontrivial solution of (1.1) in.

Proof. If, then by Proposition 1. ii) there exists a, sequence in, thus it bounded by Lemma 2. Then, there exists and we can extract a subsequence which will denoted by such that

This implies that

Moreover, by (H) and (2.4) we obtain

if we get

(4.1)

This implies that

Now, we prove that converges to strongly in. Suppose otherwise. Then, either

. By Lemma 6 there is a unique such that. Since

we have

and this is a contradiction. Hence,

Thus,

Since and, then by (4.1) and Lemma 3, we may assume that is a nontrivial nonnegative solution of (1.1). By the maximum principle, we conclude that.

Now, we complete the proof of Theorem 2. By Propositions 2 and Lemma 7, we obtain that (1.1) has two positive solutions and. Since, this implies that and are distinct.

5. Proof of Theorem 3

In this section, we consider the following Nehari submanifold of

Thus, if and only if

Firsly, we need the following Lemmas.

Lemma 8. Under the hypothesis of theorem 3, there exist such that is nonempty for any and.

Proof. Fix and let

Clearly and as. Moreover, we have

If for, then there exists such that. Thus,

and is nonempty for any.

Lemma 9. There exist M positive real such that

for and any

Proof. Let then by (2.3), (2.4) and the Holder inequality, allows us to write

Thus, if then we obtain that

(5.1)

Lemma 10. There exist r and positive constants such that

i) we have

ii) there exists when, with, such that.

Proof. We can suppose that the minima of are realized by and. The geometric conditions of the mountain pass theorem are satisfied. Indeed, we have

i) By (2.4), (5.1), the Holder inequality and the fact that, we get

Thus, for there exist such that

ii) Let, then we have for all

Letting for t large enough, we obtain For t large enough we can ensure.

Let and c defined by

and

Proof of Theorem 3.

If then, by the Lemmas 2 and Proposition 1. ii), verifying the Palais-Smale condition in. Moreover, from the Lemmas 3, 9 and 10, there exists such that

Thus is the third solution of our system such that and. Since (1.1) is odd with respect u, we obtain that is also a solution of (1.1).

Cite this paper

Mohammed El Mokhtar Ould ElMokhtar, (2015) Four Nontrivial Solutions for Kirchhoff Problems with Critical Potential, Critical Exponent and a Concave Term. Applied Mathematics,06,2248-2256. doi: 10.4236/am.2015.614198

References