Applied Mathematics
Vol.07 No.06(2016), Article ID:64929,14 pages
10.4236/am.2016.76044
Multiyear Discrete Stochastic Programming with a Fuzzy Semi-Markov Process
C. S. Kim1, Richard M. Adams2, Dannele E. Peck3
1Economic Research Service, U.S. Department of Agriculture, Washington, DC, USA
2Department of Applied Economics, Oregon State University, Corvallis, OR, USA
3Department of Agricultural and Applied Economics, University of Wyoming, Laramie, WY, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 October 2016; accepted 21 March 2016; published 24 March 2016
ABSTRACT
Drought conditions at a given location evolve randomly through time and are typically characterized by severity and duration. Researchers interested in modeling the economic effects of drought on agriculture or other water users often capture the stochastic nature of drought and its conditions via multiyear, stochastic economic models. Three major sources of uncertainty in application of a multiyear discrete stochastic model to evaluate user preparedness and response to drought are: (1) the assumption of independence of yearly weather conditions, (2) linguistic vagueness in the definition of drought itself, and (3) the duration of drought. One means of addressing these uncertainties is to re-cast drought as a stochastic, multiyear process using a “fuzzy” semi-Markov process. In this paper, we review “crisp” versus “fuzzy” representations of drought and show how fuzzy semi-Markov processes can aid researchers in developing more robust multiyear, discrete stochastic models.
Keywords:
Drought, Discrete Stochastic Economic Modeling, Fuzzy Logic, Fuzzy Markov Process, Fuzzy Semi-Markov Process
1. Introduction
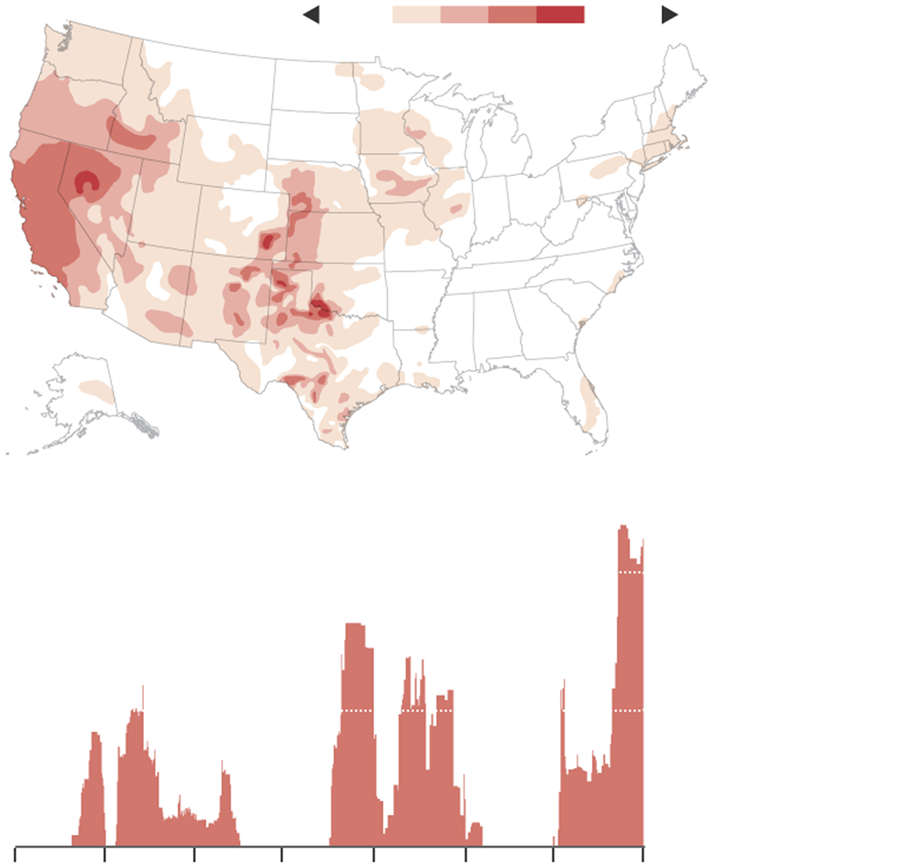
Figure 1. Severity and duration of drought in California (Source: The National Drought Miti- gation Center―USDA).
where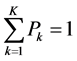 .
.
2. Linguistic Vagueness and Fuzzy Logic
To evaluate the impacts of drought conditions and associated preparedness and response plans, a clear definition of drought must be provided. One definition of drought is the case in which irrigation water supplied is less than irrigation water demanded, due to inadequate rainfall, snow pack, or other weather conditions. As the difference between irrigation water demanded and supplied increases, severity of drought intensifies along a continuous gradient. While the characterization of drought varies across studies, the following definition of drought pro- vided by Yevjevich [14] has been widely used [6] [15] [16] :
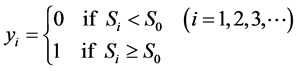 , (2.1)
, (2.1)
where 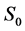 is a constant water allotment threshold (such as 40 acre-inches Peck and Adams [3] used for water allotment under normal weather condition) and Si is the ith severity state. A Bernoulli variable yi plays a significant role in estimation of the holding time (i.e., duration) probability mass function of drought in later section of semi-Markov chains.
is a constant water allotment threshold (such as 40 acre-inches Peck and Adams [3] used for water allotment under normal weather condition) and Si is the ith severity state. A Bernoulli variable yi plays a significant role in estimation of the holding time (i.e., duration) probability mass function of drought in later section of semi-Markov chains.
When economic models represent drought in binary terms (i.e., a water allocation either qualifies or does not qualify as drought), this overly-simplified or deceivingly-crisp (as opposed to fuzzy) measurement of drought severity can cause inefficient resource allocation. Unlike this crisp set (in which an element is either a member of the set or not), fuzzy sets allow elements to be included through a degree of membership, as expressed by a membership function, thus relaxing the binary state assumption [6] [17] . Introduced by Zadeh [18] , fuzzy logic and fuzzy set theory have since been widely adopted to deal with linguistic vagueness in various mathematical optimization models, including fuzzy dynamic programming [19] [20] , and optimal fuzzy control [21] .
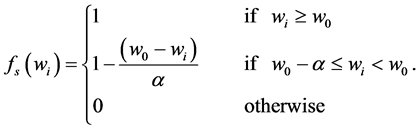 (2.2)
(2.2)
3. Fuzzy Markov and Semi-Markov Processes
Definition 2. Let 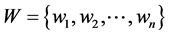 be a finite state-space of possible water allotments from an irrigation
be a finite state-space of possible water allotments from an irrigation
water district. Let 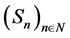 be random variables taking values in W. Now, let a fuzzy subset of W be defined as
be random variables taking values in W. Now, let a fuzzy subset of W be defined as
a set of ordered pairs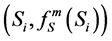 , where
, where 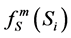 is the grade of membership of Si in W in the mth transition.
is the grade of membership of Si in W in the mth transition.
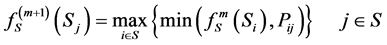 , (3.2)
, (3.2)
where the fuzzy-state grade of membership, 

and the powers of the fuzzy transition matrix, 

where 

A few empirical studies have been conducted to compare efficiencies between the use of classic Markov chains based on conventional crisp set theory and fuzzy Markov chains in the context of stochastic programming models. Mousavi et al. [20] compared a conventional stochastic dynamic programming model (which employed classic Markov chains) and a fuzzy-state stochastic dynamic programming model (which employed fuzzy Markov chains) in the operation of a multipurpose reservoir in Iran. Results from their study show that fuzzy- state stochastic dynamic programming outperforms conventional stochastic dynamic programming in achieving the flood control objective and in overall performance of the reservoir. Chandramouli and Nanduri [27] also compared a conventional stochastic dynamic model and a fuzzy-state stochastic dynamic model in the operation of a multipurpose reservoir in India. They found that the fuzzy-state stochastic dynamic programming model out performed the conventional stochastic dynamic programming model.
3.1. Fuzzy Semi-Markov Process
3.1.1. Homogeneous Fuzzy Semi-Markov Process
where Sn represents the state at the nth transition, Tn is the time of the nth transition and “t” is arrival time. Equation (3.5) expresses the probability of transitioning to state j at arrival time t, given the system has been in state i after n transitions. Unfortunately no solution has been reported for Equation (3.5) in the literature; therefore, an alternative approach for solving Equation (3.5) has been employed by Cancelliere and Salas [15] and Mirakbari and Ganji [6] .

where 
drought severity. This is estimated by 

drought before moving to the jth drought, which can be easily observed from historical data.
Mirakbari and Ganji [6] compared performances between the classic semi-Markov chains and the fuzzy semi- Markov chains by using profust reliability theory to a rangeland system in India.6 Their results indicate that the reliability of rangeland system decisions increased by 22 percent when the fuzzy semi-Markov process is used over the classic semi-Markov process.
3.1.2. Non-Homogeneous Fuzzy Semi-Markov Process
where 

4. Numerical Example
We now present a numerical example of multiyear water supply forecasts under the assumption that a pair of two random variables {Sn, Tn} follows a homogeneous fuzzy semi-Markov process (i.e., Equation (3.5) through (3.12)).7 The multiyear forecast associated with the severity and duration of droughts can be incorporated into a multiyear discrete stochastic programming model as shown in Equation (3.12).

Comparison
Due to the lagging and long-term effects of drought on vegetation and soil moisture, or on cropping choices due to agronomic constraints (e.g., rotations), the resilience of drought is equal to or longer than drought duration [38] .9 Therefore, economic impacts of individual years of drought may not necessarily be independent [3] . To compare multiyear drought probabilities between a conventional multiyear discrete stochastic program (which typically assumes the previous year’s state of nature does not influence the probability of future states of nature) and a multiyear homogeneous fuzzy semi-Markov process, the steady-state probabilities of the fuzzy transition matrix in Equation (4.2) are estimated as follows:

where π is a stationary distribution.10 The probabilities in Equation (4.4) represent Pk (k = 1, 2, 3) in Equation (1.3). In a conventional discrete stochastic programming model, the probability of severe drought (SEE) in the
first year, as well as in the second year, or any other year, is


The possibility mass function of the holding-time spent in each weather condition in a fuzzy semi-Markov
Table 2. Results of a numerical example.
N = Normal; MM = Mild/Moderate drought; SEE = Severe/Extreme/Exceptional drought. FsM = Fuzzy semi-Markov; DSPM = Discrete Stochastic Programming Model.
process is estimated with Equation (3.11) and results are presented in Table 2. In contrast to a conventional discrete stochastic programming model, the possibility of two consecutive years of SEE drought condition is 0.1875, which is 69 percent higher than the probability assumed in a conventional multiyear discrete stochastic programming approach. As the duration of consecutive years of severe drought increases to three years, the possibility of holding time in a fuzzy semi-Markov process is 0.1406, which is 280 percent higher than the probability assumed in a conventional multiyear discrete stochastic programming approach, 0.0370.
Implementation of adequate measures to control or mitigate drought consequences is a major challenge for irrigators and other water users. Our numerical example, while stylized, demonstrates how economists can use fuzzy semi-Markov processes to incorporate uncertainty about both severity of drought (which necessitates fuzzy sets) and duration of a multiyear drought (which necessitates semi-Markov processes) in stochastic modeling by using a fuzzy semi-Markov process. Such model specification may improve representation of the economic effects of drought severity and duration on water users and the efficacy of alternative mitigation actions.
5. Summary
Acknowledgements
The views expressed are those of the authors and should not be attributed to USDA or Economic Research Service.
Cite this paper
C. S.Kim,Richard M.Adams,Dannele E.Peck, (2016) Multiyear Discrete Stochastic Programming with a Fuzzy Semi-Markov Process. Applied Mathematics,07,482-495. doi: 10.4236/am.2016.76044
References
- 1. Engelhardt, T. (1983) Water Supply Optimization with Discrete Stochastic Linear Programming. Proceedings of International Crops Research Institute Workshop on the State of the Art and Management Alternatives for Optimizing the Productivity of SAT Alfisols and Related Soils, ICRISAT Center, 1-3 December 1983, Patancheru, India, 79-87.
- 2. McCarl, B. and Parandvash, G. (1988) Irrigation Development versus Hydroelectric Generation: Can Interruptible Irrigation Play a Role? Western Journal of Agricultural Economics, 13, 267-276.
- 3. Peck, D.E. and Adams, R.M. (2010) Farm-Level Impacts of Prolonged Drought: Is a Multiyear Event More than the Sum of Its Parts? The Australian Journal of Agricultural and Resource Economics, 54, 43-60.
http://dx.doi.org/10.1111/j.1467-8489.2009.00478.x - 4. Cocks, K.D. (1968) Discrete Stochastic Programming. Management Science, 15, 72-79.
http://dx.doi.org/10.1287/mnsc.15.1.72 - 5. Watanabe, Y. (1987) Errors in Availability Estimation by 2-State Models of 3-State Systems. Reliability Engineering, 18, 223-235.
http://dx.doi.org/10.1016/0143-8174(87)90100-4 - 6. Mirakbari, M. and Ganji, A. (2010) Reliability Analysis of a Rangeland System: The Application of Profust Theory. Stochastic Environmental Research and Risk Assessment, 24, 399-409.
http://dx.doi.org/10.1007/s00477-009-0329-8 - 7. Sahinidis, N. (2004) Optimization under Uncertainty: State-of-the-Art and Opportunities. Computers and Chemical Engineering, 28, 971-983.
http://dx.doi.org/10.1016/j.compchemeng.2003.09.017 - 8. Fullér, R. (1998) Fuzzy Reasoning and Fuzzy Optimization. Department of Operations, Eötvös Loránd University, Budapest.
- 9. Inuiguchi, M. and Ramit, J. (2000) Possibilistic Linear Programming: A Brief Review of Fuzzy Mathematical Programming and a Comparison with Stochastic Programming in Portfolio Selection Problem. Fuzzy Sets and System, 111, 3-28.
http://dx.doi.org/10.1016/S0165-0114(98)00449-7 - 10. Tanaka, H., Okuda, T. and Asai, K. (1974) Decision Making and Information in Fuzzy Events. Bulletin Series A, 23, 193-202.
- 11. Li, H. and Gong, Z. (2010) Fuzzy Linear Programming with Possibility and Necessity Relation. In: Cao, et al., Eds., Fuzzy Information and Engineering, Springer-Verlag, Berlin Heidelberg, 305-311.
http://dx.doi.org/10.1007/978-3-642-14880-4_32 - 12. Huang, Y.F., Baetz, B.W., Huang, G.H. and Liu, L. (2002) Violation Analysis for Solid Waste Management Systems: An Interval Fuzzy Programming Approach. Journal of Environmental Management, 65, 431-446.
http://dx.doi.org/10.1016/S0301-4797(02)90566-9 - 13. Arkov, V., Kulikov, G.G. and Breikin, T.V. (1999) Fuzzy Markov Modeling in Automatic Control of Complex Dynamic Systems. International Conference on Accelerator and Large Experimental Physics Control Systems, 4-8 October 1999, Trieste, 287-289.
- 14. Yevjevich, V. (1967) An Objective Approach to Definitions and Investigations to Continental Hydrologic Droughts. Colorado State University, Fort Collins, Colorado.
- 15. Cancelliere, A. and Salas, J.D. (2004) Drought Length Properties for Periodic-Stochastic Hydrologic Data. Water Resources Research, 40, W02503.
http://dx.doi.org/10.1029/2002wr001750 - 16. Llamas, J. and Siddiqui, M. (1969) Runs of Precipitation Series. Hydrology Paper 33, Colorado State University, Fort Collins.
- 17. Cai, K.Y., Wen, C.U. and Zhang, M.L. (1993) Fuzzy States as a Basis for a Theory of Fuzzy Reliability. Journal of Microelectronics Reliability, 33, 2253-2263.
http://dx.doi.org/10.1016/0026-2714(93)90065-7 - 18. Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353.
http://dx.doi.org/10.1016/S0019-9958(65)90241-X - 19. Bellman, R.E. and Zadeh, L.A. (1970) Decision-Making in a Fuzzy Environment. Management Science, 17, 141-164.
http://dx.doi.org/10.1287/mnsc.17.4.B141 - 20. Mousavi, S., Karamouz, K. and Menhadj, M.B. (2004) Fuzzy-State Stochastic Dynamic Programming for Reservoir Operation. Journal of Water Resources Planning and Management, 130, 460-470.
http://dx.doi.org/10.1061/(ASCE)0733-9496(2004)130:6(460) - 21. Baten, M.A. and Kamil, A.A. (2012) Optimal Fuzzy Control with Application to Discounted Cost Production Inventory Planning Problem. Proceedings of the World Congress on Engineering, Vol. III, London, 30 June-2 July 2012.
- 22. Khedun, C.P. and Singh, V. (2014) Drought Risk Management in Agriculture: Current Trends in Research. Texas A&M University, College Station.
- 23. Alves, A., Mota, G., Costa, G. and Feitosa, R. (2012) Estimation of Transition Possibilities for Fuzzy Markov Chains Applied to the Analysis of Multitemporal Image Sequences. Proceedings of the 4th GEOBIA, Rio de Janeiro, 7-9 May 2012.
- 24. Praba, B., Sujatha, R. and Srikrishna, S. (2009) A Study on Homogeneous Fuzzy Semi-Markov Model. Applied Mathematical Science, 3, 2453-2467.
- 25. Avranchenkov, K. and Sanche, E. (2002) Fuzzy Markov Chains and Decision-Making. Fuzzy Optimization and Decision Making, 1, 143-159.
http://dx.doi.org/10.1023/A:1015729400380 - 26. Schweizer, P.J. (1968) Pertubation Theory and Finite Markov Chains. Journal of Applied Probability, 5, 401-413.
http://dx.doi.org/10.2307/3212261 - 27. Chandramouli, S. and Nanduri, U. (2011) Comparison of Stochastic and Fuzzy Dynamic Programming Models for the Operation of a Multipurpose Reservoir. Water and Environment Journal, 25, 547-554.
http://dx.doi.org/10.1111/j.1747-6593.2011.00255.x - 28. Bardossy, A. and Plate, E.J. (1991) Modeling Daily Rainfall Using a Semi-Markov Representation of Circulation Pattern Occurrence. Journal of Hydrology, 122, 33-47.
http://dx.doi.org/10.1016/0022-1694(91)90170-M - 29. Masruroh, N. (2012) Introduction to Discrete Time Semi Markov Process.
http://slideplayer.com/slide/4757341/ - 30. Praba, B., Sujatha, R. and Srikrishna, S. (2009) Fuzzy Reliability Measures of Fuzzy Probabilistic Semi-Markov Model. International Journal of Recent Trends in Engineering, 2, 25-29.
- 31. Vassiliou, P.C. (2013) Fuzzy Semi-Markov Migration Process in Credit Risk. Fuzzy Sets and Systems, 223, 39-58.
http://dx.doi.org/10.1016/j.fss.2013.02.016 - 32. De Medici, J.J. and Manca, R. (2012) The Aggregate Claim Amount Discrete Time Semi-Markov Model. Working Paper, Department of Mathematics of Economic Decisions on Finance and Insurance, University of Rome, La Sapienza.
- 33. Janssen, J., Manca, R. and di Prignano, E.V. (2012) Non Homogeneous Interest Rate Structure in a Semi-Markov Framework. Working Paper.
http://www.actuaries.org - 34. Gildeh, B.S. and Dadgar, A. (2007) Reducible Fuzzy Markov Chain and Fuzzy Absorption Probability. 1st Joint Congress on Fuzzy and Intelligent Systems, Ferdowsi University of Mashhad, Iran, 29-31August 2007.
- 35. Li, J. and He, P. (2010) The Application of Fuzzy Markov Chains in the Analysis of Internet Glance Behavior. 3rd IEEE International Conference on Computer Science and Information Technology (ICCSIT), Vol. 7, Chengdu, 9-11 July 2010, 608-611.
- 36. Sanchez, E. (1976) Resolution of Composite Fuzzy Relation Equation. Information and Control, 30, 38-48.
http://dx.doi.org/10.1016/S0019-9958(76)90446-0 - 37. Meenakshi, A.R. and Kaliraja, M. (2010) Regular Interval Valued Fuzzy Matrices. Advances in Fuzzy Mathematics, 5, 7-15.
- 38. Rossi, G., Benedini, M., Tsakiris, G. and Giakoumakis, S. (1992) On Regional Drought Estimation and Analysis. Water Resources Management, 6, 249-277.
http://dx.doi.org/10.1007/BF00872280
NOTES
1Both possibilistic and flexible fuzzy programming can be presented in interval fuzzy programming [12] .
2However, we use the terms possibility and probability interchangeably in this paper.
3The max-min operations of fuzzy sets are as follows. For fuzzy subsets A and B of a crisp set W ≠ ϕ, the intersection of A and B is defined as: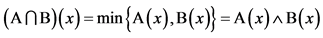 ,
,  Similarly, the union of A and B is defined as follows:
Similarly, the union of A and B is defined as follows: ,
, 
4The set of all subsets of W is called the power set of W.
5Markov kernel is also called a transition probability function that maps from a measureable space to another space.
6Profust reliability theory consists of two parts, the fuzzy part which considers vagueness in rangeland system failure and the probabilistic part which incorporates randomness of rangeland failure [6] [17] .
7Multiyear water supply forecast is a forecast in dij = 1, dij = 2, dij = 3, etc. for all drought severities i = 1, 2, ×××, n.
8See Avrachenkov and Sanchez [25] , Gildeh and Dadgar [34] , Li and He [35] , Mousavi et al. [20] , and Sanchez [36] for fuzzy transition matrix, and Meenakshi and Kaliraja [37] for interval transition matrix.
9Resilience is a measure of the recovery time of the system [38] .
10The stationary distribution must satisfy







