Applied Mathematics
Vol.06 No.12(2015), Article ID:61025,8 pages
10.4236/am.2015.612176
MHD Fluctuating Flow of Non-Newtonian Fluid through a Porous Medium Bounded by an Infinite Porous Plate
Dhiman Bose, Uma Basu
Department of Applied Mathematics, University of Calcutta, Kolkata, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 13 January 2015; accepted 8 November 2015; published 11 November 2015

ABSTRACT
In present paper, an investigation has been made on the fluctuating flow of a non-Newtonian second grade fluid through a porous medium over a semi-infinite porous plate in presence of a transverse magnetic field B0. The governing equations have been solved analytically and the expressions for the velocity and stress fields are obtained. The free stream velocity U(t) fluctuates in time about a non-zero constant mean. The effects of the permeability parameter K and magnetic field parameter M on velocity field have been analyzed quantitatively with the help of figures. It is noticed that the velocity field asymptotically approaches free stream velocity as it goes far away from the plate.
Keywords:
Fluctuating Flow, Second Grade Fluid, Porous Medium, Transverse Magnetic Field, Free Stream Velocity

1. Introduction
The fluctuating flows of viscous incompressible fluid through porous medium over an infinite porous plate have been investigated rigorously by many researchers because of its wide application in different fields. The phenomenon of flows through porous medium has been a subject of interest of many researchers because of its wide range of application in different fields such as petroleum engineering, chemical engineering etc. In petroleum engineering, it is dealt with the movement of natural gas and oil through reservoirs. Further, the study on underground water resources, seepage of water in river bed is also related to the flow through porous medium.
Soundalgekar and Puri [1] investigated on fluctuating flow of an elastic-viscous fluid past an infinite plate with variable suction. Shen, Tan, Zhao and Masuoka [2] studied the Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative model. Varshney [3] studied fluctuating flow of viscous fluid through a porous medium bounded by a porous plate. In his work, he has used Lighthill’s method in finding the solution of the field equation and shows that the results obtained reduce those of Messiha [5] . Lighthill [4] initiated the work on fluctuating flows. He studied the response of laminar skin friction and heat transfer to fluctuations in the stream velocity. An important class of two dimensional time dependent flow problems dealing with the response of the boundary layer to unsteady fluctuations about a mean value has been studied by him. Messiha [5] investigated laminar boundary layer in oscillating flow along an infinite flat plate with variable suction. Stuart [6] studied a solution of the Navier-Stokes and energy equations illustrating the response of skin friction and temperature of an infinite plate thermometer to fluctuations in the stream velocity. Gholizadeh [7] discussed MHD oscillatory flow past a vertical porous plate through porous medium in the presence of thermal and mass diffusion with constant heat source. Moniem and Hassanin [8] investigated solution of MHD flow past a vertical porous plate through a porous medium under oscillatory suction. Venkateswarlu, Reddy and Lakshmi [9] studied unsteady MHD flow of a viscous fluid past a vertical porous plate under oscillatory suction velocity. Soundalgekar and Takhar [10] discussed MHD oscillatory flow past a semi infinite plate.
In the present study, we have investigated the fluctuating flow of non-Newtonian fluid in a semi-infinite region through a porous medium bounded by a porous plate in presence of transverse magnetic field. The non- Newtonian fluid considered here is of second grade type and fluctuating flow related to such type of fluid is different from all those works that have been done earlier. The analytical solutions for the velocity and stress fields have been obtained by Lighthill’s method. The effects of permeability parameter K, Hartmann number M, frequency of fluctuation
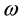 on the velocity field and skin friction have been illustrated graphically.
on the velocity field and skin friction have been illustrated graphically.
2. Mathematical Analysis of the Problem
Let us consider the flow of a second grade fluid of density ρ and viscosity µ through a porous medium of permeability K occupying a semi infinite region of the space bounded by a porous plate in presence of a transverse magnetic field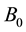 . At time
. At time
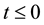 the fluid and the plate are at rest and at
the fluid and the plate are at rest and at
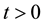 the fluid begins to move due
the fluid begins to move due
to a pressure gradient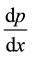 . Let u and v are the components of velocity in x and y directions taken along and
. Let u and v are the components of velocity in x and y directions taken along and
perpendicular to the porous plate. It is assumed that
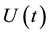 be the free stream velocity parallel to the plate which fluctuates in magnitude about a mean free stream velocity
be the free stream velocity parallel to the plate which fluctuates in magnitude about a mean free stream velocity
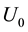 in the direction of x-axis. Since the plate be situated in the xz-plane and the plate is of infinite dimension in x and z direction, all the quantities are only functions of y and t.
in the direction of x-axis. Since the plate be situated in the xz-plane and the plate is of infinite dimension in x and z direction, all the quantities are only functions of y and t.
The equation of motion for the incompressible viscous generalized second grade fluid can be written as
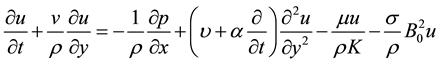 (1)
(1)
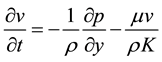 (2)
(2)
The equation of continuity
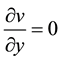 (3)
(3)
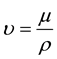 is the kinematic viscosity,
is the kinematic viscosity,
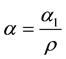 ,
,
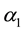 is normal stress moduli, ρ is the fluid density, µ is the viscosity of the fluid, K is the permeability of the porous medium,
is normal stress moduli, ρ is the fluid density, µ is the viscosity of the fluid, K is the permeability of the porous medium,
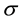 is the electrical conductivity.
is the electrical conductivity.
For free stream
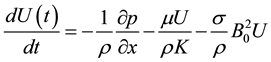 (4)
(4)
Let the fluctuating stream and suction velocities of the form


where





The boundary conditions can be written as:
No slip boundary condition
And

Eliminating


3. Method of Solution
Let us introduce the following non-dimensional quantities

where


The Equation (8) in terms of non-dimensional variables reduces to (Dropping


where
In non-dimensional variables Equation (5) and Equation (6) becomes

The boundary conditions (7) in non-dimensional variables can be written as

Let the velocity in the neighborhood of the plate be

Substituting for u and U from Equation (13) and Equation (11) respectively in Equation (10) and separating harmonic and non-harmonic terms and neglecting the squares of ε we obtain


subject to the boundary conditions

Using the boundary conditions the solution of Equation (14) and Equation (15) are given by respectively


where

Further
Therefore the velocity field u is given by

where
The non-dimensional form of the skin friction at the plate is given by

where
4. Results and Discussions
In the present study, the fluctuating flow of an unsteady incompressible fluid of second grade type through a porous medium occupying a semi-infinite region of the space bounded by a porous plate has been discussed. The analytical solution for the velocity field has been obtained by the method of Lighthill. The skin friction is also obtained at the plate



Graphical representations have been illustrated to see the effects of Hartmann number M, permeability parameter K and normal stress moduli α on the fluctuating parts






































Figure 1. The velocity is depicted against y for different values of magnetic field parameter M.
Figure 2. The velocity is depicted against y for different values of permeability parameter K.
Figure 3. The fluctuating part


Figure 4. Fluctuating part


Figure 5. Fluctuating part



Figure 6. Fluctuating part


Figure 7. The amplitude offluctuation



which the skin friction fluctuates at the plate is plotted against





Cite this paper
DhimanBose,UmaBasu, (2015) MHD Fluctuating Flow of Non-Newtonian Fluid through a Porous Medium Bounded by an Infinite Porous Plate. Applied Mathematics,06,1988-1995. doi: 10.4236/am.2015.612176
References
- 1. Soundalgekar, V.M. and Puri, P. (1969) On Fluctuating Flow of an Elastic-Viscous Fluid past an Infinite Plate with Variable Suction. Journal of Fluid Mechanics, 35, 561-573.
http://dx.doi.org/10.1017/S0022112069001297 - 2. Shen, F., Tan, W., Zhao, Y. and Masuoka, T. (2006) The Rayleigh-Stokes Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative Model. Nonlinear Analysis: Real World Applications, 7, 1072-1080.
http://dx.doi.org/10.1016/j.nonrwa.2005.09.007 - 3. Varshney, C.L. (1979) Fluctuating Flow of Viscous Fluid through a Porous Medium Bounded by a Porous Plate. Indian Journal of Pure and Applied Mathematics, 10, 1558-1564.
- 4. Lighthill, M.J. (1954) The Response of Laminar Skin Friction and Heat Transfer to Fluctuations in the Stream Velocity. Proceedings of the Royal Society A, 224, 1-23.
http://dx.doi.org/10.1098/rspa.1954.0137 - 5. Messiha, S.A.S. (1966) Laminar Boundary Layer in Oscillating Flow along an Infinite Flat Plate with Variable Suction. Proceedings of the Cambridge Philosophical Society, 62, 329-337.
http://dx.doi.org/10.1017/S030500410003989X - 6. Stuart, J.T. (1955) A Solution of the Navier-Stokes and Energy Equations Illustrating the Response of Skin Friction and Temperature of an Infinite Plate Thermometer to Fluctuations in the Stream Velocity. Proceedings of the Royal Society A, 231, 116-130.
http://dx.doi.org/10.1098/rspa.1955.0160 - 7. Gholizadeh, A. (1990) MHD Oscillatory Flow past a Vertical Porous Plate through Porous Medium in the Presence of Thermal and Mass Diffusion with Constant Heat Source. Astrophysics and Space Science, 174, 303-310.
http://dx.doi.org/10.1007/BF00642515 - 8. Moniem, A.A. and Hassanin, W.S. (2013) Solution of MHD Flow past a Vertical Porous Plate through a Porous Medium under Oscillatory Suction. Applied Mathematics, 4, 694-702.
http://dx.doi.org/10.4236/am.2013.44096 - 9. Venkateswarlu, M., Ramana Reddy, G.V. and Lakshmi, D.V. (2013) Unsteady MHD Flow of a Viscous Fluid past a Vertical Porous Plate under Oscillatory Suction Velocity. Advances in Applied Science Research, 4, 52-67.
- 10. Soundalgekar, V.M. and Takhar, H.S. (1977) MHD Oscillatory Flow past a Semi Infinite Plate. AIAA Journal, 15, 457-458.
http://dx.doi.org/10.2514/3.60646


















