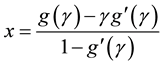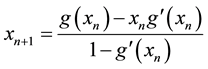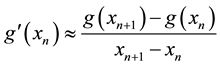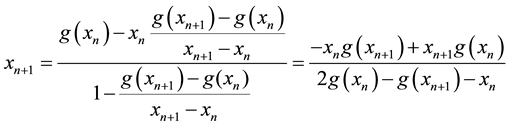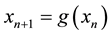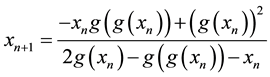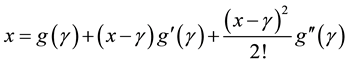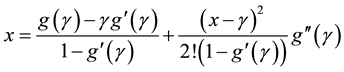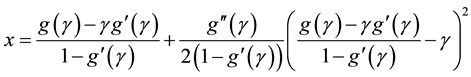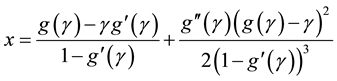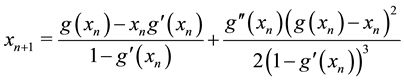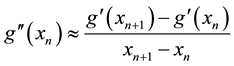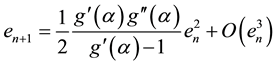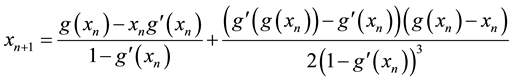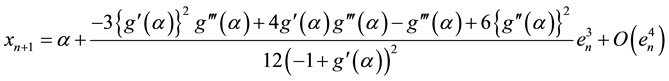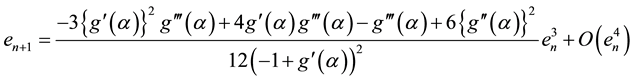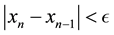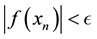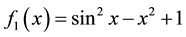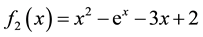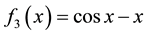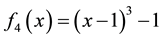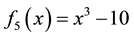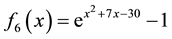Applied Mathematics
Vol.06 No.11(2015), Article ID:60493,6 pages
10.4236/am.2015.611163
New Modification of Fixed Point Iterative Method for Solving Nonlinear Equations
Muhammad Saqib1, Muhammad Iqbal2, Shahzad Ahmed2, Shahid Ali2, Tariq Ismaeel3
1Department of Mathematics, Govt. Degree College, Kharian, Pakistan
2Department of Mathematics, Lahore Leads University, Lahore, Pakistan
3Department of Mathematics, GC University, Lahore, Pakistan
Email: saqib270@yahoo.com, iqbal66dn@yahoo.com, proshahzad88@gmail.com, Shahidali.2029@gmail.com, Tariqismaeel@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 August 2015; accepted 19 October 2015; published 22 October 2015
ABSTRACT
In this paper, we have modified fixed point method and have established two new iterative methods of order two and three. We have discussed their convergence analysis and comparison with some other existing iterative methods for solving nonlinear equations.
Keywords:
Modifications, Fixed Point Method, Nonlinear Equations

1. Introduction
In recent much attention has been given to establish new higher order iteration schemes for solving nonlinear equations. Many iteration schemes have been established by using Taylor series, Adomain decomposition, Homotopy pertrubation technique and other decomposition techniques [1] -[6] . We shall modify the fixed point method using taylor series on the functional equation
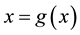 of nonlinear equation
of nonlinear equation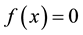 . Initially, we do not put any restrictions on the original function f. In fixed point method, we rewrite
. Initially, we do not put any restrictions on the original function f. In fixed point method, we rewrite
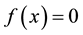 as
as
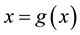 where
where
1) There exist
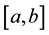 such that
such that
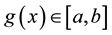 for all
for all
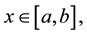
2) There exist
 such that
such that
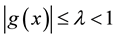 for all
for all
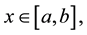
The order of convergence of a sequence of approximation is defined as:
Definition 1.1 [7] Let the sequence
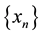 converges to
converges to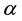 . If there is a positive integer p and real number C such that
. If there is a positive integer p and real number C such that
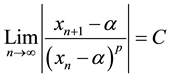
then p is order of convergence.
Theorem 1.2 (see [6] ). Suppose that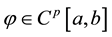 . If
. If , for
, for
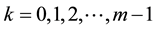 and
and
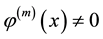
2. New Iteration Scheme
Consider the nonlinear equation
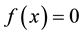
we can rewrite the above equation as
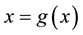
We suppose that
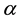
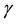
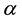
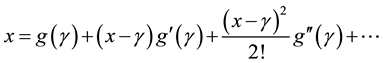
if we truncate Equation (2.3) after second term then, we obtained
From above formulation we suggest the following algorithm for solving nonlinear Equation (2.1).
In algorithem form, we can write
we approximate
Thus
if we take
then we have the following algorithem;
Algorithm 2.1 For a given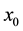
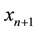
If we truncate Equation (2.3) after third term then we have
In algorithem form, we can write
we approximate
By substituting in above, we have
Thus, we have the following algorithem;
Algorithm 2.2 For a given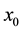
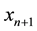
3. Convegence Analysis
In this section, we discuss the convergence of Algorithm (2.1) and (2.2).
Theorem 3.1 Let
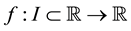
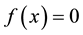
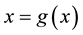
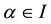
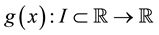
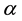
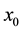
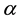
Proof. Let
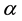
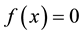
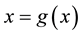
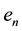
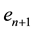
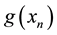
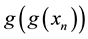
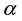
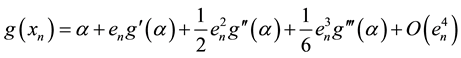
and
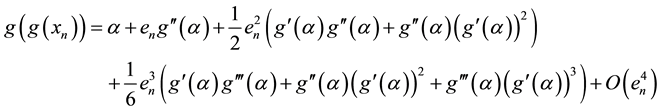
Algorithem (2.1) is given by
By substituting values from Equations (3.1) and (3.2) in above, we get
Hence algorithem (2.1) has second order convergence.
Theorem 3.2 Let
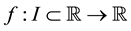
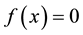
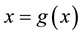
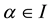
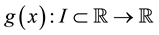
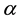
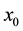
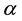
Proof. Let
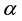
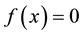
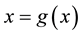
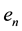
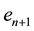
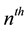
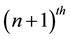
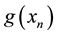
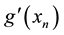
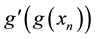
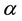
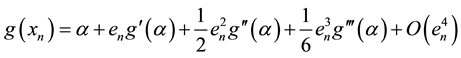
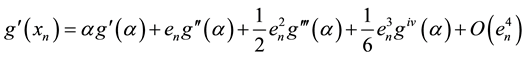
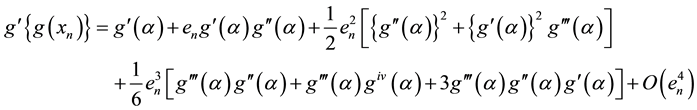
Algorithem (2.2) is given by
By substituting values from Equations (3.3), (3.4) and (3.5) in above, we get
Hence the order of convergence fo algorithm 2.2 is least 3.
4. Numerical Results
In this section, we present some example to make the comparitive study of fixed point method (FPM), Newton method (NM), Abbasbandy method (AM), Homeier method (HM), Chun method (CM), Householder method (HHM), Algorithem 2.1 and Algorithm 2.2 developed in this paper. We use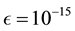
1)
2)
We consider the following examples to illustarate the performance of our newly established iteration scheme.
Comparison Table
5. Conclusion
We have modified the fixed point method for solving nonlinear equations. We have established two new algorithems of convergence order two and three. We have solved some nonlinear equations to show the performance and efficiency of our newly developed iteration schemes. From comparison table, we conclude that these schemes perform much better than Newton method, Abbasbandy method, Chun method, Homeier method, Householder method etc.
Cite this paper
MuhammadSaqib,MuhammadIqbal,ShahzadAhmed,ShahidAli,TariqIsmaeel, (2015) New Modification of Fixed Point Iterative Method for Solving Nonlinear Equations. Applied Mathematics,06,1857-1863. doi: 10.4236/am.2015.611163
References
- 1. Abbasbandy, S. (2003) Improving Newton-Raphson Method for Nonlinear Equations by Modified Adomain Decomposition Method. Applied Mathematics and Computation, 145, 887-893.
http://dx.doi.org/10.1016/S0096-3003(03)00282-0 - 2. Adomain, G. (1989) Nonlinear Atochastic Systems and Applications to Physics. Kluwer Academy Publishers, Dordrecht.
http://dx.doi.org/10.1007/978-94-009-2569-4 - 3. Chun, C. (2005) Iterative Methods Improving Newton’s Method by Decomposition Method. Applied Mathematics and Computation, 50, 1595-1568.
http://dx.doi.org/10.1016/j.camwa.2005.08.022 - 4. Noor, M.A. and Inayat, K. (2006) Three-Step Iterative Methods for Nonlinear Equations. Applied Mathematics and Computation, 183, 322-327.
- 5. Noor, M.A., Inayat, K. and Tauseef, M.D. (2006) An Iterative Method with Cubic Convergence for Nonlinear Equations. Applied Mathematics and Computation, 183, 1249-1255.
http://dx.doi.org/10.1016/j.amc.2006.05.133 - 6. Babolian, E. and Biazar, J. (2002) On the Order of Convergence of Adomain Method. Applied Mathematics and Computation, 130, 383-387.
http://dx.doi.org/10.1016/S0096-3003(01)00103-5 - 7. Kang, S.M., et al. (2013) A New Second Order Iteration Method for Solving Nonlinear Equations. Handawi Publishing Company, Abstract and Applied Analysis, 2013, Article ID: 487062.