Applied Mathematics
Vol.06 No.08(2015), Article ID:57798,7 pages
10.4236/am.2015.68111
Entropy Change of Lungs: Determinant of the Static Properties of the Lungs
Kyongyob Min
Respiratory Division, Department of Internal Medicine, Itami City Hospital, Itami, Japan
Email: in1007@poh.osaka-med.ac.jp
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 June 2015; accepted 5 July 2015; published 8 July 2015
ABSTRACT
The static properties of the lungs have been explained by energy-change considerations on the elasticity, but this article explains the elasticity of the lungs by entropy-change considerations. Entropy of the individual lobule was defined by application of stochastic geometry on aggregated alveolar polyhedrons. Entropy of the lungs is the result of integrating a number of lobular entropies through the fractal bronchial tree. Entropy of the lungs was thus determined by the individual lobular entropy and the connectivity of the bronchial tree to the lobular bronchioles. Thermodynamic considerations on the static conditions of the pulmonary system composed of the lungs and the chest wall have provided a theoretical approach to understand the subdivisions of lung volume as the entropy-change of lungs. Entropy-change considerations on the elasticity of the lungs have shown that alveolar collapse and subsequent alveolar induration as the primary pathway for the loss of elasticity in the lungs is an acceptable hypothesis.
Keywords:
Energy Elasticity, Entropy-Change Considerations, Elastic Properties of Lungs, Thermodynamics

1. Introduction
From a physical viewpoint, the lung can be described as an elastic body. Elasticity is the property of matter that causes matter to return to its resting size after prior stretching by an external force. Classic physiology has explained that this elastic property originates from the basic components of the lung skeleton: 1) a continuous network of elastic fibers that connects arteries, airways, and interstitial space, and 2) the surface force generated at the surface between the air and the alveolar lining layer of surfactant. The elastic properties of the interwoven network are formed by elastin and collagen fibers within the lungs like a nylon stocking [1] . Recent computational studies have tried to explain the pathogenesis of idiopathic pulmonary fibrosis (IPF) and emphysema as a transitional shift of the interwoven network from elastin to collagen in stochastic and/or percolated fashions [2] . The basic concept for understanding the elasticity of the lung described above is based on the energy-change consideration. However, the recent pathological and physiological study of Lutz et al. has showed that alveolar collapse and collapse induration (irreversible collapse) without deposits of collagen fibers lead to significant degradation of lung function [3] . Lutz et al. have suggested that surfactant inactivation leading to alveolar collapse and subsequent collapse induration might be the primary pathway for loss of lung function in human IPF. This observation cannot be explained by the energy change consideration because there is no change in the components of the elastic network of the lung skeleton.
Stretching a rubber band or elastic polymers (elastomers) causes a rubber band to release heat, and releasing the band after being stretched causes a cooler temperature. Temperature affects the elasticity of rubber such that healing causes contraction and cooling can cause expansion. The rubber behaves somewhat like an ideal monoatomic gas, in as much as elastic polymers in the rubber do not store any potential energy in stretched chemical bands or elastic work done in stretching molecules, when work is done upon them. All work done on the rubber is “released” and appears immediately in the polymer as thermal energy [4] . This is an important clue that the elastic ability of the lung to work depends on entropy-change considerations. The author of this paper provides a proposal to explain that the elastic property of the lung as the entropy-change of alveoli in the pulmonary parenchyma integrated into the whole lung through lobular structures with a fractal bronchial tree and that the entropy of the lung would determine the subdivisions of lung volume as the thermal equilibrium as well.
2. Origami-Model of Alveoli and Gibbs Free Energy
High-resolution computer-assisted tomography (HRCT) images have shown that Miller’s secondary lobule is the important structure for integrating pulmonary parenchyma into the lung through the bronchial tree [5] . The alveoli and small airways in the secondary lobule are closely anatomically interrelated and functionally undiscriminated. Intra-lobular arterioles and capillaries are also constructed in the lobular vascular network including alveolar walls as a united polyhedron body. In the pulmonary parenchyma in vivo, both air and blood flows in the lobule cause dynamic changes in the position of the walls of the alveoli due to the physiological function of the surfactant molecules.
Kitaoka proposed an origami model for explaining change in alveolar volume concerning the functional structure of the pulmonary parenchyma (Figure 1) [6] , which is an appropriate model to introduce entropy change considerations of lung volume. When alveoli in a secondary lobule j are observed, the angles between the adjacent walls of alveoli can be measured by probability density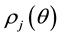 , where
, where 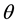 is radian between zero and
is radian between zero and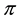 . The probability density of
. The probability density of 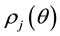 is a quantitative expression for the degree of inflation in lobule j. Each
is a quantitative expression for the degree of inflation in lobule j. Each  would be different each time of observation because each wall of alveoli in vivo continuously changes in the angle.
would be different each time of observation because each wall of alveoli in vivo continuously changes in the angle.
According to statistical mechanics, [7] probability density 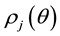 in lobule j is assumed to be expressed as follows,
in lobule j is assumed to be expressed as follows,
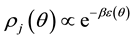 (1.1a)
(1.1a)
 (1.1b)
(1.1b)
where 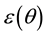 is a surface energy for holding angle
is a surface energy for holding angle 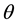 between adjacent walls of alveolar polyhedron, and
between adjacent walls of alveolar polyhedron, and  is a common parameter to define the state of field among lobules in the lung system, from which we can introduce a new state parameter temperature T by
is a common parameter to define the state of field among lobules in the lung system, from which we can introduce a new state parameter temperature T by . Then, total surface energy
. Then, total surface energy 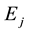 in lobule j is obtained as follows,
in lobule j is obtained as follows,
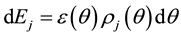 (1.2)
(1.2)
It is also possible to introduce a state function of entropy 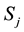 for lobule j as a logarithmic function as follows,
for lobule j as a logarithmic function as follows,
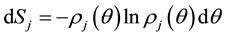 (1.3)
(1.3)
A Gibbs free energy for lobule j 



Figure 1. Origami models for pulmonary parenchyma from Kitaoka, H. (from reference [6] ). (a) Origami model for alveolar polyhedron. Note that the volume of alveolus is changing dependent on changes in angles of adjacent walls; (b) Origami models for alveolar duct.
3. Chest Wall and Gibbs Free Energy
Rohrer proposed that movement of the respiratory system is caused by pressure differences across the system to overcome the elastic resistance to volume change [8] . When the pulmonary system is under conditions in which there is a constant volume, only elastic forces are evident. In one of the first experimental descriptions of the static properties of the pulmonary system, normal subjects were asked to inspire a volume of air from a spirometer and then to relax for a few seconds against an occluded airway with the glottis open. This was repeated at various lung volumes. The pressure at the mouth was measured together with the lung volume and recorded as a P-V curve. Rahn’s diagram displayed the static P-V curves of the pulmonary system, lungs, and chest wall in normal human subjects, and revealed the volume of the pulmonary system where mouth pressure = 0 is the functional reserve volume (FRC) [9] . Several years after the publication of Rahn’s diagram, the esophageal balloon technique for measuring transpulmonary pressure 


Agostoni and Rahn were the first to measure transdiaphragmatic pressure as the difference between gastric and esophageal pressures [11] . This allowed direct determination of the pressures developed by the diaphragm either due to its active contraction or to passive stretching. By measuring gastric and esophageal pressures as an index of pleural pressure, Agostoni and Rahn accomplished the pressure partitioning necessary to determine the pressure displacing the abdomen and that acting on the inner surface of the chest wall. When the entropy of chest wall is thus designated by 
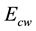


4. Thermodynamic Laws for the Pulmonary System in Vivo
According to the first law of thermodynamics [7] , the law of conservation of energy at lobule j is stated in the following equation,

where 

By combining (1.4) and (3.1), the following equation is obtained as,

The law of conservation of energy for the chest wall is also expressed by the following equation,

where 
Thus, by combining (2.1) and (3.3), the following equation is also obtained as,

At any time the pulmonary system should be in mechanical equilibrium among the components of the pulmonary system, the lung and the chest wall. Thus, the equation of equilibrium is as follows,

where N is the number of lobules in the whole lung. Divided by a time differential of dt, (3.5) is transformed to the following equation,

Miller’s [12] anatomical study has shown that each lobule has a corresponding single bronchiole and single arteriole (Figure 2). There is an important relation between lobular volume 


Thus, by combination (3.6) and (3.7) the pulmonary system obeys the relationship as follows,

5. Entropy-Change Considerations on Static Properties of the Pulmonary System
Lung volumes and lung capacities in vivo refer to the volume of air associated with different phases of the resting respiratory cycle. Subdivisions of the lung volume are easily seen through the motion trajectories in the flow-volume plane using a spirometry (Figure 3): tidal volume (TV), vital capacity (VC), total lung capacity (TLC), reserve volume (RV), functional reserve capacity (FRC), expiratory reserve volume (ERV), and inspiratory capacity (IC). When the lung volume changes along with the thoracic volume, subdivisions of the lung volume are determined as the static condition of the chest wall, that is, 

where 

Figure 2. A secondary lobule with a single corresponding bronchiole and arteriole. Left: a cast model of the secondary lobule from a human lung by Pump (1964), Right: a drawing of the secondary lobule by Miller (1961).
Figure 3. Subdivisions of the pulmonary system in vivo Flow-volume trajectories of spontaneous breathing and a forced expiratory flow-volume curve of a patient with mild COPD. Note that the symbols are TV = tidal volume, VC = vital capacity, TLC = total lung capacity, RV = reserve volume, FRC = functional reserve capacity, ERV = expiratory reserve volume, and IC = inspiratory capacity, respectively. Symbols SFRC, STLC, and SRV are the entropy of the lung at FRC, TLC, and RV, respectively.


where M is the number of lobules connecting to the bronchial tree, and N or less. Thus, the static properties of lung system 


6. Discussion
6.1. Entropy-Change Considerations on Lung Elasticity
Elasticity is the tendency of solid materials to return to their original shape after being deformed. In metals or other usual materials, the atomic lattice of a usual material changes size and shape when external forces are applied or when energy is added to the material. When the forces are removed, the lattice returns to the original lower energy state. This is called the energy-change consideration of elasticity. Bates et al. have proposed a network model of springs representing the lung parenchyma, which behaves as the system of energy-change elasticity [2] . Their primary study protocol is that starting from some initial configuration of the network, and the total energy is calculated by minimizing the elastic energy of the springs array, which is a numerical technique mimicking the gradual cooling of atoms in metal or glass. Bates et al. were able to simulate configurations of pulmonary fibrosis and emphysema, which are often seen in pathological pictures of pulmonary fibrosis and emphysema in humans. However, Lutz and colleagues have recently reported that idiopathic pulmonary fibrosis (IPF) and bleomycin-induced pulmonary fibrosis are associated with surfactant system dysfunction, alveolar collapse and irreversible collapse (induration) without deposits of collagen at the early phase [3] . Their experimental study has suggested that alveolar collapse and subsequent alveolar induration might be the primary pathway for the loss of elasticity of the lung in vivo. The energy-change considerations for elasticity cannot explain this phenomenon because of no change in energy of each spring in the network.
An entropic force acting in a system is a phenomenological force resulting from the entire system’s statistical tendency to increase its entropy, rather than from a particular underlying microscopic force [4] . A standard example of the entropic force is the elasticity of rubber bands. Rubber bands are made from polymers, but the chains are crosslinked to provide a network. When the network is stretched, entropic forces come into play to return the network to its original unstretched state. Loss of entropy upon stretching means that there is a retractive force for recovery when the external stress is removed. For entropy-change considerations on the elasticity of the pulmonary parenchyma, the author took the origami model of alveoli proposed by Kitaoka for describing the pulmonary parenchyma [6] . The origami model of alveoli has showed that the volume of alveoli is determined by angle 





6.2. Temperature
In any thermodynamic consideration on a system [4] , the most important variable is temperature, which is usually measured by a thermometer. However, temperature parameter T introduced in this paper is not this usual temperature measured physically but is defined mathematically by the statistical parameter in (1.1a). The question is how parameter T can be understood physiologically in the pulmonary system. From (3.11), parameter T is defined as the ratio of the surface energy change to the entropy change in the pulmonary system. In the lung in vivo, each alveolar wall would always be changing its angle due to the impact caused by both air and blood flows. All microscopic motions of the alveolar walls would be accumulated and normalized to an average value across the whole lung. This is the physiological understanding of T.
6.3. Determinant of the Subdivisions of the Lung Volume
From the study of Rahn, FRC is well known as the resting state of the pulmonary elasticity in vivo. At the resting state of FRC, the alveolar pressure is zero, and entropy 



6.4. Statistical Consideration on Alveolar Collapse
We have introduced surface energy 






Z is maximized at the proportion of collapsed and non-collapsed alveoli as follows,

Thus, when 
This is explained by the relation between the energy-change 


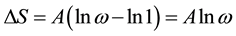

(4.3) explains that alveolar collapse would be caused by a struggle between surface energy-change and entropy-change.
6.5. The Entropy-Change Considerations on IPF
Pulmonary parenchyma is made from alveolar polyhedrons packed densely, among which are crosslinks. In general the number of crosslinks in the elastomers determines the entropic elasticity [4] . Alveolar collapse would behave to increase the number of crosslinks in the parenchyma, and as a result the parenchyma with numerous collapsed alveoli would become stiffer. This is a rational explanation for changes in elasticity of IPF or bleomycin-induced fibrosis at early phase of onset.
This study has also revealed that the entropy change of lungs is caused by change in the connectivity of the bronchial tree to the lobular bronchioles. In subdivisions of lung volume, the expiratory reserve volume (ERV) would correspond to the process in which all lobular bronchioles enter a completely closed state from an open one. Forced vital capacity (FVC) has been adopted as the major clinical indicator for evaluating the severity of IPF in all clinical studies. However, this study of entropy change by alveolar collapse and induration has suggested that the subdivision of IC (=the volume between FRC and TLC) would be a more appropriate indicator, because that FVC includes ERV. It is necessary to evaluate IC in place of FVC as the clinical indicator of severity in IPF.
6.6. The Entropy-Change Considerations on COPD
Entropy-change considerations are also applicable to understand the pathophysiology of chronic obstructive pulmonary disease (COPD). Since emphysematous COPD lungs are characterized by the disappearance of alveolar walls resulting in the decrease in the number of crosslinks among alveolar polyhedrons, COPD lungs would become more compliant based on the entropy change of pulmonary parenchyma.
Dynamic hyperinflation is one of the clinically important patho-physiological conditions to be explained in COPD during exercise or on artificial ventilation. The lung at the end-expiratory lung volume (EELV) should obey (3.9) from the entropy change considerations. When some clusters including lobular flows without connection to the bronchial tree emerge by functional airway obstruction, the clusters of lobules obeying the relation of 
References
- Grassino, A.E. and Roussos, C. (1997) Static Properties of the Lung and Chest Wall. In: Crystal, R.G. and West, J.B., et al., The Lung: Scientific Foundations, 2nd Edition, Lippincott-Raven Publishers, Philadelphia, 1187-1201.
- Bates, J.H., Davis, G.S., Majumdar, A., Butnor, K.J. and Suki, B. (2007) Linking Parenchymal Disease Progression to Changes in Lung Mechanical Function by Percolation. American Journal of Respiratory and Critical Care Medicine, 176, 617-623. http://dx.doi.org/10.1164/rccm.200611-1739OC
- Lutz, D., Gazdhar, A., Lopez-Rodriguez, E., Ruppert, C., Mahavadi, P., Günther, A., Klepetko, W., Bates, J.H., Smith, B., Geiser, T., Ochs, M. and Knudsen, L. (2015) Alveolar Derecruitment and Collapse Induration as Crucial Mechanisms in Lung Injury and Fibrosis. American Journal of Respiratory Cell and Molecular Biology, 52, 232-243. http://dx.doi.org/10.1165/rcmb.2014-0078OC
- Kubo, R. (1996) Gum Elasticity. Shyo-Ka-Boh, Tokyo, 36-42. (In Japanese)
- Min, K., Hosoi, K., Kinoshita, Y., Hara, S., Degami, H., Takada, T. and Nakamura, T. (2012) Use of Fractal Geometry to Propose a New Mechanism of Airway-Parenchymal Interdependence. Open Journal of Molecular and Integrative Physiology, 2, 14-20. http://dx.doi.org/10.4236/ojmip.2012.21003
- Kitaoka, H. (2013) Let’s Make Origami Models, in Welcome to 4D Respirology. http://www7b.biglobe.ne.jp/~lung4cer/indexEng.html
- Uffink, J. (2006) Compendium of the Foundations of Classical Statistical Physics. http://philsci-archive.pitt.edu/2691/1/UffinkFinal.pdf
- Rohrer, F. (1916) Der Zusammenhang der Atemkräfte und ihre Abhängigkeit vom Dehnungszustand der Atmungsorgane. Archiv für die gesamte Physiologie des Menchen und der Tiere, 165, 419-444. http://dx.doi.org/10.1007/BF01681079
- Agostoni, E. and Mead, J. (1964) Statics of the Respiratory System. In: Fenn, W.O. and Rahn, H., Eds., Handbook of Physiology Respiration, Sec. 3, Vol. 1, American Physiological Society, Washington DC, 387-409.
- Campbell, E.J.M. (1958) The Respiratory Muscles and the Mechanics of Breathing. Year Book Publishers, Chicago.
- Agostoni, E. and Rahn, H. (1960) Abdominal and Thoracic Pressures at Different Lung Volumes. Journal of Applied Physiology, 15, 1087-1092.
- Miller, W.S. (1950) The Lung. 2nd Edition, Charles C Thomas Publishers, Springfield.





