Applied Mathematics
Vol.06 No.03(2015), Article ID:54506,7 pages
10.4236/am.2015.63045
A Special Case on the Stability and Accuracy for the 1D Heat Equation Using 3-Level and  -Schemes
-Schemes
Pedro Pablo Cárdenas Alzate1, José Gerardo Cardona1, Luz María Rojas2
1Department of Mathematics, Universidad Tecnológica de Pereira, Pereira, Colombia
2Fundación Universitaria del Area Andina, Pereira, Colombia
Email: ppablo@utp.edu.co, gerardo7@utp.edu.co, lmrojas@funandi.edu.co
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 15 February 2015; accepted 5 March 2015; published 10 March 2015

ABSTRACT
We establish the conditions for the compute of the stability restriction and local accuracy on the time step and we prove the consistency and local truncation error by using 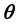 -scheme and 3-level scheme for Heat Equation with smooth initial conditions and for some parameter
-scheme and 3-level scheme for Heat Equation with smooth initial conditions and for some parameter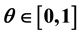 .
.
Keywords:
Global Truncation, Local Accuracy, Stability Restriction

1. Introduction
In this paper we have considered the heat equation 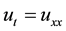 with
with . Using
. Using 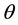 -scheme and 3-level scheme in space we compute the order of local accuracy in space and time and stability restriction as a function of
-scheme and 3-level scheme in space we compute the order of local accuracy in space and time and stability restriction as a function of 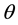 on the time step
on the time step . Much attention has been paid to the development, analysis and implementation of accurate methods for the numerical solution of this problem in the literature. Many problems are modeled by smooth initial conditions and Dirichlet boundary conditions. A number of procedures have been suggested (see, for instance [1] - [3] ). We can say that three classes of solution techniques have emerged for solution of PDE: the finite difference techniques, the finite element methods and the spectral techniques (see [4] and [5] ). The last one has the advantage of high accuracy attained by the resulting discretization for a given number of nodes [6] - [8] .
. Much attention has been paid to the development, analysis and implementation of accurate methods for the numerical solution of this problem in the literature. Many problems are modeled by smooth initial conditions and Dirichlet boundary conditions. A number of procedures have been suggested (see, for instance [1] - [3] ). We can say that three classes of solution techniques have emerged for solution of PDE: the finite difference techniques, the finite element methods and the spectral techniques (see [4] and [5] ). The last one has the advantage of high accuracy attained by the resulting discretization for a given number of nodes [6] - [8] .
We consider Scheme (1) for the 1D heat equation for some parameter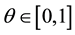 . We compute the order of local accuracy in space and time as a function of
. We compute the order of local accuracy in space and time as a function of 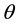 and its the stability restriction. Until
and its the stability restriction. Until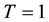 , we compute the solution with some fixed
, we compute the solution with some fixed 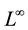 error with the smallest amount of CPU time, and finally we can see this findings producing the relevant convergence and efficiency plot. For the 3-level scheme we consider (11) for the 1D heat equation and we compute the local truncation error. For different values of
error with the smallest amount of CPU time, and finally we can see this findings producing the relevant convergence and efficiency plot. For the 3-level scheme we consider (11) for the 1D heat equation and we compute the local truncation error. For different values of  and
and  we find the stability criterion of the scheme and its accuracy.
we find the stability criterion of the scheme and its accuracy.
2.  -Scheme
-Scheme
Let
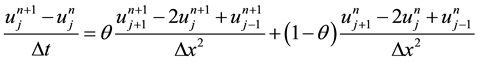 (1)
(1)
be the 

Now for the order of local accuracy in space and time as a function of 
where 


We can write the LHS of (1) as


here 


As we are solving the heat equation, the previous expression is

Now, at time 


therefore, applying Taylor expansion with respect to 
So (8) becomes

Here RHS of (1) becomes
After the elimination of some terms we have
Now simplifying we obtain
Cancelling 

Scheme (10) is first order in time, second order in space. If for example

Stability Restriction as a Function of
Here we will apply Von Neumann stability. Let 

Now dividing by 
Therefore by using 

By using the identity 
We can say this scheme is stable only for

thus
Now multiplying by the denominator we have
The expression in the absolute value becomes
Therefore by the Von Neumann stability condition, the scheme is stable if
In this case we can say the following about the best combination for 






In Figure 1 the convergence plot equation (varying the radio r) is
with matrix A described in the heat equation. We can say the scheme is unconditionally stable. We can see in Figure 1 that we have a linear convergence with respect to r.
3. Three-Level Scheme
We start by computing the stability restriction one has to impose on
Let

where
Figure 1. E vs. r for 1D-heat equation, 



and

By using (12) and (13) we can rewrite (11) as

or as
The local truncation error for this scheme 
where 

Now expanding 

however,
Expanded this expression becomes
Finally we have
4. Stability Criterion for the Three-Level Scheme and Its Accuracy When 
By using Equation (14) we have
Now applying Von Neumann stability again, the aim is to use 

Multiplying both sides by 

Using the cosine identity that 
We have a quadratic equation in

After some cancellations, we can write
Here, if all 
Acknowledgements
We would like to thank the referee for his valuable suggestions that improved the presentation of this paper.
References
- Strikwerda, J.C. (1989) Finite Difference Schemes and Partial Differential Equations. Wadsworth & Brooks, Siam, Madison, Wisconsin.
- McRea, G.J. and Godin, W.R. (1967) Numerical Solution of Atmospheric Diffusion for Chemically Reacting Flows. Journal of Computational Physics, 77, 1-42.
- Cárdenas Alzate, P.P. (2014) A Survey of the Implementation of Numerical Schemes for Linear Advection Equation. Advances in Pure Mathematics, 4, 467-479. http://dx.doi.org/10.4236/apm.2014.48052
- Cárdenas Alzate, P.P. (2014) A Survey of the Implementation of Numerical Schemes for the Heat Equation Using for- ward Euler in Time. Journal of Applied Mathematics and Physics, 2, 1153-1158. http://dx.doi.org/10.4236/jamp.2014.213135
- Hundsdorfer, W. and Koren, B. (1995) A Positive Finite-Difference Advection Scheme Applied on Locally Refined Grids. Journal of Computational Physics, 117, 35-36. http://dx.doi.org/10.1006/jcph.1995.1042
- Canuto, C. and Hussaini, M. (1988) Spectral Methods in Fluids Dynamics. Springer Series in Computational Physics, Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-84108-8
- Dehghan, M. (2007) The One-Dimensional Heat Equation Subject to a Boundary Integral Specification. Chaos, Solitons & Fractals, 32, 661-675. http://dx.doi.org/10.1155/MPE.2005.61
- Lu, X., et al. (2005) A New Analytical Method to Solve the Heat Equation for a Multi-Dimensional Composite Slab. Journal of Physics, 38, 2873.










































