Applied Mathematics
Vol.06 No.02(2015), Article ID:53791,22 pages
10.4236/am.2015.62024
U-Type Designs via New Generalized Partially Balanced Incomplete Block Designs with m = 4, 5 and 7 Associated Classes
Imane Rezgui1, Zebida Gheribi-Aoulmi1, Hervé Monod2
1Department of Mathematics, University of Constantine 1, Constantine, Algeria
2INRA, UR MaIAGE, Jouy-en-Josas, Paris, France
Email: rezgui_imane@yahoo.fr, gheribiz@yahoo.fr, herve.monod@jouy.inra.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 January 2015; accepted 28 January 2015; published 4 February 2015
ABSTRACT
The traditional combinatorial designs can be used as basic designs for constructing designs of computer experiments which have been used successfully till now in various domains such as engineering, pharmaceutical industry, etc. In this paper, a new series of generalized partially balanced incomplete blocks PBIB designs with m associated classes (m = 4, 5 and 7) based on new generalized association schemes with number of treatments v arranged in w arrays of n rows and l columns (w ≥ 2, n ≥ 2, l ≥ 2) is defined. Some construction methods of these new PBIB are given and their parameters are specified using the Combinatory Method (s). For n or l even and s divisor of n or l, the obtained PBIB designs are resolvable PBIB designs. So the Fang RBIBD method is applied to obtain a series of particular U-type designs U (wnl;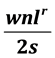 ) (r is the repetition number of each treatment in our resolvable PBIB design).
) (r is the repetition number of each treatment in our resolvable PBIB design).
Keywords:
Association Scheme, Combinatory Method (s), Resolvable Partially Balanced Incomplete Block Design, U-Type Design

1. Introduction
Designs of computer experiments drew a wide attention in the previous two decades and were still being used successfully till now in various domains. Among the various construction methods of these designs, the traditional combinatorial designs can be used as basic designs (example: [1] [2] ) and particularly the PBIB designs. The association schemes of two or three associated classes have been widely studied, while it is not the case of those over three associated classes. However, some association schemes with five associated classes have been studied (example: [3] ). Besides, a method to obtain new association schemes by crossing or nesting other association schemes was given by Bailey [4] using the character tables and strata of the initial association schemes to find the parameters of the obtained association schemes.
In this paper, new association schemes with 4, 5 and 7 associated classes are described starting by a geometric representation. The parameter expressions of these association schemes are given. Moreover, some methods to construct the PBIB designs based on these association schemes are explained using an accessible construction method called the Combinatory Method (s) [5] , which allows obtaining a series of PBIB designs by only using these association schemes. The parameters expressions of these new designs are given. In addition, for n or l even
and s divisor of n or l, the obtained PBIB are resolvable PBIB. Then, a series of U-type designs U
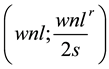
(r is the repetition number of each treatment in the resolvable PBIB design) is obtained by applying the RBIBD method [6] on these designs.
The paper is organized as follows. In Section 2, we give new definitions of generalized association schemes with m (= 4, 5 and 7) associated classes, starting by geometric representation and we give their parameters as properties. Section 3 describes a series of construction method using the Combinatory Method (s) for obtaining the PBIB designs associated to our generalized association schemes. We give the series of the U-type designs associated to our constructed PBIB designs in Section 4. We achieve our paper with a Conclusion.
Recall some definitions:
Definition 1. An m-association scheme (m ≥ 2) of v treatments [7] is a relation satisfying the following conditions:
1) Any two treatments are either 1st, 2nd, ∙∙∙, or mth associates. The relation of association is symmetric, i.e., if the treatment
 is an ith associate of β, then β is an ith associate of
is an ith associate of β, then β is an ith associate of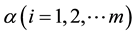 .
.
2) Each treatment
 has ni ith associates, the number ni being independent of
has ni ith associates, the number ni being independent of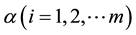 .
.
3) If any two treatments
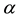 and β are ith associates, then the number of treatments that are jth associates of
and β are ith associates, then the number of treatments that are jth associates of
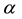 and kth associates of β is
and kth associates of β is
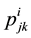 and is independent of the pair of ith associates
and is independent of the pair of ith associates
 and β
and β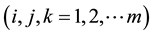 .
.
The numbers v, ni
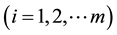 and
and
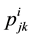
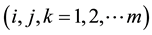 are called the parameters of the association scheme.
are called the parameters of the association scheme.
Definition 2. A PBIB design [7] , based on an m-association scheme (m ≥ 2), with parameters v, b, r, k, λi,
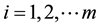 , is a block design with v treatments and b blocks of size k each such that every treatment occurs in
, is a block design with v treatments and b blocks of size k each such that every treatment occurs in
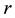 blocks and any two distinct treatments being ith associate occur together in exactly λi blocks. The number λi is independent of the pair of ith associates
blocks and any two distinct treatments being ith associate occur together in exactly λi blocks. The number λi is independent of the pair of ith associates
A parallel class of PBIB is a collection of disjoint blocks from the b blocks whose union is V. A partition of the b blocks into

The Combinatory Method (s) [5] :
Let an array of n rows and l columns as follows:
Consider s different elements of the same row i




Definition 3. Let U








2. Generalized Rectangular Right Angular Association Schemes (m) (m = 4, 5 and 7 Associated Classes)
2.1. Generalized Rectangular Right Angular Association Scheme (4)
Let V be a set of v = wnl treatments, (w ≥ 2, n ≥ 2, l ≥ 2), to which we associate a geometrical representation in the following way:
Each treatment of V is associated with a unique triplet of the set

Let

・

・


・


・


This geometric representation describes a new association scheme, we call it for convenience, generalized rectangular right angular association scheme (4) with four associated classes, to which we give the following equivalent definition:
Definition 4. A generalized rectangular right angular association scheme (4) is an arrangement of v = wnl (w ≥ 2, n ≥ 2, l ≥ 2) treatments in w arrays of n rows and l columns such that, with respect to each treatment
1) The first associates of

2) The second associates of

3) The third associates of

4) The fourth associates of

Property 1. The parameters of generalized rectangular right angular association schemes (4) are:





Definition 5. A PBIB design based on a generalized rectangular right angular association scheme (4) is called generalized rectangular right angular GPBIB4 design.
2.2. Generalized Rectangular Right Angular Association Scheme (5)
Let V be a set of v = wnl treatments, (w ≥ 2, n ≥ 2, l ≥ 2), to which we associate a geometrical representation in the following way:
Each treatment of V is associated with a unique triplet (of coordinates) of the set

Let

・

・


・


・


・


This geometric representation describes a new association scheme, we call it for convenience, generalized rectangular right angular association scheme (5) with five associated classes, to which we give the following equivalent definition:
Definition 6. A generalized rectangular right angular association scheme (5) is an arrangement of v = wnl (w ≥ 2, n ≥ 2, l ≥ 2) treatments in w (n × l) rectangular arrays such that, with respect to each treatment
1) The first associates of

2) The second associates of

3) The third associates of

4) The fourth associates of


5) The fifth associates of

Property 2. The parameters of the generalized rectangular right angular association schemes (5) are:






Definition 7. A PBIB design based on a generalized rectangular right angular association scheme (5) is called generalized rectangular right angular GPBIB5 design.
2.3. Generalized Rectangular Right Angular Association Scheme (7)
Let V be a set of v = wnl treatments, (w ≥ 2, n ≥ 2, l ≥ 2), to which we associate a geometrical representation in the following way:
Each treatment of V is associated with a unique triplet of the set

Let

・

・


・


・


・


・


・


This geometric representation describes a new association scheme, we call it for convenience, generalized rectangular right angular association scheme (7) with seven associated classes, to which we give the following equivalent definition:
Definition 8. A generalized rectangular right angular association scheme (7) is an arrangement of v = wnl (w ≥ 2, n ≥ 2, l ≥ 2) treatments in w arrays of n rows and l columns such that, with respect to each treatment
1) The first associates of

2) The second associates of

3) The third associates of

4) The fourth associates of


5) The fifth associates of



6) The sixth associates of



7) The seventh associates of

Property 3. the parameters of generalized rectangular right angular association schemes (7) are:








Definition 9. A PBIB design based on a generalized rectangular right angular association scheme (7) is called generalized rectangular right angular GPBIB7 design.
3. Construction Method of GPBIBm Designs (m = 4, 5 and 7 Associated Classes)
Let v = wnl (w ≥ 2, n ≥ 2, l ≥ 2) treatments be arranged in w arrays of n rows and l columns


3.1. Construction Method of GPBIB4 Designs
3.1.1. First Construction Method of GPBIB4 Designs
Applying the Combinatory Method (s) on each of the w arrays, with chosen
Theorem 1. The partially balanced incomplete block designs with the parameters:







are generalized rectangular right angular GPBIB4 designs.
Proof. For each array of the w arrays, we obtain a rectangular design with parameters:






For the w arrays we obtain a generalized rectangular right angular GPBIB4 design with parameters:













Lemma 1. For the special case s = l, the previous method can also be used for the construction of nested group divisible designs, with parameters:






Remark 1.
・ For w = 1, the GPBIB4 design of Theorem 1 is a rectangular design with parameters as in the Theorem 1 of [5] .
・ For w = 2, the GPBIB4 design of Theorem 1 is a rectangular right angular PBIB4 design with parameters as in Proposition 1 of [8] .
Proposition 2. Let GPBIB4 be a design with parameters:








For n or l even and s divisor of l or s, the GPBIB4 design is a resolvable PBIB designs (RGPBIB4) with r parallel classes where each parallel classes contain

Proof.
n or l is even and s is divisor of n or l, then
Example 1. Let v = 3 × 4 × 4 treatments be arranged in the three following arrays:
The construction method for (s = 2), give the following resolvable generalized rectangular right angular GPBIB4 design, with the parameters:
3.1.2. Second Construction Method of GPBIB4 Designs with
Let



Applying the Combinatory Method








Theorem 3. The partially balanced incomplete block designs with the parameters:








are generalized rectangular right angular GPBIB4 designs.
Proof.
・ The v and k values are obvious.
・ r: For each treatment



○ On an array











○ On an array




other elements of the same row. There is













Thus:
・



















・






○ In an array










○ In the array







In total
・



















・






○ If


times. For the array



have









In total
○ If
























In total
・













Remark 2. For w = 2, the GPBIB4 design of Theorem 3 is a rectangular right angular PBIB4 design with parameters as in Proposition 2 of [8] .
Proposition 4 Let GPBIB4 be a design with parameters:








For n or l even and s divisor of l or s, the GPBIB4 design is a resolvable PBIB designs (RGPBIB4) with r parallel classes where each parallel classes contain

3.2. Construction Method of GPBIB5 Designs
Let


thod (s) with s chosen





Theorem 5. The incomplete block designs with parameters:









are generalized rectangular right angular GPBIB5 designs.
Remark 3. For w = 2, the GPBIB5 design of Theorem 5 is a rectangular right angular PBIB5 design with parameters as in Proposition 3 of [8] .
Proposition 6. Let GPBIB5 be a design with parameters:









For n or l even and s divisor of l or s, the GPBIB5 design is a resolvable PBIB designs (RGPBIB5) with r parallel classes where each parallel classes contain

Example 2. Let v = 3 × 2 × 3 treatments be arranged in the two following arrays:
The construction method for (s = 3), give the following generalized rectangular right angular GPBIB5 design, with parameters:
3.3. Construction Method of GPBIB7 Designs
3.3.1. First Construction Method of GPBIB7 Designs
Applying the Combinatory Method (s) on each of the w arrays, with chosen and fixed



Theorem 7. The incomplete block designs with parameters:







are generalized rectangular right angular GPBIB7 designs.
Proof. The design parameters are deduced from the construction method.
Remark 4.
・ For w = 1, the GPBIB7 design of Theorem 7 is a rectangular design with parameters as in Theorem 1 of [5] .
・ For w = 2, the GPBIB7 design of Theorem 7 is a rectangular right angular PBIB7 design with parameters as in Proposition 4 of [8] .
Proposition 8. Let GPBIB7 be a design with parameters:






For n or l even and s divisor of l or s, the GPBIB7 design is a resolvable PBIB designs (RGPBIB7) with r parallel classes where each parallel classes contain

Example 3. Let v = 3 × 4 × 4 treatments be arranged in the three following arrays:
The construction method for (s = 2), give the following resolvable generalized rectangular right angular GPBIB7 design, with the parameters:
3.3.2. Second Construction Method of GPBIB7 Designs with

Let


of the gth array

array of the form







treatments that always contain a component of the column


Theorem 9. The partially balanced incomplete block designs with the parameters:











are generalized rectangular right angular GPBIB7 designs.
Proof. The design parameters are deduced from the construction method.
Remark 5. For w = 2, the GPBIB7 design of Theorem 9 is a rectangular right angular PBIB7 design with parameters as in Proposition 5 of [8] .
Proposition 10. Let GPBIB7 be a design with parameters:











For n or l even and s divisor of l or s, the GPBIB7 design is a resolvable PBIB designs (RGPBIB7) with r parallel classes where each parallel classes contain

Example 4. Let v = 3 × 3 × 3 treatments be arranged in the three following arrays:
The construction method for (s = 3), give a generalized rectangular right angular GPBIB7 design with parameters:
To illustrate the method, we applying the construction method for the columns and rows of the first array, where each column represents a block:
4. Construction of the U-Type Designs Based on Resolvable GPBIBm Designs (m = 4, 5 and 7)
In this section we apply the RBIBDmethod (see [6] ) on our resolvable rectangular right angular RGPBIBm designs (m = 4, 5 and 7) to obtain a series of U-type designs
Let a resolvable GPBIBm designs (m = 4, 5 and 7) with r parallel classes



Algorithm RGPBIBm − UD
・ Step 1. Give a natural order


・ Step 2. For each PCj, construct a q-level column



・ Step 3. The r q-level columns constructed from PCj,


Proposition 11. For v = wnl runs (w ≥ 2, n ≥ 2, l ≥ 2), a series of U-type

・ U
・ U
・ U
・ U
・ U
Proof. applying the RGPBIBm − UD Algorithm on each resolvable rectangular right angular GPBIBm (m = 4, 5 and 7) of the Proposition 1, 5.
Example 5. Applying the RGPBIBm − UD Algorithm on the resolvable rectangular right angular GPBIB7 of Example 1, we obtain the following U-type U (48, 49) with 48 runs and nine 4-level factors.
5. Conclusions
New association schemes with m = 4, 5 and 7 associated classes called generalized rectangular right angular association schemes for v = wnl treatments arranged in w ≥ 2 (n × l) arrays were described and their parameters expressions were given exactly and directly. Some construction methods of PBIB designs based on these association schemes accommodated by accessible method called the Combinatory Method (s) which facilitates the
construction application were explained. Moreover, a series of U-type designs U
Fang RBIBD method on resolvable generalized rectangular right angular GPBIBm designs (m = 4, 5 and 7) was constructed.
We note that all the construction methods described in this article were programmed with the R-package “CombinS” [9] (the ameliorated version).
References
- Fang, K.T., Ge, G.N., Liu, M. and Qin, H. (2004) Construction of Uniform Designs via Super-Simple Resolvable t-Designs. Utilitas Mathematica, 66, 15-32.
- Fang, K.T., Tang, Y. and Yin, J.X. (2005) Resolvable Partially Pairwise Balanced Designs and Their Applications in Computer Experiments. Utilitas Mathematica, 70, 141-157.
- Benmatti, A. (1983) Un schéma d’association partiellement équilibré appliqué aux croisements dialléles. Magister Thesis. http://biblio.cca-paris.com/index.php?lvl=author_see&id=1181
- Bailey, R.A. (2004) Association Schemes: Designed Experiments, Algebra and Combinatorics. Cambridge University Press, Cambridge. www.cambridge.org/9780521824460
- Rezgui, I. and Gheribi-Aoulmi, Z. (2014) New Construction Method of Rectangular PBIB Designs and Singular Group Divisible Designs. Journal of Mathematics and Statistics, 10, 45-48. http://dx.doi.org/10.3844/jmssp.2014.45.48
- Fang, K.T., Li, R. and Sudjianto, A. (2006) Design and Modeling for Computer Experiments. Taylor & Francis Group, LLC, London.
- Bose, R.C. and Nair, K.R. (1939) Partially Balanced Incomplete Block Designs. Sankhya, 4, 337-372.
- Rezgui, I., Gheribi-Aoulmi, Z. and Monod, H. (2013) New Association Schemes with 4, 5 and 7 Associate Classes and Their Associated Partially Balanced Incomplete Block Designs. Advances and Applications in Discrete Mathematics, 12, 207-215.
- Laib, M., Rezgui, I., Gheribi-Aoulmi, Z. and Monod, H. (2013) Package “CombinS”: Constructions Method of Rectangular PBIB and Rectangular Right Angular PBIB(m) (m = 4, 5 and 7) Designs. Version 1.0. http://cran.r-project.org/web/packages/CombinS/CombinS.pdf















































