Received 10 November 2014; revised 29 November 2014; accepted 15 December 2014

ABSTRACT

Based on Nehari manifold, Schwarz symmetric methods and critical point theory, we prove the existence of positive radial ground states for a class of Schrodinger-Poisson systems in, which doesn’t require any symmetry assumptions on all potentials. In particular, the positive potential is interesting in physical applications.

Keywords:

Ground States, Schrodinger-Poisson Systems

1. Introduction

In this paper, we consider the following nonlinear Schrodinger-Poisson systems

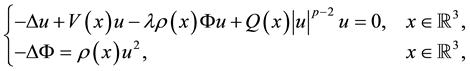(1.1)

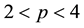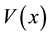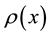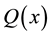where,;, and are positive potentials defined in.

In recent years, such systems have been paid great attention by many authors concerning existence, non- existence, multiplicity and qualitative behavior. The systems are to describe the interaction of nonlinear Schrodinger field with an electromagnetic field. When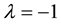, , 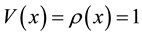, 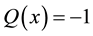the existence of non- trivial solution for the problem (1.1) was proved as 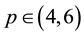in [1] , and non-existence result f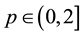or or 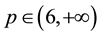was proved in [2] . When, , , using critical point theory, Ruiz [3] obtained some multiplicity results for, and existence results for. Later, Ambrosetti and Ruiz [4] , and Ambrosetti [5] generalized some existence results of Ruiz [3] , and obtained the existence of infinitely solutions for the problem (1.1).

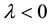In particular, Sanchel and Soler [6] considered the following Schrodinger-Poisson-Slater systems

(1.2)

where. The problem (1.2) was introduced as the model of the Hartree-Foch theory for a one-compo- nent plasma. The solution is obtained by using the minimization argument and as a Lagrange multiplier. However, it is not known if the solution for the problem (1.2) is radial. Mugani [7] considered the following generalized Schrodinger-Poisson systems

(1.3)

where, and, and proved the existence of radially symmetric solitary waves for the problem (1.3).

In this paper, without requiring any symmetry assumptions on, and, we obtain the existence of positive radial ground state solution for the problem (1.1). In particular, the positive potential implies that we are dealing with systems of particles having positive mass. It is interesting in physical applications.

The paper is organized as following. In Section 2, we collect some results and state our main result. In Section 3, we prove some lemmas and consider the problem (1.1) at infinity. Section 4 is devoted to our main theorem.

2. Preliminaries and Main Results

Let, denotes a Lebesgue space, the norm in is,

is the completion of with respect to the norm

be the usual Sobolev space with the usual norm

.

Assume that the potential satisfies

H1), ,.

Let be the Hilbert subspace of such that

(2.1)

Then, with the corresponding embeddings being continuous (see [8] ). Furthermore, assume the potential satisfies

H2), ,.

It is easy to reduce the problem (1.1) to a single equation with a non-local term. Indeed, for every, we have

(2.2)

Since, and (2.1), by the Lax-Milgram theorem, there exists a

unique such that

(2.3)

It follows that satisfies the Poisson equation

and there holds

Because, we have when, and, is positive constant.

Substituting in to the problem (1.1), we are lead to the equation with a non-local term

. (2.4)

In the following, we collect some properties of the functional, which are useful to study our problem.

Lemma 2.1. [9] For any, we have

1) is continuous, and maps bounded sets into bounded sets;

2) if weakly in, then weakly in;

3) for all

Now, we state our main theorem in this paper.

Theorem 2.2. Assume that, , the potential satisfies condition H1), the potential satisfies condition H3) and, the potential satisfies

H3), ,

and, on positive measure. Then there exists a positive radial ground state solution for the problem (1.1).

Remark 2.3. If, , and are positive potentials defined in, and, be a solution for the problem (1.1). Then, Indeed, we have

Since, this implies. By Lemma 2.1, we have.

3. Some Lemmas and the Problem (1.1) at Infinity

Now, we consider the functional given by

Since satisfies condition H2), by (2.2), the Holder inequality and Sobolev inequality, we have

, (3.2)

where and. Since the potential satisfies condition Q,

, we have

By Sobolev inequality, we obtain that

(3.3)

Combining (3.2) and (3.3), we obtain that the functional is a well defined functional, and if is critical point of it, then the pair is a weak solution of the problem (1.1).

Now, we define the Nehari manifold ([10] ) of the functional

,

where

Hence, we have

(3.4)

Lemma 3.1. 1) For any, , there exists a unique such that. Moreover, we have

2) is bounded from below on by a positive solution.

Proof. 1) Taking any and, we obtain that there exists a unique such

that. Indeed, we define the function. We note that if only if. Since is equivalent to

.

By, and, we have

.

By, , the equation has a unique and the corresponding point and.

2) Let, by (3.4) and, we have

By the definition of Nehari manifold of the functional, we obtain that

is a critical point of if and only if is a critical point of constrained on (3.5)

Now, we set

By 2) of Lemma 3.1, we have

Since, , , we consider the problem (1.1) at infinity

(3.6)

Similar to (2.2), we obtain that there exists a unique such that

.

It follows that satisfies the Poisson equation

(3.7)

Hence substituting into the first equation of (3.6) we have to study the equivalent problem

(3.8)

The weak solution of the problem (3.8) is the critical point of the functional

where is endowed with the norm

Define the Nehari manifold of the functional

,

where

and

The Nehari manifold has properties similar to those of

Lemma 3.2. The problem (3.8) has a positive radial ground state solution such that

For the proof of Lemma 3.2, we make use of Schwarz symmetric method. We begin by recalling some basic properties.

Let such that, then there is a unique nonnegative function, called the Schwarz symmetric of, such that it depends only on, whose level sets

.

We consider the following Poisson equation

From Theorem 1 of [11] , we have

.

Hence, let, and, , we have

. (3.9)

The Proof of Lemma 3.2. Let be such that Let such that then we have

,

and

.

Hence, we obtain that

. (3.10)

Since and, (3.10) implies that. Therefore, we can assume that.

On the other hand, let be the Schwartz symmetric function associated to, then we have

(3.11)

Let be such that, and, by (3.9) and (3.11), we have

This implies that. Therefore, we have, and we can suppose that is radial

in. Since is compactly embedded into for, we obtain that is achieved at some which is positive and radial. Therefore, Lemma 3.2 is proved.

4. The Proof of Main Theorem

In this section, we prove Theorem 2.2. Firstly, we consider a compactness result and obtain the behavior of the (PS) sequence of the functional.

Lemma 4.1. Let be a (PS)_d sequence of the functional constrained on, that is

(4.1)

Then there exists a solution of the problem (2.4), a number, functions of and sequences of points, such that

1), , if,;

2);

3);

4) are non-trivial weak solution of the problem (3.8).

Proof. The proof is similar to that of Lemma 4.1 in [9] .

By Lemma 4.1, taking into account that for all and, we obtain that

and in (strongly), i.e. is relatively compact for all. Hence we only need to prove that the energy of a solution of the problem (2.4) cannot overcome the energy of a ground state solution of the problem (3.8).

The proof of Theorem 2.2. By Lemma 4.1, we only prove that. Indeed, let such that, and let such that. Since, and, we have

(4.2)

Since and, we have

Therefore, we have

By, we have. If, we have and. Hence, by, we have

(4.3)

and by, we have

. (4.4)

Combining (4.3) and (4.4), we have

Since, , , and on a positive measure, we have

which is not identically zero, and is contradiction. Hence, we have. By (4.2), we have

Then there exists a positive radial ground state solution for the problem (1.1).

Acknowledgements

This research is supported by Shanghai Natural Science Foundation Project (No. 15ZR1429500), Shanghai Leading Academic Discipline Project (No. XTKX2012) and National Project Cultivate Foundation of USST (No. 13XGM05).

References

NOTES

^*Corresponding author.