Applied Mathematics
Vol.5 No.11(2014), Article
ID:47061,12
pages
DOI:10.4236/am.2014.511160
Measurement Error for Age of Onset in Prevalent Cohort Studies
Yujie Zhong, Richard J. Cook
Department of Statistics and Actuarial Science, University of Waterloo, Waterloo, Canada
Email: zyujie@uwaterloo.ca, rjcook@uwaterloo.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 March 2014; revised 20 April 2014; accepted 27 April 2014
ABSTRACT
Prevalent cohort studies involve screening a sample of individuals from a population for disease, recruiting affected individuals, and prospectively following the cohort of individuals to record the occurrence of disease-related complications or death. This design features a response-biased sampling scheme since individuals living a long time with the disease are preferentially sampled, so naive analysis of the time from disease onset to death will over-estimate survival probabilities. Unconditional and conditional analyses of the resulting data can yield consistent estimates of the survival distribution subject to the validity of their respective model assumptions. The time of disease onset is retrospectively reported by sampled individuals, however, this is often associated with measurement error. In this article we present a framework for studying the effect of measurement error in disease onset times in prevalent cohort studies, report on empirical studies of the effect in each framework of analysis, and describe likelihood-based methods to address such a measurement error.
Keywords:Disease Onset Time, Left Truncation, Measurement Error, Model Misspecification, Prevalent Cohort

1. Introduction
Prevalent cohort studies of chronic diseases involving screening populations and sampling individuals with the condition of interest for prospective follow-up [1] . Examples of such studies include cancer screening trials [2] , studies of HIV prevalence [3] and studies of dementia [4] [5] . The prevalent cohort design is both more efficient and more practical than the incident cohort design [6] in which a cohort of disease-free individuals are followed for disease onset, and only the subset of individuals developing the disease yields information on the time from disease onset to death. The prevalent cohort design features a form of response-dependent sampling, however, in the sense that diseased individuals with long survival times are preferentially selected for inclusion into the cohort [1] [2] [7] ; some authors refer to the resulting data as “length-biased”. Valid statistical inference depends critically on adequately addressing the sampling scheme in the likelihood construction, and there are two broad frameworks for analysis, both of which make use of the retrospectively reported time of disease onset recorded at the time of sampling.
Analysis in the conditional framework is based on the fact that individuals who died before the time of screening cannot be sampled, and so the survival times among sampled individuals are left-truncated by the time from disease onset to enrollment. The unconditional framework is based on the density of the survival times derived under the prevalent cohort sampling scheme. That is, if the disease incidence is stationary, the onset times follow a time homogeneous Poisson process, and the resulting left truncation times have a constant density. If the probability that an individual is sampled is proportional to their survival time, the density of times subject to this sampling scheme can be derived and used for likelihood construction.
For the conditional approach, parametric, nonparametric and semiparametric methods are relatively straightforward and have seen considerable application [3] [8] [11] . Wang [10] proposed a product-limit estimator for left-truncated survival times which maximizes the conditional likelihood and loses no information when the distribution of the truncation time variable is unspecified. For semiparametric Cox models, the partial likelihood approach can be adopted for left-truncated data but with an adjusted risk set [8] [11] [12] . Wang et al. [12] argued that the nonparametric and semiparametric estimators are efficient when the distribution of the truncation time is unspecified but can be inefficient when the distribution of truncation time is parameterized.
Unconditional analyses [5] [13] -[16] are based on the joint distribution of the backward recurrence time (time from disease onset to sampling) and the forward recurrence time (time from sampling to death). Vardi [13] [14] and Asghrian et al. [5] developed the nonparametric maximum likelihood estimator (NPMLE) for right-censored length-biased survival times, but this NPMLE does not have closed form and its limiting distribution is intractable [15] [16] . Huang and Qin [17] derived a new closed-form nonparametric estimator that incorporates the information about the length-biased sampling. Wang [18] proposed pseudo-likelihood for length-biased failure times under the Cox proportional hazards model, but this method cannot be applied to right-censored failure times. Luo and Tsai [19] and Tsai [20] derived pseudo-partial-likelihood estimators for right-censored lengthbiased data which have closed-form and retain high efficiency. Shen et al. [21] considered modeling covariate effects for length-biased data under time transform and accelerated failure time models. Qin and Shen [22] recently proposed two estimating equations for fitting the Cox proportional hazards model that are formulated based on different weighted risk sets.
Both conditional and unconditional analyses make use of the retrospectively reported times of disease onset, with the latter further based on the assumption of a stationary (Poisson) incidence process. However, there is often considerable error and uncertainty in the retrospectively reported onset times. This is particularly true for onset times related to disease featuring cognitive impairment or mental health disorders. In some settings the reported times may better represent times of symptom onset, rather than the actual start of the disease process which may lead to underestimation of disease duration. In other settings the errors may lead to earlier or later reported onset times.
The purpose of this article is to examine the impact of measurement error in the retrospectively reported onset time for both the conditional and unconditional frameworks. The remainder of the paper is organized as follows. In Section 2, we introduce notation and likelihood construction for prevalent cohort data. The impact of misspecification of the disease onset time is explored in Section 3 by simulation for the unconditional and conditional approaches, and methods for correcting for this measurement error are described in Section 4. General remarks and topics for further research are given in Section 5.
2. Approaches to Statistical Analysis
2.1. Notation and Likelihood Construction
Consider a population and a chronic disease such that at any time an individual in the population is in one of three states: alive and disease-free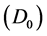 , alive with disease
, alive with disease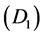 , and dead
, and dead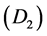 . For individuals who develop the disease, the path is
. For individuals who develop the disease, the path is 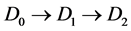 and interest often lies in the distribution of the survival time with the disease, or equivalently the sojourn time distribution for state
and interest often lies in the distribution of the survival time with the disease, or equivalently the sojourn time distribution for state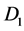 . For individual i, let
. For individual i, let 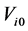 be the calendar time of disease onset and
be the calendar time of disease onset and 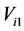 be the calendar time of death (time of entry to state
be the calendar time of death (time of entry to state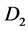 ); then
); then 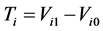 denotes the time of interest.
denotes the time of interest.
Consider a study starting at calendar time R (recruitment time), when individuals in the population are screened for the disease of interest and those who are diseased are to be recruited into the study. Figure 1 shows a hypothetical situation in the prevalent cohort study, where calendar time is represented on the horizontal axis. Individuals who are sampled must have developed the disease of interest at some point over the calendar time interval , and be still alive at the recruitment time R. Those who develop the disease over
, and be still alive at the recruitment time R. Those who develop the disease over 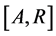 but die before the recruitment time cannot, of course, be selected for inclusion in the sample. Those who develop the disease after the recruitment time are also not eligible for recruitment. The times
but die before the recruitment time cannot, of course, be selected for inclusion in the sample. Those who develop the disease after the recruitment time are also not eligible for recruitment. The times  and
and 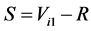 are called the backward and forward recurrence times for individual i respectively, and
are called the backward and forward recurrence times for individual i respectively, and 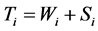 is the survival time of interest. To accommodate incomplete follow-up, let
is the survival time of interest. To accommodate incomplete follow-up, let 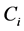 denote the right censoring time for individual i from disease onset, and
denote the right censoring time for individual i from disease onset, and 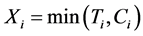 denote the survival time from disease onset;
denote the survival time from disease onset;  is a indicator of whether death is observed.
is a indicator of whether death is observed.
Let 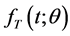 and
and 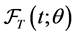 be the so-called unbiased probability density and survivor functions for
be the so-called unbiased probability density and survivor functions for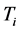 , which characterize the distribution in the target population, where a
, which characterize the distribution in the target population, where a 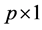 parameter vector
parameter vector  indexes the distribution. The relevant density function for the observed left-truncated survival data for individual
indexes the distribution. The relevant density function for the observed left-truncated survival data for individual 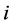 is
is
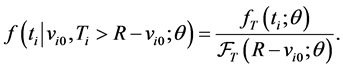 (1)
(1)
The conditional likelihood for right-censored left-truncated survival data is
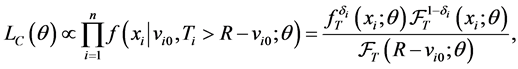 (2)
(2)
assuming 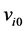 is recorded correctly. By conditioning on the observed truncation time, it is not necessary to model the distribution of the onset times.
is recorded correctly. By conditioning on the observed truncation time, it is not necessary to model the distribution of the onset times.
If the disease onset process is a stationary Poisson process,  and the resulting sample is right-censored length-biased sample. If the distribution of the onset time is known and can be parameterized, the conditional approach may be inefficient and it is natural to want to make use of the information contained in the onset process.
and the resulting sample is right-censored length-biased sample. If the distribution of the onset time is known and can be parameterized, the conditional approach may be inefficient and it is natural to want to make use of the information contained in the onset process.
We now consider the distribution of the onset times over the interval 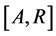 in the target population. Let
in the target population. Let 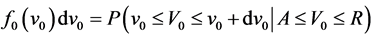 be the probability an onset time occurs in an interval
be the probability an onset time occurs in an interval 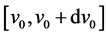 given it happens over
given it happens over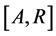 . We assume
. We assume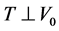 , so that the distribution of the survival time since disease onset does not depend on onset time. We also define the sample onset time density for individuals who satisfy the inclusion criterion,
, so that the distribution of the survival time since disease onset does not depend on onset time. We also define the sample onset time density for individuals who satisfy the inclusion criterion,
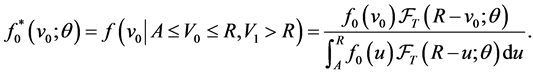 (3)
(3)
When the onset process is stationary, as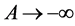 , the sample density function for the onset time (3) can be simplified to be
, the sample density function for the onset time (3) can be simplified to be
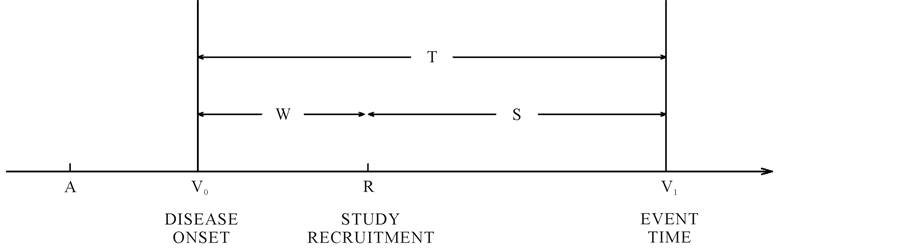
Figure 1. Diagram of calendar times and study times of disease onset, left-truncation and survival.
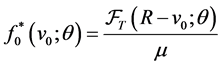 (4)
(4)
where  is the population mean survival time with disease.
is the population mean survival time with disease.
From (3) and (4), one can see that the onset time among sampled individuals contains information regarding the survival distribution. The unconditional likelihood utilizing this information is based on the joint distribution of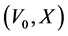 , which can be written as
, which can be written as
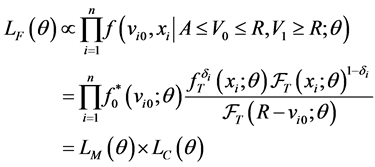 (5)
(5)
where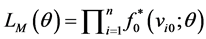 . Thus the full likelihood is the product of the conditional likelihood and the marginal likelihood of sample onset times,
. Thus the full likelihood is the product of the conditional likelihood and the marginal likelihood of sample onset times, 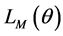 indexed by
indexed by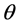 .
.
Under the assumption of a stationary disease process and based on (4), the unconditional likelihood for rightcensored length-biased sample can be written as
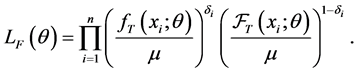 (6)
(6)
Thus the unconditional approach exploits information in the disease onset times to improve efficiency over the conditional approach, but it does so by making stationary assumption for the disease onset process, which makes it less robust.
The estimators 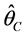 and
and 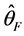 can be found by maximizing the conditional (2) or unconditional (5) likelihoods respectively when parametric models are applied. Further, the resulting estimators have an asymptotic normal distribution, so
can be found by maximizing the conditional (2) or unconditional (5) likelihoods respectively when parametric models are applied. Further, the resulting estimators have an asymptotic normal distribution, so

where 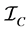 and
and 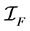 are the Fisher information matrices for conditional and unconditional likelihoods.
are the Fisher information matrices for conditional and unconditional likelihoods.
2.2. Nonparametric Estimation of the Survival Function Estimation
Nonparametric methods are often more appealing than parametric methods when there is limited knowledge regarding the distribution of survival times. Wang et al. [23] and Wang [10] derived the product-limit estimator for left-truncated survival data. Let 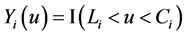 indicate whether individual i has been recruited into the study and under observation at time u, where
indicate whether individual i has been recruited into the study and under observation at time u, where 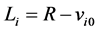 is the left-truncation time, and let
is the left-truncation time, and let  be an indicator they are at risk of an event. Let
be an indicator they are at risk of an event. Let 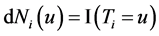 be the event indicator, and
be the event indicator, and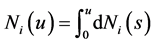 . Then the logarithm of the likelihood for left-truncated data (2), can be rewritten as
. Then the logarithm of the likelihood for left-truncated data (2), can be rewritten as
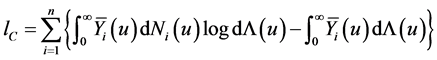
where 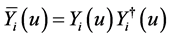 and
and 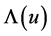 is the cumulative hazard function. The nonparametric maximum likelihood estimator (NPMLE) of the survivor function for right-censored left-truncated data is
is the cumulative hazard function. The nonparametric maximum likelihood estimator (NPMLE) of the survivor function for right-censored left-truncated data is
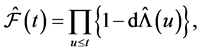 (7)
(7)
where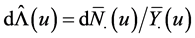 ,
, 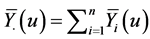 , and
, and .
.
The conditional NPMLE is consistent, but a more efficient estimator can be obtained when the onset process is stationary. Vardi [14] proposed a nonparametric maximum likelihood estimator for survival distribution function  based on a length-biased sample under the multiplicative censoring. The NPMLE of
based on a length-biased sample under the multiplicative censoring. The NPMLE of 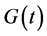 is found by an expectation-maximization algorithm which maximizes the likelihood function of the form
is found by an expectation-maximization algorithm which maximizes the likelihood function of the form
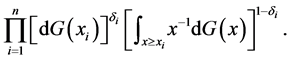 (8)
(8)
Vardi [14] also argued that, based on the renewal theory, the joint distribution of 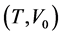 under length-biased sampling is
under length-biased sampling is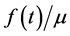 . Hence the density function for the observed length-biased event time is
. Hence the density function for the observed length-biased event time is 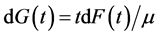 , and then the survivor function for event time in the population is
, and then the survivor function for event time in the population is . The full likelihood (6) under length-biased sampling can be rewritten as
. The full likelihood (6) under length-biased sampling can be rewritten as
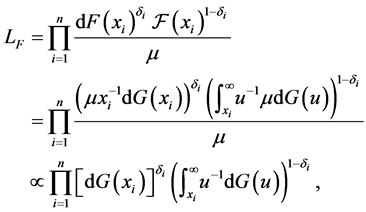
which is exactly the same as Vardi (8). The Vardi [14] algorithm can therefore be used to obtain the NPMLE of , and by using the relationship between
, and by using the relationship between 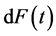 and
and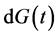 , the NPMLE of
, the NPMLE of  can be easily obtained by
can be easily obtained by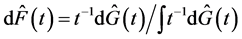 .
.
Qin et al. [24] developed an expectation-maximization algorithm for the analysis of length-based data by constructing a complete data likelihood using the Turnbull [9] approach and considering contributions from “ghosts”; these are individuals not sampled into the cohort because they died before the screening assessment. Unlike Vardi [14] method, their likelihood function is derived from the unbiased distribution of event time and EM algorithm directly estimates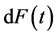 , which allows one to impose any model and parameter constraints for this distribution function.
, which allows one to impose any model and parameter constraints for this distribution function.
3. Error in the Reported Onset Time
3.1. Introduction
Both the conditional and unconditional analyses make use of the reported onset time, and the latter requires the additional assumption of a stationary disease incidence process. For individuals determined to have the disease at the time of assessment, the disease may have begun several years earlier, making accurate recall of the onset time difficult. There may therefore be considerable uncertainty about the reported onset time and the difference between the true onset time and the reported onset time represents recall, reporting, or measurement error; we will henceforth use the term measurement error.
Both the conditional and unconditional approaches to the analysis of prevalent cohort data will in general lead to biased estimators in the presence of measurement error. We therefore investigate the impact of this measurement error in both the conditional and unconditional frameworks for parametric and nonparametric settings.
3.2. The Classical Measurement Error Model
In retrospective studies, selected patients need to recall their disease onset times. In this case, the recall times are very likely different from the exact disease onset times, even though perhaps they are quite close. Consider disease incidence over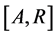 , and a sample of the prevalent cohort is selected at recruitment time R. Let
, and a sample of the prevalent cohort is selected at recruitment time R. Let 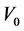 be the exact disease onset time which is not observed and
be the exact disease onset time which is not observed and 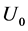 be the retrospectively reported disease onset time. A classical error model Carroll et al. [25] leads to
be the retrospectively reported disease onset time. A classical error model Carroll et al. [25] leads to
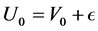 (9)
(9)
where 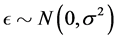 is random measurement error, and
is random measurement error, and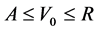 .
.
The data obtained in this case are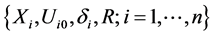 , where
, where 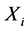 is observed event time or censoring time, and
is observed event time or censoring time, and  is a censoring indicator. Notice that diseased individuals who are still alive at the recruitment time and selected into the study need to report their onset time retrospectively, and their reported onset time should also satisfy the condition
is a censoring indicator. Notice that diseased individuals who are still alive at the recruitment time and selected into the study need to report their onset time retrospectively, and their reported onset time should also satisfy the condition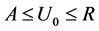 . In this case the sample distribution of
. In this case the sample distribution of  given
given  becomes a truncated normal distribution, with density function written as
becomes a truncated normal distribution, with density function written as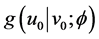 , suppressing the condition
, suppressing the condition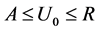 ,
,
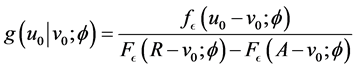 (10)
(10)
where 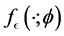 and
and 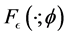 are the density and cumulative distribution functions of
are the density and cumulative distribution functions of 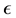 with parameter
with parameter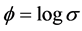 , where
, where 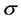 is the standard deviation; we let
is the standard deviation; we let 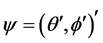 denote the vector of all parameters.
denote the vector of all parameters.
3.3. Empirical Study of Measurement Error
If we ignore the measurement error and treat 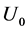 as the true onset time, both the left-truncation time and survival time will be in error. Conditional and unconditional parametric analyses will lead to biased estimators for parameters of interest. To examine this impact, we conduct the following simulation study which follows the same strategy of Huang and Qin (2011) to generate length-biased data. We let the true disease onset time
as the true onset time, both the left-truncation time and survival time will be in error. Conditional and unconditional parametric analyses will lead to biased estimators for parameters of interest. To examine this impact, we conduct the following simulation study which follows the same strategy of Huang and Qin (2011) to generate length-biased data. We let the true disease onset time 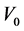 be uniformly distributed over
be uniformly distributed over , and the underlying survival time T be independently generated from a Weibull distribution with survival function
, and the underlying survival time T be independently generated from a Weibull distribution with survival function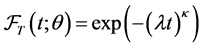 ;
;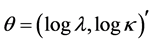 , and consider
, and consider  and
and . Hence the event happens at
. Hence the event happens at 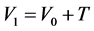 at the calender time scale which can be recorded. Suppose the censoring time, measured from the time of recruitment, is independently and uniformly distributed over
at the calender time scale which can be recorded. Suppose the censoring time, measured from the time of recruitment, is independently and uniformly distributed over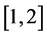 , which leads to a 30% true censoring rate. To incorporate the measurement error in the onset time, we adapt the classical measurement error model (9) and assume that
, which leads to a 30% true censoring rate. To incorporate the measurement error in the onset time, we adapt the classical measurement error model (9) and assume that 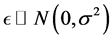 with
with 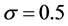 or 1.0 to reflect mild and strong measurement error, respectively. In presence of measurement error, although the ascertainment criteria is still
or 1.0 to reflect mild and strong measurement error, respectively. In presence of measurement error, although the ascertainment criteria is still 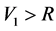 to form a prevalent cohort sample, both the left truncation time and survival time are affected by the random error and are recorded as
to form a prevalent cohort sample, both the left truncation time and survival time are affected by the random error and are recorded as 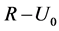 and
and , respectively. We set the sample size as n = 500 and simulation nsim = 1000 data sets. To examine the impact of measurement error in disease onset time, naive, conditional and unconditional parametric and nonparametric approaches are applied to the resulting data, all of which involved treating
, respectively. We set the sample size as n = 500 and simulation nsim = 1000 data sets. To examine the impact of measurement error in disease onset time, naive, conditional and unconditional parametric and nonparametric approaches are applied to the resulting data, all of which involved treating  as the “true” onset time. Table 1 summarizes the average bias (EBIAS), empirical standard error (ESE), average model-based standard error (ASE), and empirical 95% coverage probability of estimators based on naive (NAIVE), conditional (COND) and unconditional (UNCOND) likelihoods.
as the “true” onset time. Table 1 summarizes the average bias (EBIAS), empirical standard error (ESE), average model-based standard error (ASE), and empirical 95% coverage probability of estimators based on naive (NAIVE), conditional (COND) and unconditional (UNCOND) likelihoods.
From Table 1, we see that all three likelihood methods lead to biased estimators, since they all ignore the measurement error in the disease onset time. Although the ESE and ASE agree with each other, the empirical
Table 1. Empirical properties of estimators in presence of measurement error in disease onset time using Naive likelihood (NAIVE), Conditional likelihood (COND) and Unconditional likelihood (UNCOND); n = 500, nsim = 1000.
coverage probability is far away from the nominal value. Further, when the variance of the measurement error becomes smaller, the biases of estimators reduce a lot and the empirical coverage probabilities become better. This makes sense because the smaller the variance of measurement error, the closer of reported onset time to the true onset time, which reduces the impact of using the reported onset time.
Table 2 and Table 3 summarize the nonparametric estimates of the survivor functions and percentiles based on naive, conditional and unconditional approaches, along with the estimates based on parametric models for comparison. Similar conclusions can be drawn about the effect of measurement error in disease onset time for nonparametric analyses. One thing needs to mention is that even when the variance of measurement error becomes smaller, the biases are still quite large for the naive approach, under parametric and nonparametric analyses. This is because the naive approach treats the recruited sample as a representative sample of the population and does not correct for the selection bias for left-truncated or length-biased data.
To clearly understand the importance of correcting for measurement error in disease onset time for prevalent cohort samples, we plot the true survivor function versus estimated survivor functions based on the naive, conditional and unconditional likelihoods without correcting for measurement error, both parametric and nonparametric models are considered. Figure 2 shows that ignoring the measurement error in onset time, both conditional and unconditional likelihoods lead to biased estimate of survivor function.
4. The Corrected Likelihood
4.1. Corrected Parametric Conditional Likelihood
A “correct” likelihood approach can be used to account for the measurement error in the onset time and will
Table 2. Empirical properties of nonparametric and parametric survivor estimators at certain time points based on naive (NAIVE), conditional (COND) and unconditional (UNCOND) likelihoods; n = 500, nsim = 1000.
Table 3. Empirical properties of nonparametric and parametric percentile estimators based on naive (NAIVE), conditional (COND) and unconditional (UNCOND) likelihoods; n = 500, nsim = 1000.
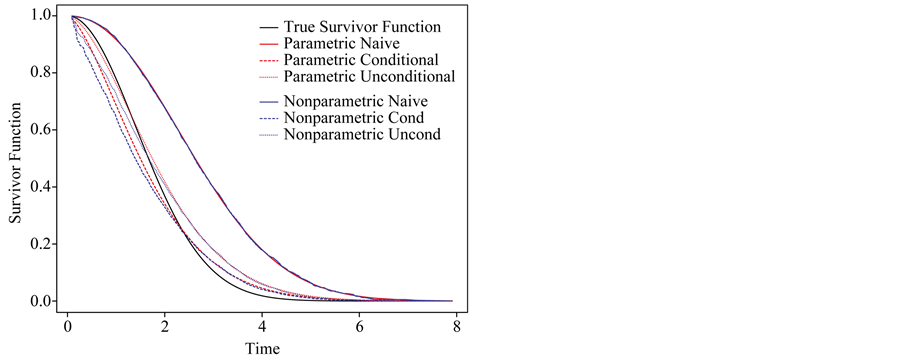 (a)
(a)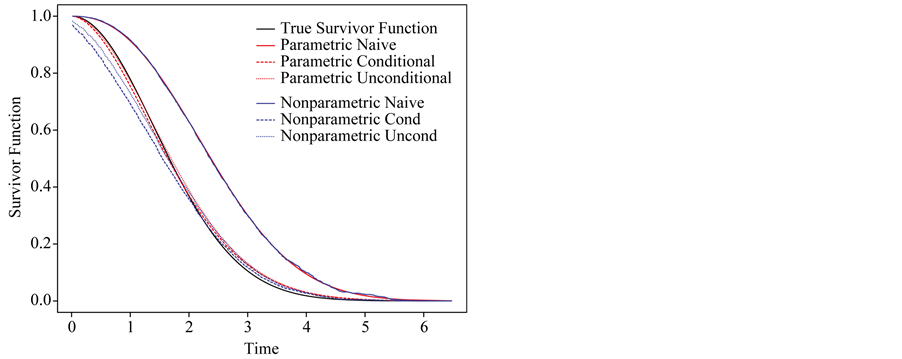 (b)
(b)
Figure 2. Nonparametric and parametric estimates of survivor function based on the naive, conditional and unconditional likelihoods in presence of measurement error in disease onset time when ignoring the measurement error; n = 5000. (a) σ = 1; (b) σ = 0.5.
yield unbiased estimators of the parameters of interest if the component model assumptions are correctly specified. Such a likelihood should be based on the reported onset time and the (possibly censored) survival time, which will require explicit modeling of the measurement error process. Let 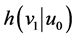 be the density function of the calendar time of death given the reported onset time, i.e.
be the density function of the calendar time of death given the reported onset time, i.e.
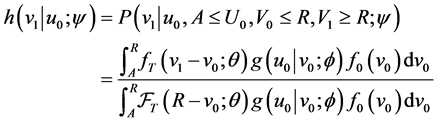 (11)
(11)
The “correct” conditional likelihood for right-censored left-truncated data  is of the form
is of the form
 (12)
(12)
Similarly, the joint density of the observed onset time and calendar time of death is
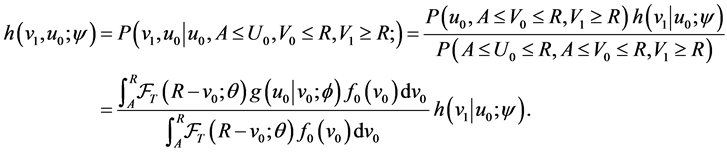 (13)
(13)
where the last equality is derived by (10).
The “correct” unconditional likelihood can then be constructed as follows,
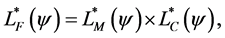 14)
14)
where
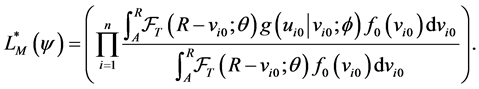 (15)
(15)
Since 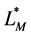 might contain the information about parameters we are interested in, the “correct” unconditional likelihood might be more efficient than the “correct” conditional likelihood. Further, when the underlying onset time is a stationary process, then we can let
might contain the information about parameters we are interested in, the “correct” unconditional likelihood might be more efficient than the “correct” conditional likelihood. Further, when the underlying onset time is a stationary process, then we can let 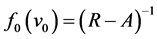 and let
and let 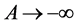 to obtain both “correct” likelihoods for length-biased data.
to obtain both “correct” likelihoods for length-biased data.
The maximum likelihood estimators  and
and 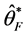 under (un)conditional likelihoods can be easily found by maximizing (12) and (14) respectively and have asymptotic normal distribution, as
under (un)conditional likelihoods can be easily found by maximizing (12) and (14) respectively and have asymptotic normal distribution, as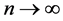 ,
,
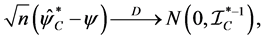
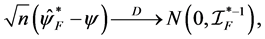
where 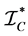 and
and 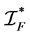 are information matrices based on conditional
are information matrices based on conditional  and unconditional
and unconditional 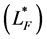 likelihoods function.
likelihoods function.
4.2. Empirical Study of Corrected Likelihood
To examine the performance of “correct” likelihoods in the presence of measurement error in disease onset time, we use the same strategy to generate length-biased survival data with measurement error in disease onset times as in Section 3.2. The “correct” likelihood is considered here in two scenarios: the variance of the measurement error  is known or unknown. Figure 3 shows the estimated survivor functions based on the conditional and unconditional likelihood approaches which ignoring the measurement error and “correct” conditional and unconditional likelihood approaches based on (12) and (14). From this figure, we can find that the proposed “correct” likelihood approach adjusts the measurement error well and leads to better estimates of the survivor functions. Table 4 summarizes the empirical properties of the estimates based on the naive parametric conditional likelihood, the “correct” parametric conditional likelihood, the naive parametric unconditional likelihood, and the “correct” parametric unconditional likelihood. For the corrected likelihood we maximize (12) and (14) both with respect to
is known or unknown. Figure 3 shows the estimated survivor functions based on the conditional and unconditional likelihood approaches which ignoring the measurement error and “correct” conditional and unconditional likelihood approaches based on (12) and (14). From this figure, we can find that the proposed “correct” likelihood approach adjusts the measurement error well and leads to better estimates of the survivor functions. Table 4 summarizes the empirical properties of the estimates based on the naive parametric conditional likelihood, the “correct” parametric conditional likelihood, the naive parametric unconditional likelihood, and the “correct” parametric unconditional likelihood. For the corrected likelihood we maximize (12) and (14) both with respect to 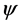 (i.e. when
(i.e. when 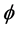 is treated as unknown) and with respect to
is treated as unknown) and with respect to 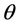 when
when 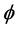 is fixed at the true value. Whether the variance of error
is fixed at the true value. Whether the variance of error 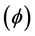 is known or unknown, the “correct” likelihood approach reduces the bias of estimates, and the resulting empirical coverage probabilities are all within the acceptable range. These simulations therefore provide empirical support to the claim that the “correct” likelihood approach adjusts for the measurement error and yields consistent estimators. Notable is the only modest increase in the empirical or average standard errors of parameter estimates when the variance of the measurement error distribution is estimated, especially for the shape parameter
is known or unknown, the “correct” likelihood approach reduces the bias of estimates, and the resulting empirical coverage probabilities are all within the acceptable range. These simulations therefore provide empirical support to the claim that the “correct” likelihood approach adjusts for the measurement error and yields consistent estimators. Notable is the only modest increase in the empirical or average standard errors of parameter estimates when the variance of the measurement error distribution is estimated, especially for the shape parameter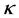 . The “correct” likelihood approach also provides a good estimator of
. The “correct” likelihood approach also provides a good estimator of , and the empirical bias of estimator for
, and the empirical bias of estimator for 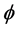 is small at 0.03 with standard error 0.27 for the conditional analysis and 0.01 with standard error 0.11 for the unconditional analysis, when
is small at 0.03 with standard error 0.27 for the conditional analysis and 0.01 with standard error 0.11 for the unconditional analysis, when , for example.
, for example.
5. Discussion
Statistical models and methods for the analysis of prevalent cohort data have been reviewed here from both the conditional and unconditional frameworks. It is well known that naive analyses which ignore the selection bias lead to overestimation of the survivor probabilities. The conditional likelihood based on the density for lefttruncated event times can be used to correct for this selection bias. The unconditional likelihood approach is based on the joint density of the backwards and forward recurrence times yield more efficient estimators by incorporating the information contained in the onset times. The typical assumption required to formulate the associated model is of a stationary disease incidence process. Since both approaches make use of the onset time information to correct for selection effects, misspecification of the retrospectively reported disease onset time can have serious implications on the estimation. We investigate the impact of measurement error in disease onset time for prevalent cohort sample and propose “correct” conditional and unconditional likelihoods to account for the measurement error.
The methods we proposed to correct for measurement error in this paper are based on the parametric model. It
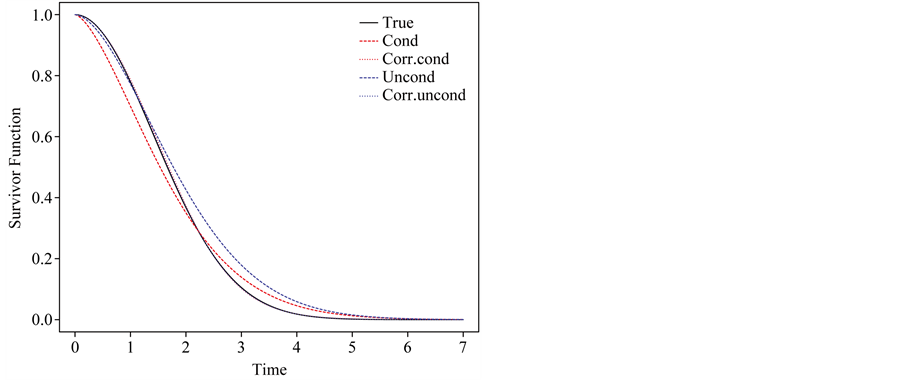
Figure 3. Comparison of the true survivor function with estimated survivor functions based on conditional likelihood and “correct” conditional likelihood approach; σ = 1, n = 500, nsim = 1000.
Table 4. Empirical properties of estimators based on the naive conditional likelihood (COND.NA), the corrected conditional likelihood (COND.C), the naive unconditional likelihood (UNCOND.NA), and the corrected unconditional likelihood (UNCOND.C); n = 500, nsim = 1000.
1Denotes case of unknown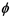 ; 2Denotes case of known
; 2Denotes case of known .
.
is of interest to investigate what the limiting value is of standard nonparametric estimators for both the conditional and unconditional frameworks. The modest increase in the standard error of the Weibull shape and scale parameters when 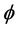 is estimated, suggests that it is promising to consider nonparametric estimation in the corrected conditional and unconditional settings. Extending the corrected likelihoods to accommodate misspecification of the onset times is also of interest for both frameworks.
is estimated, suggests that it is promising to consider nonparametric estimation in the corrected conditional and unconditional settings. Extending the corrected likelihoods to accommodate misspecification of the onset times is also of interest for both frameworks.
We focused on the classical error model in this study, but other measurement error models are also of interest; often individuals will report later onset times since their views on disease onset may be more closely tied to the onset of symptoms than the actual disease. Methods to correct for this kind of measurement error are also important and are under development.
References
- Zelen, M. and Feinleib, M. (1969) On the Theory of Screening for Chronic Diseases. Biometrika, 56, 601-614. http://dx.doi.org/10.1093/biomet/56.3.601
- Zelen, M. (2004) Forward and Backward Recurrence Times and Length Biased Sampling: Age Specific Models. Lifetime Data Analysis, 10, 325-334. http://dx.doi.org/10.1007/s10985-004-4770-1
- Lagakos, S.W., Barraj, L.M. and De Gruttola, V. (2006) Nonparametric Analysis of Truncated Survival Data, with Applications to AIDS. Biometrika, 75, 515-523. http://dx.doi.org/10.1093/biomet/75.3.515
- Wolfson, C., Wolfson, D.B., Asgharian, M., M’Lan, C.E., ?stbye, T., Rockwood, K. and Hogan, D.B. (2001) A Reevaluation of the Duration of Survival after the Onset of Dementia. New England Journal of Medicine, 344, 1111-1116. http://dx.doi.org/10.1056/NEJM200104123441501�
- Asgharian, M., M’Lan, C.E. and Wolfson, D.B. (2002) Length-Biased Sampling with Right Censoring: An Unconditional Approach. Journal of the American Statistical Association, 97, 201-209. http://dx.doi.org/10.1198/016214502753479347
- Rothman, K.J., Greenland, S. and Lash, T.L. (2008) Modern Epidemiology. Lippincott Williams & Wilkins, Philadelphia.
- Cox, D.R. and Miller, H.D. (1965) The Theory of Stochastic Processes. Chapman, London.
- Kalbfleisch, J.D. and Lawless, J.F. (1991) Regression Models for Right Truncated Data with Applications to AIDS incubation Times and Reporting Lags. Statistica Sinica, 1, 19-32.
- Turnbull, B.W. (1976) The Empirical Distribution Function with Arbitrarily Grouped, Censored and Truncated Data. Journal of the Royal Statistical Society, Series B (Methodological), 38, 290-295.
- Wang, M.-C. (1991) Nonparametric Estimation from Cross-Sectional Survival Data. Journal of the American Statistical Association, 86, 130-143. http://dx.doi.org/10.1080/01621459.1991.10475011
- Keiding, N. and Moeschberger, M. (1992) Independent Delayed Entry, Survival Analysis: State of the Art. Springer, New York, 309-326. http://dx.doi.org/10.1007/978-94-015-7983-4_18
- Wang, M.-C., Brookmeyer, R. and Jewell, N.P. (1993) Statistical Models for Prevalent Cohort Data. Biometrics, 49, 1-11. http://dx.doi.org/10.2307/2532597
- Vardi, Y. (1982) Nonparametric Estimation in the Presence of Length Bias. The Annals of Statistics, 10, 616-620. http://dx.doi.org/10.1214/aos/1176345802
- Vardi, Y. (1989) Multiplicative Censoring, Renewal Processes, Deconvolution and Decreasing Density: Nonparametric Estimation. Biometrika, 76, 751-761. http://dx.doi.org/10.1093/biomet/76.4.751
- Vardi, Y. and Zhang, C.-H. (1992) Large Sample Study of Empirical Distributions in a Random-Multiplicative Censoring Model. The Annals of Statistics, 20, 1022-1039. http://dx.doi.org/10.1214/aos/1176348668
- Asgharian, M. and Wolfson, D.B. (2005) Asymptotic Behavior of the Unconditional NPMLE of the Length-Biased Survivor Function from Right Censored Prevalent Cohort Data. The Annals of Statistics, 33, 2109-2131. http://dx.doi.org/10.1214/009053605000000372
- Huang, C.-Y. and Qin, J. (2011) Nonparametric Estimation for Length-Biased and Right-Censored Data. Biometrika, 98, 177-186. http://dx.doi.org/10.1093/biomet/asq069
- Wang, M.-C. (1996) Hazards Regression Analysis for Length-Biased Data. Biometrika, 83, 343-354. http://dx.doi.org/10.1093/biomet/83.2.343
- Luo, X.D. and Tsai, W.Y. (2009) Nonparametric Estimation for Right-Censored Length-Biased Data: A Pseudo-Partial Likelihood Approach. Biometrika, 96, 873-886. http://dx.doi.org/10.1093/biomet/asp064
- Tsai, W.Y. (2009) Pseudo-Partial Likelihood for Proportional Hazards Models with Biased-Sampling Data. Biometrika, 96, 601-615. http://dx.doi.org/10.1093/biomet/asp026
- Shen, Y., Ning, J. and Qin, J. (2009) Analyzing Length-Biased Data with Semiparametric Transformation and Accelerated Failure Time Models. Journal of the American Statistical Association, 104, 1192-1202. http://dx.doi.org/10.1198/jasa.2009.tm08614
- Qin, J. and Shen, Y. (2010) Statistical Methods for Analyzing Right-Censored Length-Biased Data under Cox Model. Biometrics, 66, 382-392. http://dx.doi.org/10.1111/j.1541-0420.2009.01287.x
- Wang, M.-C., Jewell, N.P. and Tsai, W.-Y. (1986) Asymptotic Properties of the Product Limit Estimate under Random Truncation. The Annals of Statistics, 14, 1597-1605. http://dx.doi.org/10.1214/aos/1176350180
- Qin, J., Ning, J., Liu, H. and Shen, Y. (2011) Maximum Likelihood Estimations and EM Algorithms with Length-Biased Data. Journal of the American Statistical Association, 106, 1434-1449. http://dx.doi.org/10.1198/jasa.2011.tm10156
- Carroll, R.J., Ruppert, D., Stefanski, L.A. and Crainiceanu, C.M. (2006) Measurement Error in Nonlinear Models. Chapman & Hall, London. http://dx.doi.org/10.1201/9781420010138


