Applied Mathematics
Vol.5 No.5(2014), Article ID:44068,8 pages DOI:10.4236/am.2014.55078
The Construction of Locally D-Optimal Designs by Canonical Forms to an Extension for the Logistic Model
Irene García Camacha Gutiérrez, Raúl Martín Martín
Mathematics Department, Castilla-La Mancha University, Toledo, Spain
Email: Irene.GarciaCamacha@uclm.es, Raul.MMartin@uclm.es
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 8 December 2013; revised 8 January 2014; accepted 15 January 2014
Abstract
Logistic regression models for binary response problems are present in a wide variety of industrial, biological, social and medical experiments; therefore, optimum designs are a valuable tool for experimenters, leading to estimators of parameters with minimum variance. Our interest in this contribution is to provide explicit formulae for the D-optimal designs as a function of the unknown parameters for the logistic model  where
where 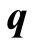 is an indicator variable. We have considered an experiment based on the dose-response to a fly insecticide in which males and females respond in different ways, proposed in Atkinson et al. (1995) [1] . To find the D-optimal designs, this problem has been reduced to a canonical form.
is an indicator variable. We have considered an experiment based on the dose-response to a fly insecticide in which males and females respond in different ways, proposed in Atkinson et al. (1995) [1] . To find the D-optimal designs, this problem has been reduced to a canonical form.
Keywords:Binomial Response; D-Optimal Design; Canonical Form

1. Introduction
There are many natural phenomena or external factors to which males and females respond differently; this feature happens in most live species and has received several book length treatments. The interest of the present work focuses on a particular insect specie: flies. The experiment consists of supplying a dose of insecticide on and analysing its effectiveness. The characterization of this process is the impossibility of identifying the gender of the flies before and during the treatment application. The behaviour is studied on the total population and, due to the experimental differences on the response, it is considered that sex is distributed according to binomial with success probability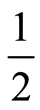 . The theory of optimal design is used to calculate the optimal dose levels with a determinate probability of death.
. The theory of optimal design is used to calculate the optimal dose levels with a determinate probability of death.
To model the experiment, the logistic model for binary data was chosen. Denoting 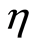 as the probability of death,
as the probability of death,  as the logarithm of dose (in micrograms per millilitre) and
as the logarithm of dose (in micrograms per millilitre) and  as the number of deaths, it must be:
as the number of deaths, it must be:

where 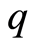 is a factor with values 0 for males and 1 for females and being
is a factor with values 0 for males and 1 for females and being 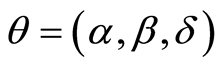 the unknown parameters vector. This model can be linearized by the logarithm of the probability ratio:
the unknown parameters vector. This model can be linearized by the logarithm of the probability ratio: 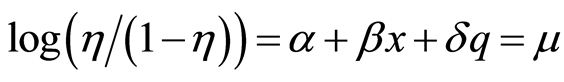
Atkinson et al. (1995) [1] . A wide range of dichotomous response-mechanisms can be expressed in terms of the previous model.
2. Optimum Design
The main objective of optimal experimental design is to select where and how many trials are necessary to be collected in order to achieve an optimal estimation of the model parameters. The observations will be taken into experimental region,  , which will be in most cases a closed interval of the real line,
, which will be in most cases a closed interval of the real line, . On
. On  it is defined an approximated design as
it is defined an approximated design as
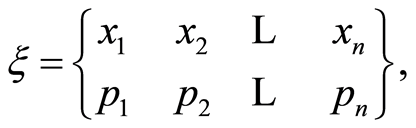
where 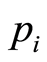 denotes a probability measure with support on
denotes a probability measure with support on . The number of support points is guaranteed to be finite, or at least it is possible to find one finite equivalent, as consequence of Caratheodory’s theorem. Due to the continuity of probability measure chosen, it may occur not to obtain an exact number of trials for each dose level. However, the theory assures us that when the number of observations is sizeable, the integer approximation of the values is enough good.
. The number of support points is guaranteed to be finite, or at least it is possible to find one finite equivalent, as consequence of Caratheodory’s theorem. Due to the continuity of probability measure chosen, it may occur not to obtain an exact number of trials for each dose level. However, the theory assures us that when the number of observations is sizeable, the integer approximation of the values is enough good.
To proceed with this type of problems, a certain functional from the called Fisher information matrix is required to achieve its maximum value. According to the considered model, it is built the information matrix to a single observation  on an insect of known sex as
on an insect of known sex as

being  the variance used in fitting a generalized model by weighted least squares
the variance used in fitting a generalized model by weighted least squares
(McCullagh and Nelder, 1989 [2] ). Nevertheless, the matrix just defined does not take into account the differences on the response previously mentioned. In spite of the experimental limitations about the lack of sex knowledge, it is possible to modify the above matrix to consider this uncertainly as it is shown:

In this work, the function of the information matrix chosen is D-optimality criteria. This criterion minimizes the volume of the confidence ellipsoid of the parameters and it is given by 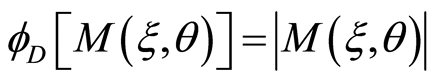 or equivalently
or equivalently 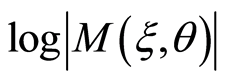 which has the advantage of being a concave function. This optimality criterion has received much attention in the literature because of its direct interpretation (Silvey, 1980 [3] ).
which has the advantage of being a concave function. This optimality criterion has received much attention in the literature because of its direct interpretation (Silvey, 1980 [3] ).
3. Canonical Forms
The use of canonical forms in the present paper greatly simplifies the process to obtain the optimal one. If the problem is transformed through a suitable choice from  to
to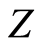 , the dependence of the optimal design on the true value of
, the dependence of the optimal design on the true value of  for given design space
for given design space 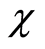 will be replaced, in the transformed problem for arbitrary
will be replaced, in the transformed problem for arbitrary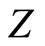 , which will vary with
, which will vary with . Then, if we are able to solve the transformed problem, we have implicitly solved the original design problem (Ford et al. (1992) [4] ). The invariance of the design criteria chosen by the transformation is an indispensable requirement for performing this canonical version of the problem.
. Then, if we are able to solve the transformed problem, we have implicitly solved the original design problem (Ford et al. (1992) [4] ). The invariance of the design criteria chosen by the transformation is an indispensable requirement for performing this canonical version of the problem.
First, we consider the chosen model as a distribution function which is denoted by .
.
Let’s suppose the insect sex is known. The following argument is valid for both males and females, so we will denote with the factor q an individual regardless of gender. Applying the change of variable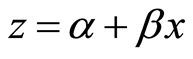 , the original problem can be reformulated as
, the original problem can be reformulated as

with  or
or 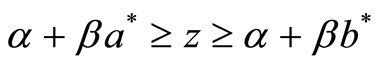 depending on
depending on ’s sign. The information matrix can be built using the chain's rule for
’s sign. The information matrix can be built using the chain's rule for 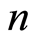 dose levels as below:
dose levels as below:
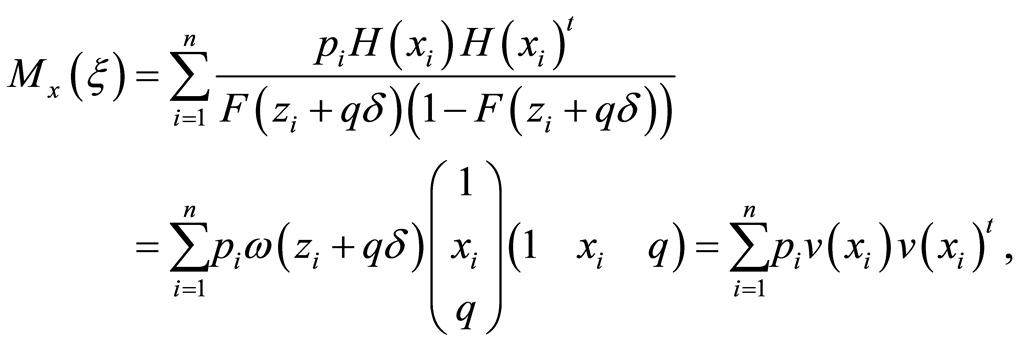
being
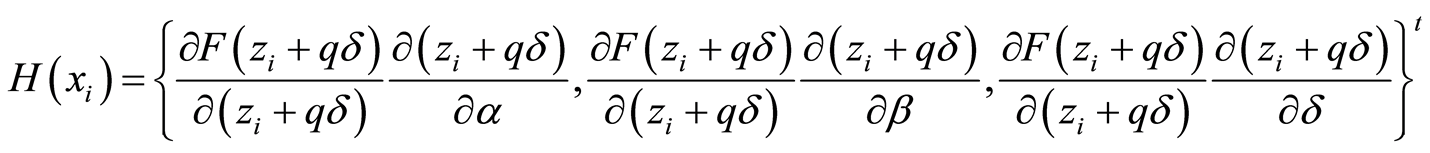
the partial-derivative vector from the chain's rule,  the probability density function and
the probability density function and
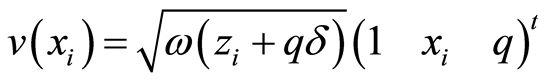 . Note we have defined
. Note we have defined

abusing notation. The previous transformation can be expressed in matrix form as
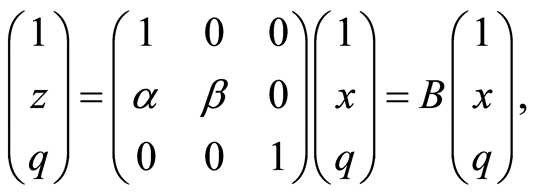
and defining,

the partial-derivative vector 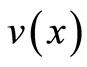 can be expressed in terms of
can be expressed in terms of  through
through 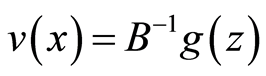 since
since  is invertible for being
is invertible for being . Let us write the information matrix using the formula for change of basis as
. Let us write the information matrix using the formula for change of basis as
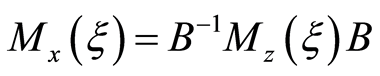 (Fedorov, 1972 [5] ). Since the D-optimal criterion does not vary by non-singular linear transformations of the design space, the maximization problem of
(Fedorov, 1972 [5] ). Since the D-optimal criterion does not vary by non-singular linear transformations of the design space, the maximization problem of 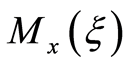 determinant reduces to maximize
determinant reduces to maximize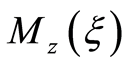 . Hereafter, it will only work with the information matrix depending on
. Hereafter, it will only work with the information matrix depending on  and then it will carry the inverse change out for solving the original problem without loss of concept. Note the parameter dependence has been considerably reduced:
and then it will carry the inverse change out for solving the original problem without loss of concept. Note the parameter dependence has been considerably reduced:
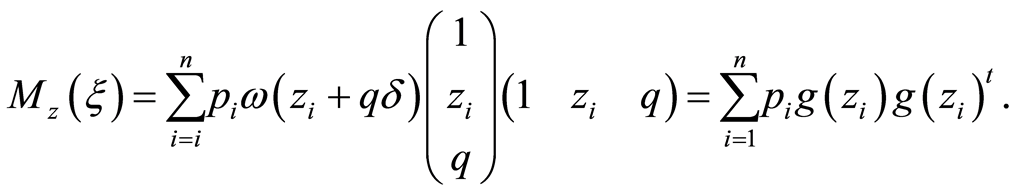
By adding uncertainty about sex, the information matrix to the design 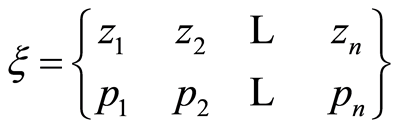 with
with
 for
for 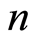 dose levels results
dose levels results
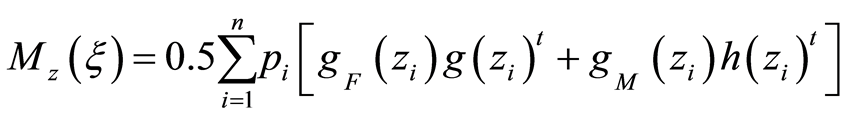
being,
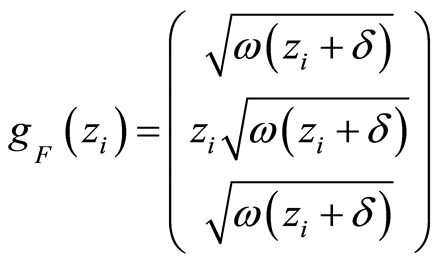 and
and 
The above expression can be reformulated into a more general formula
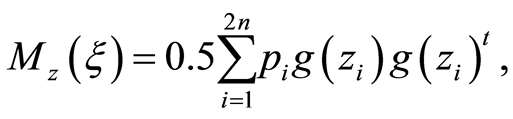 (1)
(1)
where the ’s are repeated to consider the information by each possibility about sex since their partial derivatives are different. The novelty of this paper is described in the previous lines. The simplified formulation of the information matrix will allow us to achieve analytical expressions for the optimal weights for several cases in the next section.
’s are repeated to consider the information by each possibility about sex since their partial derivatives are different. The novelty of this paper is described in the previous lines. The simplified formulation of the information matrix will allow us to achieve analytical expressions for the optimal weights for several cases in the next section.
4. Results
The aim of our study is to select where and how many observations must be collected in order to reduce the volume of confidence ellipsoid of the parameters as possible. For this purpose, it is necessary to obtain an expression of the determinant of the information matrix which will be maximized later. To calculate the determinant to the information matrix written as (1), it is possible to apply the following formula to its explicit expression given by Ardanuy et al. (1999) [6] :
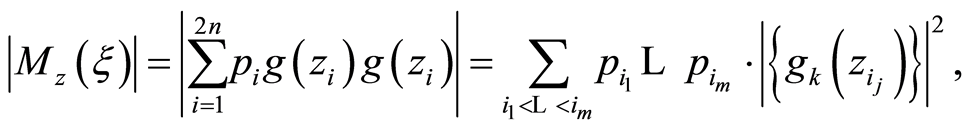 (2)
(2)
being  the number of parameters and
the number of parameters and  the elements of
the elements of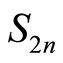 , the symmetrical group of
, the symmetrical group of 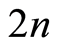 -order permutations. We focus the study to calculate optimal designs to a small size of observations, two and three design points. The reason for this choice is that the upper and lower bound for the number of point suffers a slight modification due to each trial has two reading. Then the system will be non-singular if there are at least
-order permutations. We focus the study to calculate optimal designs to a small size of observations, two and three design points. The reason for this choice is that the upper and lower bound for the number of point suffers a slight modification due to each trial has two reading. Then the system will be non-singular if there are at least
 point since
point since 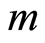 is odd and the Caratheodory upper's bound will be halved with
is odd and the Caratheodory upper's bound will be halved with . The only possibilities are the considered in the present work.
. The only possibilities are the considered in the present work.
4.1. Two Points Design
Using the formula (2), it is possible to obtain the following expression:
 (3)
(3)
where  and
and  are the squares of the determinants which result from combining the column matrices
are the squares of the determinants which result from combining the column matrices
 with
with 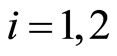 and operating conveniently. An analytical expression to the optimal weights can be obtained calculating the critical points for the last expression:
and operating conveniently. An analytical expression to the optimal weights can be obtained calculating the critical points for the last expression:

To compute the optimal points  will be enough to replace
will be enough to replace  in the determinant expression and to use a maximization routine. Note the parameter dependence still persists due to non-linearity of the model. To avoid such dependence, Chernoff (1953) [7] suggests providing a prior guess for the parameters
in the determinant expression and to use a maximization routine. Note the parameter dependence still persists due to non-linearity of the model. To avoid such dependence, Chernoff (1953) [7] suggests providing a prior guess for the parameters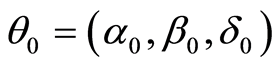 . In that sense, the achieved designs in the present work will be called locally
. In that sense, the achieved designs in the present work will be called locally 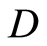 -optimal. The parameter estimates were obtained in Atkinson et al. (1995) [1] . The last step will be to calculate the value of the original variables through inverse change
-optimal. The parameter estimates were obtained in Atkinson et al. (1995) [1] . The last step will be to calculate the value of the original variables through inverse change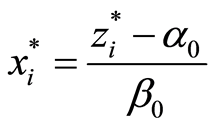 . The obtained result is shown in table 1.
. The obtained result is shown in table 1.
4.2. Three Points Design
It is known from other previous works that it can consider a symmetrical design for the present case. Let's us assume such design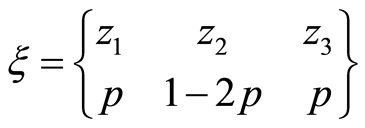 . Applying the determinant formula and proceeding analogously as
. Applying the determinant formula and proceeding analogously as
(3), it is possible to achieve a tractable expression for the determinant and an analytical formula for the optimal weights in a way:
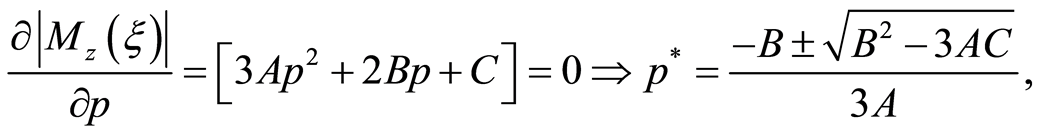
being A, B and C the squares of the determinants which result from applying the formula to its fast calculation grouped conveniently. Taking into account the previous considerations, the results are shown in Table 2.
An advantage of working with approximate designs is that the optimality of a design can be easily checked. Kiefer and Wolffowitz (1960) [8] provided a main result for optimal experimental design theory: the general equivalence theorem. The central point of this theorem establishes a necessary condition to check whether a proposed design is  -optimal or not. It consists of verifying if the standardized variance of the prediction, which is known as sensitivity function and is defined as
-optimal or not. It consists of verifying if the standardized variance of the prediction, which is known as sensitivity function and is defined as

is equal to number of parameters in the support points of the design. However, for the present case it is not possible to apply directly the above formula due to lack of knowledge about gender. It requires to use an extension of the equivalence theorem motivated by Chaloner and Larntz (1989) [9] :
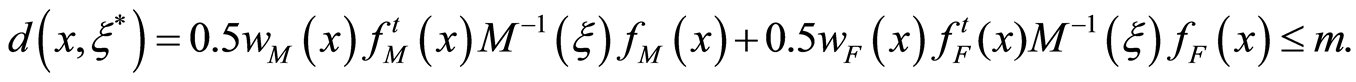
The results shown in Figure 1 allows us to validate the optimal designs proposed in this work. As we can observe from the figures, the points where the sensitivity function intersects the number-parameter line represent the optimal points obtained with the procedure described in this paper.
5. Conclusions
In this paper, it is proposed the use of canonical forms to solve a problem non-standard of optimal experimental designs laid out by Atkinson et al. (1995) [1] upon calculating the optimum dose of a fly insecticide. The main difficulty arises by adding uncertainty about gender since they differ in the response and the experiment only senses applied on the whole population. The witty transformation of the problem to a canonical version reduces the parameter dependence leading to analytical expression of the optimal weights. From these, we are able to compute D-optimal designs for several cases. In particular, it is constructed optimal designs for two and three dose levels.
Regarding future work, we will try to take advantage of the transformation geometry,  , for identifying
, for identifying
Table 2. Locally D-optimal designs for three points design.
 (a)
(a)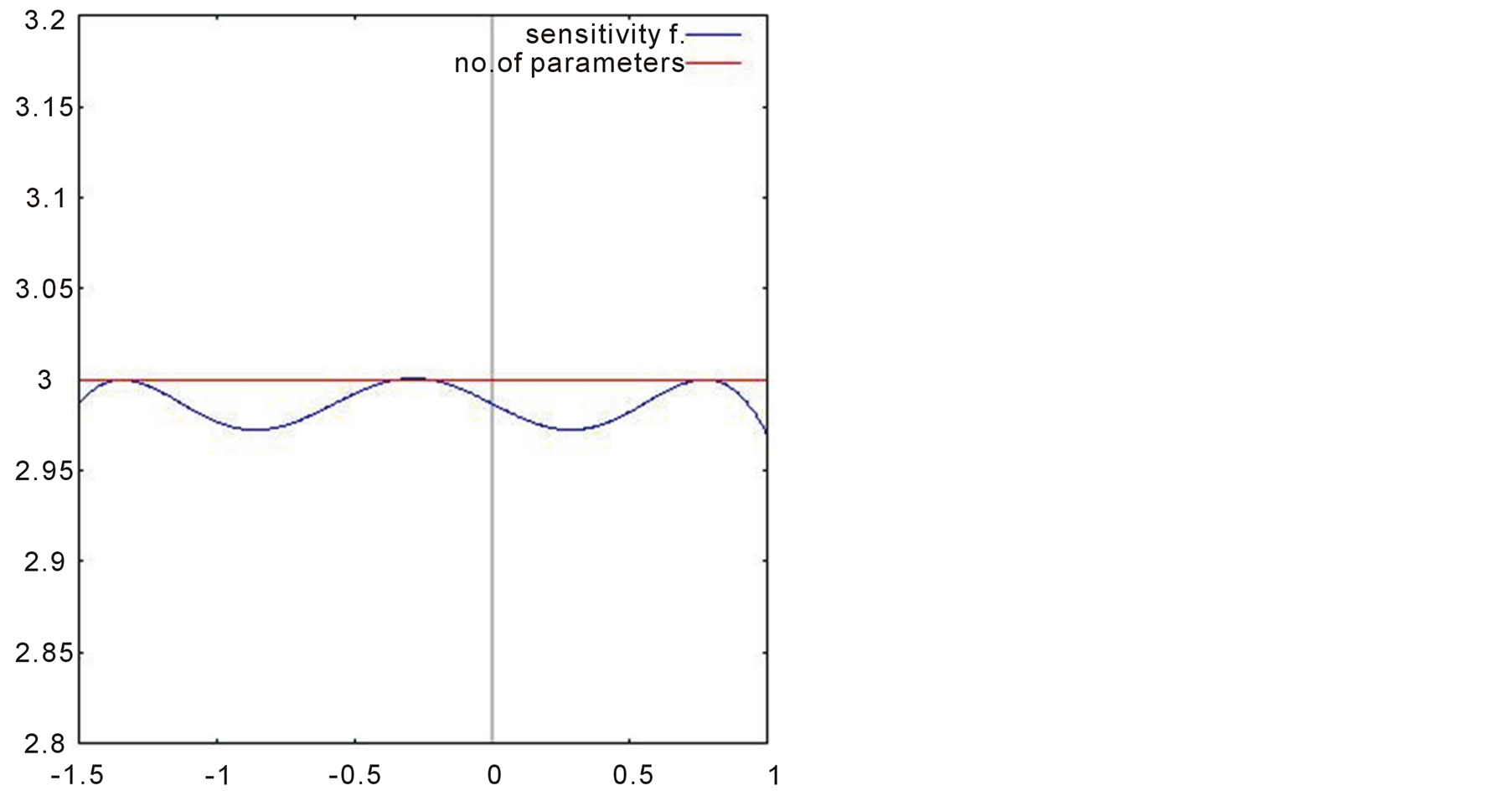 (b)
(b)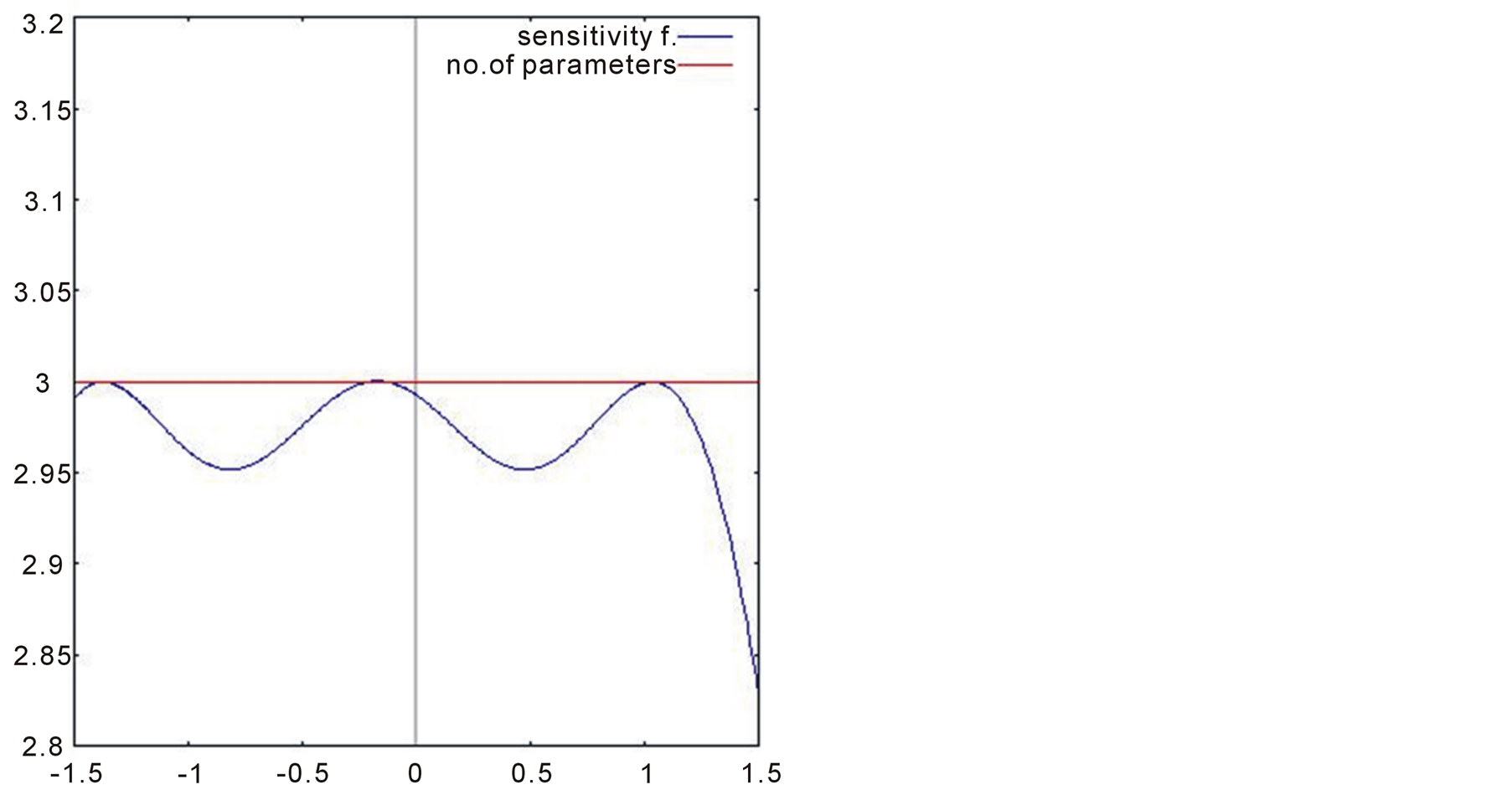 (c)
(c)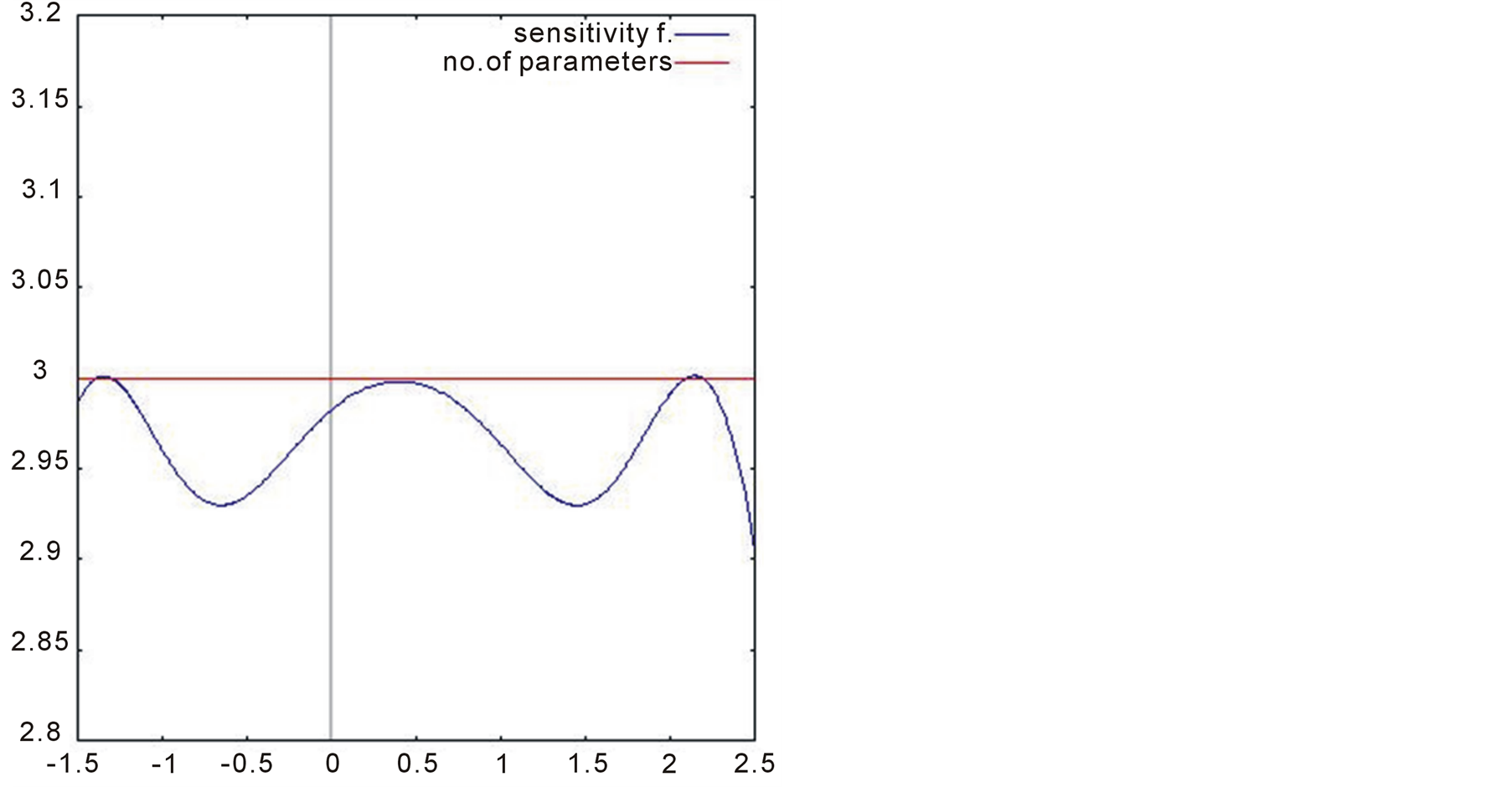 (d)
(d)
Figure 1. Testing locally D-optimal designs ( ,
,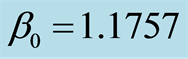 ). (a) 2 points:
). (a) 2 points: ; (b) 3 points:
; (b) 3 points: ; (c) 3 points:
; (c) 3 points: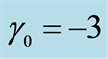 ; (d) 3 points:
; (d) 3 points: .
.
the support point. It is known that these are the points of contact between 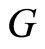 and the smallest ellipsoid centred on the origin containing
and the smallest ellipsoid centred on the origin containing  (Sibson, 1972 [10] , Silvey and Tittetington, 1973 [11] , Silvey, 1980 [3] , and Torsney and Musrati, 1993 [12] ). However, this procedure must be adapted non-trivially to add two readings by observation with their corresponding probabilities.
(Sibson, 1972 [10] , Silvey and Tittetington, 1973 [11] , Silvey, 1980 [3] , and Torsney and Musrati, 1993 [12] ). However, this procedure must be adapted non-trivially to add two readings by observation with their corresponding probabilities.
References
- Atkinson, A.C., Demetrio, C.G.B. and Zochhi, S.S. (1995) Optimun Dose Levels When Males and Females Differ en Response. Applied Statistics, 44, 213-226.
- McCullagh, P. and Nelder, J.A. (1992) Generalized Linear Models. Chapman and Hall, London.
- Silvey, S.D. (1980) Optimal Design. Chapman and Hall, London. http://dx.doi.org/10.1007/978-94-009-5912-5
- Ford, I., Tosney, B. and Wu, C.F.J. (1992) The Use of a Canonical form in the Construction of Locally Optimal Designs for Non-Linear Problems. Journal of the Royal Statistical Society: Series B, 54, 569-583.
- Fedorov, V.V. (1972) Theory of Optimal Experiments. Academic Press, New York.
- Ardanuy, R., Lopez-Fidalgo, J., Laycock, P.J. and Wong, W.K. (1999) When Is an Equally-Weihted Design D-Optimal? Annals of the Institute of Statistical Mathematics, 51, 531-540. http://dx.doi.org/10.1023/A:1003954207112
- Chernoff, H. (1953) Locally Optimal Designs for Estimating Parameters. The Annals of Mathematical Statistics, 24, 586-602. http://dx.doi.org/10.1214/aoms/1177728915
- Kiefer, J. and Wolfowitz, J. (1960) The Equivalence of Two Extremun Problems. Canadian Journal of Mathematics, 12, 363-366.
- Chaloner, K. and Larntz, K. (1989) Optimal Bayesian Design Applied to Logistic Regression Experiments. Journal of Statistical Planning and Inference, 21, 191-208. http://dx.doi.org/10.1016/0378-3758(89)90004-9
- Sibson, R. (1972) Discussion on Results in the Theory and Construction of D-Optimun Experimental Designs (by H. P. Wynn). Journal of the Royal Statistical Society, 34, 174-175.
- Silvey, S.D. and Titterington, D.M. (1973) A Geometrical Approach to Optimal Design Theory. Biometrika, 60, 21-32. http://dx.doi.org/10.1093/biomet/60.1.21
- Torsney, B. and Musrati, A.K. (1993) On the Construction of Optimal Designs with Applications to Binary Response and to Weighted Regression Models. Model Oriented Data Analysis, Physica-Verlag, Heidelberg.


