Applied Mathematics
Vol.5 No.3(2014), Article ID:42645,5 pages DOI:10.4236/am.2014.53036
The Unified Geometrical Theory of Fields and Particles
Department of Physics and Mathematics, Federal University of Technology, Owerri, Nigeria
Email: amaghnduka@yahoo.com.au
Received October 23, 2013; revised November 23, 2013; accepted November 30, 2013
ABSTRACT
Wave-particle duality is a familiar concept in the theories of the fundamental processes. We have, for example, electromagnetic waves with the photon as the corresponding particle, gravitational waves with the graviton as the corresponding particle, and Dirac waves with the electron as the corresponding particle. All these theories are stand-alone theories having nothing in common. The outstanding problem is a unified theory of particles and fields. In this paper, we discuss a unified geometrical theory of fields and particles.
Keywords:Wave-Particle Duality; Boson; Fermion; Euclidean; Pseudoeuclidean; Reducible; Irreducible; Discrete Geometry; 4-Operator; Invariant Operator
1. Introduction
We have today a unified particle theory of fermions and a unified particle theory of force particles (bosons), i.e. a synthesis of gravitation, electromagnetism, weak and strong nuclear interactions into a single electro-gravinuclear force [1]. It is therefore natural to seek for a unified theory of particles and fields.
A fundamental entity in the geometrical theory of science is the 4-tensor space of rank one, a pseudoeuclidean space. The only physical resident in this space (an observable) outside the nuclear realm is characterized geometrically by the fact that its temporal displacement (cdt) between any two points of the space is equal to its euclidean distance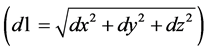 . Thus, the only known resident in this space is the photon, a particle whose state is characterized by a pair of 4-operators (pm, Am) [1]. This space has no known material resident.
. Thus, the only known resident in this space is the photon, a particle whose state is characterized by a pair of 4-operators (pm, Am) [1]. This space has no known material resident.
The most important fact is that this 4-tensor space is reducible. In the quantum domain, it is reducible to a pair of irreducible 2-dimensional subspaces whose residents are fermions. In fact, a 4-tensor space of arbitrary order (n) is reducible to a number of 2-dimensional subspaces [1]. Here the corresponding state is again characterized by a pair of 4-operators (pm, gm) [2].
In the classical domain, the 4-tensor space of rank one is reducible to a pair of irreducible subspaces of 1 and 3 dimensions. The subspace of 3-dimenstion is the familiar euclidean space whose residents are well-known as 3-dimensional material objects. The subspace of dimension one has the graviton, an antiparticle, as its only resident. Being an antiparticle, a force particle, the graviton is absolutely separated (remote) from us; hence its velocity relative to us must be vanished! Thus, its state is again characterized by (pm, Am) subject to the constraint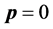 .
.
2. The Algebra of 4-Operators
The admissible 4-operators are either null, time-like or space-like 4-operators. Examples of 4-operators include space-time, 4-momentum, 4-angular momentum, 4-wave, and 4-spin 4-operators. 4-operators do not have the usual algebraic properties as ordinary linear operators of analysis: 4-operators can be multiplied by real numbers and two 4-operators of the same type can be added together to give 4-operators of the same type, thus the multiplicative axiom of ordinary algebra is not valid. By repeated application of the process of adding 4-operators one can form sums of more than two of them, and one can proceed to build up an algebra with them. In this algebra all the axioms of ordinary algebra, with the exception of the multiplicative axiom, are valid. 4-operators, however, have the additional property that 4-invariants (Einstein products) can be constructed with any two of them.
3. The Coordinate Representation
The fundamental dynamical variables are the 4-coordinates, qm = (x0, x1, x2, x3), where x0 = ct is the temporal displacement, and pm = (p0, p1, p2, p2), where p0 = E/c. These observables satisfy the generalized fundamental quantum conditions.
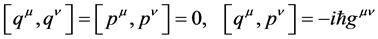 . (1)
. (1)
Here m, n take the values 0, 1, 2, 3 and gmn is the metric tensor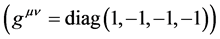 . Equation (1) differs from the conventional quantum conditions of quantum mechanics in that it treats x0 and p0 on equal footing with the space coordinates. Equation (1) constitutes the basic equations of the new theory.
. Equation (1) differs from the conventional quantum conditions of quantum mechanics in that it treats x0 and p0 on equal footing with the space coordinates. Equation (1) constitutes the basic equations of the new theory.
Equations (1) show that the q’s and p’s separately form a complete commuting set of observables. Each set by itself constitutes a geometrical basis for a representation. The last equation of (1) shows that in the classical limit (h ® 0), the q’s commute with the p’s, so that all eight dynamical variables are needed for the determination of the state of a classical system. This is, however, not the case in the quantum domain. That representation in which the q’s take simultaneous values and the p’s are given by
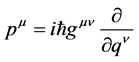 (2)
(2)
is called the coordinate representation. A symmetrical representation, called the momentum representation, is that for which pm ® pm and qm is given by
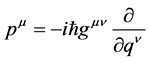 (3)
(3)
Thus, the momentum representation is that in which the p’s take simultaneous values and the q’s are represented by differential operators. In this paper we work entirely in the coordinate representation so that the coordinates, qm = (x0, x1, x2, x3), span the space of observation, called space-time (E4). It follows that the set of kets 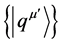 constitutes a basis of space-time; consequently we must have at each point of space-time,
constitutes a basis of space-time; consequently we must have at each point of space-time,
 , (4)
, (4)
called the orthonormality condition, and
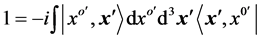 , (5)
, (5)
called the closure relation.
4. Invariant Operator Theorem
Let a denote the complete set of eight commuting observables of the system under study so that the state ket is given by 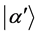 (the state may also be represented by a bra)
(the state may also be represented by a bra) 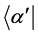 [1]. We obtain the expansion of the state ket
[1]. We obtain the expansion of the state ket 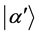 in terms of the basic kets of E4 by multiplying (5) from the right by
in terms of the basic kets of E4 by multiplying (5) from the right by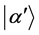 ,
,
 (6)
(6)
where 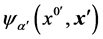 is the state (wave) function at the point
is the state (wave) function at the point  of
of 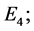
 is the component of the state ket
is the component of the state ket  at this point of
at this point of 
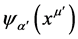 is physically the probability amplitude for a particular result of observation at the point xm¢ of E4, while its square gives the probability density for the particular result. The amplitude at another point xm² of E4 is obtained by multiplying equation 6) from the left by the bra
is physically the probability amplitude for a particular result of observation at the point xm¢ of E4, while its square gives the probability density for the particular result. The amplitude at another point xm² of E4 is obtained by multiplying equation 6) from the left by the bra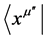 ,
,
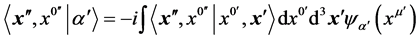 (7)
(7)
where  is the well known Feynman’s transformation function that connects the two sets of basis kets.
is the well known Feynman’s transformation function that connects the two sets of basis kets.
Equation (7) is fundamental in that it poses the crucial question: Suppose that we know the amplitude at the point xm¢ of E4 what is the amplitude at any other point xm² of E4. R.P. Feynman gave a solution to this problem in his space-time approach to quantum mechanics based on path integrals [3]. We note that Equation (7) is consistent in that the temporal coordinate x0 appears explicitly in the theory unlike the original equations of Feynman.
In this paper we give another solution to this problem. It is desired to find the equation of motion that determines 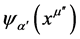 once
once 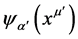 is known. The key point here is the observation that the state ket
is known. The key point here is the observation that the state ket  remains the same at all points of E4, as is obvious from Equation (7). In other words the state ket
remains the same at all points of E4, as is obvious from Equation (7). In other words the state ket 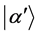 remains unchanged during the motion of the system, while the state function depends on the space-time point in question. We infer that there exists an invariant (Killing) operator F, which is in general a function of the q’s, p’s and any other distinct dynamical variable, l say, that may be required for the complete characterization of the dynamical system, such that the equation,
remains unchanged during the motion of the system, while the state function depends on the space-time point in question. We infer that there exists an invariant (Killing) operator F, which is in general a function of the q’s, p’s and any other distinct dynamical variable, l say, that may be required for the complete characterization of the dynamical system, such that the equation,
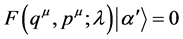 , (8)
, (8)
is satisfied. The determination of the probability amplitude at any point xm¢ of E4 is then reduced to the problem of finding the representatives of Equation (8) in the coordinate representation, and solving the differential equations that arise there from. In other words 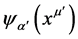 is determined by the differential equation
is determined by the differential equation
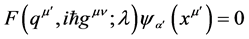 . (9)
. (9)
Equation (9) is the embodiment of a new physical theory. As we shall see Equation (9) gives all the well known wave theories of theoretical physics excluding the non-relativistic Schrodinger’s equation. This theory, called the invariant operator theory, thus gives the unified field and particle theory of the fundamental processes. Consequently the problem of finding the equation of motion of a dynamical system (classical or quantum) is reduced to the problem of determining the 4-invariant operators F(qm, pm; l) appropriate for the system under study. This in turn implies the determination of the 4-operators that determine the states of the system under study. This is the content of the 4-operator theorem of theoretical physics.
5. Applications
As our first application, we consider a dynamical system consisting of an isolated material particle. Such a system does not have internal degrees of freedom, hence its associated 4-operator is the 4-momentum pm = (p0, p1p2, p3), and the corresponding 4-invariant operator is just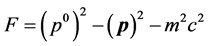 , where m is the mass of the particle. Equation (9) gives the wave equation for the wave function in the form,
, where m is the mass of the particle. Equation (9) gives the wave equation for the wave function in the form,
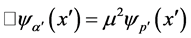 , (10)
, (10)
where  is the d’ Alembertian operator, m = mc/h, x¢ = xm¢, and p¢ = pm¢. Equation (10) is the wellknown Klein-Gordon (KG) equation [4].
is the d’ Alembertian operator, m = mc/h, x¢ = xm¢, and p¢ = pm¢. Equation (10) is the wellknown Klein-Gordon (KG) equation [4].
The energy E¢ and velocity v¢ of the KG – particle are given by E¢ = c(m2c2 + p¢2) and v¢ = c2p¢/E¢ respectively. The frequency and wavelength of the associated KG – wave are given by n = E¢/h and l = h/p¢ respectively, so that the velocity of the KG-wave is given by ln = E¢/p¢ = c2/v¢, which is greater than c. Thus, the KG – wave cannot represent a physical state in agreement with the dimensionality theorem [1].
As our second example, we consider the free electromagnetic field. The state of the system is defined by a pair of 4-vectors (pm, Am), and hence is represented by the ket  The associated invariant operators are pmpm, pmAm, AmAm. The first invariant operator, pmpm, gives, on using Equation (9) the usual wave equation for
The associated invariant operators are pmpm, pmAm, AmAm. The first invariant operator, pmpm, gives, on using Equation (9) the usual wave equation for 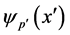 and
and  which are KG-equations with m = 0. On putting
which are KG-equations with m = 0. On putting  and
and , we find that the second invariant operator,
, we find that the second invariant operator, 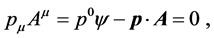 which in the coordinate representation becomes
which in the coordinate representation becomes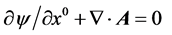 . This is the well-known Lorentz condition of electromagnetism. Thus, the Lorentz condition is seen to arise naturally as a constraint on
. This is the well-known Lorentz condition of electromagnetism. Thus, the Lorentz condition is seen to arise naturally as a constraint on 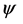 and
and 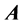 and not merely imposed as an arbitrary subsidiary condition. Finally the third invariant operator,
and not merely imposed as an arbitrary subsidiary condition. Finally the third invariant operator, 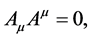 gives a new constraint on the potentials
gives a new constraint on the potentials 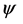 and
and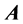 .
.
Further, we consider the problem of a charged material particle of 4-momentum 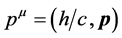 in a fixed external electromagnetic field of 4-potential
in a fixed external electromagnetic field of 4-potential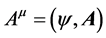 . The combined system can be considered as a single dynamical system, a particle, having 4-momentum
. The combined system can be considered as a single dynamical system, a particle, having 4-momentum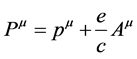 , which is simply the sum of pm and Am, with e/c a constant required by dimensional considerations. Thus, a charged particle interacting with an external electromagnetic field is analogous to a free particle of 4-momentum
, which is simply the sum of pm and Am, with e/c a constant required by dimensional considerations. Thus, a charged particle interacting with an external electromagnetic field is analogous to a free particle of 4-momentum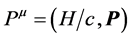 , where
, where and
and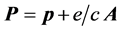 . On putting h = mgc2,
. On putting h = mgc2,  where
where 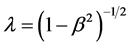 and b = n/c, we find that
and b = n/c, we find that
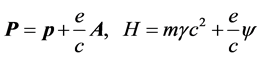 . (11)
. (11)
From the hamiltonian H one can find the lagrangian (L) of the particle from the general formula 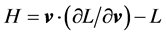 ,
,
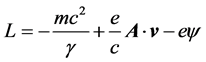 . (12)
. (12)
With the Lagrangian known one can proceed to obtain the equations of motion of a charged particle in a field [5]. Our solution is more natural than the conventional method which uses variational method.
The conclusion to be drawn from our two examples of a free material particle and a charged material particle interacting with a fixed electromagnetic field is that such physical systems have only particle states, and no wave states, because they are described by a single 4-operator. The situation is completely different when one considers the Dirac electron described by a pair of 4-operators (pm, gm) and Dirac electron in an external electromagnetic field described by a pair of 4-operators (Pm, gm). Our approach gives elegant and simple solutions to these problems in contradistinction to the conventional methods [2].
As our final example, we consider gravitation, an influence mediated by the graviton, a force particle. This influence is only along the temporal axis, and its existence is only manifested by its interaction with massive objects. In other words the graviton is an antiparticle of dimension , and because it is not an object one can see, its velocity relative to us is zero. Since it is now known that the graviton has rest mass (m) [6], we infer that its momentum
, and because it is not an object one can see, its velocity relative to us is zero. Since it is now known that the graviton has rest mass (m) [6], we infer that its momentum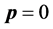 . Unlike electromagnetism gravitation is not known to exhibit such effects as polarization, interference, etc. Consequently gravitation is characterized by a pair of 4-operators (pm, Am), where
. Unlike electromagnetism gravitation is not known to exhibit such effects as polarization, interference, etc. Consequently gravitation is characterized by a pair of 4-operators (pm, Am), where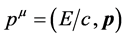 , and
, and ; with associated invariants, pmpm = m2c2, pmAm = m2c2, AmAm = m2c2. The last two invariants are mere constraints on y, implying that y is time-independent and has the dimension of energy per unit mass. pmpm = m2c2 on the other hand gives the invariant operator F = pmpm – m2c2 = 0, so that the equation of motion is given by
; with associated invariants, pmpm = m2c2, pmAm = m2c2, AmAm = m2c2. The last two invariants are mere constraints on y, implying that y is time-independent and has the dimension of energy per unit mass. pmpm = m2c2 on the other hand gives the invariant operator F = pmpm – m2c2 = 0, so that the equation of motion is given by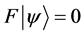 . On multiplying this equation from the left by the bra
. On multiplying this equation from the left by the bra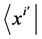 , i = 1, 2, 3, we obtain in the coordinate representation the important equations.
, i = 1, 2, 3, we obtain in the coordinate representation the important equations.
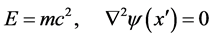 , (13)
, (13)
where , and
, and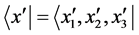 . The second of (13) is the familiar Newton’s equation of gravitation, and E is the rest mass energy. We associate the potential y with gravitational field intensity
. The second of (13) is the familiar Newton’s equation of gravitation, and E is the rest mass energy. We associate the potential y with gravitational field intensity , then
, then 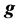 satisfies the field equations
satisfies the field equations
 . (14)
. (14)
Thus, the gravitational field equations of Newton are derivable from the invariant operator theory.
6. Conclusions
An important development arising from our considerations is the geometrical definition of the photon and graviton, the two fundamental particles without corresponding antiparticle and particle respectively. The photon is a particle whose temporal displacement (cdt) is equal to its euclidean distance. Its speed is thus seen to be the speed of light. It follows that for the photon and hence other relativistic material particles, the quantity dt/g, where g = (1 – b2)–1/2, b = v/c, not dt, is an invariant quantity, and that dt/g is zero, positive, or negative for light-like, time-like, or space-like processes respectively. The graviton, on the other hand, is a physical entity whose temporal and Euclidean displacements vanish. Consequently, a relativistic theory of gravitation is meaningless.
The invariant operator theory is a powerful physical theory. As we have seen, the theory reduces the problem of finding the equations of motion for a physical system to that of finding invariant operators, F(qm, pm; l), appropriate for the system. An important consequence of this assertion is the invariant operator theorem: A necessary and sufficient condition for the realization of a physical theory of a given dynamical system (classical or quantum) is that the system is endowed with 4-operators. If the system is endowed with a single 4-operator, only a particle theory in which the space-time background (xm) plays a dynamical role is possible. If, however, the system is endowed with a pair of 4-operators, only a wave theory is possible, in which case the space-time background plays a passive role serving only as the observation points. This conclusion is in complete agreement with the dimensionality theorem [1].
In the limit of low speed, H = mgc2 ® mc2 + (mv2/2), and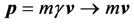 , where the term mc2 in H is irrelevant because it is impotent in the derivation of the equations of motion. Thus, in the Newtonian limit, the 4-momentum pm goes over into a decoupled form
, where the term mc2 in H is irrelevant because it is impotent in the derivation of the equations of motion. Thus, in the Newtonian limit, the 4-momentum pm goes over into a decoupled form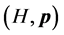 , and via the equation
, and via the equation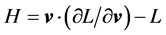 , one obtains the lagrangian L of the system and hence the equations of motion. Integration of Lagrange’s equations of motion gives the states of the system in the familiar form (t, xi; H, pi).
, one obtains the lagrangian L of the system and hence the equations of motion. Integration of Lagrange’s equations of motion gives the states of the system in the familiar form (t, xi; H, pi).
Finally, Erwin Schrodinger (1926) obtained a “wave theory” of the hydrogen atom electron, which is called Schrodinger’s equation. This theory treats the electron of atomic hydrogen as a bare particle having no internal degrees of freedom. This treatment is deficient and hence is inconsistent with the invariant operator theory. P.A.M. Dirac’s treatment of the same system is more realistic and is in excellent agreement with the invariant operator theory.
Our present work is concerned with the problem of the determination of the states of a single particle system in interaction or free. We have seen that the invariant operator theory solves this problem with pristine beauty. The outstanding problems relate to the determination of the states of multiparticle systems. This problem has already been solved for a system of fermions (atoms, nuclei, and molecules) [7], and also for a system of bosons using the arsenal of discrete geometry [1]. The remaining problem is the determination of the states of fermion-boson systems, which is the theory of weak and strong nuclear interactions. The theory of weak and strong nuclear interactions is the subject of our next paper.
REFERENCES
- A. Nduka, “The Geometrical Theory of Science,” Applied Mathematics, Vol. 3, No. 11, 2012, pp. 1598-1600. http://dx.doi.org/10.4236/am.2012.311220
- V. B. Berestetskii, E. M. Lifshitz and L. P. Pithaevskii, “Relativistic Quantum Theory,” Pergamon Press, Oxford, 1971.
- R. P. Feynman and A.R. Hibbs, “Quantum Mechanics and Path Integrals,” Mcgraw-Hill Book Company, New York, 1964.
- J. J. Sakurai, “Advanced Quantum Mechanics,” Addison-Wesley Publishing Company, Reading, 1967.
- L. D. Landau and E. M. Lifshitz, “The Classical Theory of Fields,” Pergamon Press, Oxford, 1971.
- A. Nduka, “The Neutrino Mass,” Applied Mathematics, Vol. 4, No. 2, 2013, pp. 310-131.
- A. Nduka, “The Structure of Atoms, Nuclei, and Molecules,” AJP, Vol. 5, 2013, to appear.

