Applied Mathematics
Vol.4 No.12(2013), Article ID:39794,7 pages DOI:10.4236/am.2013.412218
A Forward-Looking Nash Game and Its Application to Achieving Pareto-Efficient Optimization
1School of Electronics and Information Engineering, Beijing Jiaotong University, Beijing, China
2Department of Electronic and Electrical Engineering, University College London, Torrington Place, London, UK
Email: jee.ren@live.cn, kai-kit.wong@ucl.ac.uk, houjj@bjtu.edu.cn
Copyright © 2013 Jie Ren et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 19, 2013; revised October 19, 2013; accepted October 26, 2013
Keywords: Belief; Cognition; Iterative Algorithm; Nash Equilibrium; Pareto-Optimality; Stackelberg
ABSTRACT
Recognizing the fact that a player’s cognition plays a defining role in the resulting equilibrium of a game of competition, this paper provides the foundation for a Nash game with forward-looking players by presenting a formal definition of the Nash game with consideration of the players’ belief. We use a simple two-firm model to demonstrate its fundamental difference from the standard Nash and Stackelberg games. Then we show that the players’ belief functions can be regarded as the optimization parameters for directing the game towards a much more desirable equilibrium.
1. Introduction
Game theory has been very well recognized as a branch of applied mathematical tools, best for analyzing the phenomenon of selfish competition, which arises in numerous real-life applications ranging from economics to social sciences, and even to engineering problems. Many optimization problems can be viewed as a competition problem.
If there are shared resources, then inherently there will be competition in the allocation of such resources. An individual who participates in the resource allocation always wishes to maximize its payoff. Nevertheless, the player’s return not only depends on its own strategy, but is also dependent on competitors’ responses. As a result, ideally, a player should choose or optimize its strategy based on not only its immediate return but also the possible outcomes of how others might respond to its strategy. Apparently, a player’s cognition (i.e., its belief on how the environment as a whole would react to any of its action) will be pivotal in the optimization of its strategy for maximizing its payoff and in defining the equilibrium of the game.
In the literature, there are a number of game-theoretic models and they differ in their assumptions on the players’ cognition. Due to this fundamental difference, these models represent different competition environmentsthereby resulting in very different outcomes, which at the steady state are referred to as equilibria. When the competition process reaches an equilibrium, by definition, no player would have incentive to change their strategies further to deviate from the equilibrium which is therefore usually considered as a satisfactory outcome to all players.
The most popular model has to be the Nash game [1] in which a player has the belief that other players’ strategies are fixed and will not change regardless of what it does. A Nash game is based on such assumption on the players’ cognition. It is noted that the game is still very well defined, although the player’s belief is totally inaccurate.
On the other hand, in a Stackelberg game [2], there is a super player, commonly known as leader, who knows all the information about its competitors, known as followers. In this case, the leader is considered to have perfect cognition and therefore can obtain the most rewarding strategy.
In most practical competition situations, the efficiency of a Nash game resulting in the most celebrated Nash equilibrium is often poor (which will be revealed by a two-firm example later in this paper). The main reason is that the assumption for the Nash game is too much simplified, and it fails to account for the interaction between the players. In contrast, the assumption for the Stackelberg model is too stringent and it is often too difficult to be qualified to be a leader in most practical scenarios. Nevertheless, the Stackelberg equilibrium is highly beneficial to the leader. The limitation is that if there were two or more leaders, all of which possess perfect cognition and wish to be the biggest winner, this would lead to a tragedy [3].
In this paper, we recognize the importance of players’ cognition in a game, and focus on how the assumption of the players’ cognition affects the equilibrium. Based on the analysis of Nash and Stackelberg equilibria, we provide a new definition for the Nash game with considera tion of the players’ belief. As a useful byproduct, the new definition facilitates the interpretation of the players’ belief as the optimization parameters, which, if optimized properly, can direct the game towards a Pareto-efficient equilibrium.
2. Preliminaries
2.1. The Two-Firm Model
For illustrative purpose, in this paper, we use a simple two-firm model in economics as an example. In this simple model, there are two firms, Firm A and Firm B. They manufacture an identical product and its unit cost is the same for both firms. In addition, the profit per unit product diminishes as the number of products available in the market increases. In particular, let  denote the number of products manufactured by Firm A, and
denote the number of products manufactured by Firm A, and 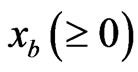 be that manufactured by Firm B. The unit cost is denoted by
be that manufactured by Firm B. The unit cost is denoted by 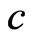 and the price per product which is set the same by both Firm A and Firm B is assumed to be
and the price per product which is set the same by both Firm A and Firm B is assumed to be 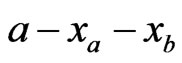 for some constant
for some constant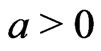 . Therefore, the profit functions for Firm A and Firm B are, respectively, given by
. Therefore, the profit functions for Firm A and Firm B are, respectively, given by
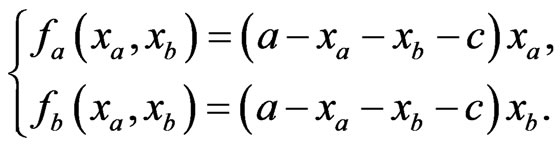 (1)
(1)
In various game-theoretic models, the objective would be for Firm A and Firm B to iteratively optimize their respective strategies, 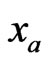 and
and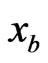 , for maximizing their profits (1) in a competitive fashion. Before we examine different equilibria of this two-firm game, we find it useful to first present the general notations of a game.
, for maximizing their profits (1) in a competitive fashion. Before we examine different equilibria of this two-firm game, we find it useful to first present the general notations of a game.
For a game with  players, we denote the strategy profile for player
players, we denote the strategy profile for player 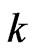 as
as 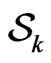 and use
and use
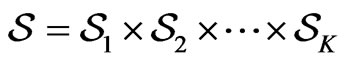 (2)
(2)
to represent the strategy profile for all the players. Moreover, we use 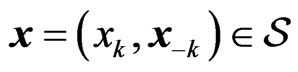 to denote a specific choice of strategy from all the players, where
to denote a specific choice of strategy from all the players, where 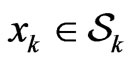 is the strategy adopted by player
is the strategy adopted by player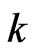 , and
, and
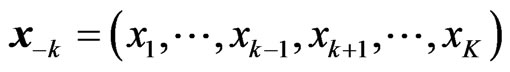 (3)
(3)
denotes the adopted strategy by all the players except player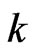 . Likewise, the reward function for player
. Likewise, the reward function for player 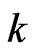 is denoted by
is denoted by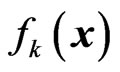 . If the game converges to an equilibrium, then we will use the superscript
. If the game converges to an equilibrium, then we will use the superscript 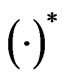 to highlight that the corresponding parameters are at the equilibrium. For instance, we have
to highlight that the corresponding parameters are at the equilibrium. For instance, we have 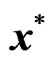 and
and 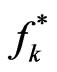 at the equilibrium.
at the equilibrium.
2.2. Nash Competition
Given the competition of K players, if at some point, no one can gain any further by deviating from its present strategy, then the strategy of all the players is said to have reached to an equilibrium [4]. Mathematically, we have
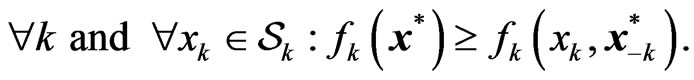 (4)
(4)
Now, proceed to derive the Nash equilibrium for the two-firm example. According to (4), Firm A solves
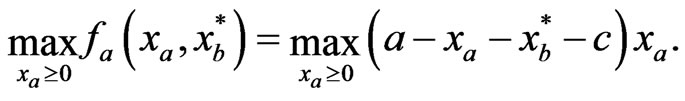 (5)
(5)
As such, it can be easily shown that
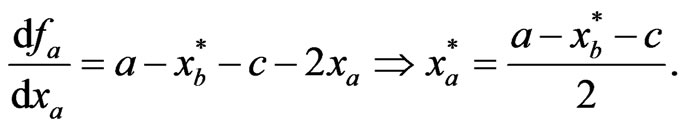 (6)
(6)
Similarly,  can be derived, resulting the set of simultaneous equations
can be derived, resulting the set of simultaneous equations
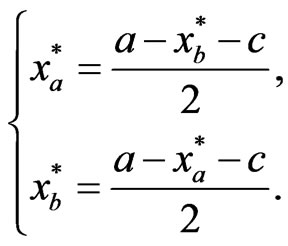 (7)
(7)
As a result, the game governed by (7) will reach the Nash equilibrium
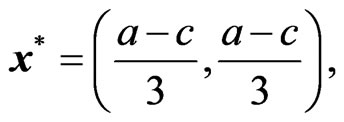 (8)
(8)
which leads to the profits
 (9)
(9)
It is worth pointing out here that in Nash equilibrium when taking 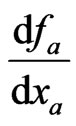 in the optimization for player A, player A believes that
in the optimization for player A, player A believes that 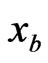 at any given time instance is optimal and fixed, or
at any given time instance is optimal and fixed, or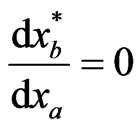 . This is obviously inaccurate. At the Nash equilibrium in particular, from (1.7), we actually have
. This is obviously inaccurate. At the Nash equilibrium in particular, from (1.7), we actually have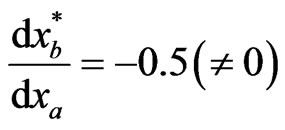 . This shows that a Nash player’s cognition and the reality have considerable difference and the profit function
. This shows that a Nash player’s cognition and the reality have considerable difference and the profit function  is in fact only the profit in the ideal situation
is in fact only the profit in the ideal situation 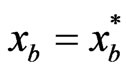 but does not represent the actual profit function due to interaction from player B.
but does not represent the actual profit function due to interaction from player B.
2.3. Stackelberg Competition
A player can benefit more from the rest of the players in a game if this player has perfect cognition about how others would react to its strategy. This is studied formally by the Stackelberg equilibrium. In the general setting with 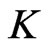 players, if player
players, if player  is the leader, it should know perfectly the response function
is the leader, it should know perfectly the response function 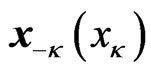 and therefore is able to obtain the most effective strategy such that
and therefore is able to obtain the most effective strategy such that
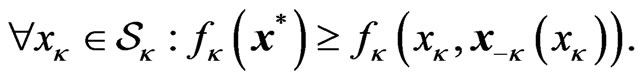 (10)
(10)
For other players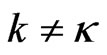 , as they do not have any information about any of the other players’ strategies, they can only assume that other players’ strategies are fixed, and will act like a Nash player, see (4). As a result, we have
, as they do not have any information about any of the other players’ strategies, they can only assume that other players’ strategies are fixed, and will act like a Nash player, see (4). As a result, we have
 (11)
(11)
In a Stackelberg game, there is a very strict order of how the players play the game [1,5]. In particular, leader  needs to first give out its strategy and lets other players compete to reach a Nash equilibrium against this strategy before it revises its strategy for another round of competition among the rest of the players. Achieving the Stackelberg equilibrium will thus require a two-level game.
needs to first give out its strategy and lets other players compete to reach a Nash equilibrium against this strategy before it revises its strategy for another round of competition among the rest of the players. Achieving the Stackelberg equilibrium will thus require a two-level game.
The merit of Stackelberg equilibrium is that leader 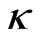 has an absolute advantage over other players but the drawback is that knowing the function
has an absolute advantage over other players but the drawback is that knowing the function  would be too difficult to achieve in practice, if not impossible. A standard approach would require the leader to try exhaustively all possible
would be too difficult to achieve in practice, if not impossible. A standard approach would require the leader to try exhaustively all possible 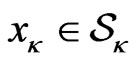 to identify the best strategy.
to identify the best strategy.
Recalling from the two-firm example, if we let Firm A be the leader and Firm B be the follower, then according to (11), player B’s cognition is that player A’s strategy is optimal and fixed and player B therefore aims to solve
 (12)
(12)
which by setting 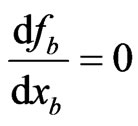 gives
gives
 (13)
(13)
which is the exact response function of player B with respect to any action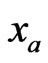 .
.
According to (10) and using (13), player A finds its best strategy by
 (14)
(14)
As a result, the best strategy for player A can be analytically obtained as
 (15)
(15)
and the corresponding strategy for player B is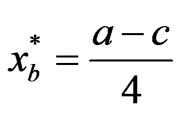 .
.
Hence, at the Stackelberg equilibrium, we have
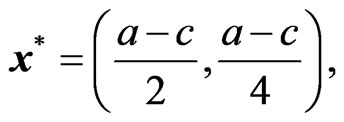 (16)
(16)
which leads to the profits
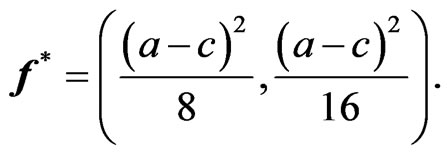 (17)
(17)
Note that in order to achieve the Nash equilibrium earlier, there is no specific order of obtaining 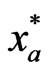 and
and 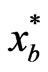 in solving the simultaneous Equations (7) and the equilibrium can be achieved by free competition. This is however not true for the Stackelberg equilibrium where the leader’s strategy,
in solving the simultaneous Equations (7) and the equilibrium can be achieved by free competition. This is however not true for the Stackelberg equilibrium where the leader’s strategy, 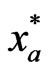 , must be obtained first and the follower(s) respond. As the number of players increases, the complexity of the Stackelberg game will increase considerably and the simplicity of the Nash game will prevail. In addition, a game with all leaders degenerates to a Nash game.
, must be obtained first and the follower(s) respond. As the number of players increases, the complexity of the Stackelberg game will increase considerably and the simplicity of the Nash game will prevail. In addition, a game with all leaders degenerates to a Nash game.
In the two-firm example, because Firm A knows precisely the strategy adopted by Firm B (13), it is able to achieve a higher profit than what is achieved by the Nash equilibrium. However, the key questions are:
• If (13) is not known by Firm A, or Firm A only knows partial information about (13), e.g.,  or only
or only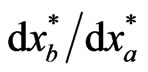 , would it still help Firm A to obtain a better or even Stackelberg strategy? If the answer is yes, this would mean that the level of cognition for a leader could be significantly reduced.
, would it still help Firm A to obtain a better or even Stackelberg strategy? If the answer is yes, this would mean that the level of cognition for a leader could be significantly reduced.
• Also, what if two players have partial information about each other’s strategies? What will happen?
This has motivated us to investigate the Nash game with simultaneous forward-looking players, in which each player optimizes its strategy based on its own belief.
3. Forward-Looking Competition
After the discussion of Nash and Stackelberg equilibria above, it is clear that players’ cognition is key to defining the resulting equilibrium of a game. At the same time, we understand the beauty of the Nash game where players can compete freely (without following a specific order) to reach the equilibrium. Based on these two points, we present the Nash game with forward-looking players.
To facilitate our analysis, we find it useful to have the following definitions.
• Environmental function—In a competition process, the reward for player 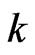 depends not only its own strategy
depends not only its own strategy  but also others’ strategies
but also others’ strategies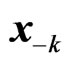 , at any given time instant
, at any given time instant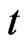 . We use the environmental function
. We use the environmental function  to quantify the influence of other players’ strategies (at time instant
to quantify the influence of other players’ strategies (at time instant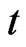 ) onto player
) onto player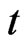 ’s reward. Obviously, other players’ strategies can always be treated as some form of response to a given player’s strategy at time instant
’s reward. Obviously, other players’ strategies can always be treated as some form of response to a given player’s strategy at time instant .
.
• Belief function—A player’s understanding on its environmental function reflects its cognition about the competition in the game. We assume that player 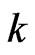 possesses the knowledge of a belief function, which is denoted as
possesses the knowledge of a belief function, which is denoted as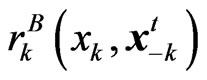 , where
, where 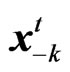 denotes the strategies from all the players at time instant
denotes the strategies from all the players at time instant 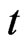 except player
except player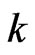 , and clearly
, and clearly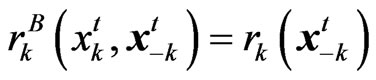 . The latter relationship further suggests to formulate the belief response using some form of Taylor series expansion. For example, we may write
. The latter relationship further suggests to formulate the belief response using some form of Taylor series expansion. For example, we may write
 (18)
(18)
where 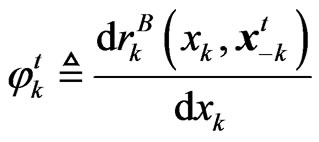 is regarded as the interference derivative (to be discussed in Section 3.3). The belief function
is regarded as the interference derivative (to be discussed in Section 3.3). The belief function  is player
is player ’s cognition on what the environmental function
’s cognition on what the environmental function 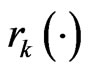 would be, given a strategy
would be, given a strategy  and the present state
and the present state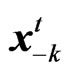 . If
. If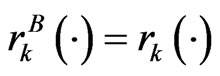 , then player
, then player ’s cognition will be perfect. Otherwise, it is only a prediction.
’s cognition will be perfect. Otherwise, it is only a prediction.
• Predicted reward—The predicted reward function, denoted by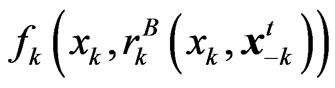 , indicates the amount of reward player
, indicates the amount of reward player  believes to achieve by the strategy
believes to achieve by the strategy 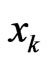 and other players’ strategies at time instant
and other players’ strategies at time instant ,
,  , based on the belief function
, based on the belief function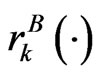 .
.
3.1. A Motivating Example
In Section 2.3, if player A is a Stackelberg leader, then it has the environmental function (or response) 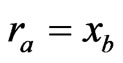 and knows perfectly the strategy of player B (13). Therefore, it has the perfect belief function
and knows perfectly the strategy of player B (13). Therefore, it has the perfect belief function
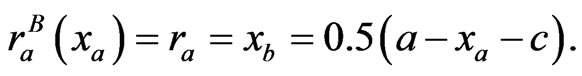 (19)
(19)
If player A’s cognition is reduced; for instance, knows at any given time instant 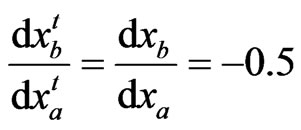 in (13) and can observe the environmental function at present time
in (13) and can observe the environmental function at present time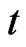 , i.e.,
, i.e., 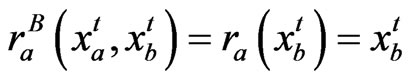 , player A can formulate its belief function, using a first-order Taylor series, as
, player A can formulate its belief function, using a first-order Taylor series, as
 (20)
(20)
and its predicted reward function can be expressed as
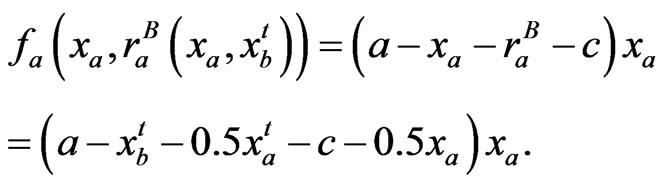 (21)
(21)
From the side of player B, if it has as low cognition as a Nash player, then it will have the belief function . Hence, player B’s reward function will be
. Hence, player B’s reward function will be
 (22)
(22)
As a result, player A’s strategy can be optimized by
 (23)
(23)
By setting , this suggests an updating process
, this suggests an updating process
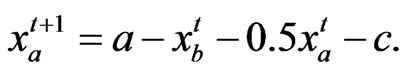 (24)
(24)
On the other hand, for player B, it aims to solve
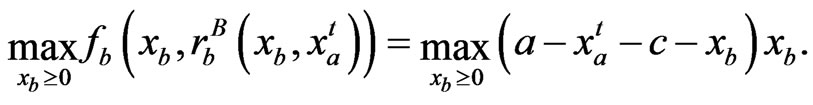 (25)
(25)
By setting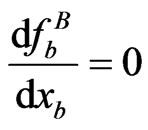 , player B updates its strategy by
, player B updates its strategy by
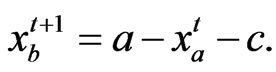 (26)
(26)
Applying the two updating rules (24) and (26) repeatedly, as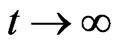 , we get
, we get
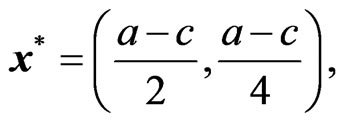 (27)
(27)
which ends up the same strategy in the Stackelberg equilibrium (16), but via a completely different process.
The striking result here is that the Stackelberg equilibrium can now be achieved by a free competition between the players without following a specific order of how the game should be played and that the so-called leader, i.e., player A here, does not need perfect cognition of the environmental function (13), but a good belief (20).
3.2. Definition of the New Equilibrium
Motivated by the potential of being forward-looking, we here present the Nash equilibrium with forward-looking players (i.e., with some cognition in the form of belief functions). Mathematically, it is written as
 (28)
(28)
where  is the belief function reflecting player
is the belief function reflecting player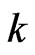 ’s cognition ability and
’s cognition ability and 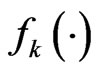 is the predicted reward function for player
is the predicted reward function for player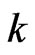 . Note that (28) can be rewritten as
. Note that (28) can be rewritten as
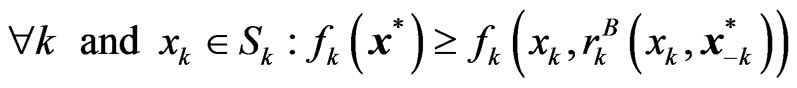 (29)
(29)
because according to (18), 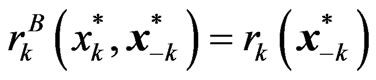 and as such, at the equilibrium, we have
and as such, at the equilibrium, we have
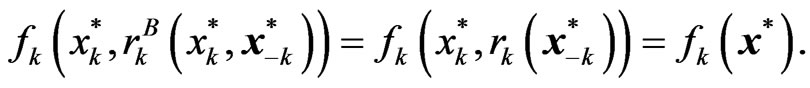 (30)
(30)
In this model, the belief function 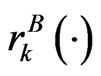 can be chosen arbitrarily and it only serves to indicate player
can be chosen arbitrarily and it only serves to indicate player ’s understanding about the competition environment. In fact, (29) embraces the conventional Nash equilibrium (4) in which players have the belief function
’s understanding about the competition environment. In fact, (29) embraces the conventional Nash equilibrium (4) in which players have the belief function  which effectively treats the environment player
which effectively treats the environment player  observes at any present time instant
observes at any present time instant  as fixed and constant and ignores the subsequent changes in other players’ strategies provoked by player
as fixed and constant and ignores the subsequent changes in other players’ strategies provoked by player ’s new strategy.
’s new strategy.
We refer to the equilibrium of a Nash game with belief functions as a belief-directed Nash equilibrium (BNE).
3.3. From Interference Derivative to Pareto-Optimality
In the proposed model of the Nash game with forwardlooking players, every player is free to choose its own belief function. Altogether, the combination of the players’ belief functions defines the resulting equilibrium of the players’ competition and has numerous possibilities. To examine this, we consider in the two-firm example that
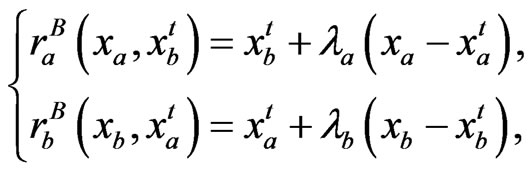 (31)
(31)
where 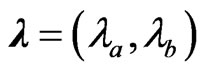 are regarded as the interference derivatives which can be interpreted as the rate of change of the environmental function with respect to one’s strategy. Also, (31) can be viewed as a first-order Taylor series approximation for the response. With (31), we can express the predicted reward functions for the players as
are regarded as the interference derivatives which can be interpreted as the rate of change of the environmental function with respect to one’s strategy. Also, (31) can be viewed as a first-order Taylor series approximation for the response. With (31), we can express the predicted reward functions for the players as
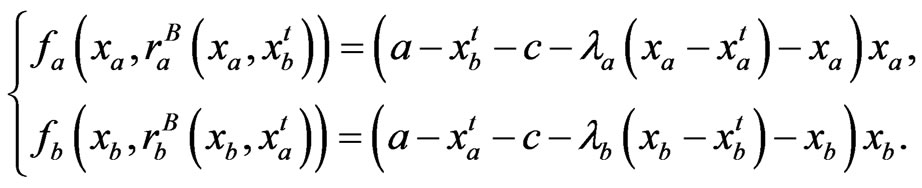 (32)
(32)
For convenience, we refer to this two-firm example as a BNE game by BNE(λ). In this game, player A aims to
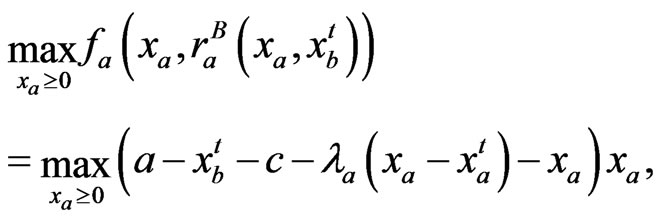 (33)
(33)
which can be solved by setting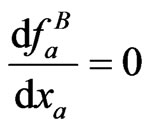 . This then gives
. This then gives
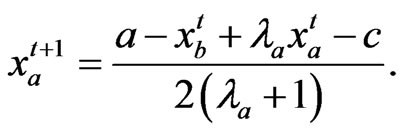 (34)
(34)
Similarly, we can easily derive the corresponding result for optimizing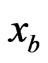 . As
. As 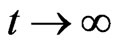 (after a sufficient number of iterations), at the equilibrium, we have
(after a sufficient number of iterations), at the equilibrium, we have
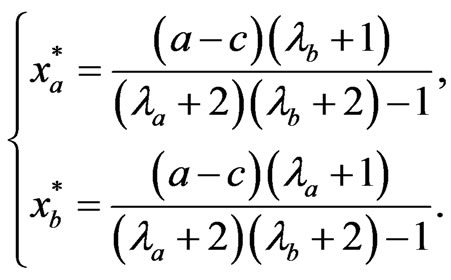 (35)
(35)
The above strategies will lead to the profits (or rewards)
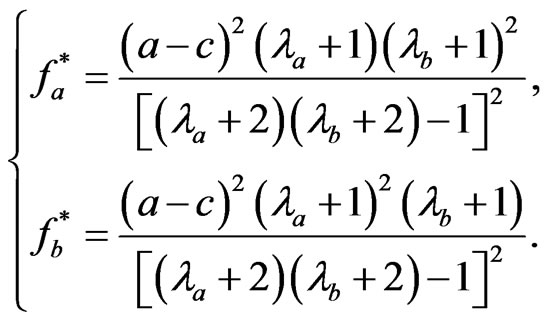 (36)
(36)
Very interestingly, we can observe that the equilibrium varies according to the belief parameters of the players,  , which offers an opportunity to optimize the equilibrium.
, which offers an opportunity to optimize the equilibrium.
In order to illustrate this, we let 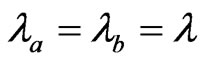 and consider that
and consider that 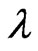 is an optimization parameter of the game. Then
is an optimization parameter of the game. Then  can be optimized by
can be optimized by
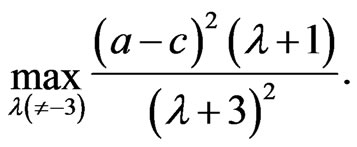 (37)
(37)
The above optimization maximizes both the sum-profit and the individual profits of the players, and therefore is Pareto-optimal. Note that 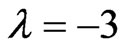 is not permitted as this would lead to unbounded solutions to
is not permitted as this would lead to unbounded solutions to  and
and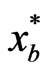 .
.
It can be easily shown that the optimal value of 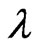 is
is , which gives
, which gives
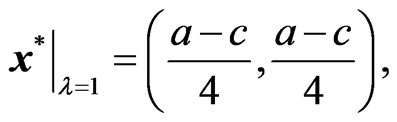 (38)
(38)
and
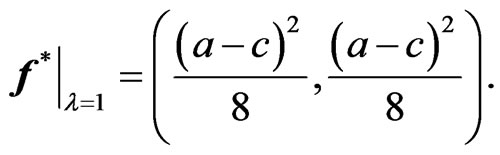 (39)
(39)
We summarize our results and include some interesting scenarios in Table 1. Note that in this two-firm example, the Stackelberg equilibrium is not Paretooptimal. It can be seen by comparing it with BNE(1) that if the leader is being less aggressive, its profit is not reduced but the profit for the follower can be further increased.
Another observation is that achieving Pareto-optimum does not require that the players’ cognition be accurate. In particular, for the case of Pareto-optimum, i.e., 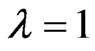 , we see from (34) that at the equilibrium, we have
, we see from (34) that at the equilibrium, we have
 (40)
(40)
However, intriguingly, the player’s cognition is very different and for player A, we have
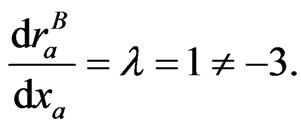 (41)
(41)
This reveals that the belief function a player has is not required to reflect the true reality but can still achieve the best outcome from the competition of the players. This has changed our understanding on how player’s cognition influences the equilibrium of a game. A beautiful world may be an outcome from people’s mistakes.
On the contrary, if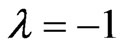 , then it can be shown that
, then it can be shown that

Table 1. Strategies and profits for various equilibria.
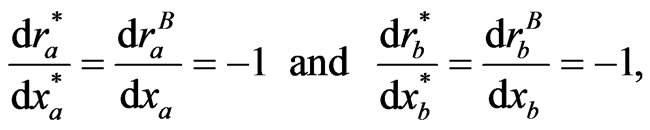 (42)
(42)
and the belief functions are perfect in terms of representing the reality. Unfortunately, the profits for both players at the equilibrium will be , showing that if both players are perfectly smart, the outcome could be a tragedy.
, showing that if both players are perfectly smart, the outcome could be a tragedy.
In this table, we also included the case with  which interestingly results in the same profits as the Nash equilibrium but with half production. To show how the belief (or the interference derivative
which interestingly results in the same profits as the Nash equilibrium but with half production. To show how the belief (or the interference derivative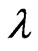 ) affects the strategy
) affects the strategy 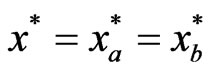 and the reward
and the reward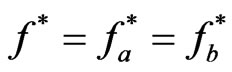 , we provide the results in Figure 1 assuming that
, we provide the results in Figure 1 assuming that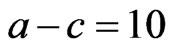 .
.
3.4. Existence
Since the birth of game theory, the quest for the existence of an equilibrium has been the focal point in this area. In [6], Nash proved the existence of the widely known Nash equilibrium we know today. Later, numerous researchers presented further theorems and proofs about the existence of the game-theoretic equilibria [7,8]. Based on what is known in the literature, we provide the sufficient condition for the existence of the general BNE game.
Corollary 1 Consider a 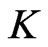 -player game, with the strategy spaces
-player game, with the strategy spaces 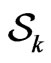 for
for , which are not empty, compact and convex subsets of an Euclidean space. If the predicted reward function
, which are not empty, compact and convex subsets of an Euclidean space. If the predicted reward function 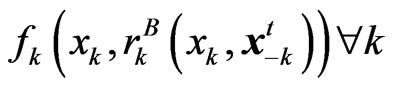 is continuous and quasi-concave in
is continuous and quasi-concave in  for any fixed
for any fixed , then there exists an equilibrium.
, then there exists an equilibrium.
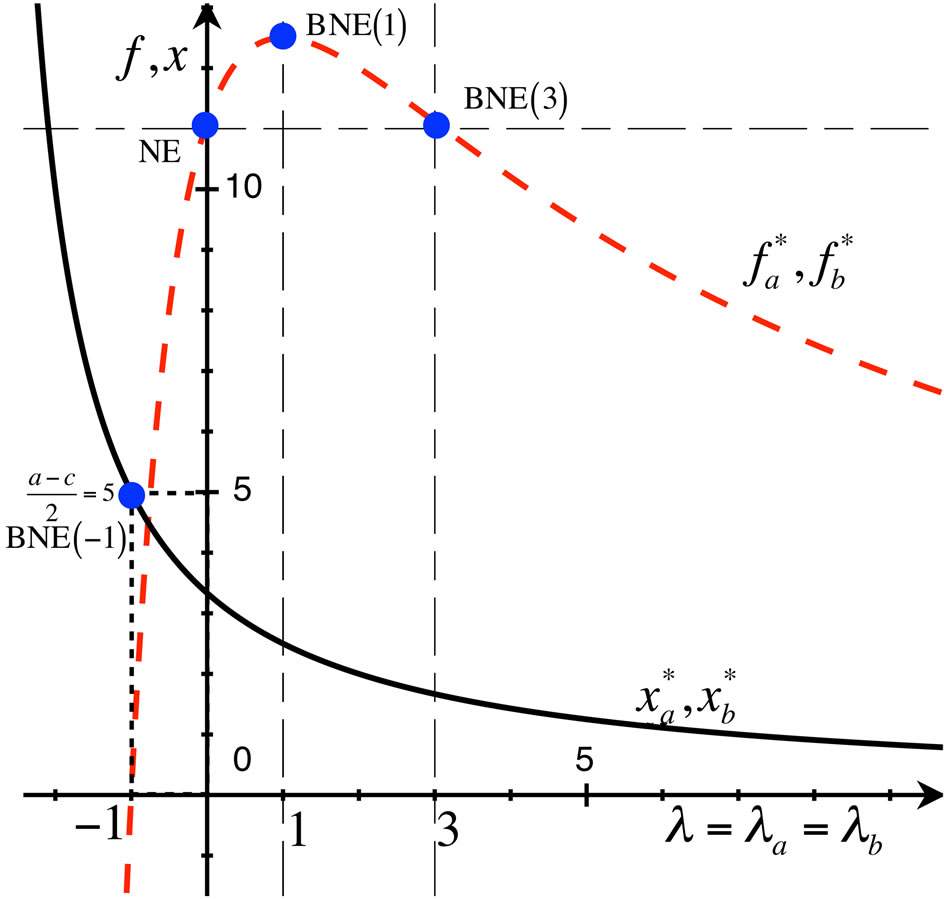
Figure 1. The strategy and reward at various equilibria against the belief 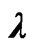 assuming
assuming . The solid line refers to the results for the strategy while the dash line shows the rewards.
. The solid line refers to the results for the strategy while the dash line shows the rewards.
Proof The BNE game (with forward-looking players) presented in Section 3.2 follows the same spirit as a typical Nash game where any player acts towards an equilibrium assuming that other players’ strategies are fixed. Their only difference lies in their understanding about the payoff functions due to different level of cognition to the environment. Consequently, the same result regarding existence of Nash equilibrium [7] can be directly applied to BNE by simply replacing the pay off function by the predicted reward function, which completes the proof.
4. Conclusion
This paper showed the importance of players’ cognition to the equilibrium of the game and presented the Nash equilibrium of forward-looking players. Using a two-firm example, we demonstrated how a Nash game with belief (referred to as BNE) can be made to achieve the Nash and Stackelberg equilibria. On the other hand, this paper has also illustrated the potential of using the belief function as an optimization parameter which makes possible the game converging to a Pareto-optimal equilibrium. However, this is a new regime in game theory and future work is required to better understanding of belief-directed games.
REFERENCES
- M. J. Osborne and A. Rubinstein, “A Course in Game Theory,” MIT Press, Cambridge, 1994.
- G. H. Von Stackelberg, “Market Structure and Equilibrium,” Springer-verlag, Berlin, Heidelberg, 2011. http://dx.doi.org/10.1007/978-3-642-12586-7
- E. Rasmusen, “Game and Information,” Basil Backwell Ltd., Oxford, 1989.
- J. Nash, “Non-Cooperative Games,” The Annals of Mathematics, Vol. 54, No. 2, 1951, pp. 286-295. http://dx.doi.org/10.2307/1969529
- D. Fudenberg and J. Tirole, “Game Theory,” MIT Press, Cambridge, 1991.
- J. Nash, “Equilibrium Pints in n-Person Games,” Proceedings of the National Academy of Science, Vol. 36, No. 1, 1950, pp. 48-49. http://dx.doi.org/10.1073/pnas.36.1.48
- D. A. Debreu, “Social Equilibrium Existence,” Proceedings of the National Academy of Science, Vol. 38, No. 10, 1952, pp. 886-893. http://dx.doi.org/10.1073/pnas.38.10.886
- R. B. Myerson, “Game Theory: Analysis of Conflict,” Harvard University, Cambridge, 1991.

