Applied Mathematics
Vol.5 No.8(2014), Article ID:45615,9 pages DOI:10.4236/am.2014.58106
A Model of Cellular Automata for the Fuzzy Control of Aphids
Magda da Silva Peixoto1, Laécio Carvalho de Barros2, Rodney Carlos Bassanezi2
1Departamento de Física, Química e Matemática, Universidade Federal de São Carlos, Sorocaba, Brazil
2Departamento de Matemática Aplicada, IMECC, Universidade Estadual de Campinas, Campinas, Brazil
Email: magda@ufscar.br, laeciocb@ime.unicamp.br, rodney@ime.unicamp.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 22 January 2014; revised 22 February 2014; accepted 1 March 2014
Abstract
Pesticides are substances used to prevent, destroy or mitigate any pest. We have adopted in this paper the Cellular Automata model to study the dispersion of the aphids in the block of citric trees using the pesticides (chemical control) and the biological agent (biological control). The main purpose of this research is the development of a simple and specific methodology to study Citrus Sudden Death (CSD). CSD is a disease that has affected sweet orange trees grafted on Rangpur lime in the state of São Paulo-Brazil. Some studies suggest that this disease has been caused by a virus and it is transmitted by insects known as aphids (vector). The ladybug was selected among the most known enemies of aphids in citrus in Brazil. In order to elaborate a predator-prey type of model to study the interaction between aphids (preys) and ladybugs (predators) in citriculture we have used a fuzzy rule-based system (FRBS). The states of the variables of the system (inputs) are the density of preys and the density of predators and their variations are the outputs. Therefore we take into account the effect of the wind in the space covered by the aphid, since the wind is important for the flight of the aphid as described in Peixoto et al. (2008) [1] . After, we used a FRBS to establish the relationship between the quantity of pesticides and the density of the preys. The simulations have been performed and have been compared between blocks with the presence of both aphids and ladybugs without the use of pesticides and the presence of them with the use of these ones using the Cellular Automata model. Numerical simulations allow us to foresee the behavior of the system, hence creating a spectrum of possibilities and proposing control techniques for different initial scenarios.
Keywords:Fuzzy Sets, Fuzzy Rule Base, Cellular Automata, Simulations, Pesticides

1. Introduction
Brazil is currently the world greatest exporter of frozen and concentrated orange juice (74.6% of the production is exported). This leadership is directly connected to the quality and productivity of our orchards when compared to our competitors. Brazil is also the biggest world producer of orange juice with 49.3% of the total. The state of São Paulo is responsible for 97% of the Brazilian export and it is the biggest core of the Brazilian citric complex (of which 313 cities come from of the state of São Paulo and 7 come from Minas Gerais). São Paulo has the biggest citrus orchard complex in the world and it is responsible for more than 80% of the national production of the citric fruits.
Citrus Sudden Death (CSD) is a disease that has affected sweet orange trees grafted on Rangpur lime in the state of São Paulo-Brazil [2] .
Some studies suggest that this disease has been caused by a virus and it is transmitted by insects known as aphids (vector).
The ladybug (predator) was selected among the most known enemies of aphids in citrus in Brazil.
On the order hand, the producers have used the pesticides indiscriminately. Nevertheless, we have used a fuzzy rule-based system to establish the relationship between the quantity of pesticides and the density of aphids, i.e., if the density of aphids is low, the quantity of pesticides is also low.
We have adopted in this paper the Cellular Automata model to study 1) the dispersion of the aphids in the block of citric trees using biological agent (biological control) and 2) the dispersion of the aphids in the block of citric trees using the pesticides (chemical control).
2. Preliminares
2.1. Cellular Automata
Cellular Automata (CA) was introduced in the 1950s by the mathematician John von Neumann who considered the suggestions from Stanislaw Ulam and tried to model the natural process of self-reproduction [3] .
Biological systems are ripe for modeling with CA methods. The spatial and temporal patterns are diverse and fascinating. Our knowledge of the details of a particular mechanism is often full of gaps and, unlike physics, there are few “laws” such as the Navier-Stokes equations or laws of Newton. Thus simplified models can be useful in precluding certain mechanisms as being impossible or at least unlikely. The speed by which calculations can be made allows the investigator to examine a huge number of parameter ranges that would be otherwise impractical for more “realistic” simulations [4] . In particular, it can be employed in the ecological context to represent heterogeneous and dynamic habitat structures [5] .
In short, CA consists of a simulation which is discrete in time, space and state of the systems. The idea of these models consists in considering each position (or region) of the spatial dominion as a cell which is attributed to a state. The state of each cell is modified regarding both its own state and the state of its neighbors during the former time stage through a series of simple rules that try to imitate the physical or the biological laws, which are, in our case, the ones that rules the system. In this approach, the system state variables, as well as the time, are discrete.
We have used a Cellular Automata model to study the dispersion of the aphids in the block of citric tree. The system is represented in space through a cell lattice that interacts obeying some rules for the changing of the state among the cells. Each cell represents a tree that can be with the absence of aphids and ladybugs, the presence of aphids and the absence of ladybugs and the presence of aphids and ladybugs.
Next, we have used a Cellular Automata model to study the dispersion of the aphids in the block of citric tree using the pesticides.
2.2. Fuzzy Rule-Based System
Fuzzy sets and fuzzy logic have become one of the emerging areas in contemporary technologies of information processing. Fuzzy Logic was first developed by [6] in the mid-1960s to represent uncertain and imprecise knowledge. It provides an approximate but effective means of describing the behavior of the system that is too complex, ill-defined, or not easily analyzed mathematically.
A fuzzy subset is characterized by a membership function mapping the elements of a domain, space, or universe of discourse X to the unit interval 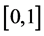 [6] That is,
[6] That is,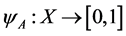 . Thus, a fuzzy set A in X may be represented as a set of ordered pairs of a generic element and its grade of membership:
. Thus, a fuzzy set A in X may be represented as a set of ordered pairs of a generic element and its grade of membership: . Clearly, a fuzzy set is a generation of the concept of a set whose membership function takes on only two values
. Clearly, a fuzzy set is a generation of the concept of a set whose membership function takes on only two values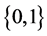 , that is, the characteristic function of A,
, that is, the characteristic function of A,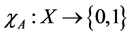 .
.
Fuzzy variables are processed using a fuzzy rule-based system.
Fuzzy rule-based system (FRBS): Basically, fuzzy rule-based systems have four components: an input processor (fuzzification), a collection of linguistic rules called rule base; a fuzzy inference method and an output processor (defuzzification). These components process real-valued inputs in order to provide real-valued outputs. Figure 1 illustrates a FRBS.
The fuzzification is the process in which the input values of the system are translated into fuzzy sets of their respective universes. It is a mapping of the dominion of the real numbers led to the fuzzy dominion. Expert knowledge plays an important role to build the membership functions for each fuzzy set associated with the inputs.
The rule base characterizes the objectives and strategies used by specialists in the area through of a linguistic rule set. It is composed by a collection of fuzzy conditional propositions in the form if-then rules. An expert can articulate associations of linguist inputs/outputs.
The fuzzy inference method performs an approximate reasoning using the compositional rule of inference. A particular form of fuzzy inference of interest here is the Mamdani method [8] . In this case, it aggregates the rules through the logical operator OR, modeled by the maximum operator and, in each rule, the logical operators AND and THEN are modeled by the minimum operator [9] . The logic of decision to be made, incorporated to the structure of inference of the rule base, uses fuzzy implications to simulate the decisions that are wanted. It generates actions inferred from consequents a set of input conditions-antecedents.
Finally, in defuzzification, the value of the output linguistic variable inferred from the fuzzy rule is translated to a real value. The output processor task is to provide real-valued outputs using defuzzification which is a process that chooses a real number that is representative of the inferred fuzzy set. A typical defuzzification scheme, the one adopted in this paper, is the centroid or center of mass method [8] .
According to [6] fuzzy set approaches have been developed for special purposes where the information basis has been vague and imprecise. Under these conditions fuzzy techniques allow more accurate conclusions in comparison to the other approaches which cannot be applied successfully because of lack of data.
We suggest [8] and [9] for a detailed study of the fundamentals of fuzzy set and the systems theory and applications.
3. Fuzzy Predator-Prey Model
In this work, we have used fuzzy rule-based systems to elaborate a predator-prey type of model to study the interaction between aphids (preys) and ladybugs (predators) in citriculture.
In this paper we suggest using fuzzy set theory [6] to create a model that studies the interaction between a prey (aphid) and its predator (ladybug), instead of using the usual differential equations which characterize the classic deterministic model of Lotka-Volterra [10] . Since we do not have sufficient information about our phenomena, it is difficult to express the variations as functions of the states. On the other hand, qualitative information from specialists allows us to propose rules that relate (at least partially), to the state variables, with their own variations. In particular, our interest here is to elaborate a predator-prey model that represents the interaction between aphids (preys) and ladybugs (predators) in citriculture by using a fuzzy rule-based system. The

Figure 1. Structure of fuzzy rule-based system. Source: [7] .
mathematical models that describe prey and predator relationship are used to study interactions between two populations, when one of them depends on the other for food and for survival. Such dynamic relationship between preys and predators are prominent subjects in ecology [10] .
In short, we present hypotheses that characterize a predator-prey model of Lotka-Volterra, whose trajectories show the following features:
• The number of prey population and the number of predator population have an oscillatory character;
• An increase in the prey population is followed (with a delay) by an increase in the predator population;
• A decrease in the prey population is followed (with a delay) by a decrease in the predator population;
• If the number of predators is small, the number of preys increases;
• If the number of predators is large, the number of preys decreases;
• If the number of preys is large, the number of predators increases;
• If the number of preys is small, the number of predators.
So this dynamics is characterized by enchained oscillations in both populations: predator and prey. What is most interesting is that these oscillations have the following property: the peak of the prey population will always occur sometime before the natural enemy’s population peak.
According to the information above, our purpose is to elaborate a fuzzy rule base that replaces differential equations, which characterize the classic deterministic models that are used to model the dynamics between preys and predators. Qualitative information from specialists permits to propose rules that relate the state variables with their own variations.
The variables of the system are the number of preys, x, (very small, small, medium1, medium2, large, very large) and the number of the predators, y, (very small, small, medium1, medium2, large, very large) and their variations, x' and y', (increases a little, increases a lot, decreases a little, decreases a lot) (outputs). However, accurate knowledge about the input variables and theirs variations is not available. Thus, the hypotheses of LotkaVolterra model allow us to propose rules that relate the variables of state to their own variations, that is, they come from the phase-plane of Lotka-Volterra model.
The fuzzy rule base is given by 16 rules of the type: “If (x is low) and (y is low) then (x' increases a lot) and (y' decreases a lot)”; “If (x is medium1) and (y is medium2) then (x' decreases a little) and (y' decreases a little)”; “If (x is large) and (y is large) then (x' decreases a lot) and (y' increases a lot)”.
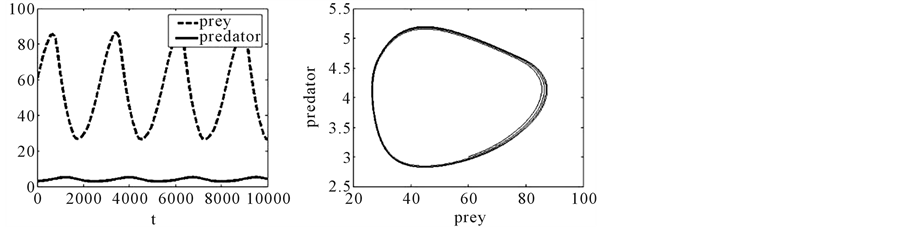
From Mamdani’s Inference Method and defuzzification of the center-of-gravity, we have obtained the variation rates of the preys and the potential of predation. In each moment t, the number of preys and the number of predation are given by Euler’s Method. The evolution of the population contingents of the preys and potential of predation given by the fuzzy model over time, and its respective phase-plane, are illustrated in Figure 2.
We would like to point out that even without any equations, we have managed to obtain a phase-plane where the trajectories appear to converge to a limit cycle.
4. Cellular Automata Model
The wind is a decisive factor for the insect dispersion and the information about the time of aphid flight is imprecise. In [1] , we have adopted the CA model to study the temporal evolution of the disease. We take into account the effect of the wind in the space covered by the aphid. We have adopted the FRBS in order to establish
 (a) (b)
(a) (b)
Figure 2. (a) The evolution of the population contingents in time, and (b) Phase-plane of the fuzzy model, with x0 = 60 and y0 = 3.
the relationship between the space covered by the aphid and the intensity of the wind. In this work, we have considered the hypothesis and the results of [1] to determine that the space covered by the aphid.
The attribute of each cell is described by two simultaneous values, one is the population density of aphids and the other is the potential of predation. Therefore, the attribute of dynamic system in the moment t is described by two matrixes. These matrixes are updated every single moment. Each cell of lattice represents a plant, that is, a tree.
The interaction between aphids and ladybugs occurs inside each cell through the predator-prey dynamic given by FRBS model of Section 3.
It is important to remember that the trees are shared uniformly by lines and columns in the block of citric trees.
Some hypotheses are essential to establish the rules of CA model:
• Brief contacts between the bodies of adults without wings facilitate the production of a greater number of winged descendents, in other words, it is supposed to come forth winged aphids when the population of these ones reaches its carrying capacity;
• The winged aphids create new colonies in other trees;
• Ladybugs are very inefficient in the capture of aphids as long as they only distinguish the presence of aphids when they are very close to their preys.
According to the previous hypotheses, we establish the further rules of movement:
1) Ladybugs capture aphids which are closer to them. The search is done among the “nearest neighbors”. Each cell in two-dimensional square lattice has eight nearest neighbors conveniently addressed as points on the compass. The four neighbors sharing a common face are: N, E, S, and W. Those that can be reached diagonally are: NE, SE, NW, and SW. If they find aphids in one of these cells, the choice is random. Otherwise, the search is done until they find food (i.e. aphids).
2) Only adult ladybugs move among cells.
3) Winged aphids leave overcrowded cells and occupy other cells according to the dynamic of the flight, that is determined by the intensity of the wind as described in Peixoto et al. (2008) [1] .
We have used a Cellular Automata model to study the dispersion of the aphids and ladybugs in the block of citric tree. The system is represented in space through a cell lattice that interacts obeying the previous rules for the changing of the state among the cells. Each cell represents one tree that can be in one of the two states: presence of aphids (black) and absence of aphids (white).
Simulations
In the numerical simulations, the initial trees with aphids, ladybugs or both are chosen randomly. The initial number of insects in each tree is random as well. The block consists in 10 × 20 trees arranged homogenously. The dispersion of the insects is plotted for a period of five days at each figure.
Simulation 1: In this example, we have accomplished two simulations. In the first one, there are aphids in one tree in the block (Figure 3) and in the second, there are aphids and ladybugs (Figure 4).
Simulation 2: Similar to the example 1, we have accomplished two simulations. There are aphids in five trees in the first one (Figure 5) and in the second simulation, there are ladybugs in the same five trees in the block (Figure 6).
In the graphic (Figure 7), we have compared the difference between the quantity of tree with the presence of aphids and ladybugs and the trees with the presence of aphids and absence of ladybugs in the block.
5. Fuzzy Control
The producer aims to eliminate the plague when using the pesticides. It is natural that the quantity of the pesticide depends of the quantity of aphids presents in the trees, that is, if the quantity of aphids is large then the quantity of the pesticide is high. Then, we have used a FRBS to establish the relationship between the quantity of pesticides and the density of aphids.
The variables of the system are the number of aphids (very small, small, medium1, medium2, large) (input) and quantity of pesticides (low, medium, high) (output).
The rule base is:
1) If (number of aphids is very small) then (quantity of pesticides is low);

Figure 3. Absence of predator in the block. Initial condition: one tree with the presence of aphids.

Figure 4. Presence of predator in the block. Initial condition: one tree with the presence of aphids and ladybugs.

Figure 5. Absence of predator in the block. Initial condition: five trees with the presence of aphids.
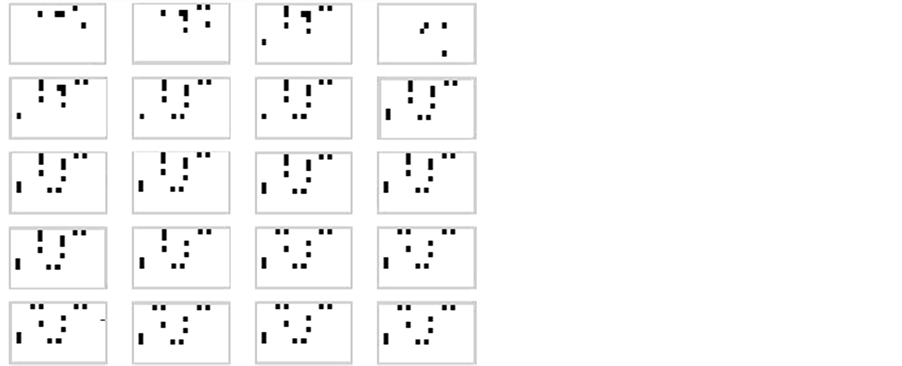
Figure 6. Presence of predator in the block. Initial condition: five trees with the presence of aphids and ladybugs.
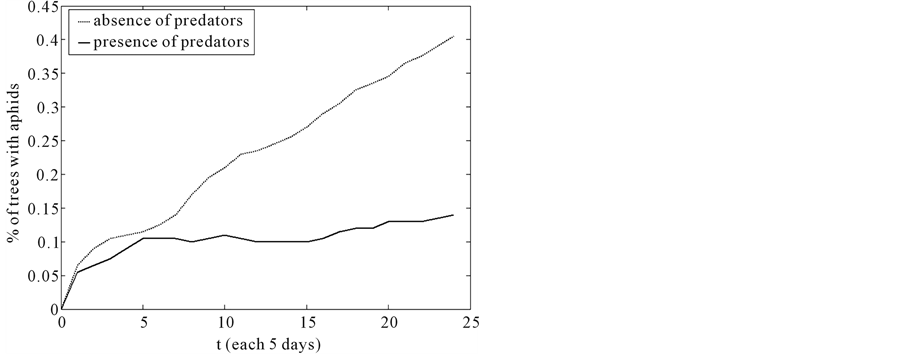
Figure 7. Percentage of trees with the presence of predators and the absence of predators.
2) If (number of aphids is small) then (quantity of pesticides is low);
3) If (number of aphids is medium1) then (quantity of pesticides is low);
4) If (number of aphids is medium2) then (quantity of pesticides is medium);
5) If (number of aphids is large) then (quantity of pesticides is medium);
6) If (number of aphids is very large) then (quantity of pesticides is large).
From Mamdani Inference Method and defuzzification of the center-of-gravity, we have obtained the curve represented in Figure 8.
6. Simulations by Cellular Automata Model
Now, we have used a Cellular Automata model to study the dispersion of the aphids in the block of citric tree using the pesticides, that is, the dispersion of the aphids with one application of the pesticides. Similar Section 4.1, in the numerical simulations the initial trees with aphids, ladybugs or both are chosen randomly.
The initial number of insects in each tree is random as well. From this number, the fuzzy model of Section 5 provides the quantity of pesticides. Then, the insects are removed according to this quantity.
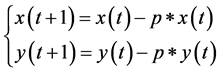
where 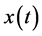 is the number of the aphids,
is the number of the aphids,  is the number of the ladybugs in the instant t in each tree and p is the quantity of the pesticides applied.
is the number of the ladybugs in the instant t in each tree and p is the quantity of the pesticides applied.
Finally, the interaction predator-prey occurs in each tree according to fuzzy model (Section 3) as the diagram in Figure 9.
The block consists in 10 × 20 trees arranged homogenously. The dispersion of the insects is plotted for a period of one month at each following figure.
In this example we have accomplished two simulations.
Simulation 1: In Figure 10, there are aphids are ladybugs in the same five trees in the block without using pesticides.
Simulation 2: In the second, there are aphids and ladybugs. There are ladybugs in the same five trees in the block using pesticides once. We have observed few aphids in only two trees after using the pesticides (Figure 11). But, the population of the ladybugs decreased also. Thus, the population of the aphids increased quickly.
7. Conclusions
This paper has suggested applying Fuzzy Sets Theory and Cellular Automata to Ecology. We have evaluated the dynamics of the aphids population with the presence of ladybugs (aphids predators) without the use of pesticides and the presence of them with the use of these ones. It is possible to observe this difference: the ladybugs are not capable of eliminating the entire population of aphids which is expected in a predator-prey model. It is considered impossible to eradicate the population of aphids, though it is probable to control its spread velocity. When
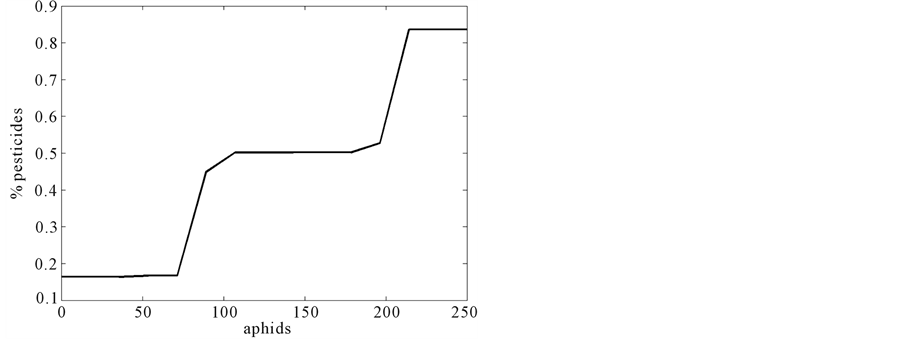
Figure 8. Solution given by fuzzy model.
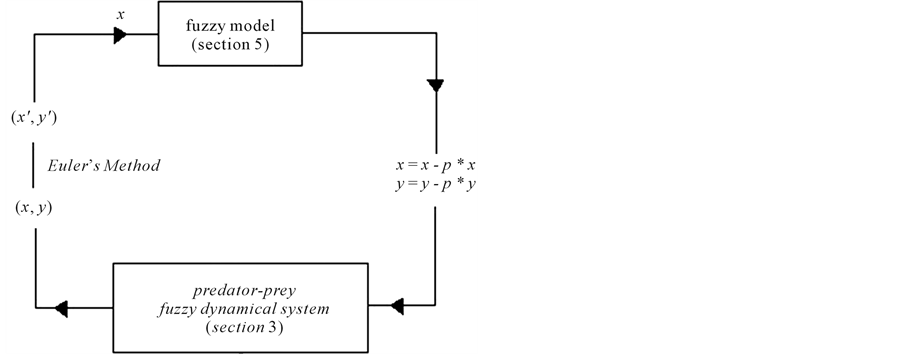
Figure 9. The model consists of two fuzzy systems: predatorprey fuzzy dynamical system and fuzzy control system.

Figure 10. Initial condition: five trees with the presence of aphids and ladybugs.

Figure 11. Initial condition: five trees with the presence of aphids and ladybugs using pesticides once.
we compare the simulations that have been done with Cellular Automata in each example and graph above. On the other hand, we have observed the population of the aphids and ladybugs decreased after using the pesticides. Thus, the population of the aphids increased quickly. The use of pesticides is more harmful.
Finally, the Cellular Automata approach developed in this work enhances understanding and contributes to investigating and to predicting the spread of the insects which transmit the suspect virus responsible for Citrus Sudden Death.
Acknowledgements
The first and second authors acknowledge the National Council for Scientific and Technological Development (CNPq), process 305862/2013-8, for the financial support.
References
- Peixoto, M.S., Barros, L.C. and Bassanezi, R.C. (2008) A Model of Cellular Automata for the Spatial and Temporal Analysis of Citrus Sudden Death with the Fuzzy Parameter. Ecological Modelling, 214, 45-52. http://dx.doi.org/10.1016/j.ecolmodel.2008.01.018
- Bassanezi, R.B., Bergamin Filho, A., Amorim, L., Gimenes-Fernandes, N. and Gottwald, T.R. (2003) Spatial and Temporal Analysis of Citrus Sudden Death as a Tool to Generate Hypothesis Its Etiology. Phytopathology, 93, 502-512. http://dx.doi.org/10.1094/PHYTO.2003.93.4.502
- Wolfram, S. (1994) Cellular Automata and Complexity. Addison-Wesley Publishing Company, Massachusetts.
- Ermentrout, G.B. and Edelstein-Keshet, L. (1993) Cellular Automata Approaches to Biological Modeling. Journal of Theoretical Biology, 160, 97-133. http://dx.doi.org/10.1006/jtbi.1993.1007
- Breckling, B., Muller, F., Reuter, H., Hölker, F. and Fränzle, O. (2005) Emergent Properties in Individual-Based Ecological Models—Introducing Case Studies in a Ecosystem Research Context. Ecological Modelling, 186, 376-388. http://dx.doi.org/10.1016/j.ecolmodel.2005.02.008
- Zadeh, L.A. (1965) Fuzzy Sets. Informat. Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Jafelice, R.M., Barros, L.B., Bassanezi, R.C. and Gomide, F. (2003) Fuzzy Modeling Symptomatic HIV Virus Infected Population. Bulletin of Mathematical Biology, 66, 1597-1620. http://dx.doi.org/10.1016/j.bulm.2004.03.002
- Klir, G.J. and Yuan, B. (1995) Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall, New Jersey.
- Pedrycs, W. and Gomide, F. (1998) An Introduction to Fuzzy Sets: Analysis and Design. Massachusets Institute of Technology, Cambridge.
- Edelstein-Keshet, L. (1987) Mathematical Models in Biology. McGraw-Hill, Inc., New York.

