Applied Mathematics
Vol.4 No.11A(2013), Article ID:38843,4 pages DOI:10.4236/am.2013.411A1004
Spectra of 2 × 2 Upper-Triangular Operator Matrices
College of Mathematics and Information Science, Shangqiu Normal University, Shangqiu, China
Email: csqam@163.com
Copyright © 2013 Haiyan Zhang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 25, 2013; revised June 25, 2013; accepted August 2, 2013
Keywords: Spectra; Upper-Triangular Operator Matrix; Fredholm Operator
ABSTRACT
In [Perturbation of Spectrums of 2 × 2 Operator Matrices, Proceedings of the American Mathematical Society, Vol. 121, 1994], the authors asked whether there was an operator  such that
such that  for a given pair
for a given pair  of operators, where the operator
of operators, where the operator 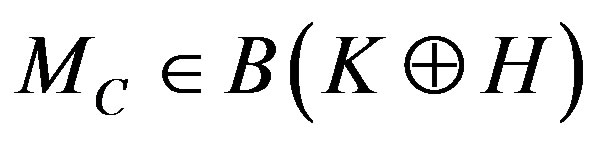 was defined by
was defined by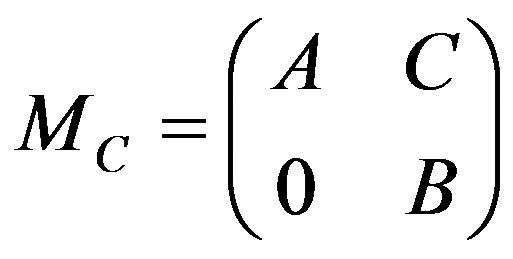 . In this note, a partial answer for the question is given.
. In this note, a partial answer for the question is given.
1. Introduction
In the last decades considerable attention has been paid to upper triangular operator matrices, particularly to spectra of operator matrices, see [1-8]. H. Du and J. Pan firstly researched the intersection of the spectra of 2 × 2 upper triangular operator matrices, and also proposed some open problems. In this note, we mainly study these problems.
For the context, we give some notations. Let  and
and 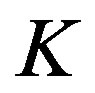 be Hilbert spaces,
be Hilbert spaces, 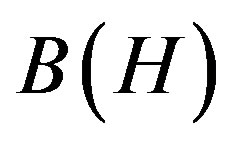 ,
, 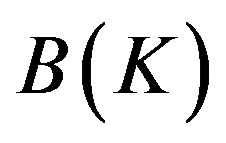 and
and 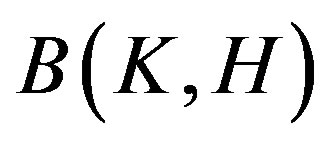 denote the sets of all linear bounded operators on
denote the sets of all linear bounded operators on ,
,  and from
and from  into
into , respectively. For
, respectively. For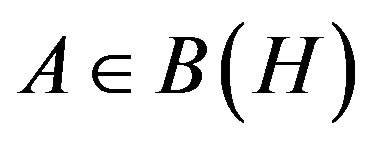 ,
, 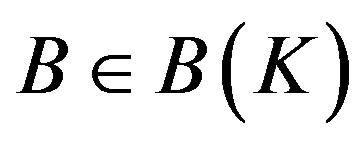 ,
,  , define an operator
, define an operator 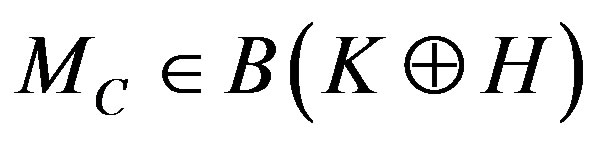 by
by
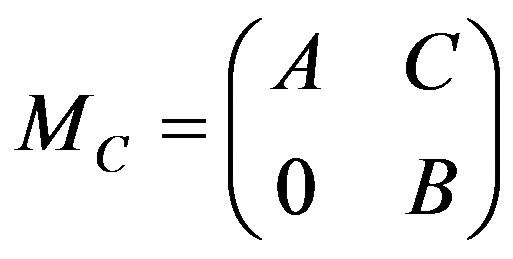 .
.
Let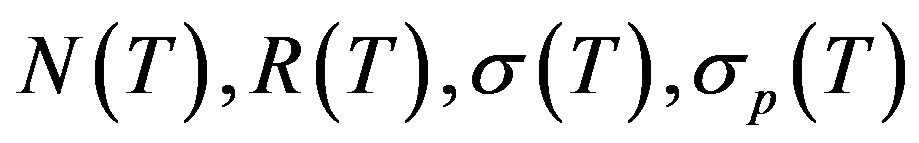 ,
, 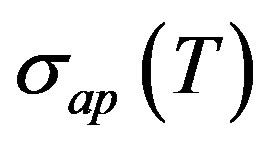 ,
, 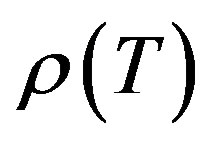 ,
, 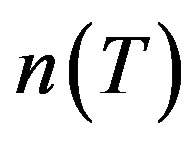 and
and 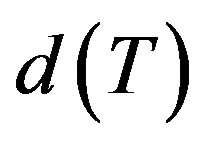 denote the nullspace, the range, the spectrum, the point spectrum, the approximation point spectrum of the resolvent set, the nullity and the deficiency of an operator
denote the nullspace, the range, the spectrum, the point spectrum, the approximation point spectrum of the resolvent set, the nullity and the deficiency of an operator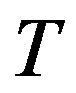 , respectively, where
, respectively, where
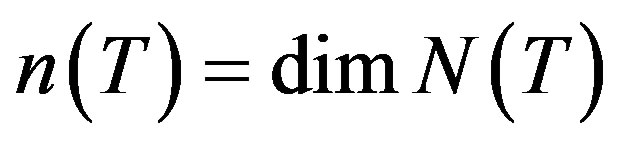 and
and 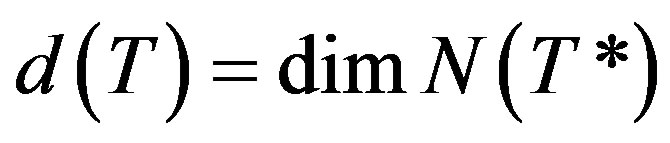
use ,
,  and
and 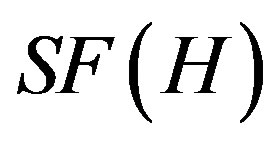 to denote the sets of left Fredholm operators, right Fredhlom operators and semi-Fredholm operators in
to denote the sets of left Fredholm operators, right Fredhlom operators and semi-Fredholm operators in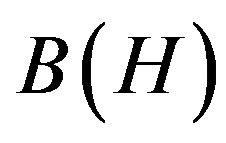 , respectively. If T is a semi-Fredholm operator, define the index of T,
, respectively. If T is a semi-Fredholm operator, define the index of T,  , by
, by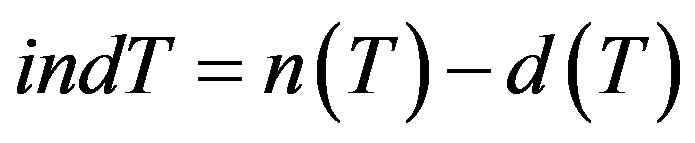 . Note that
. Note that  and it is necessary for either
and it is necessary for either  or
or 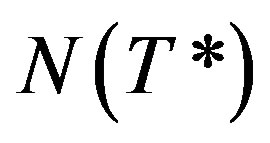 to be finite dimensional in order for (1) to make sense ([3]).
to be finite dimensional in order for (1) to make sense ([3]).
For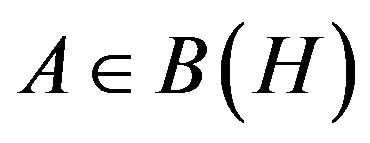 ,
, 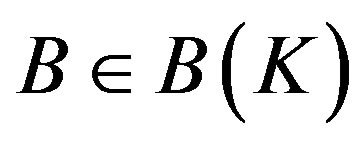 , denote
, denote

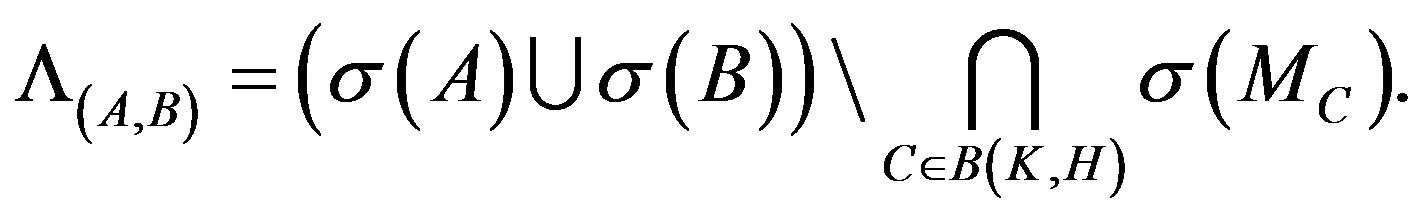
Under the situation that do not cause confusion, we simplify 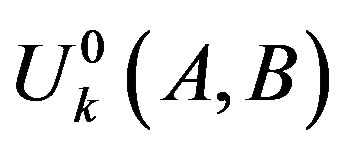 as
as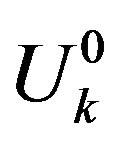 .
.
In [2], H. Du and J. Pan have proved that,
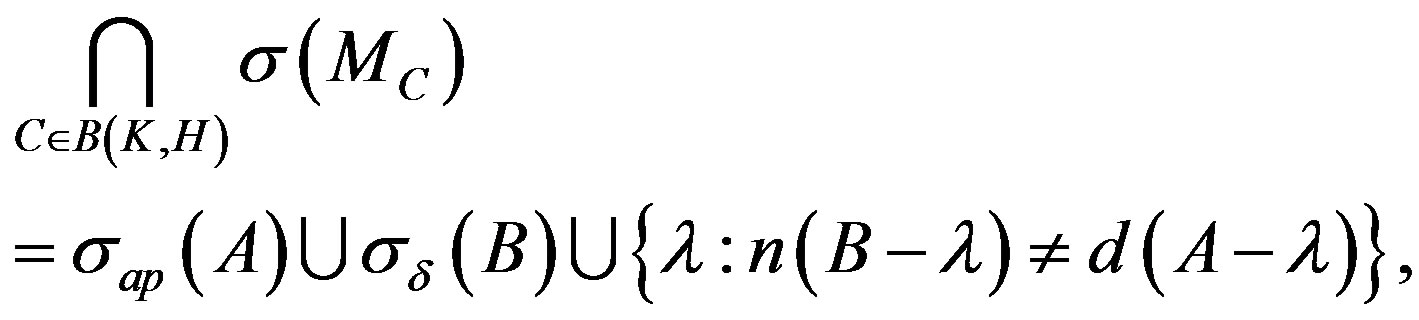 (1)
(1)
for given 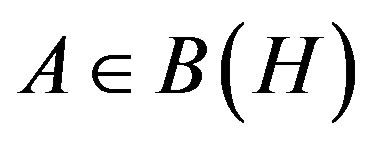 and
and , the author asked a question that whether there exists an operator
, the author asked a question that whether there exists an operator 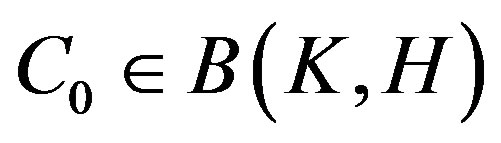 such that
such that
 ?
?
In this note, when 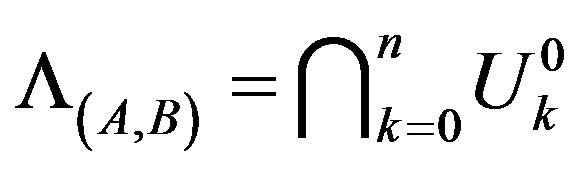 (n is a natural number), an affirmative answer of the question has been obtained.
(n is a natural number), an affirmative answer of the question has been obtained.
2. Main Results and Proofs
To prove the main result, we begin with some lemmas.
Lemma 1. ([2]). Given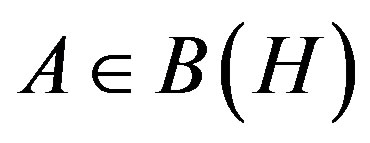 ,
, 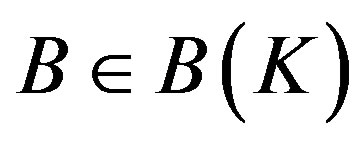 , then
, then
 .
.
Lemma 2. ([9]). Let 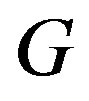 be an open connected subset of
be an open connected subset of 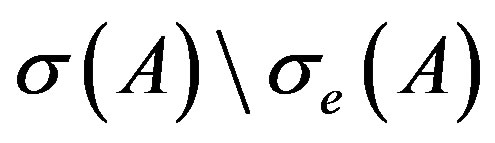 and suppose
and suppose 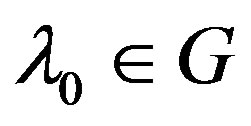 such that
such that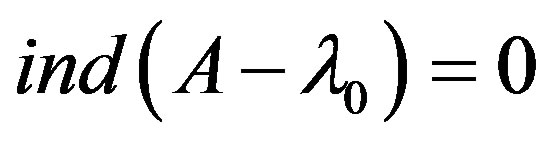 , then there is a finite-rank operator
, then there is a finite-rank operator  such that
such that 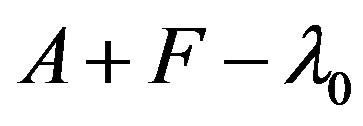 is invertible, and also
is invertible, and also 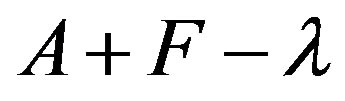 is invertible for every
is invertible for every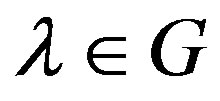 .
.
For any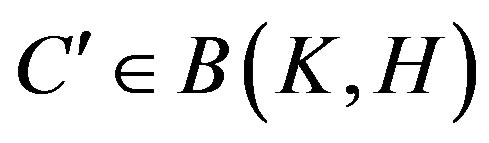 , it is clear that
, it is clear that
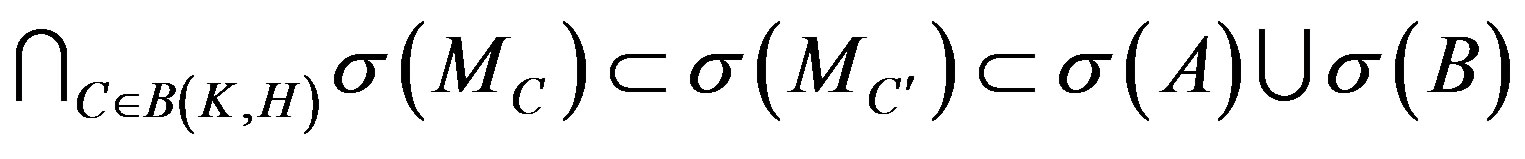 .
.
If there exists a 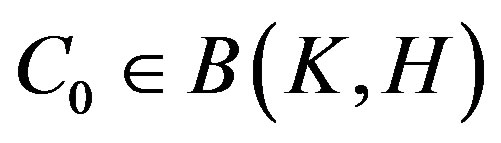 such that
such that
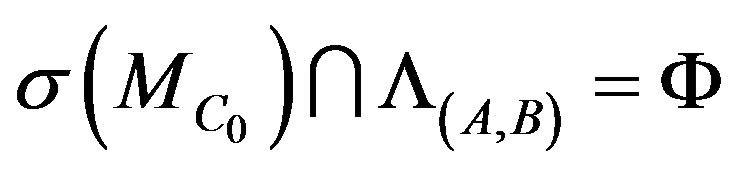 then
then
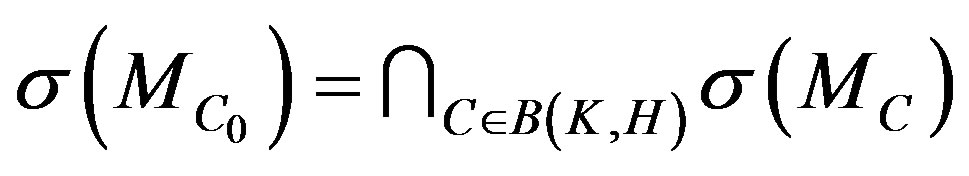 .
.
But how to construct the operator such that
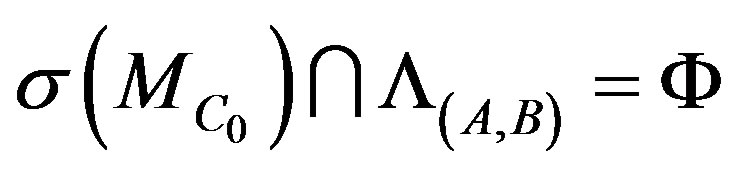 ?
?
In the next theorem, we give a necessary condition of the answer of the question.
Theorem 3. For a given pair  of operators, where
of operators, where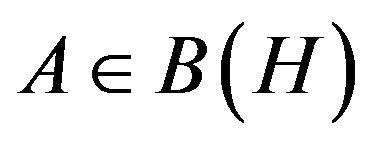 ,
,  , if
, if  (n is a natural number) and each
(n is a natural number) and each 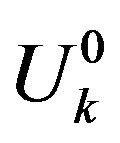 has finite simple connected open sets, then there exists an operator
has finite simple connected open sets, then there exists an operator 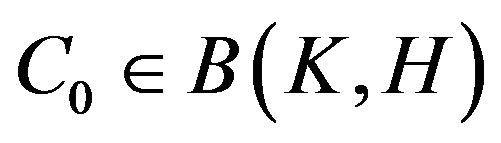 such that
such that
 .
.
Proof. For convenience, we divide the proof into two cases.
Case 1. If n = 0, that is, 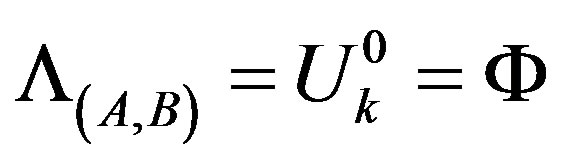 , let
, let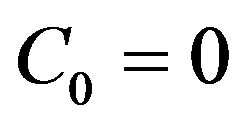 .
.
It is easy to see that 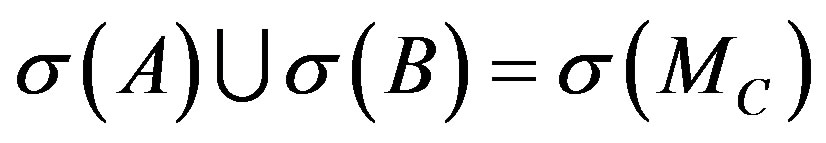 from lemma 1. Thus
from lemma 1. Thus
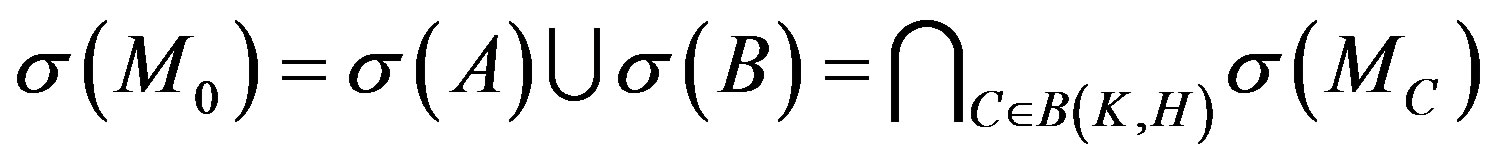 so the result is obtained.
so the result is obtained.
Case 2. If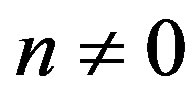 , that is,
, that is,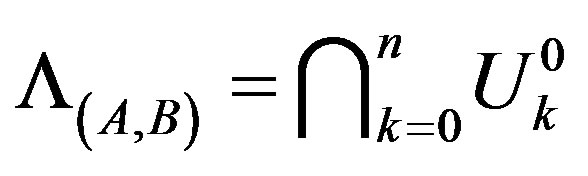 . Then
. Then
 has finite simple connected open sets, now reordering and denoting by
has finite simple connected open sets, now reordering and denoting by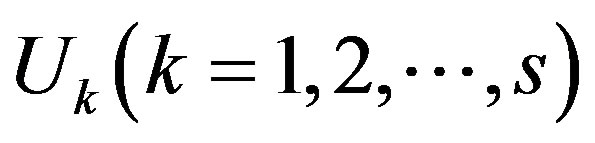 . Thus there exists a natural number
. Thus there exists a natural number 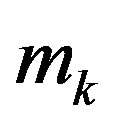 such that
such that
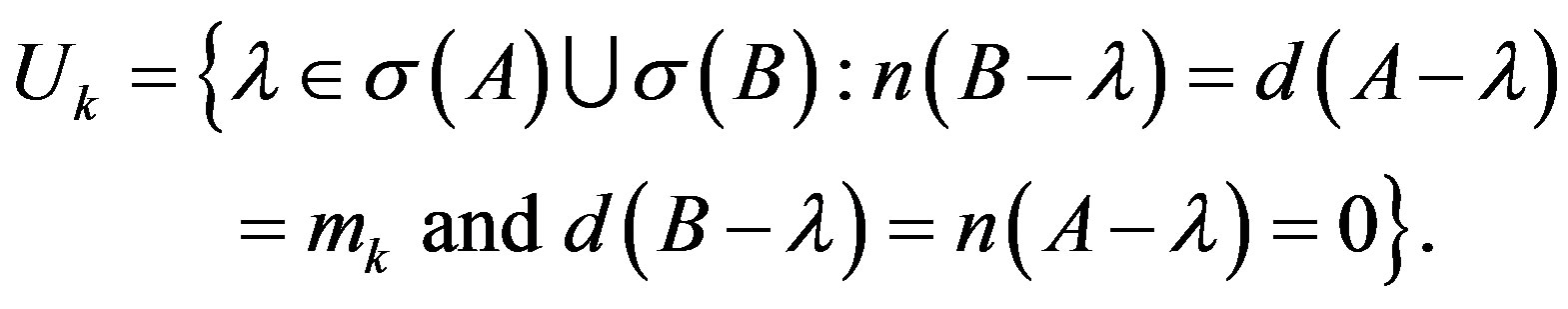
For each  choose a
choose a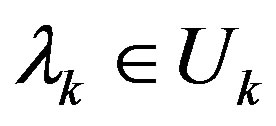 , then
, then 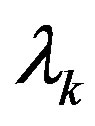 is a finite subset of
is a finite subset of 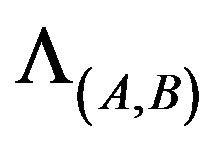 and
and
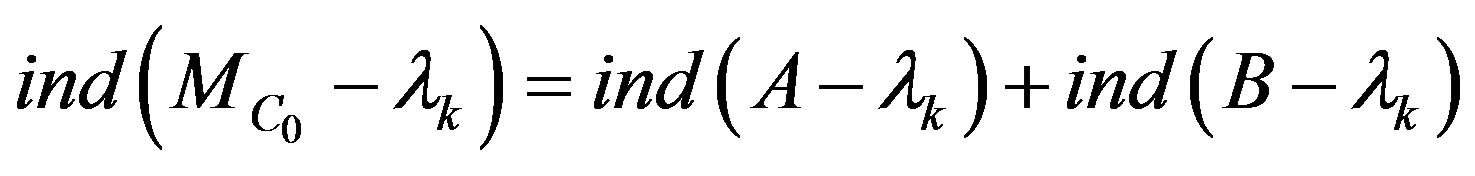 .
.
Next, the rest of proof is divided into two steps.
Step 1. We construct 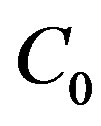 as follows:
as follows:
Let 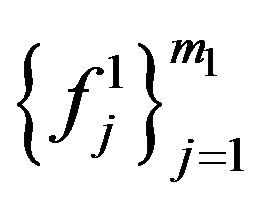 and
and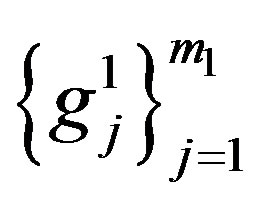 are orthonormal basis for
are orthonormal basis for
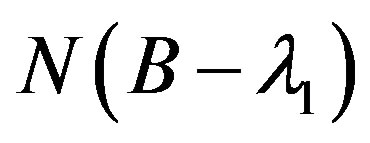 and
and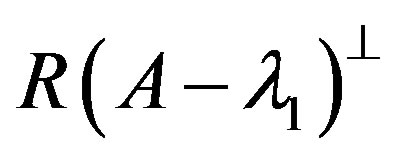 , respectively and denote
, respectively and denote
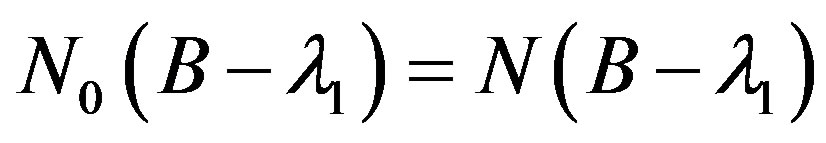 ,
,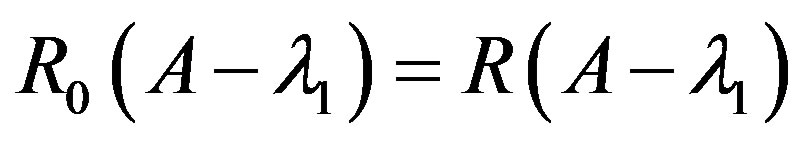 .
.
First define an operator  from
from 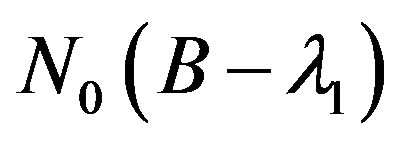 onto
onto 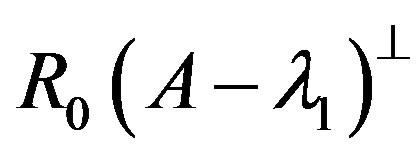 by
by ,
,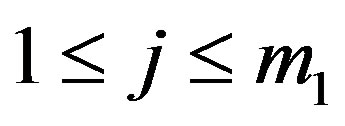 . Then define
. Then define 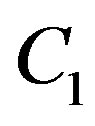 by
by

It is clear that 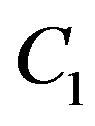 is well defined and
is well defined and .
.
If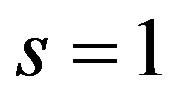 , then let
, then let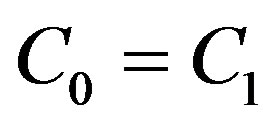 .
.
If , let
, let 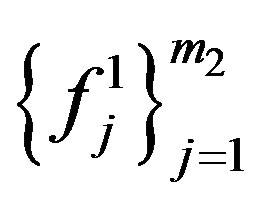 and
and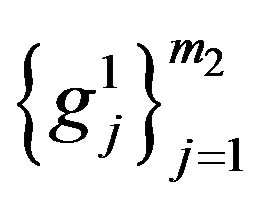 be orthonormal basis for
be orthonormal basis for 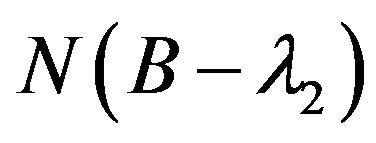 and
and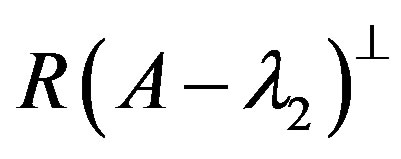 , respectively.
, respectively.
It is clear that  and
and 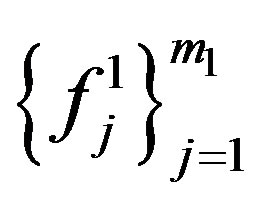 are linear independent. then there must be unit vectors
are linear independent. then there must be unit vectors
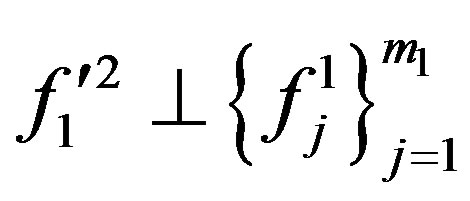 ,
, 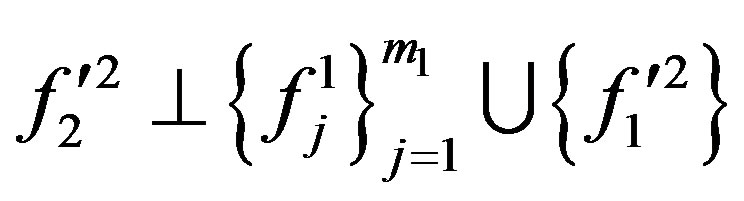 ,···,
,···,

such that
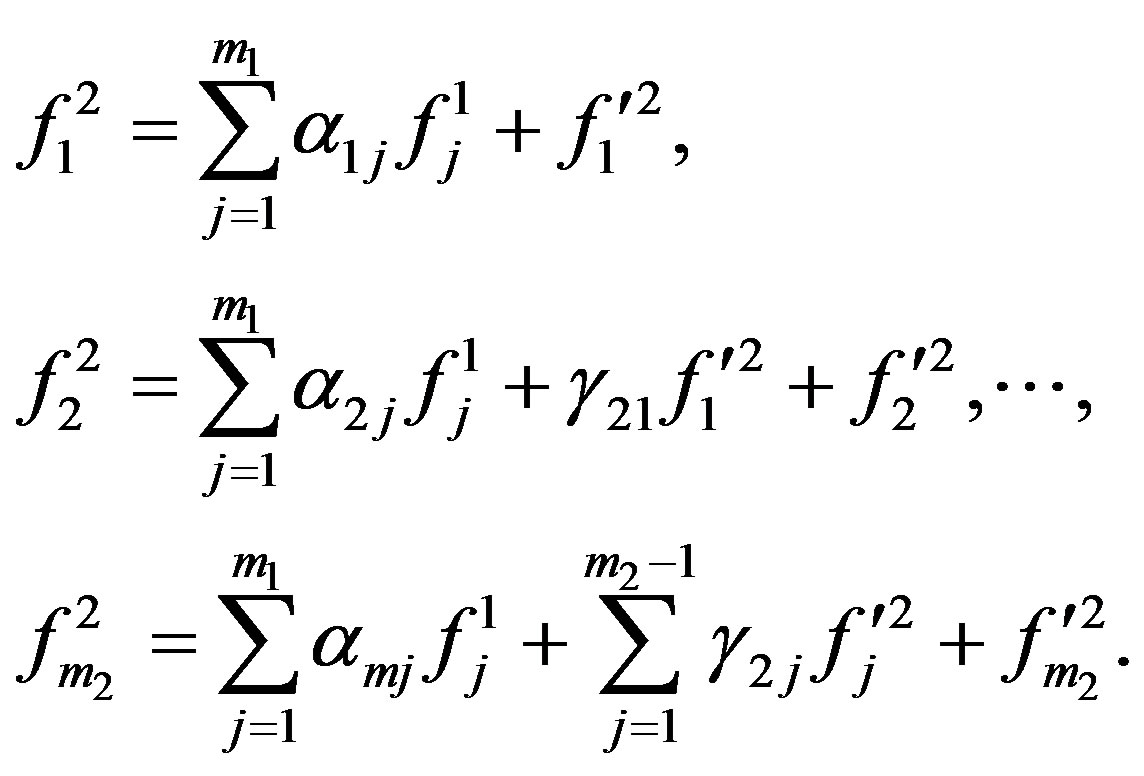
Define an operator 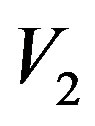 as follows:
as follows:
Let
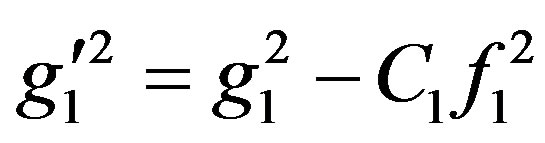 and
and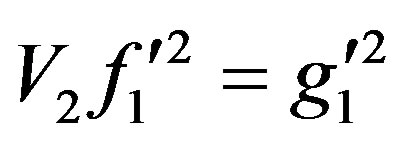 ,
,
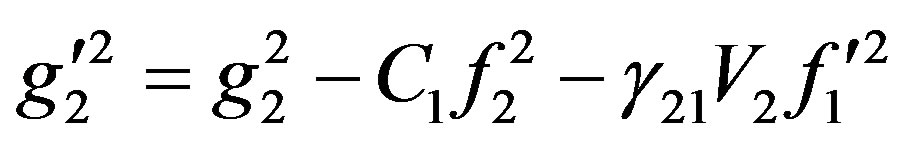 and
and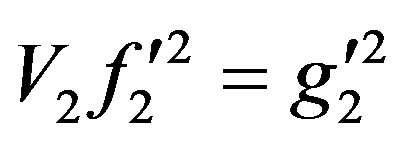 ,
,
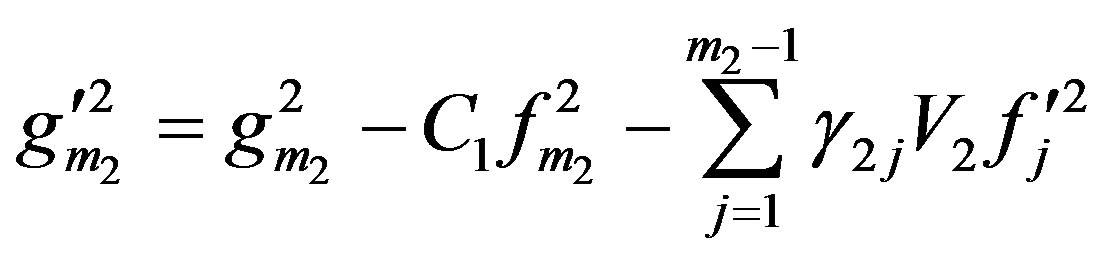 and
and .
.
Since 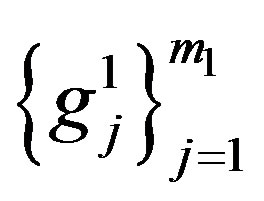 be and
be and 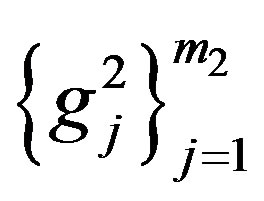 be are linear independent,
be are linear independent, 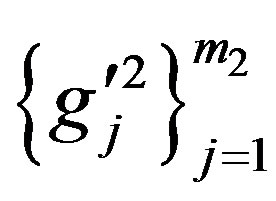 is linear independent. Let
is linear independent. Let
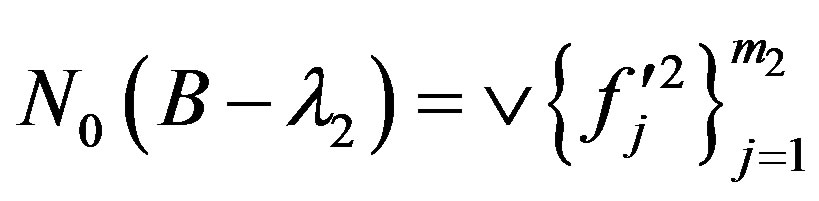
and
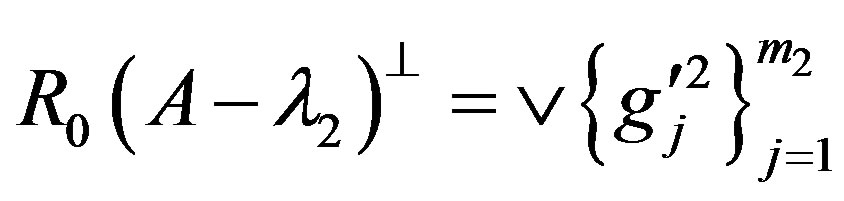 .
.
Then 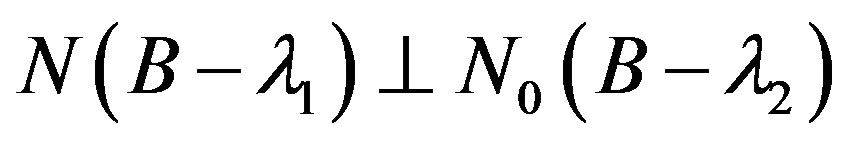 and
and 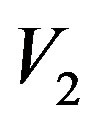 is an operator from
is an operator from 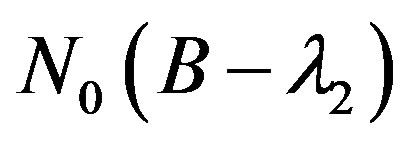 onto
onto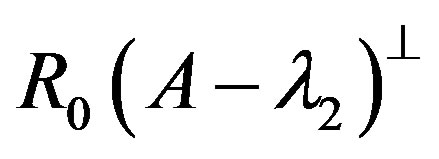 . Define
. Define  by
by
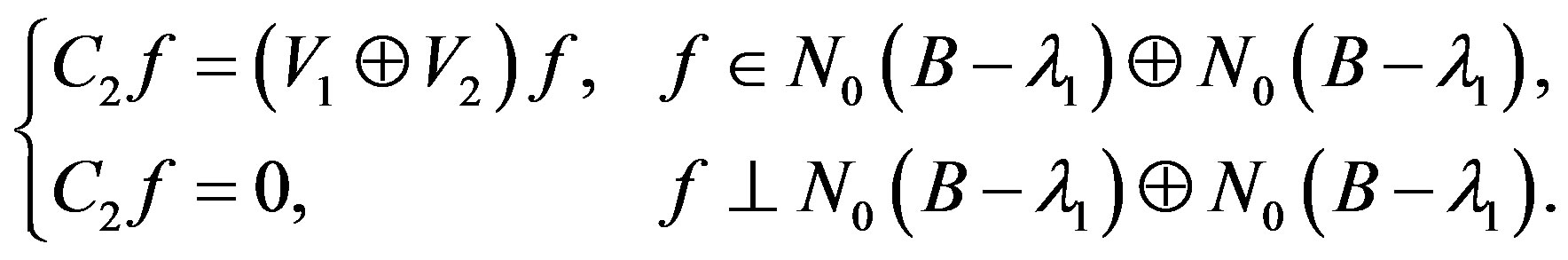
The process can be similarly done continuously.
Let 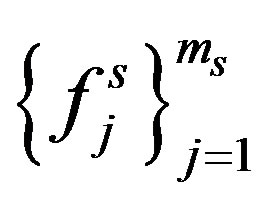 and
and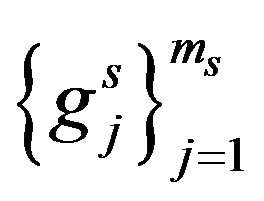 be orthonormal basis for
be orthonormal basis for
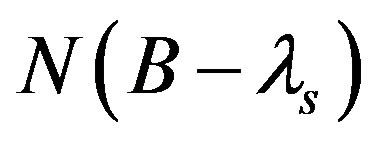 and
and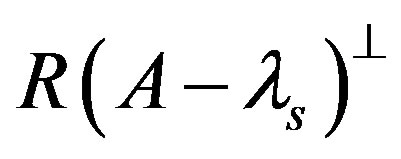 , respectively. It is clear that
, respectively. It is clear that 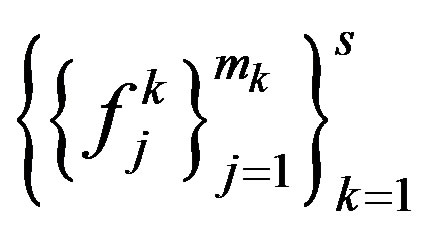 is linear independent. Then there must be unit vectors
is linear independent. Then there must be unit vectors
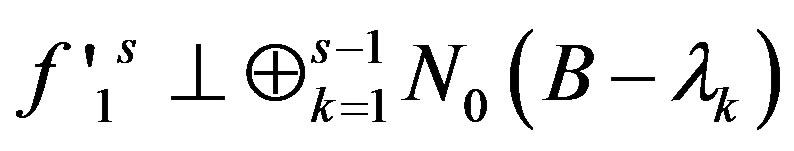 ,
,
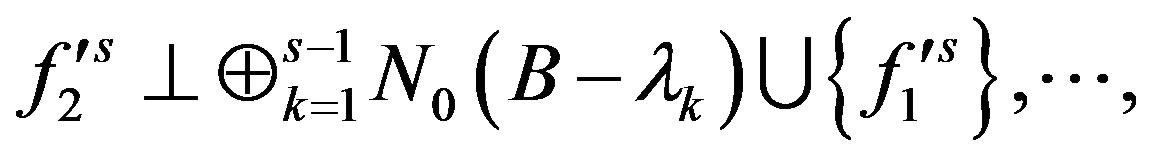

such that


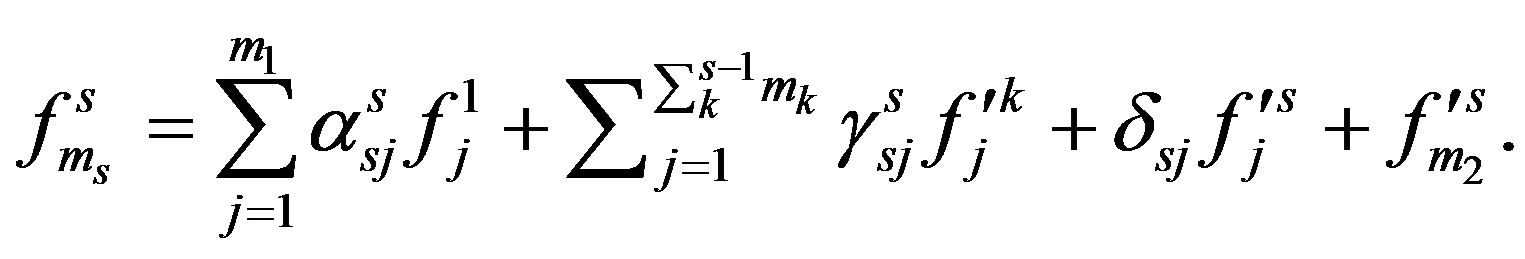
Define an operator 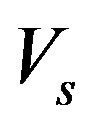 as follows:
as follows:
Let
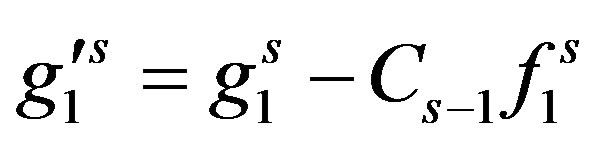 and
and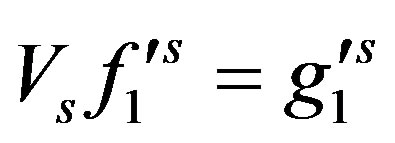 ,
,
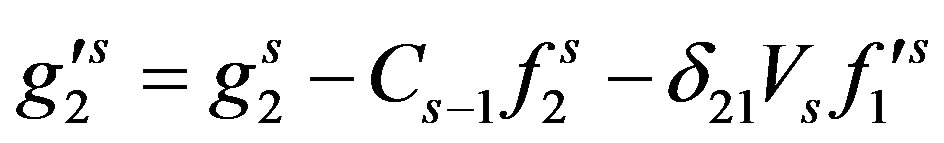 and
and 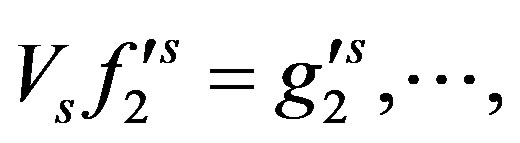
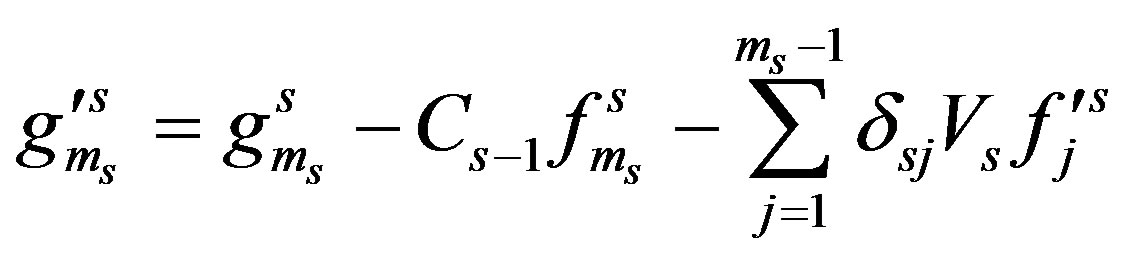 and
and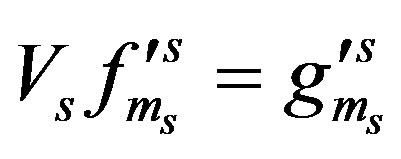 .
.
Since  is linear independent,
is linear independent, 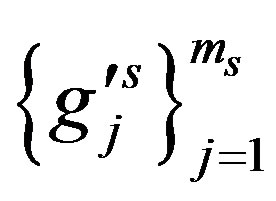 is linear independent. Denote
is linear independent. Denote
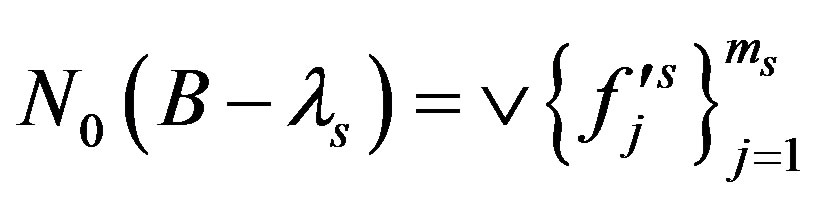 and
and .
.
Then
 ,
,
 and
and 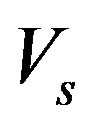 is an operator from
is an operator from 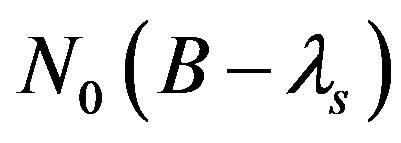 onto
onto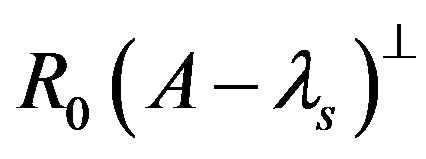 . Define
. Define 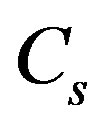 by
by
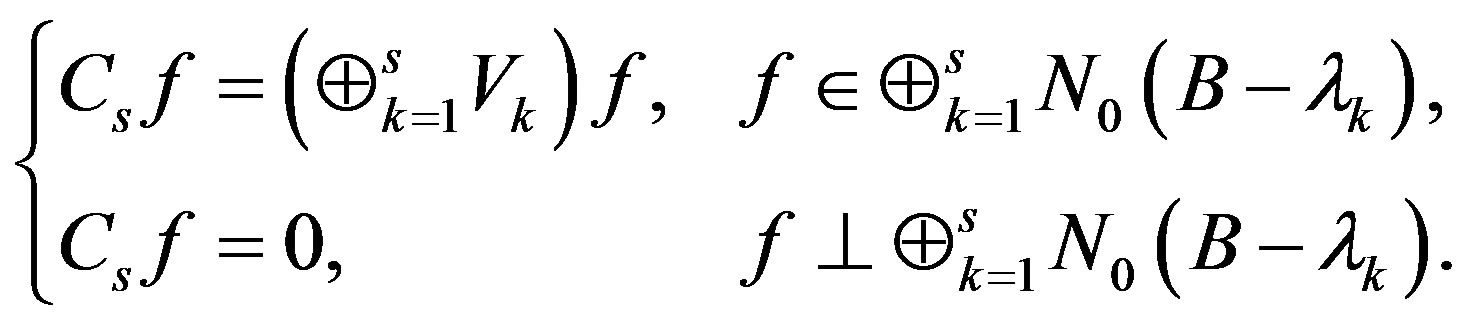
Let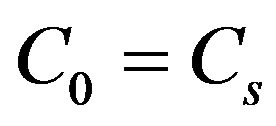 . It is clear that
. It is clear that  is well defined and bounded with finite rank. By directly computation, we can get
is well defined and bounded with finite rank. By directly computation, we can get
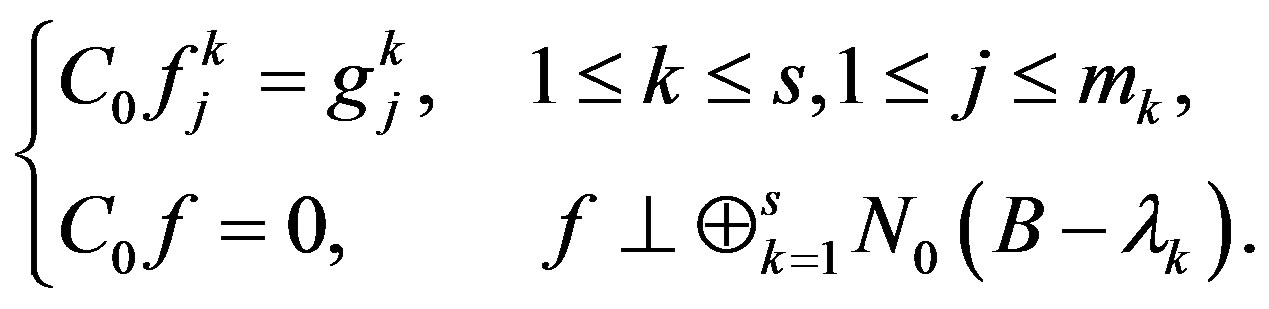
Step 2. We prove that 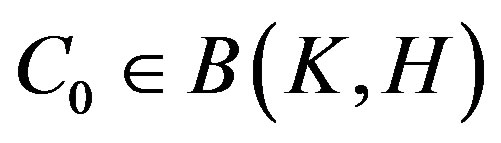 defined as above such that
defined as above such that
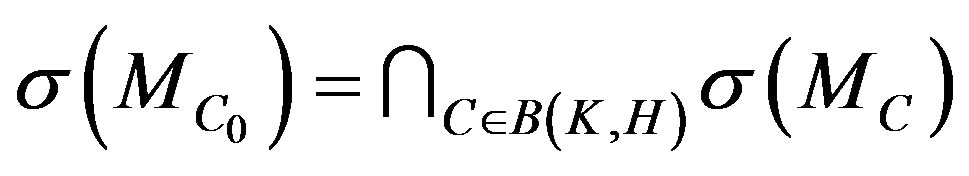 .
.
It is sufficient to prove that for any ,
,  is invertible. From Lemma 2, it is only to prove for any
is invertible. From Lemma 2, it is only to prove for any ,
, 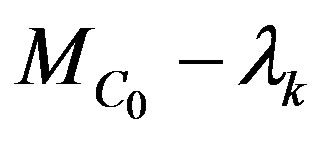 is invertible. To finish it, it is to prove that
is invertible. To finish it, it is to prove that  is injective and surjective.
is injective and surjective.
If there exists a vector 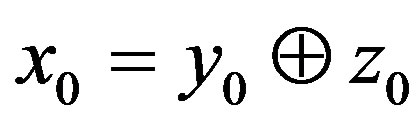 with
with
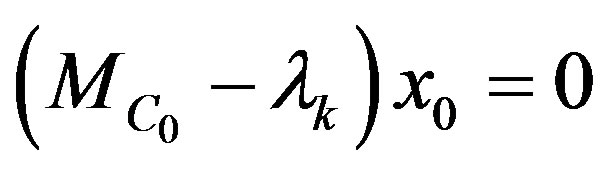 where
where  and
and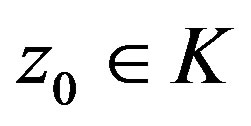 , then
, then 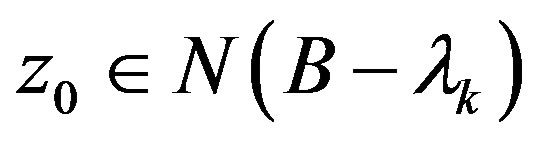 and
and
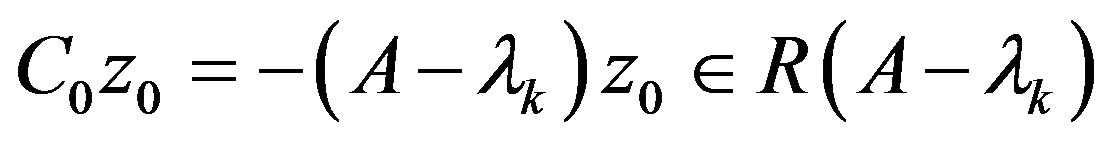 . By definition of
. By definition of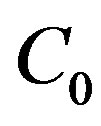 then
then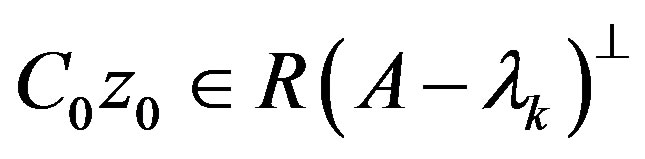 , thus
, thus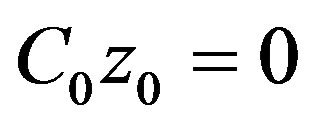 . On the other hand, since
. On the other hand, since 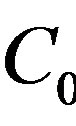 is injective on
is injective on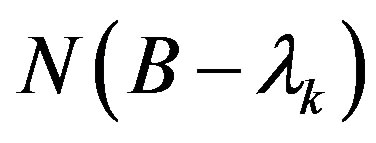 , then
, then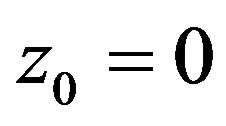 and so,
and so,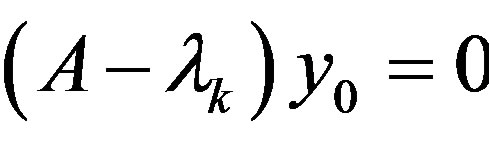 . By assumption that
. By assumption that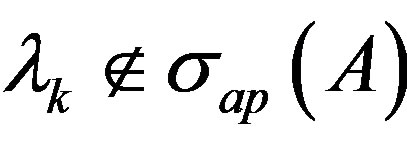 hence
hence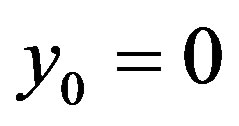 . Therefore
. Therefore  is injective.
is injective.
For any vector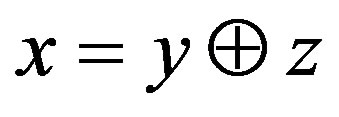 , where
, where 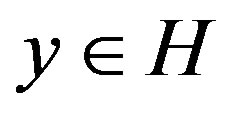 and
and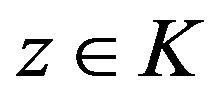 .
.
Since  and
and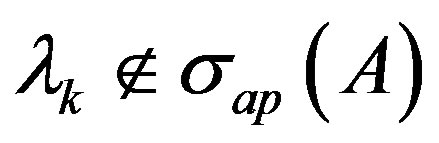 ,
, 
and 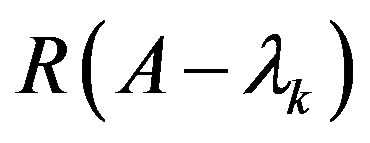 is closed. Thus there is a vector
is closed. Thus there is a vector 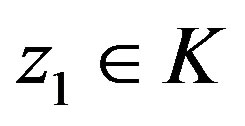
such that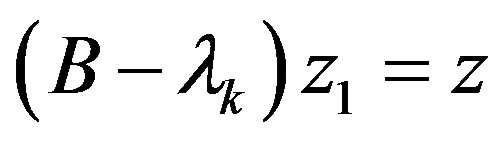 . Because
. Because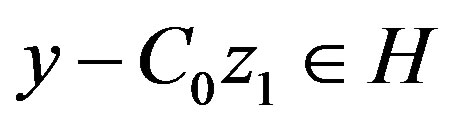 , there exist
, there exist 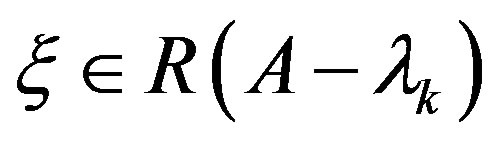 and
and 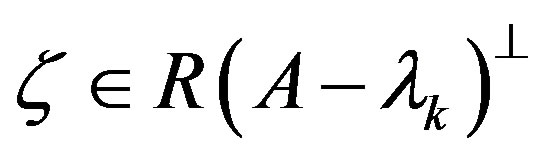 such that
such that
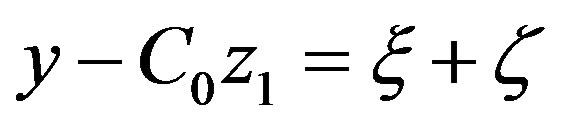 . Hence there exist
. Hence there exist 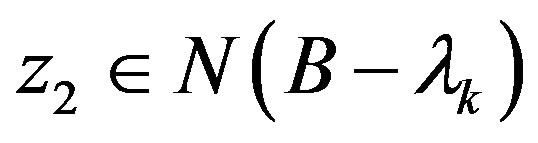
and 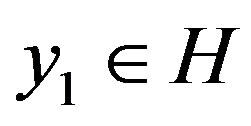 such that
such that 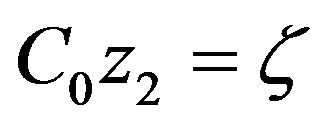 and
and . The last equality is possible, because
. The last equality is possible, because  is onto
is onto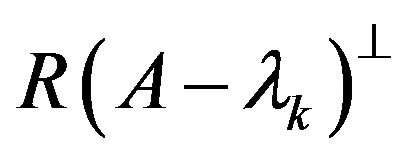 . Therefore,
. Therefore,
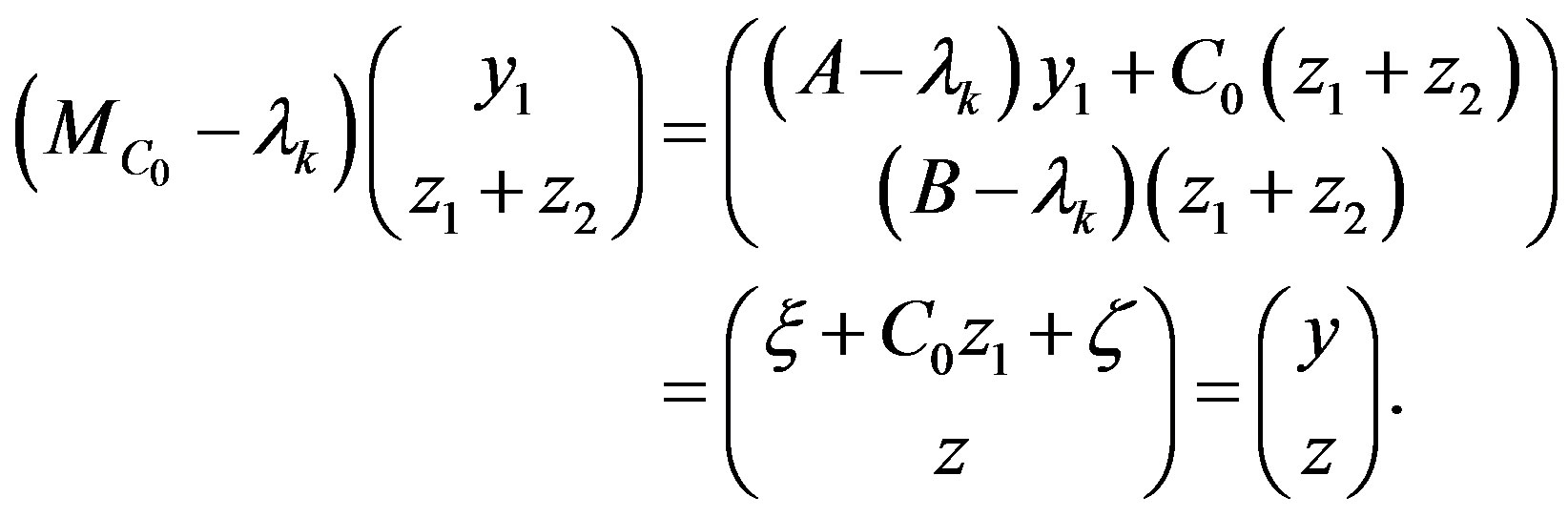
As  is arbitrary,
is arbitrary, 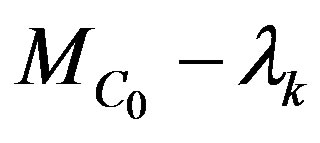 is surjective.
is surjective.
Hence, for any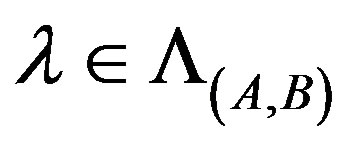 ,
, 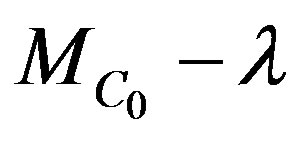 is invertible, i.e.,
is invertible, i.e.,
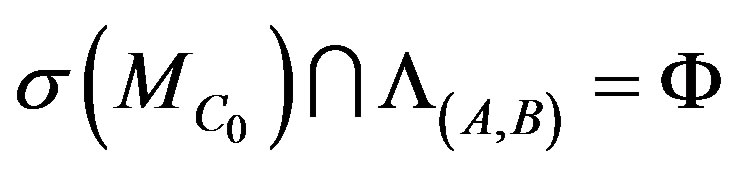 . So
. So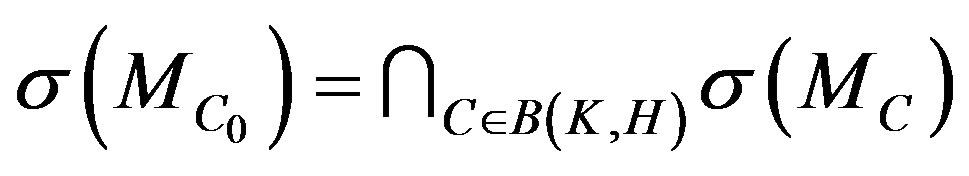 .
.
The proof is completed.
Example 4. If  and
and ,
, 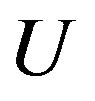 is the shift operator on
is the shift operator on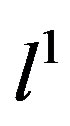 , let
, let
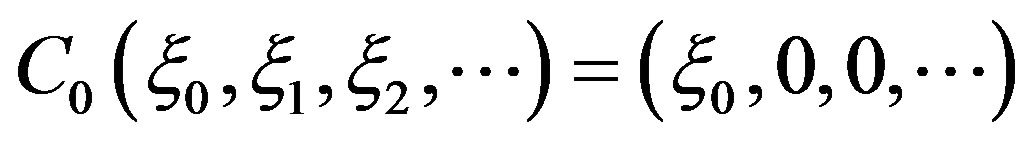 then
then  is invertible. From directly computation,
is invertible. From directly computation, 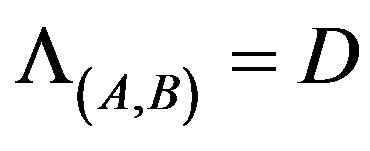 and
and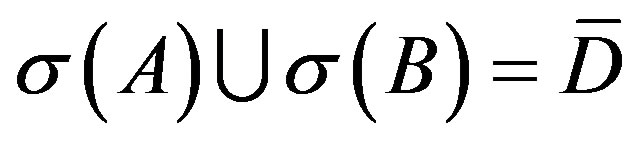 , where
, where  is the interior of unit disk. For any
is the interior of unit disk. For any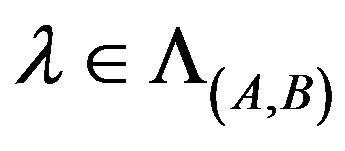 ,
,  is invertible. Thus
is invertible. Thus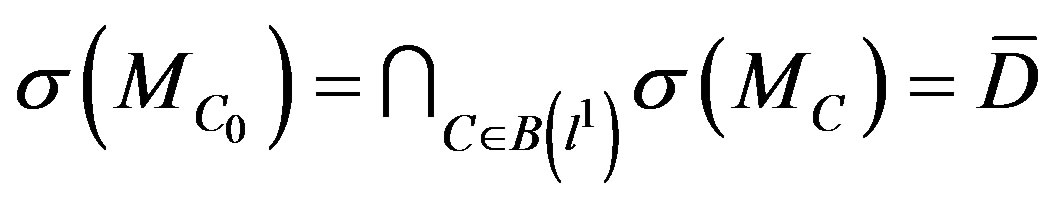 .
.
3. Acknowledgements
This subject is supported by NSF of China (No. 11171197) and the Natural Science Basic Research Plan of Henan Province (No. 122300410420, 122300410427).
REFERENCES
- H. K. Du and J. Pan, “Perturbation of Spectrums of 2 × 2 Operator Matrices,” Proceedings of the American Mathematical Society, Vol. 121, 1994, pp. 761-766. http://dx.doi.org/10.1090/S0002-9939-1994-1185266-2
- H. Y. Zhang and H. K. Du, “Browder Spectra of Upper Triangular Operator Matrices,” Journal of Mathematical Analysis and Applications, Vol. 323, No. 1, 2006, pp. 700-707. http://dx.doi.org/10.1016/j.jmaa.2005.10.073
- M. Barrua and M. Boumazgour, “A Note on the Spectra of an Upper Triangular Operator Matrix,” Proceedings of the American Mathematical Society, Vol. 131, 2003, pp. 3083-3088. http://dx.doi.org/10.1090/S0002-9939-03-06862-X
- X. H. Cao and B. Meng, “Essential Appoximate Point Spectra and Weyl’s Theorem for Operator Matices,” Journal of Mathematical Analysis and Applications, Vol. 304, No. 2, 2005, pp. 759-771. http://dx.doi.org/10.1016/j.jmaa.2004.09.053
- D. S. Djordjevic, “Perturbations Spectra of Operator Matrices,” Journal of Operator Theory, Vol. 48, 2002, pp. 467-486.
- J. K. Han, H. Y. Lee and W. Y. Lee, “Invertible Completions of 2 × 2 Operator Matrices,” Proceedings of the American Mathematical Society, Vol. 128, 2000, pp. 119- 123. http://dx.doi.org/10.1090/S0002-9939-99-04965-5
- Y. Li, X. H. Sun and H. K. Du, “Inversctions of the Left and Right Essential Spectra of 2 × 2 Upper Triangular Operator Matrices,” Bulletin London Mathematical Society, Vol. 36, 2004, pp. 811-819.
- H. Y. Zhang, X. H. Zhang and H. K. Du, “Drazin Spectra of 2 × 2 Upper Triangular Operator Matrices,” Acta Mathematica Scientia, Vol. 29, 2009, pp. 272-282.
- J. B. Conwey, “A Course in Functional Analysis,” Springer-verlag, New York, Heidelberg, Berlin, Tokyo, 1985. http://dx.doi.org/10.1007/978-1-4757-3828-5

