ABSTRACT

Received June 15, 2013; revised July 15, 2013; accepted July 23, 2013

The design of telecommunication network with capacity constraints of links, routers and ports of routers is considered in this paper. Specially, we limit each demand flow traversed through a pre-specified maximal number of links (called hops) under node failure scenarios in IP layer network. Such a design must be the most cost-effec- tive and ensure that feasible flows continue to exist even when any relay node of the network fails. We propose a reliable mixed-integer programming (MIP) model with multi-scenario constraints to optimally design a mini- mum-cost survivable IP network that continues to support a good communication under any node failure scena- rio. Then we transform the MIP model into many single scenario models, that is, simplified MIPs, nonlinear programming (NLP) models and MIP models under Benders decomposition Then we transform the MIP model into many single scenario models, that is, simplified MIPs, nonlinear programming (NLP) models and MIP mod- els under Benders decomposition. Three heuristic methods are proposed to solve these models including branch-and-bound algorithm, global algorithm for NLP, and heuristic algorithm based on benders decomposition. We mainly study the application of Benders decomposition method, where dual model and bounding procedures are given for each MIP model under Benders decomposition at each scenario. The results of our computational experiments validate the effectiveness of the proposed models and algorithms.

Keywords:

Mixed-Integer Programming; Benders Decomposition; Network Design; Node Failure

1. Introduction

Network design problems [1-3] involve a number of applications including logistics, power systems, transporta- tion, telecommunication and military scenarios. The idea is to establish a network of links (roads, bridges, air- lines, optical fibers, electric lines, etc.) that enables the flow of commodities (people, rescue materials, data packets, electricity, etc.) in order to satisfy some demand characteristics like minimum cost. In addition, the idea con- taining design of survivable or reliable networks has become a major objective for telecommunication operators [4,5].

Telecommunication network has been developed rapidly in China with the characteristics of more complex flow, wider bandwidth, and higher level of QoS (quality of service) in recent years. Network survivability is de- fined as the ability of a network to maintain its communication capabilities in the face of equipment failure [6]. In most cases, it means that a network is still functional after the failure of certain network components like node failure. In this paper, we treat the concept of reliability the same as survivability. Take IP-over-WDM network in telecommunication as an example, IP layer nodes employ optical cross-connects and IP routers and they are connected by fibers to form a mesh topology. Unlike physical layer, an important and special case in IP layer

is that IP nodes are more vulnerable than the links. A common reason for interrupted connections with node failures is caused by hardware failures or by an overloaded network. A node has to cope with more traffic than it is able to handle [7], and it usually happens in uncertain issues such as disruptions from disasters. So contin- gency plans for providing relief to affected areas in IP network design need to consider the potential failure of certain vulnerable nodes. Many measures have been taken like installing redundant communication lines and connecting equipment, design node-disjoint (and edge-disjoint) path [8] or enough link capacity [9]. And there have been lots of researches on the related issues.

The main contributions of this paper can be summarized as follows. First, we provide a reliable mixed-integer programming model for telecommunication network design problem from a more practical point of view. Al- though the model has been designed to be mostly technology-independent for a single layer IP network, it can be extended easily with practical needs.

Second, according to origin model, we transformed it to other three mathematical models including simple MIP model, NLP model, and MIP model with Benders decomposition form.

Third, we present various model-specific algorithms including branch-and-bound algorithm, global algorithm for NLP, and heuristic algorithm based on benders decomposition, and compare them by looking at the results and computing time. Meanwhile, we show that our methods are effective by comparing the price of robustness between our methods and the method using 1 + 1 dedicated path protection, and highlight the performance of the heuristic algorithm based on benders decomposition and the gap design is influenced by convergence of Benders algorithm bounds.

The remainder of the paper is organized as follows. In Section 2, we review the related literature. We then define our problem and build a reliable network design model and some smart model transformations in Section 3. In Section 4, a heuristic algorithm is developed based on benders decomposition, followed by computational re- sults in Section 5 and conclusions in Section 6.

2. Literature Review

As stated in the introduction, design of survivable or reliable networks has been addressed by a number of researchers and the network design problem considering reliability constraints is NP-hard [4,5]. Soni provided a classification scheme as physical survivability and logical survivability and further classification within each group. Actually, logical survivability would be achieved if and only if the underlying physical network was survivable. In order to handle the reliable problem, protection schemes have been proposed mainly in three aspects including dedicated path protection, shared path protection and demand-wise shared protection [10,11]. These schemes are different within measures like good reaction times, good bandwidth requirements and simple network management.

In particular, some authors used failure probability as the factor of reliability [8] and some used scenario-base failure without probability factor to support robust solutions [6,9]. For simplicity, it usually makes sense to try and protect the network against single link or single node failures only [6,7,9,12]. And it can be expand to the general scenarios of arbitrary set of failure configurations, including multiple link and node failures. Our paper concentrates on single node failure. A node represents equipment, such as a switch or router. The diameter bound, also called “hop constraints”, ensures efficient use of node resources and limits the maximum delay, which is usually used as a surrogate for service restrictions. The node degree bound models the limited number of physical ports on a node, which often has capacity constraints. Therefore, more and more papers have focused on hop constrained network design problem [13,14] and capacitated network design problem [7,9,15].

Uncertainty in the traffic requirements is an important factor that affects reliable network design, and we must take it into account. Lots of researchers have studied the network design with demand uncertainty [15-20]. Alper [18] allows one to control conservatism of the solutions by means of an allowed “budget for demand uncertainty.” The idea is robust optimization, which was first proposed by Soyster [21]. In our reliable network design, we consider the worst node failure scenario and try to get the robust solutions.

Our problem is very closely related to the well-known hub location problem [22-25], but differs in the fact that the demand nodes can communicate with each other directly and we consider more constrains together in the model such as various capacity constraints and hop constraints. On the other hand, hierarchical or layered topological network design [26-28] is common in real telecommunication networks. But we concentrate IP layer for simplicity and consider multi-layer network design later.

Network design problems are usually modeled as mixed-integer programming formulation or two-stage mixed-integer program formulation. The models are often large-scale and hard to solve. Many solution approaches or heuristics have been proposed for these problems in recent years, such as Benders decomposition

[29-33], branch and bound, branch and cut, branch cut and price, column generation, Lagrangian relaxation, dy- namic programming and so on. Benders [29] proposed benders decomposition methods first for solving mixed variables programming problems followed by many researchers. In Section 4, we prefer Benders decomposition for structured optimization.

3. Reliable Network Design Model

The network design problem that we consider examines the network as a graph with a set of nodes and potential links. The nodes are divided into two types, demand nodes as a set of communication pairs (or origin-destination pairs) and relay nodes with fixed router construction cost and port cost in the router. Every origin-destination pair has a flow demand and the hop constraint. Associated with each link is a construction cost and a capacity. Meanwhile, we consider the failure of any potential relay node that may necessarily render the remaining operational links incapable of transmitting the information flow and we denote such a situation with a failing node as a failure scenario. So the aim of this article is to build a reliable network design model to minimize network construction cost with node failure scenarios and develop heuristic algorithms to get robust solutions. The robust solutions contain the number of ports of every router (that is relay node), whether link is established, and the amount of flow of every link.

3.1. Notation and Model Parameters

First of all, we define a network in telecommunication with parameters as follows:

: A graph 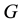standing for the IP network with node setand potential directed link set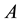.We substitute 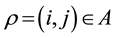where convenient in this discussion.

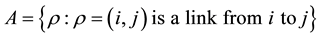
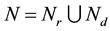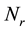, denotes a set of relay nodes, 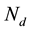denotes a set of demand nodes

is a set of origin-destination pairs, and

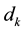: The amount of flow demand for the kth pair from to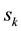

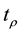: The capacity of link

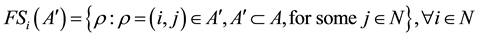is the set of links in 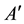that exit node

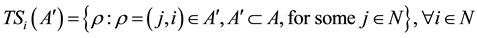is the set of links in that enter node

: A set of links operating normally when there is a failure scenario

: The maximum number of ports of the router

: The flow amount of each port of the router

: The per-unit cost of flow on link, a construction cost of the router and a port cost in a router respectively

: The maximum number of hops in the network.

The decision variables in our models are as follows:

:

: The number of ports of relay node in IP network, where

: A designed flow demand satisfying formal communication under any failure scenario

: The amount of the kth origin-destination flow demand satisfied on arc under failure scenario

: Under the failure scenario, if the arc is constructed in the kth origin-destination pair, it denotes 1; otherwise, it denotes 0.

3.2. The Basic Model

With the above parameters, the model of our original problem can be stated as follows:

(1)

(1a)

(1b)

(1c)

(1d)

(1e)

(1f)

(1g)

(1h)

(1i)

(1j)

(1k)

The objective function (1) serves to minimize the total cost of constructing routers and flows of links, in which parameter is used to describe the construction cost of the router in advance, not consider whether to use. Constraints (1a) limit the amount of every flow on the link to be no more than its designed flow demand in each failure scenario. Constraints (1b) require that the required amount of demand is shipped from each origin in each failure scenario, while constraints (1c) enforce the flow balance for delay nodes in each failure scenario. (1d) enforce the enter flows or exit flows of each relay node within the limit of the router’s capacity. Constraints (1e) stipulate that the hops of every origin-destination pair should be no more than the maximum hops in order to satisfy the telecommunication quality and (1f) insures that the amount of the kth origin-destination flow exists on the link only when the link is constructed in the kth origin-destination pair under failure scenario. (1g) limits that the designed flow on each link should be no more than its capacity. (1g) to (1k) state the admissible range of decision variables.

Remark 1. The model (1) above considers a reliable telecommunication network design problem. Its advantage is that the reliable flow allocation is designed in advance with the possible failure nodes. Under the design, the network operates with little jitter or delay connection specially when there is enough bandwidth. Survivable network design deals with the problem of designing telecommunication networks that can survive a specified number of node or link failures. Although considering failure with only one relay node here, it can be applied to the occasion that a set of nodes or arcs could simultaneously fail.

3.3. Model Transformation

The Model (1) is a large-scale mixed-integer programming problem, and the variables contain binary variables, integer variables and continuous variables. Overall, there are constraints, decision variables including, , , and. Hence, we try to employ model transformations to simplify the original model and design effective algorithms.

Proposition 1 Model (1) is a multi-scenario model and can be transformed to many simplified single scenario model (2) for every scenario. And we can get the optimal objective value and optimal solutions of Model (1) from the optimal solutions of Model (2).

(2)

(2a)

(2b)

(2c)

(2d)

(2e)

(2f)

(2g)

(2h)

Proof Since requires, and means. So the binary variables can be dropped

from model (1) where its value can be deduced from. In fact,. At the same time, (Note that “” as rounded up). Therefore model (1) can be transformed

approximately to Model (3) with the same optimal solutions as follows:

(3)

(3a)

(3b)

(3c)

(3d)

(3e)

(3f)

(3g)

(3h)

In model (3), means the number of relay nodes which is a given value, and the item in the objective function can be omitted which doesn’t change the optimal solution. As for the item

in the objective function, the optimal solution will not be changed by dropping

“”. Given a scenario, then the approximate sub-problem can be stated as Model (2) where the failure scenario index w has been dropped for simplicity. So the optimal objective value of Model (1) can be obtained from the optimal solutions of Model (2). □

Here the simplified form of model (1) is obtained, and it is a mixed integer programming model with decision variables and, we note it as MIP model.

Remark 2 The MIP model (2) has either detected infeasibility or has an optimal solution to the original problem and gets its optimal solution on the extreme points.

Notice that the model (2) is a multi-commodity flow problem with hop constraints from actual telecommunication background. If it has feasible solutions, the feasible solution region is a bounded polyhedral region. So it will get its optimal solution on the extreme points to make the minimum total cost. Otherwise, the problem is infeasible because of limited capacity and hops or other conditions.

We can also transform the MIP model (2) into a nonlinear programming model with only one decision variables as Liu et al. [10] built. Since if, then link will be constructed. Therefore, constraints (2e)

equals, where is a little positive number. Here we show the model as follows

and we note it as NLP model:

(4)

(4a)

(4b)

(4c)

(4d)

(4e)

(4f)

4. Heuristic Algorithms

The algorithmic approaches apply robust ideas such as using a worst-case approach, and this idea is often useful in practice. Initial results on robust linear optimization were given by Soyster in [21]. His model is equivalent to the LP in which all uncertain parameters have been fixed at their worst-case values from the uncertainty set. However, our model has the uncertain parameter of node failure which may influence flow allocation. We can choose uncertain part of node failure scenarios but not all of the node failure necessarily. To avoid considering the probability of choosing node failure, we consider every node failure scenario.

Here we propose three methods to solve the model (2). First, solve it directly with branch-and-bound algorithm provided by lingo or Xpress optimizer software. Second, it can be transformed to model (4) and solve model (4) with global algorithm by the similar software. Third, we can employ a Benders decomposition approach [29] which may get solutions more effectively. As Benders decomposition approach is concerned, it is a classical method for combinatorial optimization problem, especially mixed integer programming model, such as routing, distribution and location problems. It begins by partitioning the model to be solved into two simpler problems, named master problem and sub-problem [31]. The master problem is a relaxed version of original problem, containing only a subset of the original variables and the associated constraints. The sub-problem is the dual problem of original problem with the variables obtained in the master problem fixed. Specifically, we can divide the variables of a problem into two vectors and. It fixes to define a sub-problem that contains only. If the solution of the sub-problem reveals that the trial value of is unacceptable, the solution of the sub-problem’s dual is used to identify a new values of. We will propose the decomposition approach with our problem in the next section with detail.

4.1. Heuristic Algorithms to Solve Model (2) and Model (4) Directly

Since model (2) and model (4) has the similar basic process to solve except the inner algorithm in Lingo, we describe them in the same framework here.

Initialization: Set iteration counter., let.

Step 1: Choose a scenario w satisfying arbitrarily and solve model (2) (or model (4)). If there is an optimal solution and (for model (4)), set and increment by one, and proceed to Step 2. Otherwise, terminate the algorithm with no optimal solution.

Step 2: If, return to Step 1. Otherwise, proceed to Step 3.

Step 3: We obtain the final optimal solution and

.

The Algorithm will be executed iterations. Thus, the complexity of this heuristic is given by, where represents the complexity of solving model (2) (or model (4)), and represents the instance of the model.

4.2. Heuristic Algorithm Based on Benders Decomposition to Solve Model (2)

In the MIP model (2), is identified as real variables and is identified as binary variables. We may thus employ a Benders decomposition approach and the problem can be expressed as

(5)

(5a)

(5b)

(5c)

(5d)

(5e)

(5f)

(5g)

Where.

The inner minimization model (5) is a linear program. For a given value for, associating dual variables, with constraints (5b), , with constraints (5c) and (5d), , with constraints (5e) and, with constraints (5f), therefore the dual to (5) for scenario is given by

(6)

(6a)

(6b)

(6c)

(6d)

(6e)

(6f)

Since the original problem has optimal solution if it is feasible, and then by duality theory of linear programming, we have:

(7)

Using the partitioning and delayed constraint generation ideas [30], we can now decompose model (2) into two small problems referred to as the Benders sub-problem (SP) and the Benders relaxed master problem (MP), in that, SP and MP will be employed for computing upper bound UB and lower bound LB on model (2) in an iterative procedure called the Benders algorithm.

Here SP for every scenario is expressed as model (8), that is:

(8)

Next, let be the extreme points, and, be the extreme (i.e. unbounded) rays of SP poly-tope. Then MP in scenario w can be stated as follows:

(9)

(9a)

(9b)

(9c)

(9d)

where is a free variable. We use the idea behind delayed constraint generation which is to solve MP using only a small subset of the constraints, and to check afterward whether any of the non-included constraints are violated. Therefore, the constraints (9a)-(9b) will be generated whenever they are needed, and these are not de- fined for all and at the beginning.

To obtain optimal solution of model (9), consider only the extreme points and extreme rays that will be generated one-by-one by solving SP. If SP is feasible and bounded, one can identify an optimal extreme point, if

,

where is the optimal value of the former MP, then add constraint (9a) to MP and re-solve MP. If SP is unbounded, one can identify an extreme ray, if

,

then add constraint (9b) to MP and re-solve MP. However, to find the extreme rays in practice is often difficult. A method is to solve the auxiliary sub-problem AP [32], which is the same as SP except that the objective function of model (6) set to zero, and the right side of the constraints (6a)-(6c) are forced to be zero, that is

(10)

However, when model (6) has an unbounded solution, that is we find an extreme ray, we often don’t find the extreme ray in practical operation, but adopt to add the following constraint to model (6) that assures a bounded solution:

(11)

where is an enough large positive number.

In order to reduce running time to solve Model (2) with benders decomposition, and get an acceptable solution, we define the relative gap of our algorithm:

(12)

This gives the accuracy of the approximation for the optimal solution value, which provides a stopping criterion or convergence criterion of iterative algorithms. Then start with a partial network solution from the current network design, and add arcs to the network as necessary until a feasible solution is obtained. Although we need not get extreme ray in our problem, we write the entire frame of the algorithm in favor of algorithm expansions. The heuristic algorithm based on the Benders decomposition is given as follows.

Algorithm: Heuristic algorithm based on benders decomposition

So the optimal solutions of the original model (1) are:

The algorithm is provably finite. When our problem has feasible solutions, it results in the optimal solution and at any time during its execution lower and upper bounds on the optimal solution of the original MP can be obtained. In our implementation, the heuristic will follow the detail steps in the reference of multiple models and parallel solving with Mosel [32].

5. Computational Experiments

We propose three methods to solve three transformations of the same model of our problem in telecommunication background, and they are the branch-and-bound algorithm provided by Lingo9.0 used in the MIP model (BBMIP), global algorithm provided by Lingo9.0 used in the NLP model (GNLP) and the heuristic algorithm based on benders decomposition applied in the MIP model (BDMIP). The BDMIP is implemented with Mosel in Xpress-ive and solved with Xpress optimizer (version 19.00). All results are collected on a Dell computer with 2.0 GB memory and 2.93 GHz dominant frequency. Here let’s compare them by looking at the results and computing times (in CPU seconds).

Considering a random example as Figure 1 illustrated. Here we compare the methods by looking at the processes and results, including solver iterations. is the origin-destination pair. Initialize common data as follows:

, , , , , , , h = 3, is shown in Table 1.

Case 1:, , , Gap = 0.

In this simple instance, the results in Table 2 demonstrate different solver iterations for different methods, and they can get the same objective values and robust solutions. The program execution time of each method is very little, but we can see the BBMIP has the fewest solver iterations.

In order to show the price of robustness with our method is acceptable, we can compare our reliable protection (called “reliable node failure protection”) with the method using 1 + 1 dedicated path protection [12,13].

To ensure service connectivity in case of single network element failures, two link- or node disjoint paths (depending on planning requirements) are set up for 1 + 1 dedicated path protection. The signal is broadcasted over both the working and the backup path simultaneously. In case of a single link or node failure, the sink of the demand still receives a copy of the data from one of the two paths.

If we don’t consider the node failure scenario, that is no node of the network will fail, then the results of this case can be computed from our model (2) without the factors of node failure scenarios. We list the objective value of original model with 1 + 1 dedicated path protection and with reliable node failure protection in the last row of Table 2, from which we can compare total cost of the telecommunication network design problem and the price of robustness. Here we note “objective value of original model with reliable node failure protection” as OV1, and note “objective value of original model 1 + 1 dedicated path protection” as OV2. The savable price of

network is noted as SPN, and it equals (OV2-OV1)/OV1.

For the BDMIP, when experimented on this illustrative example of node E failure, it converged to the optimal solution in 46 iterations. The convergence of the algorithm and the bounds obtained at each iteration are illustrated in Figure 2. The final network topology from this example is shown in Figure 3.

Case 2:, ,.

For the purpose of demonstrating the influence of numbers of demands, we consider more demands than Case 1 and the results are displayed in Table 3, Figures 4 and 5. By comparing Case 1 and Case 2, we can observe that the methods with the increasing speed of solver iterations from low to high are BBMIP, GNLP and BDMIP respectively. For the savable price robustness, the value is 21.8% in case 1% and 4.3% in Case 2 which guarantee the reliability of the network and save more price of the network than that of the 1 + 1 dedicated path protection.

Since the CPU time to solve the model (2) with BDMIP mainly depends on the numbers of the master problem [8], and solving the master problem will spend more and more time as the solver iterations increase,. This can be seen clearly in Figure 6. So we must decrease the solver iterations by making the Gap > 0 and permit an approximate solution.

Here we compare the different Gap to allow the approximate solutions with BDMIP in Table 4. A very important observation from the results is that the value to set the Gap is influenced by convergence of Benders algorithm bounds which is partly shown in Figures 7 and 8.

For example, by examining the results for node E failure in Case 2, the Gap equals 0.05 and the Gap equals 0.1 make no difference at the iterations. That’s because the lower bound and the upper bound of Benders algorithm here at the 281st iteration is very close. But for node F failure, the gap is enough small until the algorithm iterate constantly to get optimal solution.

6. Concluding Remarks

Our models are to obtain a minimum cost network with some flow constraints, capacity constraints and especially hop constraints under uncertain node failure scenario. This is in fact a network design problem in telecommunication background which can be formulated as mixed integer programming models and can also be transformed to other mathematical models. Many other practical applications such as logistics, power systems, and transportations can be abstracted as similar network design problems. The idea of reliability or survivability is applied to the network design problem which is mainly embodied in considering the node failure scenarios here. We propose three methods including BBMIP, GNLP and BDMIP with a worst-case idea behind robust op- timization. And mainly study the Benders Decomposition for our model. Our computational experiments have indicated that Benders decomposition is an efficient method for solving network design problems, and can be controlled more easily than traditional techniques such as Branch-and-Bound, Lagrangian relaxation or global non-linear algorithms.

There are several variations and extensions of this work that could be considered for future research. In addition to the two extensions of our model in Remark 1 in Section 2.2, we can find some extensions of our problem. First, we study the network reliability under certain demands, but uncertain demands need to be considered. Se- cond, in the context of emergency service deployment, disasters such as earthquakes may damage several com- municational device nodes or links. Multi-link failures or failures of both links and nodes are difficult to handle in modeling and computing. For these difficult and practical problems, effective and efficient algorithms like Benders decomposition or combining Benders decomposition with other techniques are urgently needed.

Acknowledgements

We would like to thank Jiye Han very much for his constructive remarks and suggestions. This work is sup-

ported by National Natural Science Foundation of China (No:71171189, No:71271204, No:11101420) and Knowledge Innovation Program (No:KGCX2-RW-329) of the Chinese Academy of Sciences.

References

NOTES

^*Corresponding author.