Applied Mathematics
Vol. 4 No. 8A (2013) , Article ID: 35077 , 9 pages DOI:10.4236/am.2013.48A004
Model-Based Analysis of a Phenol Bio-Oxidation Process by Adhered and Suspended Candida tropicalis
1Grupo de Tecnología Bioquímica, Departamento de Bioquímica y Biología Molecular, Universidad de La Laguna, San Cristóbal de La Laguna, Spain
2Departamento de Ingeniería Bioquímica, Escuela Nacional de Ciencias Biológicas, IPN, Mexico D.F., Mexico
Email: *ntorres@ull.edu.es
Copyright © 2013 Hugo Velasco-Bedrán et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 14, 2013; revised April 15, 2013; accepted April 24, 2013
Keywords: Candida tropicalis; Phenol Biodegradation; Fluidized Bed Reactor; Adhered; Suspended Yeast; Mathematical Modeling
ABSTRACT
Phenol is an important commodity for the chemical industry, used for many processes and deemed to be a major pollutant due its xenobiotic nature and high toxicity. For the purpose of phenol bioremediation a biotechnological set up consisting of a continuous packed column bioreactor with Candida tropicalis adhered onto activated carbon beads has been previously described. In this work, we show how the integration of available experimental data of such a biotechnological set up into a mathematical model, can lead both to a better comprehension of the underlying physiological mechanisms operating in the cell culture, and to the identification of the system parameters optimum performance. The model so constructed describes the dynamics of phenol uptake and growth rates by the adhered and suspended biomass; the lethality rates; the adhered biomass removal into suspension or adherence onto carbon beads rates and the phenol and biomass (adhered and suspended) concentrations. It also serves to identify different physiological states for the adhered and the suspended biomass; its predictions being verified by comparing with experimental observations. Based on the model description, different optimization strategies are proposed, some of which have been experimentally tested, encompassing changes in bioreactor operation conditions, process development and strain development.
1. Introduction
Phenol is an important commodity for the chemical industry, used for resins production, synthetic fibers and pharmaceuticals [1]. Altogether these industries account for 80% of the utilization of the 6 million tons/year of the phenol world production [2]. It is also the by-product of petrochemical plants and paper mills. Phenol, due to its xenobiotic nature paired to a high toxicity at low concentrations in water [3], is a major pollutant.
The last two decades have witnessed an increasing awareness for cleaner manufacturing practices and for preserving water resources. Given the toxic and harmful effect of the phenol effluents coming from industries, increasing attention has been devoted to phenol removal from wastewater streams [3-5]. The current treatment for phenol physical removal involves adsorption plus oxidation or desorption, both being energy consuming and costly [5]. Thus, bio-oxidation has become a suitable, low-energy consuming alternative, albeit at slower rates than sorption processes [6]. Therefore, attempting higher bioprocess rates is a biotechnologically relevant goal.
Yeasts show the ability to oxidize and cleave aromatic rings where phenol, being a reduced carbon source, can serve as an energy rich nutrient [7-9]. In this regard several process strategies have been proposed [5]. Among the reported strategies for phenol bioremediation are the use of aerobic granulated consortiums [3] and cell immobilization [10-12]. In the second case, where selfadherence of cells onto porous solid surfaces occurs, an increased conversion rate of substrates by yeasts is observed [13]. Reference [9] has shown that, in a phenoldegrading granular consortium, a film of Candida tropicalis on the surface is formed. However, it has been also demonstrated that phenol displays growth inhibiting and lethal effects on yeast cultures [9,14].
A strategy employing at a trade-off between higher phenol uptake and growth-inhibition and lethality has been recently reported [11]. In the present work, based in the experimental observations made by these authors, we have built a mathematical model of this set up. In the report alluded to, the experimental results are presented graphically and described phenomenologically. Reference [11] reports total phenol removal for most of the experimental conditions tested. Overall phenol removal rates could be calculated from the experimental measurements performed as also adhered and suspended biomass concentrations were measured. Several processes can be inferred from the experimental set-up, namely the process of cell adherence to, and disengagement form, the activated carbon beads; adhered and suspended cell lethality and, most importantly, the phenol removal discriminated for the adhered and suspended cell populations. Since the experimental set-up did not allow the calculation of the rates of these processes a model of this bioprocess in power law formalism [15,16] was built. Based in this model we aim first, to get insight on the basic mechanisms involved in the phenol mineralization and cell growth and then, to use this knowledge to define optimization goals.
2. Material and Methods
2.1. The Experimental Set up
The modeled process is described in [11]. It consists of a sparged, packed column bioreactor running in continuous mode with phenol-saturated activated carbon beads previously colonized with Candida tropicalis. In addition to the suspended cell culture, activated carbon beads provided a bed where adhered Candida tropicalis cells grew; both cultures (either in liquid or onto solid phase) being in a dynamic equilibrium (Galíndez-Mayer; personal communication). Micrographs in the paper alluded to, show yeasts growing discretely on the carbon beads, and no biofilm formation.
The process start-up was reported by [11,17]. After the saturation of the carbon beads with phenol, colonization was carried out and transient process kinetics ensued at a low feed at the necessary rates to achieve the experimenttal dilution rates. Phenol concentration was measured in the bio-reactor. The transient kinetics experimental conditions are used to simulate the phenol uptake batch process employing the suitable kinetic equation and parameter values.
The system was fed with a phenol-compounds mixture as sole carbon source. Steady state biomass (total and suspended) and unconverted phenols concentrations were measured at three different phenol inlet concentrations and feeding rates.
Two types of experimental behavior were observed. At low to medium phenol load rates (up to 50 mg∙L-1∙h-1), an almost null outlet phenol concentration and a high biomass concentration with a high adhered/total biomass ratio resulted. At higher phenol load rates, reduced biomass concentration and high phenol outlet concentrations were observed. In these conditions the adhered/total biomass ratio observed was lower than in the previous conditions.
2.2. The Model
Figure 1 shows the proposed kinetic model of the experimental set up for phenol bioremediation by using C. tropicalis [11]. According to this scheme there are three independent variables, the medium phenol concentration, PhS; and the suspended XS and adhered XA biomass concentrations. The physiology of phenol biodegradation shows the importance of oxygen in the process [18,19]. Nonetheless, the bioreactor configuration and operation provided an oxygen transfer rate and mixing assuring an abundant supply of oxygen [11]. Stoichiometric calculations (results not shown) demonstrate the oxygen culture medium concentration to be almost constant, so it was discarded as a variable.
Phenol is fed to the system at a constant rate VPhin and leaves the bioreactor at a rate VPhout. These rates are a function of the phenol concentrations PhS and the volumetric flow rate. Once within the culture medium, phenol is taken up at a rate (RPhA) by the adheredand a rate (RPhS) by the suspended-yeast biomass and used for biomass growth and energy production. The growth yields on phenol are described in the model by the parameters GS and GA for the XS and XA, respectively. The XA and XS yeasts decay at different rates (RXAD and RXSD, respectively) and are dislodged (Rd) or immobilized (Ra) at rates according to each experimental condition. Suspended cells (XS) leave the system at the VXSout rate. In
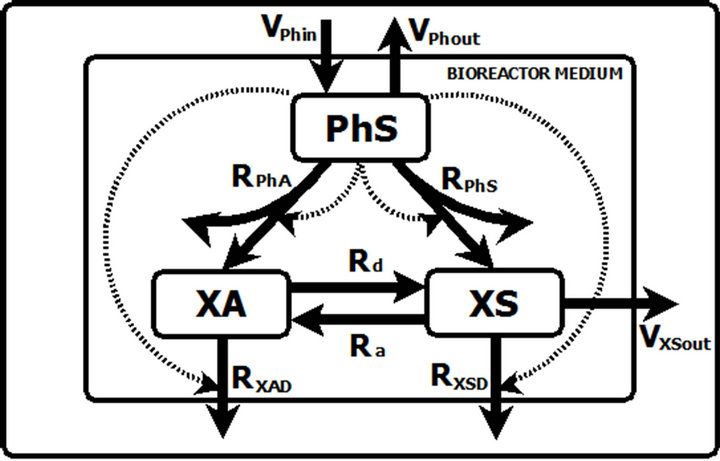
Figure 1. Kinetic model of the phenol degradation with C. tropicalis in a fluidized-bed bioreactor. Solid arrows represent input and output or process rates while dotted lines represent regulatory signals (curved dotted line for phenol effect on its uptake, straight dotted line for phenol effect on yeast cell decay rate). The curved arrows from PhS to the medium represent phenol mass conversion to metabolites and/or end products other than biomass.
the chosen power law formalism [15,16] the transport and bio-kinetic phenomena rates are expressed as a kinetic rate multiplied by the variables concentrations influenced by a kinetic coefficient to weight the impact of the concentration on the rate assessed.
In the model there are two types of regulatory signals. Those from PhS to the phenol uptake rates, RPhA and RPhS and those from PhS to the yeasts decay rates RXAD and RXSD. The first ones are represented in the model equations by the kinetic order parameters gPhA1 and gPhS1. In this case the values of the regulatory parameters quantify the net influence of the phenol concentration on the biomass growth. In the second ones, the corresponding parameters gXAD2 and gXSD2, account for the negative effect of phenol on yeast biomass due to its toxic nature.
The mass balance equations for the kinetic model thus described are:
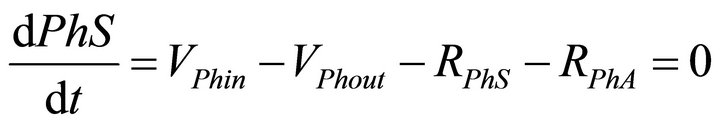 (1)
(1)
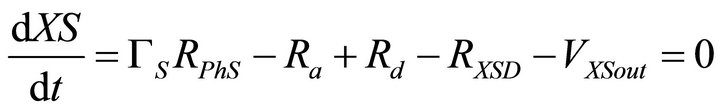 (2)
(2)
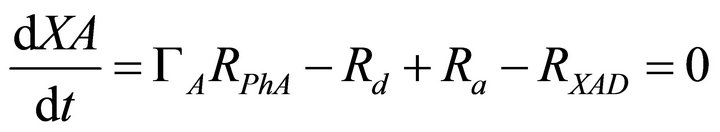 (3)
(3)
The corresponding rate equations in Equations (1)-(3) are given by the following power law kinetics:
 (4)
(4)
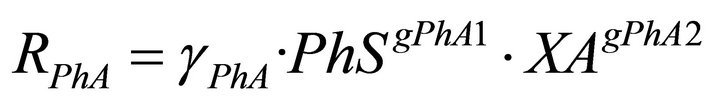 (5)
(5)
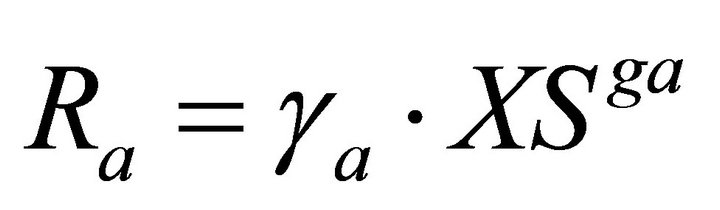 (6)
(6)
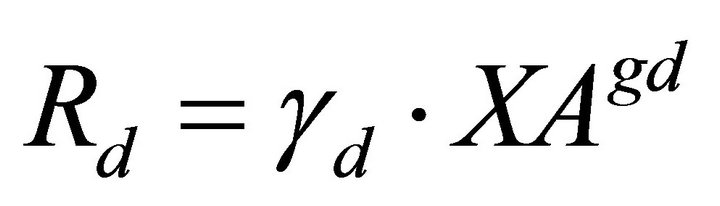 (7)
(7)
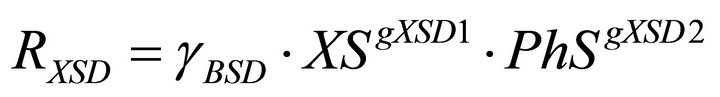 (8)
(8)
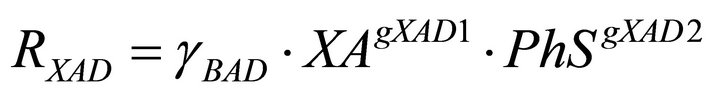 (9)
(9)
In Equations (4)-(9) each biochemical rate is expressed as a product of a rate constant (g) and the variables of the system subject to characteristic kinetic orders (g). Their metabolic meanings are listed in Table 1. Kinetic orders can have non-integer values [16]. This features greatly facilitate the modeling process since, in the absence of data on the detailed reaction mechanisms (see [20,21]), we proceed by condensing several processes into simplified representations. This aggregation of information is conveniently represented by power-law expressions [16, 20,22-24].
The model involves eighteen parameters (rate constants, kinetic orders and G; see Table 1) to be deter-
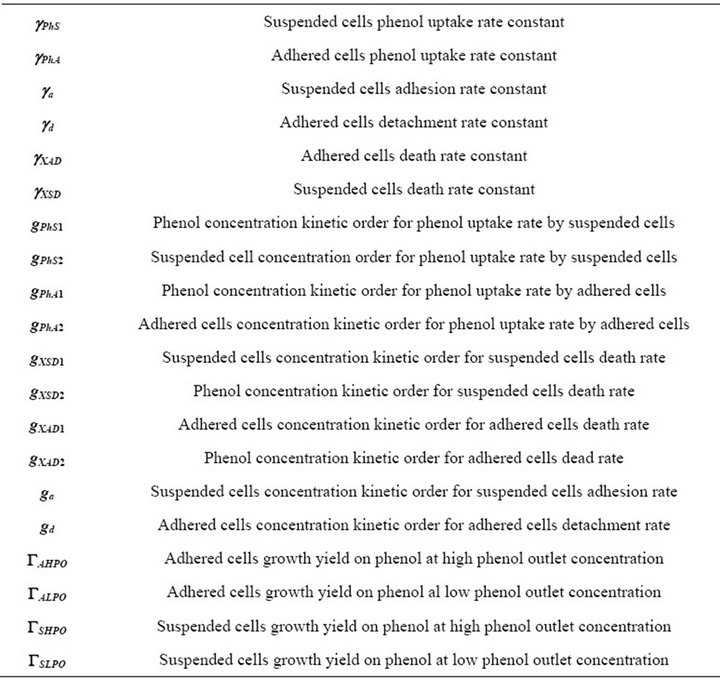
Table 1. Model parameters.
mined from seven different sets of experimental steadystates data taken from [11]. These parameter sets were estimated from two series of experimental data, as provided by [11]; corresponding to conditions of low phenol output (LPO) and high phenol output (HPO). Estimates so obtained are unique for each parameter, except for the G where the estimation method yields a couple of them, GHPO and GLPO, which correspond to LPO and HPO conditions respectively. Five of these steady state are characterized by a low phenol input flux (VPhin) and an even lower phenol output flux (VPhout) while two show higher values of VPhin and VPhout.
Each steady state is determined by the values of the independent variables and rates (3 concentrations and 3 rates) and the eighteen parameters. Since there are less variables that parameters we have to face an identifiability problem; that is, different sets of parameters can account for the same steady state [25]. We deal with this problem by searching for the parameter sets able to represent the maximum number of experimental data at the most different operating conditions.
For this purpose a Modified Genetic Algorithm was used for steady state parameter estimation [23,26]. The objective-function defined with this aim was set up in order to simultaneously accomplish with two wanted features of the solutions: to be stable and integrable. Stability is a prerequisite for any solution to be biologically relevant while integrability refers to as the capacity of each parameter set to produce a numerical solution with an integration time lower than the actual experimental time when using a standard integration method. Both, stability and integrability were weighted by different factors, in order to allow the fast discrimination among similar sets of parameters. This composed objective function is defined as:
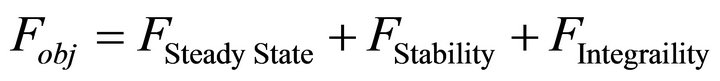 (10)
(10)
where
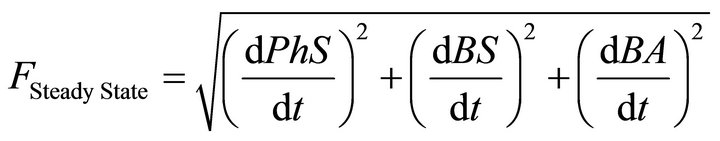 (11)
(11)
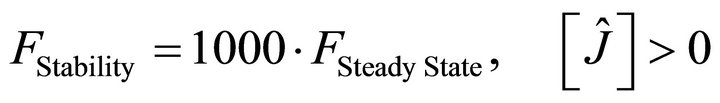 (12)
(12)
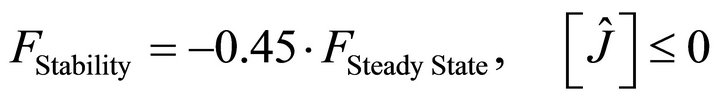 (13)
(13)
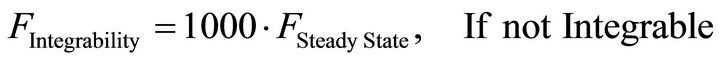 (14)
(14)
 (15)
(15)
being [Ĵ] the Jacobi matrix determinant.
A third requirement for the selection of the suitable solution parameter set is the system robustness. Robustness is defined in terms of the sensitivities of the systems response to changes is the system parameters. There are two types of sensitivities, those of the rate constants and those of the kinetics orders sensitivities [16,27,28]. A rate constant sensitivity is defined as the ratio of a relative change in a dependent concentration, Xi or flux, Ri, to a relative change in a rate constant (gj). The corresponding expression is where the subscript 0 refers to the steady state. Similarly, the kinetic order sensitivity coefficients are defined as:
 (16)
(16)
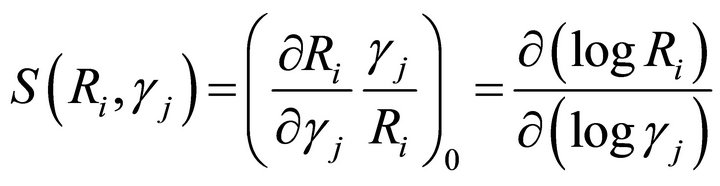 (17)
(17)
where the subscript 0 refers to the steady state. Similarly, the kinetic order sensitivity coefficients are defined as:
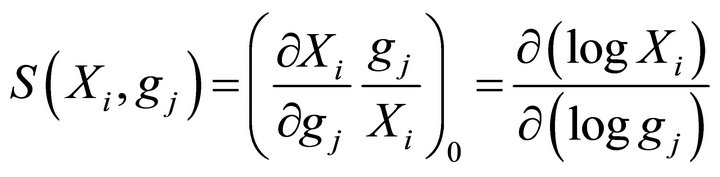 (18)
(18)
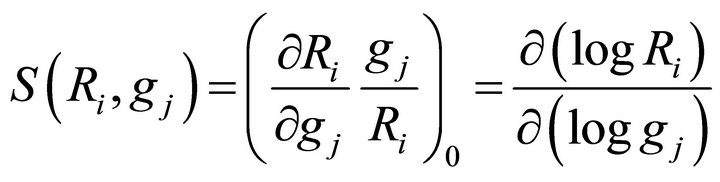 (19)
(19)
Sensitivity analysis offers a characterization of the quality of a model, since it indicates whether the model is able to tolerate structural changes.
The systematic application of the above described search together with the sensitivity analyses of the model performance led us to the identification of five sets of parameters yielding stable, integrable and robust steady states. All of them showed congruence with the experimental growth yield and phenol concentrations measurements observed in different, independent experiments.
2.3. Model Selection
The experimental data of the startup transient kinetics [17] were used for the selection of the parameter set that best represents the observed behavior.
3. Results and Discussion
As described in the previous sections, the model analysis leads to a final selection of five sets of parameters, each of which is able to describe the whole range of observed experimental behavior. However, these 5 sets can be grouped into 4 distinct operating scenarios as represented in Figure 2. In this figure, panels A and B correspond to situations where only one component of biomass shows significant uptake of phenol, RPhS (panel A) or RPhA (panel B). In both cases there is a high value of RXAD. However, while the rates in panel A Ra and Rd are negligible, in panel B Ra and Rd have significant values, being always Rd greater than Ra. The remaining scenarios
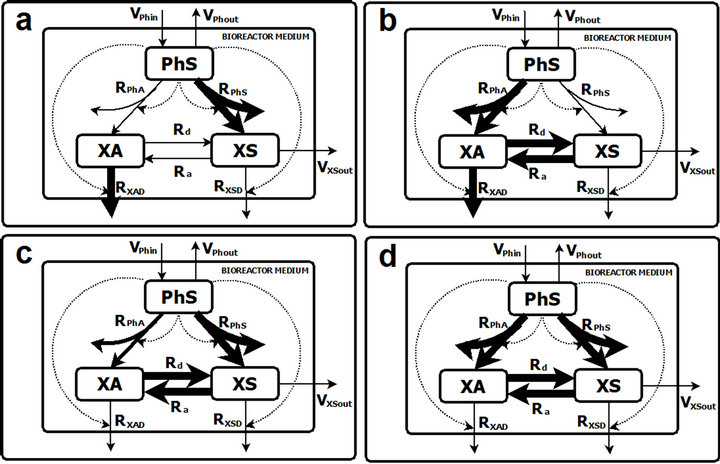
Figure 2. Model predicted operating scenarios. In every panel a possible bioprocess operating scenario is presented as predicted by the model analysis. In all cases the arrow thickness reflects its relative value. A. Solution characterized by showing only one significant Ph absorption rate (RPhS); negligible values of Ra and Rd and a high value of RXAD. B. Solution characterized by showing only one significant phenol absorption flow rate (RPhA); significant values of Ra and Rd and a high value of RXAD. C. Solution characterized by showing significant values of RPhS, RPhA, Ra and Rd (Rd being greater than Ra); RXSD lesser than RXAD and RPhS greater than RPhA. D. This solution is the same as C except for the fact that RPhS is of the same magnitude as RPhA.
(panels C and D) correspond to intermediate situations between panels A and B. In these cases RPhS, RPhA, Ra and Rd have significant values (Rd being greater than Ra). The only differences are that in panel C RXSD is lesser than RXAD and RPhS greater than RPhA while in panel D these are of the same magnitude.
Regarding the sensitivity analysis for the selected five sets showed varied values but the mean values in each of them was 8, thus indicating that in all the scenarios the model is robust enough.
However, two of the scenarios showed in Figure 2 (Panels A and B) are mutually exclusive, that is, each of them ascribe phenol uptake wholly to either suspended or adhered biomass, which is contrary to the observed process performance. Therefore these two sets are not further used for analysis. Note that all these alternative scenarios adjust to the experimental measurements carried out, and that the experimental set up and measurements made precluded the calculation of some of these process rates.
For model selection and verification we compared the remaining scenarios (Panels C and D) with the observed dynamics in the same experimental set up but in different conditions.
In Figure 3 it can be seen that, by using unpublished experimental transient kinetics data obtained by [17] in transient process at 1500 mg/L phenol feed, model predictions based in the parameters set 3 (Panel C in Figure 2; see Table 2) fits well with the system evolution in one of its key variables (the Phenol concentration); other predicted variables (adhered biomass and suspended biomass concentrations) showing physiologically acceptable values.
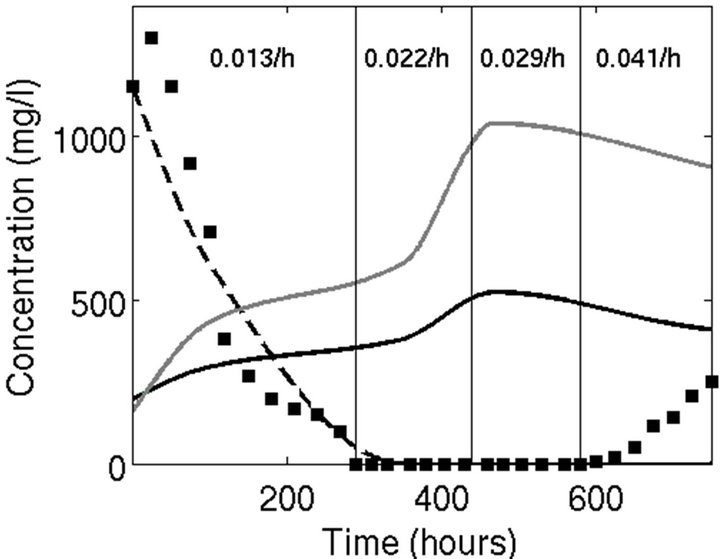
Figure 3. Transient and steady state measurements of unconverted phenol concentrations as compared to simulated phenol and suspended and adhered biomass concentrations using the parameters set 3 as reported in Table 2. Experimental data of phenol concentration (■) were taken from Ramon-Gallegos (2008) while continuous lines indicate the model predicted values. Black discontinuosus line: Phenol concentration; gray continuous line: adhered biomass; black continuous line: suspended biomass concentrations. Startup transient process (0 - 280 h) and steady-state processes at different dilution rates (the values of which are shown in bold type) for continuous process at 1500 mg/L phenol feed.

Table 2. Estimated parameter values for the identified parameter set yielding a verified stable, integrable and robust steady state.
Accordingly, this parameter set was used to simulate the rates of the model. The rates were calculated versus phenol and adhered or suspended yeast concentrations, according to Equations (4)-(9). This is shown as Figure 4.
An interesting observation regarding the comparison of the calculated adhered (RPhS) and suspended (RPhA) biomass phenol uptake rates is that the first one is greater, as shown in Figure 4(a). Moreover, the estimated values of the suspended (GS) and adhered (GA) biomass growth yield parameters show that the values for the suspended biomass yield is higher (see Table 2). These results suggest that, in these conditions, the adhered biomass is subject to a higher stress than the suspended cells, resulting in an approximately 20% lesser growth yield for adhered yeasts. Several research reports provide experimental confirmation of this model finding [12,13,29].
Figure 4(a) also illustrates another feature of the model of the system; namely that the RPhA rate is less sensitive to the medium phenol concentration (PhS). Some possible mechanisms can account for this prediction. One is related to the supposition that XA mainly takes phenol from the liquid phase, the phenol in the carbon beads being depleted. Another explanation is based in the negative regulatory influence of PhS on RPhA through the combined kinetic order gPhA1 (see Figure 1 and Equations (4) and (5)). This kinetic order quantifies two opposite effects of PhS on the RPhS rate; one being the positive influence of PhS as substrate for growth and one negative, as an stressing factor. A similar insensitivity pattern is observed with respect to RPhS rate, although of lesser magnitude. In this case the mechanism responsible could be the negative regulatory influence of PhS on RPhS through the combined kinetic order gPhS1.

Figure 4. A. Predicted dependence of the adhered (RPhA) and suspended (RPhS) biomass phenol uptake rates on the system variables XA, XS and PhS. B. Predicted dependence for the biomass lethality rates of the adhered (RXAD) and suspended (RXSD) biomass on the system variables XA, XS and PhS. C. Dependence of the biomass adhesion (Ra) and detachment (Rd) rates with respect to the dependent variables XS and XA, respectively.
In the same vein, it is observed (Figure 4(b)) that the highest rate of adhered biomass decay, RXAD, is higher than the highest rate of suspended biomass decay, RXSD. This model prediction has been experimentally observed in phenol biodegradation system using free and immobilized cells [12] and is in accordance to the hypothesized higher stress for adhered cell. Also, it is observed that the RXAD and RXSD rates are mostly insensitive to macroscopic changes in phenol concentration at the higher phenol concentrations. One of the underlying mechanisms to explain this alludes to the different phenol concentrations in the solid and the liquid phases. As it has been experimentally observed [29], adhered yeasts show higher stress response, the RXAD rate expression (see Equation (2)) reflects this fact through the estimated values of the kinetic order gXAD2 and gXAD. In the same Figure 4(b) it can be seen that both rates show saturation kinetics with respect to the biomass.
In Figure 4(c), the evolution of the Ra and Rd values for the selected solution with respect to the biomass, XS and XA, respectively, is presented. It is observed that the Rd values are more linearly dependent on the adhered population concentration than Ra. Ra shows a steep linearity with respect to the suspended yeas concentration at its lower values, and then more pronounced saturationtype kinetics, suggesting that adhesion surface becomes scarce.
Optimization Strategies
From the above analysis four optimization strategies can be suggested. The experimental observations and our model predictions show that the total amount of phenol degraded increases as the phenol inflow increases too. This seems to be in contradiction with the fact that the phenol concentration negatively affects the biomass, in fact, the biomass decreases when the inflow of phenol in the bioreactor (VPhin) is high. However, our model also predicts that these adverse effects on biomass are less dependent of the phenol concentration at high phenol loads. In this line, reference [30] found, in a spiral packed-bed reactor, that an activated-sludge culture maintained its phenol uptake rate constant up to a 150 mg∙L–1∙h–1 with almost complete phenol conversion. Also, reference [31] found that while C. tropicalis growth is inhibited by increasing phenol concentration, the inhibition rate decreases with phenol concentration. Thus, we can conclude that the bioprocess is more efficient degrading phenol when VPhin is high. This could be attributed to the fact that yeast invests part of the consumed phenol in counteracting the stress condition. Accordingly, we propose the utilization of higher phenol input rates VPhin and the use of bioreactors in series, the first ones degrading most of the phenol and in the following the remains.
A second line of improvement can be attained by increasing the adhered biomass rate Ra. In fact several reports emphasize the higher substrate up take rates by adhered as compared to suspended yeast cultures [13,29]. Since Ra is a function of XS it is advisable to increase the adhered biomass through the implementation of a cell recycler system.
A third line of improvement refers to the carbon beads. We suggest the use of a greater area of the solid carriers in the reactor able to support higher levels of biomass, as reference [32] found when treating Pyrene with suspended or “chemicaly supported” (entrapment) or “physicaly supported” (adhered) C. tropicalis cells. This research concluded that adhered cells on large area carriers converted 62% Pyrene compared to 42% for suspended cells in batch culture.
Finally, our model indicates that we should address the lethality rate. The choice of a more resistant strain against high phenol concentrations, rather than a faster growing strain, since it reduces the biomass loss, would enhance the biotransformation.
4. Conclusion
Our work suggests, based in a well informed mathematical model, a set of improvements to a phenol bioremediation biotechnological process. The modeled system consists in a continuous bioreactor of adhered and suspended Candida tropicalis yeast where phenol is incurporated at a constant rate to the bioreactor. We found out that increasing phenol input over the values used in previous studies (about 50 mg∙L–1∙h–1, [1]) and increasing the amount of particle adhered yeasts produced an increase in the phenol degradation rate. Also it is found that the arrangement in series of a set of bioreactors combined with the increase of the phenol input rate can upgrade the phenol elimination yield. Our result also shows that the death rate of biomass is critical in limiting the phenol uptake. We conclude that a key strategy to significantly improve the phenol bioremediation process is through the use of more resistant strain against phenol of Candida tropicalis.
5. Acknowledgements
The authors gratefully acknowledge Dr Carlos GonzálezAlcon, Nora Ruíz-Ordaz (ENCB-IPN) and Juvencio Galíndez-Mayer (ENCB-IPN) for their helpful observations. This work was funded by research Grants from Spanish MICINN, Ref. No. BIO2011-29233-C02-02. Hugo Velasco-Bedrán is on sabbatical leave from the Escuela Nacional de Ciencias Biológicas (Instituto Politécnico Nacional) and enjoys scholarship grants from the Comisión de Fomento de las Actividades Académicas (COFAA) and Consejo Nacional de Ciencia y Tecnología (CONACYT).
REFERENCES
- Agency for Toxic Substances and Disease Registry, “Toxicological Profile for Phenol,” USA Public Health Service, Department of Health and Human Services, Atlanta, 1989.
- W. Jordan, X. Ran, H. Arneveld, O. Gerlich, M. KleineBoyman and J. Ullrich, “Phenol,” In: L. Pilato, Ed., Ullman’s Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag, Berlin Heidelberg, 2002.
- A. M. Maszenan, Y. Liu and W. Ng, “Bioremediation of Wastewaters with Recalcitrant Organic Compounds and Metals by Aerobic Beads,” Biotechnology Advances, Vol. 29, No. 1, 2011, pp. 111-123. doi:10.1016/j.biotechadv.2010.09.004
- S. E. Agarry, A. O. Durojaye and B. O. Solomon, “Microbial Degradation of Phenols. A Review,” International Journal of Environment and Pollution, Vol. 32, No. 1, 2008, pp. 12-28. doi:10.1504/IJEP.2008.016895
- G. Busca, S. Berardinelli, C. Resini and C. Arrighi, “Technologies for the Removal of Phenol from Fluid Streams. A Short Review of Recent Developments,” Journal of Hazardous Materials, Vol. 160, No. 2-3, 2009, pp. 265- 288. doi:10.1016/j.jhazmat.2008.03.045
- A. S. Whiteley and M. J. Bailey, “Bacterial Community Structure and Physiological Cell-State within an Industrial Phenol Bioremediation System,” Applied and Environmental Microbiology, Vol. 66, No. 6, 2000, pp. 2400- 2407. doi:10.1128/AEM.66.6.2400-2407.2000
- M. Mörtberg and H. J. Neujahr, “Uptake of Phenol by Trichosporon cutaneum,” Journal of Bacteriology, Vol. 161, No. 2, 1985, pp. 615-619.
- K. H. Hoffman and F. Schauer, “Utilization of Phenol by Hydrocarbon Assimilating Yeasts,” Antonie van Leeuwenhoek, Vol. 54, No. 2, 1988, pp. 179-188. doi:10.1007/BF00419204
- S. S. Adav, M. Y. Chen, D. J. Lee and N. Q. Ren, “Degradation of Phenol by Aerobic Beads and Isolation of Candida tropicalis,” Biotechnology and Bioengineering, Vol. 96, No. 5, 2007, pp. 844-852. doi:10.1002/bit.21148
- K. T. O’Reilly and R. L. Crawford, “Degradation of Pentachlorophenol by Polyurethane-Immobilized Flavobacterium Cells,” Applied and Environmental Microbiology, Vol. 55, No. 9, 1999, p. 2113.
- J. Galíndez-Mayer, J. Ramón-Gallegos, N. Ruiz-Ordaz, C. Juárez-Ramírez, A. Salmerón-Alcocer and H. M. PoggiVaraldo, “Phenol and 4-Chlorophenol Biodegradation by Yeast Candida tropicalis in a Fluidized-Bed Reactor,” Biochemical Engineering Journal, Vol. 38, No. 2, 2008, pp. 147-157. doi:10.1016/j.bej.2007.06.011
- Y. J. Liu, A. N. Zhang and X. C. Wang, “Biodegradation of Phenol by Using Free and Immobilized Cells of Acinetobacter sp X405 and Sphingomonas sp FG03,” Biochemical Engineering Journal, Vol. 44, No. 2-3, 2009, pp. 187-192. doi:10.1016/j.bej.2008.12.001
- G. A. Junter, L. Coquet, S. Vialin and T. Jouenne, “Immobilized-Cell Physiology: Current Data and the Potentialities of Proteomics,” Enzyme and Microbial Technology, Vol. 31, No. 2, 2002, pp. 201-212. doi:10.1016/S0141-0229(02)00073-X
- N. Ruiz-Ordaz, E. Hernández-Manzano, J. C. Ruiz-Lagunes, E. Cristiani-Urbina and J. Galíndez-Mayer, “Growth Kinetic Model That Describes the Inhibitory and Lytic Effects of Phenol on Candida tropicalis Yeast,” Biotechnology Progress, Vol. 14, No. 6, 1998, pp. 966-969. doi:10.1021/bp980095x
- M. A. Savageau, “Biochemical Systems Analysis. A Study on Design and Function in Molecular Biology,” Addison-Wesley Publishing Company, Massachusetts, 2009.
- E. O. Voit, “Computational Analysis of Biochemical Systems. A Practical Guide for Biochemists and Molecular Biologists,” Cambridge University Press, Cambridge, 2000.
- J. Ramón-Gallegos, “Degradación de Fenol y 4-CloroFenol por Candida tropicalis CC1 Inmovilizada en Carbón Activado Granular en un Reactor Aerobio en Lecho Fluidizado,” M.S. Thesis, Escuela Nacional de Ciencias Biológicas, Instituto Politécnico Nacional, 2008.
- A. G. Moat J. W. Foster and M. P. Spector, “Microbial Physiology,” Wiley-Liss, Inc, New York, 2002. doi:10.1002/0471223867
- D. Ahuatzi-Chacón, G. Ordorica-Morales, N. Ruiz-Ordaz, E. Cristiani-Urbina, C. Juárez-Ramirez and J. GalíndezMayer, “Kinetic Study of Phenol Hydroxylase and Chatechol 1-2 Dioxygenase Biosynthesis by Candida tropicalis Cells Grown in Different Phenolic Substances,” World Journal of Microbiology and Biotechnology, Vol. 20, No. 7, 2004, pp. 695-702. doi:10.1007/s11274-004-2622-5
- J. Vera, E. Balsa-Canto, P. Wellstead and O. Wolkenhauer, “Power-Law Models of Signal Transduction Pathways,” Cellular Signalling, Vol. 19, No. 7, 2007, pp. 1531- 1541. doi:10.1016/j.cellsig.2007.01.029
- M. A. Savageau, “Development of Fractal Kinetic Theory for Enzyme-Catalysed Reactions and Implications for the Design of Biochemical Pathways,” Biosystems, Vol. 47, No. 1-2, 1998, pp. 9-36. doi:10.1016/S0303-2647(98)00020-3
- M. R. Atkinson, M. A. Savageau, J. T. Myers and A. J. Ninfa, “Development of Genetic Circuitry Exhibiting Toggle Switch or Oscillatory Behavior in Escherichia coli,” Cell, Vol. 113, No. 5, 2003, pp. 597-607. doi:10.1016/S0092-8674(03)00346-5
- J. Vera, J. Bachmann, A. C. Pfeifer, V. Becker, J. A. Hormiga, N. V. Torres Darias, J. Timmer, U. Klingmüller and O. Wolkenhauer, “A Systems Biology Approach to Analyse Amplification in the JAK2-STAT5 Signalling Pathway,” BMC Systems Biology, Vol. 2, 2008, p. 38. doi:10.1186/1752-0509-2-38
- J. A. Hormiga, J. Vera, I. Frías and N. Torres, “Growth and Ligninolytic System Production Dynamics of the Phanerochaete chrysosporium Fungus. A Modelling and Optimization Approach,” Journal of Biotechnology, Vol. 137, No. 1-4, 2008, pp. 50-58. doi:10.1016/j.jbiotec.2008.07.1814
- P. K. Polisetty, E. O. Voit and E. P. Gatzke, “Identification of Metabolic System Parameters Using Global Optimization Methods,” Theoretical Biology and Medical Modelling, Vol. 3, 2006, p. 4. doi:10.1186/1742-4682-3-4
- J. Hormiga, C. González-Alcón, A. Sevilla, M. Cánovas and N. Torres, “Quantitative Analysis of the Dynamic Signalling Pathway Involved in the cAMP Mediated Induction of L-Carnitine Biosynthesis in E. coli,” Molecular BioSystems, Vol. 6, No. 4, 2010, pp. 699-710. doi:10.1039/b913063b
- D. D. Siljak, “Nonlinear System the Parameter Analysis and Design,” Wiley, New York, 1969.
- P. M. Frank, “Introduction to System Sensitivity Theory,” Academic Press, New York, 1978.
- G. Inei-Shizukawa, H. Velasco-Bedrán, G. Gutiérrez-López and H. Hernández-Sánchez, “Statistical Approach to Optimization of Ethanol Fermentation by Saccharomyces cerevisiae in the presence of VALFOR® 100 Zeolite NAA,” Revista Mexicana de Ingenieria Quimica, Vol. 8, No. 3, 2009, pp. 265-270.
- C. W. Lin, C. H. Yen and S. L. Tsai, “Biotreatment of Phenol-Contaminated Wastewater in a Spiral Packed-Bed Bioreactor,” Bioprocess and Biosystems Engineering, Vol. 32, No. 5, 2009, pp. 575-580. doi:10.1007/s00449-008-0279-4
- R. Varma and B. G. Gaikwan, “Biodegradation and Phenol Tolerance in Recycled Cell of Candida tropicalis NCIM 3556 Cells,” International Biodeterioration & Biodegradation, Vol. 63 No. 4, 2009, pp. 539-542
- X. Wang, Z. Gong, P. Li and L. Zhang, “Degradation of Pyrene in Soils by Free and Immobilized Yeasts, Candida tropicalis,” Bulletin of Environmental Contamination and Toxicology, Vol. 78, No. 6, 2007, pp. 522-526. doi:10.1007/s00128-007-9156-0
NOTES
*Corresponding author.

