Applied Mathematics
Vol.5 No.6(2014), Article ID:44582,9 pages DOI:10.4236/am.2014.56083
Mathematical Modeling and Analysis of Torsional Surface Waves in a Transverse Isotropic Elastic Solid Semi-Infinite Medium with Varying Rigidity and Density under a Rigid Layer
Anjana P. Ghorai1, Rekha Tiwary2
1Department of Applied Mathematics, BIT, Mesra, Ranchi, India
2Department of Mathematics, RVSCET, Jamshedpur, India
Email: rekha.tiwari68@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 25 December 2013; revised 25 January 2014; accepted 5 February 2014
ABSTRACT
In this paper, mathematical modeling of the propagation of torsional surface waves in a transverse isotropic elastic medium with varying rigidity and density under a rigid layer has been considered. The equation of motion has been formulated in the elastic medium using suitable boundary conditions. The frequency equation containing Whittaker’s function for phase velocity due to torsional surface waves has been derived. The effect of rigid layer in the propagation of torsional surface waves in a transverse isotropic elastic medium with varying rigidity and density has been discussed. The numerical results have been shown graphically. It is observed that the influence of transverse and longitudinal rigidity and density of the medium have a remarkable effect on the propagation of the torsional surface waves. Frequency equations have also been derived for some particular cases, which are in perfect agreement with some standard results.
Keywords:Torsional Surface Waves, Transverse Isotropic Elastic Medium, Phase Velocity

1. Introduction
Surface waves in elastic medium have been well recognized in the study of earthquake waves, seismology, geophysics and geodynamics. A good amount of work in respect of surface waves in classical elasticity is available in the standard books of Bullen [1] , Ewing et al. [2] , Love [3] [4] and Stonely [5] . Much information is available on the propagation of surface waves, such as Rayleigh waves, Love waves and Stonely waves but torsional surface waves have not drawn much attention.
In seismogram, some disturbances are observed between the arrival of Rayleigh and Love wave disturbances. As sufficient information was not available earlier, these disturbances were termed as “noise” and are ignored in the study of seismic waves and these “noise” may be due to the torsional wave. A wave motion in which the vibrations of the medium are periodic rotational motions around the direction of propagation is known as torsional wave. It gives twist to the medium during the propagation of earthquake thus producing torque in the medium involve circumferential displacement which is independent of q coordinate of cylindrical coordinate axes. But only scanty of literature is available about torsional surface waves.
Lord Rayleigh [6] , in his paper, showed that isotropic homogeneous elastic half space does not allow torsional surface waves to propagate. Meissner [7] showed that torsional surface waves may propagate in an inhomogeneous elastic half space with quadratic variation of shear modulus and density varying with depth. Vardoulakis [8] has observed that torsional surface waves also propagate in a Gibson half-space in which shear modulus varies linearly with depth but the density remains unchanged. Georgiadis et al. [9] have studied tortional surface waves in a gradient elastic halfspace. In a series of papers, Dey et al. [10] -[12] have studied torsional waves in different media. They have discussed the existence and the propagation of torsional surface waves in an elastic half-space with pores, in a homogeneous substrum over a heterogeneous half-space and in initially stressed anisotropic porous media. The effect of irregularity on the propagation of torsional surface waves in a heterogeneous elastic half space has been studied by Selim [13] and concluded that the surface irregularity has a notable effect on the propagation of torsional surface waves in heterogeneous medium with irregular free surface. Propagation of torsional surface wave in anisotropic poroelastic medium under initial stress has been discussed by Chattaraj et al. [14] . They observed that there is a significant effect of porosity, initial stress and inhomogeneity in the propagation of torsional surface wave in a layered anisotropic porous media under initial stress.
Gupta et al. [15] studied the propagation of torsional surface waves in a homogeneous layer of finite thickness over a heterogeneous half space and observed that such a medium allows torsional surface wave to propagate. Again Gupta et al. [16] studied the propagation of torsional surface waves in an initially stressed non-homogeneous layer over a non-homogeneous half space and observed that as the non-homogeneity parameter in the layer as well as half space increases, the velocity of torsional surface wave also increases. It has also been observed that an increase in compressive initial stresses decreases the velocity of torsional surface wave. Chattopadhyay et al. [17] studied the propagation of the same waves in a heterogeneous anisotropic half space under the initial compressive stress. They found that the phase velocity of torsional waves decreases with increase of initial stress and inhomogenity.
In this paper, we have discussed the effect of rigid layer in the propagation of torsional surface waves in a transverse isotropic elastic medium with varying rigidity and density. It is found that in-homogeneity of rigidity and density of the medium influence the velocity of the torsional surface wave. When the longitudinal and transverse rigidity are the same, our result is similar to that of Dey et al. [18] . All results have been computed and presented using MAT lab.
2. Formulation and Solution of the Problem
We consider a transversely isotropic elastic solid semi-infinite medium with varying rigidity and density under a rigid layer. The constitute equation for transversely isotropic linear elastic material with preferred direction 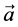 is (A. J. M. Spencer [19] )
is (A. J. M. Spencer [19] )
 (1)
(1)
where  are the components of stress,
are the components of stress,  are the components of infinitesimal strain and for homogeneous material,
are the components of infinitesimal strain and for homogeneous material,  and
and 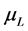 are elastic shear modules in transverse and longitudinal shear respectively,
are elastic shear modules in transverse and longitudinal shear respectively,  is elastic constant,
is elastic constant, 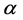 and
and 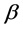 are reinforcement elastic coefficients,
are reinforcement elastic coefficients,  are the components of
are the components of 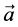 referred to the cylindrical coordinate system and
referred to the cylindrical coordinate system and 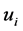 are the displacement vector components. Taking the origin of cylindrical coordinate system at the interface of rigid layer and z-axis positive downwards (Figure 1), we consider the following variations in rigidity and density:
are the displacement vector components. Taking the origin of cylindrical coordinate system at the interface of rigid layer and z-axis positive downwards (Figure 1), we consider the following variations in rigidity and density:
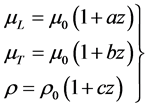 (2)
(2)
where a, b, c are constants having dimensions of inverse of length.
It is assumed that torsional surface wave travels in the radial direction and all the mechanical properties associated with it are independent of q. So it is characterized by the displacements
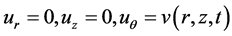 (3)
(3)
and hence
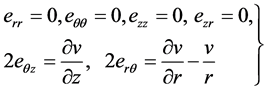 (4)
(4)
Using (3) and (4) in Equation (1) and setting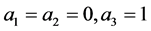 , we have the following non-zero stress components
, we have the following non-zero stress components
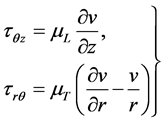 (5)
(5)
For the torsional surface wave motion in the radial direction, the equation of motion may be written as
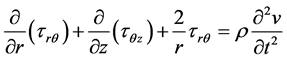 (6)
(6)
Equation (6) with the help of (5) becomes
 (7)
(7)
For the wave propagating along the r-direction, we may assume the solution of (7) as
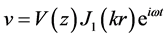 (8)
(8)
where J1(kr) is the Bessel function of first kind.
Now substituting (8) into (7) and using (2) we have
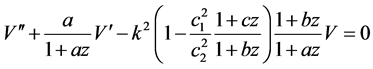 (9)
(9)
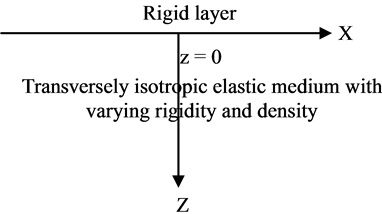
Figure 1. Geometry of the problem.
in which (') represents differentiation with respect to z, 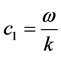 and
and .
.
On substitution of , Equation (9) takes the form
, Equation (9) takes the form
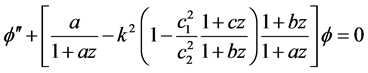 (10)
(10)
Using the following dimensionless quantities
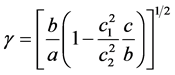 and
and in the Equation (10), we get
in the Equation (10), we get
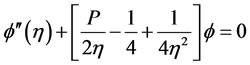 (11)
(11)
where
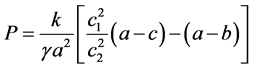 (12)
(12)
Equation (11) is a standard Whittaker’s equation and whose solution is 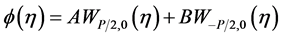
where 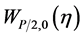 and
and 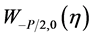 are Whittaker functions.
are Whittaker functions.
As the lower medium is a half space, the solution should vanish at z®µ i.e. for h®µ.
So in view of the above condition the solution may be taken as
 (13)
(13)
And hence we have displacement component as
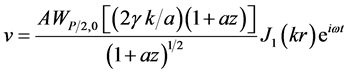 (14)
(14)
3. Boundary Condition
At the interface, the displacement component vanishes i.e.
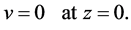 (15)
(15)
Expanding the Whittaker function up to linear terms and substituting the boundary condition (15), we find the velocity equation from (14) as
 (16)
(16)
From which we have either
 (17)
(17)
or,
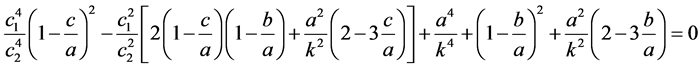 (18)
(18)
4. Observations
Case-1:
When c ® 0 i.e. the medium is of constant density and rigidity components vary linearly with depth, the Equation (18) is reduced to
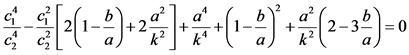 (19)
(19)
Case-2:
When a = b the equation (18) reduced to
 (20)
(20)
which is similar to the result obtained by Dey et al. [18] .
Case-3:
When a = b ® 0 and c® 0 i.e. the medium is of constant rigidity and density,  i.e. torsional surface wave does not propagate in such a medium.
i.e. torsional surface wave does not propagate in such a medium.
5. Numerical Calculation and Discussions
The values of 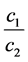 have been computed from Equation (17) for
have been computed from Equation (17) for 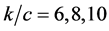 for different values of
for different values of 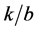 and shown in Figure 2.
and shown in Figure 2.
The values of 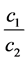 have also been computed from Equation (18) for
have also been computed from Equation (18) for 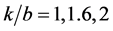 and
and 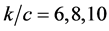 for different values of
for different values of 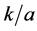 and shown in Figures 3-5.
and shown in Figures 3-5.
When a = b i.e. longitudinal and transverse rigidity are same, the change of phase velocity 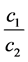 computed from the Equation (20) with respect to
computed from the Equation (20) with respect to 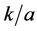 for
for 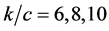 has been shown in Figure 6.
has been shown in Figure 6.
Figure 7 shows the change of phase velocity 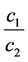 with the changes in the longitudinal and transverse rigidity for
with the changes in the longitudinal and transverse rigidity for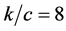 .
.
Figure 2. Torsional wave dispersion curve for different values of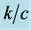 .
.

Figure 3. Torsional wave dispersion curve for different values of 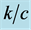 when
when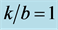 .
.

Figure 4. Torsional wave dispersion curve for different values of 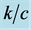 when
when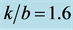 .
.
6. Conclusion
It has been found that there are two torsional wave fronts propagating in a transversely isotropic elastic solid semi-infinite medium with varying rigidity and density under a rigid layer, one of which is shown in Figure 2 and the second one is given by Equation (18) [Figure 3-5]. It is also observed that as the density and the rigidity
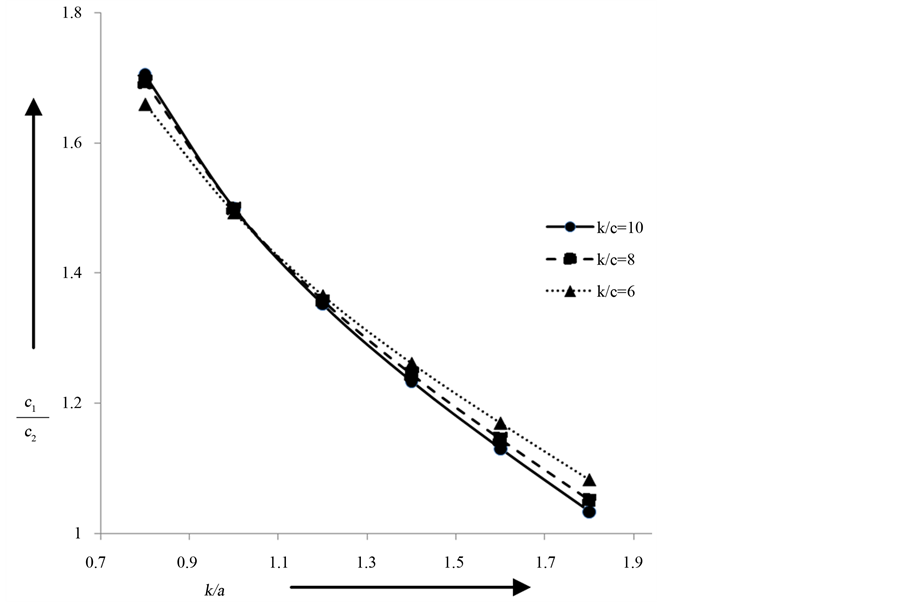
Figure 5. Torsional wave dispersion curve for different values of  when
when .
.
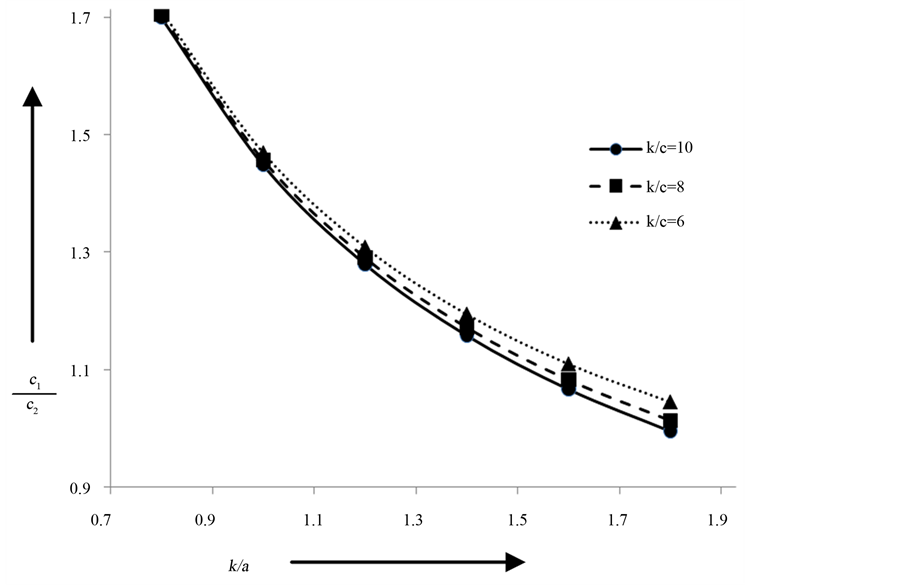
Figure 6. Torsional wave dispersion curve for different values of 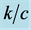 when a = b.
when a = b.
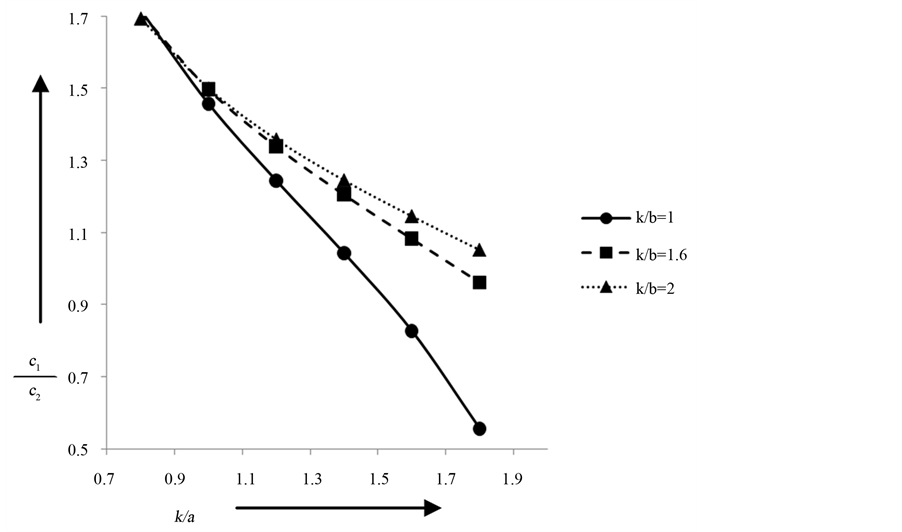
Figure 7. Torsional wave dispersion curve for different values of  when
when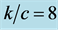 .
.
of the medium increases, the velocity of the torsional wave decreases. In the lower ranges of rigidity, the dispersions of torsional surface waves are less significant as compared to the higher ranges. Also from Figure 7, it has been shown that the longitudinal and transverse rigidity has inverse effect in the propagation of torsional surface waves in the medium of fixed density. Lastly when the medium is homogeneous and isotropic in nature, torsional surface wave does not propagate there.
References
- Bullen, K.E. (1963) An Introduction to the Theory of Seismology. Cambridge University Press, London.
- Ewing, M., Jardetzky, W. and Press, F. (1957) Elastic Waves in Layered Media. McGraw-Hill, New York.
- Love, A.E.H. (1911) Some Problems of Geodynamics. Cambridge University Press, London.
- Love, A.E.H. (1944) A Treatise on the Mathematical Theory of Elasticity. 4th Edition, Dover Publication, New York.
- Stonely, R. (1934) Transmission of Love Waves in a Half-Space with a Surface Layer Whose Thickness Varies Hyperbolically. Bulletin of the Seismological Society of America, 54, 611.
- Rayleigh, L. (1885) On Wave Propagated along the Plane Surface of an Elastic Solid. Proceedings London Mathematical Society, 17, 4-11. http://dx.doi.org/10.1112/plms/s1-17.1.4
- Meissner, E. (1921) Elastic Oberflanchenwellen MIT Dispersion in Einem Inhomogeneous Medium. Viertelgahrsschr Naturforsch. Gses. Zurich, 66, 181-195.
- Vardoulakis, I. (1984) Torsional Surface Wave in Inhomogeneous Elastic Medium. International Journal for Numerical and Analytical Methods in Geomechanics, 8, 287-296. http://dx.doi.org/10.1002/nag.1610080306
- Georgiadis, H.G., Vardoulakis, I. and Lykotrafitis, G. (2000) Tortional Surface Waves in a Gradient-Elastic Half-Space. Wave Motion, 31, 333-348. http://dx.doi.org/10.1016/S0165-2125(99)00035-9
- Dey, S., Gupta, S. and Gupta, A.K. (1993) Torsional Surface Waves in an Elastic Half-Space with Void Pores. International Journal for Numerical and Analytical Methods in Geomechanics, 17, 197-204. http://dx.doi.org/10.1002/nag.1610170305
- Dey, S., Gupta, A.K. and Gupta, S. (1996) The Propagation of Torsional Surface Waves in a Homogeneous Substratum over a Hetero-Geneous Half-Space. International Journal for Numerical and Analytical Methods in Geomechanics, 20, 287-294. http://dx.doi.org/10.1002/(SICI)1096-9853(199604)20:4<287::AID-NAG822>3.0.CO;2-2
- Dey, S. and Sarkar, M.G. (2002) Torsional Surface Waves in an Initially Stressed Anisotropic Porous Medium. Journal of Engineering Mechanics, 128, 184-189. http://dx.doi.org/10.1061/(ASCE)0733-9399(2002)128:2(184)
- Selim, M.M. (2007) Propagation of Torsional Surface Waves in Heterogeneous Half-Space with Irregular Free Surface. Applied Mathematical Sciences, 1, 1429-1437.
- Chattaraj, R., Samal, S. and Mahanti, N.C. (2011) Propagation of Torsional Surface Wave in Anisotropic Poroelastic Medium under Initial Stress. Wave Motion, 48, 184-195. http://dx.doi.org/10.1016/j.wavemoti.2010.10.003
- Gupta, S., Chattopadhyay, A., Kundu, S.K. and Gupta, A.K. (2009) Propagation of Torsional Surface Waves in Gravitating Anisotropic Porous Half-Space with Rigid Boundary. International Journal of Applied Mathematics and Mechanics, 6, 76-89.
- Gupta, S., Majhi, D.K. and Vishwakarma, S.K. (2012) Torsional Surface Wave Propagation in an Initially Stressed Non-Homogeneous Layer over a Non-Homogeneous Half Space. Applied Mathematics and Computation, 219, 3209- 3218. http://dx.doi.org/10.1016/j.amc.2012.09.058
- Chattopadhyay, A., Gupta, S., Sahu, S.A. and Dhua, S. (2013) Torsional Surface Waves in Heterogeneous Anisotropic Half-Space under Initial Stress. Archive of Applied Mechanics, 83, 357-366. http://dx.doi.org/10.1007/s00419-012-0683-8
- Dey, S., Gupta, S., Gupta, A.K. and Prasad, A.M. (2001) Propagation of Torsional Surface Waves in a Heterogeneous Half-Space under Rigid Layer. Acta Geophysica Polonica, XLLX, 113-118.
- Spencer, A.J.M. (1972) Deformation of Fiber-Reinforced Material. Oxford University Press, London.

