Applied Mathematics
Vol.4 No.2(2013), Article ID:28190,9 pages DOI:10.4236/am.2013.42044
On Removable Sets of Solutions of Neuman Problem for Quasilinear Elliptic Equations of Divergent Form
Institute of Mathematics of Academy Sciences, Baku, Azerbaijan
Email: tgadjiev@mail.az
Received November 21, 2012; revised December 25, 2012; accepted January 3, 2013
Keywords: Removable; Elliptic; Degenerate; Neumann Problem
ABSTRACT
In this paper we consider a nondivergent elliptic equation of second order whose leading coefficients are from some weight space. The sufficient condition of removability of a compact with respect to this equation in the weight space of Hölder functions was found.
1. Introduction
Let D be a bounded domain situated in ![]() -dimensional Euclidean space
-dimensional Euclidean space 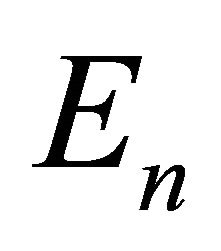 of the points
of the points 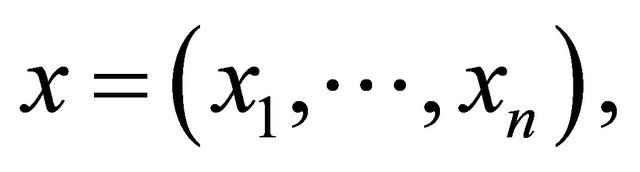
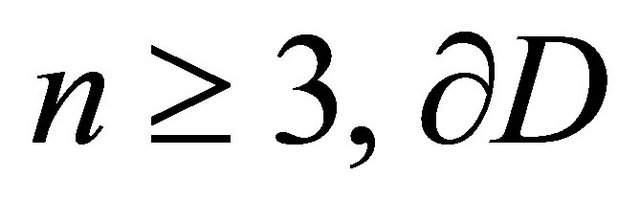 be its boundary. Consider in
be its boundary. Consider in 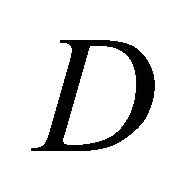 the following elliptic equation
the following elliptic equation
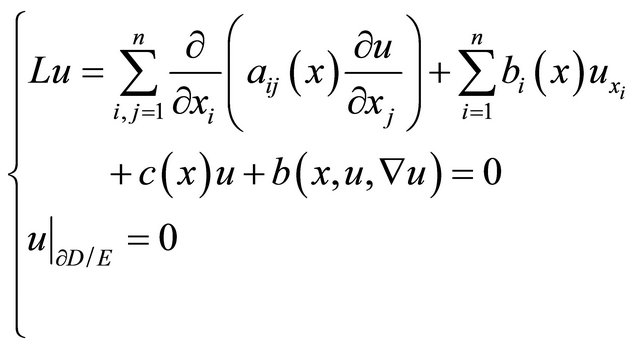 (1)
(1)
in supposition that 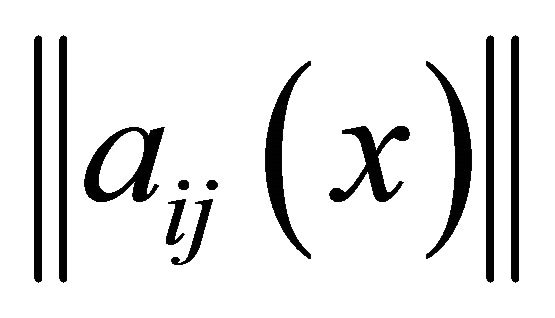 is a real symmetric matrix, moreover
is a real symmetric matrix, moreover
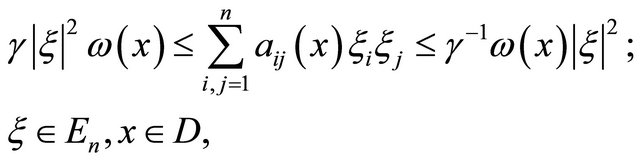 (2)
(2)
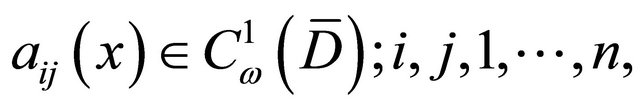 (3)
(3)
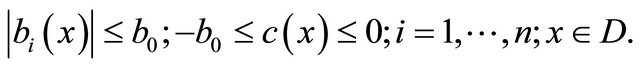 (4)
(4)
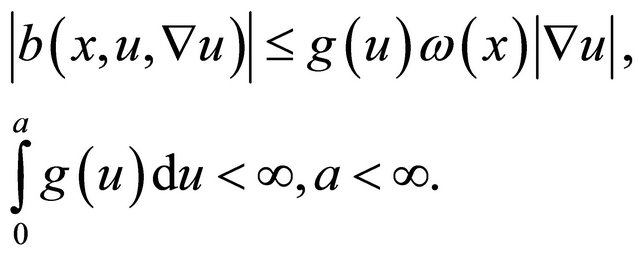 (5)
(5)
Here 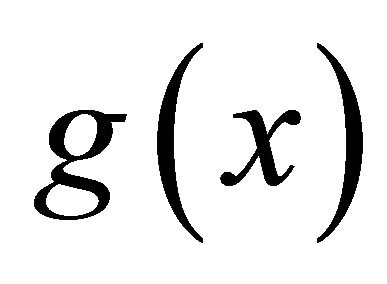 is non-negative function from
is non-negative function from
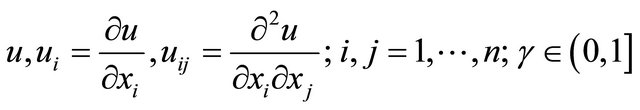
and 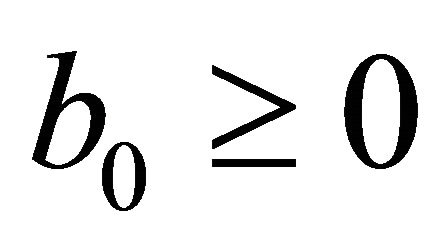 are constants. Besides we’ll assume that the minor coefficients of the operator
are constants. Besides we’ll assume that the minor coefficients of the operator ![]() are measurable in
are measurable in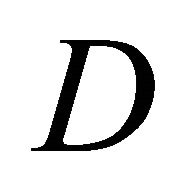 . Let
. Let 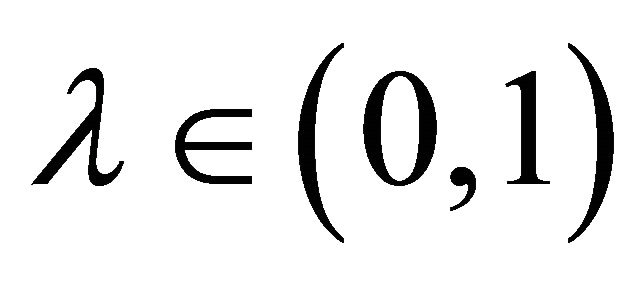 be some number.
be some number.
The compact  is called removable with respect to the Equation (1) in the space
is called removable with respect to the Equation (1) in the space 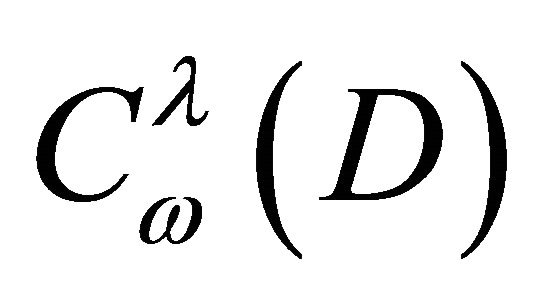 if from
if from
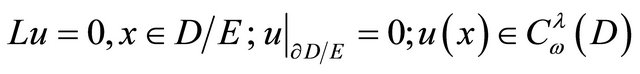 (6)
(6)
it follows that 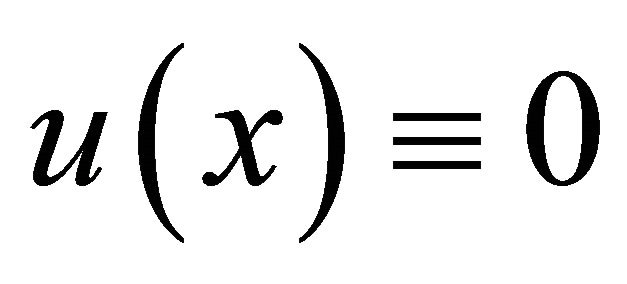 in
in .
.
2. Auxiliary Results
The paper is organized as follows. In Section 2, we present some definitions and auxiliary results. In Section 3 we give the main results of the sufficient condition of removability of compact.
The aim of the given paper is finding sufficient condition of removability of a compact with respect to the Equation (1) in the space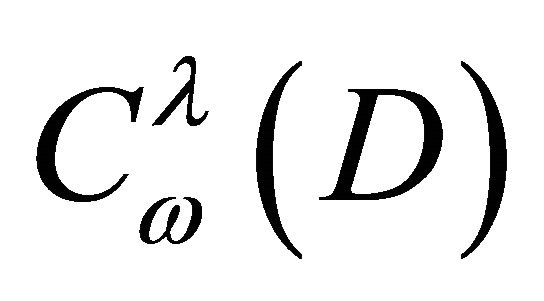 . This problem have been investigated by many researchers. For the Laplace equation the corresponding result was found by L. Carleson [1]. Concerning the second order elliptic equations of divergent structure, we show in this direction the papers [2,3]. For a class of non-divergent elliptic equations of the second order with discontinuous coefficients the removability condition for a compact in the space
. This problem have been investigated by many researchers. For the Laplace equation the corresponding result was found by L. Carleson [1]. Concerning the second order elliptic equations of divergent structure, we show in this direction the papers [2,3]. For a class of non-divergent elliptic equations of the second order with discontinuous coefficients the removability condition for a compact in the space 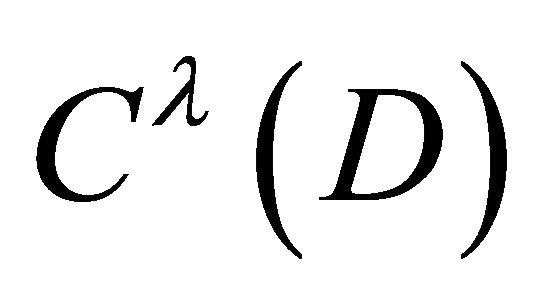 was found in [4]. Mention also papers [5-9] in which the conditions of removability for a compact in the space of continuous functions have been obtained.The removable sets of solutions of the second order elliptic and parabolic equations in nondivergent form were considered in [10-12]. In [13], T. Kilpelainen and X. Zhong have studied the divergent quasilinear equation without minor members, proved the removability of a compact. Removable sets for pointwise solutions of elliptic partial differential equations were found by J.
was found in [4]. Mention also papers [5-9] in which the conditions of removability for a compact in the space of continuous functions have been obtained.The removable sets of solutions of the second order elliptic and parabolic equations in nondivergent form were considered in [10-12]. In [13], T. Kilpelainen and X. Zhong have studied the divergent quasilinear equation without minor members, proved the removability of a compact. Removable sets for pointwise solutions of elliptic partial differential equations were found by J.
Diederich [14]. Removable singularities of solutions of linear partial differential equations were considered in R. Harvey, J. Polking paper [15]. Removable sets at the boundary for subharmonic functions have been investigated by B. Dahlberg [16]. Also we mentioned the papers of A.V.Pokrovskii [17,18].
In previous work, authors considered Direchlet problems for linear equations in some space of functions. In this work we consider Newman problem for quasilinear equations and sufficient conditions of removability of a compact in the weight space of Holder functions is obtained. The application value of the research in many physic problems.
Denote by 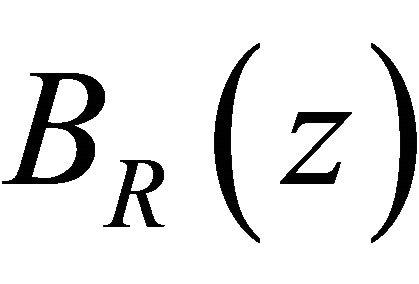 and
and 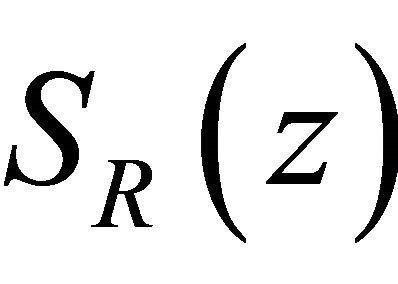 the ball
the ball 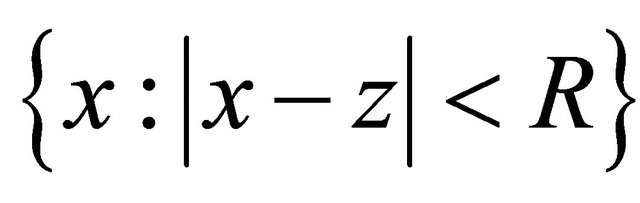 and the sphere
and the sphere 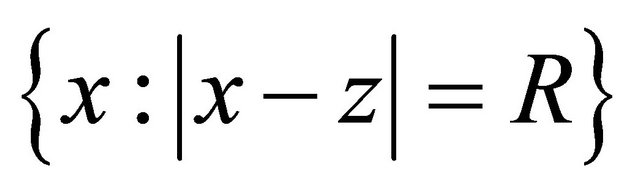 of radius
of radius 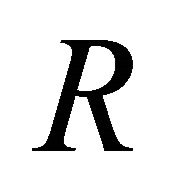 with the center at the point
with the center at the point 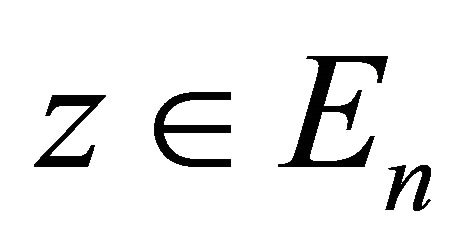 respectively. We’ll need the following generalization of mean value theorem belonging to E.M. Landis and M.L. Gerver [8] in weight case.
respectively. We’ll need the following generalization of mean value theorem belonging to E.M. Landis and M.L. Gerver [8] in weight case.
Lemma. Let the domain 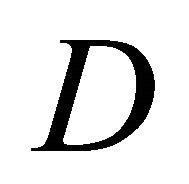 be situated between the spheres
be situated between the spheres 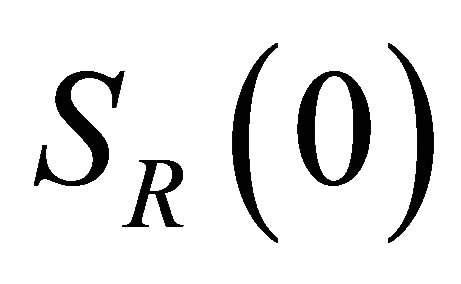 and
and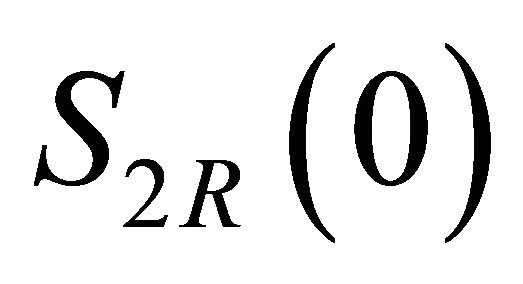 , moreover the intersection
, moreover the intersection 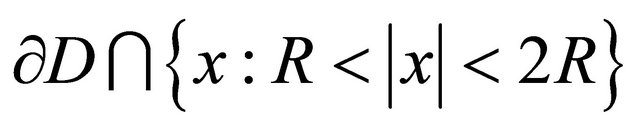 be a smooth surface. Further, let in
be a smooth surface. Further, let in 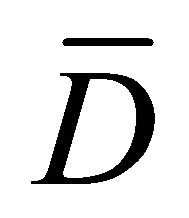 the uniformly positive definite matrix
the uniformly positive definite matrix
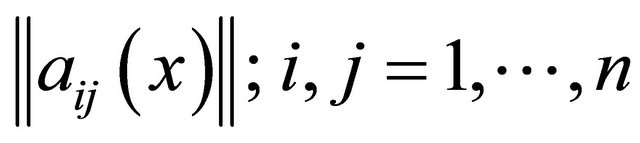
and the function 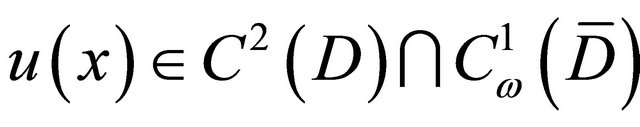 be given. Then there exists the piece-wise smooth surface
be given. Then there exists the piece-wise smooth surface ![]() dividing in
dividing in 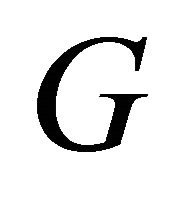 the spheres
the spheres 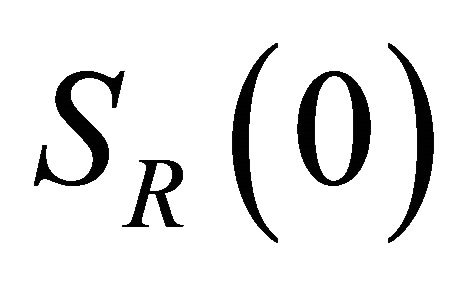 and
and 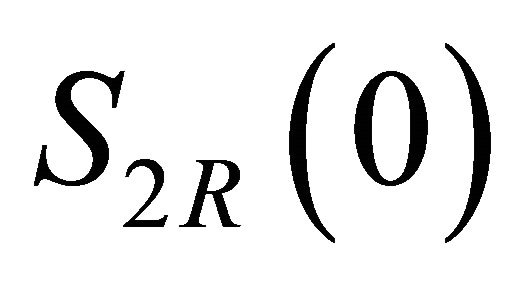 such that
such that
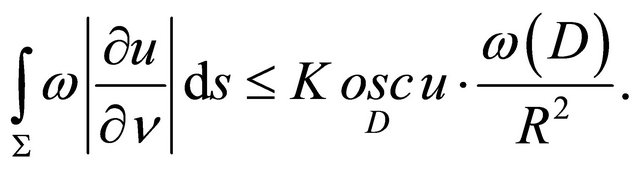
Here 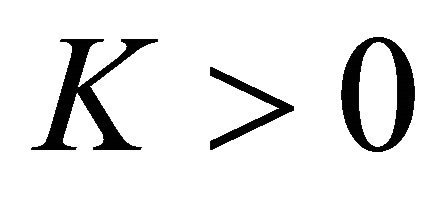 is a constant depending only on the matrix
is a constant depending only on the matrix 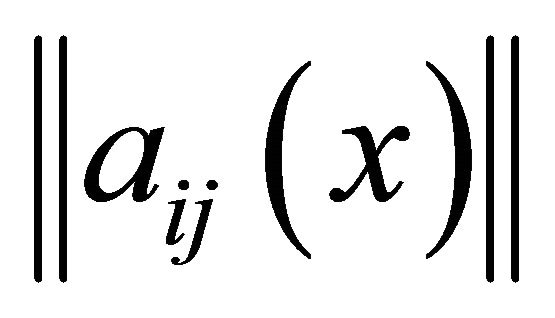 and
and![]() ,
, 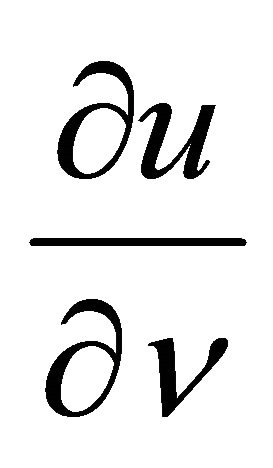 is a derivative by a conormal determined by the equality
is a derivative by a conormal determined by the equality
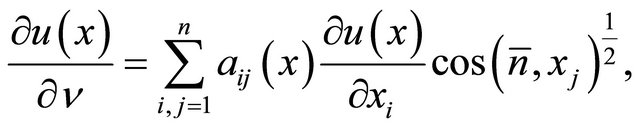
where 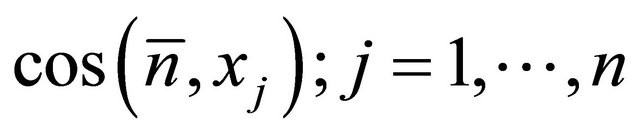 are direction cosines of a unit external normal vector to
are direction cosines of a unit external normal vector to![]() .
.
Proof. Let 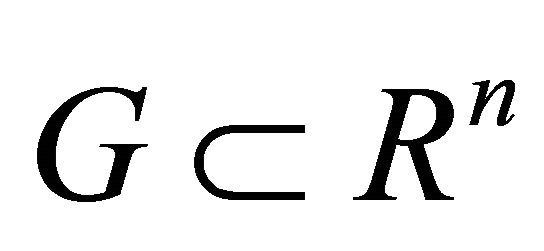 be a bounded domain
be a bounded domain
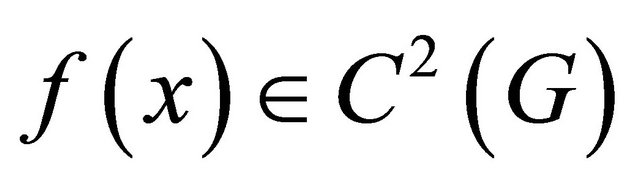 . Then for any there exists a finite number of balls
. Then for any there exists a finite number of balls 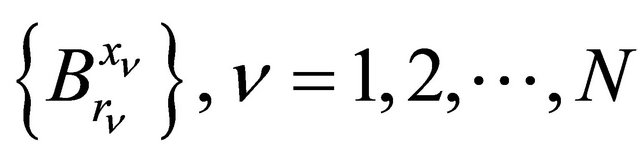 which cover
which cover  and such that if we denote by
and such that if we denote by , the surface of
, the surface of ![]() -th ball, then
-th ball, then
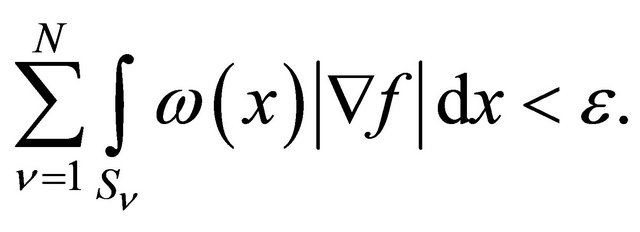
Decompose 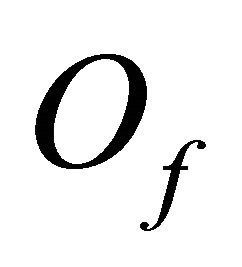 into two parts:
into two parts: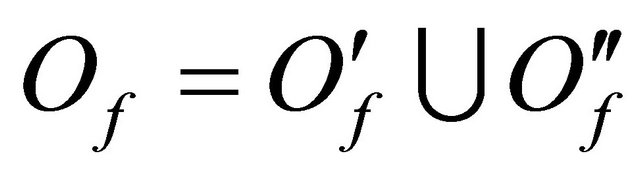 , where
, where
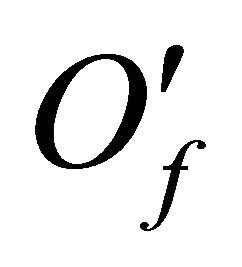 is a set of points
is a set of points 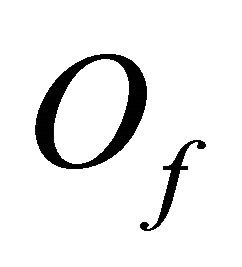 for which
for which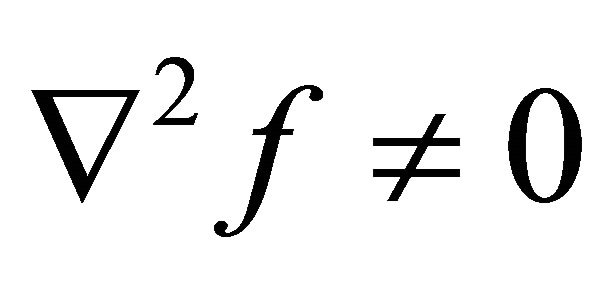 ,
, 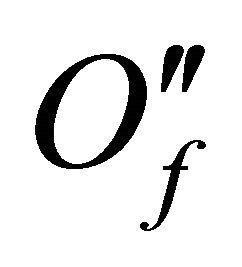 is a set of points for which
is a set of points for which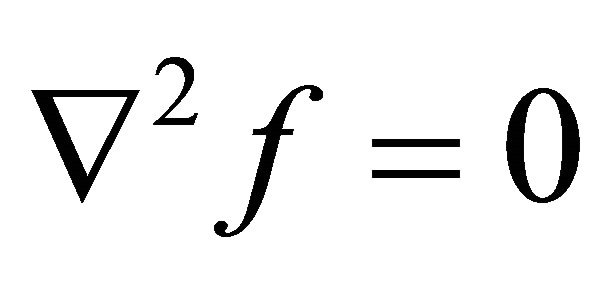 .
.
The set 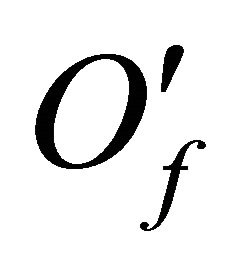 has
has ![]() -dimensional Lebesque measure equal zero, as on the known implicit function theorem, the
-dimensional Lebesque measure equal zero, as on the known implicit function theorem, the 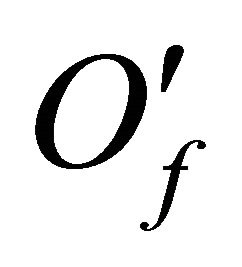 lies on a denumerable number of surfaces of dimension
lies on a denumerable number of surfaces of dimension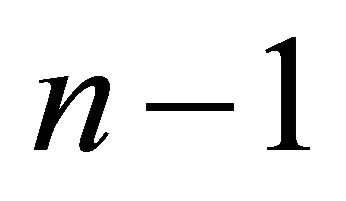 . If we use the absolute continuity of integral
. If we use the absolute continuity of integral
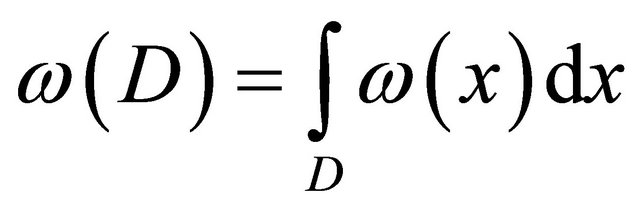
with respect to Lebesque measure 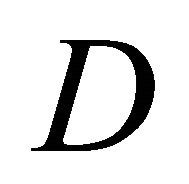 and above said we get that the set
and above said we get that the set 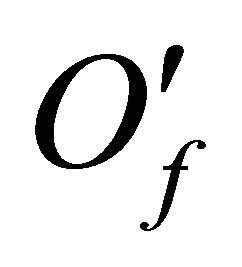 may be included into the set
may be included into the set 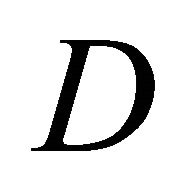 for which
for which 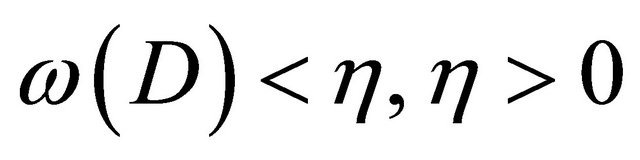 will be choosen later. Let for each point
will be choosen later. Let for each point 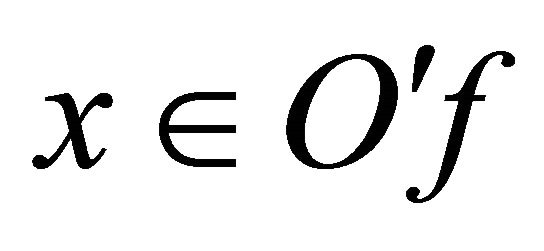 there exist such
there exist such ![]() that
that 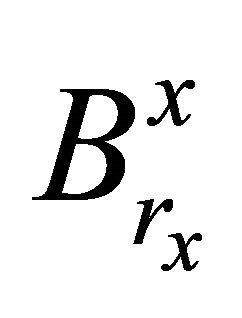 and
and 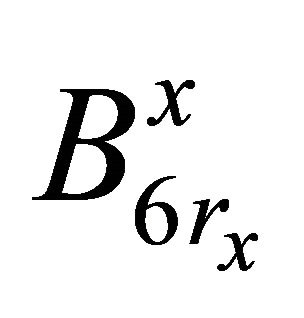 are contained in
are contained in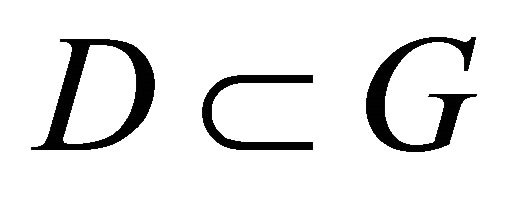 . Then
. Then
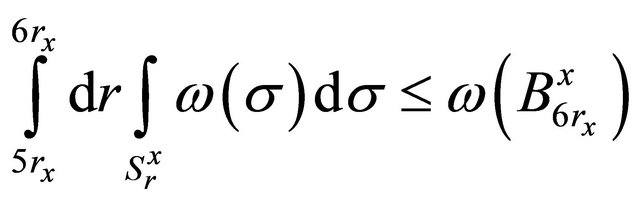
therefore there exists such 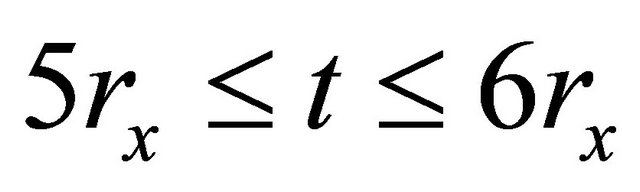 that
that
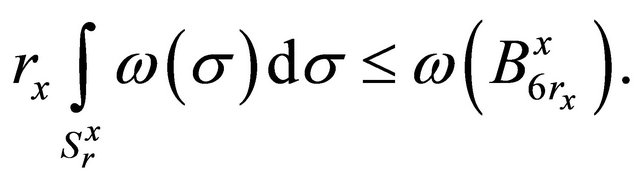
Then
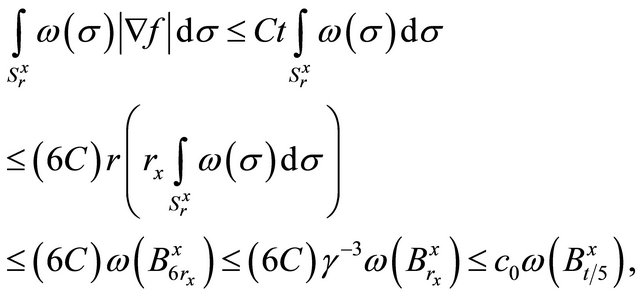
where
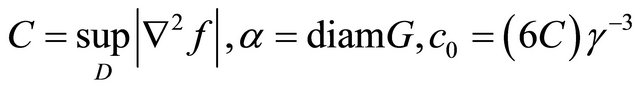 .
.
Now by a Banach process ([4], p.126) from the ball system 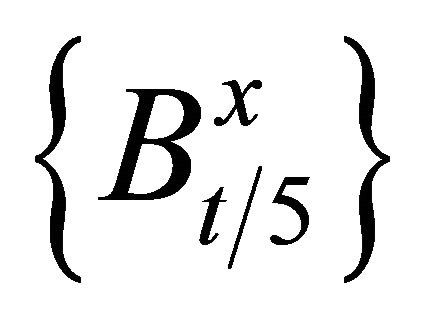 we choose such a denumerable number of not-intersecting balls
we choose such a denumerable number of not-intersecting balls 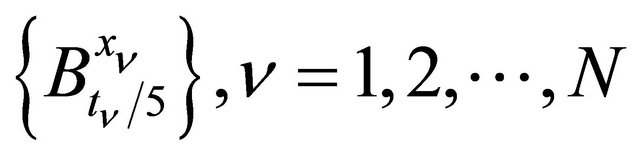 that the ball of five times greater radius
that the ball of five times greater radius 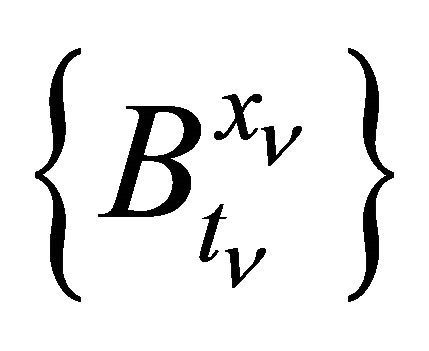 cover the whole
cover the whole 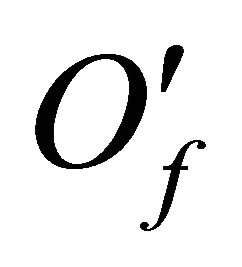 set. We again denote these balls by
set. We again denote these balls by
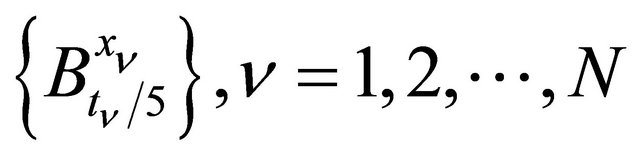
and their surface by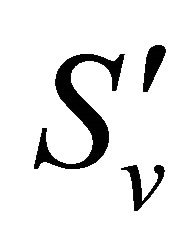 . Then by virtue of (4)
. Then by virtue of (4)
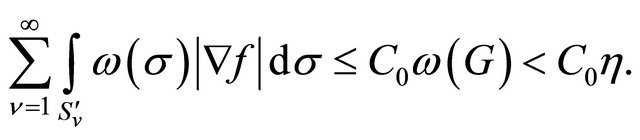
Now let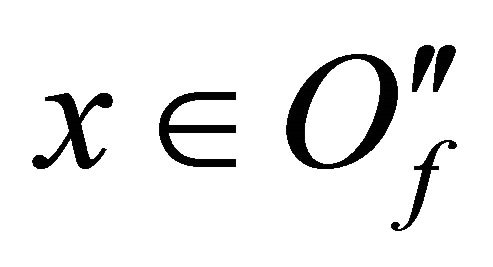 . Then
. Then
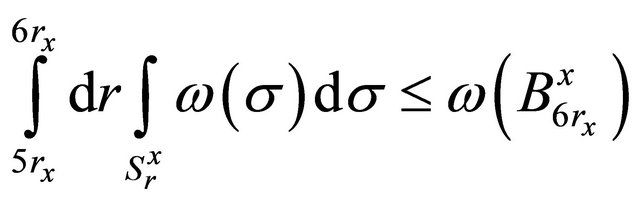
Therefore there exists such 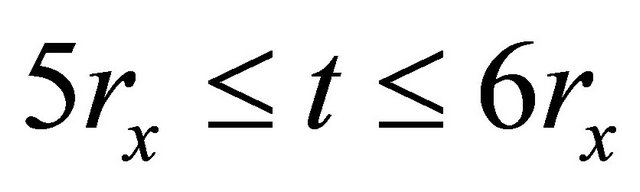 that
that
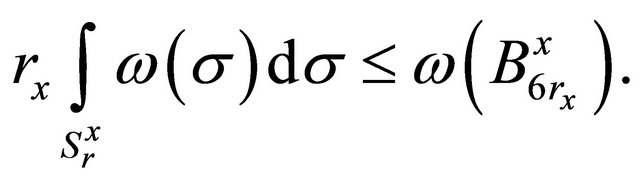
Assign arbitrary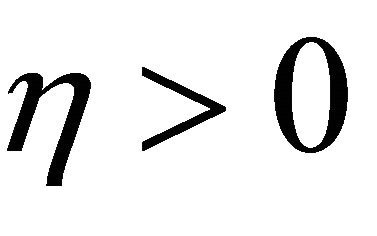 . By virtue of that
. By virtue of that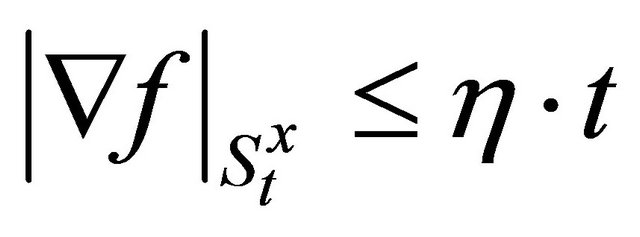 , for sufficiently small
, for sufficiently small 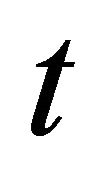 we have
we have
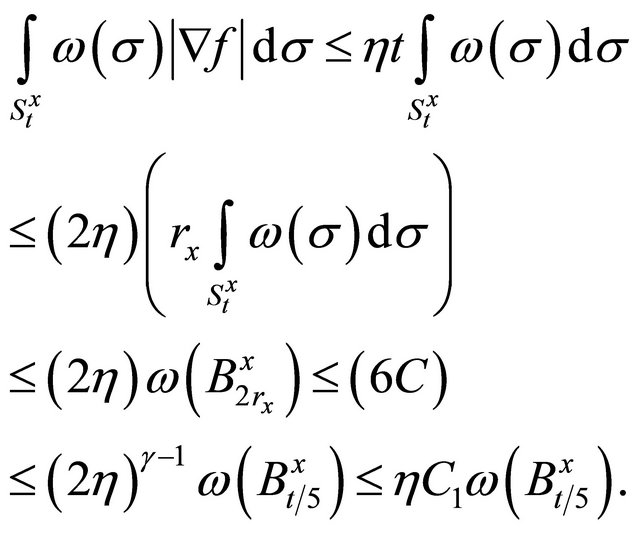
Again by means of Banach process and by virtue of (6) we get
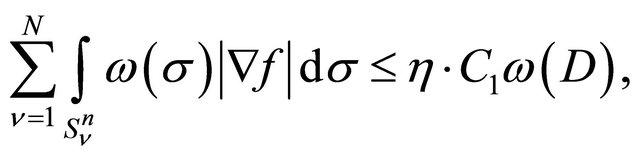
where 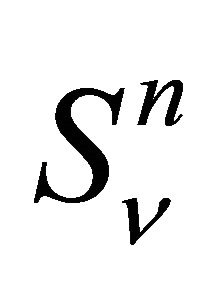 is the surface of balls in the second covering.
is the surface of balls in the second covering.
Combining the spherical surfaces 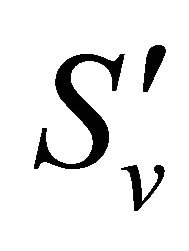 and
and 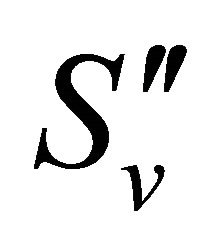 we get that the open balls system cover the closed set
we get that the open balls system cover the closed set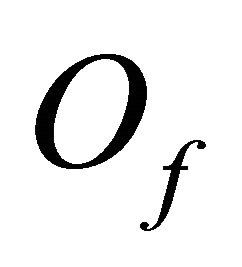 . Then a finite subcovering may be choosing from it. Let they be the balls
. Then a finite subcovering may be choosing from it. Let they be the balls 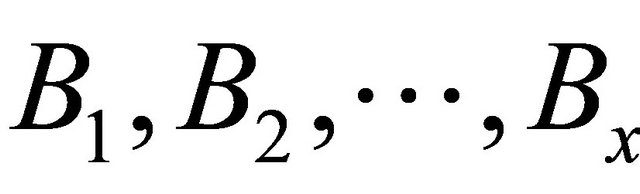 and their surfaces is
and their surfaces is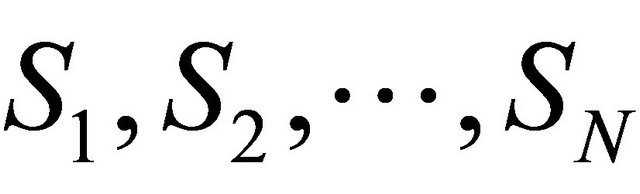 .
.
We get from inequalities (3) and (5)
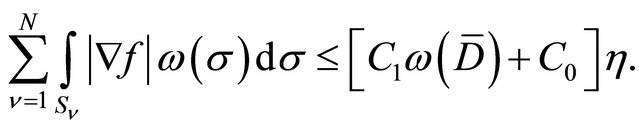
Put now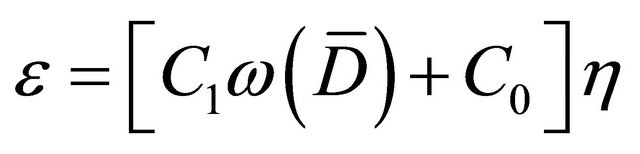 .
.
Following [2], assume
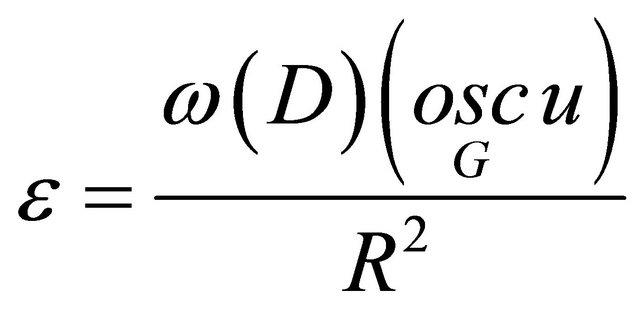
and according to lemma 1 well find the balls 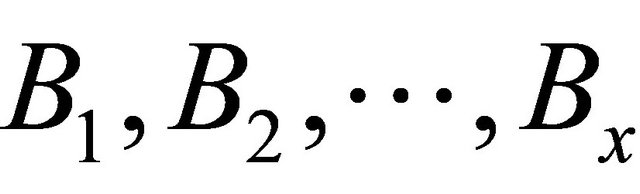 for given and exclude then from the domain
for given and exclude then from the domain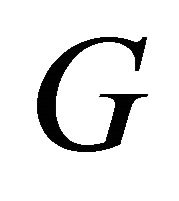 . Put
. Put
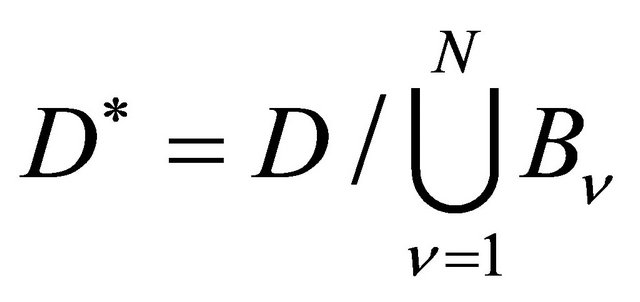 intersect with
intersect with 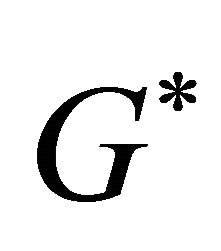 a closed spherical layer
a closed spherical layer
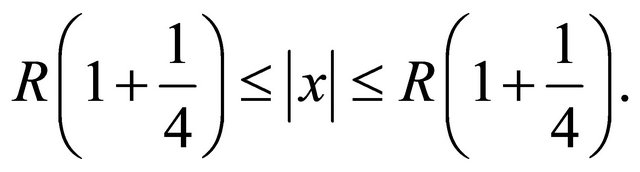
We denote the intersection by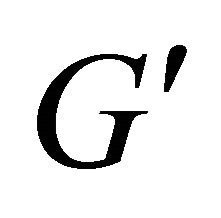 . We can assume that the function
. We can assume that the function 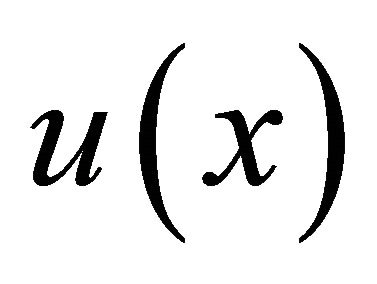 is defined in some
is defined in some ![]() vicinity
vicinity
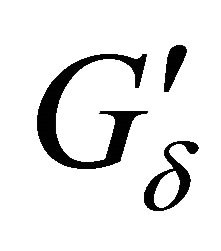 of set
of set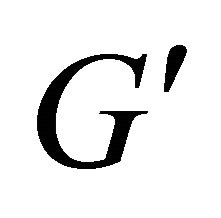 . Take
. Take 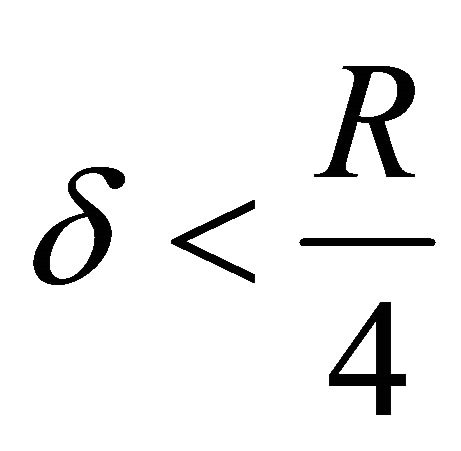 so that
so that
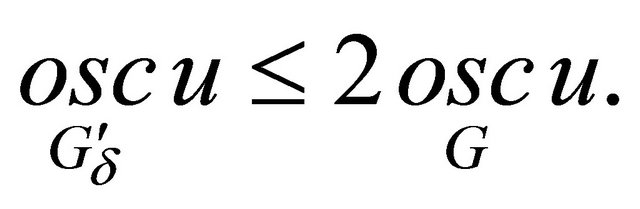
On a closed set 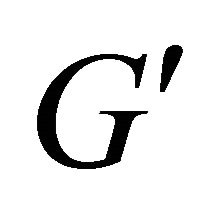 we have
we have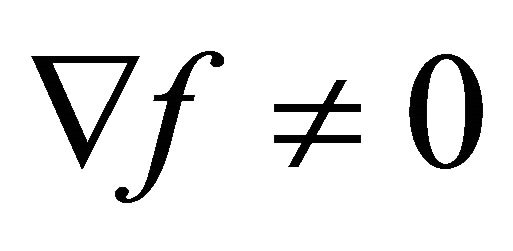 . Consider on
. Consider on 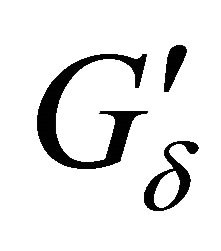 the equation system
the equation system
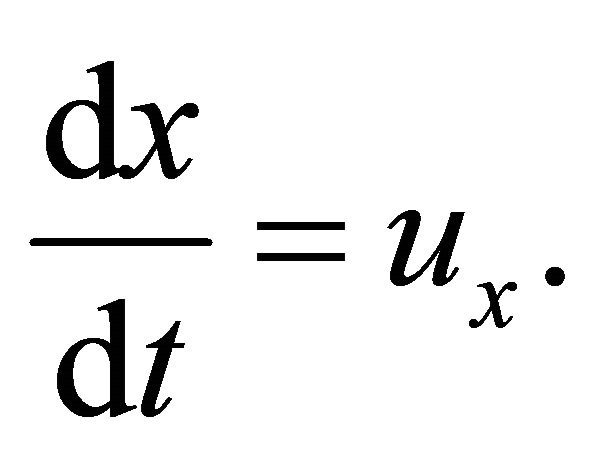
Let ![]() a such from surface that it touches to field direction at any his point, then
a such from surface that it touches to field direction at any his point, then
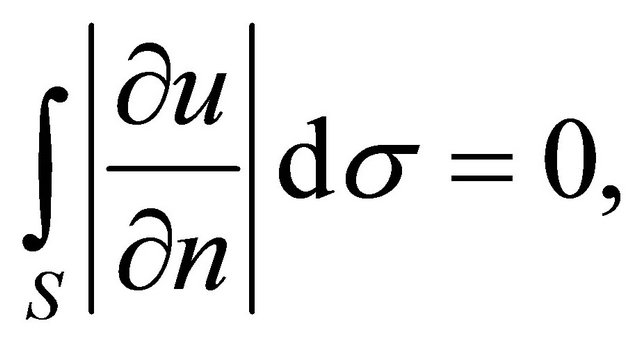
since 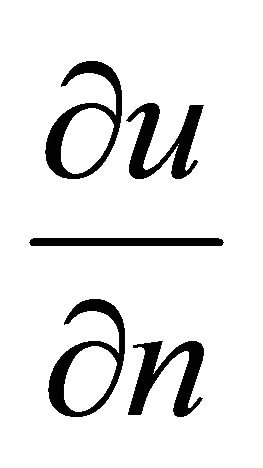 is identically equal to zero at
is identically equal to zero at![]() .
.
We shall use it in constructing the needed surface of![]() . Tubular surfaces whose generators will be the trajectories of the system (10) constitute the basis of
. Tubular surfaces whose generators will be the trajectories of the system (10) constitute the basis of![]() .
.
They will add nothing to the integral we are interested in. These surfaces will have the form of thin tubes that cover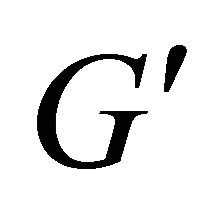 . Then we shall put partitions to some of these tubes. Lets construct tubes. Denote by
. Then we shall put partitions to some of these tubes. Lets construct tubes. Denote by 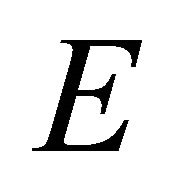 the intersection of
the intersection of 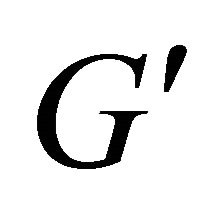 with sphere
with sphere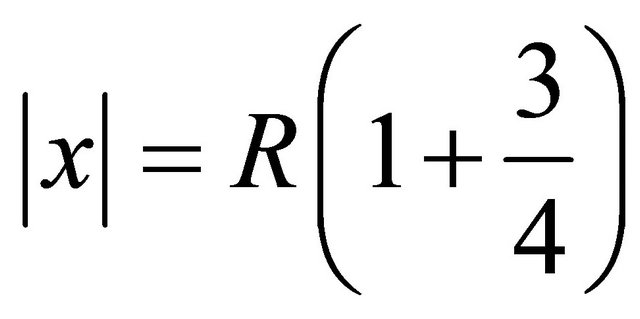 .
.
Let 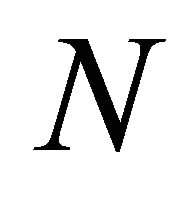 be a set of points
be a set of points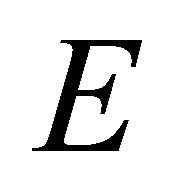 . Where field direction of system (10) touches the sphere
. Where field direction of system (10) touches the sphere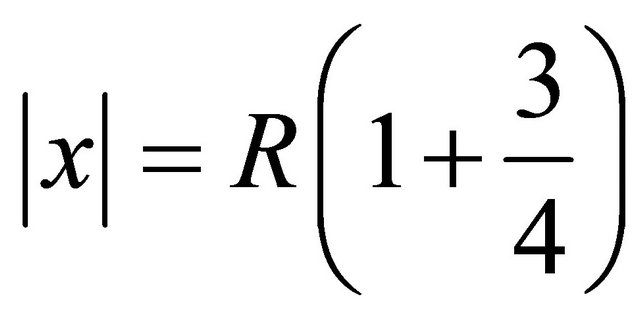 . Cover
. Cover 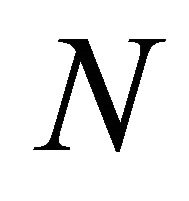 with such an open on the sphere
with such an open on the sphere 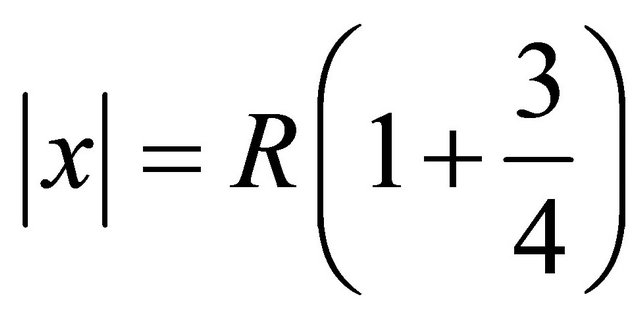 set
set  that
that
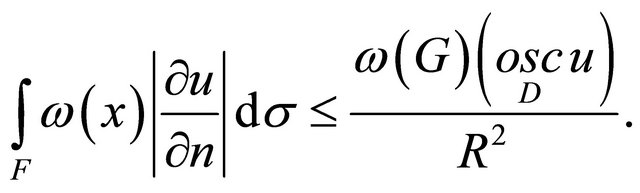
It will be possible if on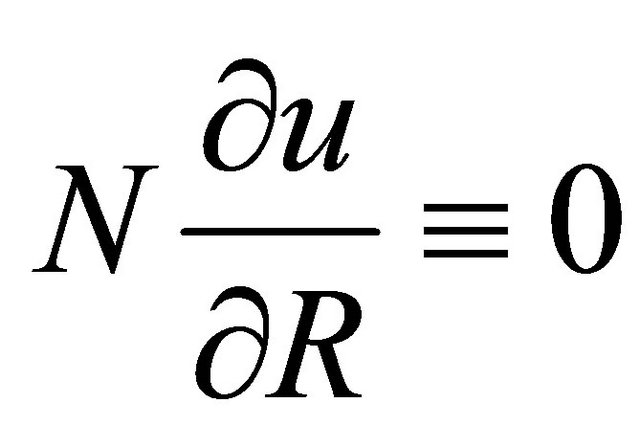 .
.
Put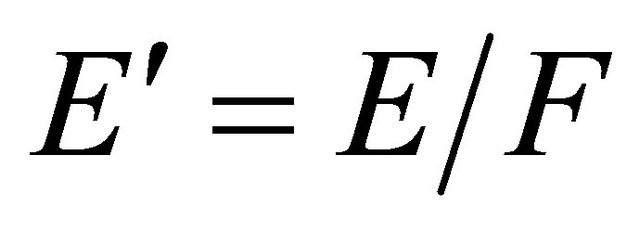 . Cover
. Cover 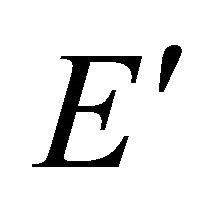 on the sphere by a finite number of open domains with piece-wise smooth boundaries. We shall call them cells. We shall control their diameters in estimation of integrals that we need. The surface remarked by the trajectories lying in the ball
on the sphere by a finite number of open domains with piece-wise smooth boundaries. We shall call them cells. We shall control their diameters in estimation of integrals that we need. The surface remarked by the trajectories lying in the ball
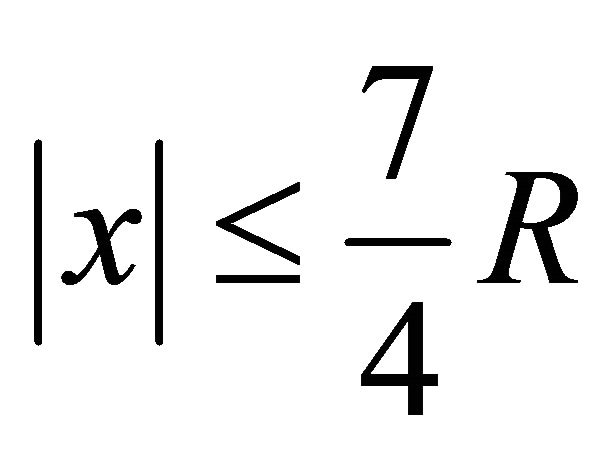 and passing through the bounds of cells we shall call tube.
and passing through the bounds of cells we shall call tube.
So, we obtained a finite number of tubes. The tube is called open if not interesting this tube one can join by a broken line the point of its corresponding cell with a spherical layer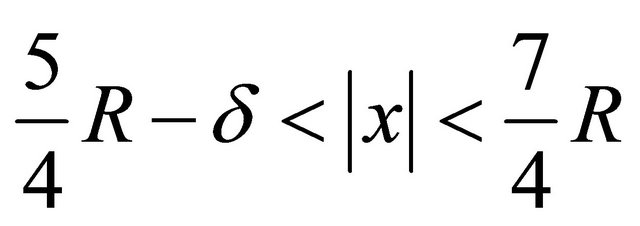 . Choose the diameters of cells so small that the trajectory beams passing through each cell, could differ no more than
. Choose the diameters of cells so small that the trajectory beams passing through each cell, could differ no more than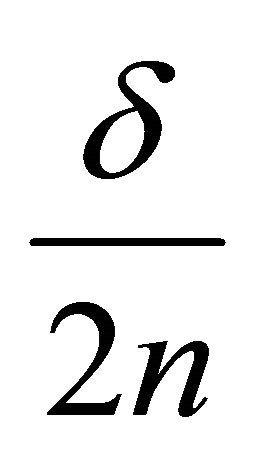 .
.
By choose of cells diameters the tubes will be contained in
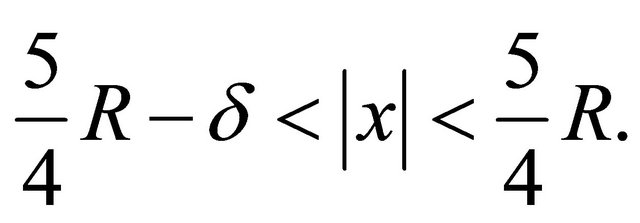
Let also the cell diameter be chosen so small that the surface that is orthogonal to one trajectory of the tube intersect the other trajectories of the tube at an angle more than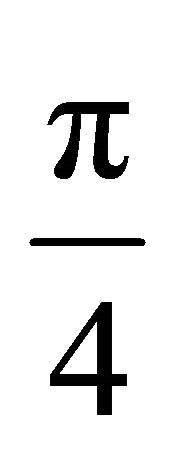 .
.
Cut off the open tube by the hypersurface in the place where it has been imbedded into the layer
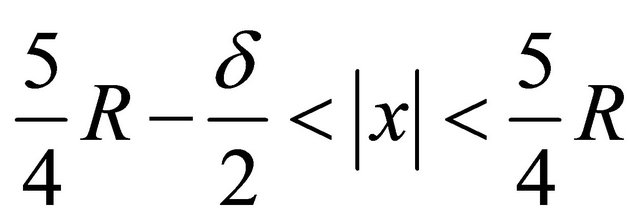
at first so that the edges of this tube be embedded into this layer.
Denote these cut off tubes by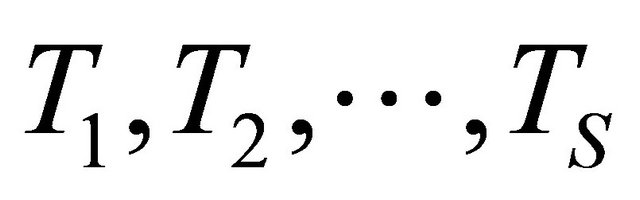 . If each open tube is divided with a partition, then a set-theoretical sum of closed tubes, tubes
. If each open tube is divided with a partition, then a set-theoretical sum of closed tubes, tubes 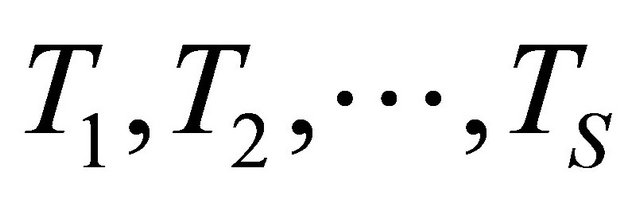 their partitions spheres
their partitions spheres 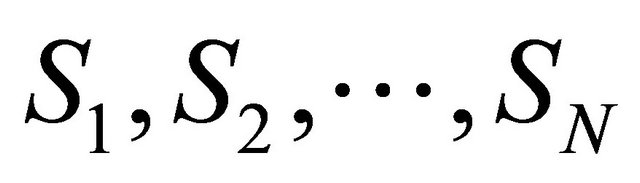 and the set
and the set  on the sphere
on the sphere 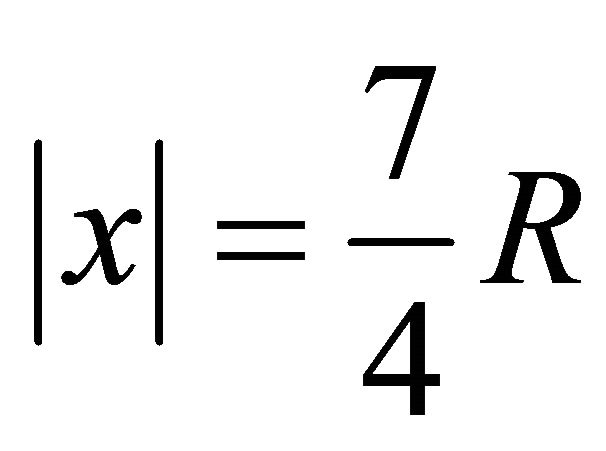 divides the spheres
divides the spheres 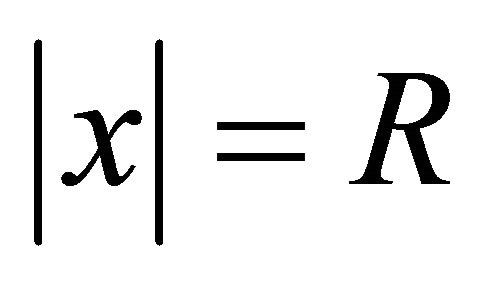 and
and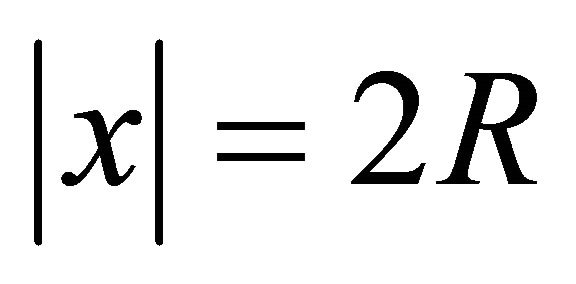 . Note that
. Note that 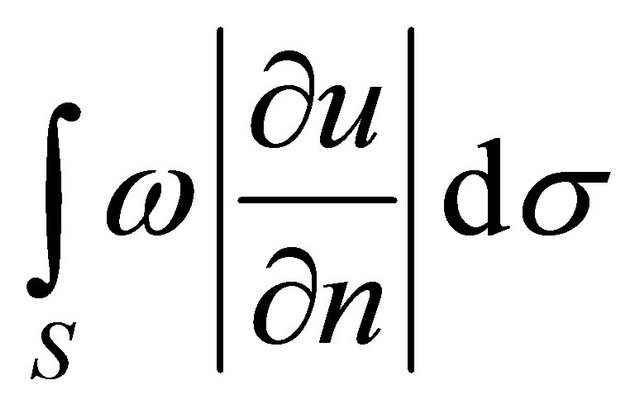 along the surface of each tube equals to zero, since
along the surface of each tube equals to zero, since 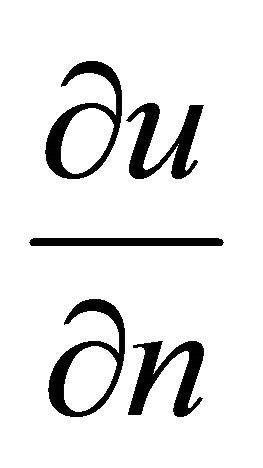 identically equals to zero.
identically equals to zero.
Now we have to choose partitions so that the integral
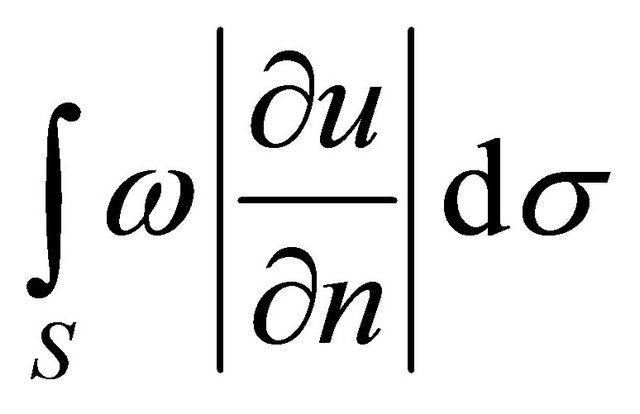 was of the desired value. Denote by
was of the desired value. Denote by 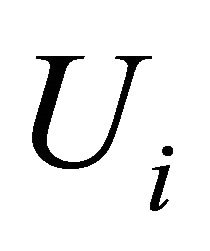 the domain bounded by
the domain bounded by ![]() with corresponding cell and hypersurface cutting off this tube. We have
with corresponding cell and hypersurface cutting off this tube. We have 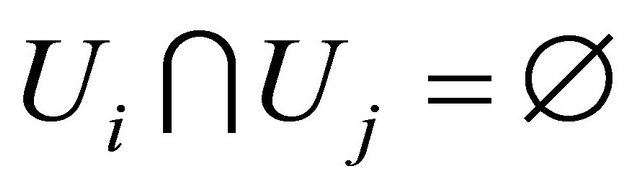 and therefore
and therefore
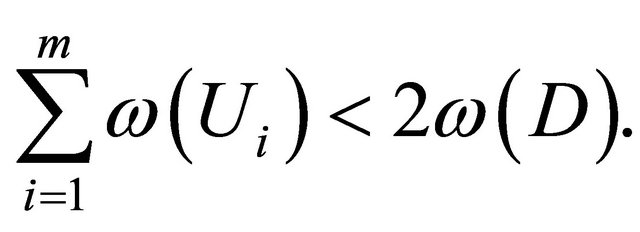
Consider a tube ![]() and corresponding domain
and corresponding domain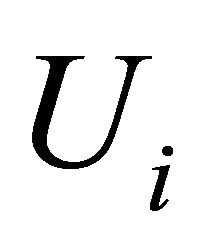 . Choose any trajectory on this tube. Denote it by
. Choose any trajectory on this tube. Denote it by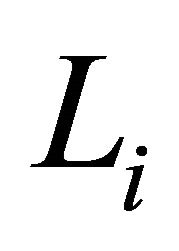 . The length
. The length 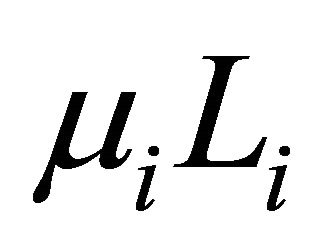 of the curve
of the curve 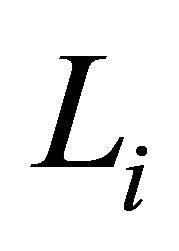 satisfies the inequality
satisfies the inequality
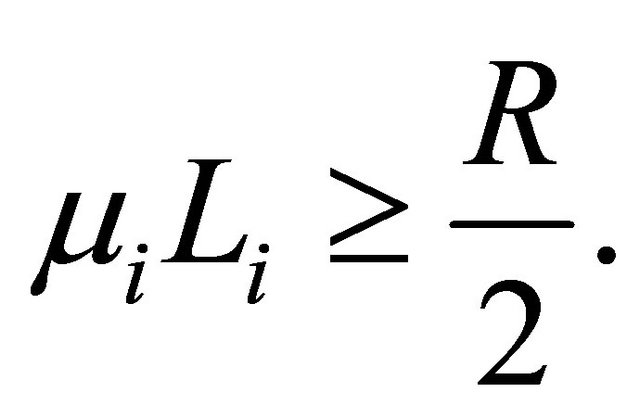
On 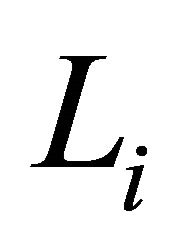 introduce a parameter in
introduce a parameter in  -length of the are counted from cell. By
-length of the are counted from cell. By 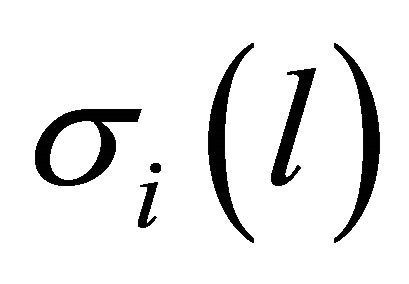 denote the cross-section by
denote the cross-section by 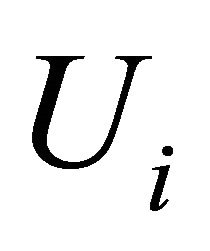 hypersurface passing thought the point, corresponding to
hypersurface passing thought the point, corresponding to  and orthogonal to the trajectory
and orthogonal to the trajectory 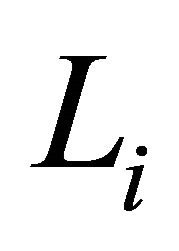 at this point. Let the diameter of cells be so small
at this point. Let the diameter of cells be so small
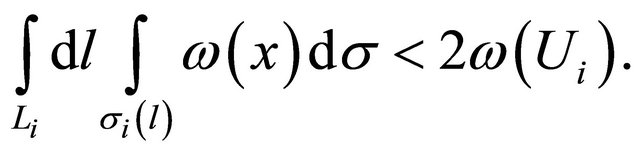
Then by Chebyshev inequality a set  points
points 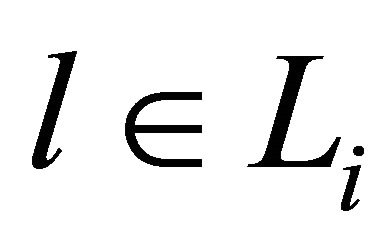 where
where
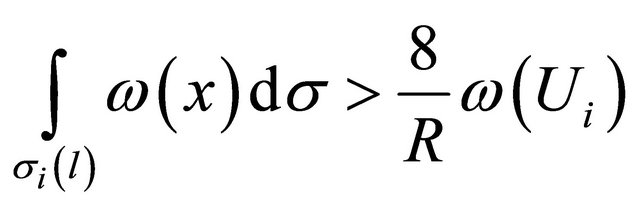
satisfies the inequality 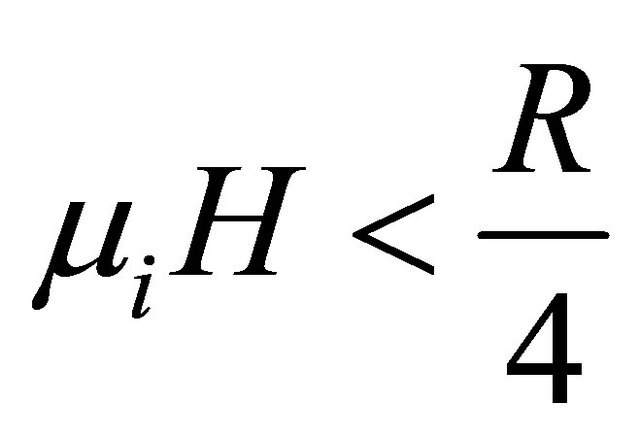 and hence by virtue of (13) for
and hence by virtue of (13) for 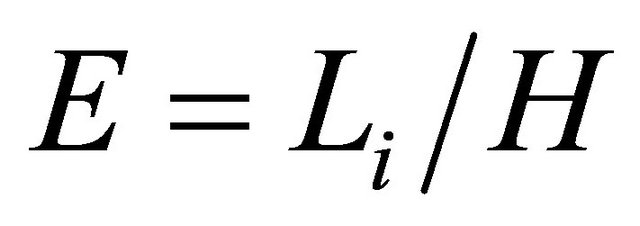 it is valid and
it is valid and
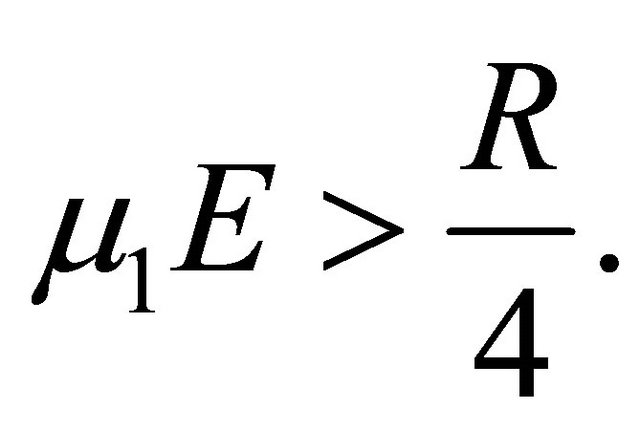
At the points of the curve 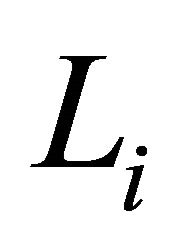 the derivative
the derivative 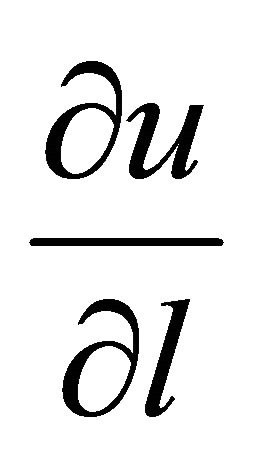 preserves its sign, and therefore
preserves its sign, and therefore
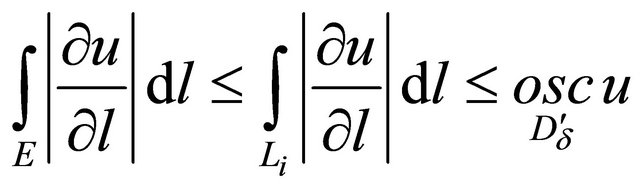
Hence, by using (15) and a mean value theorem for one variable function we find that there exists 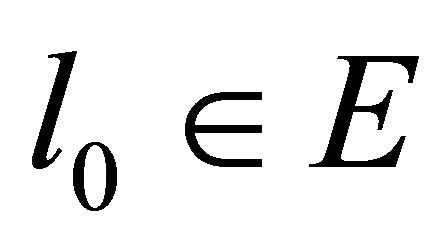
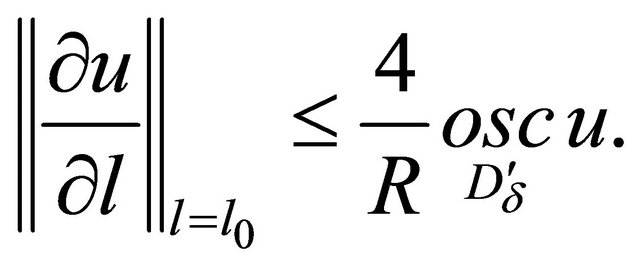
But on the other hand
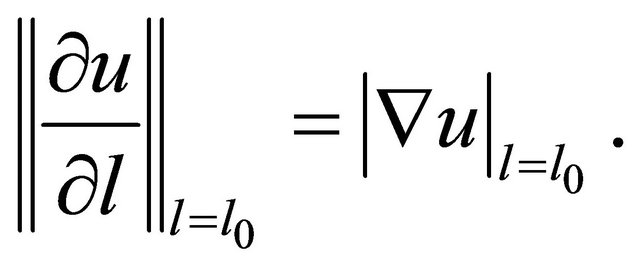
Together with (16) it gives
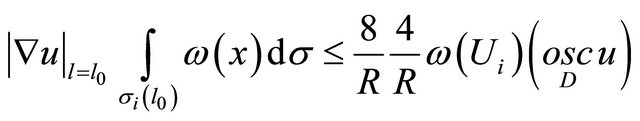
Now, let the diameter of cells be still so small that
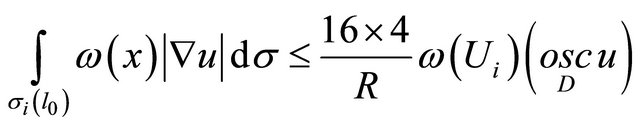
(we can do it, since the derivatives 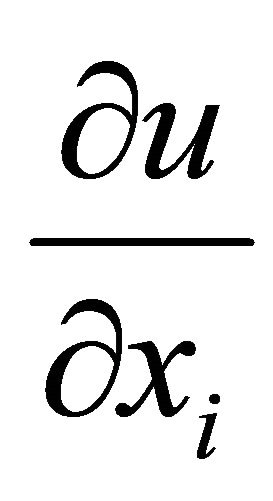 are uniformly continuous). Therefore according to (12)
are uniformly continuous). Therefore according to (12)
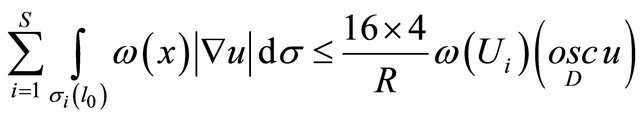
Now by ![]() we denote a set-theoretic sum of all open tubes all thought tubes
we denote a set-theoretic sum of all open tubes all thought tubes ![]() all
all 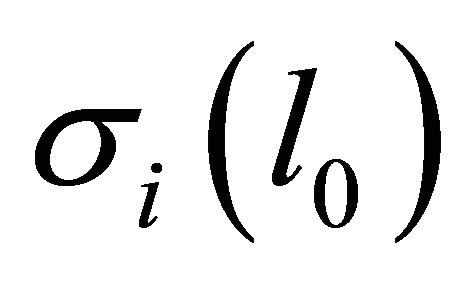 all spheres
all spheres 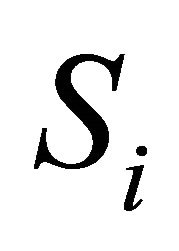
and sets  on the sphere
on the sphere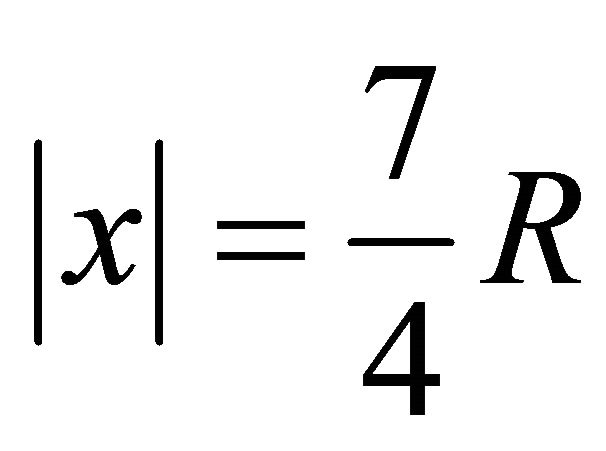 .
.
Then, we get by Equations (3), (9), (11) and (17)
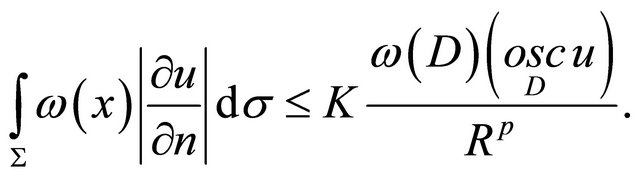
The lemma is proved.
Denote by 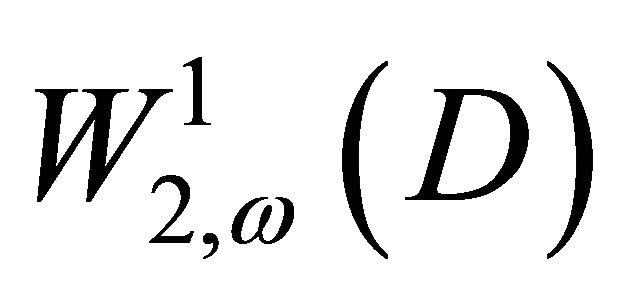 the Banach space of the functions
the Banach space of the functions 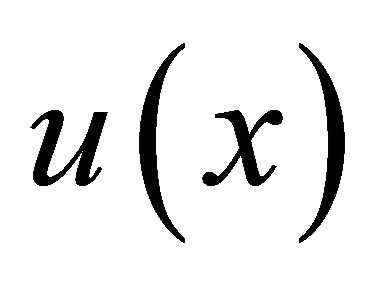 defined in
defined in 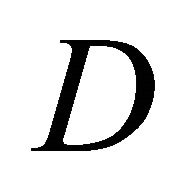 with the finite norm
with the finite norm
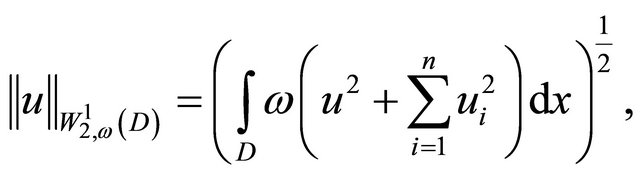
and let 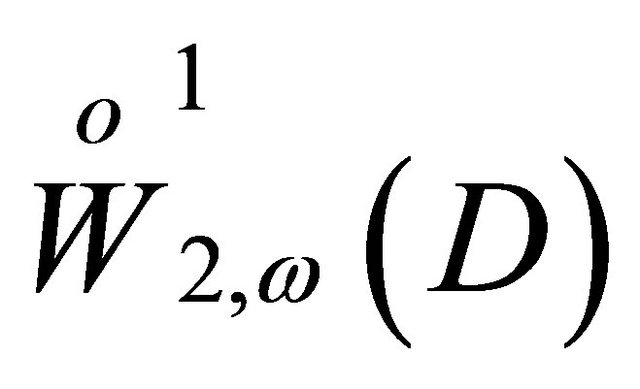 be a completion of
be a completion of 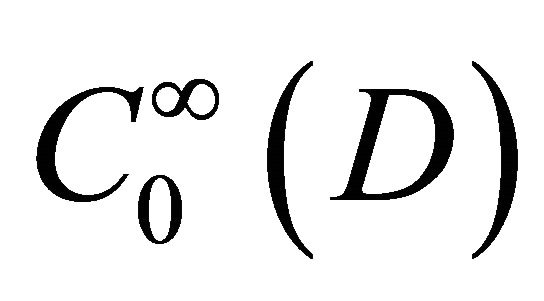 by the norm of the space
by the norm of the space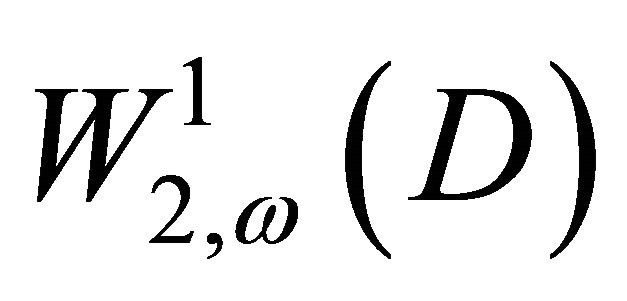 .
.
By 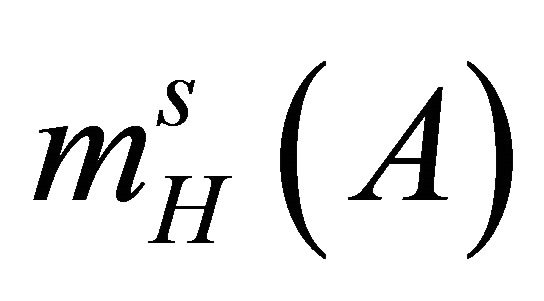 we’ll denote the Hausdorff measure of the set
we’ll denote the Hausdorff measure of the set  of order
of order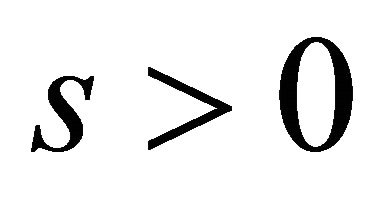 . Further everywhere the notation
. Further everywhere the notation 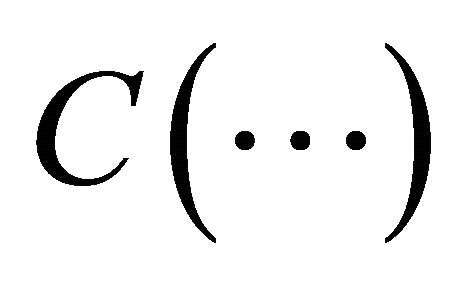 means, that the positive constant
means, that the positive constant 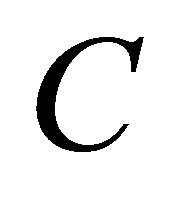 depends only on the content of brackets.
depends only on the content of brackets.
3. Main Results
Theorem 1. Let 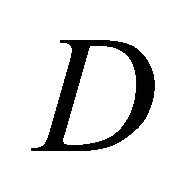 be a bounded domain in
be a bounded domain in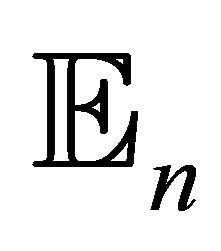 ,
,  be a compact. If with respect to the coefficients of the operator
be a compact. If with respect to the coefficients of the operator ![]() the conditions (2)-(5) are fulfilled, then for removability of the compact
the conditions (2)-(5) are fulfilled, then for removability of the compact 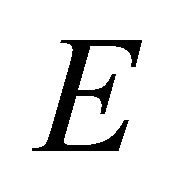 with respect to the Equation (1) in the space
with respect to the Equation (1) in the space 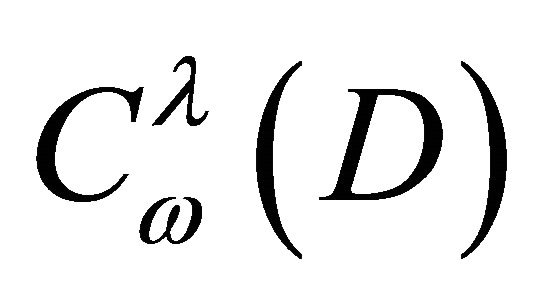 it sufficies that
it sufficies that
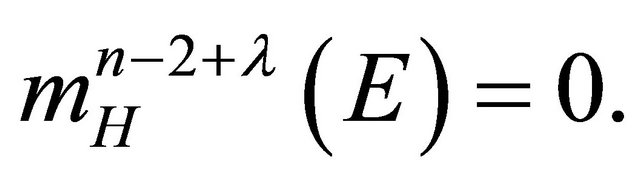 (7)
(7)
Proof. At first we show that without loss of generality we can suppose the condition  is fulfilled. Suppose, that the condition (7) provides the removability of the compact
is fulfilled. Suppose, that the condition (7) provides the removability of the compact 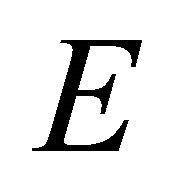 for the domains, whose boundary is the surface of the class
for the domains, whose boundary is the surface of the class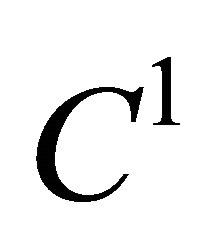 , but
, but  and by fulfilling (7) the compact
and by fulfilling (7) the compact 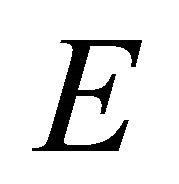 is not removable. Then the problem (6) has non-trivial solution
is not removable. Then the problem (6) has non-trivial solution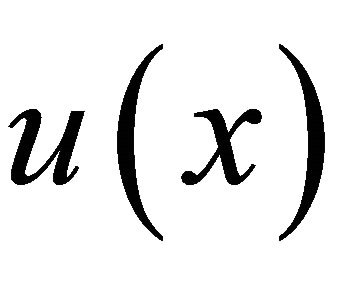 , moreover
, moreover 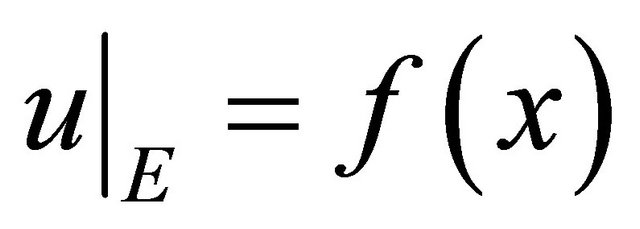 and
and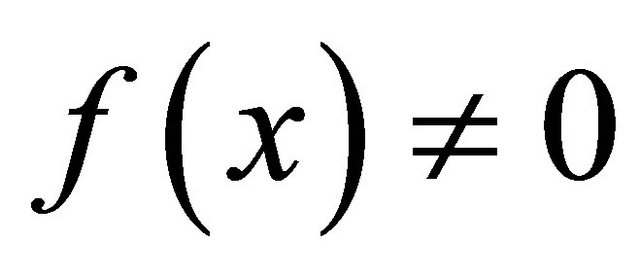 . We always can suppose the lowest coefficients of the operator
. We always can suppose the lowest coefficients of the operator ![]() are infinitely differentiable in
are infinitely differentiable in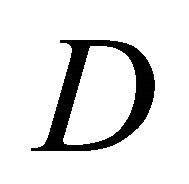 . Moreover, without loss of generality, we’ll suppose that the coefficients of the operator
. Moreover, without loss of generality, we’ll suppose that the coefficients of the operator ![]() are extended to a ball
are extended to a ball 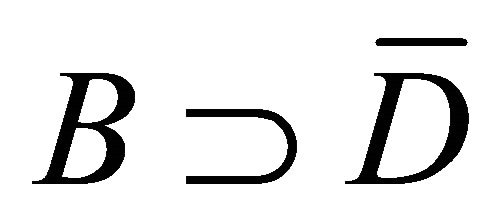 with saving the conditions (2)- (5). Let
with saving the conditions (2)- (5). Let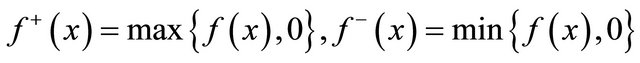 , and
, and 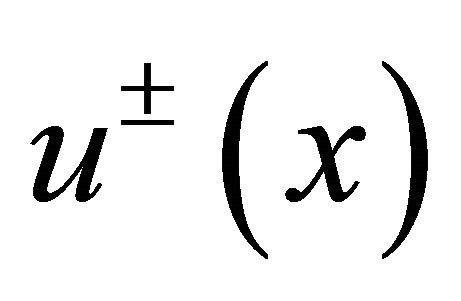 be generalized by Wiener (see [8]) solutions of the boundary value problems
be generalized by Wiener (see [8]) solutions of the boundary value problems
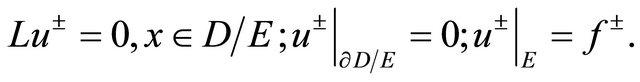
Evidently, by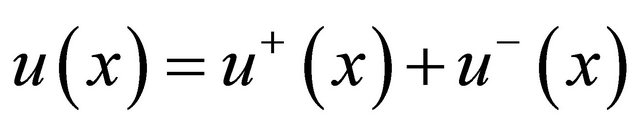 . Further, let
. Further, let 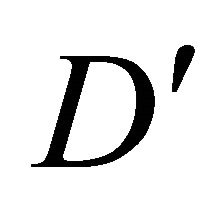
be such a domain, that 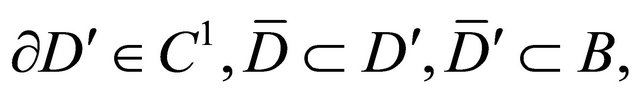 and
and 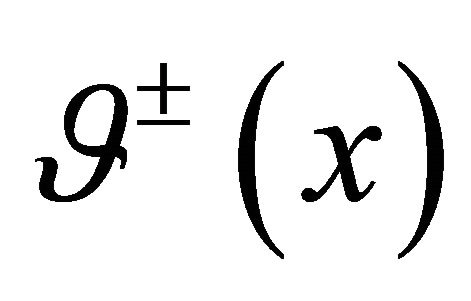 be solutions of the problems
be solutions of the problems
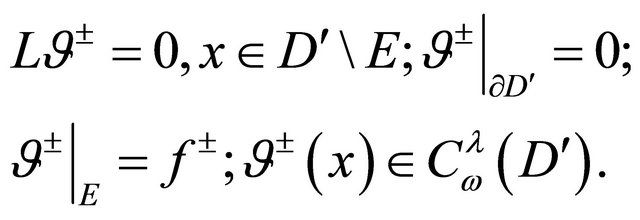
By the maximum principle for 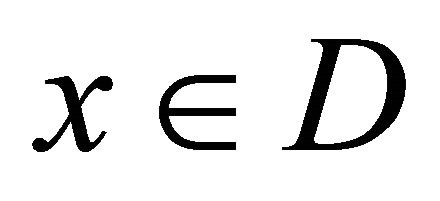
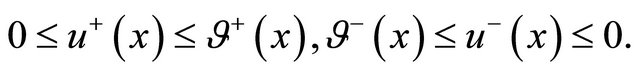
But according to our supposition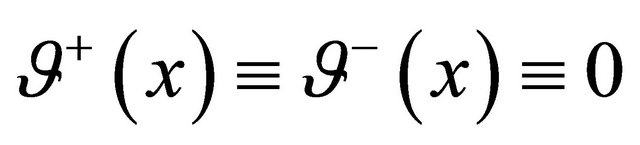 . Hence, it follows, that
. Hence, it follows, that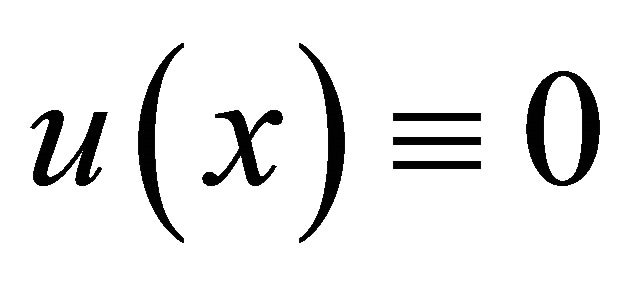 . So, we’ll suppose that
. So, we’ll suppose that . Now, let
. Now, let 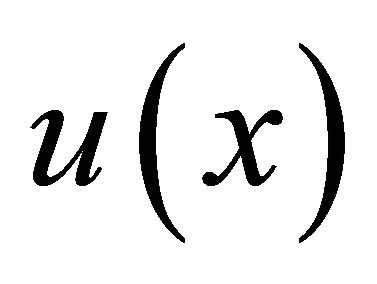 be a solution of the problem (6), and the condition (7) be fulfilled. Give an arbitrary
be a solution of the problem (6), and the condition (7) be fulfilled. Give an arbitrary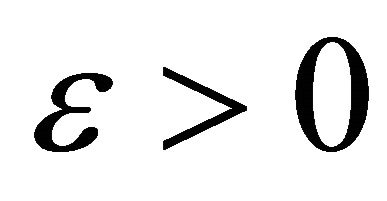 . Then there exists a sufficiently small positive number
. Then there exists a sufficiently small positive number ![]() and a system of the balls
and a system of the balls 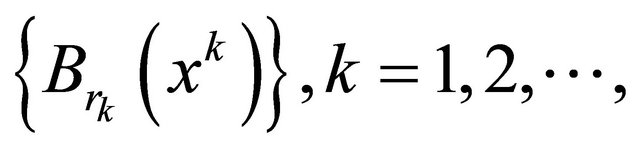
such that 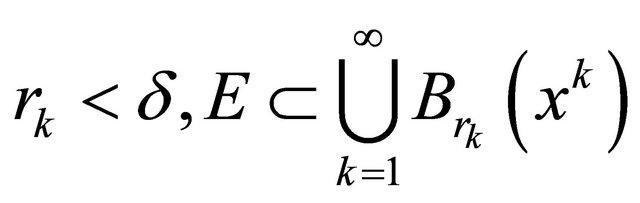 and
and
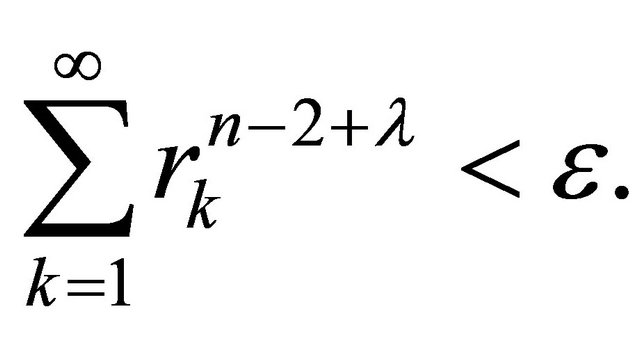 (8)
(8)
Consider a system of the spheres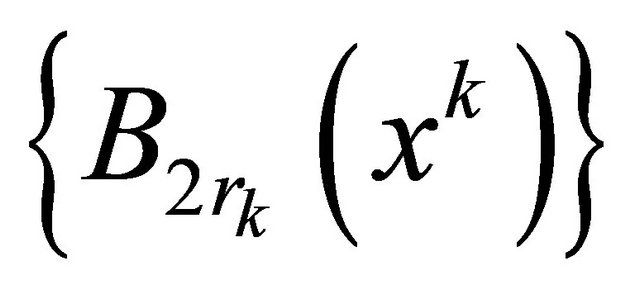 , and let
, and let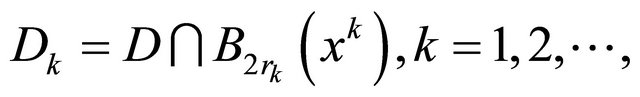 . Without loss of generality we can suppose that the cover
. Without loss of generality we can suppose that the cover 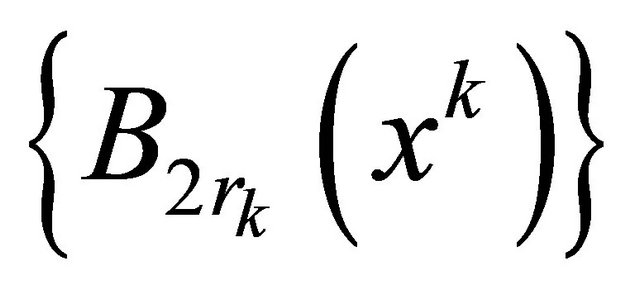 has a finite multiplicity
has a finite multiplicity . By lemma for every
. By lemma for every 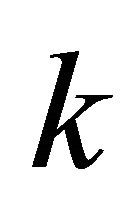 there exists a piece-wise smooth surface
there exists a piece-wise smooth surface 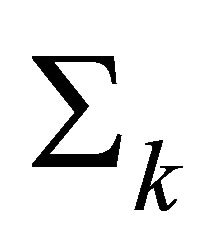 dividing in
dividing in 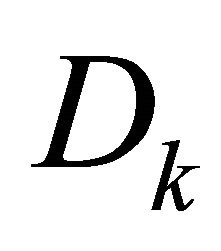 the spheres
the spheres 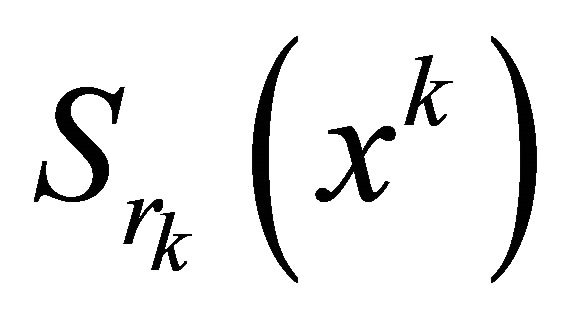 and
and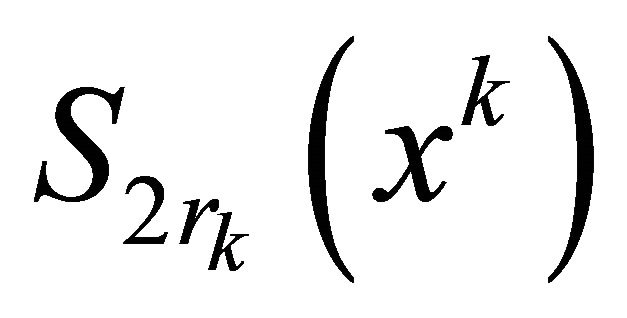 , such that
, such that
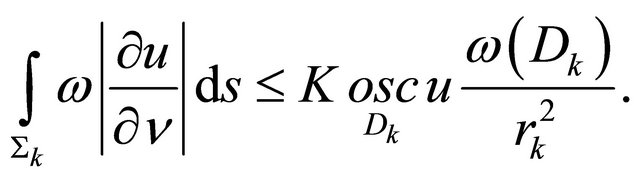 (9)
(9)
Since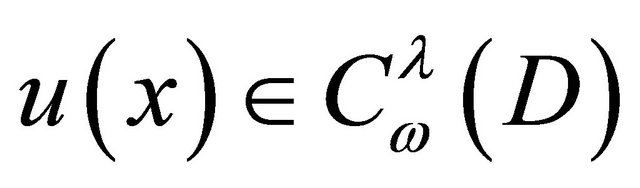 , there exists a constant
, there exists a constant  depending only on the function
depending only on the function 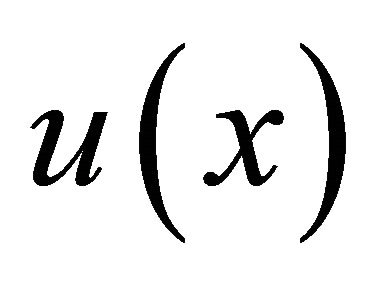 such that
such that
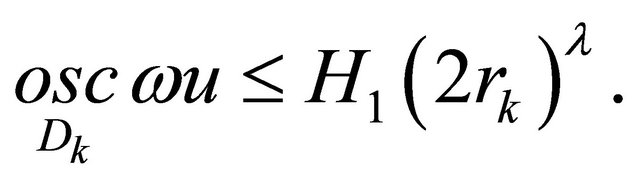 (10)
(10)
Besides,
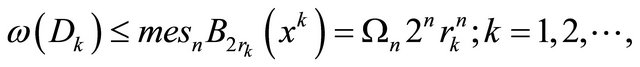 (11)
(11)
where . Using (10) and (11) in (9), we get
. Using (10) and (11) in (9), we get
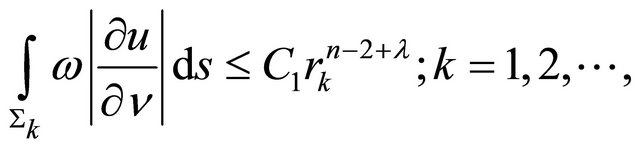 (12)
(12)
where .
.
Let 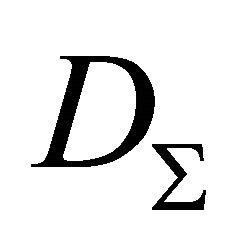 be an open set situated in
be an open set situated in 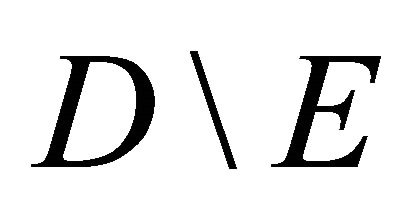 whose boundary consists of unification of
whose boundary consists of unification of ![]() and
and![]() , where
, where
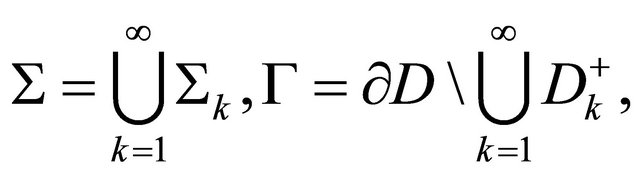
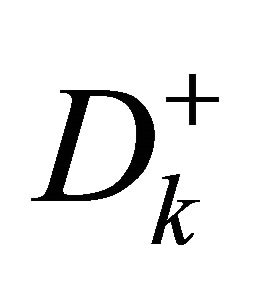 is a part of
is a part of 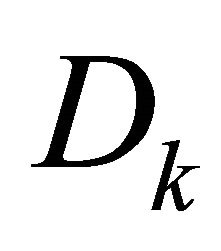 remaining after the removing of points situated between
remaining after the removing of points situated between ![]() and
and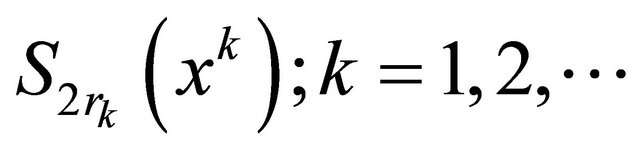 . Denote by
. Denote by 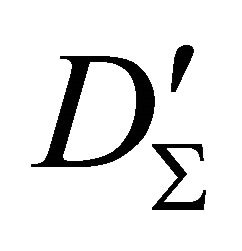 the arbitrary connected component
the arbitrary connected component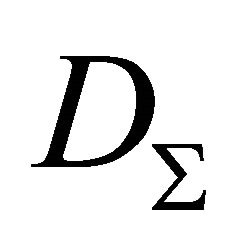 , and by
, and by 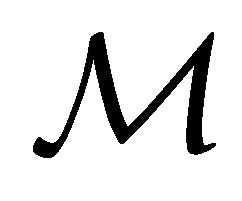 we denote the elliptic operator of divergent structure
we denote the elliptic operator of divergent structure
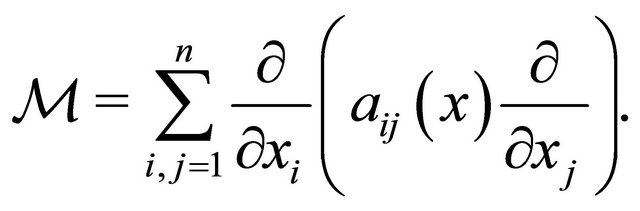
According to Green formula for any functions 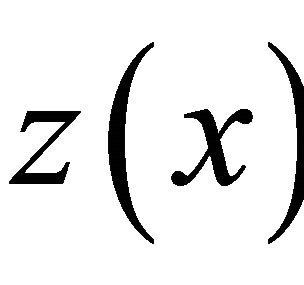 and
and
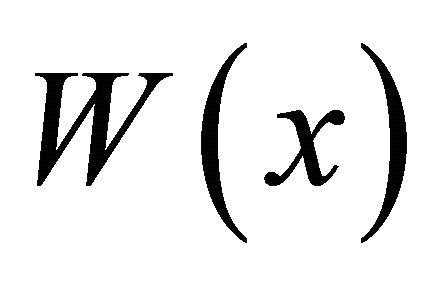 belonging to the intersection
belonging to the intersection 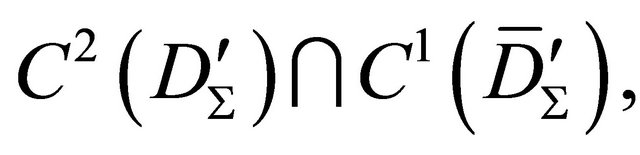
we have
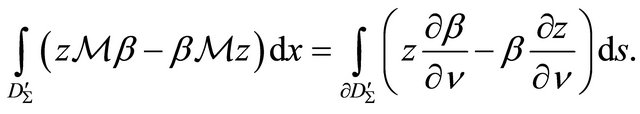 (13)
(13)
Since 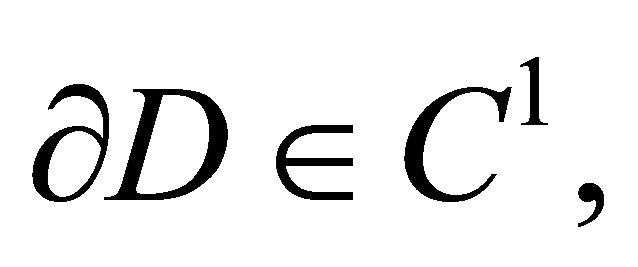 then
then
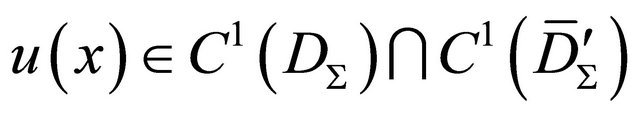
(see [9]). From (13) choosing the functions 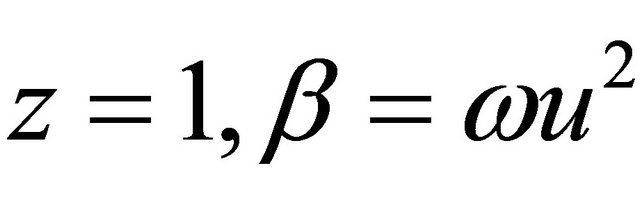 we have
we have
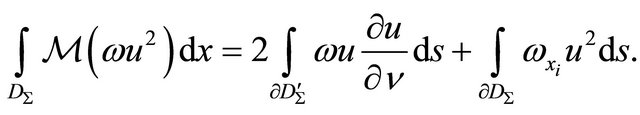
But 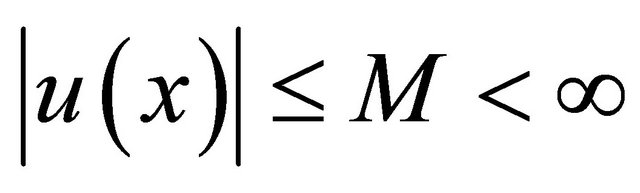 for
for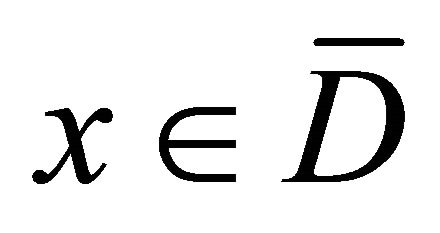 . Let’s assume that the condition
. Let’s assume that the condition
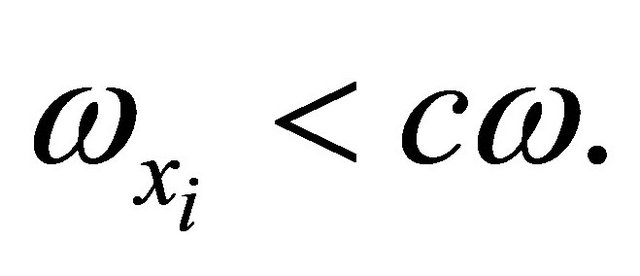 (*)
(*)
is fulfilled. By virtue of condition (*) and
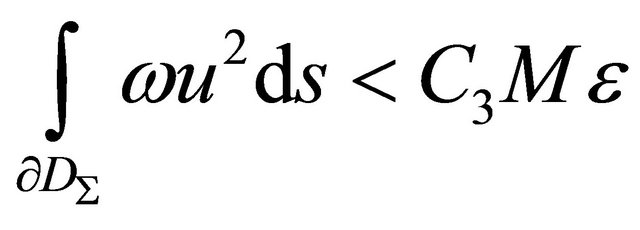
subject to (12) and (8) we conclude
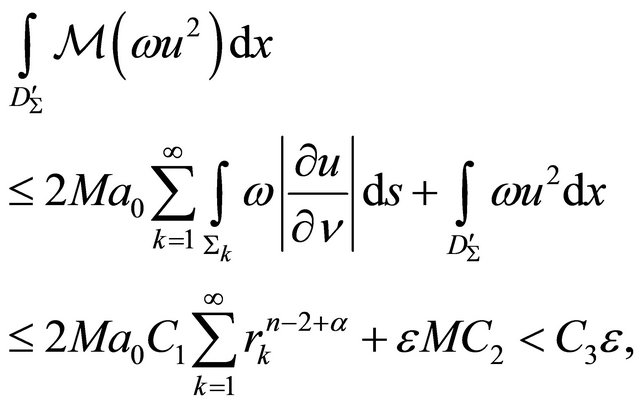 (14)
(14)
where 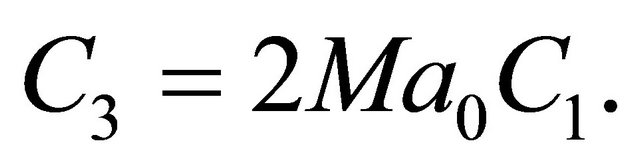
On the other hand
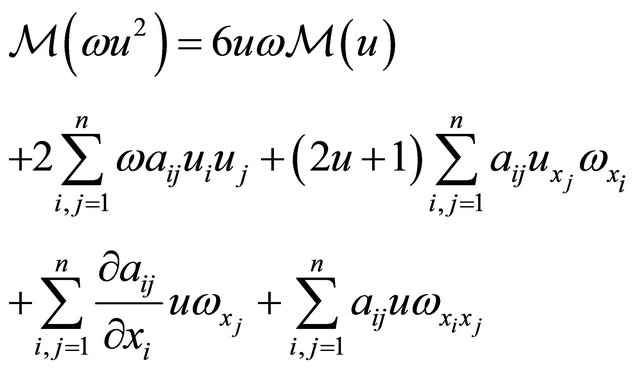
and besides,
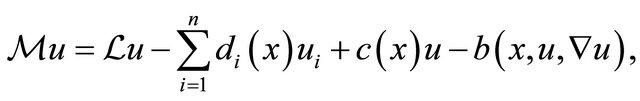
where ![]()
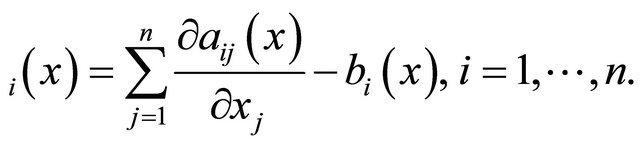
It is evident that by virtue of conditions (3)-(4) 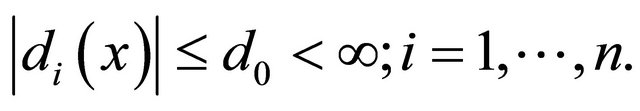 Thus, from (13) we obtain
Thus, from (13) we obtain
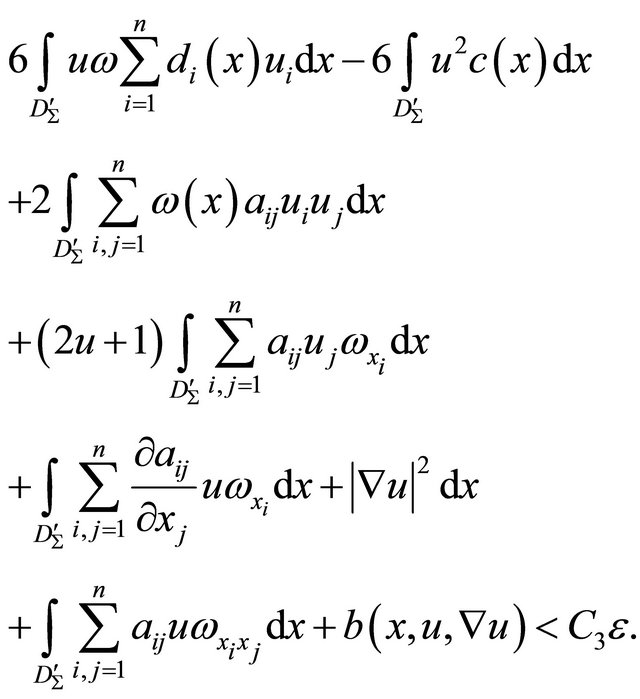 (15)
(15)
Let’s estimate the nonlinear member on the right part applying the inequality
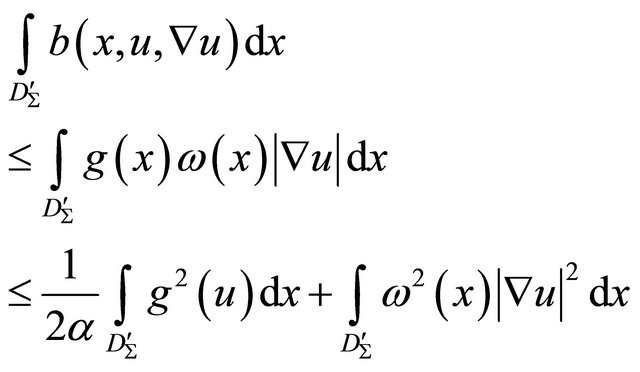
Hence, for any 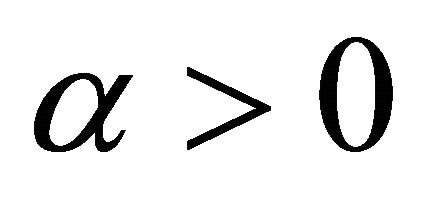 applying Cauchy inequality we have
applying Cauchy inequality we have
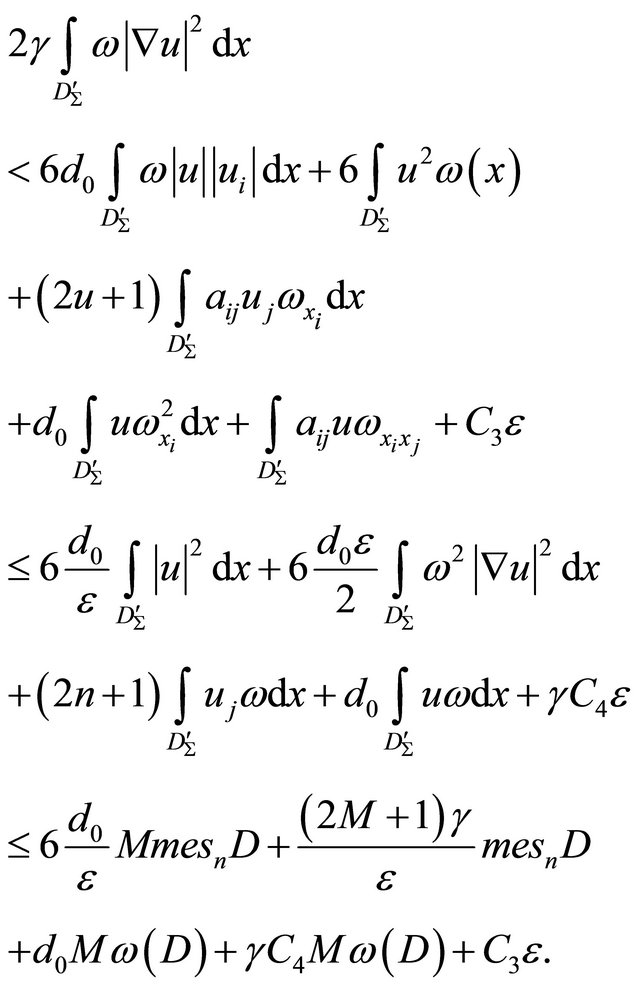
If we’ll take into account that
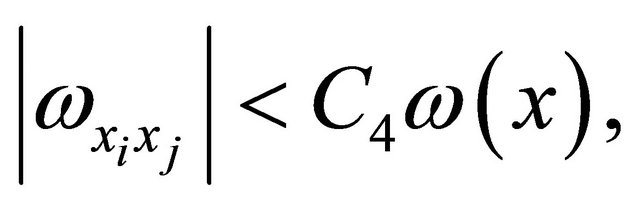
then from here we have that
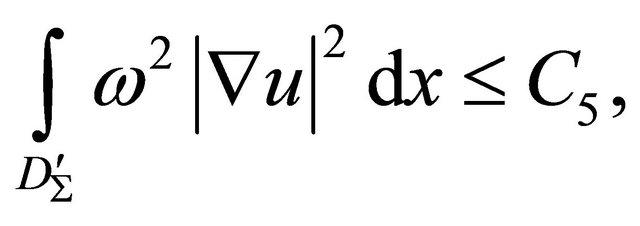
where
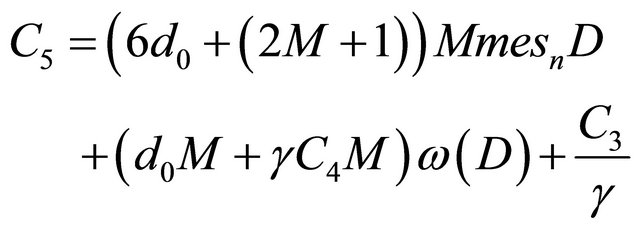 .
.
Without loss of generality we assume that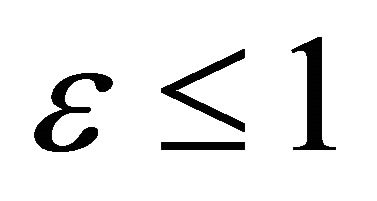 . Hence we have
. Hence we have
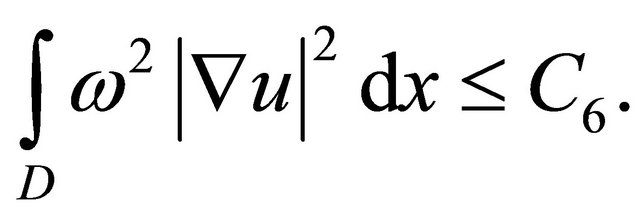
Thus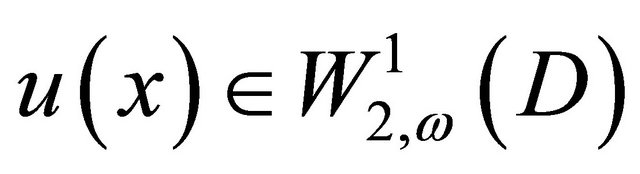 . From the boundary condition and
. From the boundary condition and 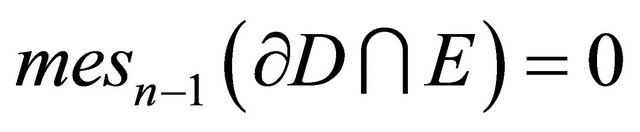 we get
we get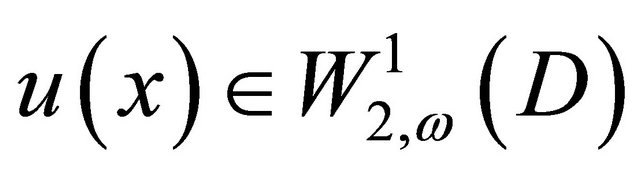 . Now, let
. Now, let 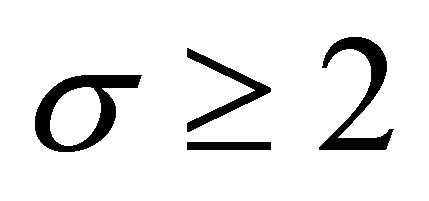 be a number which will be chosen later,
be a number which will be chosen later,
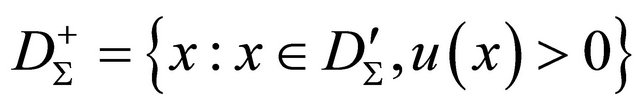 . Without loss of generalitywe suppose that the set
. Without loss of generalitywe suppose that the set 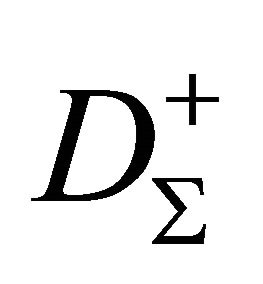 isn’t empty. Supposing in (13)
isn’t empty. Supposing in (13) 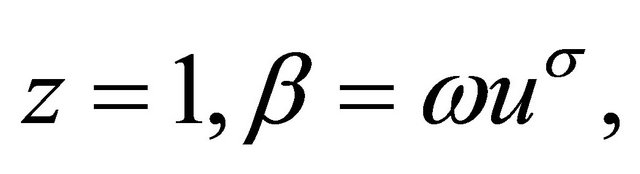 we get
we get
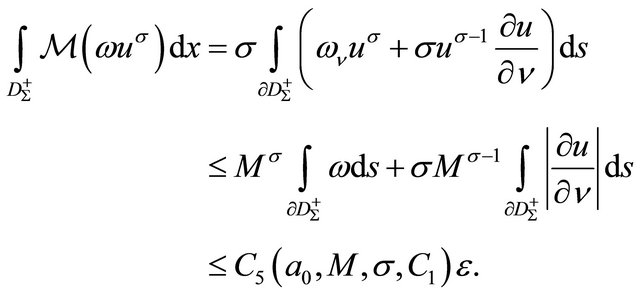
But, on the other hand
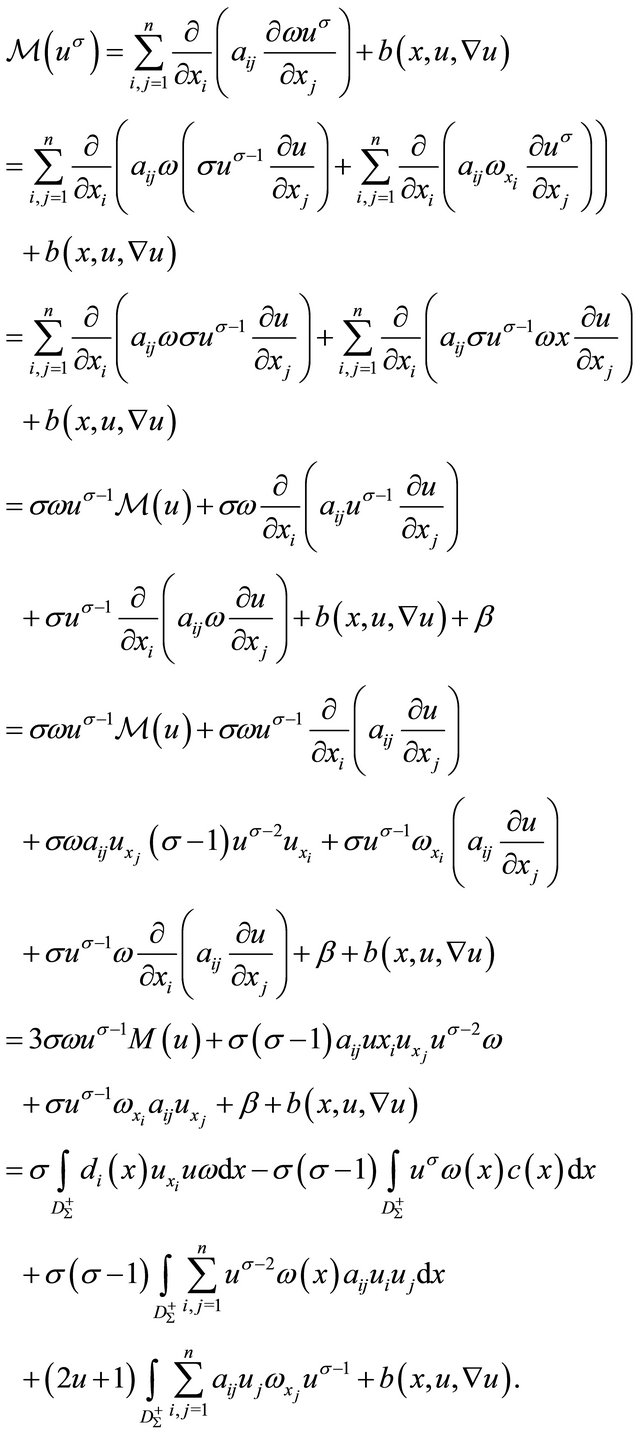
Hence, we conclude
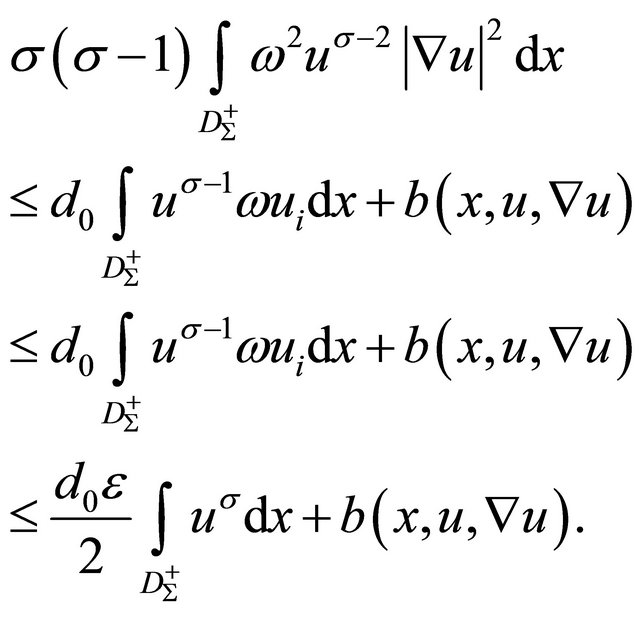 (16)
(16)
Let ,
, 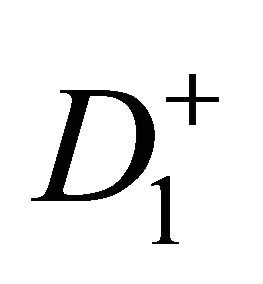 be an arbitrary connected component of
be an arbitrary connected component of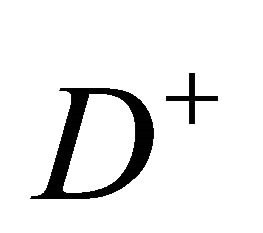 . Subject to the arbitrariness of
. Subject to the arbitrariness of ![]() from (16) we get
from (16) we get
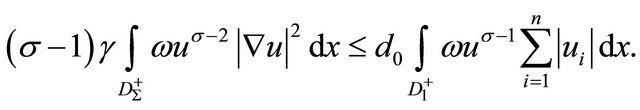
Thus, for any 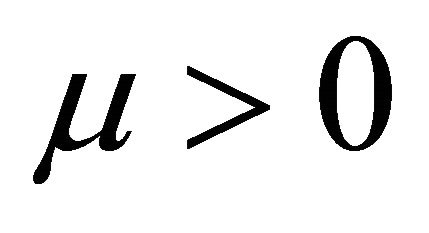
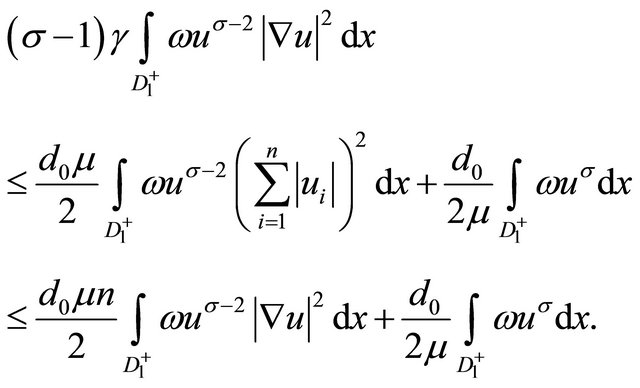 (17)
(17)
But, on the other hand
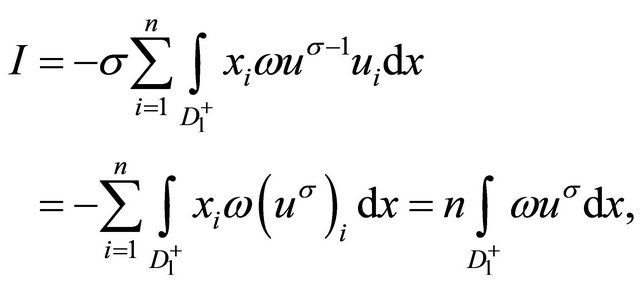
and besides, for any 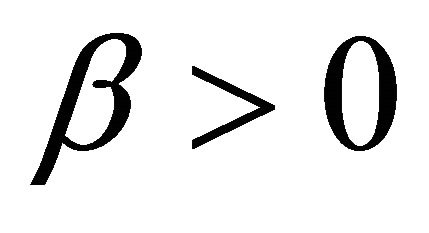
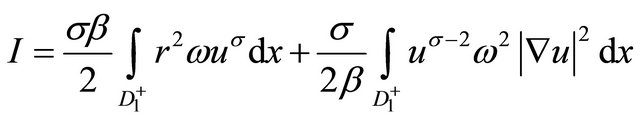
Then
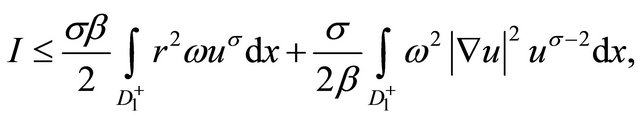
where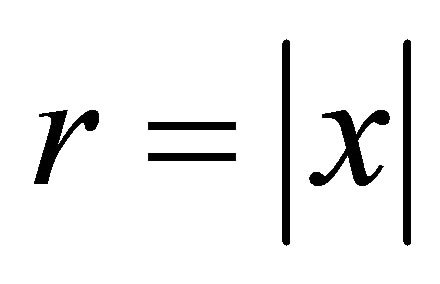 . Denote by
. Denote by 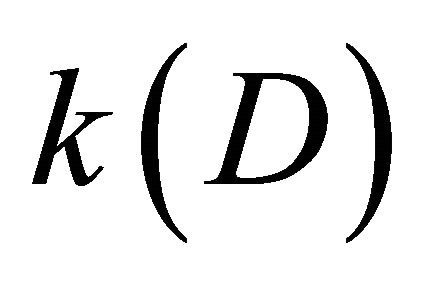 the quantity
the quantity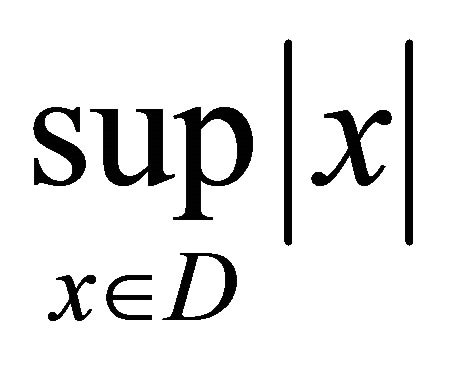 .
.
Without loss of generality we’ll suppose, that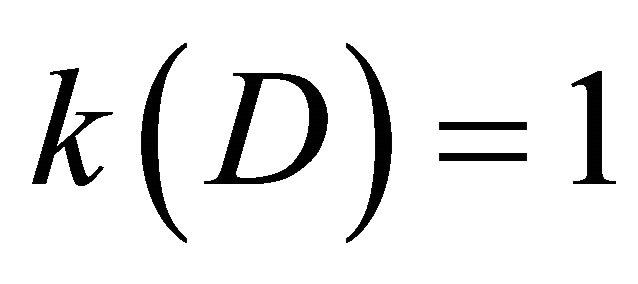 . Then
. Then
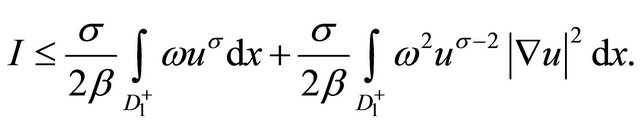
Thus,
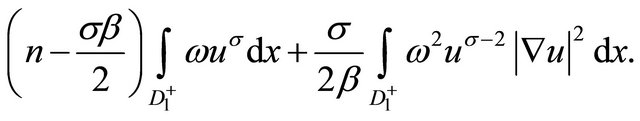
Now, choosing 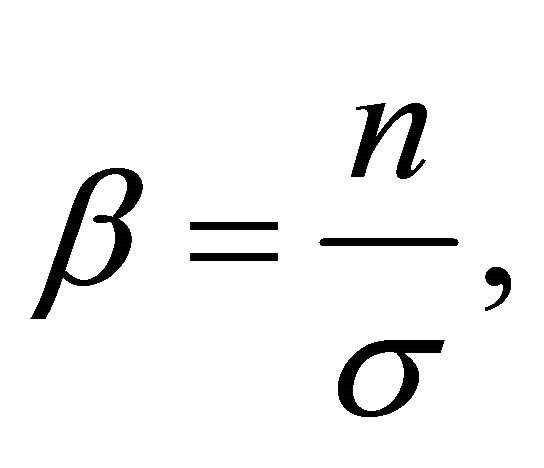 we finnaly obtain
we finnaly obtain
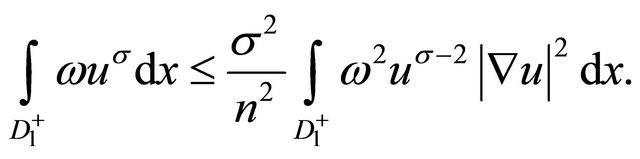 (18)
(18)
Subject to Equation (18) in Equation (17) ,we conclude
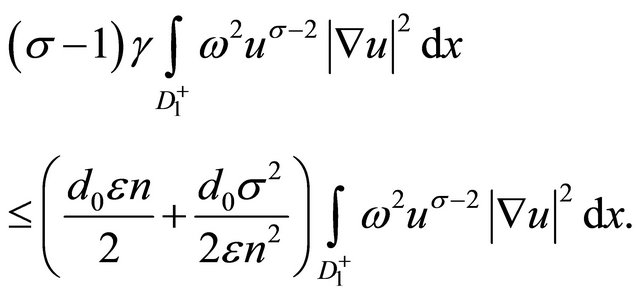 (19)
(19)
Now choose 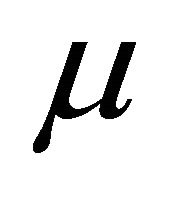 such that
such that
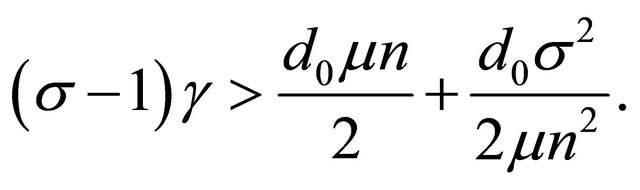 (20)
(20)
Then from Equations (18)-(20) it will follow that 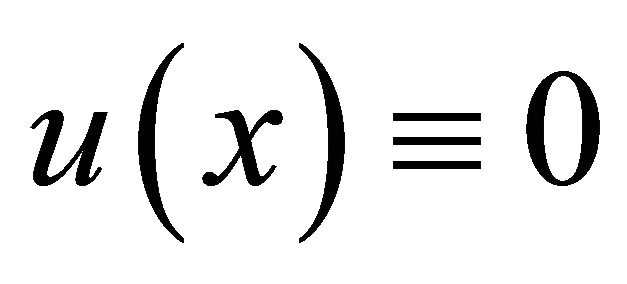 in
in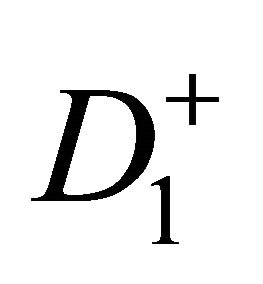 , and thus
, and thus 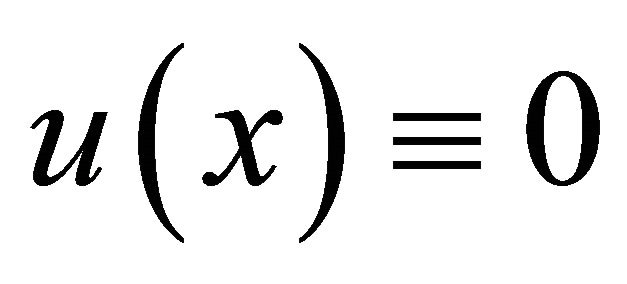 in
in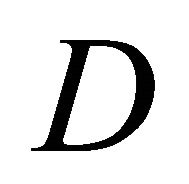 . Suppose that
. Suppose that
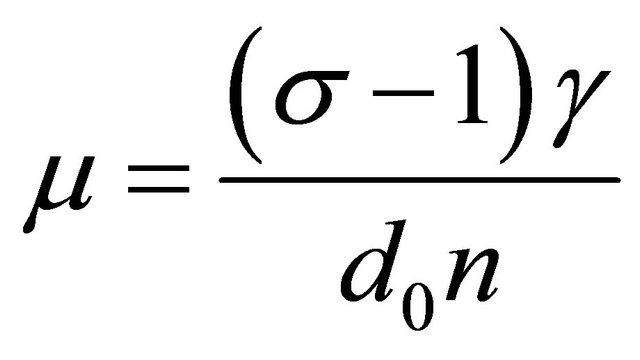 .
.
Then Equation (20) is equivalent to the condition
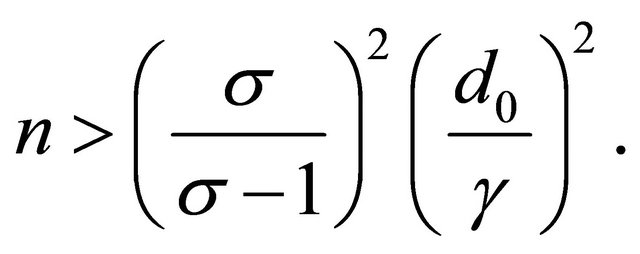 (21)
(21)
At first, suppose that
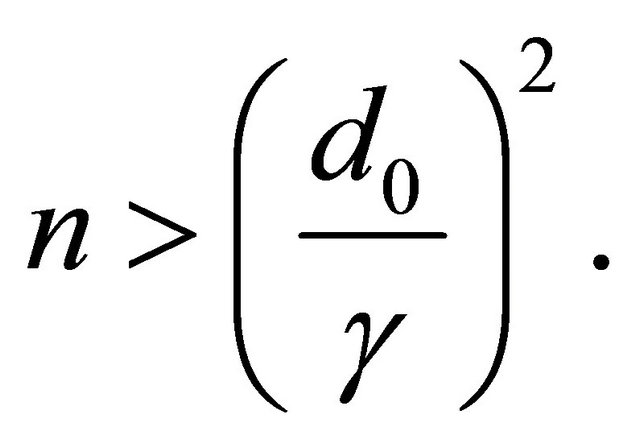 (22)
(22)
Let’s choose and fix such a big 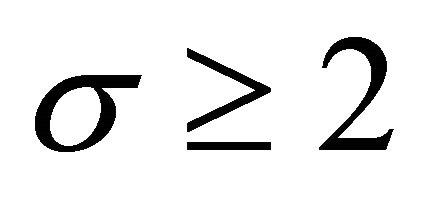 that by fulfilling (22) the inequality (21) was true. Thus, the theorem is proved, if with respect to
that by fulfilling (22) the inequality (21) was true. Thus, the theorem is proved, if with respect to ![]() the condition (22) is fulfilled. Show that it is true for any
the condition (22) is fulfilled. Show that it is true for any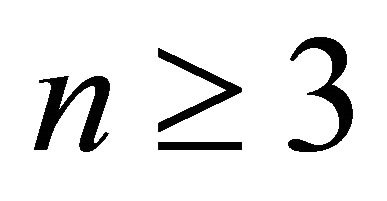 . For that, at first, note that if
. For that, at first, note that if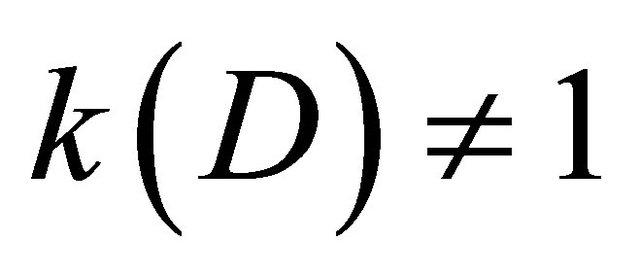 , then condition (22) will take the form
, then condition (22) will take the form
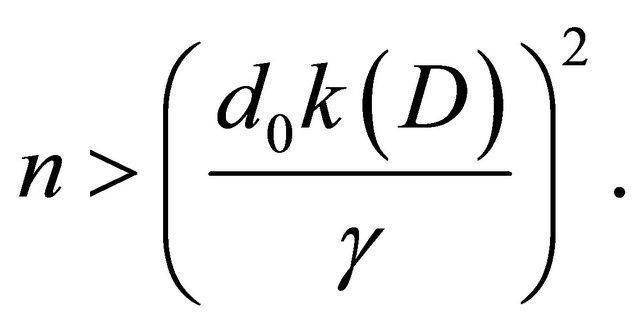
Now, let the condition (22) be not fulfilled. Denote by 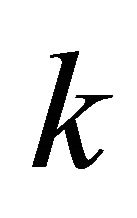 the least natural number for which
the least natural number for which
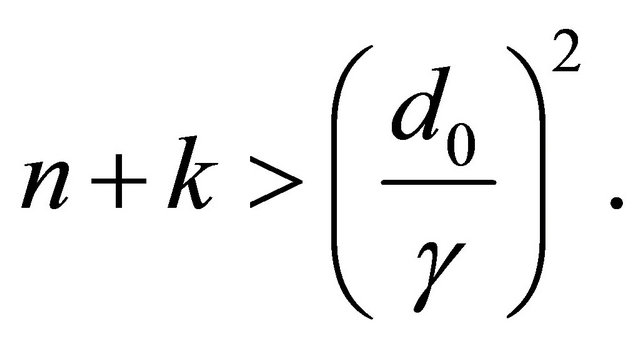 (23)
(23)
Consider 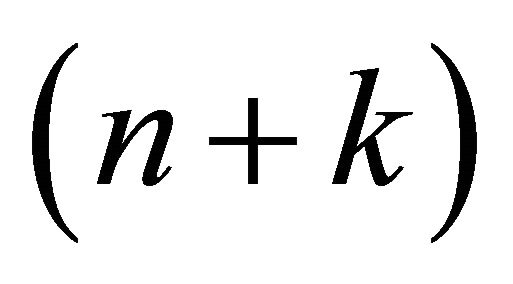 -dimensional semi-cylinder
-dimensional semi-cylinder
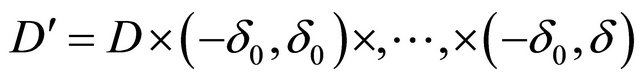 where the number
where the number 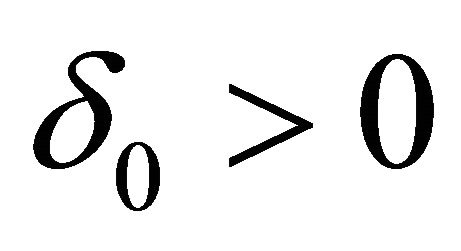 will be chosen later. Since
will be chosen later. Since
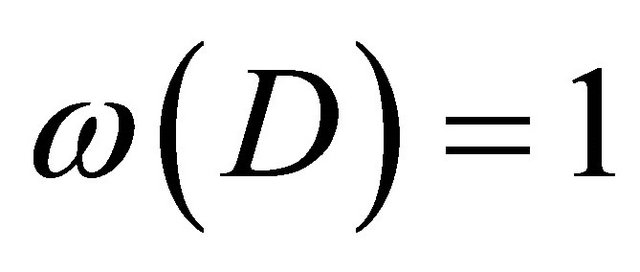 , then
, then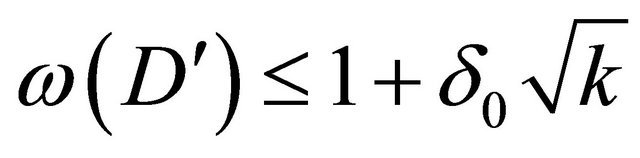 . Let’s choose and fix
. Let’s choose and fix
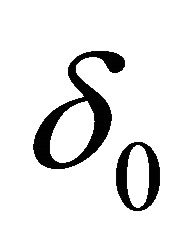 so small that along with the condition (23) the condition
so small that along with the condition (23) the condition
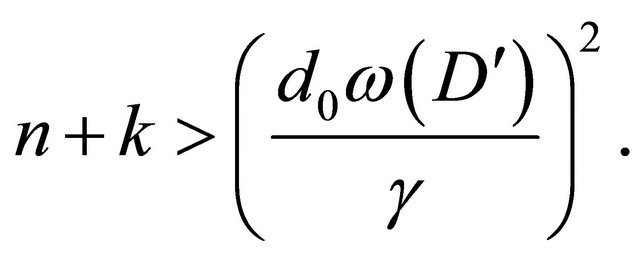 (24)
(24)
was fulfilled too.
Let
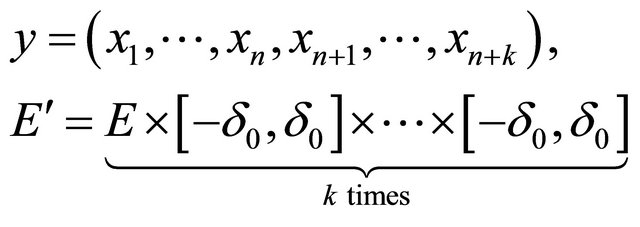
Consider on the domain 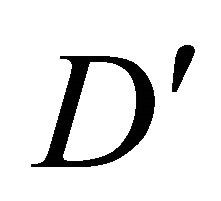 the equation
the equation
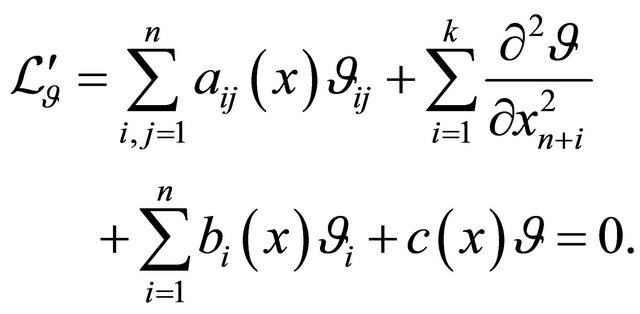 (25)
(25)
It is easy to see that the function 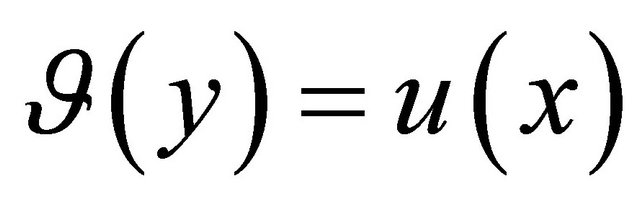 is a solution of the Equation (25) in
is a solution of the Equation (25) in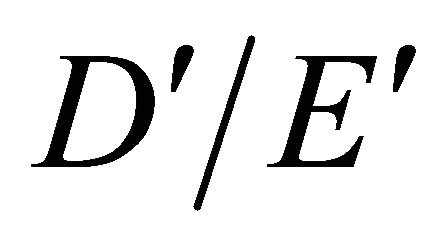 . Besides,
. Besides,
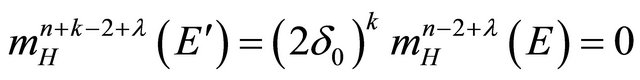 the function
the function 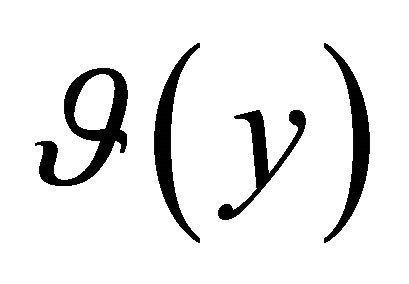 vanishes on
vanishes on
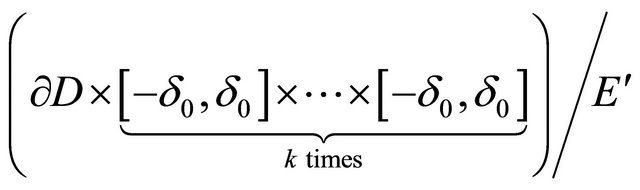 and
and 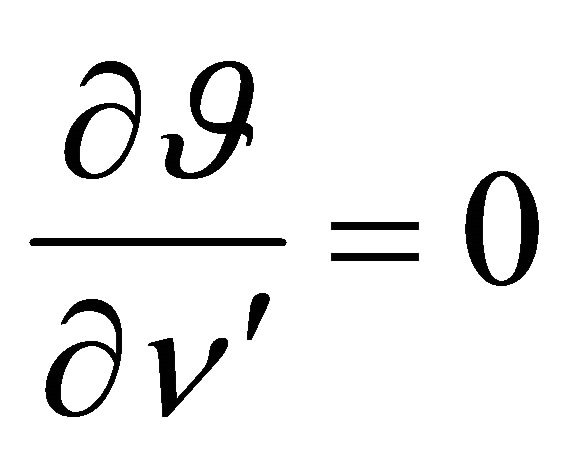
at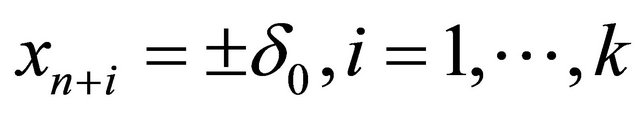 , where
, where 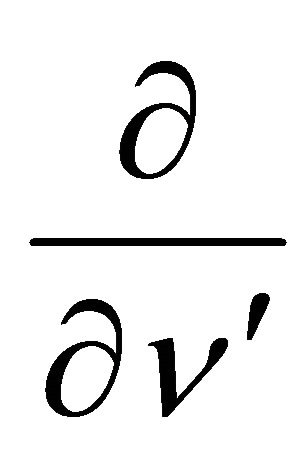 is a derivative by the conormal generated by the operator
is a derivative by the conormal generated by the operator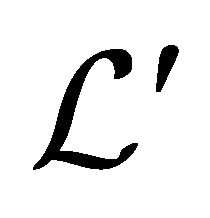 . Noting that
. Noting that 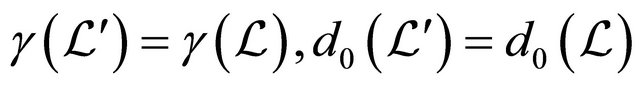 and subject to the condition (24), from the proved above we conclude that
and subject to the condition (24), from the proved above we conclude that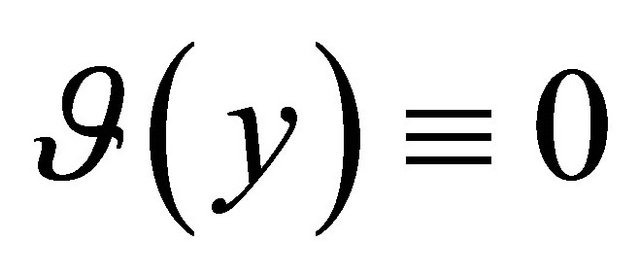 , i.e.
, i.e.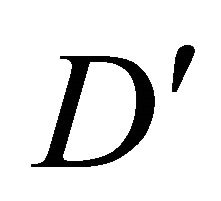 . The theorem is proved.
. The theorem is proved.
Remark. As is seen from the proof, the assertion of the theorem remains valid if instead of the condition (3) it is required that the coefficients 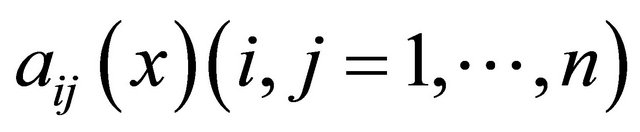 have to satisfy in domain
have to satisfy in domain 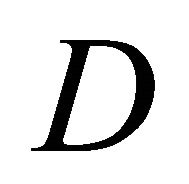 the uniform Lipschitz condition with weight.
the uniform Lipschitz condition with weight.
Thus in this paper the sufficient condition for removability of the compact respect Newman problem for quasilinear equation in classes in the weight space of Holder functions is obtained.
REFERENCES
- L. Carleson, “Selected Problems on Exceptional Sets,” D. Van Nostrand Company, Toronto, 1967, 126 p.
- E. I. Moiseev, “On Neumann Problems in Piecewise Smooth Domains,” Differentsial’nye Uravneniya, Vol. 7, No. 9, 1971, pp. 1655-1656.
- E. I. Moiseev, “On Existence and Non-Existence Boundary Sets of Neumann Problem,” Differentsial’nye Uravneniya, Vol. 9, No. 5, 1973, pp. 901-911.
- E. M. Landis, “To Question on Uniqueness of Solution of the First Boundary Value Problem for Elliptic and Parabolic Equations of the Second Order,” Uspekhi Matematicheskikh Nauk, Vol. 33, No. 3, 1978, p. 151.
- V. A. Kondratyev and E. M. Landis, “Qualitative Theory of Linear Partial Differential Equations of Second Order,” Modern Problems of Mathematics, Fundamental Directions, Partial Differential Equations, Vol. 3, Itogi Nauki i Tekhniki, Seriya, VINITI, 1988, pp. 99-212.
- I. T. Mamedov, “On Exceptional Sets of Solutions of Dirichlet Problem for Elliptic Equations of Second Order with Discontinuous Coefficients,” Proceedings of Institute of Mathematics and Mechanics of Academy of Science of Azerbaijan, Vol. 3, No. 16, 1998, pp. 137-149.
- M. L. Gerver and E. M. Landis, “One Generalization of a Theorem on Mean Value for Multivariable Functions,” Doklady Akademii Nauk USSR, Vol. 146, No. 4, 1962, pp. 761-764.
- E. M. Landis, “Second Order Equations of Elliptic and Parabolic Types,” Nauka, 1971, 288 p.
- D. Gilbarg and N. S. Trudinger, “Elliptic Partial Differential Equations of Second Order,” Springer-Verlag, Berlin, 1977, 401 p. doi:10.1007/978-3-642-96379-7
- V. Kayzer and B. Muller, “Removable Sets for Heat Conduction,” Vestnik, Moscow University, Moscow, 1973, pp. 26-32.
- V. A. Mamedova, “On Removable Sets of Solutions of Boundary Value Problems for Elliptic Equations of Second Order,” Transactions of the NAS of Azerbaijan, Vol. 25, No. 1, 2005, pp. 101-106.
- T. S. Gadjiev and V. A. Mamedova, “On Removable Sets of Solutions of Second Order Elliptic and Parabolic Equations in Nondivergent Form,” Ukrainian Mathematical Journal, Vol. 61, No. 11, 2009, pp. 1485-1496.
- T. Kilpelainen and X. Zhong, “Removable Sets for Continuous Solutions of Quasilinear Elliptic Equations,” Proceedings of the American Mathmatical Society, Vol. 130, No. 6, 2002, pp. 1681-1688. doi:10.1090/S0002-9939-01-06237-2
- J. Diederich, “Removable Sets for Pointwise Solutions of Elliptic Partial Differential Equations,” Transactions of the American Mathmatical Society, Vol. 165, 1972, pp. 333-352. doi:10.1090/S0002-9947-1972-0293235-X
- R. Harvey and J. Polking, “Removable Singularities of Solutions of Linear Partial Differential Equations,” Acta Mathematica, Vol. 125, No. 1, 1970, pp. 39-56. doi:10.1007/BF02838327
- B. E. J. Dahlberg, “On Exceptional Sets at the Boundary for Subharmonic Functions,” Arkiv för Matematik, Vol. 15, No. 2, 1977, pp. 305-312.
- A. V. Pokrovskii, “Removable Singularities of Solutions of Linear Uniformly Elliptic Second Order Equations,” Funktsionalnyj Analiz i Prilozhenija, Vol. 42, No. 2, 2008, pp. 44-55.
- A. V. Pokrovskii, “Removable Singularities for Solutions of Second-Order Linear Uniformly Elliptic Equations in Non-Divergence Form,” Mathematics Sbornik, Vol. 199, No. 6, 2008, pp. 137-160.

