Applied Mathematics
Vol.3 No.12A(2012), Article ID:25988,6 pages DOI:10.4236/am.2012.312A280
Discrete-Time Langevin Motion in a Gibbs Potential
1Department of Mathematics, Iowa State University, Ames, USA
2Department of Electrical and Computer Engineering, University of California San Diego, San Diego, USA
3Department of Mathematics, Grand Valley State University, Allendale, USA
Email: rastegar@iastate.edu, roiterst@iastate.edu, roytersh@gmail.com, suhj@gvsu.edu
Received September 8, 2012; revised October 8, 2012; accepted October 15, 2012
Keywords: Langevin Equation; Dynamics of a Moving Particle; Multivariate Regular Variation; Chains with Complete Connections
ABSTRACT
We consider a multivariate Langevin equation in discrete time, driven by a force induced by certain Gibbs’ states. The main goal of the paper is to study the asymptotic behavior of a random walk with stationary increments (which are interpreted as discrete-time speed terms) satisfying the Langevin equation. We observe that (stable) functional limit theorems and laws of iterated logarithm for regular random walks with i.i.d. heavy-tailed increments can be carried over to the motion of the Langevin particle.
1. Introduction
We start with the following equation describing a discrete-time motion in 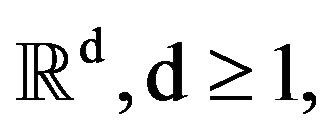 of a particle with mass
of a particle with mass ![]() in the presence of a random potential and a viscosity force proportional to velocity:
in the presence of a random potential and a viscosity force proportional to velocity:
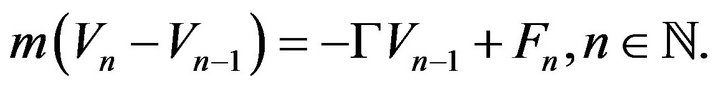
Here d-vector  is the velocity at time
is the velocity at time 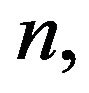
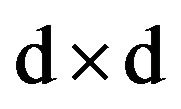 matrix
matrix ![]() represents an anisotropic damping coefficient, and d-vector
represents an anisotropic damping coefficient, and d-vector 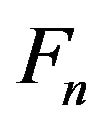 is a random force applied at time
is a random force applied at time ![]() The above equation is a discrete-time counterpart of the Langevin SDE
The above equation is a discrete-time counterpart of the Langevin SDE 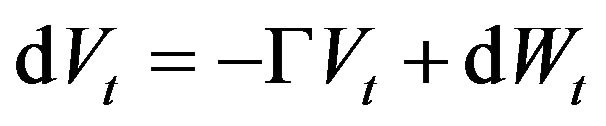 [1,2]. Applications of the Langevin equation with a random non-Gaussian term
[1,2]. Applications of the Langevin equation with a random non-Gaussian term 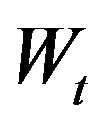 are addressed, for instance, in [3,4]. Setting
are addressed, for instance, in [3,4]. Setting  and
and  we obtain:
we obtain:
 (1)
(1)
The random walk 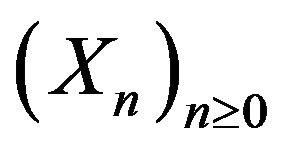 associated with this equation is given by
associated with this equation is given by
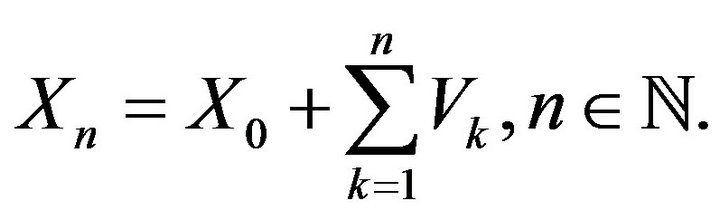 (2)
(2)
Similar models of random motion in dimension one, with i.i.d. forces 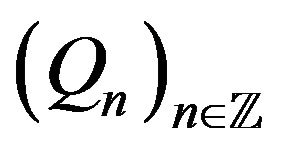 were considered in [5-8], see also [9,10] and references therein. See, for instance, [11-14] for interesting examples of applications of Equation (1) with i.d.d. coefficients in various areas.
were considered in [5-8], see also [9,10] and references therein. See, for instance, [11-14] for interesting examples of applications of Equation (1) with i.d.d. coefficients in various areas.
In this paper we will assume that the coefficients
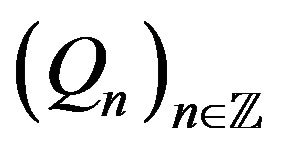 are induced (in the sense of the following definition) by certain Gibbs’s states.
are induced (in the sense of the following definition) by certain Gibbs’s states.
Definition 1. Coefficients  are said to be induced by random variables
are said to be induced by random variables  each valued in a finite set
each valued in a finite set  if there exists a sequence of independent random d-vectors
if there exists a sequence of independent random d-vectors ![]() which is independent of
which is independent of 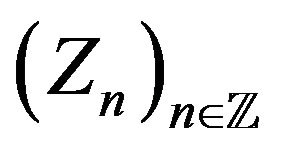 and is such that for a fixed
and is such that for a fixed
 are i.i.d. and
are i.i.d. and 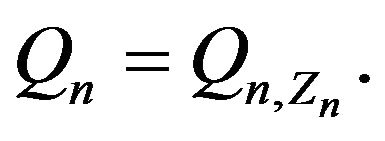
The randomness of 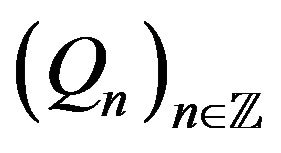 is due to two factors:
is due to two factors:
1) Random environment  which describes a “state of Nature”; and, given the realization of
which describes a “state of Nature”; and, given the realization of 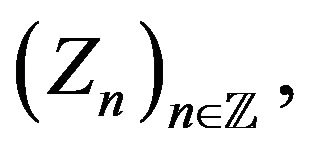
2) The “intrinsic” randomness of systems’ characteristics which is captured by the random variables 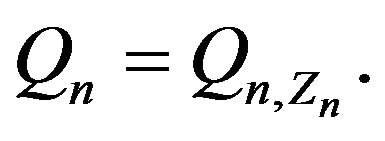
Note that when 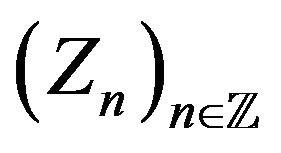 is a finite Markov chain,
is a finite Markov chain,
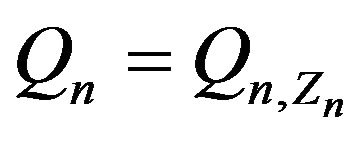 is a Hidden Markov Model. See, for instance, [15] for a survey of HMM and their applications. Heavy tailed HMM as random coefficients of multivariate linear time-series models have been considered, for instance, in [16,17]. In the context of financial time series,
is a Hidden Markov Model. See, for instance, [15] for a survey of HMM and their applications. Heavy tailed HMM as random coefficients of multivariate linear time-series models have been considered, for instance, in [16,17]. In the context of financial time series, 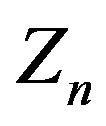 can be interpreted as an exogenous factor determined by the current state of the underlying economy. The environment changes due to seasonal effects, response to the news, dynamics of the market, etc. When
can be interpreted as an exogenous factor determined by the current state of the underlying economy. The environment changes due to seasonal effects, response to the news, dynamics of the market, etc. When 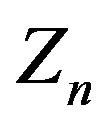 is a function of the state of a Markov chain, stochastic difference Equation (1) is a formal analogue of the Langevin equation with regime switches, which was studied in [18]. The notion of regime shifts or regime switches traces back to [19,20], where it was proposed in order to explain the cyclical feature of certain macroeconomic variables.
is a function of the state of a Markov chain, stochastic difference Equation (1) is a formal analogue of the Langevin equation with regime switches, which was studied in [18]. The notion of regime shifts or regime switches traces back to [19,20], where it was proposed in order to explain the cyclical feature of certain macroeconomic variables.
In this paper we consider 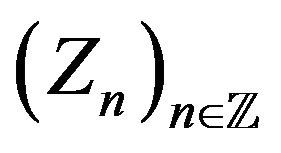 that belong to the following class of random processes:
that belong to the following class of random processes:
Definition 2 ([21]). A C-chain is a stationary random process  taking values in a finite set (alphabet)
taking values in a finite set (alphabet)
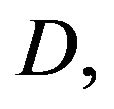 such that the following holds:
such that the following holds:
i) For any 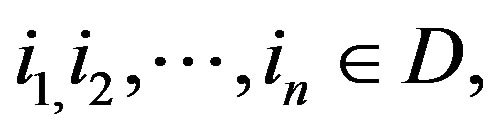

ii) For any 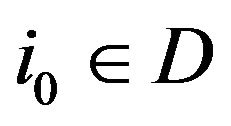 and any sequence
and any sequence 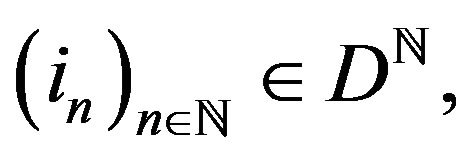 the following limit exists:
the following limit exists:

where the right-hand side is a regular version of the conditional probabilities.
iii) Let
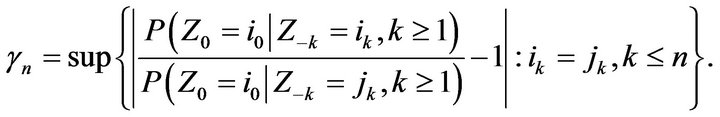
Then, 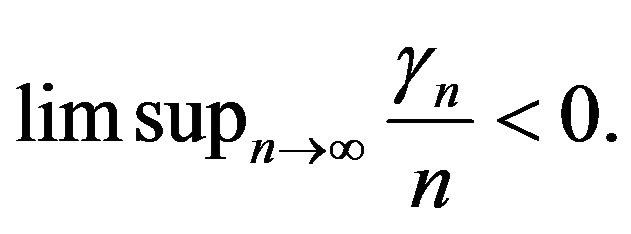
C-chains form an important subclass of chains with complete connections/chains of in-finite order [22-24]. They can be described as exponentially mixing full shifts, and alternatively defined as an essentially unique random process with a given transition function (g-measure) 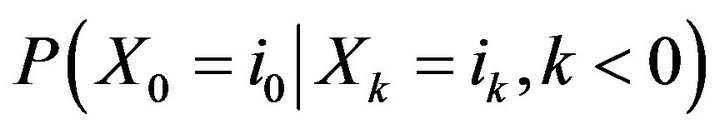 [25]. Stationary distributions of these processes are Gibbs states in the sense of Bowen
[25]. Stationary distributions of these processes are Gibbs states in the sense of Bowen
[21,26]. For any C-chain 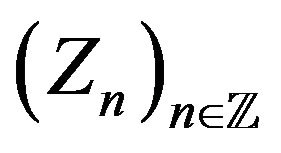 there exists a Markovian representation [21,25], that is a stationary irreducible Markov chain
there exists a Markovian representation [21,25], that is a stationary irreducible Markov chain 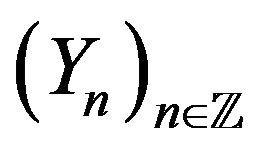 in a countable state space and a function
in a countable state space and a function  such that
such that 
where 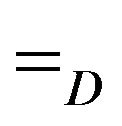 means equivalence of distributions. Chains of infinite order are well-suited for modeling of long range-dependence with fading memory, and in this sense constitute a natural generalization of finite-state Markov chains [24,27-30].
means equivalence of distributions. Chains of infinite order are well-suited for modeling of long range-dependence with fading memory, and in this sense constitute a natural generalization of finite-state Markov chains [24,27-30].
We will further assume that the vectors 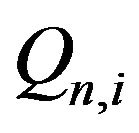 are multivariate regularly varying. Recall that, for
are multivariate regularly varying. Recall that, for  a function
a function 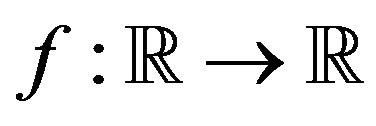 is said to be regularly varying of index
is said to be regularly varying of index ![]() if
if 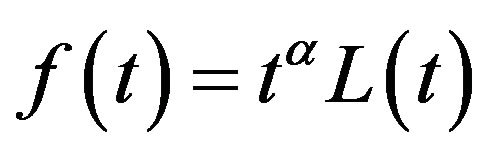 for some function
for some function
 such that
such that 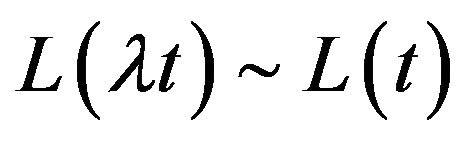 for any positive real
for any positive real  (i.e.,
(i.e., ![]() is a slowly varying function). Let
is a slowly varying function). Let

Definition 3 ([31]). A random vector 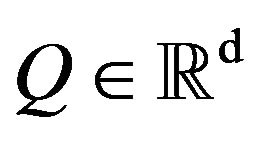 is regularly varying with index
is regularly varying with index 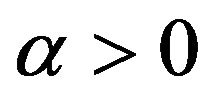 if there exist a function
if there exist a function  regularly varying with index
regularly varying with index 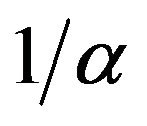 and a Radon measure
and a Radon measure 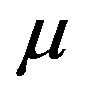 in the space
in the space 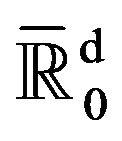 such that
such that
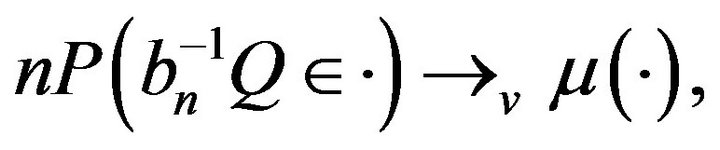 as
as  where
where  denotes the vague convergence and
denotes the vague convergence and 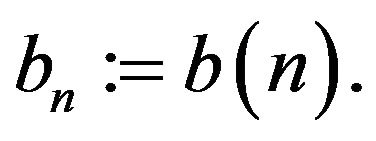
We denote by  the set of all d-vectors regularly varying with index
the set of all d-vectors regularly varying with index  associated with function
associated with function ![]()
The corresponding limiting measure ![]() is called the measure of regular variation associated with
is called the measure of regular variation associated with 
We next summarize our assumptions on the coefficients 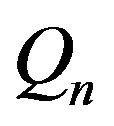 and
and 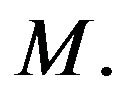 Let
Let  and
and
![]() for, respectively, a vector
for, respectively, a vector 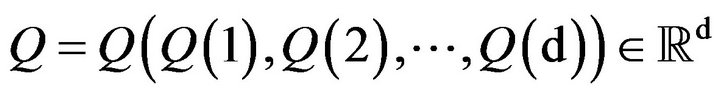 and a
and a  matrix
matrix
Assumption 1. Let 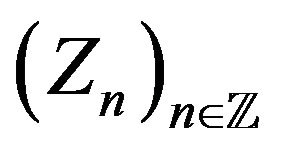 be a stationary C-chain defined on a finite state space
be a stationary C-chain defined on a finite state space  and suppose that
and suppose that 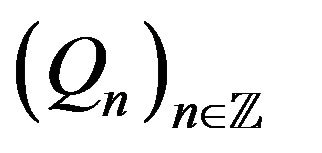 is induced by
is induced by 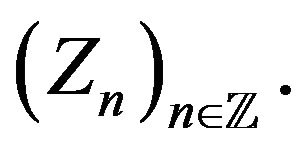 Assume in addition that:
Assume in addition that:
A1) 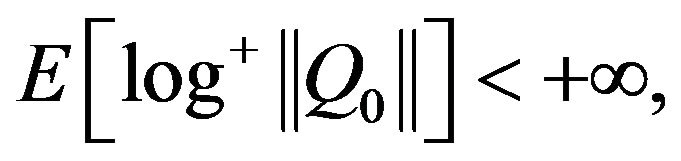 where
where  for
for 
A2) The spectral radius  is strictly between zero and one.
is strictly between zero and one.
A3) There exist a constant 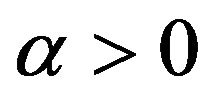 and a regularly varying function
and a regularly varying function 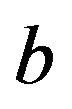 with index
with index  such that for all
such that for all  with associated measure of regular variation
with associated measure of regular variation 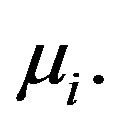
2. Statement of Results
For any (random) initial vector  the series
the series 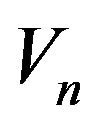 converges in distribution, as
converges in distribution, as 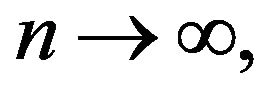 to
to
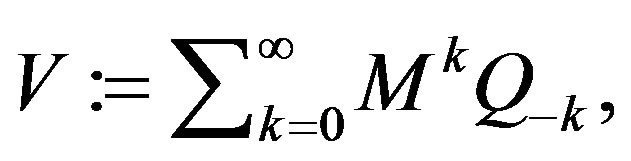
which is the unique initial value making 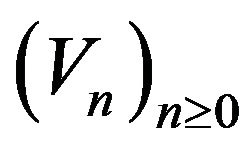 into a stationary sequence [32]. The following result, whose proof is omitted, is a “Gibssian” version of a “Markovian” [16, Theorem 1]. The claim can be established following the line of argument in [16] nearly verbatim, exploiting the Markov representation of C-chains obtained in [21].
into a stationary sequence [32]. The following result, whose proof is omitted, is a “Gibssian” version of a “Markovian” [16, Theorem 1]. The claim can be established following the line of argument in [16] nearly verbatim, exploiting the Markov representation of C-chains obtained in [21].
Theorem 1. Let Assumption 1 hold. Then  with associated measure of regular variation
with associated measure of regular variation
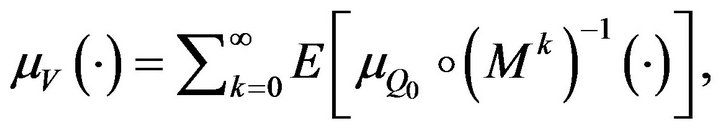
where 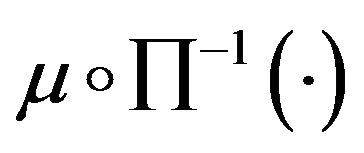 stands for
stands for  and
and 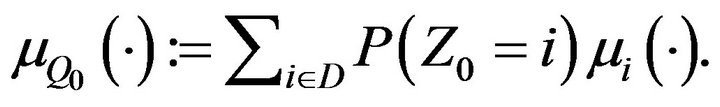
In a slightly more general setting, the existence of the limiting velocity suggests the following law of large numbers, whose short proof is included in Section 3.1.
Theorem 2. Let Assumption 1 hold with A3) being replaced by the condition  Then1
Then1
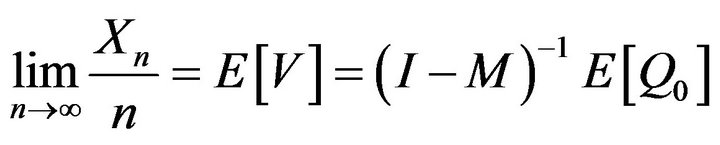 , a.s.
, a.s.
Let ![]() denote independent copies of
denote independent copies of 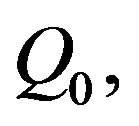 and let be
and let be  a sequence of vectors such that the sequence of processes
a sequence of vectors such that the sequence of processes
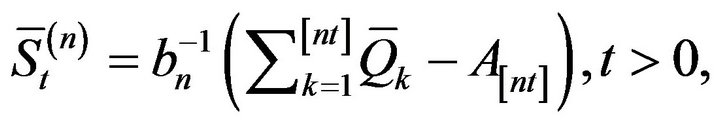
converges in law as ![]() in the Skorokhod space
in the Skorokhod space
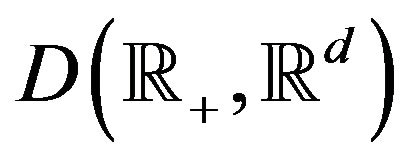 to a Lévy process
to a Lévy process ![]()
where 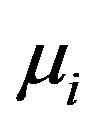 are introduced in A3) with stationary independent increments,
are introduced in A3) with stationary independent increments, 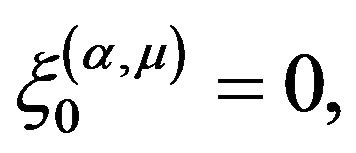 and
and  being distributed according to a stable law of index
being distributed according to a stable law of index ![]() whose domain of attraction includes
whose domain of attraction includes 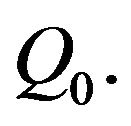 For an explicit form of the centering sequence
For an explicit form of the centering sequence 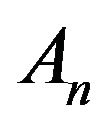 and the characteristic function of
and the characteristic function of 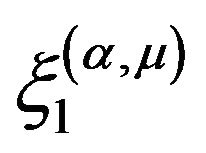 see, for instance, [33] or [34]. Remark that one can set
see, for instance, [33] or [34]. Remark that one can set  if
if 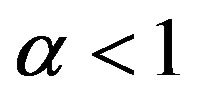 and
and  if
if
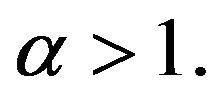 For each
For each 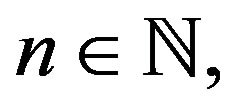 define a process
define a process 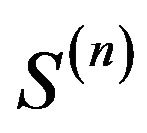 in
in
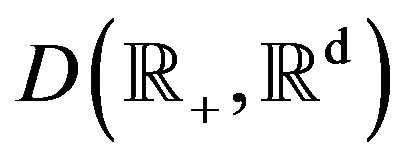 by setting
by setting
 (3)
(3)
Theorem 3. Let Assumption 1 hold with 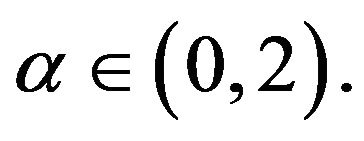 Then the sequence of processes
Then the sequence of processes 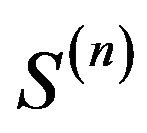 converges weakly in
converges weakly in 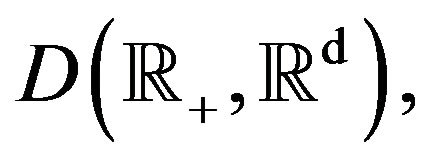 as
as 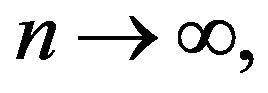 to
to 
It follows from Definition 3 (see, for instance, [31])
that if 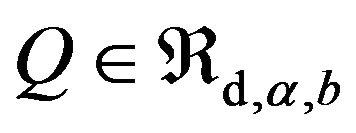 then the following limit exists for any vector
then the following limit exists for any vector 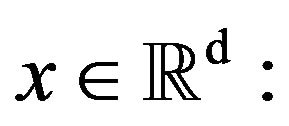
![]() (4)
(4)
Theorem 4. Assume that the conditions of Theorem 3 hold. If 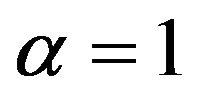 assume in addition that the law of
assume in addition that the law of  is symmetric for any
is symmetric for any  Let
Let 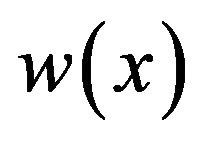 be defined by Equation (4) with
be defined by Equation (4) with  Then, for any
Then, for any 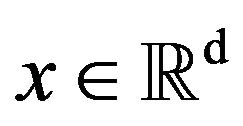 such that
such that 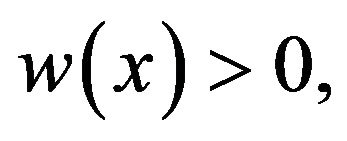 we have
we have
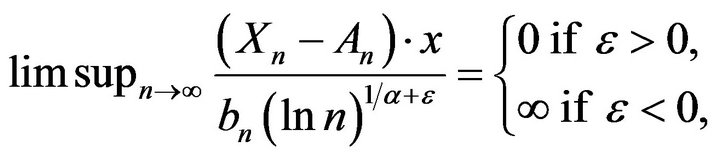 a.s. (5)
a.s. (5)
In particular,
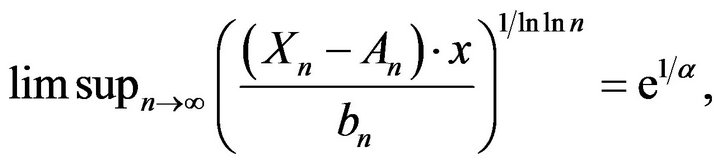 a.s.
a.s.
If either Assumption 1 holds with  or
or
 is assumed instead of A3), then, in view of Equation (6), a Gaussian counterpart of Theorem 3 can be obtained as a direct consequence of general CLTs for uniformly mixing sequences (see, for instance, [35, Theorem 20.1] and [36, Corollary 2]) applied to the sequence
is assumed instead of A3), then, in view of Equation (6), a Gaussian counterpart of Theorem 3 can be obtained as a direct consequence of general CLTs for uniformly mixing sequences (see, for instance, [35, Theorem 20.1] and [36, Corollary 2]) applied to the sequence 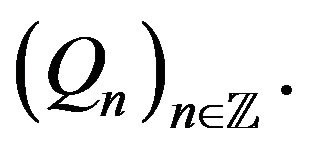 If
If 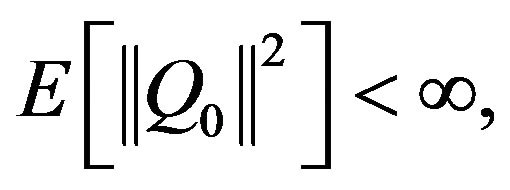 then a law of iterated logarithm in the usual form follows from Equation (5) and, for instance, [37, Theorem 5] applied to the sequence
then a law of iterated logarithm in the usual form follows from Equation (5) and, for instance, [37, Theorem 5] applied to the sequence 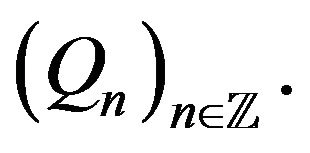
We remark that in the case of i.i.d. additive component 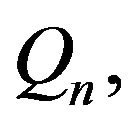 similar to our results are obtained in [7] for a more general than Equation (1) mapping
similar to our results are obtained in [7] for a more general than Equation (1) mapping 
3. Proofs
3.1. Proof of Theorem 2
It follows from the definition of the random walk  and Equation (1) that
and Equation (1) that
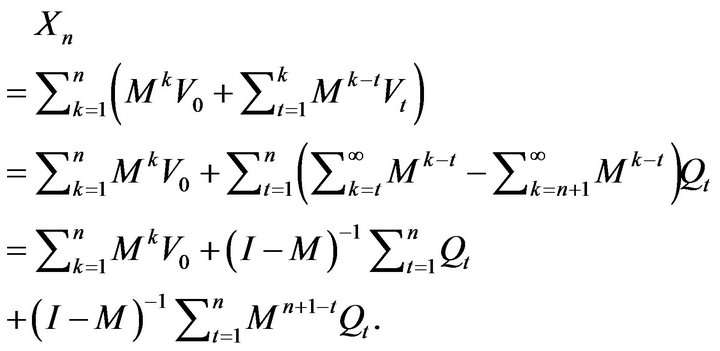 (6)
(6)
Note that  implies
implies
![]()
It follows then from the Borel-Cantelli lemma that
 a.s.
a.s.
Furthermore, we have
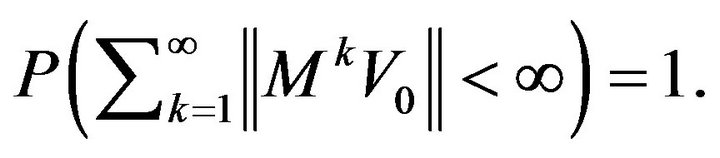
Thus the law of large numbers for 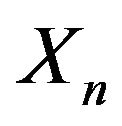 follows from the ergodic theorem applied to the sequence
follows from the ergodic theorem applied to the sequence 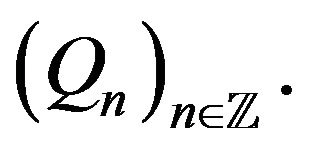 □
□
3.2. Proof of Theorem 3
Only the second term in the right-most side of Equation (5) contributes to the asymptotic behavior of 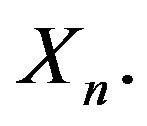 The proof rests on the application of Corollary 5.9 in [34] to the partial sums
The proof rests on the application of Corollary 5.9 in [34] to the partial sums  In view of condition iii) in Definition 2 and the decomposition shown in Equation (6), we only need to verify that the following “local dependence” condition (which is condition (5.13) in [34]) holds for the sequence
In view of condition iii) in Definition 2 and the decomposition shown in Equation (6), we only need to verify that the following “local dependence” condition (which is condition (5.13) in [34]) holds for the sequence 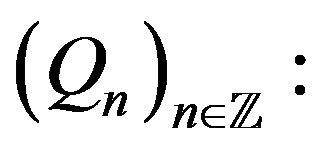
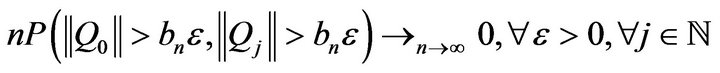
The above convergence to zero follows from the mixing condition iii) in Definition 2 and the regular variation, as t goes to infinity, of the marginal distribution tail
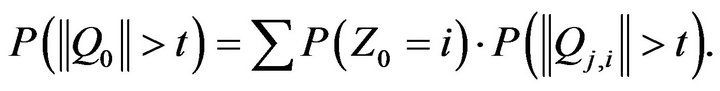 □
□
3.3. Proof of Theorem 4
For  let
let  be the number of occurrences of
be the number of occurrences of  in the set
in the set  That is,
That is,
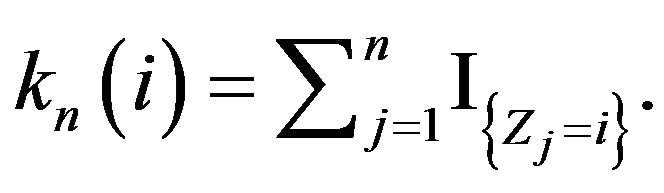
Define recursively 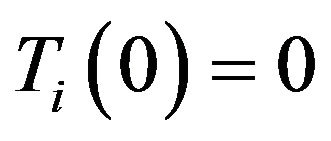 and
and
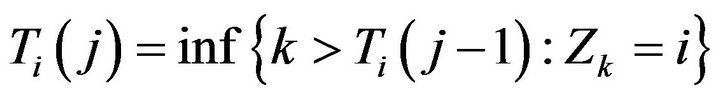
(with the usual convention that the greatest lower bound over an empty set is equal to infinity). For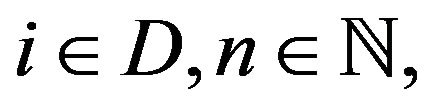 let
let
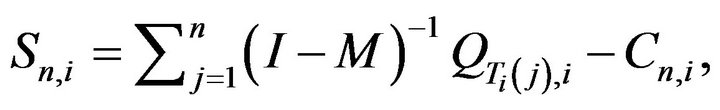
where
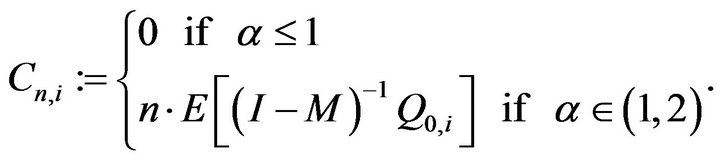
Denote
![]()
Further, for each 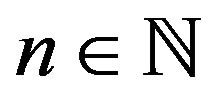 let
let 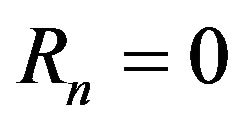 if
if 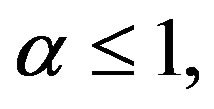 whereas if
whereas if 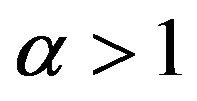 let
let
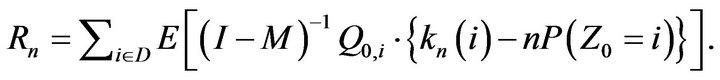
Then  and hence
and hence

It follows from the decomposition given by Equation (6) along with the Borel-Cantelli lemma that for any 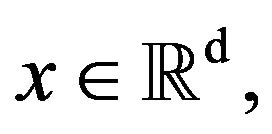
 a.s.
a.s.
Let 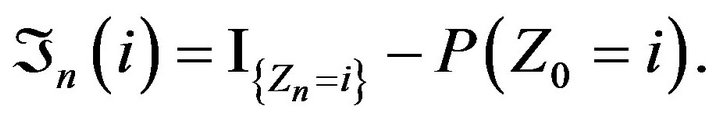 Then
Then
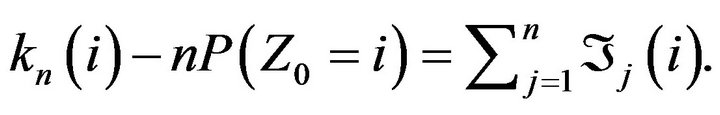
It follows, for instance, from Theorem 5 in [37] that if  then for any
then for any 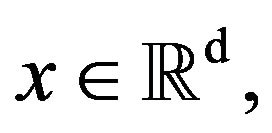 the following limit exists and the identity holds with probability one:
the following limit exists and the identity holds with probability one:
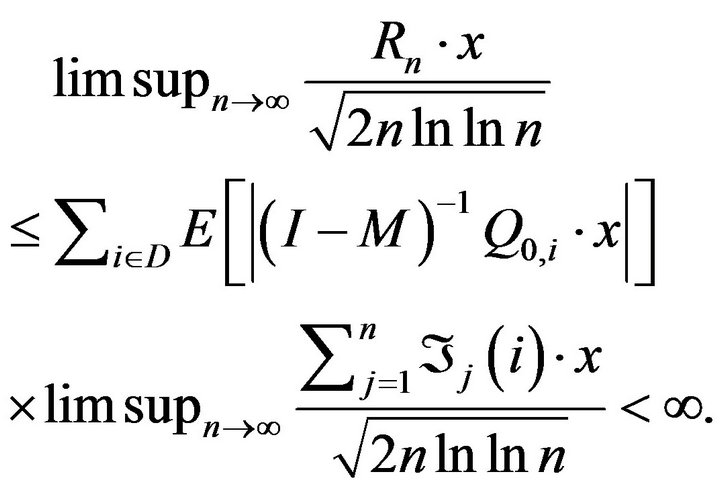
Therefore (since  is regularly varying with index
is regularly varying with index ), in order to complete the proof Theorem 4 it suffices to show that for any
), in order to complete the proof Theorem 4 it suffices to show that for any  that satisfies the condition
that satisfies the condition 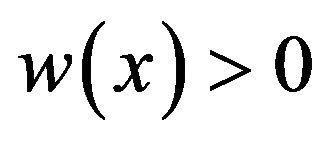 of the theorem, we have
of the theorem, we have
 a.s.
a.s.
We first observe that by the law of iterated logarithm for heavy-tailed i.i.d. sequences (see Theorems 1.6.6 and 3.9.1 in [33]),
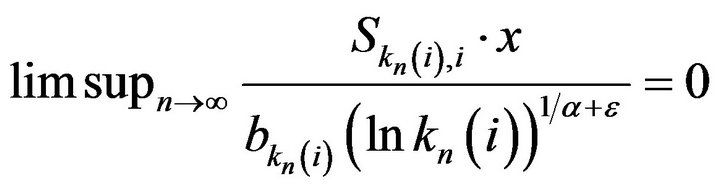 , a.s.
, a.s.
for any 
 and
and  Since by the ergodic theorem,
Since by the ergodic theorem,
![]() a.s.this yields
a.s.this yields
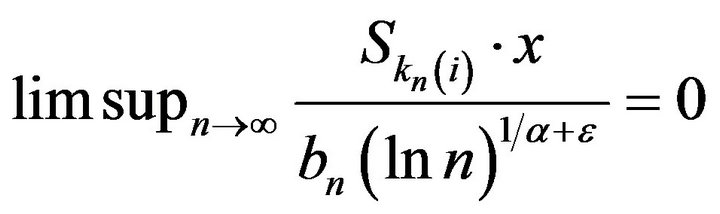 , a.s.and hence
, a.s.and hence
 , a.s.
, a.s.
On the other hand, if 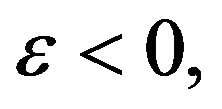 Theorem 3.9.1 in [33] implies that for any
Theorem 3.9.1 in [33] implies that for any  and any
and any  such that
such that 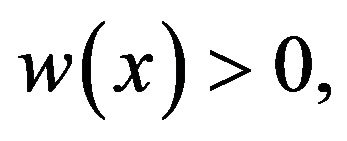 we have
we have
 a.s.
a.s.
To conclude the proof of the theorem it thus remains to show that for any 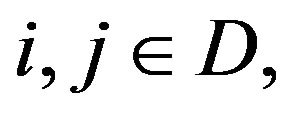 any
any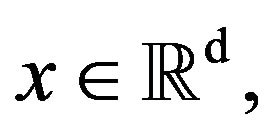 and all
and all 
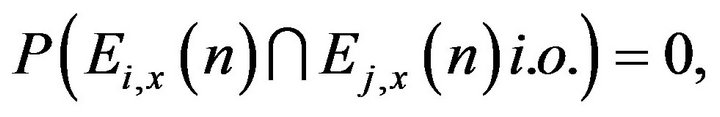 (7)
(7)
where, for  the events
the events 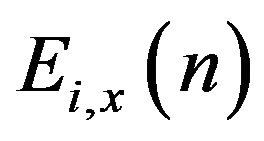 are defined as follows:
are defined as follows:
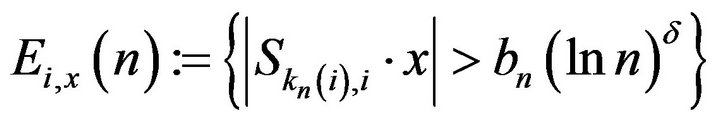 .
.
For  let
let 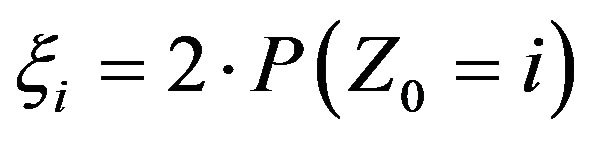 and define
and define
 .
.
Then
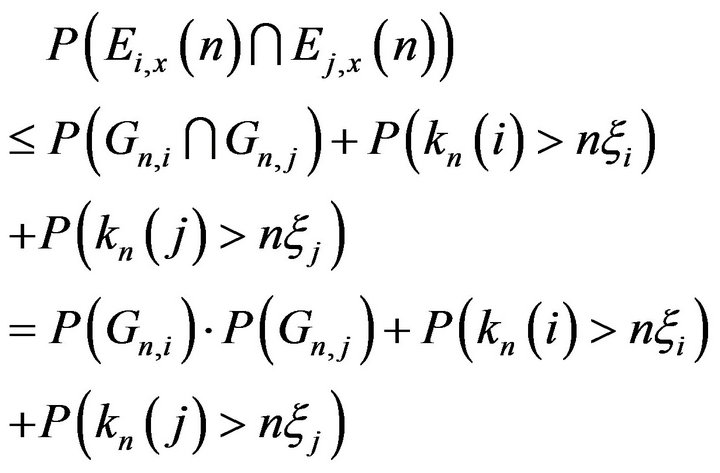
The Ruelle-Perron-Frobenius theorem (see [26]) implies that the sequence 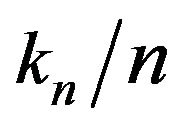 satisfies the large deviation principle (by the Gärtner-Ellis theorem), and hence
satisfies the large deviation principle (by the Gärtner-Ellis theorem), and hence
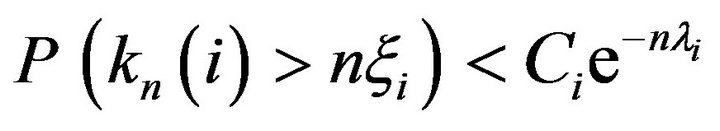 for some constants
for some constants 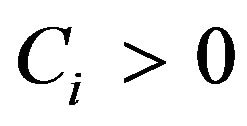
and 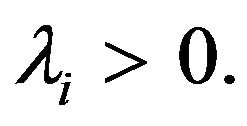 Furthermore, for any
Furthermore, for any 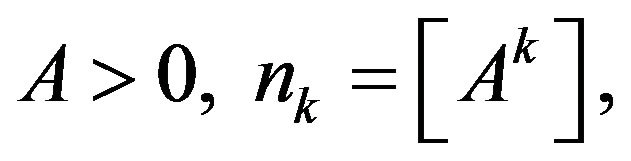
and 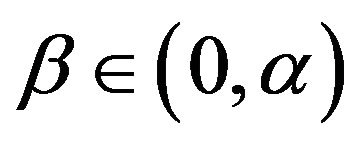 there exists a constant
there exists a constant  such that (see [33, p. 177]),
such that (see [33, p. 177]), 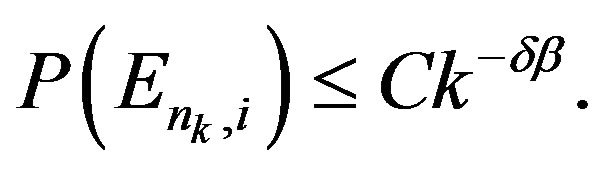 Therefore, since
Therefore, since 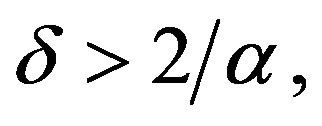 we can choose
we can choose  such that
such that  with suitable
with suitable 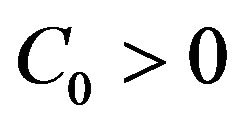
and 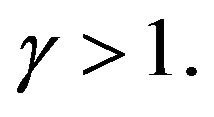 A standard argument using the Borel-Cantelli lemma imply then the identity in Equation (7). □
A standard argument using the Borel-Cantelli lemma imply then the identity in Equation (7). □
REFERENCES
- W. T. Coffey, Yu. P. Kalmykov and J. T. Waldron, “The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering,” 2nd Edition, World Scientific Series in Contemporary Chemical Physics, Vol. 14, World Scientific Publishing Company, Singapore City, 2004.
- N. G. Van Kampen, “Stochastic Processes in Physics and Chemistry,” 3th Edition, North-Holland Personal Library, Amsterdam, 2003.
- O. E. Barndorff-Nielsen and N. Shephard, “Non-Gaussian Ornstein-Uhlenbeck-Based Models and Some of Their Uses in Financial Economics (with Discussion),” Journal of the Royal Statistical Society: Series B (Statistical Methodology), Vol. 63, No. 2, 2001, pp. 167-241. doi:10.1111/1467-9868.00282
- S. C. Kou and X. S. Xie, “Generalized Langevin Equation with Fractional Gaussian Noise: Sub-Diffusion within a Single Protein Molecule,” Physical Review Letters, Vol. 93, 2004, Article ID: 18.
- D. Buraczewski, E. Damek and M. Mirek, “Asymptotics of Stationary Solutions of Multivariate Stochastic Recursions with Heavy Tailed Inputs and Related Limit Theorems,” Stochastic Processes and Their Applications, Vol. 122, No. 1, 2012, pp. 42-67. doi:10.1016/j.spa.2011.10.010
- H. Larralde, “A First Passage Time Distribution for a Discrete Version of the Ornstein-Uhlenbeck Process,” Journal of Physics A, Vol. 37, No. 12, 2004, pp. 3759- 3767. doi:10.1088/0305-4470/37/12/003
- H. Larralde, “Statistical Properties of a Discrete Version of the Ornstein-Uhlenbeck Process,” Physical Review E, Vol. 69, 2004, Article ID: 027102.
- E. Renshaw, “The Discrete Uhlenbeck-Ornstein Process,” Journal of Applied Probability, Vol. 24, No. 4, 1987, pp. 908-917. doi:10.2307/3214215
- M. Lefebvre and J.-L. Guilbault, “First Hitting Place Probabilities for a Discrete Version of the OrnsteinUhlenbeck Process,” International Journal of Mathematics and Mathematical Sciences, Vol. 2009, 2009, Article ID: 909835.
- A. Novikov and N. Kordzakhia, “Martingales and First Passage Times of AR(1) Sequences,” Stochastics, Vol. 80, No. 2-3, 2008, pp. 197-210. doi:10.1080/17442500701840885
- P. Embrechts and C. M. Goldie, “Perpetuities and Random Equations,” Proceedings of 5th Prague Symposium, Physica, Heidelberg, 1993, pp. 75-86.
- R. F. Engle, “ARCH. Selected Readings,” Oxford University Press, Oxford, 1995.
- S. T. Rachev and G. Samorodnitsky, “Limit Laws for a Stochastic Process and Random Recursion Arising in Probabilistic Modelling,” Advances in Applied Probability, Vol. 27, No. 1, 1995, pp. 185-202.
- W. Vervaat, “On a Stochastic Difference Equations and a Representation of Non-Negative Infinitely Divisible Random Variables,” Advances in Applied Probability, Vol. 11, No. 4, 1979, pp. 750-783. doi:10.2307/1426858
- Y. Ephraim and N. Merhav, “Hidden Markov Processes,” IEEE Transactions on Information Theory, Vol. 48, No. 6, 2002, pp. 1518-1569. doi:10.1109/TIT.2002.1003838
- D. Hay, R. Rastegar and A. Roitershtein, “Multivariate Linear Recursions with Markov-Dependent Coefficients,” Journal of Multivariate Analysis, Vol. 102, No. 3, 2011, pp. 521-527. doi:10.1016/j.jmva.2010.10.011
- R. Stelzer, “Multivariate Markov-Switching ARMA Processes with Regularly Varying Noise,” Journal of Multivariate Analysis, Vol. 99, No. 6, 2008, pp. 1177-1190. doi:10.1016/j.jmva.2007.07.001
- P. Eloe, R. H. Liu, M. Yatsuki, G. Yin and Q. Zhang, “Optimal Selling Rules in a Regime-Switching Exponential Gaussian Diffusion Model,” SIAM Journal of Applied Mathematics, Vol. 69, No. 3, 2008, pp. 810-829. doi:10.1137/060652671
- E. F. Fama, “The Behavior of Stock Market Prices,” Journal of Business, Vol. 38, No. 1, 1965, pp. 34-105. doi:10.1086/294743
- J. D. Hamilton, “A New Approach to the Economic Analysis of Non-Stationary Time Series and the Business Cycle,” Econometrica, Vol. 57, No. 2, 1989, pp. 357-384. doi:10.2307/1912559
- S. Lalley, “Regenerative Representation for One-Dimensional Gibbs States,” Annals of Probability, Vol. 14, No. 4, 1986, pp. 1262-1271. doi:10.1214/aop/1176992367
- R. Fernández and G. Maillard, “Chains with Complete Connections and One-Dimensional Gibbs Measures,” Electronic Journal of Probability, Vol. 9, 2004, pp. 145- 176. doi:10.1214/EJP.v9-149
- R. Fernández and G. Maillard, “Chains with Complete Connections: General Theory, Uniqueness, Loss of Memory and Mixing Properties,” Journal of Statistical Physics, Vol. 118, No. 3-4, 2005, pp. 555-588. doi:10.1007/s10955-004-8821-5
- M. Iosifescu and S. Grigorescu, “Dependence with Complete Connections and Its Applications,” Cambridge Tracts in Mathematics, Vol. 96, Cambridge University Press, Cambridge, 2009.
- H. Berbee, “Chains with Infinite Connections: Uniqueness and Markov Representation,” Probability Theory and Related Fields, Vol. 76, No. 2, 1987, pp. 243-253. doi:10.1007/BF00319986
- R. Bowen, “Equillibrium States and the Ergodic Theory of Anosov Diffeomorthisms,” Lecture Notes in Mathematics, Vol. 470, Springer, Berlin, 1975.
- F. Comets, R. Fernández and P. A. Ferrari, “Processes with Long Memory: Regenerative Construction and Perfect Simulation,” Annals of Applied Probability, Vol. 12, No. 3, 2002, pp. 921-943. doi:10.1214/aoap/1031863175
- A. Galves and E. Lӧcherbach, “Stochastic Chains with Memory of Variable Length,” TICSP Series, Vol. 38, 2008, pp. 117-133.
- J. Rissanen, “A Universal Data Compression System,” IEEE Transactional on Information Theory, Vol. 29, No. 5, 1983, pp. 656-664. doi:10.1109/TIT.1983.1056741
- R. Vilela Mendes, R. Lima and T. Araújo, “A ProcessReconstruction Analysis of Market Fluctuations,” International Journal of Theoretical Applied Finance, Vol. 5, No. 8, 2002, pp. 797-821. doi:10.1142/S0219024902001730
- S. I. Resnick, “On the Foundations of Multivariate Heavy Tail Analysis,” Journal of Applied Probability, Vol. 41, 2004, pp. 191-212. doi:10.1239/jap/1082552199
- A. Brandt, “The Stochastic Equation
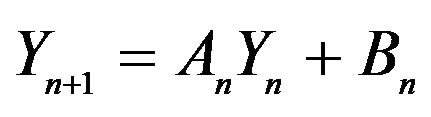 with Stationary Coefficients,” Advances in Applied Probability, Vol. 18, No. 1, 1986, pp. 211-220. doi:10.2307/1427243
with Stationary Coefficients,” Advances in Applied Probability, Vol. 18, No. 1, 1986, pp. 211-220. doi:10.2307/1427243 - A. A. Borovkov and K. A. Borovkov, “Asymptotic Analysis of Random Walks: Heavy-Tailed Distributions,” Encyclopedia of Mathematics and Its Applications, Vol. 118, Cambridge University Press, Cambridge, 2008.
- M. Kobus, “Generalized Poisson Distributions as Limits for Sums of Arrays of Dependent Random Vectors,” Journal of Multivariate Analysis, Vol. 52, No. 2, 1995, pp. 199-244. doi:10.1006/jmva.1995.1011
- P. Billingsley, “Convergence of Probability Measures,” John Wiley & Sons, New York, 1968.
- Z. S. Szewczak, “A Central Limit Theorem for Strictly Stationary Sequences in Terms of Slow Variation in the Limit,” Probability and Mathematical Statistics, Vol. 18, No. 2, 1998, pp. 359-368.
- H. Oodaria and K. Yoshihara, “The Law of the Iterated Logarithm for Stationary Processes Satisfying Mixing Conditions,” Kodai Mathematical Seminar Reports, Vol. 23, No. 3, 1971, pp. 311-334. doi:10.2996/kmj/1138846370

