Applied Mathematics
Vol.3 No.10(2012), Article ID:23378,4 pages DOI:10.4236/am.2012.310165
Absolutely Stable of Takagi-Sugeno Fuzzy Control System by Using Popov’s Criterion
Department of Mathematics, Payame Noor University, Tehran, Iran
Email: asad8700@gmail.com, soleymanpoor@phd.pnu.ac.ir, a_heidari@pnu.ac.ir, aghilehheydari@yahoo.com
Received August 14, 2012; revised September 14, 2012; accepted September 21, 2012
Keywords: Fuzzy Control; Fuzzy Systems; Popov’s Criterion
ABSTRACT
In this paper, we presented a sufficient condition on the frequency domain for the absolutely stable analysis of the Takagi-Sugeno (T-S)fuzzy control system, based on the Popov’s criterion. we use some numerical examples to illustrate the efficiency of frequency domain-based condition.
1. Introduction
Among various fuzzy modeling themes, the Takagi-Sugeno (T-S) model [1] has been one of the most popular modeling frameworks. T-S fuzzy models can be as universal approximator then any smooth nonlinear control systems cab be approximated by T-S fuzzy models and also any smooth nonlinear state feedback controller can be approximated by the parallel distributed compensation (PDC) controller [2]. The predictive controller and T-S model-based linearization controller are, respectively, studied in [3,4]. However,most of these results are in the time domain instead of frequency domain.
On the other hand, the frequency response methods have been well developed and widely used in industrial applications with many advantages. for instance, the effect of noise in a control system can be evaluated in a straightforward way by its frequency response. In addition, Bode and Nyquist plots, which are often used in the frequency response methods, can also provide a graphic insight into the control system under investigation.
Stability is one of the most important nocepts concerning the design of control strategies. In [5] the stability of the Mamdani fuzzy control system is explored based on the Popov’s criterion, which is a frequency domain-based sufficient condition, so as to guarantee the stability of nonlinear feedback systems. Popov’s criterion is a frequency response method and it evaluate absolutely stable for a system that the forward path is a linear timeinvariant system, and the feedback part is a memoryless nonlinearity. In this paper, Popov’s criterion is utilized to drive the frequency domain-based sufficient condition, which provide a graphical interpretation for the stability analysis of the T-S fuzzy control systems.
2. Absolute Stability
The systems considered in this work have the interesting structure shown in Figure 1. The forward path is a linear time-invariant system, and the feedback part is a memoryless nonlinearity, i.e., a nonlinear static mapping.
The equations of such systems can be written as:
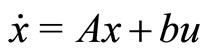 (1)
(1)
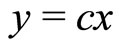 (2)
(2)
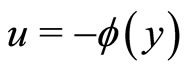 (3)
(3)
where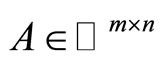 ,
,  ,
,  and
and . G(p) is transfer function for linear system of
. G(p) is transfer function for linear system of . The nonlinear system (1)-(3) has various physical applications. The nonlinear system in Figure 1 has a special structure. If the feedback path simply contains a constant gain, i.e.,
. The nonlinear system (1)-(3) has various physical applications. The nonlinear system in Figure 1 has a special structure. If the feedback path simply contains a constant gain, i.e., 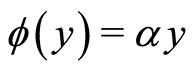 , then the stability of the whole system, a linear feedback system, can be simply determined by examining the eigenvalues of the closed-loop system matrix
, then the stability of the whole system, a linear feedback system, can be simply determined by examining the eigenvalues of the closed-loop system matrix . However, the stability analysis of the whole system with an arbitrary nonlinear feedback function
. However, the stability analysis of the whole system with an arbitrary nonlinear feedback function 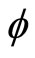 is much more difficult. for using Popov’s criterion we usually require the nonlinearity to satisfy a so-called sector condition, whose definition is given below [6,7].
is much more difficult. for using Popov’s criterion we usually require the nonlinearity to satisfy a so-called sector condition, whose definition is given below [6,7].
Definition 1. A continuous function 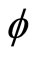 is said to belong to the sector
is said to belong to the sector , if there exists two nonnegative numbers
, if there exists two nonnegative numbers 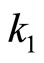 and
and  such that
such that
 (4)
(4)
Geometricaly, condition (4) implies that the nonlinear function always lies between the two straight lines 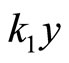 and
and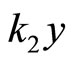 . Two properties are implied by Equation (4).
. Two properties are implied by Equation (4).
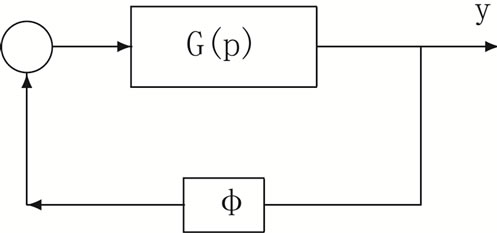
Figure 1. System structure in absolute stability problems.
First, it implies that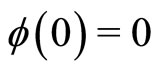 . Secondly, it implies that
. Secondly, it implies that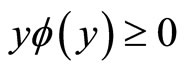 , such that the graph of
, such that the graph of 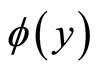 lies in the first and third quadrants. Assume that both the nonlinearity
lies in the first and third quadrants. Assume that both the nonlinearity 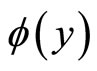 is a function belonging to the sector
is a function belonging to the sector 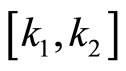 and that the
and that the 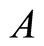 matrix of the linear subsystem in the forward path is stable (Hurwitz matrix). What additional constraints are needed to guarantee the stability of the whole system?
matrix of the linear subsystem in the forward path is stable (Hurwitz matrix). What additional constraints are needed to guarantee the stability of the whole system?
Definition 2. If the piont 0 (origin) is globally asymptotically stable for all nonlinearitys that belong to the sector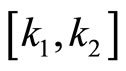 , Then system in Figure 1 by equations of (1), (2) and (3) will be absolute stability.
, Then system in Figure 1 by equations of (1), (2) and (3) will be absolute stability.
We will see that Popov’s criterion creat conditions for asymptotic stability.
Popov’s Criterion
Many researchers attempted to seek conditions that guarantee the stability of the nonlinear system in Figure 1. Popov’s criterion imposes additional conditions on the linear subsystem, leading to a sufficient condition for asymptotic stability reminiscent of Nyquist’s criterion(a necessary and sufficient condition) in linear system analysis.
A number of versions have been developed for Popov’s criterion [7]. The following basic version is fairly simple and useful.
Theorem 1. If the system described by (1), (2) and (3) satisfies the conditions:
• The matrix  is Hurwitz (i.e., has all its eigenvalus strictly in the left half-plan)and the pair
is Hurwitz (i.e., has all its eigenvalus strictly in the left half-plan)and the pair  is controllable.
is controllable.
• The nonlinearity  belongs to the sector
belongs to the sector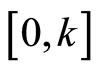 .
.
• 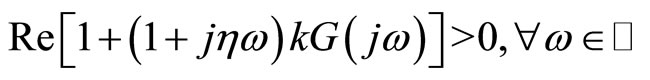 is equivalent:
is equivalent:
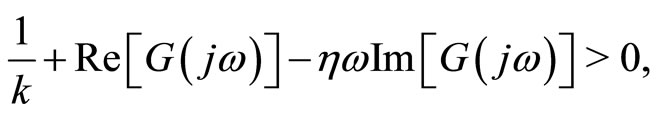
 (Popov’s inequality)(5)
(Popov’s inequality)(5)
then the point 0 is globally asymptotically stable.
Proof. see [7].
Remark 1. If 
and 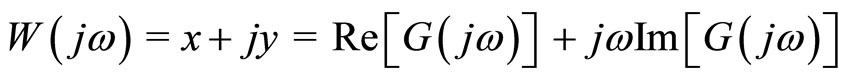
then inequality (5) is equivalent that the polar plot of 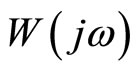 be below the line
be below the line .
.
3. The T-S Fuzzy Control System
Let us consider  in Figure 2 which can be described by the following state model:
in Figure 2 which can be described by the following state model:
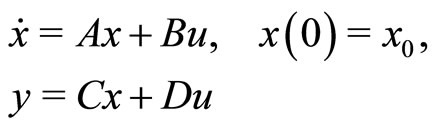 (6)
(6)
where ,
, 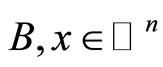 , and
, and . D is a scalar. We assume that the pair
. D is a scalar. We assume that the pair 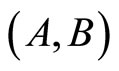 is controllable, i.e.,
is controllable, i.e.,  , and that the pair
, and that the pair 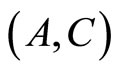 is observable, i.e.,
is observable, i.e.,
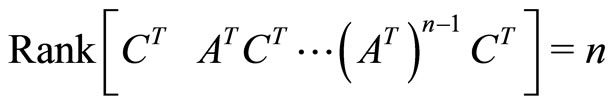 .
.
The T-S fuzzy controller consists of the following two rules (Figure 2):
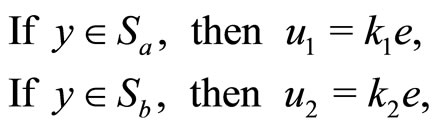
where both  and
and  are controller inputs, and
are controller inputs, and ,
, 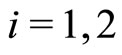 , are the outputs of the two local proportional controllers. Then by using the center-of-gravity method for defuzzification, We can represent the
, are the outputs of the two local proportional controllers. Then by using the center-of-gravity method for defuzzification, We can represent the  vector controller as:
vector controller as:
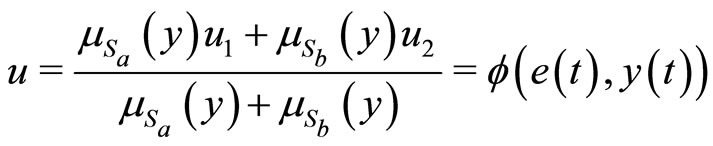 (7)
(7)
We use the triangular membership functions 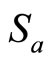 and
and  of the following form (Figure 3):
of the following form (Figure 3):
where both 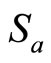 and
and  are given by the following equations:
are given by the following equations:
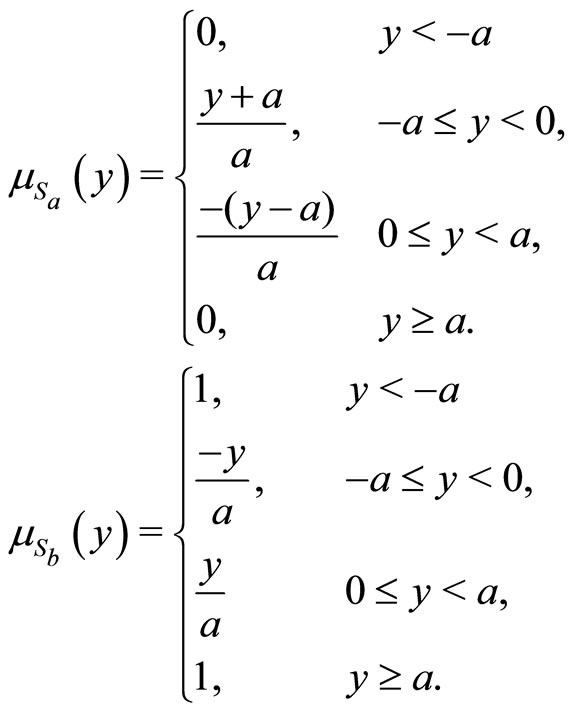 (8)
(8)
We assume that ,
,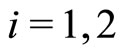 which are the proportional gains of the local controllers, are positive and
which are the proportional gains of the local controllers, are positive and . If both
. If both 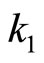 and
and  to be negative then we can recast the nonlinear system by an equivalent system according to Theorem 2. In this case the local proportional gains can be made positive with the plant multiplied by
to be negative then we can recast the nonlinear system by an equivalent system according to Theorem 2. In this case the local proportional gains can be made positive with the plant multiplied by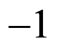 .
.
Theorem 2. Two Systems in Figures 2 and 4 are equivalent.
Proof. We first observe that from (7) and (8) we have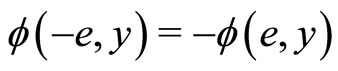 . For example, when
. For example, when , we have:
, we have:
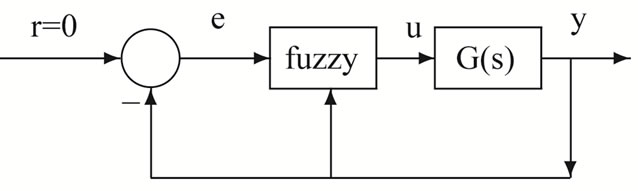
Figure 2. Structure of T-S system.
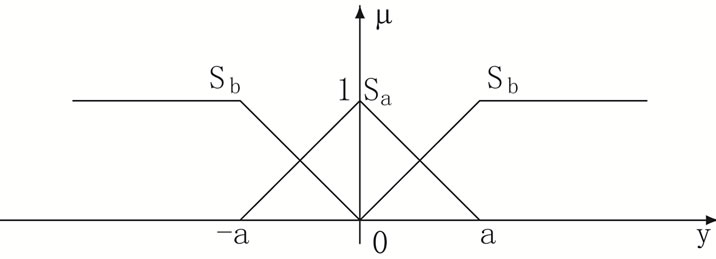
Figure 3. The membership functions of Sa and Sb.
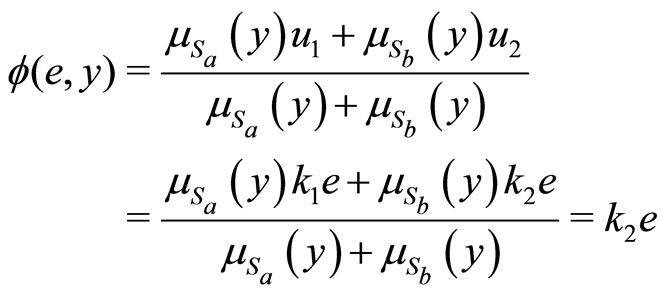
It is clear that:
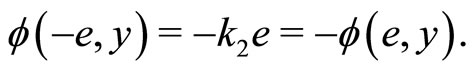
from Figure 2, we observe that:
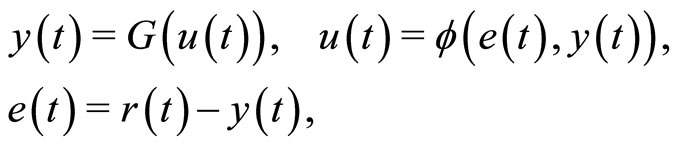 (9)
(9)
equations in (9) are equivalent the following equations:
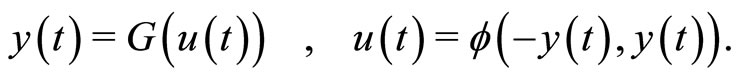 (10)
(10)
from , we get:
, we get:
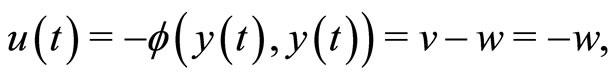 (11)
(11)
 in (11) is equivalent
in (11) is equivalent 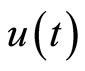 in Figure 3 and
in Figure 3 and 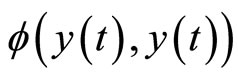 represents the functional mapping achived by the following fuzzy rules:
represents the functional mapping achived by the following fuzzy rules:

Then Two Systems in Figures 2 and 3 are equivalent.
Therefore, if the functional mapping achieved by the T-S fuzzy controller belongs to some sector, then Popov’s criterion can be employed directly.
Theorem 3. Let 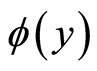 denote the mapping of the T-S fuzzy control system in Figure 3, i.e.,
denote the mapping of the T-S fuzzy control system in Figure 3, i.e.,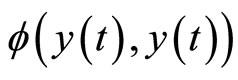 . Then
. Then  belong to the sector
belong to the sector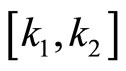 .
.
Proof. from relation 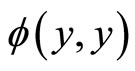 we have:
we have:
 (12)
(12)
We know, 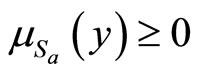 and
and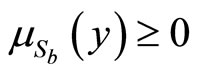 . Consequently, with the assumption that
. Consequently, with the assumption that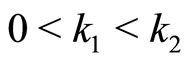 , we have:
, we have:
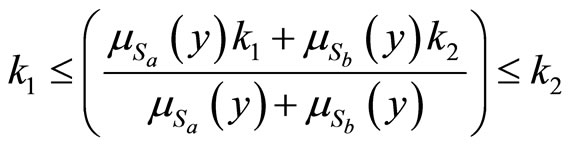
If multiply 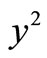 to the last inequality then we have
to the last inequality then we have .
.
Theorem 4. Let 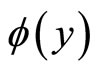 denote the mapping of the T-S fuzzy control system in Figure 3, i.e.,
denote the mapping of the T-S fuzzy control system in Figure 3, i.e., . Then
. Then 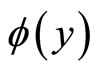 belong to the sector
belong to the sector  where
where  .
.
Proof. clearly we have:

and also it is obvious that:

Then 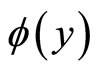 belongs to the sector
belongs to the sector 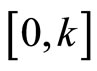 where
where .
.
Numerical Applications
As an example we consider a stable plant 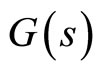 is described by:
is described by:
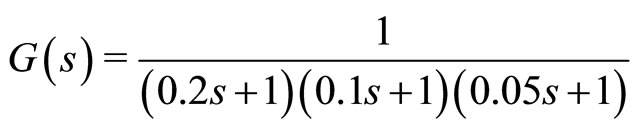 (13)
(13)
We obtain proportional gains  and
and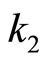 , based on the Bode plot of
, based on the Bode plot of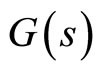 . The Bode plot of
. The Bode plot of 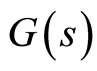 is given in the Figure 5. When the phase magnitudes are
is given in the Figure 5. When the phase magnitudes are  and
and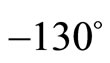 , the corresponding log magnitudes are
, the corresponding log magnitudes are  and
and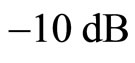 , respectively. Then
, respectively. Then 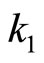 and
and 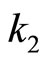 are:
are:

Phase margins of open loop for gains 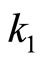 and
and 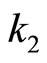 are, respectively
are, respectively  and
and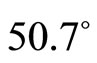 . Next, the T-S fuzzy con-
. Next, the T-S fuzzy con-
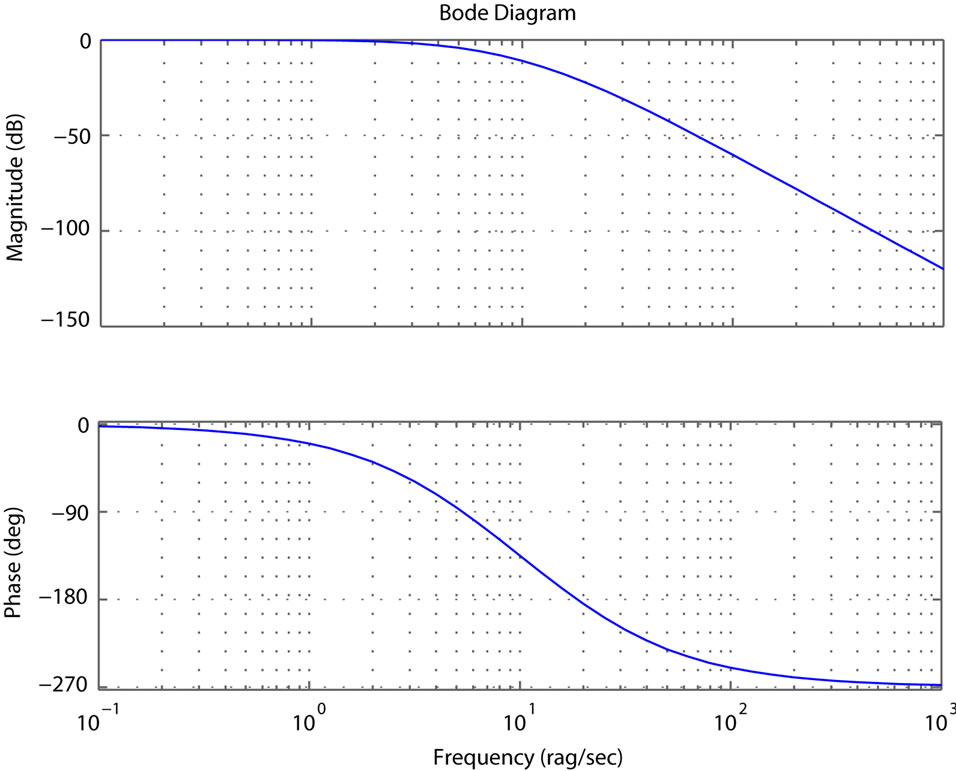
Figure 5. The bode plot of G(s).
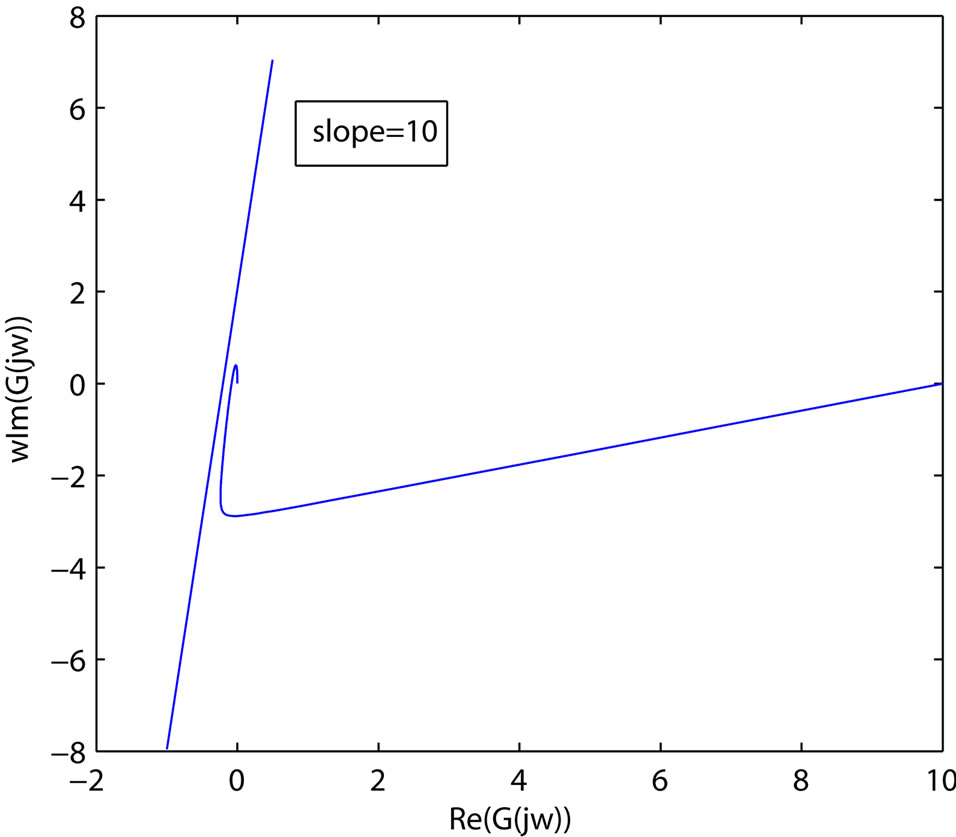
Figure 6. Popov’s plot and line of: y = 10(x + 1/4.89).
troller rules are:

Hear,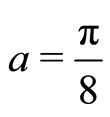 . We shall point out that this is chosen only for convenience. In fact,
. We shall point out that this is chosen only for convenience. In fact, 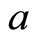 has no effect on the closed-loop stability. Popov’s plot are shown in Figure 6, this figure reveals that the system is stable because Popov’s plot is below line of
has no effect on the closed-loop stability. Popov’s plot are shown in Figure 6, this figure reveals that the system is stable because Popov’s plot is below line of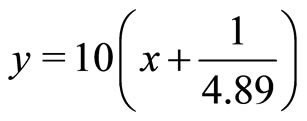 . Popov’s plot is obtained for
. Popov’s plot is obtained for . but for
. but for 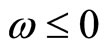 is the same, because functions of
is the same, because functions of 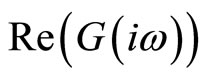 and
and 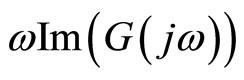 are even functions.
are even functions.
4. Conclusion
In this paper, we presented a condition on the frequency domain for the global stability analysis of the T-S fuzzy control system based on the Popov’s criterion and it’s graphical interpretation. We said T-S fuzzy control system can be like to system of Figure 1, Then Popov’s criterion imposes conditions for stability. We conclude T-S fuzzy control system in the Figure 2 is absolute stable.
REFERENCES
- T. Takagi and Sugeno, “Fuzzy Identification of Systems and Its Applications to Modeling and Control,” IEEE Transactions on Systems, Man, and Cybernet, Vol. 15, 1985, pp. 116-132. doi:10.1109/TSMC.1985.6313399
- H. O. Wang, J. Li, D. Niemann and Tanaka, “T-S Fuzzy Model with Linear Rule Consequence and PDC Controller: A Universal Framework for Nonlinear Control Systems,” Proceedings of FUZZ-IEEE 2000, San Antonio, 7-10 May 2000, pp. 549-554.
- N. Li, S. Y. Li and Y. G. Xi, “Multi-Model Predictive Control Based on the Takagi-Sugeno Fuzzy Models: A Case Study,” Information Sciences, Vol. 165, No. 3-4, 2004, pp. 247-263. doi:10.1016/j.ins.2003.10.011
- C. W. Park, “LMI-Based Robust Stability Analysis for Fuzzy Feedback Linearization Regulator with Its Applications,” Information Sciences, Vol. 152, 2003, pp. 287- 301. doi:10.1016/S0020-0255(03)00057-4
- A. Kandel, Y. Luo and Y. Q. Zhang, “Stability Analysis of Fuzzy Control Systems,” Fuzzy Sets and Systems, Vol. 105, No. 1, 1999, pp. 33-48. doi:10.1016/S0165-0114(97)00234-0
- J. J. E. Slotine and W. Li, “Applied Nonlinear Control,” Prentice-Hall, New York, 1991.
- H. K. Khalil, “Nonlinear Systems Design and Control,” Vol. 2, 1950.


