Applied Mathematics
Vol.3 No.9(2012), Article ID:22996,7 pages DOI:10.4236/am.2012.39145
Common Fixed Point Theorems for Weakly Compatible Mappings in Fuzzy Metric Spaces Using (JCLR) Property*
1R. H. Government Postgraduate College, Kashipur, India
2Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, Thailand
Email: sun.gkv@gmail.com, #poom_teun@hotmail.com, #poom.kum@kmutt.ac.th
Received July 10, 2012; revised August 10, 2012; accepted August 17, 2012
Keywords: Fuzzy Metric Space; Weakly Compatible Mappings; (E.A) Property; (CLR) Property; (JCLR) Property
ABSTRACT
In this paper, we prove a common fixed point theorem for a pair of weakly compatible mappings in fuzzy metric space using the joint common limit in the range property of mappings called (JCLR) property. An example is also furnished which demonstrates the validity of main result. We also extend our main result to two finite families of self mappings. Our results improve and generalize results of Cho et al. [Y. J. Cho, S. Sedghi and N. Shobe, “Generalized fixed point theorems for compatible mappings with some types in fuzzy metric spaces,” Chaos, Solitons & Fractals, Vol. 39, No. 5, 2009, pp. 2233-2244.] and several known results existing in the literature.
1. Introduction
In 1965, Zadeh [1] investigated the concept of a fuzzy set in his seminal paper. In the last two decades there has been a tremendous development and growth in fuzzy mathematics. The concept of fuzzy metric space was introduced by Kramosil and Michalek [2] in 1975, which opened an avenue for further development of analysis in such spaces. Further, George and Veeramani [3] modified the concept of fuzzy metric space introduced by Kramosil and Michalek [2] with a view to obtain a Hausdoroff topology which has very important applications in quantum particle physics, particularly in connection with both string and  theory (see, [4] and references mentioned therein). Fuzzy set theory also has applications in applied sciences such as neural network theory, stability theory, mathematical programming, modeling theory, engineering sciences, medical sciences (medical genetics, nervous system), image processing, control theory, communication etc.
theory (see, [4] and references mentioned therein). Fuzzy set theory also has applications in applied sciences such as neural network theory, stability theory, mathematical programming, modeling theory, engineering sciences, medical sciences (medical genetics, nervous system), image processing, control theory, communication etc.
In 2002, Aamri and El-Moutawakil [5] defined the notion of (E.A) property for self mappings which contained the class of non-compatible mappings in metric spaces. It was pointed out that (E.A) property allows replacing the completeness requirement of the space with a more natural condition of closedness of the range as well as relaxes the complexness of the whole space, continuity of one or more mappings and containment of the range of one mapping into the range of other which is utilized to construct the sequence of joint iterates. Subsequently, there are a number of results proved for contraction mappings satisfying (E.A) property in fuzzy metric spaces (see [6-11]). Most recently, Sintunavarat and Kumam [12] defined the notion of “common limit in the range” property (or (CLR) property) in fuzzy metric spaces and improved the results of Mihet [10]. In [12], it is observed that the notion of (CLR) property never requires the condition of the closedness of the subspace while (E.A) property requires this condition for the existence of the fixed point (also see [13]). Many authors have proved common fixed point theorems in fuzzy metric spaces for different contractive conditions. For details, we refer to [14-25].
The aim of this paper is to introduce the notion of the joint common limit in the range of mappings property called (JCLR) property and prove a common fixed point theorem for a pair of weakly compatible mappings using (JCLR) property in fuzzy metric space. As an application to our main result, we present a common fixed point theorem for two finite families of self mappings in fuzzy metric space using the notion of pairwise commuting due to Imdad et al. [15]. Our results improve and generalize the results of Cho et al. [26], Abbas et al. [7] and Kumar [8].
2. Preliminaries
Definition 2.1 [27] A binary operation
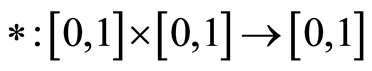 is a continuous t-norm if it satisfies the following conditions:
is a continuous t-norm if it satisfies the following conditions:
1)  is associative and commutative
is associative and commutative
2)  is continuous
is continuous
3) 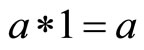 for all
for all
4) 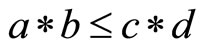 whenever
whenever 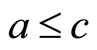 and
and 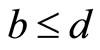 for all
for all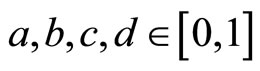 .
.
Examples of continuous t-norms are 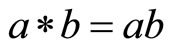 and
and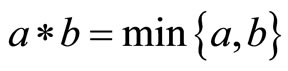 .
.
Definition 2.2 [3] A 3-tuple 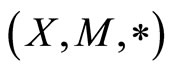 is said to be a fuzzy metric space if X is an arbitrary set, * is a continuous t-norm and M is a fuzzy set on
is said to be a fuzzy metric space if X is an arbitrary set, * is a continuous t-norm and M is a fuzzy set on  satisfying the following conditions: For all
satisfying the following conditions: For all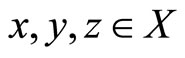 ,
, 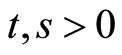 ,
,
1)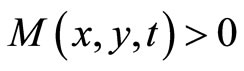
2) 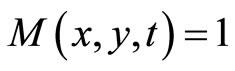 if and only if
if and only if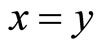
3)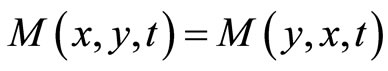
4)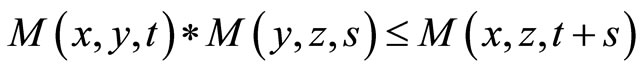 5)
5) 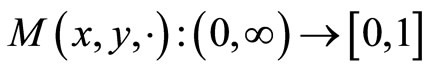 is continuous.
is continuous.
Then M is called a fuzzy metric on X and 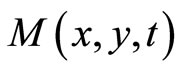 denotes the degree of nearness between x and y with respect to t.
denotes the degree of nearness between x and y with respect to t.
Let  be a fuzzy metric space. For
be a fuzzy metric space. For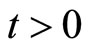 , the open ball
, the open ball 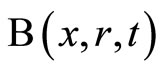 with center
with center 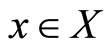 and radius
and radius 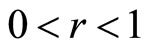 is defined by
is defined by
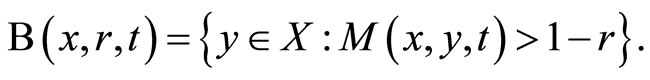
Now let 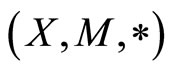 be a fuzzy metric space and
be a fuzzy metric space and 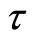 the set of all
the set of all 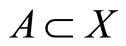 with
with 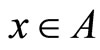 if and only if there exist
if and only if there exist  and
and 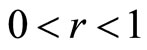 such that
such that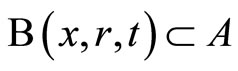 . Then
. Then 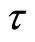 is a topology on X induced by the fuzzy metric M.
is a topology on X induced by the fuzzy metric M.
In the following example (see [3]), we know that every metric induces a fuzzy metric:
Example 2.1 Let 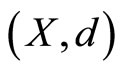 be a metric space. Denote
be a metric space. Denote 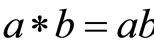 (or
(or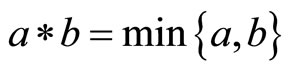 ) for all
) for all 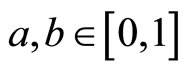 and let
and let 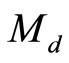 be fuzzy sets on
be fuzzy sets on 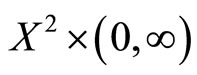 defined as follows:
defined as follows:
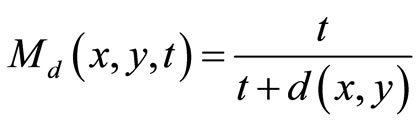 .
.
Then 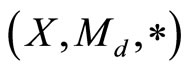 is a fuzzy metric space and the fuzzy metric M induced by the metric d is often referred to as the standard fuzzy metric.
is a fuzzy metric space and the fuzzy metric M induced by the metric d is often referred to as the standard fuzzy metric.
Definition 2.3 Let 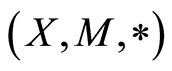 be a fuzzy metric space. M is said to be continuous on
be a fuzzy metric space. M is said to be continuous on  if
if

whenever a sequence 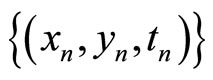 in
in 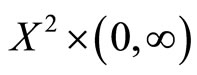 converge to a point
converge to a point , i.e.,
, i.e.,
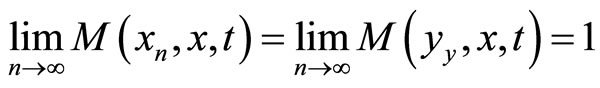
and
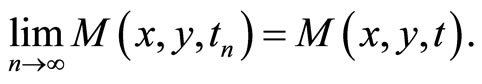
Lemma 2.1 [28] Let 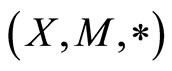 be a fuzzy metric space. Then
be a fuzzy metric space. Then  is non-decreasing for all
is non-decreasing for all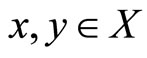 .
.
Lemma 2.2 [29] Let 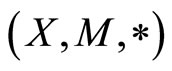 be a fuzzy metric space. If there exists
be a fuzzy metric space. If there exists 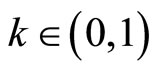 such that
such that

for all 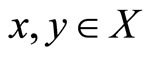 and
and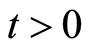 , then
, then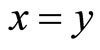 .
.
Definition 2.4 [30] Two self mappings f and g of a non-empty set X are said to be weakly compatible (or coincidentally commuting) if they commute at their coincidence points, i.e. if 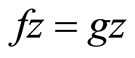 some
some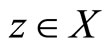 , then
, then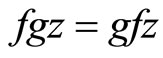 .
.
Remark 2.1 [30] Two compatible self mappings are weakly compatible, but the converse is not true. Therefore the concept of weak compatibility is more general than that of compatibility.
Definition 2.5 [7] A pair of self mappings f and g of a fuzzy metric space 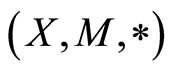 are said to satisfy the (E.A) property, if there exists a sequence
are said to satisfy the (E.A) property, if there exists a sequence 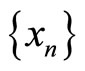 in X for some
in X for some 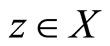 such that
such that
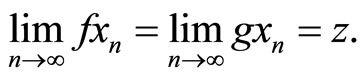
Remark 2.2 It is noted that weak compatibility and (E.A) property are independent to each other (see [31], Example 2.1, Example 2.2).
In 2011, Sintunavarat and Kumam [12] defined the notion of “common limit in the range” property in fuzzy metric space as follows:
Definition 2.6 A pair 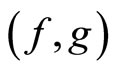 of self mappings of a fuzzy metric space
of self mappings of a fuzzy metric space 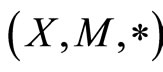 is said to satisfy the “common limit in the range of g” property (shortly, (CLRg) property) if there exists a sequence
is said to satisfy the “common limit in the range of g” property (shortly, (CLRg) property) if there exists a sequence 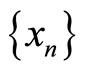 in X such that
in X such that
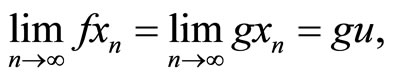
for some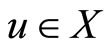 .
.
Now, we show examples of self mappings f and g which are satisfying the (CLRg) property.
Example 2.2 Let  be a fuzzy metric space with
be a fuzzy metric space with 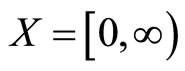 and
and
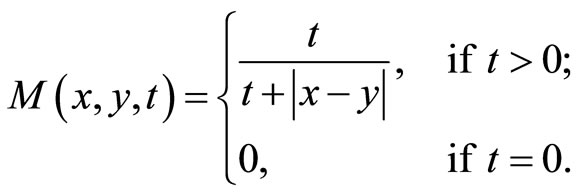
for all . Define self mappings f and g on X by
. Define self mappings f and g on X by 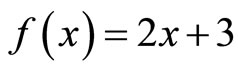 and
and 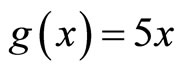 for all
for all . Let a sequence
. Let a sequence 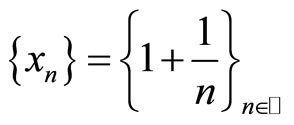 in X, we have
in X, we have

which shows that f and g satisfy the (CLRg) property.
Example 2.3 The conclusion of Example 2.2 remains true if the self mappings f and g is defined on X by
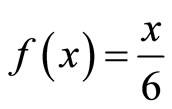 and
and 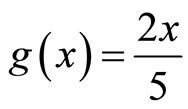 for all
for all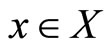 . Let a sequence
. Let a sequence 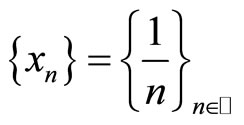 in X. Since
in X. Since
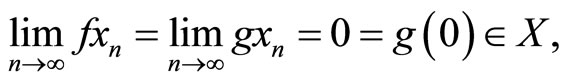
therefore f and g satisfy the (CLRg) property.
The following definition is on the lines due to Imdad et al. [32].
Definition 2.7 [32] Two families of self mappings
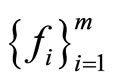 and
and 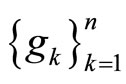 are said to be pairwise commuting if
are said to be pairwise commuting if
1) 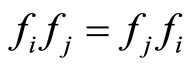 for all
for all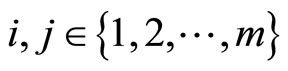
2) 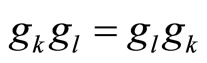 for all
for all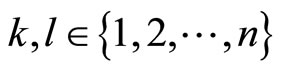
3) 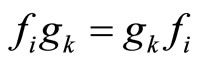 for all
for all 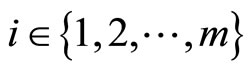 and
and 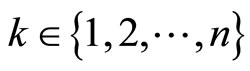 .
.
Throughout this paper, 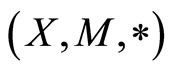 is considered to be a fuzzy metric space with condition
is considered to be a fuzzy metric space with condition
 for all
for all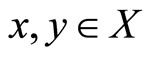 .
.
3. Main Results
In this section, we first introduce the notion of “the joint common limit in the range property” of two pairs of self mappings.
Definition 3.1 Let 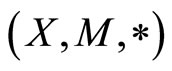 be a fuzzy metric space and
be a fuzzy metric space and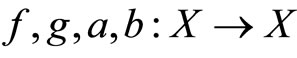 . The pair
. The pair  and
and  are said to satisfy the “joint common limit in the range of b and g” property (shortly, (JCLRbg) property) if there exists a sequence
are said to satisfy the “joint common limit in the range of b and g” property (shortly, (JCLRbg) property) if there exists a sequence 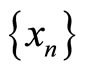 and
and 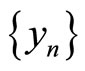 in X such that
in X such that
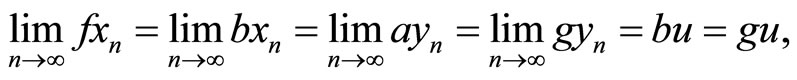 (1)
(1)
for some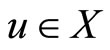 .
.
Remark 3.1 If ,
, 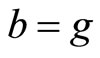 and
and  in (1), then we get the definition of (CLRg).
in (1), then we get the definition of (CLRg).
Throughout this section, 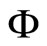 denotes the set of all continuous and increasing functions
denotes the set of all continuous and increasing functions 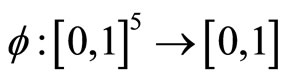 in any coordinate and
in any coordinate and 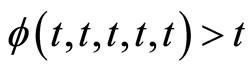 for all
for all .
.
Following are examples of some function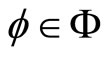 :
:
1)  for some
for some .
.
2)  for some
for some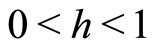 .
.
3) 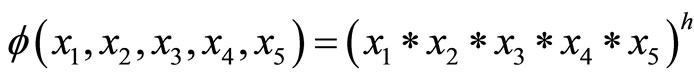 for some
for some 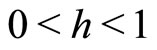 and for all t-norm
and for all t-norm  such that
such that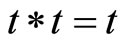 .
.
Now, we state and prove main results in this paper.
Theorem 3.1 Let 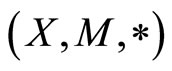 be a fuzzy metric space, where
be a fuzzy metric space, where  is a continuous t-norm and f, g, a and b be mappings from X into itself. Further, let the pair
is a continuous t-norm and f, g, a and b be mappings from X into itself. Further, let the pair 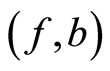 and
and  are weakly compatible and there exists a constant
are weakly compatible and there exists a constant  such that
such that
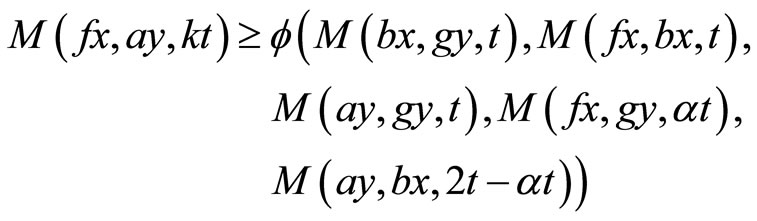 (2)
(2)
holds for all ,
, 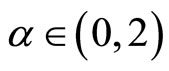 ,
, 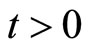 and
and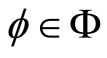 . If
. If 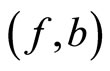 and
and  satisfy the (JCLRbg) property, then f, g, a and b have a unique common fixed point in X.
satisfy the (JCLRbg) property, then f, g, a and b have a unique common fixed point in X.
Proof. Since the pairs 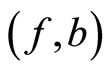 and
and  satisfy the (JCLRbg) property, there exists a sequence
satisfy the (JCLRbg) property, there exists a sequence 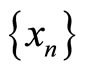 and
and 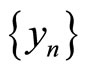 in X such that
in X such that

for some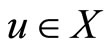 .
.
Now we assert that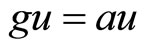 . Using (2), with
. Using (2), with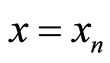 ,
, 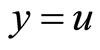 , for
, for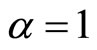 , we get
, we get
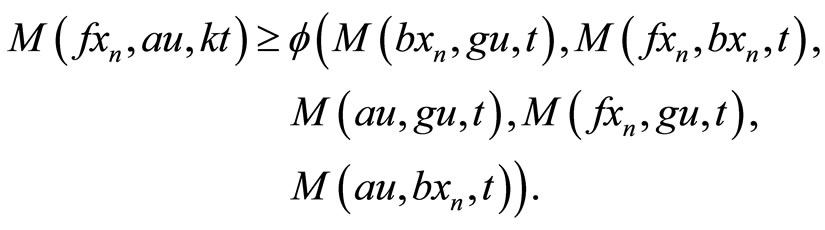
Taking the limit as , we have
, we have

Since  is increasing in each of its coordinate and
is increasing in each of its coordinate and 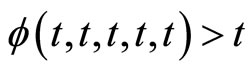 for all
for all , we get
, we get  . By Lemma 2.2, we have
. By Lemma 2.2, we have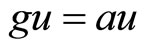 .
.
Next we show that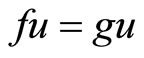 . Using (2), with
. Using (2), with ,
, 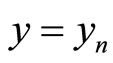 , for
, for , we get
, we get
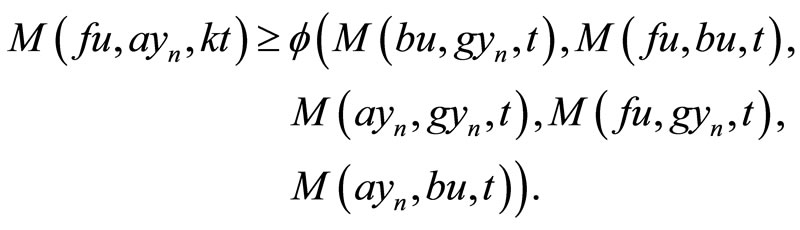
Taking the limit as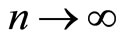 , we have
, we have
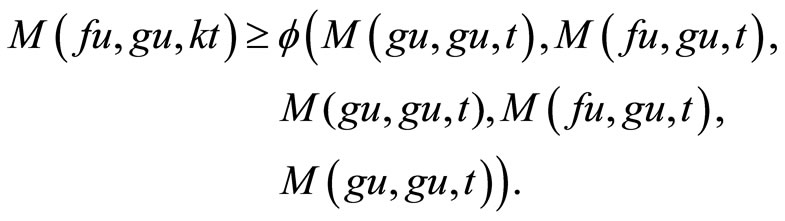
Since  is increasing in each of its coordinate and
is increasing in each of its coordinate and 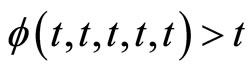 for all
for all , we get
, we get
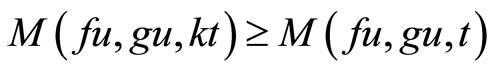 . By Lemma 2.2, we have
. By Lemma 2.2, we have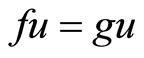 .
.
Now, we assume that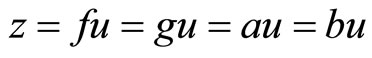 . Since the pair
. Since the pair 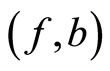 is weakly compatible,
is weakly compatible, 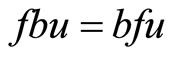 and then
and then . It follows from
. It follows from 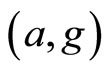 is weakly compatible,
is weakly compatible, 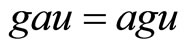 and hence
and hence 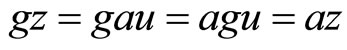 .
.
We show that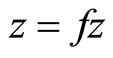 . To prove this, using (2) with
. To prove this, using (2) with ,
, 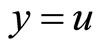 , for
, for , we get
, we get
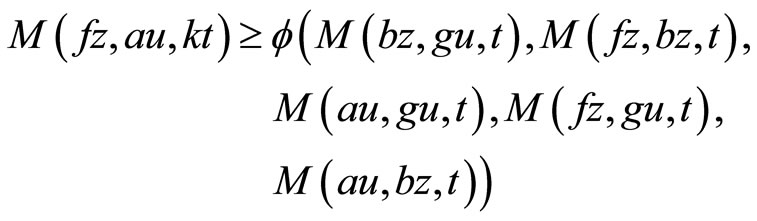
and so

Since 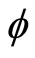 is increasing in each of its coordinate and
is increasing in each of its coordinate and 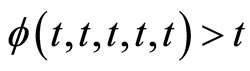 for all
for all ,
,  , which implies that
, which implies that . Hence
. Hence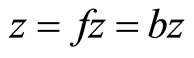 .
.
Next, we show that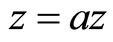 . To prove this, using (2) with
. To prove this, using (2) with ,
,  , for
, for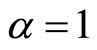 , we get
, we get
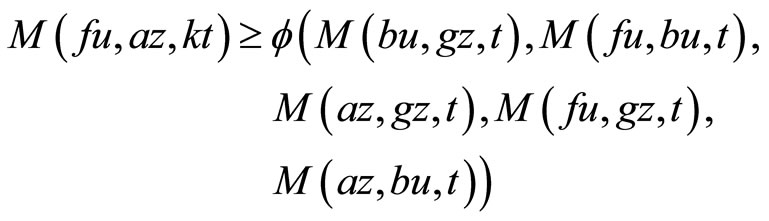
and so
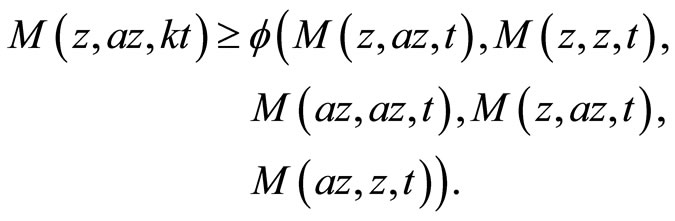
Since  is increasing in each of its coordinate and
is increasing in each of its coordinate and 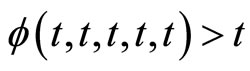 for all
for all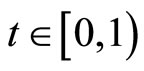 ,
, 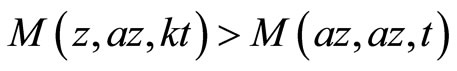 , which implies that
, which implies that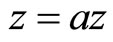 . Hence
. Hence . Therefore, we conclude that
. Therefore, we conclude that 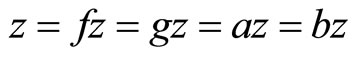 this implies f, g, a and b have common fixed point that is a point z.
this implies f, g, a and b have common fixed point that is a point z.
For uniqueness of common fixed point, we let w be another common fixed point of the mappings f, g, a and b. On using (2) with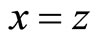 ,
, 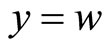 , for
, for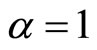 , we have
, we have

and then
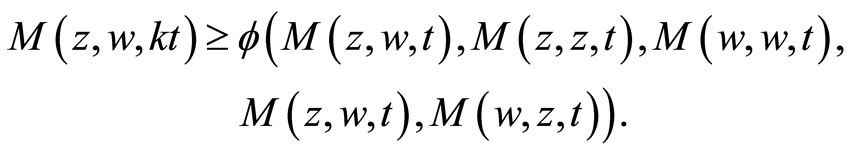
Since 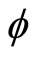 is increasing in each of its coordinate and
is increasing in each of its coordinate and 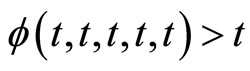 for all
for all ,
, 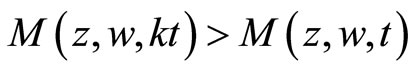 , which implies that
, which implies that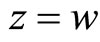 . Therefore f, g, a and b have a unique a common fixed point.
. Therefore f, g, a and b have a unique a common fixed point.
Remark 3.2 From the result, it is asserted that (JCLRgb) property never requires any condition closedness of the subspace, continuity of one or more mappings and containment of ranges amongst involved mappings.
Remark 3.3 Theorem 3.1 improves and generalizes the results of Abbas et al. ([7], Theorem 2.1) and Kumar ([8], Theorem 2.3) without any requirement of containment amongst range sets of the involved mappings and closedness of the underlying subspace.
Remark 3.4 Since the condition of t-norm with 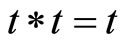 for all
for all 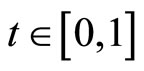 is replaced by arbitrary continuous t-norm, Theorem 3.1 also improves the result of Cho et al. ([26], Theorem 3.1) without any requirement of completeness of the whole space, continuity of one or more mappings and containment of ranges amongst involved mappings.
is replaced by arbitrary continuous t-norm, Theorem 3.1 also improves the result of Cho et al. ([26], Theorem 3.1) without any requirement of completeness of the whole space, continuity of one or more mappings and containment of ranges amongst involved mappings.
Corollary 3.1 Let 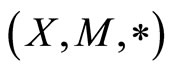 be a fuzzy metric space, where
be a fuzzy metric space, where  is a continuous t-norm and f, g, a and b be mappings from X into itself. Further, let the pair
is a continuous t-norm and f, g, a and b be mappings from X into itself. Further, let the pair 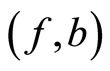 and
and  are weakly compatible and there exists a constant
are weakly compatible and there exists a constant 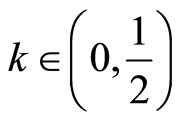 such that
such that
 (3)
(3)
holds for all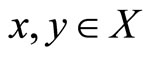 ,
,  ,
, 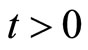 and
and 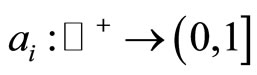 such that
such that . If
. If 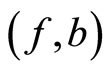 and
and 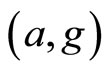 satisfy the (JCLRbg) property, then f, g, a and b have a unique common fixed point in X.
satisfy the (JCLRbg) property, then f, g, a and b have a unique common fixed point in X.
Proof. By Theorem 3.1, if we define

then the result follows.
Remark 3.5 Corollary 3.1 improves the result of Cho et al. ([26], Corollary 3.4) without any requirement of completeness of the whole space, continuity of one or more mappings and containment of ranges amongst involved mappings while the condition of t-norm 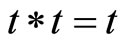 for all
for all 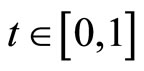 is replaced by arbitrary continuous t-norm.
is replaced by arbitrary continuous t-norm.
Corollary 3.2 Let 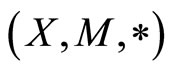 be a fuzzy metric space, where
be a fuzzy metric space, where  is a continuous t-norm and f and g be mappings from X into itself. Further, let the pair
is a continuous t-norm and f and g be mappings from X into itself. Further, let the pair 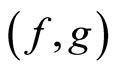 is weakly compatible and there exists a constant
is weakly compatible and there exists a constant 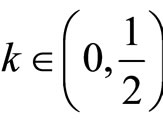 such that
such that
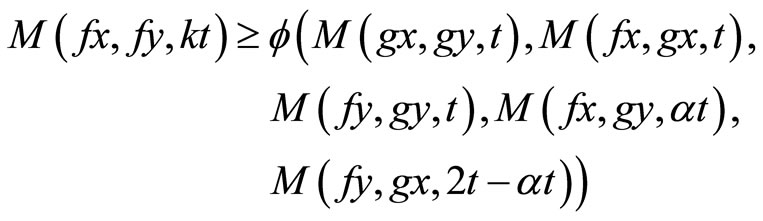 (4)
(4)
holds for all ,
,  ,
, 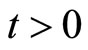 and
and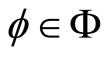 . If
. If 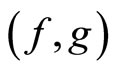 satisfies the (CLRg) property, then f and g have a unique common fixed point in X.
satisfies the (CLRg) property, then f and g have a unique common fixed point in X.
Proof. Take 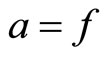 and
and 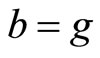 in Theorem 3.1, then we get the result.
in Theorem 3.1, then we get the result.
Our next theorem is proved for a pair of weakly compatible mappings in fuzzy metric space 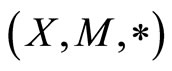 using (E.A) property under additional condition closedness of the subspace.
using (E.A) property under additional condition closedness of the subspace.
Theorem 3.2 Let 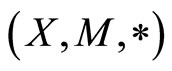 be a fuzzy metric space, where
be a fuzzy metric space, where  is a continuous t-norm. Further, let the pair
is a continuous t-norm. Further, let the pair 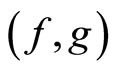 of self mappings is weakly compatible satisfying inequality (4) of Corollary 3.2. If f and g satisfy the (E.A) property and the range of g is a closed subspace of X, then f and g have a unique common fixed point in X.
of self mappings is weakly compatible satisfying inequality (4) of Corollary 3.2. If f and g satisfy the (E.A) property and the range of g is a closed subspace of X, then f and g have a unique common fixed point in X.
Proof. Since the pair  satisfies the (E.A) property, there exists a sequence
satisfies the (E.A) property, there exists a sequence 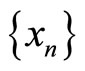 in X such that
in X such that
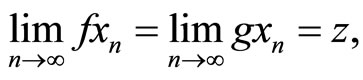
for some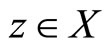 . It follows from
. It follows from 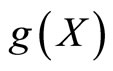 being a closed subspace of X that there exists
being a closed subspace of X that there exists 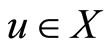 in which
in which . Therefore f and g satisfy the (CLRg) property. From Corollary 3.2, the result follows.
. Therefore f and g satisfy the (CLRg) property. From Corollary 3.2, the result follows.
In what follows, we present some illustrative examples which demonstrate the validity of the hypotheses and degree of utility of our results.
Example 3.1 Let 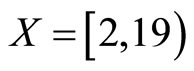 with the metric d defined by
with the metric d defined by 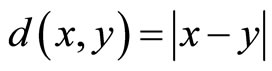 and for each
and for each 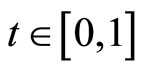 define
define
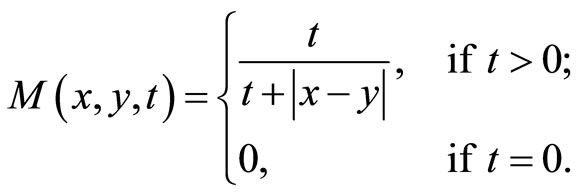
for all . Clearly
. Clearly  be a fuzzy metric space with t-norm defined by
be a fuzzy metric space with t-norm defined by 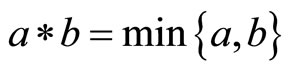 for all
for all
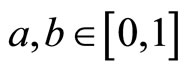 . Consider a function
. Consider a function 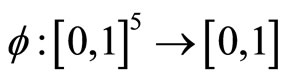 defined by
defined by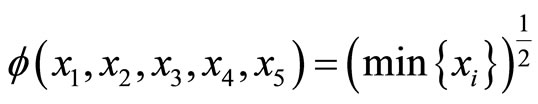 . Then we have
. Then we have
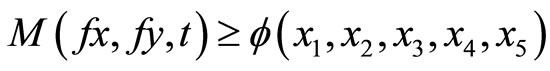 . Define the self mappings f and g on X by
. Define the self mappings f and g on X by

and
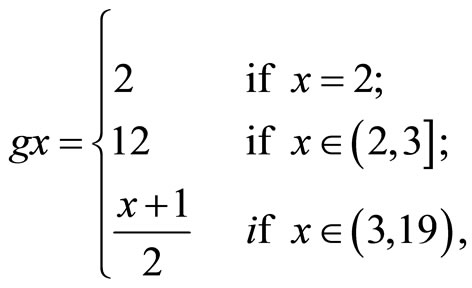
Taking 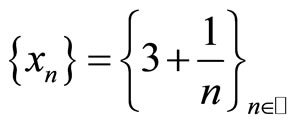 or
or , it is clear that the pair
, it is clear that the pair 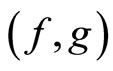 satisfies the (CLRg) property since
satisfies the (CLRg) property since
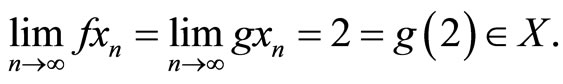
It is noted that . Thus, all the conditions of Corollary 3.2 are satisfied for a fixed constant
. Thus, all the conditions of Corollary 3.2 are satisfied for a fixed constant  and 2 is a unique common fixed point of the pair
and 2 is a unique common fixed point of the pair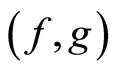 . Also, all the involved mappings are even discontinuous at their unique common fixed point 2. Here, it may be pointed out that
. Also, all the involved mappings are even discontinuous at their unique common fixed point 2. Here, it may be pointed out that 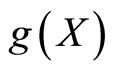 is not a closed subspace of X.
is not a closed subspace of X.
Example 3.2 In the setting of Example 3.1, replace the mapping g by the following, besides retaining the rest:

Taking  or
or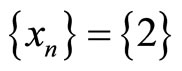 , it is clear that the pair
, it is clear that the pair  satisfies the (E.A) property since
satisfies the (E.A) property since
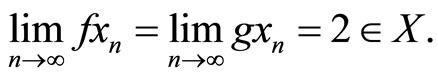
It is noted that . Thus, all the conditions of Theorem 3.2 are satisfied and 2 is a unique common fixed point of the mappings f and g. Notice that all the involved mappings are even discontinuous at their unique common fixed point 2. Here, it is worth noting that
. Thus, all the conditions of Theorem 3.2 are satisfied and 2 is a unique common fixed point of the mappings f and g. Notice that all the involved mappings are even discontinuous at their unique common fixed point 2. Here, it is worth noting that 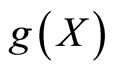 is a closed subspace of X.
is a closed subspace of X.
Now, we utilize Definition 2.7 which is a natural extension of commutativity condition to two finite families of self mappings. Our next theorem extends Corollary 3.2 in the following sense:
Theorem 3.3 Let 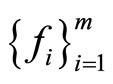 and
and  be two finite families of self mappings in fuzzy metric space
be two finite families of self mappings in fuzzy metric space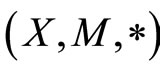 , where
, where  is a continuous t-norm such that
is a continuous t-norm such that 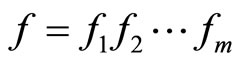 and
and 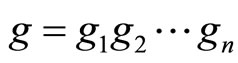 which satisfy the inequalities (4) of Corollary 3.2. If the pair
which satisfy the inequalities (4) of Corollary 3.2. If the pair 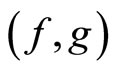 shares (CLRg) property, then f and g have a unique point of coincidence.
shares (CLRg) property, then f and g have a unique point of coincidence.
Moreover, 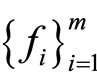 and
and 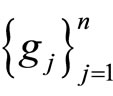 have a unique common fixed point provided the pair of families
have a unique common fixed point provided the pair of families 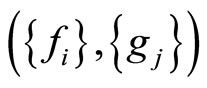
commutes pairwise, where 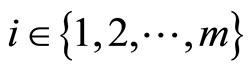 and
and  .
.
Proof. The proof of this theorem can be completed on the lines of Theorem 3.1 contained in Imdad et al. [15], hence details are avoided.
Putting  and
and
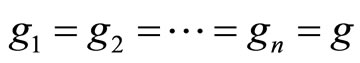 in Theorem 3.3, we get the following result:
in Theorem 3.3, we get the following result:
Corollary 3.3 Let f and g be two self mappings of a fuzzy metric space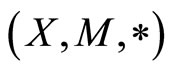 , where
, where  is a continuous t-norm. Further, let the pair
is a continuous t-norm. Further, let the pair 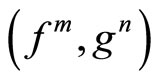 shares (CLRg) property. Then there exists a constant
shares (CLRg) property. Then there exists a constant  such that
such that
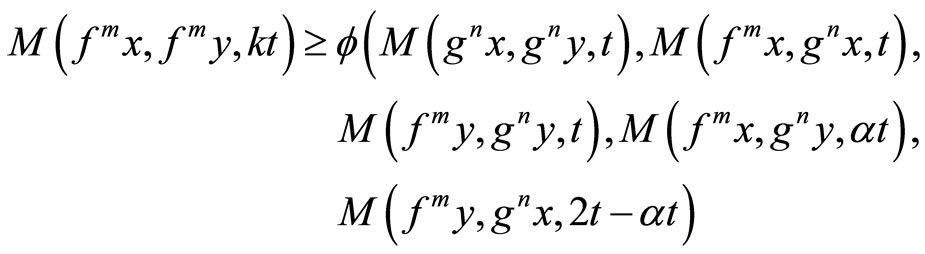
holds for all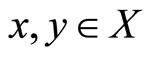 ,
,  ,
, 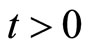 ,
, 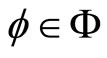 and m and n are fixed positive integers, then f and g have a unique common fixed point provided the pair
and m and n are fixed positive integers, then f and g have a unique common fixed point provided the pair  commutes pairwise.
commutes pairwise.
Remark 3.6 Theorem 3.2, Theorem 3.3 and Corollary 3.3 can also be outlined in respect of Corollary 3.1.
Remark 3.7 Using Example 2.2, we can obtain several fixed point theorems in fuzzy metric spaces in respect of Theorems 3.2 and 3.3 and Corollaries 3.2, 3.1 and 3.3.
4. Acknowledgements
The authors would like to express their sincere thanks to Professor Mujahid Abbas for his paper [18]. The second author would like to thank the Research Professional Development Project under the Science Achievement Scholarship of Thailand (SAST). This study was supported by the Higher Education Research Promotion and National Research University Project of Thailand, Office of the Higher Education Commission under the Computational Science and Engineering Research Cluster (CSEC Grant No. 55000613).
REFERENCES
- L. A. Zadeh, “Fuzzy Sets,” Information and Control, Vol. 8, No. 3, 1965, pp. 338-353. doi:10.1016/S0019-9958(65)90241-X
- I. Kramosil and J. Michalek, “Fuzzy Metric and Statistical Metric Spaces,” Kybernetika (Prague), Vol. 11, No. 5, 1975, pp. 336-344.
- A. George and P. Veeramani, “On Some Result in Fuzzy Metric Space,” Fuzzy Sets & Systems, Vol. 64, No. 3, 1994, pp. 395-399. doi:10.1016/0165-0114(94)90162-7
- M. S. El Naschie, “On a Fuzzy Kahler-Like Manifold Which Is Consistent with Two-Slit Experiment,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 6, No. 2, 2005, pp. 95-98. doi:10.1515/IJNSNS.2005.6.2.95
- M. Aamri and D. El Moutawakil, “Some New Common Fixed Point Theorems under Strict Contractive Conditions,” Journal of Mathematical Analysis and Applications, Vol. 270, No. 1, 2002, pp. 181-188. doi:10.1016/S0022-247X(02)00059-8
- I. Aalam, S. Kumar and B. D. Pant, “A Common Fixed Point Theorem in Fuzzy Metric Space,” Bulletin of Mathematical Analysis and Applications, Vol. 2, No. 4, 2010, pp. 76-82.
- M. Abbas, I. Altun and D. Gopal, “Common Fixed Point Theorems for Non Compatible Mappings in Fuzzy Metric Spaces,” Bulletin of Mathematical Analysis and Applications, Vol. 1, No. 2, 2009, pp. 47-56.
- S. Kumar, “Fixed Point Theorems for Weakly Compatible Maps under E. A. Property in Fuzzy Metric Spaces,” Applied Mathematics & Information Sciences, Vol. 29, No. 1-2, 2011, pp. 395-405.
- S. Kumar and B. Fisher, “A Common Fixed Point Theorem in Fuzzy Metric Space Using Property (E. A.) and Implicit Relation,” Thai Journal of Mathematics, Vol. 8, No. 3, 2010, pp. 439-446.
- D. Mihet, “Fixed Point Theorems in Fuzzy Metric Spaces Using Property E. A.,” Nonlinear Analysis, Vol. 73, No. 7, 2010, pp. 2184-2188. doi:10.1016/j.na.2010.05.044
- S. Sedghi, C. Alaca and N. Shobe, “On Fixed Points of Weakly Commuting Mappings with Property (E. A.),” Journal of Advanced Studies in Topology, Vol. 3, No. 3, 2012.
- W. Sintunavarat and P. Kumam, “Common Fixed Point Theorems for a Pair of Weakly Compatible Mappings in Fuzzy Metric Spaces,” Journal of Applied Mathematics, Vol. 2011, 2011, Article ID: 637958.
- W. Sintunavarat and P. Kumam, “Common Fixed Points for R-Weakly Commuting in Fuzzy Metric Spaces,” Annali dell’Universita di Ferrara, Vol. 58, No. 2, 2012, pp. 389-406. doi:10.1007/s11565-012-0150-z
- Y. J. Cho, “Fixed Points in Fuzzy Metric Spaces,” Journal of Fuzzy Mathematics, Vol. 5, No. 4, 1997, pp. 949- 962.
- M. Imdad and J. Ali, “Some Common Fixed Point Theorems in Fuzzy Metric Spaces,” Mathematical Communications, Vol. 11, No. 2, 2006, pp. 153-163.
- S. Kutukcu, D. Turkoglu and C. Yildiz, “Common Fixed Points of Compatible Maps of Type (β) on Fuzzy Metric Spaces,” Communications of the Korean Mathematical Society, Vol. 21, No. 1, 2006, pp. 89-100.
- P. P. Murthy, S. Kumar and K. Tas, “Common Fixed Points of Self Maps Satisfying an Integral Type Contractive Condition in Fuzzy Metric Spaces,” Mathematical Communications, Vol. 15, No. 2, 2010, pp. 521-537.
- D. O’Regan and M. Abbas, “Necessary and Sufficient Conditions for Common Fixed Point Theorems in Fuzzy Metric Space,” Demonstratio Mathematica, Vol. 42, No. 4, 2009, pp. 887-900.
- B. D. Pant and S. Chauhan, “Common Fixed Point Theorems for Two Pairs of Weakly Compatible Mappings in Menger Spaces and Fuzzy Metric Spaces,” Scientific Studies and Research. Series Mathematics and Informatics, Vol. 21, No. 2, 2011, pp. 81-96.
- S. Sedghi, D. Turkoglu and N. Shobe, “Common Fixed Point of Compatible Maps of Type (γ) on Complete Fuzzy Metric Spaces,” Communications of the Korean Mathematical Society, Vol. 24, No. 4, 2009, pp. 581-594. doi:10.4134/CKMS.2009.24.4.581
- S. L. Singh and A. Tomar, “Fixed Point Theorems in FM-Spaces,” Journal of Fuzzy Mathematics, Vol. 12, No. 4, 2004, pp. 845-859.
- W. Sintunavarat, Y. J. Cho and P. Kumam, “Coupled Coincidence Point Theorems for Contractions without Commutative Condition in Intuitionistic Fuzzy Normed Spaces,” Fixed Point Theory and Applications, Vol. 2011, No. 81, 2011.
- W. Sintunavarat and P. Kumam, “Fixed Point Theorems for a Generalized Intuitionistic Fuzzy Contraction in Intuitionistic Fuzzy Metric Spaces,” Thai Journal of Mathematics, Vol. 10 No. 1, 2012, pp. 123-135.
- P. V. Subrahmanyam, “A Common Fixed Point Theorem in Fuzzy Metric Spaces,” Information Sciences, Vol. 83, No. 3-4, 1995, pp. 109-112. doi:10.1016/0020-0255(94)00043-B
- R. Vasuki, “Common Fixed Points for R-Weakly Commuting Maps in Fuzzy Metric Spaces,” Indian Journal of Pure and Applied Mathematics, Vol. 30, No. 4, 1999, pp. 419-423.
- Y. J. Cho, S. Sedghi and N. Shobe, “Generalized Fixed Point Theorems for Compatible Mappings with Some Types in Fuzzy Metric Spaces,” Chaos, Solitons & Fractals, Vol. 39, No. 5, 2009, pp. 2233-2244. doi:10.1016/j.chaos.2007.06.108
- B. Schweizer and A. Sklar, “Probabilistic Metric Spaces,” In: North-Holland Series in Probability and Applied Mathematics, North-Holland Publishing Co., New York, 1983.
- M. Grabiec, “Fixed Points in Fuzzy Metric Spaces,” Fuzzy Sets & System, Vol. 27, No. 3, 1988, pp. 385-389. doi:10.1016/0165-0114(88)90064-4
- S. N. Mishra, N. Sharma and S. L. Singh, “Common Fixed Points of Maps on Fuzzy Metric Spaces,” International Journal of Mathematics and Mathematical Sciences, Vol. 17, No. 2, 1994, pp. 253-258. doi:10.1155/S0161171294000372
- G. Jungck, “Common Fixed Points for Noncontinuous Nonself Maps on Nonmetric Spaces,” Far East Journal of Mathematical Sciences, Vol. 4, No. 2, 1996, pp. 199- 215.
- H. K. Pathak, R. R. López and R. K. Verma, “A Common Fixed Point Theorem Using Implicit Relation and Property (E. A.) in Metric Spaces,” Filomat, Vol. 21, No. 2, 2007, pp. 211-234. doi:10.2298/FIL0702211P
- M. Imdad, J. Ali and M. Tanveer, “Coincidence and Common Fixed Point Theorems for Nonlinear Contractions in Menger PM Spaces,” Chaos, Solitons & Fractals, Vol. 42, No. 5, 2009, pp. 3121-3129. doi:10.1016/j.chaos.2009.04.017
NOTES
*This work was supported by the Higher Education Research Promotion and National Research University Project of Thailand, Office of the Higher Education Commission (NRU-55000613).
#Corresponding authors.

