ABSTRACT

This paper studies the generalized (2 + 1)-dimensional Zakharov-Kuznetsov Equation using the (G'/G)-expand method, we obtain many new explicit solutions of the generalized (2 + 1)-dimensional Zakharov-Kuznetsov Equation, which include hyperbolic function solutions, trigonometric function solutions and rational function solutions and so on.

1. Introduction

Nonlinear evolution equations in many areas play an important role. Thus solving nonlinear evolution equations (NLEEs) has become a valuable task. For this purpose, in the past few decades, due to availability of computer symbolic system like Mathematica or Maple, many significant methods have been developed, such as inverse scattering transformation (IST) [1], Jacobi elliptic function method [2], Hirota bilinear method [3], Sinecose function method [4], classic and non-classic Lie symmetry method [5-7], the Exp-function expansion method [8] and so on.

Recently, Wang [9] introduced a new method called the (G'/G)-expansion method to look for exact solutions of mathematical physics. Lot of studies have been conducted with NLEEs by using this method [10-12]. This method is direct, concise, elementary and effective, and can be used for NLEEs involving higher order nonlinear terms.

Let us consider the generalized (2 + 1)-dimensional ZK Equation with high-order nonlinear terms in the form as follows:

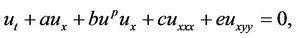(1)

where a, b, c and e are nonzero arbitrary constants and. When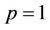, Equation (1) can be reduced to the standard (2 + 1)-dimensional ZK Equation. In 1974, Zakharov and Kuznetsov (ZK) [13] derived an equation which describes weakly nonlinear ion-acoustic waves in a strongly magnetized lossless plasma composed of coldions and hot isothermal electrons. The ZakhrovKuznetsov (ZK) Equation is also known as one of twodimensional generalizations of the KdV equation, another one being the Kadomtsev-Petviashvili (KP) Equation for example. The ZK Equation has been derived in the context of plasma physics [14,15]. Biswas and Zerrad [16] considered the ZK Equation with dual-power law nonlinearity and obtained 1-soliton solution by using the solitary wave ansatze. He [17] applied the homotopy perturbation method to the (2 + 1)-dimensional ZK Equation to search for traveling wave solutions. Using a subequation method (the elliptic equation is taken as a transformation), the traveling wave solutions for the (2 + 1) dimensional-ZK Equation are also studied by Fu [18]. I. Aslan has obtained solitary and periodic wave solutions [19].

In this paper, by use of the (G'/G)-expansion method to construct some new exact solutions of the generalized (2 + 1)-dimensional ZK Equation with nonlinear terms of any order.

2. The (G'/G)-Expansion Method

Wang (Wang and Zhang, 2008) has summarized for using (G'/G)-expansion method:

Step 1: Combining the independent variables x and t into one variable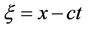, we suppose that   , which permits us reducing a partial differential equation (PDE)

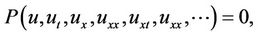(2.1)

to an ordinary differential equation (ODE) for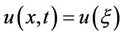

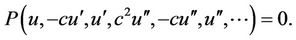(2.2)

Step 2: Suppose that the solution of ODE (2.2) can be expressed by a polynomial in (G'/G) as follows:

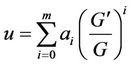(2.3)

where satisfies the second order LODE in the form

(2.4)

the integer m can be determined by considering the homogeneous balance between the highest order derivatives and the nonlinear terms appearing in ODE (2.2).

Step 3: By substituting (2.3) into (2.2) and using the second order linear ODE (2.4), collecting all terms with the same order of (G'/G) together, the left-hand side of Equation (2.2) is converted into another polynomial in (G'/G). Equating each coefficient of this polynomial to zero yields a set of algebraic equations for , , 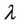c and by using Maple, along with the general solutions of Equation (2.4) into (2.3), we can have more travelling wave solutions of the nonlinear evolution Equation (2.1).

3. Exact Solutions of the Generalized (2 + 1)-Dimensional ZK Equation with Any-Order Nonlinear Terms

Firstly we take the form of the required solution as follows:

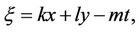
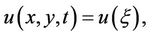(3.1)

where k, l and m are constants to be determined later, Equation (1) becomes an ODE

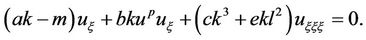(3.2)

Suppose that the solutions of (3.2) can be expressed by a polynomial in (G'/G) as follows:

(3.3)

where satisfies the second order LODE in the form

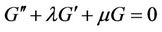(3.4)

the integer q can be determined by considering the homogeneous balance between the highest order derivatives and the nonlinear terms appearing in ODE (3.2).

Equation (3.4) can be changed into

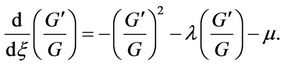(3.5)

By using Equation (3.5), by balancing the highest order partial derivative term and the nonlinear term in (3.2), we get the value of q,

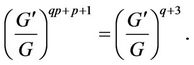
So, Thus we make transformation and transform Equation (3.2) into the following ODE

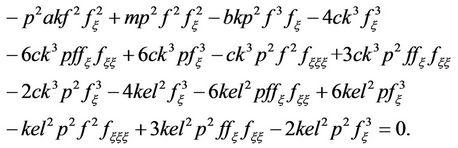(3.6)

Suppose that the solutions of (3.6) can be expressed by a polynomial in (G'/G) as follows:

(3.7)

By balancing the highest order partial derivative term and the nonlinear term in (3.6), we get the value of n = 2, thus we can write Equation (3.7) as

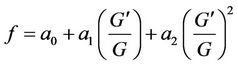(3.8)

where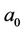, and are constants to be determined.

With the help of the symbolic software Maple15, substitution of Equation (3.8) with Equation (3.4) into Equation (3.6), collecting the coefficients of (G'/G) and setting it to zero, so the set of algebraic equations possesses the following solutions Set 1.

,

,

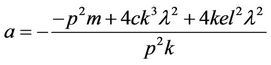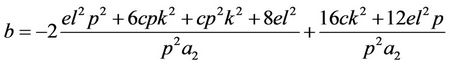Set 2.

,

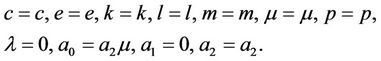
Set 3.

,

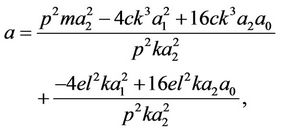
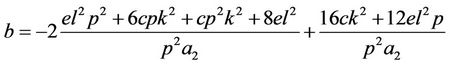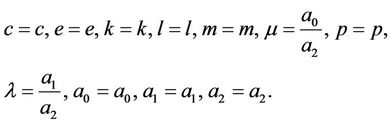
Therefore, substituting the general solutions of Equation (3.4) into (3.8), we can obtain that three types of travelling wave solutions of (3.6) as follows:

Case (Set 1).

When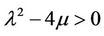, we obtain hyperbolic function solution

By using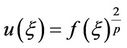, the generalized (2 + 1)-dimensional ZK Equation with high-order nonlinear terms have the solution

If setting 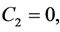then solution 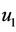becomes the wellknow kink-type solitary wave solution, namely

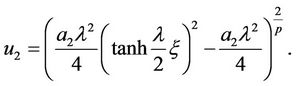
When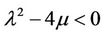, we have trigonometric function solution

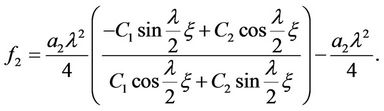
Similarly,

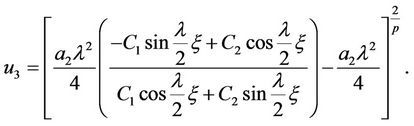
When, we have rational function solution

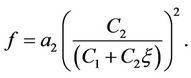
So we can get

(3.9)

Case (Set 2).

When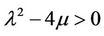, we can obtain hyperbolic function solution

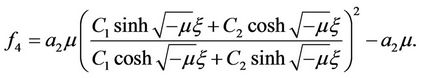
Similarly, by using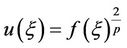, the generalized

(2 + 1)-dimensional ZK Equation with high-order nonlinear terms have the solution

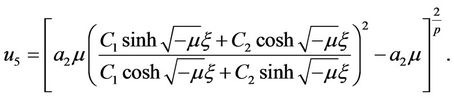
If setting then solution 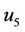can be changed

When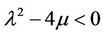, we have trigonometric function solution

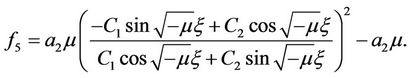
Similarly,

.

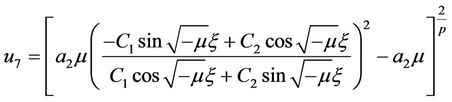If setting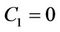, one can get

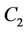When, we have rational function solution the same results as (3.9). where, and are arbitrary constants.

Case (Set 3).

When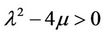, we can get hyperbolic function solution

.

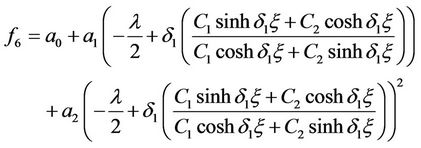By using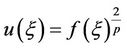, we can get the solution of Equation (1)

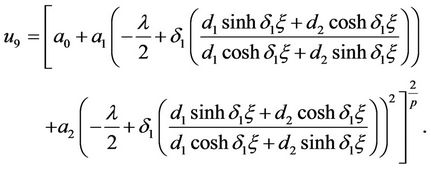
When, one can get new trigonometric function solution

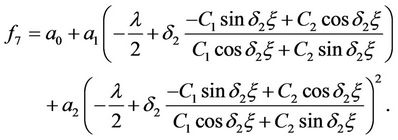
Therefore, we can have the new trigonometric function solution

When, we can obtain rational function solution

Thus

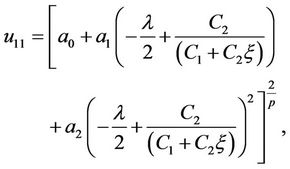
where

,

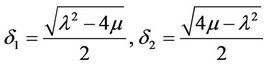and are arbitrary constants.

4. Conclusion

In this paper (G'/G)-expansion method is used for constructing some new exact solutions for the generalized (2 + 1)-dimensional ZK Equation with high-order nonlinear terms arising in mathematical physics. And above all, we have successfully obtained some new exact solutions for the generalized (2 + 1)-dimensional ZK Equation with high-order nonlinear terms, which include hyperbolic function solutions, trigonometric function solutions and rational function solutions and so on. The physical relevance of the new solutions is clear for us. The performance of the method used here, is reliable and effective, and give more and new solutions. All of the solutions obtained in this paper have been verified with the help of Maple. The new type of explicit solutions might have impact on future researches.

5. Acknowledgements

The project is supported by National Natural Science Foundation of China and China Academy of Engineering Physics (NSAF:11076015).

REFERENCES