Applied Mathematics
Vol. 3 No. 5 (2012) , Article ID: 19051 , 8 pages DOI:10.4236/am.2012.35064
Effect of Non-Uniform Basic Concentration Gradient on the Onset of Double-Diffusive Convection in Micropolar Fluid
1Department of Mathematics, Christ University, Bangalore, India
2Department of Mathematics, Faculty of Engineering, Christ University, Bangalore, India
Email: {pranesh.s, arun.kumar}@christuniversity.in
Received December 28, 2011; revised March 19, 2012; accepted March 26, 2012
Keywords: Double Diffusive Convection; Micropolar Fluid; Rayleigh Benard Convection and Non Uniform Concentration Gradients
ABSTRACT
The effect of non-uniform basic concentration gradient on the onset of double diffusive convection in a micropolar fluid layer heated and saluted from below and cooled from above has been studied. The linear stability analysis is performed. The eigen value of the problem is obtained using Galerkian method. The eigen values are obtained for 1) free-free; 2) rigid-free; 3) rigid-rigid velocity boundary combination with isothermal temperature condition on spin-vanishing permeable boundaries. The influence of various micropolar parameters on the onset of convection has been analyzed. One linear and five non linear concentration profiles are considered and their comparative influence on onset is discussed and results are depicted graphically. It is observed that fluid layer with suspended particles heated and soluted from below is more stable compare to the classical fluid without suspended particles.
1. Introduction
The convection driven by two different density gradients with differing rates of diffusion is widely known to as “double-diffusive convection” and is an important fluid dynamics phenomenon (see Mojtabi and Charrier-Mojtabi [1]). The study of double-diffusive convection has attracted attention of many researchers during the recent past due to its occurrence in nature and industry. Oceanography is the root of double-diffusive convection in natural settings. The existence of heat and salt concentrations at different gradients and the fact that they diffuse at different rates lead to spectacular double-diffusive instabilities known as “salt-fingers” (see Stern [2,3]). The formation of salt-fingers can also be observed in laboratory settings. Double-diffusive convection occurs in the sun where temperature and Helium diffusions take place at different rates. Convection in magma chambers and sea-wind formations are among other manifestations of double-diffusive convection in nature. The theory of double-diffusive convection both theoretically and experimentally is investigated by Turner [4], Chen et al. [5] and recently Malashetty and Bharati [6].
The theory of micro-fluid introduced by Eringen [7] deals with a class of fluids, which exhibits certain microscopic effects arising from the local structure and micro-motions of the fluid elements. Consequently new principles must be added to the basic principle of continuous media which deals with 1) Conservation of micro inertia moments, and 2) Balance of first stress moments. The theory of micro fluids naturally give rise to the concept of inertial spin, body moments, micro-stress averages and stress moments which have no counter part in the classical fluid theories. A detailed survey of the theory of micropolar fluid and its applications are considered in the books of Erigen [8,9], Lukasazewicz [10] and power [11]. The theory of thermomicropolar convection was studied by many authors Datta and Sastry [12], Ahmadi [13], Rama Rao [14], Lebon and Perez-Gracia [15], Bhattacharya and Jena [16], Siddheshwar and Pranesh [17-20], Y. N. Murthy [21], and more recently by Pranesh and Kiran [22] and Alloui et al. [23].
The main object of this paper is to study the onset of double diffusive convection in a micropolar fluid using one linear and five non-linear concentration profiles as a mechanism to control the onset of convection.
2. Mathematical Formulation
Consider a horizontal layer of infinite extent occupied by a Boussinesquian, micropolar fluid of depth “d” as shown in Figure 1. Let DT and DC is the difference in tempera-
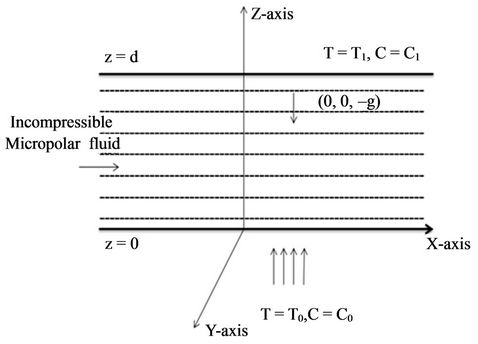
Figure 1. Schematic diagram for the problem.
ture and species concentration of the fluid between lower and upper plates. Appropriate single-phase heat and solute transport Equations are chosen with effective heat and capacity ratio and effective thermal diffusivity. A Cartesian coordinate system (x, y, z) is used with the origin at the bottom of the fluid layer and the z-axis vertically upwards.
The governing Equations for the Rayleigh-Benard situation in a Boussinesquian micropolar fluid are;
Continuity Equation:
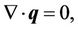 (1)
(1)
Conservation linear momentum:
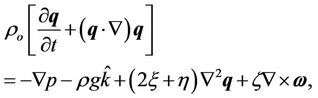 (2)
(2)
Conservation of angular velocity:
 (3)
(3)
Conservation of energy:
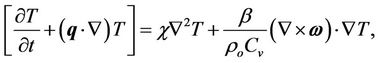 (4)
(4)
Conservation soluted concentration:
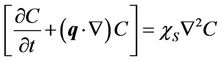 , (5)
, (5)
Equation of state:
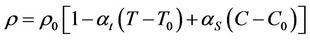 , (6)
, (6)
Here, 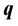 is the velocity,
is the velocity, 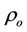 is density of the fluid at temperature T = T0, p is the pressure,
is density of the fluid at temperature T = T0, p is the pressure, 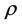 is the density,
is the density,  is acceleration due to gravity,
is acceleration due to gravity,  is coupling viscosity coefficient or vortex viscosity,
is coupling viscosity coefficient or vortex viscosity, 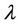 and
and  are the bulk and shear spin-viscosity coefficients,
are the bulk and shear spin-viscosity coefficients, 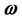 is the angular velocity, I is moment of inertia,
is the angular velocity, I is moment of inertia, 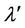 and
and 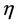 are bulk and shear spin-viscosity coefficients, T is the temperature,
are bulk and shear spin-viscosity coefficients, T is the temperature, 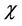 is the thermal conductivity,
is the thermal conductivity, 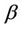 is micropolar heat conduction coefficient,
is micropolar heat conduction coefficient, 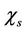 is solute thermal conductivity, C is concentration,
is solute thermal conductivity, C is concentration, 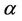 is coefficient of thermal expansion,
is coefficient of thermal expansion, 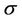 is electrical conductivity.
is electrical conductivity.
3. Basic State
The basic state of the fluid quiescent and is given by
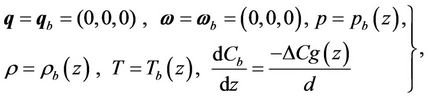 (7)
(7)
where the subscript “b” denotes the basic state. The non-dimensional basic concentration gradient g(z) which is non-negative satisfies the condition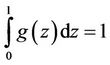 .
.
One linear and five non-linear basic concentration gradients are considered in this paper to study the onset of convection and are given below in Table 1.
Substituting Equation (7) into Equations (1)-(6), we get the equations governing the basic state;
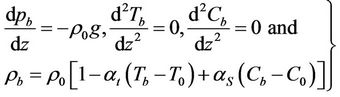 . (8)
. (8)
4. Linear Stability Analysis
We now superpose infinitesimal perturbations on the quiescent basic state and study the instability. Let the basic state be disturbed by an infinitesimal thermal perturbation, given by;
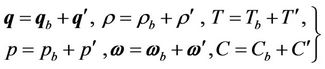 . (9)
. (9)
The prime indicates that the quantities are infinitesimal
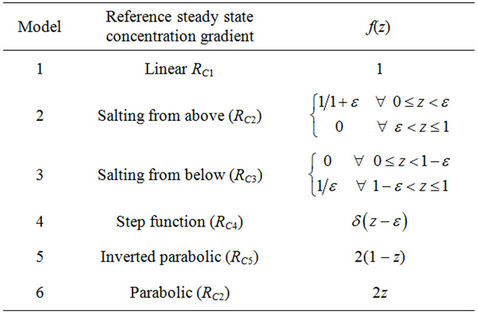
Table 1. Non-uniform basic concentration profiles.
perturbations. In the present problem we assume that principle of exchange of stability to be valid and hence deal with only stationary convection. Substituting Equation (9) into Equations (1) to (6) and using the basic state (8) we get, the linearized Equations governing the infinitesimal perturbations in the form:
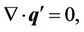 (10)
(10)
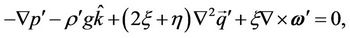 (11)
(11)
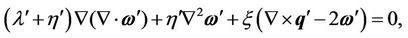 (12)
(12)
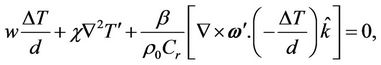 (13)
(13)
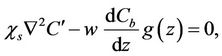 (14)
(14)
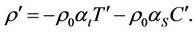 (15)
(15)
The perturbation Equations (10)-(15) are non-dimensionalised using the following definitions:
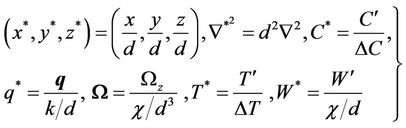 . (16)
. (16)
Using Equation (15) in Equation (11), operating curl twice on the resulting Equation, and operating curl on Equation (12), we get
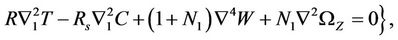 (17)
(17)
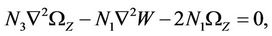 (18)
(18)
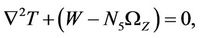 (19)
(19)
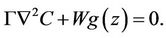 (20)
(20)
where, the asterisks have been dropped for simplicity and non-dimensional parameters are
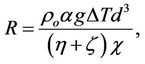 (Rayleigh number),
(Rayleigh number),
 (Solutal Rayleigh number)
(Solutal Rayleigh number)
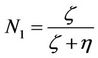 (Coupling parameter),
(Coupling parameter),
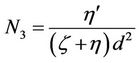 (Couple stress parameter)
(Couple stress parameter)
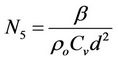 (Micropolar heat conduction parameter)
(Micropolar heat conduction parameter)
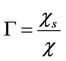 (Ratio of diffusivity)
(Ratio of diffusivity)
The infinitesimal perturbation 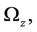
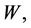 T and C are assumed to be periodic waves (see Chandrasekhar 1961) and hence these permit a normal mode solution in the form:
T and C are assumed to be periodic waves (see Chandrasekhar 1961) and hence these permit a normal mode solution in the form:
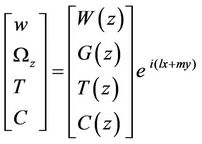 , (21)
, (21)
where  and
and 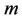 are horizontal components of the wave number
are horizontal components of the wave number , substituting Equation (21) into Equations (17)-(20), we get
, substituting Equation (21) into Equations (17)-(20), we get
 (22)
(22)
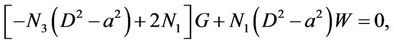 (23)
(23)
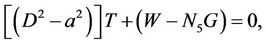 (24)
(24)
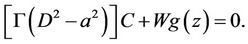 (25)
(25)
and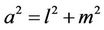 .
.
The sets of ordinary differential Equations (22)-(25) are approximations based on physical considerations to the system of partial differential Equations (17)-(20). Although the relationship between the solutions of the governing partial differential Equations and the corresponding ordinary differential Equations has not been established, these linear models reproduce qualitatively the convective phenomena observable through the full system.
When the fluid layer is heated from below, the nonuniform concentration gradient g(z) is not only nonnegative but also decreases monotonically. Thus our main interest here is to find out suitable non-uniform basic concentration profile that gives the maximum/minimum critical Rayleigh number, for this we have considered the various concentration profile as shown in the Table 1.
In the Galerkin procedure, we expand the velocity, microrotation, temperature, concentration by,
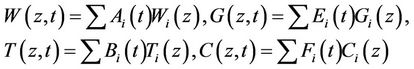
where 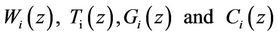 are polynomials in z that generally have to satisfy the given boundary conditions. For the single term Galerkin expansion technique we take i = j = 1. Multiplying Equation (22) by W, Equation (23) by G, Equation (24) by T and, and Equation (25) by C, integrating the resulting integrals by parts with respect to z from 0 to 1 and taking
are polynomials in z that generally have to satisfy the given boundary conditions. For the single term Galerkin expansion technique we take i = j = 1. Multiplying Equation (22) by W, Equation (23) by G, Equation (24) by T and, and Equation (25) by C, integrating the resulting integrals by parts with respect to z from 0 to 1 and taking 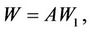
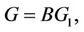
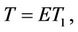
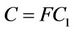 in which A, B, E and F are constants and W1, G1, T1, C1 are trial functions, yield the following Equation for the Rayleigh number,
in which A, B, E and F are constants and W1, G1, T1, C1 are trial functions, yield the following Equation for the Rayleigh number,
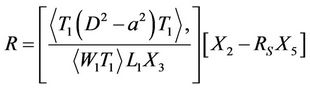 , (26)
, (26)
where
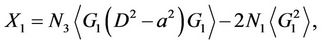
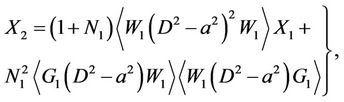

 .
.
In the Equation (26), 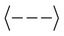 denotes integration with respect to z between z = 0 and z = 1. We note here that R in Equation (30) is a functional and the Euler-Lagrange Equations for the extremisation of R are Equations (22) to (25).
denotes integration with respect to z between z = 0 and z = 1. We note here that R in Equation (30) is a functional and the Euler-Lagrange Equations for the extremisation of R are Equations (22) to (25).
The value of critical Rayleigh number depends on the boundaries. In this paper we consider following boundary combinations.
1) Free-Free Isothermal-Permeable No-Spin condition:
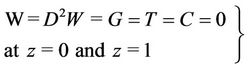 . (27)
. (27)
2) Rigid-Free Isothermal-Permeable No-Spin condition:
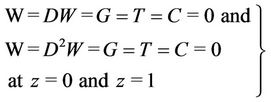 . (28)
. (28)
3) Rigid-Rigid Isothermal-Permeable No-Spin condition:
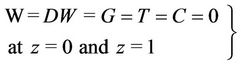 . (29)
. (29)
The trial functions satisfying the above boundary conditions are presented in Table 2.
5. Result and Discussion
In the paper, we study the effect of basic non-uniform concentration gradient on the convective instability of a micropolar fluid. One uniform, five non-uniform basic concentration gradient are chosen for the study and this have been presented in Table 1. We find that,
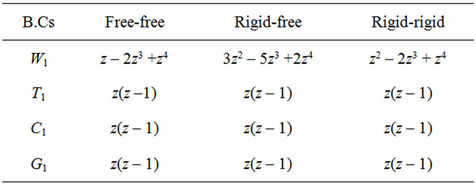
Table 2. Trial functions for the different boundary conditions.
(RC2) < (RC5) = (RC1) < (RC3) < (RC6) < (RC4)
for symmetric boundary combination(free-free and rigidrigid). In the case of non-symmetric boundary combination namely, rigid-free we find that(RC2)< (RC5) < (RC1) < (RC3) < (RC4) = (RC6)i.e., salting from above and step function profiles are most destabilizing and stabilizing respectively.
Figures 2(a), 3(a) and 4(a) are the plots of critical Rayeigh number Rc versus coupling parameter N1 for different values of solutal Rayleigh number, Rs and different non-uniform basic concentration profiles, for freefree, rigid-free and rigid-rigid isothermal permeable, nospin boundary condition. It is observed that as N1 increases, Rc also increases. Increase in N1 indicates the increase in the concentration of the microelements. These microelements consume the greater part of the energy in developing gyrational velocity and as a result the onset of convection is delayed. From this we conclude that an increase in N1 is to stabilize the system.
Figures 2(b), 3(b) and 4(b) are the plots of critical Rayeigh number Rc versus couple stress parameter N3 for different values of solutal Rayleigh number, Rs and different non-uniform basic concentration profiles, for freefree, rigid-free and rigid-rigid isothermal permeable, nospin boundary condition. We note that the role played by the shear stress in the conservation of linear momentum is played by the couple stress in angular momentum Equations. It is observed that as N3 increases the Rc decreases, because, when N3 increases the couple stress of the fluid increases, which causes the microrotation to decease. Therefore, increase in N3 destabilize the system hence, we can conclude that couple stress are operative only for small values of N3.
Figures 2(c), 3(c) and 4(c) are the plots of critical Rayeigh number Rc versus micropolar heat conduction parameter N5 for different values of solutal Rayleigh number, Rs and different non-uniform basic concentration profiles, for free-free, rigid-free and rigid-rigid isothermal permeable, no-spin boundary condition. When N5 increases, the heat induced into the fluid due to these microelements also increases, thus reducing the heat transfer from bottom to top. The decrease in heat transfer is responsible for delaying the onset of instability. Thus
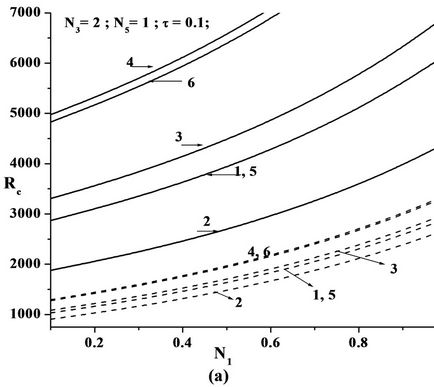
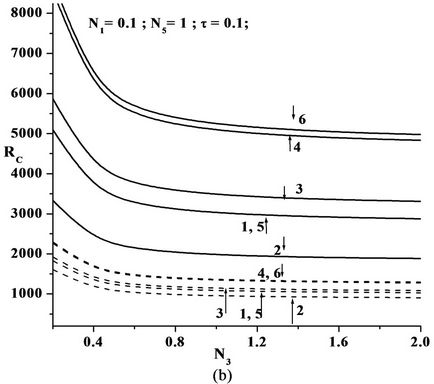
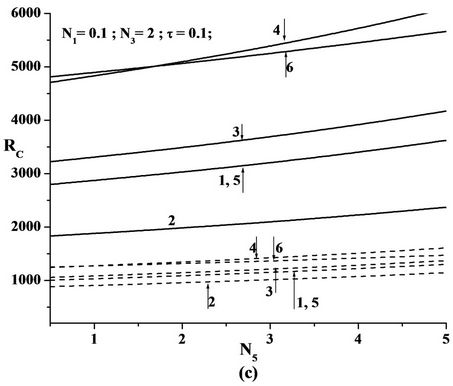
Figure 2. Plot of Critical Rayleigh number versus (a) Coupling parameter N1, (b) Couple stress parameter N3, (c) Micropolar heat conduction parameter N5 for various Solutal Rayleigh number RS for the six models as in the Table 1 in the case of free-free isothermal-permeable no spin condition (---RS = 25 & —RS = 200).
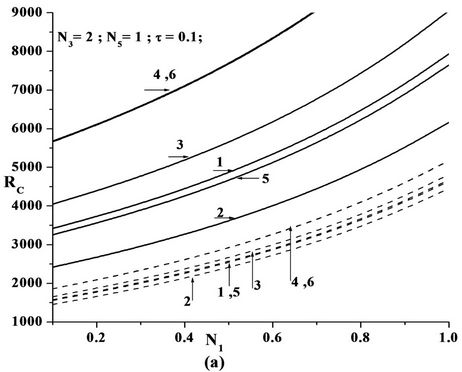

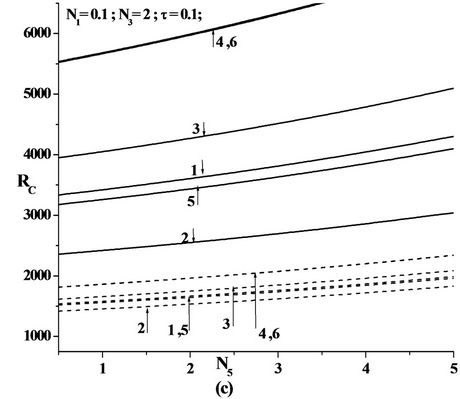
Figure 3. Plot of Critical Rayleigh number versus (a) Coupling parameter N1, (b) Couple stress parameter N3, (c) Micropolar heat conduction parameter N5 for various Solutal Rayleigh number RS for the six models as in the Table 1 in the case of rigid-free isothermal-permeable no spin condition (---RS = 50 & —RS = 200).
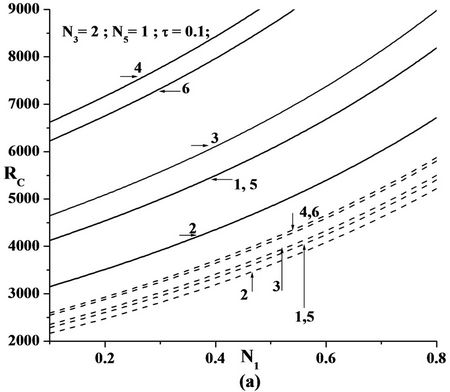
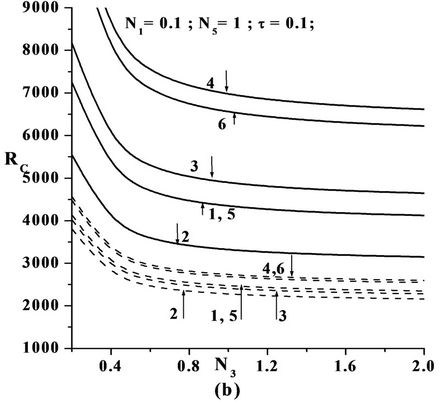
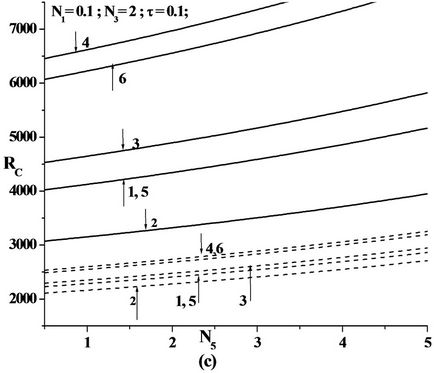
Figure 4. Plot of Critical Rayleigh number versus; (a) Coupling parameter N1; (b) Couple stress parameter N3; (c) Micropolar heat conduction parameter N5 for various Solutal Rayleigh number RS for the six models as in the Table 1 in the case of rigid-rigid isothermal-permeable no spin condition (---RS = 25 & —RS = 200).
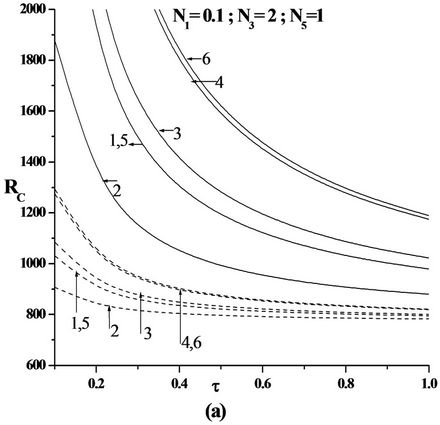
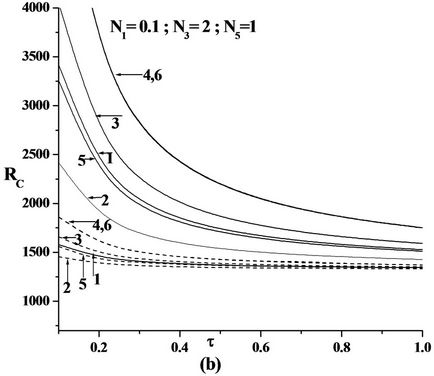
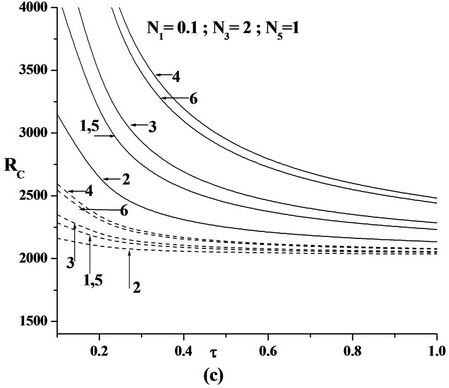
Figure 5. Plot of Critical Rayleigh number versus Ratio of diffusivity for (a) Free-free; (b) Rigid-free; (c) Rigid-rigid isothermal-permeable no spin condition for various Solutal Rayleigh number RS for the six models as in the Table 1 (---RS = 25 & —RS = 200).
N5 stabilizes the system.
Figure 5 is the plot of critical Rayeigh number Rc versus diffusivity ratio г. The increase in the value of г decreases Rc, thus advancing the onset of double diffusive convection.
From the above figures we observed that increase in solutal Rayleigh number Rs increases Rc, indicating that the additional diffusing component stabilizes the system.
From the figures we also observe that 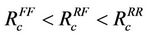 , where superscript denotes the velocity boundary combinations.
, where superscript denotes the velocity boundary combinations.
6. Conclusions
The following conclusions are drawn from the study:
1) By choosing appropriate non-uniform basic temperature profile it is possible to control the RayleighBénard convection.
2) The step function is the most stabilizing basic concentration distribution and salting from above is the most destabilizing basic concentration distribution.
3) The effect of increase in the value of solute Rayliegh number is to increase the value of Rc, thus making the system more stable.
4) It is found that the increase in the value of diffusivity ratio, decrease the value of Rc, thus advancing the onset of double diffusive convection.
5) The coupling parameter N1 and micropolar heat conduction parameter N5 stabilizes the system, whereas the couple stress parameter N3 destabilizes the system.
6) Rayleigh-Bénard double diffusive convection in Newtonian fluids may be delayed by adding micron sized suspended particles.
7. Acknowledgements
Authors would like to acknowledge the support of Christ University administration in completing the work and also Dr. Pradeep G Siddheshwar for suggesting the problem and for many stimulating discussions.
REFERENCES
- A. Mojtabi and M. C. Charrier-Mojtabi, “Double Diffusive Convection in Porous Media,” Handbook of Porous Media, Marcel Dekker, New York, 2005, pp. 269-320.
- M. E. Stern, “The Salt Fountain and Thermohaline Convection,” Tellus, Vol. 12, No. 2, 1960, pp. 172-175. doi:10.1111/j.2153-3490.1960.tb01295.x
- M. E. Stern, “Collective Instability of Salt Fingers,” Journal of Fluid Mechanics, Vol. 35, No. 2, 1969, pp. 209- 218. doi:10.1017/S0022112069001066
- J. S. Turner, “Buoyancy Effects in Fluids,” Cambridge University Press, Cambridge, 1973.
- S. Chen, J. Tolke and M. Krafczyk, “Numerical Investigation of Double-Diffusive (Natural) Convection in Vertical Annuluses with Opposing Temperature and Concentration Gradients,” International Journal of Heat and Fluid Flow, Vol. 31, No. 2, 2010, pp. 217-226. doi:10.1016/j.ijheatfluidflow.2009.12.013
- M. S. Malashetty and B. S. Biradar, “The Onset of Double Diffusive Convection in a Binary Maxwell Fluid Saturated Porous Layer with Cross Diffusion Effects,” Physics of Fluids, Vol. 23, No. 6, 2011, p. 13. doi:10.1063/1.3601482
- A. C. Eringen, “Micropolar Theory of Liquid Crystals,” In: J. F. Johnson and R. S. Porter, Eds., Liquid Crystals and Ordered Fluids, Vol. 3, Plenum Publishing, New York, 1978.
- A. C. Eringen, “Theory of Micropolar Fluids,” Journal of Mathematics and Mechanics, Vol. 16, 1966, pp. 1-18.
- A. C. Eringen, “Micro Continuum Field Theory,” Springer Verlag, New York, 1999.
- G. Lukaszewicz, “Micropolar Fluid Theory and Applications,” Birkhauser, Boston, 1999.
- H. Power, “Bio-Fluid Mechanics, Advances in Fluid Mechanics,” W.I.T. Press, UK, 1995.
- A. B. Datta and V. U. K. Sastry, “Thermal Instability of a Horizontal Layer of Micropolar Fluid Heated from Below,” International Journal of Engineering Science, Vol. 14, No. 7, 1976, pp. 631-637. doi:10.1016/0020-7225(76)90005-7
- G. Ahmadi, “Stability of a Micropolar Fluid Layer Heated from Below,” International Journal of Engineering Science, Vol. 14, No. 1, 1976, pp. 81-89.
- K. V. Rama Rao, “Thermal Instability in a Micropolar Fluid Layer Subject to Magnetic Field,” International Journal of Engineering Science, Vol. 18, No. 5, 1980, pp. 741-750. doi:10.1016/0020-7225(80)90107-X
- C. Perez-Garcia and J. M. Rubi, “On the Possibility of Overstable Motions of Micropolar Fluids Heated From Below,” International Journal of Engineering Science, Vol. 20, No. 7, 1982, pp. 873-878. doi:10.1016/0020-7225(82)90009-X
- S. P. Bhattacharyya and S. K. Jena, “On the Stability of Hot Layer of Micropolar Fluid,” International Journal of Engineering Science, Vol. 21, No. 9, 1983, pp. 1019-1024. doi:10.1016/0020-7225(83)90043-5
- P. G. Siddheshwar and S. Pranesh, “Magneto Convection in a Micropolar Fluid,” International Journal of Engineering Science, Vol. 36, No. 10, 1998, pp. 1173-1181. doi:10.1016/S0020-7225(98)00013-5
- P. G. Siddheshwar and S. Pranesh, “Linear and Weakly Non-Linear Analyses of Convection in a Micropolar Fluid,” Hydrodynamics VI-Theory and Applications, 2005, pp. 487-493.
- P. G. Siddheshwar and S. Pranesh, “Magnetoconvection in Fluids with Suspended Particles under 1g and mg,” Aerospace Science and Technology, Vol. 6, No. 2, 2001, pp. 105-114. doi:10.1016/S1270-9638(01)01144-0
- P. G. Siddheshwar and S. Pranesh, “Suction-Injection Effects on the Onset of Rayleigh-Benard-Marangoni Convection in a Fluid with Suspended Articles,” Acta Mechanica, Vol. 152, No. 1-4, 2001, pp. 241-252. doi:10.1007/BF01176958
- Y. N. Murthy and V. V. Ramana Rao, “Effect of Through Flow on Marangoni Convection in Micropolar Fluids,” Acta Mechanica, Vol. 138, No. 3-4, 1999, pp. 211-217, doi:10.1007/BF01291845
- S. Pranesh and R. V. Kiran, “Study of Rayleigh-Bénard Magneto Convection in a Micropolar Fluid with Maxwell-Cattaneo Law,” Applied Mathematics, Vol. 1, 2010, pp. 470-480, doi:10.4236/am.2010.16062
- Z. Alloui, H. Beji and P. Vasseur, “Double-Diffusive and Soret-Induced Convection of a Micropolar Fluid in a Vertical Channel,” Computers & Mathematics with Applications, Vol. 62, No. 2, 2011, pp. 725-736. doi:10.1016/j.camwa.2011.05.053

