Applied Mathematics
Vol.3 No.8(2012), Article ID:21475,7 pages DOI:10.4236/am.2012.38125
Impact of Quantum Fluctuations on the Modulational Instability of a Modified Gross-Pitaevskii Equation with Two-Body Interaction
1Laboratory of Mechanics, Department of Physics, Faculty of Science, University of Yaounde I, Yaounde, Cameroon
2Departement de Physique, Universite des Sciences et Techniques de Masuku, Franceville, Gabon
3Ecole Normale Superieure, Libreville, Gabon
4Max Planck Institute for the Physics of Complex Systems, Dresden, Germany
5Group of Nonlinear Physics and Complex Systems, Faculty of Science, University of Douala, Douala, Cameroon
Email: glatchio@yahoo.fr, tekogo@yahoo.fr, mohamali@pks.mpg.de, tckofane@yahoo.com
Received December 19, 2011; revised April 14, 2012; accepted April 21, 2012
Keywords: Modulational Instability; Modified Gross-Pitaevskii Equation; Quantum Fluctuations
ABSTRACT
Modulational instability conditions for the generation of localized structures in the context of matter waves in BoseEinstein condensates are investigated analytically and numerically. The model is based on a modified Gross-Pitaevskii equation, which account for the energy dependence of the two-body scattering amplitude. It is shown that the modified term due to the quantum fluctuations modify significantly the modulational instability gain. Direct numerical simulations of the full modified Gross-Pitaevskii equation are performed, and it is found that the modulated plane wave evolves into a train of pulses, which is destroyed at longer times due to the effects of quantum fluctuations.
1. Introduction
Bose-Einstein condensates (BEC) made of ultracold atomic alkali gases have proven to be a fertile field in the last years for the study of nonlinear matter waves in recent reviews and monographs [1,2]. Mean-field theory provides a consistent framework for the modeling of the principal characteristics of condensation and elucidates the role of the interactions between the particles. A generic theoretical model widely employed involves the Gross-Pitaevskii (GP) equation, which bears the form of a nonlinear Schrödinger-type equation with a cubic nonlinearity, taking into account boson interactions, in addition to the confinement potential imposed on the BEC in a potential trap. The scattering length as, although initially taken to be positive (accounting for repulsive interactions and prescribing condensate stability), has later been sign-inverted to negative (attractive interaction) via Feshbach resonance, in appropriately designed experiments. This allowed for the prediction of BEC state instability, eventually leading to wave collapse, which is only possible in the attractive case  [3]. Modulational instability (MI) is also an interesting issue in BEC [4]. MI is an indispensable mechanism for understanding pattern formation from a uniform medium. This phenomenon appears in continuum as well as in discrete models and finds its applications in many physical settings [5,6]. MI occurs when a constant-wave background becomes unstable to induced sinusoidal modulations under the combined effects of nonlinearity and dispersion. The slow modulation of a monochromatic plane wave in BEC can leads to an exponential growth of the unstable modes and eventually may results in the formation of envelope soliton train, which is described by the GP equation. Hence, it is important and worthful to study the properties of the MI in trapped BEC. A description based on the GP equation with cubic nonlinearity, however, is adequate only at low densities.
[3]. Modulational instability (MI) is also an interesting issue in BEC [4]. MI is an indispensable mechanism for understanding pattern formation from a uniform medium. This phenomenon appears in continuum as well as in discrete models and finds its applications in many physical settings [5,6]. MI occurs when a constant-wave background becomes unstable to induced sinusoidal modulations under the combined effects of nonlinearity and dispersion. The slow modulation of a monochromatic plane wave in BEC can leads to an exponential growth of the unstable modes and eventually may results in the formation of envelope soliton train, which is described by the GP equation. Hence, it is important and worthful to study the properties of the MI in trapped BEC. A description based on the GP equation with cubic nonlinearity, however, is adequate only at low densities.
For higher densities or stronger confinement, it has become clear that a better description of atom-atom interaction will be required. For homogeneous systems, it has been demonstrated in a recent work by Cowell et al. [7] that different potentials having the same scattering length can lead to a vastly different ground-state energy. For inhomogeneous systems, recent works on two atoms in a trap have shown that the shape-independent approximation becomes less valid under strong confinement [8]. Then, a modified GP equation, which incorporates the energy dependence of the two-body scattering amplitude through an effective-range expansion has been derived [9]. To the best of our knowledge, MI in this system has not been investigated. The principal objet of this paper is to show analytically conditions stability for the generation of localized structures in BEC via MI and to discuss the comparison between the linear analysis of plane wave solutions and the direct numerical simulations of the full modified GP equation.
2. Modified Gross-Pitaevskii Equations
The dynamic behaviour of the three dimensional (3D) modified GP equation which take into account quantum fluctuations and the shape dependence on the interaction potential can be described by [9]
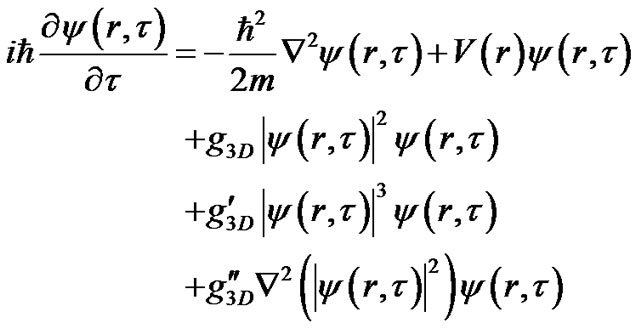 (1)
(1)
where 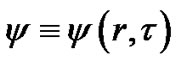 denotes the BEC wave function at position
denotes the BEC wave function at position  and time
and time 
 is the Laplacian,
is the Laplacian,  is the mass of the condensate,
is the mass of the condensate,
 characterizes the two-body interactions,
characterizes the two-body interactions, 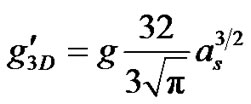 is the correction term due to quantum fluctuation. The extra correction term
is the correction term due to quantum fluctuation. The extra correction term 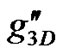 incorporates the shape dependence on the interaction potential. For a hard sphere potential,
incorporates the shape dependence on the interaction potential. For a hard sphere potential, 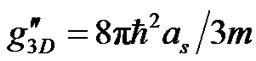 [9]. The potential
[9]. The potential 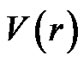 confines the atoms in a trap. For harmonic trapping,
confines the atoms in a trap. For harmonic trapping, 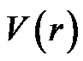 is given by
is given by
 where
where 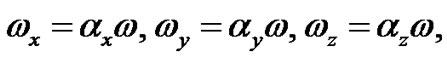 are the trap frequencies,
are the trap frequencies,  and
and 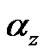 are the coupling constants along the
are the coupling constants along the  and
and 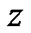 axes. When the trapping in the transverse directions is stronger, the BEC is cigar-shaped and the 3D modified GP equation can be reduced to the one dimensional (1D) modified GP equation. In order to normalize the modified GP equation, we introduce the dimensionless variables
axes. When the trapping in the transverse directions is stronger, the BEC is cigar-shaped and the 3D modified GP equation can be reduced to the one dimensional (1D) modified GP equation. In order to normalize the modified GP equation, we introduce the dimensionless variables
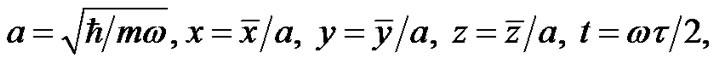
and . By substituting these new variables into Equation (1), we obtain
. By substituting these new variables into Equation (1), we obtain
 (2)
(2)
where
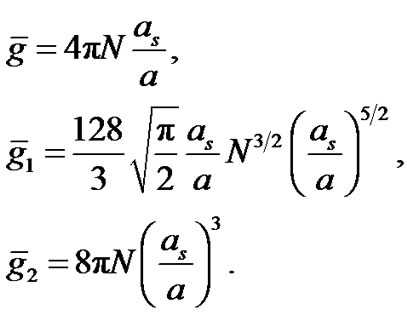
We focus our attention on the trapped BEC with attractive interaction. In this respect, the coefficient  is a complex number. The following physical parameters have been used in the rest of the paper
is a complex number. The following physical parameters have been used in the rest of the paper 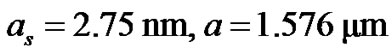 [10].
[10].
We assume a separable ansatz for the solution of Equation (2) such that [11]
 (3)
(3)
with
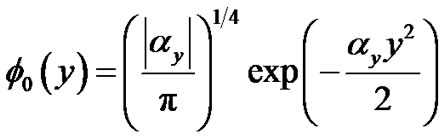
and
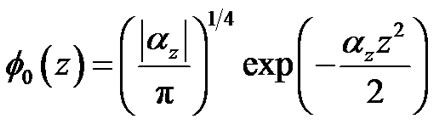
the respective ground state wave functions in yand z-directions. Using this ansatz in Equation (2), multiplying by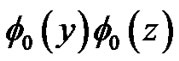 , integrating over
, integrating over  and
and , we obtain
, we obtain
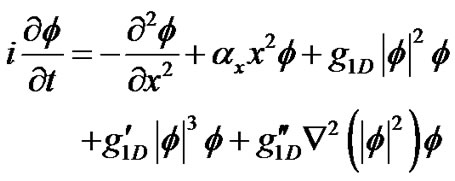 (4)
(4)
with
 (5)
(5)
3. Linear Stability Analysis
In order to investigate the MI process in the presence of harmonic trapping potential, we begin with the modified lens-type transformation of the form [12,13]
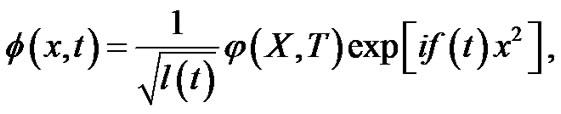 (6)
(6)
where  is a real function of time,
is a real function of time,

Upon the above conditions, the equation for 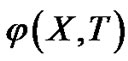 becomes
becomes
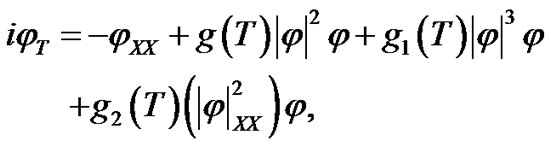 (7)
(7)
where

Now, we analyze the MI of the modified GP equation described by Equation (7). We consider the evolution of the small modulation  according to
according to
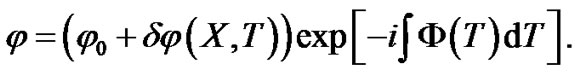 (8)
(8)
where 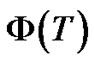 is a nonlinear frequency shift. Substituting Equation (8) into Equation (7) and neglecting second-order terms in
is a nonlinear frequency shift. Substituting Equation (8) into Equation (7) and neglecting second-order terms in  and its complex conjugate
and its complex conjugate  we obtain
we obtain
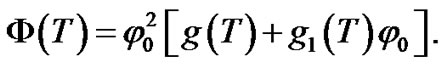 (9)
(9)
Then, the equation describing the dynamics of the perturbation take the form
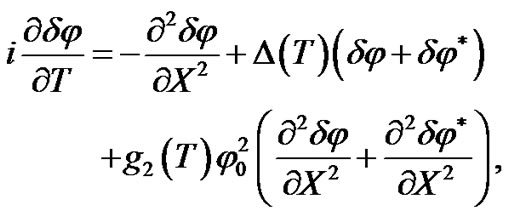 (10)
(10)
where 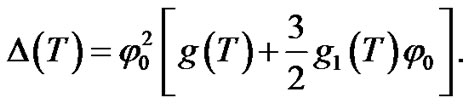
To perform a precise analysis of Equation (10), we use the complex representation  Then, Equation (10) is transformed into the following two coupled equations
Then, Equation (10) is transformed into the following two coupled equations
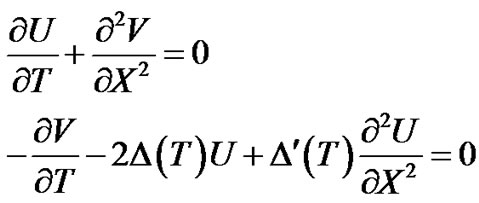 (11)
(11)
where 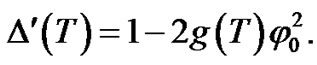 We assume that the amplitude perturbation varies as
We assume that the amplitude perturbation varies as
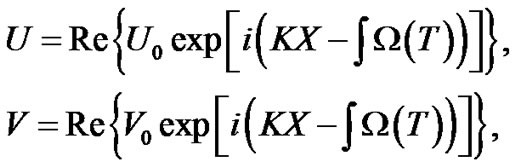
where  and
and  are, the wave number and frequency of the modulation, respectively. Substituting these expressions in Equation (11), we obtain the following time-dependent nonlinear dispersion relation
are, the wave number and frequency of the modulation, respectively. Substituting these expressions in Equation (11), we obtain the following time-dependent nonlinear dispersion relation

 (12)
(12)
If 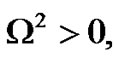 the system is stable under modulation, otherwise if
the system is stable under modulation, otherwise if 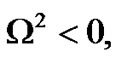 the system is unstable. Therefore, the instability growth rate can be written as
the system is unstable. Therefore, the instability growth rate can be written as
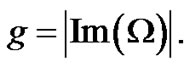
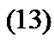
For  we recover the GP equation with two-body interaction whose MI properties have been analyzed in detail by Xu [14]. Next, we are interested in MI conditions in BEC taking the modified GP equation as model equation and discuss the following two cases.
we recover the GP equation with two-body interaction whose MI properties have been analyzed in detail by Xu [14]. Next, we are interested in MI conditions in BEC taking the modified GP equation as model equation and discuss the following two cases.
For a first case, we set 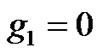 (absence of quantum fluctuations) and
(absence of quantum fluctuations) and  In this situation, the MI may develop during the time scale t < tc, where
In this situation, the MI may develop during the time scale t < tc, where
 (14)
(14)
with

From Equation (14), one can see that the external trapping parameter 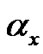 enhances the instability which occurs at short time scale for stronger trapping. Figure 1 portrays the MI gain provided by Equation (11), as a function of K, for three values of the trapping parameter
enhances the instability which occurs at short time scale for stronger trapping. Figure 1 portrays the MI gain provided by Equation (11), as a function of K, for three values of the trapping parameter . When
. When 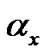 increases, both the peak gain and the MI bandwidth decrease. We have also observed that the parameter
increases, both the peak gain and the MI bandwidth decrease. We have also observed that the parameter 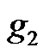 essentially does not influence the MI peak gain and the MI bandwidth.
essentially does not influence the MI peak gain and the MI bandwidth.
For the second case, the effects of quantum fluctuations have been taken into account ( and
and ). In this case, it has been extremely difficult to perform a complete analytical analysis to obtain the MI critical time. However, as can be seen from Figure 2, the parameter
). In this case, it has been extremely difficult to perform a complete analytical analysis to obtain the MI critical time. However, as can be seen from Figure 2, the parameter  extends the bandwidth of MI to the whole spectrum of the wave number
extends the bandwidth of MI to the whole spectrum of the wave number 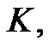 contrary to the previous case where the instability is of the finite bandwidth type. This is one of the main result of present paper.
contrary to the previous case where the instability is of the finite bandwidth type. This is one of the main result of present paper.

Figure 1. The MI gain in the modified GP equation for g1 = 0, and g2 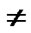 0. The parameters used are φ0 = 10, N = 50, αy = 1, αz = 1, t = 30, αs = –2.75 nm, α = 1.576 μm.
0. The parameters used are φ0 = 10, N = 50, αy = 1, αz = 1, t = 30, αs = –2.75 nm, α = 1.576 μm.

Figure 2. The MI gain in the modified GP equation for g1  0, and g2
0, and g2 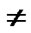 0. Other parameters are φ0 = 10, N = 50, αy = 1, αz = 1, t = 30, αs = –2.75 nm, α = 1.576 μm.
0. Other parameters are φ0 = 10, N = 50, αy = 1, αz = 1, t = 30, αs = –2.75 nm, α = 1.576 μm.
4. Numerical Simulations
To verify our results and get more insight on the development of the instability, we solve numerically Equation (4) by using the split-step Fourier method with periodic boundary conditions on the spatial domain. The initial condition used is
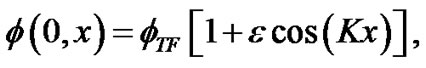 (15)
(15)
where  is the background wave function in the Thomas-Fermi approximation. In a region close to the center
is the background wave function in the Thomas-Fermi approximation. In a region close to the center 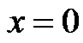 and for convenient values of the potential,
and for convenient values of the potential, 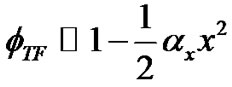 [13,14]. In all numerical simulations, we set
[13,14]. In all numerical simulations, we set 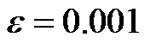 (small compared to
(small compared to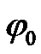 ). To illustrate our theoretical predictions, we consider two special cases. We first consider the case
). To illustrate our theoretical predictions, we consider two special cases. We first consider the case 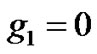 and
and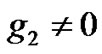 . Figure 3 depicts the spatial evolution of a modulated amplitude of the wave for the wave number
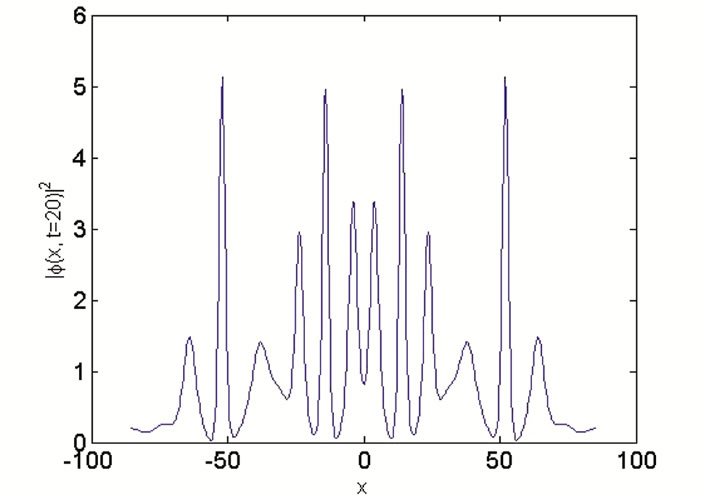
. Figure 3 depicts the spatial evolution of a modulated amplitude of the wave for the wave number . The initial wave breaks up into a pulse chain [Figure 3(a) at
. The initial wave breaks up into a pulse chain [Figure 3(a) at 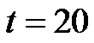 and Figure 3(b) at
and Figure 3(b) at ] as the time increases.
] as the time increases.
Figure 4 shows the time evolution of the maximal amplitude in Figures 4(a) and (c); and the spatiotemporal evolution of the modulated envelope  in Figures 4(b) and (d). By comparing Figures 4(a) and (b), we realize that for the strong trapping case in Figure 4(a), the rate of MI increases. Secondly, we consider the general modified GP equation with
in Figures 4(b) and (d). By comparing Figures 4(a) and (b), we realize that for the strong trapping case in Figure 4(a), the rate of MI increases. Secondly, we consider the general modified GP equation with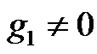 , and
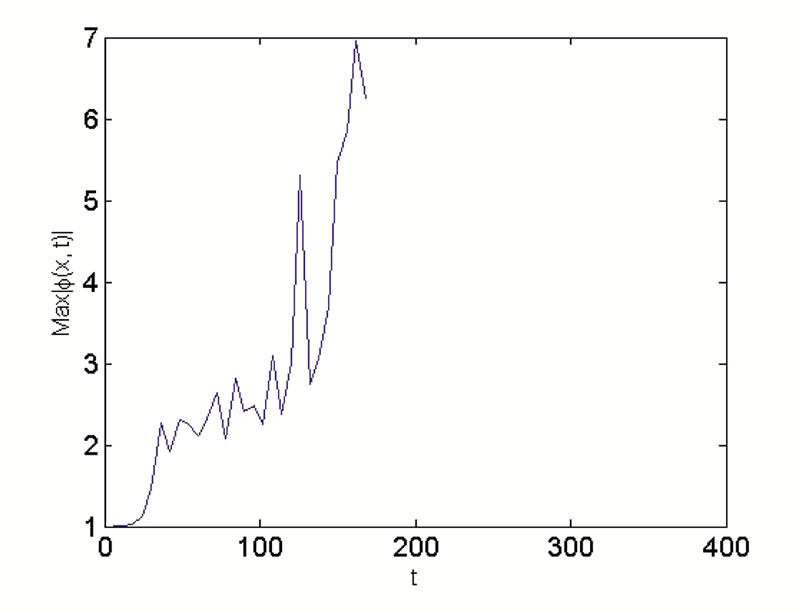
, and . From Figure 2, we choose
. From Figure 2, we choose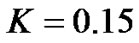 , which belongs to the MI zone. Figure 5 portrays the time evolution of the maximal amplitude in Figures 5(a) and (c); and the spatiotemporal evolution of
, which belongs to the MI zone. Figure 5 portrays the time evolution of the maximal amplitude in Figures 5(a) and (c); and the spatiotemporal evolution of  in Figures 5(b) and (d). We obtain also a soliton wave train, formed as a result of the instability. However, by comparing Figure 5 and Figure 4 obtained in the previous case, we realize that the quantum fluctuations destroyed the wave trains, which is also one of the main findings of this work.
in Figures 5(b) and (d). We obtain also a soliton wave train, formed as a result of the instability. However, by comparing Figure 5 and Figure 4 obtained in the previous case, we realize that the quantum fluctuations destroyed the wave trains, which is also one of the main findings of this work.
 (a)
(a) (b)
(b)
Figure 3. Spatial evolution of the modulated waves in terms of solitary waves on top of the Thomas-Fermi cloud, introducing the occurrence of the modulational instability through the system. (a) t = 20; (b) t = 40. The other parameters used are αx = 0.0004, αy = 1, αz = 1, K = 0.15, ε = 0.001, N = 20, αs = –2.75 nm, α = 1.576 μm.
 (a)
(a)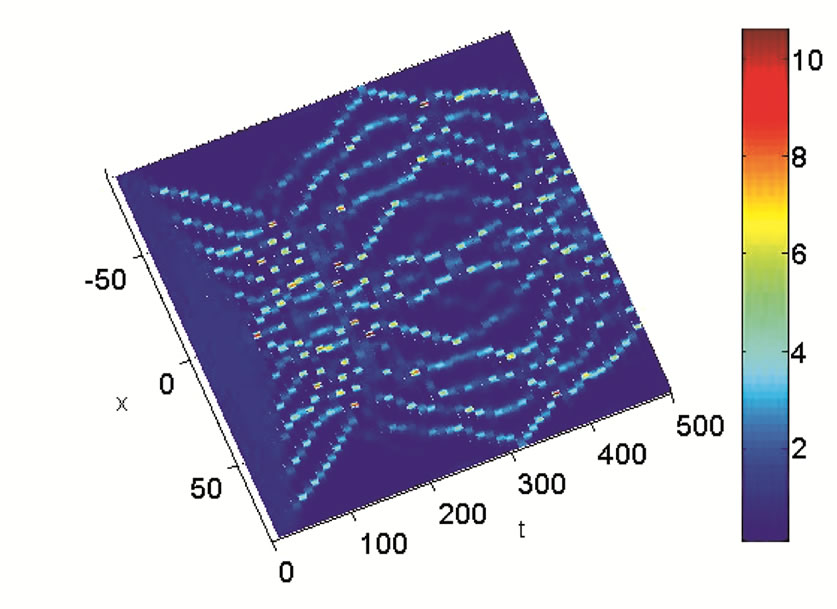 (b)
(b)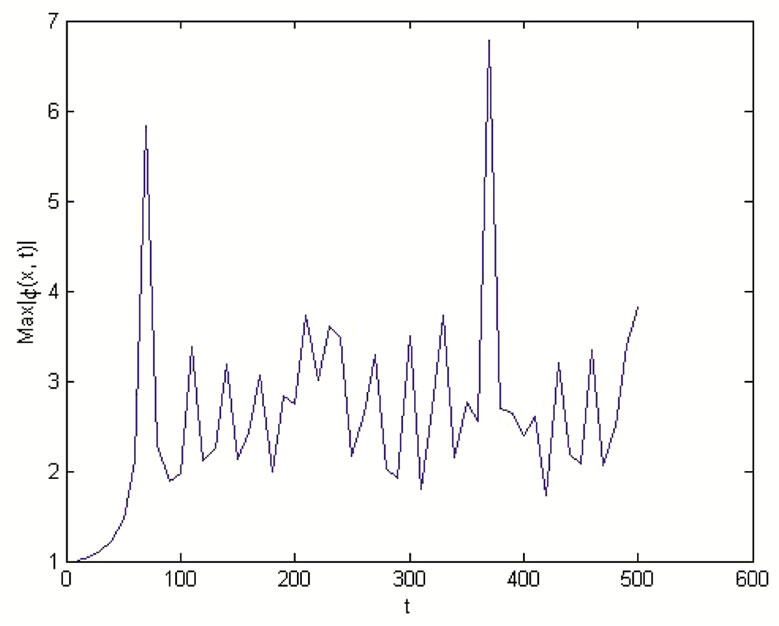 (c)
(c) (d)
(d)
Figure 4. Spatiotemporal evolution of the maximum amplitude of the waves showing the formation of wave trains in the case g1 = 0, and g2  0. The parameters used are K = 0.15, ε = 0.001, αy = 1, αz = 1, αs = –2.75 nm, α = 1.576 μm. (a)
0. The parameters used are K = 0.15, ε = 0.001, αy = 1, αz = 1, αs = –2.75 nm, α = 1.576 μm. (a)  for N = 50, αx = 0.0004 (weak trapping); (b)
for N = 50, αx = 0.0004 (weak trapping); (b) 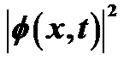 for N = 50, αx = 0.0004 (weak trapping); (c)
for N = 50, αx = 0.0004 (weak trapping); (c)  for N = 20, αx = 0.0004 (strong trapping); (d)
for N = 20, αx = 0.0004 (strong trapping); (d)  for N = 20, αx = 0.0004 (strong trapping).
for N = 20, αx = 0.0004 (strong trapping).
 (a)
(a) (b)
(b)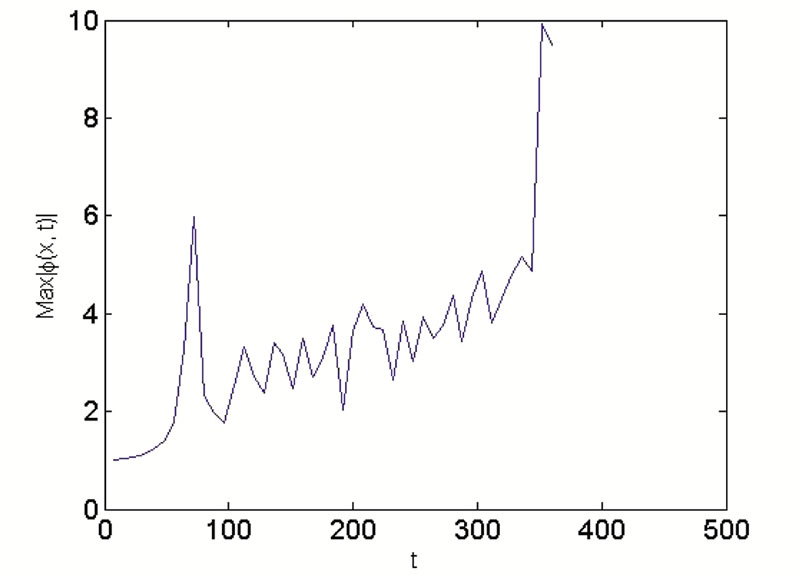 (c)
(c)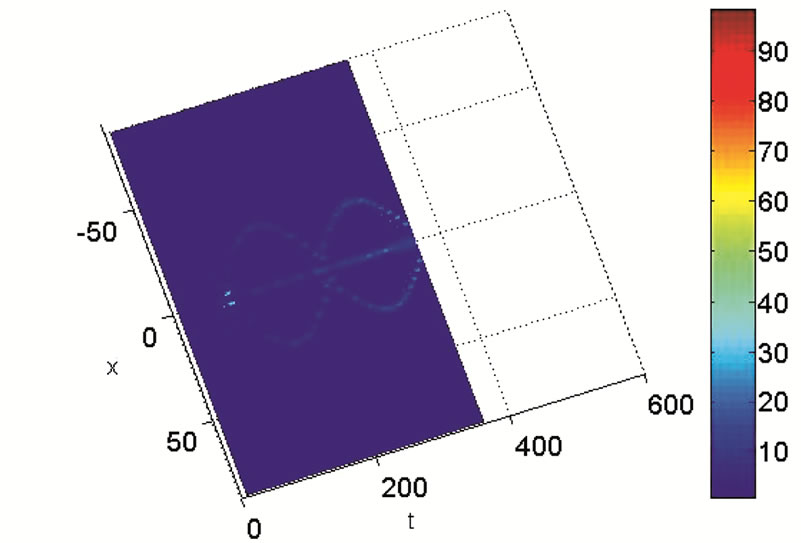 (d)
(d)
Figure 5. Spatiotemporal evolution of the maximum amplitude of the waves showing the formation of wave trains in the case g1 = 0, and g2  0. The parameters used are K = 0.15, ε = 0.001, αy = 1, αz = 1, αs = –2.75 nm, α = 1.576 μm. (a)
0. The parameters used are K = 0.15, ε = 0.001, αy = 1, αz = 1, αs = –2.75 nm, α = 1.576 μm. (a)  for N = 50, αx = 0.0004 (weak trapping); (b)
for N = 50, αx = 0.0004 (weak trapping); (b)  for N = 50, αx = 0.0004, (weak trapping); (c)
for N = 50, αx = 0.0004, (weak trapping); (c)  for N = 20, αx = 0.0004 (strong trapping); (d)
for N = 20, αx = 0.0004 (strong trapping); (d) 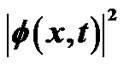 for N = 20, αx = 0.0004 (strong trapping).
for N = 20, αx = 0.0004 (strong trapping).
5. Conclusion
In summary, we have investigated analytically and numerically the MI in the modified GP equation. By using a theoretical model which includes the energy dependence of the two-body scattering amplitude, our results show that MI in the modified GP equation is qualitatively different. By taking the modified terms as 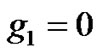 and
and , a new explicit time-dependent criteria for MI has been obtained. Moreover, both the MI gain peak and bandwidth decrease with the trapping of the condensate. In the case
, a new explicit time-dependent criteria for MI has been obtained. Moreover, both the MI gain peak and bandwidth decrease with the trapping of the condensate. In the case 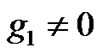 and
and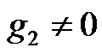 , it is shown that the quantum fluctuations extend the MI gain in the whole spectrum of the wave number K. By numerical simulations, we have observed that when the quantum fluctuations are not introduced in the system, wave patterns propagate in the medium without vanishing. When the quantum fluctuations are introduced, the wave trains are destroyed at long time. These wave trains can be exploited for the realization of laser sources adapted to ultrahigh bit-rate optical transmissions. It open also the possibilities for future applications in coherent atom optics, atom interferometry and atom transport.
, it is shown that the quantum fluctuations extend the MI gain in the whole spectrum of the wave number K. By numerical simulations, we have observed that when the quantum fluctuations are not introduced in the system, wave patterns propagate in the medium without vanishing. When the quantum fluctuations are introduced, the wave trains are destroyed at long time. These wave trains can be exploited for the realization of laser sources adapted to ultrahigh bit-rate optical transmissions. It open also the possibilities for future applications in coherent atom optics, atom interferometry and atom transport.
REFERENCES
- C. Pethick and H. Smith, “Bose-Einstein Condensation in Dilute Gases,” Cambridge University Press, Cambridge, 2003.
- L. Pitaevskii and S. Stringari, “Bose-Einstein Condensation in Dilute Gases,” Oxford University Press, New York, 2003.
- J. M. Gerton, D. Strekalov, I. Prodan and R. G. Hulet, “Direct Observation of Growth and Collapse of a BoseEinstein Condensate with Attractive Interaction,” Nature, Vol. 408, 2000, pp. 692-695. doi:10.1038/35047030B
- T. S. Raju, P. K. Panigrahi and K. Porsezian, “Modulational Instability of Two-Component Bose-Einstein Condensates in a Quasi-One Dimensional Geometry,” Physics Review A, Vol. 71, No. 3, 2005, Article ID: 035601. doi:10.1103/PhysRevA.71.035601
- A. Hasegawa and F. Tappert, “Transmission of Stationary Nonlinear Optical Pulses in Dispersive Dielectric Fibers,” Applied Physics Letter, Vol. 23, No. 3, 1973, pp. 142-144. doi:10.1063/1.1654836
- C. Tabi, A. Mohamadou and T. C. Kofane, “Modulated Wave Packets in DNA and Impact of Viscosity,” Chinese Physics Letter, Vol. 26, No. 6, 2009, Article ID: 068703. doi:10.1088/0256-307X/26/6/068703
- S. Cowell, H. Heiselberg, I. E. Mazets, J. Morales, V. R. Pandhari-Pande and C. J. Pethick, “Cold Bose Gases with Large Scattering Lengths,” Physics Review Letter, Vol. 88, 2002, pp. 210403-210406. doi:10.1103/PhysRevLett.88.210403
- E. Tiesinga, C. J. Williams, F. H. Mies and P. S. Julienne, “Interacting Atoms under Strong Quantum Confinement,” Physics Review A, Vol. 61, No. 6, 2000, Article ID: 063416. doi:10.1103/PhysRevA.61.063416
- H. Fu, Y. Wang and B. Gao, “Beyond the Fermi Pseudopotential: A Modified Gross-Pitaevskii Equation,” Physics Review A, Vol. 67, No. 5, 2003, Article ID: 053612. doi:10.1103/PhysRevA.67.053612
- G. Theocharis, Z. Rapti, P. G. Kevrekidis, D. J. Frantzeskakis and V. V. Konotop, “Modulational Instability of Gross-Pitaevskii-Type Equations in 1+1 Dimensions,” Physics Review A, Vol. 67, No. 6, 2003, Article ID: 063610. doi:10.1103/PhysRevA.67.063610
- P. Muruganandam and S. Adhikari, “Fortran Programs for the Time-Dependent Gross-Pitaevskii Equation in a Fully Anisotropic Trap,” Computer Physics Communication, Vol. 180, No. 10, 2009, pp. 1888-1912. doi:10.1016/j.cpc.2009.04.015
- L.Wu and J. F. Zhang, “Modulational Instability of (1+1)- Dimensional Bose-Einstein Condensate with Three-Body Interatomic Interaction,” Chinese Physics Letter, Vol. 24, No. 6, 2007, pp. 1471-1474. doi:10.1088/0256-307X/24/6/012
- E. Wamba, A. Mohamadou and T. C. Kofane, “Modulational Instability of a Trapped Bose-Einstein Condensate with Twoand Three-Body Interactions,” Physics Review E, Vol. 77, No. 4, 2008, Article ID: 046216. doi:10.1103/PhysRevE.77.046216
- J. K. Xu, “Modulational Instability of the Trapped BoseEinstein Condensates,” Physics Letter A, Vol. 341, No. 5-6, 2005, pp. 527-531. doi:10.1016/j.physleta.2005.05.018

