Advances in Bioscience and Biotechnology
Vol.5 No.4(2014), Article ID:43381,5 pages DOI:10.4236/abb.2014.54038
Method and Apparatus for Creating Problem-Solving Complexes from Individual Elements
Bernhard Mitterauer
Volitronics-Institute for Basic Research, Psychopathology and Brain Philosophy, University of Salzburg, Salzburg, Austria
Email: mitterauer@sbg.ac.at
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 13 December 2013; revised 6 February 2014; accepted 22 February 2014
ABSTRACT
Based on the biological key-lock-principle common in various biological systems such as the human brain, this paper relates to a method and device for creating problem-solving complexes from individual elements that can be coupled with one another and that have different properties to solve problems. The problem solution can be carried out either serially with a large computer, or with several independent, hierarchically joined computers. In this system, an independent control unit that assumes a multitude of tasks and also acts as an interface with access to all participating computers, is assigned to each problem or object class according to the amount of potential problem-oriented solutions. Such a unit prepares the partial solutions found in its computer for the totality of the solutions computed in the associated computers, finally leading to a total problem solution.
Keywords:Key-Lock-Principle; Geometrical Elements; Computer System; Composition; Problem-Solving

1. Introduction
The key-lock principle is a principle from biology [1] . The principle can be applied to many processes such as in neurotransmitters acting on perceptors or hormones and hereby requiring specialized hormone receptors for the hormonal system to work. Therefore, a function must be embodied in a material composition [2] . Conrad [3] also focused on the key-lock-principle in molecular computing.
Berkholz et al. [4] showed that protein structure determination and productive modeling have long been guided by the paradigm that the peptide backbone has a single context-independent ideal geometry. In the present paper, elements or bodies with an inverse geometrical structure fit to one another building a composition of a larger structure (body).
In the past years, attempts have been made to replace conventional electronic computers which incorporate their computer programs with new computer devices in order to solve even very complex problems if required. Adleman [5] describes “Computing with DNA” by building words from the four letters A, T, G and C (corresponding to the nucleotides Adenine, Thymine, Guanine and Cytosine) of the DNA alphabet corresponding to the partial sequences of the deoxyribonucleic acid (DNA) and then processing these words by an “enzyme” corresponding to polymerases, that is, forming complements, combining words, etc. This method can be applied, for example, to solve the known traveling salesman problem. In this problem, a path must be found through various cities, where the path begins at a city of origin and ends at a defined city of destination. The object is to identify a path where each city is visited but only once [6] .
Although this DNA computer uses new data components corresponding to the four DNA molecules mentioned, these components are connected using known nexuses corresponding to conventional electronic computer programs able to solve a known problem. Interestingly, a method is described by Koza [7] for solving problems using a non-linear genetic algorithm to find a fit composition of functions.
Another process has been recommended by Kauffman [8] in “The Origins of Order”. Kauffman uses several symbols that are connected to one another in pairs using a fixed grammar in order to build symbolic chains that contain a desired statement in their final form. In their basics, the systems and methods mentioned use the principles of a universal computer already prescribed by Turing, but always with the objective of solving a known problem with known means. The methods are always goal-oriented, where the procedure is determined by a development engineer based on his knowledge and strict specifications.
2. Outline of the Apparatus
The principal object of the present paper is to provide a method and apparatus where solutions can be found for problems that are not accessible to conventional computer programs and where surprisingly new results can be obtained. The model allows for a creative interaction of the individual elements which leads to new results with conventional methods that were unattainable until now.
The general principle of the method proposed is that a large number of elements with different shapes is generated by a generator according to a randomization principle, where statement parameters, coupling parameters, and, if required, program parameters are assigned to the individual elements. In particular, the coupling parameters are selected by a complementary principle, i.e. the lock/key principle of a lock such that virtual elements with complementary coupling parameters can dock to one another. The elements generated in this manner are provided with individual parameters and then “mixed” in a limited space according to a randomization principle using a processor, i.e. in a manner where the individual elements are turned and shifted within the prescribed space, and where at each contact the elements can check among each other if the elements can be coupled with one another at this contact based on the assigned parameters.
When a particular problem is specified, each element can be assigned a special symbolic content, where the elementary symbolic content units are selected according to the problem to be solved. The symbolic content may, for example, be an elementary logical proposition, a word, an activity command, a component of a mathematical equation or fractional description of sections of a path to a certain destination that a robot has to take.
The solution of the problem is carried out as follows: during the course of the random mixing and coupling of the individual elements chains of elementary components come into existence that are indeed meaningful. To test this, the “mixing process” is interrupted at prescribed intervals to evaluate the obtained result, and if necessary, the process is repeated until a satisfactory result is obtained (Figure 1).
A significant difference to the other calculating methods, such as described above, is that no end point is given for the solution of the problem and that the steps of the process are not goal-oriented. With the method based on the present model, new and surprisingly meaningful results can be achieved in solving a problem, where relevant results can also be implemented positively in reality. Such unexpected and meaningful solutions are closed to other methods.
Currently, we are developing a program applicable for music composition. In a space for tones, 19 elements (from D to a1) of a Doric music mode provide for the computation. In order to do this, one needs
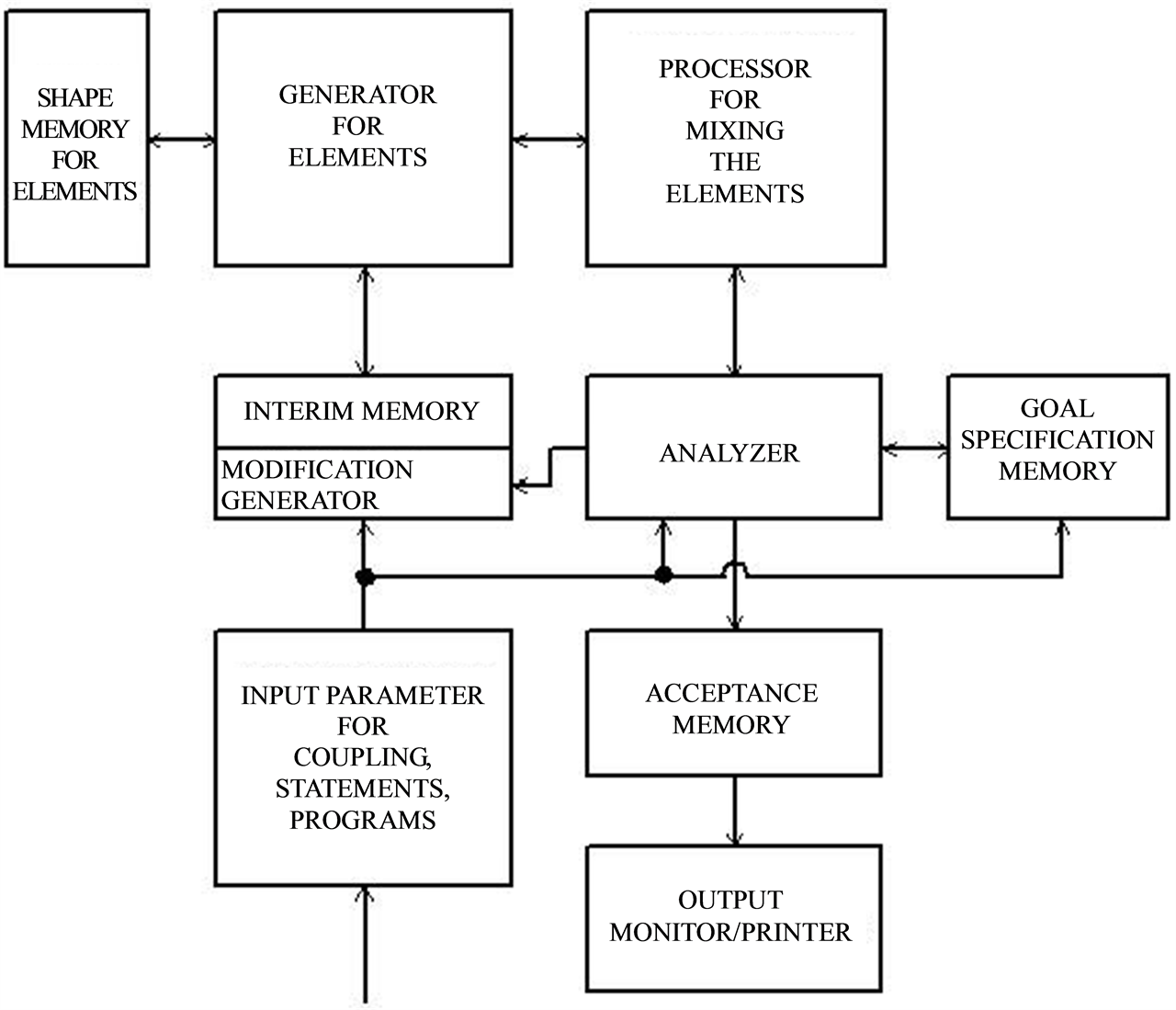
Figure 1. Block diagram of a computer system creating problem-solving complexes.
“accord-elements, melody-elements, pause-elements and time-elements”. A more detailed description and discussion of this problem-solving program would require a separate publication.
The test of the problem-solving complexes created during the mixing process can be carried out, for example, with the aid of an analyzer that tests if the problem-solving complexes formed of elements coupled to one another would be able to achieve a meaningful effect based on the parameters assigned to the individual elements, or if there are contradictions.
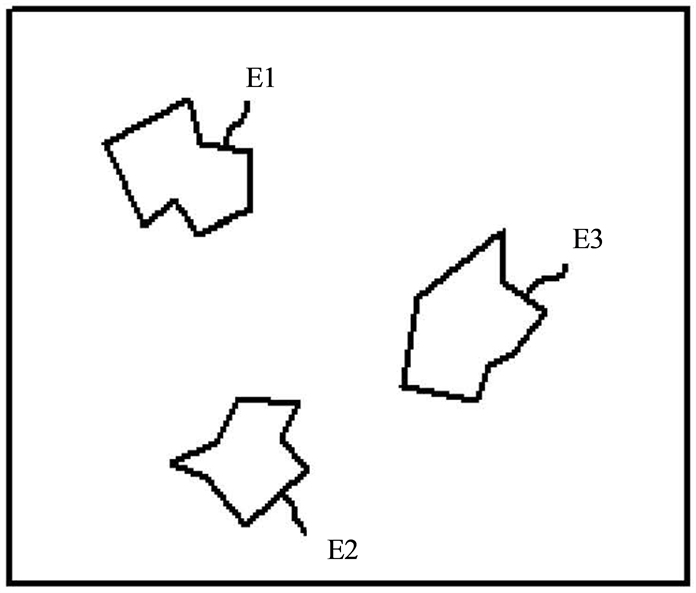
The statement parameters, coupling parameters, and potentially the program parameters that are assigned to the individual elements are decisive for the result, i.e. the creation of new problem-solving complexes. Also decisive is the stringent application of the key-lock principle that otherwise has great significance particularly in the fields of microphysics and microchemistry on the nuclear and molecular plane (Figures 2(a) and (b)).
The state parameters are, for example, statements about the entropy of the elements that is determined by its complex shape. Depending on this application, these parameters may be symbols or activity commands such as those used in recognition theory or in robotics.
For instance, the coupling parameters define the type of spatial coupling of differing elements. Additionally, they can be linked with the statement parameters for the individual elements such that conditions that are more rigorous are set for coupling two elements. The program parameters may be sequences of several logical statements, for instance IF-THEN statements.
3. Discussion
The model proposed can be applied advantageously to robotics, where the elements are activity commands to the robot, and where relevant commands can build a complex or an activity chain only when two elements meet both the statement parameter, such as activity commands, and the related coupling parameters fit to one another. It is possible to install such activity chains directly into the program of a control centre of a robot such that the control centre virtually becomes the “brain” of the robot.
It is further possible to employ the described method and apparatus to explain a new network of neurons with their axons and dendrites or of glia cells, such as oligodendrocytes or astrocytes [9] . As generally known, such cells constantly disappear due to their short life span and are replaced by new cells which then again must be integrated and correspondingly linked into the cell conglomerate [10] . Such a new linking can be explained through the respective selection of elements with their parameters. At a minimum, one receives stimulation for new explanations through the creation of the problem-solving complex.
It is also possible to change the entered parameters based on the evaluation of the respective problem-solving complex in order to optimize the creation of problem-solving conplexes. In this manner, a certain learning effect is achieved (Figure 3).
An additional step, if required, is to implement the problem-solving complexes created to solve a problem in practical applications, such as in testing the chain of activity commands derived from the problem-solving
 (a)
(a) (b)
(b)
Figure 2. (a) Schematic diagram of individual elements (E1...E3); (b) Schematic diagram of coupled elements.
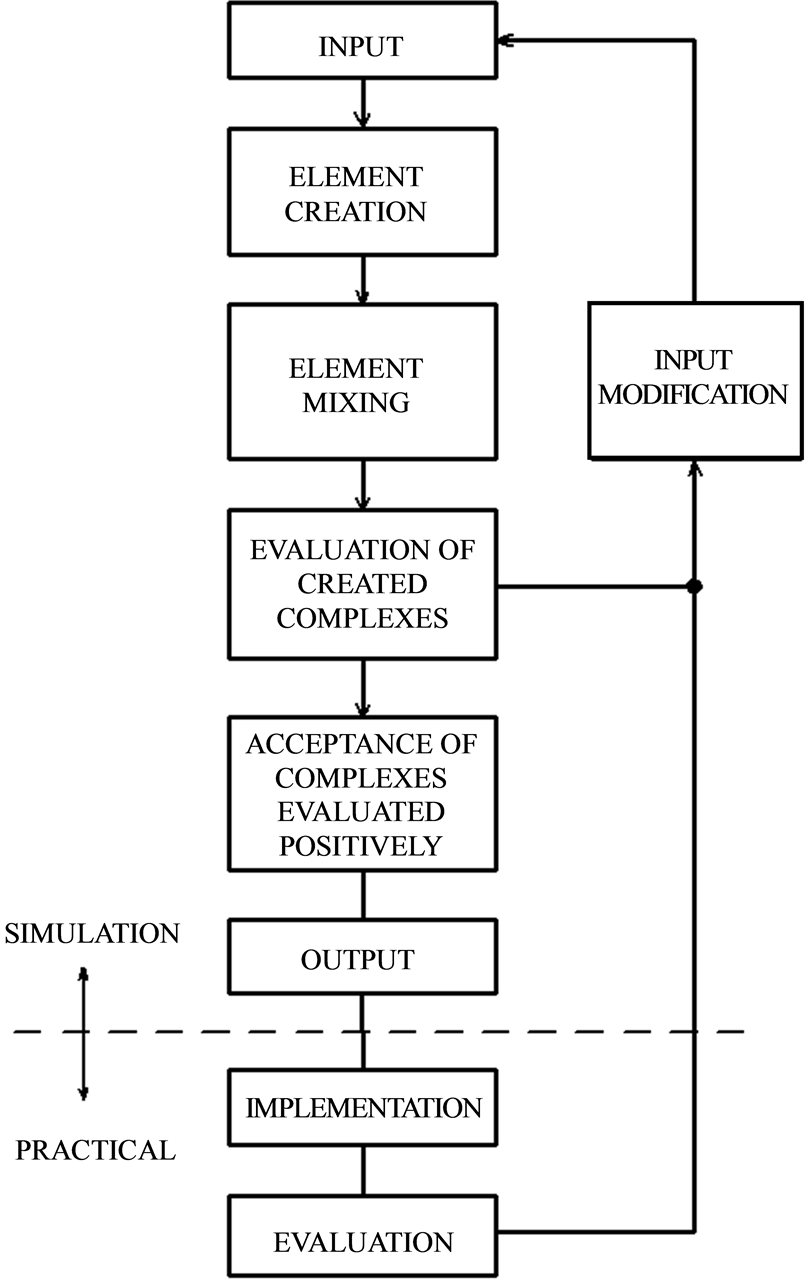
Figure 3. Flow diagram for the individual steps in the calculation phase and in the phase of implementation into practical applications.
complex on a robot in reality. In putting the problem-solving complexes into practical application, it is also possible to provide feedback to the computer in order to achieve a learning effect and to optimize the problemsolving complexes, i.e. the activity commands.
The model can also be employed in the field of recognition theory. In this case, ideas are in existence about a semantic feature listing; i.e. to classify a concept according to semantic axes. The specified elements may each have shapes corresponding to semantic axes. With elements that are shaped in star or zigzag shape, each point may be assigned a semantic feature. Statement parameters can specify that the further the point is from the centre of the element, the more effective the semantic element will be. When mixing these elements, features complementary to each other will dock to one another and combine to form a new semantic concept. The described method may be observed on a monitor, for example. Of course, three-dimensional presentations are possible as well (Figure 3).
For a full understanding of the present model, reference should also be made to the detailed description of the preferred embodiments (see [11] ). Admittedly, genetic algorithms can be efficient for function optimization [12] . The present model may also work in a “biomimetic” manner, since the key-lock principle is technically implemented [13] .
The computer system proposed here needs the experience of its technical implementation. Since it does not work algorithmically and is not goal-oriented, we must learn from its problem-solving results where it must be optimized and if it shows advantages in comparison with conventional computers.
References
- Behr, J.P. (1994) The Lock-and-Key Principle, the State of the Art-100 Years on. John Wiley and Sons, West Sussex.
- Mitterauer, B. (1989) Architektonik. Entwurf einer Metaphysik der Machbarkeit. Brandstätter, Wien.
- Conrad, M. (1992) Molecular Computing: The Lock-Key Paradigm. Computer, 25, 11-20. http://dx.doi.org/10.1109/2.166400
- Berkholz, D.S., Shapovalov, M.V., Dunbrack, R.L. and Karplus, P.A. (2009) Conformation Dependence of Backbone Geometry in Proteins. Structure, 17, 1316-1325.
- Adleman, L.M. (1998) Computing with DNA. Scientific American, 276, 54-61. http://dx.doi.org/10.1038/scientificamerican0898-54
- Mitterauer, B. (2007) Where and How Could Intentional Programs Be Generated in the Brain? A Hypothetical Model Based on Glial-Neuronal Interactions. BioSystems, 88, 101-112. http://dx.doi.org/10.1016/j.biosystems.2006.04.003
- Koza, J.R. (1992) Non-Linear Genetic Algorithms for Solving Problems by Finding a Fit Composition of Functions. US Patent 5, 136, 686.
- Kauffman, St.A. (1993) The Origins of Order. Self-Organization and Selection in Evolution. Oxford University Press, Oxford.
- Mitterauer, B. (2004) Computer System, Particularly for Simulation of Human Perception via Sense Organs. United States Patent 6, 697, 789B2.
- Raff, M.C., Barres, B.A., Burne, J.F., Coles, H.S., Ishizaki, Y. and Jacobson, M.D. (1993) Programmed Cell Death and the Control of Cell Survival: Lessons from the Nervous System. Science, 262, 695-700. http://dx.doi.org/10.1126/science.8235590
- Mitterauer, B. (2000) Verfahren und Einrichtung zur Bildung von Problemkomplexen aus Einzelnen Elementen Sowie Deren Verwendung. German Patentschrift, DE19844652C1.
- Taherdangkoo, M., Paziresk, M, Yazdi, M. and Bagheri, M.H. (2012) An Efficient Algorithm for Function Optimization: Modified Stem Cells Algorithm. Central European Journal of Engineering, 3, 36-50. http://dx.doi.org/10.2478/s13531-012-0047-8
- Mitterauer, B. (2000) Some Principles for Conscious Robots. Journal of Intelligent Systems, 10, 27-56. http://dx.doi.org/10.1515/JISYS.2000.10.1.27

