Received 14 April 2015; accepted 12 May 2015; published 15 May 2015

ABSTRACT

This paper extends Long and Staehler’s model and studies optimal export tax in the case of privatization. The authors find that optimal export tax increases with the degree of privatization if product differentiation exists. The authors provide a counterexample to Long and Staehler’s model and reach a different conclusion. This finding emphasizes that the relationship between the variables of optimal export tax and conditions of asymmetric cost and product differentiation is quite different from Long and Staehler’s model. Since optimal export tax is endogenous in the model, the authors also consider the potential endogeneity of privatization decision, which is an important issue in a traditional mixed duopoly analysis.

Keywords:

Cost Asymmetry, Privatization, Product Differentiation, Optimal Export Tax

1. Introduction

Since the 1980s, governments have begun to privatize state-owned enterprises. In keeping with this trend, many countries have changed the focus of their government policies towards international trade. Consequently, the relationship between privatization and strategic trade policies deserves further study.

Pal and White [1] were the first to study the interaction between privatization and strategic trade policies. They focused on how privatization influences the optimal tariff or subsidy. Pal and White [2] showed that the presence of state-owned firms results in decreases in optimal tariffs and subsidies. Chang [3] applied a mixed duopoly model to study privatization policy and optimal import tariffs in the presence of exogenous cost asymmetry. Chao and Yu [4] argued that partial privatization increases the optimal tariff rate but foreign competition reduces it. Wang et al. [5] demonstrated that policy choices on privatization policy and on optimal tariff depend on different sequences of firm moves.

Most existing studies examine the relationship between import tariffs and privatization. However, the export tax is also an instrument of strategic trade policy. Although several papers, including Eaton and Grossman [6] , Lee and Roland-Holst [7] , and Mitra [8] , explore the role of export taxes and subsidies under different market structures, these studies overlook the connection between privatization and optimal export taxes. Exceptions, however, can be found in Long and Staehler [9] . They showed that the optimal export tax is irrelevant to privatization in a mixed duopoly.

The innovation of this paper is as follows. First, Long and Staehler [9] ignore cost heterogeneity between firms, which seems unrealistic in view of the real world economy. Thus, we incorporate asymmetric cost into our model. This set-up follows from Chang [3] , Kamijo and Nakamura [10] , and Wang and Chen [11] . Second, Long and Staehler [9] neglect the possibility of product differentiation as shown by Wang et al. [12] , Saha [13] , and Matsumura et al. [14] .

Thus, this paper aims to study the effects of privatization on the optimal export tax in the presence of a differentiated mixed duopoly with cost asymmetry. To do this, we use a quadratic utility function, an asymmetric cost, and a Cournot-Nash equilibrium game. Within this framework, we find that the relationship between the degree of product differentiation and the optimal export tax is non-monotonic, while the optimal export tax increases with the degree of privatization. Furthermore, we find that in the presence of a cost-symmetric duopoly, privatization is independent of the optimal export tax, while optimal export taxes increase as the degree of pro- duct differentiation decreases.

Our result demonstrates that cost asymmetry plays a crucial role in the relationship between privatization and optimal export taxes. This implies that with cost asymmetry, the government may encourage the low-cost firm to export its product more; therefore, privatization will affect optimal export taxes by altering production decisions. On the contrary, with cost symmetry, the government does not adjust the export policy according to the privatization policy.

This study contributes to the existing literature in two ways. First, our finding contrasts with the research of Long and Staehler [9] , which reinforces the key result of this paper because it demonstrates that the relationship between optimal export tax and conditions of asymmetric cost and product differentiation is quite different to that in Long and Staehler’s model. Second, this study suggests that governments adopt different export taxes under different conditions.

The rest of the paper is organized as follows. Section 2 introduces our model, Section 3 solves the firm and government problems, and Section 4 concludes.

2. Model

Our model is based on Long and Staehler’s [9] model. Assume two domestic firms―Firm 1 and Firm 2―that produce a differentiated product and export their total outputs, 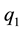and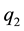, to a foreign country that does not produce the commodity. Firm 1 is a mixed enterprise and Firm 2 is a pure private enterprise. Following Vives [15] , we assume that the foreign consumer’s utility function is

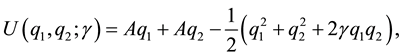
where A is a constant and 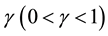measures the degree of product differentiation. The higher the value of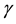, the lower the degree of product differentiation should be. When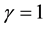 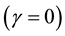, the two products are completely homogeneous or substitute (independent). The utility function gives rise to the inverse demand functions by setting:

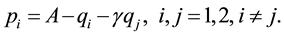
To simplify the analysis, we assume that cost function is linear, i.e., firms have a constant marginal cost of production 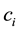, and that there is no fixed cost. The domestic government sets an export tax t to influence the quantity exported. Let the profit function for the Firm i be:

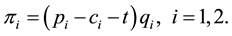(1)

As shown by Pal and White [1] and Wang et al. [5] , we assume that the mixed firm is less efficient than the private firm, i.e., 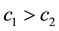, which represents a cost asymmetry. The private firm aims to maximize its profits. In addition, social welfare consists of domestic firm profits and export revenues:

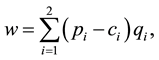(2)

where w represents the level of social welfare. It should be noted that (2) does not include consumer surplus since both firms export their entire outputs. The mixed enterprise considers both the profit and welfare in (1) and (2). Hence, the objective function of the mixed firm is given by

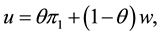(3)

where measures the degree of privatization. As is typical in privatization literature, an increase in means that the state-owned firm is more privatized while is pure nationalization (privatization).

The stages of the game involved proceed as follows. First, given, the government chooses the export tax rate t. Second, taking and t as given, each firm simultaneously and independently decides the quantity.

3. Analysis

As is standard, we first solve the firm problem and then the government problem.

3.1. The Firm Problem

Firm 1 chooses to maximize the weighted average objective in (3), subject to the constraints (1) and (2). The first-order condition is:

(4)

Next, turn to the choice of Firm 2’ s output,. The first-order condition is:

(5)

Solving the simultaneous equations of (4) and (5) for and, the Cournot equilibrium outputs are derived as

(6)

(7)

where and the superscript N refers to the Cournot-Nash equilibrium. Let

and in order to ensure interior solutions. Examine the effects of changes in export taxes, the degree of product differentiation, and the degree of privatization on the output of both domestic firms.

(8)

(9)

(10)

(11)

(12)

(13)

Equation (8) implies that increasing export taxes leads to a reduction in Firm 1’ s output if. Intuitively, if is sufficiently large, the mixed enterprise acts as a private enterprise. When the government imposes export taxes on Firm 1’ s quantity, this makes the firm produce less, as shown in (9). Contrarily, if is not sufficiently large, the mixed enterprise acts as a state-owned enterprise. Although export taxes are present, the mixed enterprise may increase the quantity produced to take into account social welfare (the total before-tax profit objective).

From Equations (10)-(13), we find that comparative statics of the optimal level of production are uncertain. We will examine a numerical example to explain the possible effect more explicitly. First, we compute the optimal level of production with respect to the degree of product differentiation by setting, , , , and. Figure 1 shows that the quantity produced by the mixed enterprise will decrease as the degree of product differentiation decreases (i.e., increases), whereas the relationship between the quantity produced by the private enterprise and the degree of product differentiation is non-monotonic. This is because as increases, the mixed enterprise will reduce its output to pursue profit more aggressively. However, when is not sufficiently large, the private enterprise will reduce its output, whereas when is sufficiently large, the resulting output will rise due to a continuing decrease in.

From Figure 1, we see that production differentiation plays an important role in firms’ production decisions. When production differentiation becomes larger, the output difference between two firms becomes smaller. The reason is that when production differentiation becomes larger, cost difference does not play a key role in firms’ production decisions. Therefore, the output difference between two firms becomes smaller. On the contrary, when production differentiation becomes smaller, cost difference does play a key role in firms’ production decisions. Therefore, the output difference between two firms becomes larger.

The following proposition summarizes what we have found:

Proposition 1: When production differentiation becomes larger, the output difference between two firms becomes smaller. On the contrary, when production differentiation becomes smaller, the output difference between two firms becomes larger.

Next, we compute the optimal level of production with respect to the degree of privatization by setting, , , , and. Figure 2 reveals that increases with, while decreases with. Intuitively, since the mixed enterprise considers tax revenues in addition to the profit objective, it still produces more although privatization increases. However, the private firm will reduce its output by pursuing the profit objective when the output of the mixed enterprise increases with.

From Figure 2, we see that the degree of privatization plays an important role in firms’ production decisions. When the degree of privatization becomes larger, the output difference between two firms becomes smaller. The reason is that when the degree of privatization becomes larger, cost difference does not play a key role in firms’ production decisions. Therefore, the output difference between two firms becomes smaller. On the contrary, when the degree of privatization becomes smaller, cost difference does play a key role in firms’ production decisions. Therefore, the output difference between two firms becomes larger.

The above allows the following result to be inferred:

Proposition 2: When the degree of privatization becomes larger, the output difference between two firms becomes smaller. On the contrary, when the degree of privatization becomes smaller, the output difference between two firms becomes larger.

3.2. The Government Problem

The optimal export tax can be found by differentiating (2) with respect to t to yield:

(14)

Substituting (6), (7), (8), and (9) into (14) yields the following optimal export tax:¹

(15)

Equation (15) shows that the optimal export tax depends on a constant A, the degree of product differentiation, Firm 1’ s marginal cost, Firm 2’ s marginal cost and the degree of privatization, i.e., .

From (15), we cannot directly calculate the comparative statics of optimal export taxes; thus, simulations are needed. First, we analyze the effect of the degree of product differentiation on optimal export taxes. Figure 3 reveals that the relationship between the degree of product differentiation and optimal export taxes is non-mo- notonic. A higher encourages optimal export taxes as long as is not sufficiently large. Conversely, if becomes sufficiently large, a higher discourages optimal export taxes. The reason is as follows. From (8),

we see that when is not sufficiently large, increasing export taxes leads to a decrease in the high-cost firm’s (Firm 1) output. However, as is sufficiently large, increasing export

taxes leads to an increase in the high-cost firm’s output. Thus, in order to improve production efficiency, the government should impose higher export taxes on output if is not sufficiently large. Contrarily, when is sufficiently large, the government should impose lower export taxes on output.

Second, we analyze the effect of the degree of privatization on optimal export taxes. Figure 4 shows that the relationship between and is monotonic. As shown in Figure 2, if the degree of privatization increases, it reduces Firm 1’ s weight on social welfare, and induces Firm 1 to increase its output while Firm 2 reduces its output. However, since Firm 2 is more cost efficient than Firm 1, privatization increases production inefficiency by reducing the output of the low-cost firm (Firm 2). To solve this inefficiency, increasing export taxes is an effective policy to correct the distortions by reducing Firm 1’ s output.

The above allows the following result to be inferred:

Proposition 3: Consider an economy in which both mixed enterprises and private firms may export from the same country to another country. We find that the relationship between the degree of product differentiation and the optimal export tax is non-monotonic. In addition, the optimal export tax increases with the degree of privatization.

Note that it is also instructive to consider some special cases. First, with and, equation (15) reduces to

(16)

Equation (16) means that the degree of privatization is independent of the optimal export tax in a homogeneous duopoly with cost symmetry. This result is consistent with that of Long and Staehler [9] (2008).

Next, with and, Equation (15) reduces to

(17)

Equation (17) means that the degree of privatization is also independent of the optimal export tax even in a differentiated duopoly with cost symmetry. To see the relationship between and, differentiating (17) with respect to yields:

(18)

Equation (18) means that if the degree of product differentiation decreases, optimal export taxes will become large. The reason is that with cost symmetry, as the degree of product differentiation decreases, both firms will reduce their output to pursue profits more aggressively. In addition, an increase in export taxes usually reduces the firms’ output. Therefore, export taxes and the degree of product differentiation are substitute relations. In

other words, optimal export taxes decrease with the degree of product differentiation.

From equations (16)-(18), we establish:

Proposition 4: Consider an economy in which both mixed enterprises and private firms may export from the same country to another country. We find that, in the presence of a cost symmetric duopoly, the degree of privatization is independent of the optimal export tax, while optimal export taxes increase as the degree of product differentiation decreases.

Finally, with and, equation (15) reduces to

(19)

Equation (19) implies that the optimal export tax depends on. To understand the relationship between and, differentiating (19) with respect to yields:

(20)

Equation (20) means that higher degree of privatization (higher value of) leads to a higher optimal export tax. The reasoning behind this result is similar to that explained in Figure 4. From (20), we establish:

Proposition 5: Consider an economy in which both mixed enterprises and private firms may export from the same country to another country. We find that in a cost asymmetric duopoly, the optimal export tax rate monotonically increases as the degree of privatization increases.

4. Concluding Remarks

Long and Staehler [9] found that the optimal export tax is irrelevant to privatization in a mixed duopoly. In this paper, we extended Long-Staehler’s model and incorporated asymmetric cost and product differentiation into our model. We conclude instead that optimal export tax increases with the degree of privatization if product differentiation exists.

Our findings are as follows. First, we show that the relationship between the degree of product differentiation and the optimal export tax is non-monotonic, while the optimal export tax monotonically increases as the degree of privatization increases. Second, we find that in the presence of a cost symmetric duopoly, the degree of privatization is independent of the optimal export tax, while optimal export tax increases as the degree of product differentiation decreases. Following these arguments, an obvious policy implication is that the optimal export tax needs to be tailored to the cost asymmetry rather than product differentiation.

The limitations of this work are as follows. First, we do not consider how foreign competitors affect the relationship between privatization and optimal export taxes. Secondly, we ignore how increasing competitive firms in the home country affect the relationship between optimal export taxes. These issues, we believe, merit future research.

References

NOTES

¹The derivation of t^N is available from the authors on request.