Received 5 August 2014; revised 6 September 2014; accepted 2 October 2014

ABSTRACT

When national financial sector regulators need to mutually harmonize macroprudential policy decisions, imperfections of cross-border information exchange may undermine fair cooperation. Attempts to overcome the effects of informational distortions by delegating macroprudential policy to a supranational body are also likely to entail welfare losses. We study the tradeoff between macroprudential policy autonomy and centralization by means of a signaling game of imperfect information played by two national regulators. The model concentrates on informational frictions in an environment with otherwise fully aligned preferences. We show that even in the absence of evident conflicting goals, the non-transferable nature of some regulatory information creates misreporting incentives. Reporting accuracy is a part of a broader problem of strategic advantage- seeking by the national regulators. Therefore, cross-border coordination mechanisms, centralized or not, that limit strategic behavior are preferable to those allowing its full deployment. The results are applicable to systemic risk management by international organizations, including the relevant EU institutions.

Keywords:

Macroprudential Regulation, Integration, Autonomy, Information, Reporting

1. Introduction

Initiatives seeking to reform the international financial architecture and regulatory framework invariably have followed each financial crisis in recent decades (see [1] and references therein). A recurrent element of the prevailing part of these initiatives is the call for establishing some form of a supranational regulatory organization (cf. [2] and [3] ).

A similar debate arose after the outbreak of the current global financial crisis, bringing about not only suggestions for the future, but also many measures that have already been implemented, including the new set of banking regulation guidelines known as Basel III, the reform roadmap of the EU banking supervision architecture under the common headline of “European banking union”, and the establishment of the European Systemic Risk Board (ESRB). In line with those changes, the new regulations pay increased attention to the so-called macroprudential policies, which are intended to prevent the emergence of systemic risks. However, the extent of macroprudential regulation powers to be entrusted to supranational bodies is still an open question. This is the motivation to address the problem of costs and benefits of supranational macroprudential control, with particular regard to small open economies, in our paper, which introduces a theoretical model dealing with the delegation of macroprudential policy decisions to a supranational body.

One argument against international unification of macroprudential policies in financial services is suggested by the generally suspected policy inefficiency in an open economy. This inefficiency is related to regulatory arbitrage: an international regulator who decides on a measure without properly understanding its country-level workings will encourage the regulated agents to circumvent it using their superior knowledge of local specifics. Accordingly, a policy mandated by an authority independent of national regulators should be doubly suboptimal in such an economy: first due to openness and second due to domestic regulation costs insufficiently taken into account by the supranational regulator.

The opposite argument in favor of a supranational regulator is that only the latter is in the position to tackle the openness problem, as by expanding the validity of policy outside national jurisdictions, it is able to eliminate regulatory arbitrage. As to the reflection of national regulation costs, the problem is usually downplayed by referring to the consensual nature of international regulatory bodies with equitable representation. This is, roughly, the conventional justification of tightening regulatory unification of the financial sector within the EU, richly fueled by the events of 2007-2009. However, this “Eurocentric” argument does not deal with the possibility of regulatory arbitrage making use of non-EU jurisdictions¹.

Supporters of internationally centralized macroprudential regulation often refer to the issue of cross-border spillovers of financial shocks and the related demand for transnational coordination of global systemic risk containment measures. It is argued that the sheer complexity of the information processing needed to efficiently counteract the threat of global financial instability calls for a centralized authority able to collect disaggregated data from individual countries and take actions based on centrally conducted analysis. On the other hand, proponents of decentralized regulation point to the fact that whatever the source of financial instability that spills across borders, it always has a “home”. This means that the particular instability invariably originated in a specific country in which the responsible authorities failed to act even if they had access to the relevant information. Further, they argue that a large portion of this information is of an intangible, human expert-dependent nature, preventing it from being quantified and shared in the timely manner necessary for useful trans-national synergies.

A considerable part of the outlined discussion overlaps with a similar debate concerning “micro-prudential” regulation of financial institutions (see [4] as a strong proponent of decentralized regulation, as opposed to, e.g., [5] , whose punch line is, essentially, a fatwa on ring-fencing practices). The systemic risk focus of macroprudential regulation adds more complexity due to interactions with inter alia, monetary policy and international competitiveness issues. That is, the macro-level provides more, and stronger, sources of international spillovers as well as more entrenched vested interests in each country involved.

The contradictory views described above often transform into a deep disagreement between policymakers on the desirable institutional arrangement. On the other hand, the same conflicting opinions have so far received little attention from a formal economic analysis perspective. The present paper contributes to the task by stating the gist of the opposing views on regulatory design in possibly abstract terms. In other words, we propose a model which strips the politically heavily laden problem down to the bare essentials and gets down to the decision-theoretical bedrock of the interplay between the two implications of (de)centralized regulation: dispersed information and regulatory costs. We believe that a first pass at understanding the problem formally can be made by abstracting from nearly all of the macroeconomic and financial intermediation specifics that occupy a prominent place in the current “post-crisis” literature on macroprudential regulation (see [6] , [7] , and [8] ).

In the present paper, we stylize the essence of the clashing policy views outlined above in a fairly primitive microeconomic setting of two (or more) imperfectly informed strategically behaving national regulators in, or without, the presence of an overarching supranational authority. Then, we consider the impact of one-dimen- sional national controls (summary statistics of local regulatory measures) on the common “supranational” fundamental variable (a summary statistic of global systemic risk factors) which co-determines the values of the two national regulatory loss functions². Each national regulator has private information about own country’s component of the said risky fundamental, and sends a signal reflecting this information, to the other regulator, either via a central authority, if it exists, or independently. The signal can never be perfect. Therefore, if, as the “centralists” in the regulation debate call for, it is the central authority who decides on regulatory controls, there is a welfare loss since a part of private information gets lost. Under the decentralized regulation preferred by the “autonomists”, all available private information is used nationally. Still, welfare losses come about for other reasons (e.g., because each regulator would like the other one to carry most of the regulatory burden―the “free rider problem”). In addition, neither the hierarchical nor the polyarchical regulatory architecture is able to prevent deliberate distortion of signals by national regulators.

In the outlined environment, regardless of centralization, a generic equilibrium is characterized by untruthful signals sent with positive probability. However, if they were given a choice between two variants of the same game with differing allowed sizes of signal distortion, rational regulators would prefer a more “honest” setting (the effect has to do with second- and higher-order effects of rationally anticipated lying by the counterparty). This fact suggests that repeated encounters between the same regulators under adjustable parameters of mutual communication would have a chance to bring information exchange very close to honesty. That is, we find that, if the main objective of centralization were accurate information processing, the corresponding regulatory integration effort would be simply wasting resources on an outcome attainable under decentralization. At the same time, it turns out that information exchange does not have to be fully honest to maximize aggregate welfare, so that integration policies with excessive stress on fair communication may end up in a suboptimal equilibrium with too much free-riding. Conversely, certain cooperation rules that seemingly neglect a part of the information content of the parties’ communication, achieve a higher social welfare thanks to their ability to shift individual responsibility back to national regulators. Still, these arrangements lack many features one normally associates with politically viable integration constructs. Instead of a “fair representation” variety of integration authority that offers its members all the necessary space for strategic interaction, a near-mechanically functioning processor of member actions with pre-defined elementary rules and an exit option might be socially preferable.

Similar dilemmas associated with strategic interaction among national policy makers have been covered by the theory of national tax competition (see [9] and references therein). Other aspects of interaction between national policymakers with imperfectly aligned incentives were extensively discussed at the time of the establishment of the EMU. The debate was naturally focused primarily on the common monetary policy, namely, on the question about how effectively the main objective of the ECB can be fulfilled in an environment of different countries following their own objectives (see [10] ). The implications of conflicting national goals were later considered for other kinds of policies, such as the borrower of last resort function in a multi-regulator environment ([11] ). However, theoretical concepts of multi-national interaction of financial regulators from a macroprudential angle have not yet been discussed intensively, although the applied policy literature recognizes the importance of this topic (see [12] ). The present paper fills this gap by discussing a number of competing approaches to multi-national regulatory interaction in a context that abstracts from quantitative details of the macroprudential policy framework. We believe such an analysis to be especially topical in the present environment of massive regulatory changes both in the EU and worldwide.

The rest of the paper is organized as follows. In Section 2 we give a verbal synopsis of the story to be later formalized as an imperfect information game between national regulators, and give an overview of the technical assumptions needed. Section 3 contains a technical description of the said communication game and states the necessary results about its equilibria in a number of alternative institutional settings. Section 4 offers an interpretation of the policy implications of the formal results obtained. Section 5 concludes. Proofs of the technical propositions in Section 3 are collected in the Appendix.

2. Global Risks, Local Costs, and Non-Transferable Knowledge

2.1. Three Depth Levels of Pro- Vs. Anti-Integration Debate

We consider financially integrated economies in which market disruptions spread across national borders quickly and financial frictions are, essentially, common. In such an environment, national authorities generally agree about what adverse developments are to be acted against. Still, they need to agree on burden sharing by implementation of the necessary policies, and conflicts between self-interests make such agreement complicated and its outcome ambiguous. The dispute between the regulatory pro- and anti-centralization sides can be then looked upon as a disagreement as to which of the two arrangements produces a more desirable outcome of the burden- sharing negotiations. The corresponding debate takes place on at least three levels of analytical sophistication. If one abstracts from the specifics of the numerous individual contributions available to date, the distinction between levels can be summarized as follows.

On the first level, one finds arguments that operate with simple cost and benefit parameters. What appears to be a beneficial policy measure from one country perspective, the autonomists say, may ignore costs incurred in other jurisdictions. A central regulatory power would always prioritize the interests of big members with a lot of political clout to the detriment of smaller ones, because no one will think of internalizing the preferences of the latter, they proceed. The unionists object that it is exactly in an integrated agency with appropriate representation of all members that a fair regard to smaller participants can be safeguarded, whereas an uncontrolled world of independent regulators would mean exactly the harm to the weak that the autonomists are campaigning against³.

The second-level debate is concerned with dispersed information, spillovers, and synergies from a common regulatory “brain”. Centralizers claim that the informational synergies of an integrated regulator will be so strong that they are bound to dominate every gain from local competence. Autonomists object that the nature of regulatory information is imminently local and partially non-transferable and that any central authority trying to take into account the totality of national economies and markets will inevitably end up as bureaucratic, slow- witted, and entirely dependent on country-level informational inputs. To support this conjecture, they offer both theoretical and empirical knowledge on the functioning of large hierarchical organizations. Formal analysis of the corresponding effects can be already found in nearly half a century-old contributions of the theory of the firm (represented by [14] , among others) and related management science literature that deal with information losses across hierarchy layers. Therefore, instead of synergies, one should mostly expect informational losses⁴. The ultimate answer on whose arguments are more val id can only be an empirical one with the formalized data at hand. Although a lot of anecdotal ev id ence on the functioning of supranational organizations supports the autonomists’ concern, it remains to be seen whether the negative experiences are indeed more numerous than the positive ones or are just more conspicuous.

The third level goes even deeper into the domain covered by game theory and mechanism design by asking whether a central regulator can prevent inefficiencies stemming from strategic non-cooperative behavior of the members and overcome welfare losses caused by asymmetric information⁵.

It is quite possible that for most practical purposes, the first two levels (or even the first level only) of the discussion are quite sufficient for a viable judgment either for or against integrated macroprudential policies. All the experience available so far on the functioning of integrated agencies (be it within or outside the EU) provides plentiful evidence for inadequate representation of smaller members and bespoke policies designed by, and in the interests of, the biggest and most influential country representations. On the contrary, an example of an underdog being protected by “common” policies is quite hard to find. Nevertheless, in order to expand the discussion beyond the limits set by current political practice, we proceed by allowing for a reasonably equitable representation (as a result of, for example, efficient coalitions among small members). Accordingly, for the sake of argument, we will assume that the autonomists’ reservations about the first two debate levels mentioned have somehow been taken care of, and deal with the third level only. Specifically, to abstract from the level-one obstacles to integration, we restrict attention to a supranational regulatory body able to harmonize at least the “symmetric-information equivalents” of its members’ preferences. That is, we demonstrate the existence of a central authority with an objective function which is optimized by the very same national macroprudential policies that each national regulator would choose given the policies of others, provided all uncertainties are common symmetrically observed random variables (In other words, the corresponding social welfare function implements the unique Nash equilibrium of a hypothetical symmetric-information game between the two regulators). In Section 3, we will work with an example of such. Also, in order to circumvent the level-two obstacles, we allow the national regulators to act on that part of local information they are unable to share, and give the central authority the capacity to process and translate into policies all information that can be shared (formal examples of Section 3 take this feature on board). In this setting, we will look at possible inefficiencies of non- cooperative behavior of national regulators when it comes to sharing local knowledge and the severity of welfare losses under different cooperation regimes.

2.2. National Regulators and Their Information

We consider two regulators, A and B, who exercise partial control over a common “global” fundamental risk factor they strive to minimize in the presence of quadratic control costs. Their preferences (loss functions) over the common fundamental are proportional. Specifically, the relative size of the losses incurred by the residual risk surviving the implementation of both national policies derives from the relative size of the respective economies themselves, and from nothing else. Among other things, this means that when the two economies’ sizes are unequal, the bigger economy (and its regulator) has a stronger impact on the loss of the smaller one than the smaller one on the loss of the bigger one. This makes the set-up formally applicable to the small open economy case.

Only a part of the information in the hands of local regulators can be credibly communicated to other parties. Several factors may cause this.

First, there may be elements of “soft” knowledge accessible to lower-rank supervisors only (e.g. confidential information on individual institutions), which the decision-making body of a supranational regulatory agency would have had to process at a prohibitively high cost. This can be illustrated by the example of regulation of international systemically important financial institutions (ISIFIs): the operation of a national affiliate of an ISIFI is often nearly impossible to follow in real time from across the border. This is so even when the countries involved are quite close and their financial regulators have a long-standing tradition of cooperation, as the case of the Fortis Bank Group resolution in the Benelux in September 2008 demonstrated.

Second, data take time to collect and the collection period often coincides with the period of the regulatory cycle itself, so that the outcome is worthless for outsiders because it is only available after the local regulatory decision has already been made. Consider, for example, a situation in which a credit bubble is forming more quickly in one country than in another. The regulator in the former country would need to have the loan-to-value (LTV) ratio limit for new loans lowered as soon as the data start to signal a bubble reliably. However, since bubble detection is generically a slow process, the latter country regulators may be still collecting evidence that, on their side, the LTV restrictions are warranted as well. Under centralized regulation, the necessary decision may have to wait until information from both national sources has been processed, and may come too late as a result. This could easily happen even if, under hypothetical (although counterfactual) symmetric and timely data pro- cessing, the socially desirable LTV caps in both countries were the same.

Third, and this is what the microeconomic literature is most familiar with, information may be impossible, or prohibitively costly, to verify for anyone else but the regulator in question. Then, analogously to what has long been taken for granted in contract theory and the microeconomics of financial intermediation, the regulator may not have the right incentives to report accurately to outsiders (in fact, it may have an incentive to misreport), for strategic reasons⁶. We will follow both the genesis of this misreporting incentive and the corresponding adjustment of the credible policy attributes in the model.

The approach is necessarily highly stylized. This is not so much a limitation as a means to highlight the essentials of the problem. Various generalizations are possible, among them such that would allow one to vary the relative effect of the global risk factor on regulators’ utility in the two national economies, keeping the utility contribution of national regulatory costs themselves fixed. The principal message would not change under this modification, although the latter may be useful for quantifying the roles of relative size and relative exposure to systemic risk (e.g. as a result of differing financial depth) separately⁷.

3. Model

3.1. Environment

Let 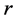be the fundamental risk factor introduced in the previous section, 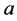and 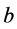its national constituent parts, an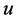d and 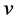the controls exercised by the two national regulators. Formally,

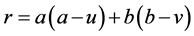. (1)

Coefficients 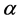and 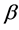reflect the relative strength of the contributions to 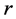-containment by regulators 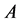and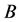. These coefficients also reflect the weights with which the common risk factor 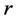enters the corres-

ponding regulator loss function: the loss of 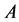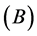is assumed to be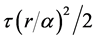 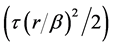, with be-

ing a positive constant, for simplicity assumed the same for both. This definition means that each regulator accounts for the loss from its own residual fundamental (for and for) one-to-one, whereas the spillover from the other country residual enters the loss function with a rescaling factor depending on the relative sizes of the two economies. For instance, if economy is bigger than, regulator cares about spillovers from more than cares about spillovers from.

Further, let the controls entail (tangible and intangible) quadratic costs so that they enter a regulator’s loss function with a common coefficient. So, when chooses control , it incurs costs . Accordingly, the overall loss functions of and are

(2)

and depend both on the regulatory policies and on the realization of the random risk factor. The latter is stochastic since there is uncertainty in the realizations of its national drivers and. Each regulator strives to minimize the expected loss given both public and his private information.

Generically, both national components of the aggregate risk factor to be controlled are affected by exogenous noises. We can think of a part of these disturbances as originating in outside world shocks, as it may be important to take account of a wider world outside the two economies in question. The remaining noises are related to the private information of the national regulators, meaning that their perception is asymmetric. The exact definitions will vary depending on the specific interaction cases, to be specified in the individual subsections of Section 3.2. However, in all cases, all participants agree on the general form of the statistical model for the national risk components. So, we can always write, , with and being means, and and being mutually independent random disturbances with zero means and standard deviations and ⁸. Differences appear as to who learns which of the values of, , , and when.

The part of the noise affecting and that reflects external shocks is likely to remain uncertain both to the national regulators and the possible overarching authority. Their statistics can be taken as common knowledge. In the chosen quadratic loss set-up chosen here, the presence of this type of uncertainty does not affect the properties of equilibrium decisions. Therefore, to make the exposition simpler we do not consider such shocks explicitly.

No less important are factors contributing to random noises and for purely “technological” reasons inside the respective regulatory systems. It is well recognized that financial oversight utilizes a lot of “soft” information, which is hard to either formalize or transfer to parties exterior to the oversight process. Apparently, such soft information would be even harder to communicate to partner regulators outside the country (see the discussion in Section 2.2). The phenomenon has been documented mainly for micro-supervision of banks, but it is reasonable to assume that, when it comes to macroprudential policy, i.e., the synergy of micro-supervisory information with inferences on aggregate systemic risks, the problem of communication of insider knowledge to outsiders becomes even more, not less, severe.

The next step in the argument is to recognize that ex ante estimates of a parameter that cannot be either measured or communicated exactly are much more likely to be manipulated than a parameter known at least to one party with certainty. In the practice of communication between national regulators, distinguishing between honest measurement error and deliberate misreporting is as good as impossible. That is why country-specific noises existing at the time of signal exchange are a natural element of the cross-border communication model we cre- ate.

For the aforementioned reasons, the presence of random disturbances to the controlled fundamental, although it does not add any analytical sophistication worth mentioning to the formal derivation of our theoretical statements, is important for conceptual reasons. The computations themselves will be made slightly simpler by assuming that each national regulator eventually resolves its own uncertainty component after the exchange of signals but before its own policy decision, i.e., knows exactly at the time of setting . Generalizing to non-zero residual uncertainty would be straightforward but is unimportant for our purposes.

3.1.1. Stages of the Game

With the above discussion in mind, we define the timeline of the model with three distinct points.

At the initial moment, the two regulators learn the parameters of the game, including the distributions of random factors and. Also, regulator learns the value of and the value of. Each of them also receives prior information about the other party’s average national risk factor, i.e., A learns value and the signal precision (the distribution of the noise), whereas B learns value and the distribution of the noise.

At the second moment, regulators send out reports about the true value of their average fundamental: sends a signal about (i.e., the statement claiming that is equal to) and a signal about. The signals do not have to be truthful.

At the third moment, and learn their respective national fundamental values and exactly and choose their controls to minimize the expected losses given their private information, i.e., they solve optimization programs

. (3)

Symbols and stand for expectations based on the two different information sets available to and, respectively.

3.1.2. Non-Verifiable Local Information and Harmonization of Preferences

In accordance with the above definitions, we can identify the transferable information with value (for) and (for) and the non-verifiable information―with realizations, at the third stage, of shock (observable only by) and shock (observable only by).

At this junction, we are able to define separate criteria for autonomous decision-making (each regulator independently and non-cooperatively) as opposed to integrated, or harmonized, regulatory decisions by a joint authority⁹. Since, in accordance with the objectives spelled out in 2.2, we are only allowing the integrator to decide prior to the private shock realizations, its loss function must be defined in terms of transferable information (and the parameters of the model). In other words, the integrated regulator has to set controls for both and based on their reported values of and and the known distributions of and. Formally, the objective can be to solve the following optimization problem:

, (4)

with being the expectation with respect to the integrated regulator’s information about the uncertain values of and, national regulators’ signals given. Coefficients and can be selected so that the integrated control choice is identical to what non-cooperative regulators would have done independently if they had had the same information. Indeed, if one sets, , the joint regulatory authority that solves (4) would select the same controls as and, solving

. (5)

The solution of (5) differs from what we will call the truthtelling non-cooperative equilibrium in 3.2.2 below, by expectations which are taken w.r.t. public information, as opposed to (3). Note that this is not a realistic Nash equilibrium notion since, in general, as discussed in 3.2.3, deviations from truthtelling are possible and profitable. In general, the joint authority information set would contain the values of the national regulators’ signals, , instead of the true values.

Given that and are private non-transferable information, (4) and, equivalently, (5) are actually the closest the integrated regulator can get to replicating the individually optimal choices of controls implied by (3). Therefore, any discussion of the advantages and disadvantages of international harmonization must take this “residual welfare discrepancy” into account. Its sign is model-specific and unobservable and, therefore, the verdict about the (dis)advantages of harmonization can be only inspired, but not determined, by the theoretical framework presented. Still, the “local expertise” factor, which we have formally associated with shocks and, clearly belongs to the “level-two debate”, as was outlined in 2.1 above, whereas our main interest in this paper is the “level-three factors” related to strategic information exchange.

The next subsection provides formal results about the decentralized equilibria under different degrees of informational friction (full symmetric information, private information with truthful reporting, misreporting). In parallel, variants of the equilibrium solutions under various assumptions about the powers of the overarching regulatory authority are provided as well.

3.2. Equilibria with Accurate and Distorted Signals

3.2.1. Benchmark: Complete Symmetric Knowledge of the Game Parameters

Purely hypothetically, and in disregard of the informational imperfections defined in 3.1, assume that and have perfect knowledge of both and, from the outset. This counterfactual example is given for further reference. We then obtain the following characterization of equilibrium policies.

Proposition 1 The Nash equilibrium of a simultaneous-move game of perfect information between regulators and is characterized by regulatory controls

. (6)

The regulator loss function values in this equilibrium are given by

■ (7)

It is easy to check that a perfectly informed central authority with preferences defined by loss function (4) with parameters, would also choose controls (6). The result would not change if the central authority observed a and b with noises, as long as the noises constitute a common uncertainty for all parties involved. This means that in the hypothetical symmetric information case, the Nash equilibrium can be implemented by a joint social welfare function, as was mentioned at the end of Subsection 2.1. Therefore, our setting is chosen in such a way that centralization is not an obstacle to a standard non-cooperative outcome of the “symmetric-information derivative” of the original game. So, from now on, one can concentrate on the role of centralization for the asymmetric information aspects of the regulators’ interaction.

3.2.2. Truthful Controls under Imperfect Information

Another counterfactual special case arises when, as defined at the end of 3.1, the non-transferable information (shocks and) is observed privately, whereas the transferable information is signaled perfectly truthfully at the first stage. In the notation introduced in 3.1, this means that,. We will call this (counterfactual if taken at face value, but with a chance to be implemented approximately; see Corollary 1 in 3.2.3) outcome T-regime, T standing for “truthful reporting”.

Proposition 2 If truthful reporting of average national risk factors by national regulators (i.e., by and by) can be enforced, then the Nash equilibrium of the simultaneous-move game between and is described by strategies

, (8a)

. (8b)

In terms of signals and noises, these strategies can be expressed as

. (9)

At the first stage of the game (i.e., before learns and learns), the ex ante loss function values are given by

, (10a)

■ (10b)

Observe that the strategies in the above game are in terms of the true national risk factor value known to the corresponding regulator and the two signals (see (6) of the complete information game; expressions (10) can be derived directly from (6) by looking at (9)).

In our setting, joint social welfare is hard to define uniquely due to the existence of non-verifiable private regulatory information in each country. It seems most natural to compare the ex ante loss functions (10) of the non-cooperative equilibrium with the losses incurred under harmonized regulation following (4) and (5), which we hereinafter call the I-regime (I for integration). Note that, thanks to the quadratic nature of the loss functions, one can all but separate the welfare consequences of -uncertainty from the rest of the parties’ problems. Indeed, (4) implies optimal controls of the form

. (11)

The expected loss functions (under expectation operator) are

, (12a)

. (12b)

Apparently, the difference from the losses under the uncoordinated Nash equilibrium given by (10) is in the noise terms. Not only does the national regulator know that by opting for decentralized policy he reduces the loss ex post, but also, ex ante, the variance terms enter (10) with coefficients strictly lower than those in (12), so that it is always true that

. (13)

The formal reason is, obviously, the possibility to take full advantage of the private information disclosed at the second stage, under decentralized policy, the same as the awareness of this possibility open to the other regulator, finding its reflection in the strategic choices.

The result of (13) could be reversed if one assumed that the central authority were somehow able to improve each regulator’s knowledge about the other regulator. Specifically, suppose that the knowledge of the other country fundamental is distorted by a stronger noise under decentralized than under centralized policies. This would mean a different set of values of, , , and in the equilibria described by (8) on the one hand and (11) on the other (Since the same true fundamentals, and, are now measured with different precision, both the mean values and the noise dispersions would have to undergo a change). This would make comparison of loss functions (10) and (12) impossible without further quantitative assumptions. The (pretty bold and speculative) assumption able to reverse the result of (13) would, obviously, have to be a superior information-collec- tion and processing ability of the central authority.

Realistically, the ability of multinational bodies to improve the informational transparency of their constituent members should be made an empirical question, which exceeds the scope of the present simple theoretical exercise. Here, we prefer to leave aside the role of informational precision under (hypothetically enforced) unbiased signals, and concentrate our attention on the case, at least as important from the pragmatic point of view, of signals with a deliberate bias.

3.2.3. Equilibria with Misreporting

In addition to the information precision problem just discussed, a more serious one arises because, once one has to give up the unnatural assumption of enforced truthtelling in the I-regime, the equilibrium solution of Proposition 2 immediately falls apart. More precisely, incentives to misreport exist both in the centralized I-regime and in the decentralized T-regime as soon as one admits the possibility of deviation from truthtelling by one party as a reaction to the truthful behavior of the other.

To see this, let us consider the T-regime for definiteness (the I-regime case is similar). We allow regulator to report a different-than-true value of, say, , while forcing to take this report as truthful and act as if the equilibrium of Proposition 2 still held. That is, is now using (8b) with replaced by, a strategy we denote by. After reporting, regulator chooses the optimal response to this strategy by (naturally, coincides with (8a)). Denote A’s ex ante (i.e., in the first stage before the revelation of a) expected loss under this behavior by. This loss is equal to (10a) when. What about small deviations of from zero? By the Envelope Theorem (A’s action is individually optimal and given by the unique internal solution to the problem of F-minimization), the -deriv- ative of at is equal to the partial derivative of w.r.t.. By looking at (8b), we find that the latter derivative is proportional to the expected value of. By simple algebra based on (9), one finds that the latter is proportional to. This means that, outside the exceptional case of, can be always improved by a small non-zero shift of x away from zero: in the positive direction when and in the negative direction when. Informally, one can say that a free-riding incentive is present, as regulator A, while saving its own costs, induces B to employ a more active policy.

In view of the existing incentives to misreport, it is reasonable to look for equilibria that allow other than truthful signals. Specifically, we cons id er below a set-up in which untruthful signals (in the notation of 3.1, and), of pre-defined sizes, are allowed with known ex ante probabilities¹⁰. We then construct an equilibrium in which and take full advantage of the offered opportunity to misreport. In other words, if regulators are prov id ed with a well-specified option to lie, they will exercise it.

Our result goes through under a fairly general representation of misreporting opportunities. Formally, we assume that operates for its signaling a randomization device according to which the difference of and is a stochastic variable distributed with density, and an analogous randomization with density ψ is employed by:

. (14)

Densities and are supposed to be common knowledge.

After the randomized signals have been generated and disclosed, the game proceeds as defined before in 3.1, i.e., the regulators wait until the exact value of their respective national fundamental becomes known with certainty and then choose their controls. One difference compared to 3.2.2 is that the value of the other country fundamental is now uncertain for two reasons: the first is the same private component as was introduced in 3.1 and the second is the signal distortion, so that the expectations must be formed differently. This seemingly minor adjustment has far-reaching consequences for equilibrium behavior. The signal randomization (misreporting, or “lying”) rules are known to both players and feed into their optimal strategies, which is why one cannot avoid mixing truth and lies in the proportion pinned down by (14) even in favor of the truth if one wants to remain credible and support the equilibrium outcome.

Analogous situations, in which the signals of game participants have to contain uncertainty in order to be believable, are known from the microeconomic literature on so-called “cheap talk” (see [21] and [22] [22] ). The latter term means costless messages by players in a non-cooperative game that help them to coordinate on the extraction of common benefit without being suspected of lying to secure an undue advantage in the zero-sum component of the payoff. In the present model, for reasons of analytical simplicity, we have chosen to represent message uncertainty by means of signal randomization. A set-up similar to that of [22] , based on fuzzy signals in the form of intervals, is equally possible.

With the defined timing, regulators’ equilibrium strategies must be functions of both signals, exact values of known variables, and distributions of uncertain ones. In particular, since the control is chosen after the resolution of both uncertainties on the regulator’s own side (and for, and for), it must depend on the signal about the own fundamental and not its true mean value (and not for, and not for), because otherwise, knowledge of the model would allow for extraction of the true value by the counterparty. The exact result is as follows.

Proposition 3 The equilibrium strategies of the signaling game with misreporting rules (14) are given by

, (15)

with, being the average signal distortion (lie) values. ■

Rule (14) was chosen for its relative simplicity in terms of representing signal distributions. However, a better interpretation can be obtained by parameterizing the space of misreporting events separately from the space of misreporting sizes. Namely, let, be two random event spaces by means of which A and B form their signals (independently of each other), and let us fix probability measures, on those spaces. Then, let a lie of size take place with probability for any . Formula (15) is not affected by this event space change.

The above result characterizes equilibrium behavior on condition that the misreporting size distributions (functions and defined on event spaces and, respectively) are fixed. As a special case, when both and are identically zero, we obtain the truthtelling solution of Proposition 2. However, the main message of Proposition 3 is that, whatever the available distribution of reporting “mistakes”, there exists an equilibrium in which these mistakes are committed. As regards the welfare comparison of equilibria under different choices of functions and, there can be no general conclusion since the loss value is significantly dependent on the distributional characteristics of the misreporting rules. However, one can conduct a simple comparison of the welfare consequences of changes in one lie magnitude under a given misreporting event (i.e., by fixing a random event or as well as well as all and realizations except for one by one regulator, and varying the latter lie size).

Since, when investigating the welfare consequences of varying misreporting magnitudes, it is more natural to compare ex ante expected losses (before random signal selection) than ex post realizations of losses after the regulators have learnt all available private information, we look at expectations with respect to the information available to immediately after it learns and to immediately after it learns. We use operator in both cases (this should not cause confusion) and denote by the -expectation of A’s losses considered a functional defined on the space of misreporting size functions x (analogously for). Let us call the outcome L-regime, or if one needs to refer to the dependence on the lie size. Then we have the following general characterization in functional analysis terms.

Proposition 4 If the values of the average national fundamentals observed by regulators and are equal to, respectively, and, the variation of the ex ante regulator -loss functional at any initial point is given by the linear functional

, (16)

and an analogous result holds for functional evaluated by regulator. ■

The abstract form of Proposition 4 was chosen to stress the generality of the result. To develop the necessary intuition about its meaning, we simplify the situation in the following.

Corollary 1 Let the signal randomization space of regulator be final and contain N elements. Then the feasible signal distortion sizes for are simply vectors of dimension N (with one component equal to zero since we want to allow for truthful reporting as one possibility), whereas the misreporting probabilities are N- vectors with positive components summing to 1. Functional becomes simply a function of N variables. In that case, (16) is equivalent to the collection of N equalities

. (17)

In the situation defined by the above elementary event spaces, Proposition 4 simply tells us that, when the signal distortion is negative (positive), A’s welfare can be increased by moving it up (down), in both cases closer to zero. The lowest losses for A are attained under truthful reporting. If one combines this finding with the intuitive fact that A’s welfare benefits from an increase in B’s truthfulness, we arrive at the natural conclusion that, in terms of social welfare, the truthtelling equilibrium of Proposition 2 dominates all other equilibria described by (15) with non-zero misreporting:,. This is an example of the general phenomenon of inefficiency caused by imperfect credibility in signaling games.

The above result should not be confused with the simplified (and false) claim that regulators would choose to signal truthfully in a given game. Remember that lie sizes are not choice variables in it. Strategies (15) are individually rational for any pre-defined distribution of lies, whilst Equations (16) and (17) offer comparison of welfare across different distributions of lies. So, Propositions 3 and 4 can be equally well interpreted in such a way that, although offered a clearly welfare-superior game of truthful reporting, regulators always run a risk of relapsing into a welfare-inferior game with lies, the supply of which is unlimited.

A more cautious interpretation of the optimistic message provided by (17) is, in our view, more appropriate. One could say that, if, for some extraneous reason, the game between regulators according to the rules of this subsection could be repeated under varying magnitudes of misreporting, both participants would tend to choose every subsequent game with lie sizes below the levels of the previous one, until, eventually, the signal distortions become negligible. Note, however, that it will still be the game with the formal distinction between signals and privately observed values, and not the game of mandatory truthfulness from 3.2.2, which has a different strategy space. Recall that a transition to the behavior which ex ante excludes misreporting by one player would immediately provide a non-negligible misreporting incentive to the other player. Therefore, one can, at most, conclude that the evolution of the lie size rules in the present misreporting game is likely to result in a near- truthtelling game. At the end of such a development, one would see (near-)maximization of welfare in the class of misreporting games defined by (14).

Comparing this fact, formally expressed by (16) or (17), with inequality (13), one sees that the equilibrium of the near-truthtelling signaling game between national regulators is superior in welfare terms to both centralized regulation (with truthtelling) and the equilibria of any signaling game with non-negligible misreporting. However, this does not mean that the welfare of decentralized signaling with potential minor strategic misreporting can- not be improved upon. Next, we discuss one possibility to reduce the losses by overcoming the limitations of strategic behavior. To do this, we will slightly change the rules of interaction between national regulators, at the same time avoiding unrealistic assumptions about the information-extraction potential of transnational authorities.

3.2.4. Full Responsibility for Misreporting

Strategically sophisticated behavior finding its expression in misreporting equilibrium (15) has its welfare limits not so much due to inefficiencies stemming from distorted signals (those are likely to recede with time, as we argued in the previous subsection) as due to excessive weight attached in the decision of one regulator to the signal statistics of the other. Put simply, this is an inefficiency caused by over-sophistication of the players. Let us now again assume an overarching authority which has no incentive to dwell in the fineries of the players’ strategic misreporting. We endow this authority with just one power: to collect signals from both regulators and implement national controls as their agent, but treating both signals as if they were fully truthful. Regulators are allowed to misreport according to the same scheme as in (14), but their own actions will be always formulated by the coordinating power on the artificial premise that the other regulator does not lie. The equilibrium of such a signaling game with delegation is described below.

Proposition 5 If the national regulators endow the coordinating authority with the power to set controls based on their signals (generated according to (14)) about the mean values of national fundamentals, on condition that those signals are treated as truthful, the equilibrium controls are (superscript d stands for “delegation”)

. (18)

By denoting the “true” average fundamental risk by and introducing the auxiliary “joint misreporting” variable, the loss function value for regulator A under (18) can be written as

(19)

when and choose misreporting values and, and an analogous expression is valid for the loss function value of regulator. ■

In the above proposition, the lie sizes and probabilities are fixed, as they were in the signaling equilibrium of Proposition 3. And, in the same way as was done in 3.2.3, we can ask how do regulators’ loss functions in equilibrium (18) depend on the level of lies. For the sake of transparency, we give an answer for the simple example of just two possible signal values for each regulator. Namely, let report truthfully with probability and give a false signal with lie size , i.e., , with the remaining probability (more general settings yield analogous results, but their statement would only require more cumbersome notation without additional insight¹¹). It turns out that, as opposed to the (maximum sophistication) equilibria of Subsection 3.2.3, the optimal misreporting size in the present case of a “credulous” central authority with delegation is non-zero.

Corollary 2 In the equilibrium of Proposition 5 with a single deviation from the truth allowed for each regulator, the regulators’ losses are minimized when the lie sizes satisfy

. (20)

Under these values of (possible) signal distortions, the losses of each regulator are strictly lower than the losses of the same regulator in the centralized regulation case with perfectly truthful reporting, as given by (12). ■

The intuition behind the above result can be found in the elementary properties of the socially optimal macroprudential controls in the settings in which they can be defined unambiguously, e.g. when information is symmetric. Aggregate welfare would be then expressed by means of a (weighted) average of national loss functions: for some weight between zero and one. It is then easy to check that, if the optimal controls constitute an internal solution to the global loss function minimization, the partial derivative of w.r.t. (w.r.t.) must be negative, i.e., the socially optimal control should, typically, lie at a higher level than the non-cooperative game control (naturally, under truthful reporting in equilibrium, since symmetric information excludes misreporting). In other words, hypothetical globally optimal national regulators usually ex- ercise greater effort than regulators in a non-cooperative setting, whereas non-cooperative outcomes entail free- riding. The myopic impartial mediator providing for our “optimal misreporting” mechanism ensures that, with their lies, the counterparties induce each other to move exactly in the desirable direction of greater effort.

In the remaining sections of the paper, we will denote the internationally coordinated regulatory regime in which the central authority is empowered to interpret the national regulator signals as truthful by -regime (for delegation) and the specific case in which optimal misreporting is described by (20) in Corollary 2 by -regime.

3.2.5. Non-Transferable Information and Exit Option

Observe that, in Corollary 2, we have compared regulators’ welfare with the centralized solution of 3.2.2 and not with the decentralized equilibria of either Proposition 2 or Proposition 3. The reason is that, as was assumed in 3.1, information on, , associated with private regulatory expertise, cannot be transferred to the central authority. Therefore, controls in a -regime cannot make use of terms, , and the ex ante welfare measures of and in equilibrium (18) include, respectively, variance terms

(21)

in the same way as in (12). On the contrary, losses in any decentralized equilibrium from Proposition 3 contain terms

. (22)

Variances and enter (22) with smaller coefficients than in (21). This is the welfare benefit from private regulatory expertise already discussed at the end of 3.2.2. Thus, although we clearly have the inequalities

(23)

analogous to (13), as stated in Corollary 2 (recall that and are loss function values as in (19), when regulatory controls are given by,), we cannot directly compare with without further assumptions. Remember that, as stated in Proposition 4, losses under truthtelling prov id e the strict upper bound of the loss functions attainable by various misreporting equilibria (15). The relation of this upper bound with is ambiguous as two opposite forces are at work here. The difference between (21) and (22) gives the welfare advantage to a decentralized control solution, whilst the effect stated in Corollary 2 (externally imposed limits to second-guessing) speaks in favor of a central power able to limit excessively sophisticated strategic behavior. Apparently, the “sophistication inefficiency” is more important when the private information significance is low and less important when it is high.

In any event, by giving the regulators an “exit option” from the delegation regime, one can make sure that the losses from unexploited private expertise under harmonized regulation do not get out of control. The exit option means that, before the game starts, each regulator is free to choose between staying in the regime of 3.2.4 (a central authority that interprets every signal as truthful) and reverting to the most elementary available version of decentralized regulation. Namely, instead of the signaling game defined in 3.2.3, one can choose a regime in which regulators act in mutual isolation (no signals), relying only on prior information. To make this last option more specific, one can assume that prior information, although very noisy, is unbiased, i.e., errors and faced by, respectively, and, have zero means¹². Then, we obtain a backstop in the form of loss from high noise in the prior information about the other regulator. For instance, for, it means deciding with prior knowledge of (instead of entailing error as was assumed in 3.2.2) and a variance of, which may be higher than and drive the loss term (22) further down away from zero. Evidently, the actual inequality sign between under low-variance noises and with high-variance noises will depend on the parameter values of the model.

More generally, an outside option in the form of reversion to non-cooperative regulatory autonomy would be useful in any environment in which the benefits of centralization are sensitive to exogenous parameters and rule- abidance by partners. The exposition in this section points, among other things, at the following three deviations from rational behavior it can put a limit to:

1) The central authority reneging on the -regime under pressure from an influential national regulator, the latter forcing evolution of cross-border regulatory coordination toward some form of strategic misreporting game similar to the one described by Proposition 3, but with welfare additionally reduced by the loss of private regulatory information;

2) One of the national regulators getting stuck in misreporting behavior with a high misreporting level (in a decentralized regime);

3) The central authority putting excessive stress on, and demanding additional resources for, the enforcement of truthful reporting (i.e., striving after the I-regime described by (11) (12) in 3.2.2), which, due to the loss of private regulatory information, would be inferior to decentralized regulation under a sufficiently low strategic misreporting magnitude.

4. Interpretation and Discussion

The different varieties of the model cons id ered in the previous section prov id e us with the following outcomes. There are two possible regulatory organizations: centralized and decentralized (when each regulator dec id es autonomously). We have discussed the indiv id ually rational decisions of national regulators under two regime types, I (integration) and D (delegation), for centralized regulatory organizations, and two further ones, T (truthful reporting) and L (lying), for autonomous regulatory organizations. The findings concerning welfare implications are summarized in Table 1 (for space economy reasons, only the loss functions of the first regulator, i.e., , , etc., are mentioned).

The centralized organization is associated with a loss of non-transferable private information held by national regulators. Decentralization gives ex post gains to each of them conditioned on maximal feasible mutual truthtelling. The latter is not deviation-proof (at least a minor misreporting deviation always pays), i.e., it remains hypothetical without an implementation device. If such a device is proposed in the form of a central authority (integrated macroprudential regulation), then 1) the previous problem of non-transferable private information returns to reduce aggregate welfare; and 2) one still needs to explain how to achieve truthful reporting. Since it is hard to justify why misreporting by integrated regulators should be prevented by the mere fact of the existence of a central authority (whose only feasible role can be to collect and disseminate data from participants), rational misreporting should realistically be counted upon under both decentralized and centralized regulatory regimes.

However, the second part of our story casts the intuition of the first part in quite a different light. We take one step further from the misreporting equilibrium under a fixed distribution of possible signal distortions and ask whether, given any fixed distribution of possible lie sizes by the counterparty, the national regulator will be better off under a bigger or a smaller own size of misreporting. And one finds that smaller (in absolute value) own lies entail higher welfare. The outcome follows from the strategic behavior of both parties, as given by (15). According to Proposition 3, each regulator conditions its own actions on both the misreporting choices of the

other side and the rational reaction of the other side to its own misreporting (“I know that you know, etc., … that I am lying to you,”―the so-called infinite regress of knowledge and beliefs explored by abstract game theory, see [23] ). This means that, given the equilibrium signaling policy of the other regulator, any regulator in this setting would, prior to the start of the actual reporting game, seek external circumstances in favor of reduced misreporting. So, if it has enough alternatives among which to seek, the same as the other side, the two regulators should eventually coordinate on a nearly-truthtelling outcome. A coordinating authority is then not needed. Recall (see (13) in Subsection 3.2.2) that the latter is unable to make use of private national information. This fact entails losses which are unlikely to be compensated by the attempts the authority can make to enforce reporting quality (it does not contribute to this quality any more than the two parties do independently and voluntarily).

The story also has a third part. The near-truthtelling equilibrium that, as we have seen, comes about as the evolutionary stable outcome of the search for optimal misreporting, is not identical to the socially optimal outcome. The latter would require more intensive controls than the non-cooperative truthtelling Nash equilibrium. The mechanism of impartial signal processing with obligatory truthful interpretation, i.e., the -regime that we discussed last, moves regulatory actions in exactly that direction.

The theoretical distinction made in the previous section between decentralized decision-making by national regulators and delegation of their powers to a central authority should by no means be confused with the actual international interaction patterns of regulatory agencies. On closer inspection, all the signaling and control strategies considered so far are perfectly imaginable under both a centralized and decentralized cross-border policy regime. So, the question is not which regulatory architecture generates which reporting behavior, but rather, which rules agreed among the participants, be it under either a hierarchical or a polyarchical architecture, create the best conditions for a given behavior. Accordingly, we shall now think about the chances of different variants of our signaling game to find a counterpart in the behavior of real-life macroprudential regulators. One needs to attribute the abstract outcomes of Section 3 to the institutional realities of regulatory cooperation.

The featured variants of the discussed strategic game with private information are all too abstract to make policy-relevant interpretation immediate. Finding an equilibrium strategy requires both rationality and sufficient cognitive abilities on the part of each policymaker. Not least, the selection of optimal reporting/signal values, as it requires knowledge of parameters whose unobservability lies at the very bottom of the problems we consider, cannot be much more than a trial-and-error exercise (supposing one designed a corresponding experiment e- conomy to test the viability of equilibrium outcomes). In this regard, the most important part seems to be to identify the most appropriate game rules and then look for the institution best able to implement them.

To that effect, we argue that an “empathy-free” arrangement between sovereigns with formal application of pre-agreed procedures may be welfare-improving compared to arrangements trying to replicate national “micro- concerns” in exchange for delegated sovereignty (as the current EU practice often does to avoid criticisms of national interest neglect). This is exactly the difference we visualized in Subsection 3.2.4 between the controls set by a mediator with a clear limit to sophistication, and maximally sophisticated controls based on infinite-regress belief processing. Having an international coordinator that allows members to deploy the full range of their second-guessing abilities in the name of fairness, i.e., a regulation harmonizer, may be detrimental to the overall welfare. Conversely, having a brainless automaton taking every member at its word, i.e., a very elementary regulation centralizer, may be welfare-improving. In addition, if cross-border coordination of this type is augmented with an exit option (the right to revert to decentralized strategic interaction), one obtains a mechanism in which the risk of downside losses from ignored private non-transferable regulatory information in the name of harmonization is cut off.

At the same time, we stress that what the model has rendered as a welfare-superior mechanism is not a supranational regulatory autocracy, as some expect to find in the recently established ESRB. As such, the central regulatory level does not have to function as an administration enforcing compliance, but should instead act as an impartial mediator. It grants the parties freedom of choice, upon which it assumes full power while acting on the choices submitted. Importantly, as opposed to the declared ideal of the EU bodies, an institution that would implement the said mechanism does not need to have its preferences aligned with those of the member regulators.

5. Conclusions

We have proposed a model of joint financial risk control in which the national regulators allow some mutually agreed central authority to take regulatory decisions based on the information they submit. In the process, a part of “soft” local information gets lost, entailing a welfare loss. Decentralized regulation avo id s this loss, but, instead, creates potential for strategically distorted supervisory information exchange between countries (misreporting). With the exception of the unlikely case of the central authority being able to verify the signals at an affordable cost, the misreporting opportunity survives regulatory integration. Still, centralization can be beneficial as long as it is able to put a limit on the strategic sophistication of the parties involved, therewith reducing the free-riding effect.

In view of the lessons from our model, the main weakness of the current mechanism of EU-wide cooperation in the macroprudential area can be summarized as too much strategic consideration in the quest for a perfect balance of national interests, but not enough space for national responsibility for one’s actions. It is too anxious to integrate claims and (often conflicting, and in any event rarely aligned) interests across member states and almost entirely unconcerned with the issue of finding appropriate contingency rules (put simply, the “crime and punishment” aspect).

Our reading of the model corrects the conventional intuition about the workings of institutional arrangements normally associated with integration and decentralization. So, according to our results, the main pitfall of integrated regulation does not seem to be insufficient respect for national rights. Institutions putting too much stress on such rights are also likely to allow excessive strategic interaction. As we have seen, the latter is harmful not primarily due to misreporting behavior (which is likely to be limited in extent), but rather, since the joint regulatory effort of strategically interacting national regulators may be socially suboptimal due to free-riding. Complete freedom of strategic behavior prevents the national regulator from bearing the full costs of its actions, i.e., not just the private costs but its fair share of the social ones as well. That is, regulators forced by a disinterested arbiter to face the full consequences of their inaccurate signals jointly achieve higher social welfare than regulators integrated in an “empathic” supranational body. This reading of the much-invoked subsidiarity principle should not be overlooked in the process of shaping international institutions responsible for systemic risk oversight. In principle, the “empathy-free” arbiter arrangement we favor can be implemented between fully sovereign states on the basis of conventional international law. Naturally, it should be much easier to transform the existing agencies for the same purpose than to create new ones from scratch.

Acknowledgements

This research was supported by the Grant Agency of the Czech Republic grant No. 13-11983S. We are grateful to Martin Fukač, Stefano Neri, Martin Vojtek, and seminar participants at the 2012 CEUPS Workshop, Otto Beisheim School of Management, Vallendar, for valuable comments and suggestions. All remaining errors and omissions are the responsibility of the authors.

References

Appendix: Proofs

Proof of Proposition 1

Although the statement is pretty straightforward, we reproduce the key steps mainly for the purposes of subsequent reference.

When regulator takes the control exercised by, i.e., , as given, the loss function has the partial -derivative equal to

. (A1)

This implies the reaction function of on and, by symmetry, the reaction function of on in the form

. (A2)

The result (6) of Proposition 1 then follows directly from solving (A2) for and, whereas (7) stems from substituting (6) into the expressions for the loss function. ■

Proof of Proposition 2

Take regulator first. minimizes expectation of loss function, i.e., he knows exactly but, regarding, only has knowledge of value, which is its unbiased estimate. Accordingly, his knowledge of is an estimate as well. Instead of (A1), the first-order condition of optimality for is

. (A3a)

By symmetry, a similar expression is valid for:

. (A3b)

Our educated guess, inspired by (A2) and (6), is that equation system (A3) must be solved by control, which is a linear function of three variables:, , and, whereas control must be a linear function of, , and. So, we write

, (A4)

then substitute (A4) into (A3) and look for coefficient values, , , , , that satisfy (A3) and (A4) identically for all values of, , , and. The result is exactly as stated in (8) or, if one replaces by and by, (9). Given that, before the exact values of and are revealed to the respective regulators, and are random noises to both, the expected loss function expressions (10) can be obtained directly by substituting (9) into (2), taking expectations, and simplifying. ■

Proof of Proposition 3

Since it does not constitute any significant increase in complexity, we shall consider the case of a slightly more general regulator loss functions than in (2), namely

. (A5)

Formulation (A5) allows one to visualize the role of differentiated significance of global systemic risk across countries. (Preferences (2) are a special case of (A5) with,.)

As was mentioned immediately prior to the statement of Proposition 3, optimal regulatory controls are formulated after both the national fundamental and the own signal uncertainty have been resolved, i.e., they depend on the exact value of the own national fundamental, the own realized signal, the observed other regulator signal and the totality of other possible signals, by both regulators. In other respects, the search for equilibrium strategies can proceed as in the proof of Proposition 2 above. Our educated guess analogous to (A4) will be

, (A6a)

, (A6b)

and our task is to find coefficients, such that the first-order conditions analogous to (A3) are satisfied identically for all, , , and. (Note that and are functions on the supports of densities and, so that one pair of realizations corresponds to the observed signals and.)

It is a matter of simple checking that the coefficients solving this problem are unique and render equilibrium strategies

, (A7a)

. (A7b)

Expressions (A7) reduce to (15) when one sets,. It is interesting to observe that, whenever one country becomes more sensitive to global systemic risk than the other (the corresponding coefficient grows ceteris paribus), the relative importance of strategic interaction concerns for its regulatory policy, expressed by the last two terms in (A7a) or (A7b), declines. ■

Proof of Proposition 4

By definition, the variation (also called the differential) of functional , evaluated at a fixed random function: giving the sizes of the lies in all possible misreporting events, is a random (i.e., dependent on) linear functional for which

(A8)

for every: from an appropriately chosen normed linear functional space. Acronym denotes all the terms converging to zero quicker than the corresponding norm of in the said functional space, as that norm goes to zero. Let the space in question be the (real) Hilbert one with scalar product defined as

.

In this case, variation is also an element of this Hilbert space (this is the so-called linear functional Representation Theorem in Hilbert spaces). We will now consider optimal controls and from (15) as (affine) functionals on the same space. Then, is a (quadratic) function of and and the well-known facts from elementary calculus imply that the scalar product of with any given trial function can be written as

. (A9)

In (A9), (which can also be written in more detail as) is the expectation over the values of all four uncertain variables of the model. Next, observe that, by the definition of the equilibrium strategy, the first-order condition of optimality of is tantamount to the equality

(A10)

for any realization of and. At the same time, from (15) it follows immediately that the functional is affine in and is independent of and. Therefore, (A10) implies that

for every (the dependence of the partial derivative of on has been dropped for notational simplicity). In view of this “Envelope Theorem”, we only have to calculate the second term in (A9). To do this, we write the risk factor as a function of random parameter and observe that

. (A11)

In (A11), denotes A’s loss function calculated at,. At the same time, by looking at the second term of the second equation in (15), we obtain

(A12)

Here, as usual, means the integral of w.r.t..

By looking again at (15), substituting with and with, and after some algebra, one arrives at

(A13)

for any. Except for the term, the rest of the right-hand s id e of (A13) is independent of and can be taken outs id e of the integral in (A12). But, has the mean value zero, so that all that remains of (A12) is

.

This is exactly the statement of (16) and, in the context of Corollary 1, of (17) as well. ■

Proof of Proposition 5

Expression (18) is an immediate consequence of the rules by which the integrated authority is instructed to function: if it has to treat signals and as if they were equal to values and actually observed by the national regulators, then, subjectively, it faces the situation of the centralized regulator in the truthful world from 3.2.2. Accordingly, controls must be set as in (11) with signaled values substituted for the actual ones.

To prove (19), rewrite the expressions for, from (18) as

and substitute this into (1). We then see that the controlled fundamental in this notation equals

.

Using the definition (2) of the loss function and taking expectations over, (recall that they are independent and have zero means), we arrive at (19). ■

Proof of Corollary 2

The proof of (20) amounts to finding under which value of A’s lie the second term in the expectation over distortions, of the loss function expression (19) attains its maximum and whether this maximum value is positive, as claimed. Since the only term in (19) dependent on the lie values is the second one, and the latter is linear-quadratic with negative coefficient by, we know that, when reports distortion, his loss is minimized in expectation if and only if

. (A14)

This implies immediately that all lie sizes are equal under optimal behavior (the same applies to B by symmetry). Therefore, it is, indeed, sufficient to consider only binary distributions of x and y, as was announced in footnote 4.

Cons id ering this simplified case, we take regulator, who knows that is zero with probability and with probability. The expected lie by is simply. Analogously, his own randomized reporting generates the truth with probability and a lie with probability. Optimal choice of by, according to (A14), implies the following reaction function:

.

By symmetry, an analogous reaction function is valid for. Solving these two equations for and, we arrive at (20).

Now observe that the loss function of under centralized regulation with truthful signals, (12a), is equal to the sum of the first and the third terms on the right-hand side of (19). Evidently, the linear-quadratic second term there is strictly positive at and around the maximum, which proves that’s (and’s) losses are lower when they misreport according to (20) than when they tell the truth. ■

NOTES

^*Corresponding author.

¹In this regard, one should remember that all efforts to spread a particular regulation globally through the G20 platform have failed so far. International consensus is especially difficult when it comes to the costs issue, as shown by the example of the envisaged Systematically Important Financial Institutions (SIFI) regulation, the burden-sharing side of which at the time of this writing remained unresolved.

²At first glance, due to its lack of specifics on the controlled fundamentals and policymakers’ objectives, such a set-up could serve for an analysis of policy coordination in any area of human activity. However, we have chosen it particularly for the discussion of macroprudential policies because formal representation of the latter in the mentioned parsimonious language is much easier than other problems of political economy. Most other controversial issues in areas of legal and institutional integration and public choice are, essentially, multidimensional. On the contrary, macroprudential regulation, expressed by across-the-board directives with a well-defined aggregate target (which makes its role in the economy resemble monetary policy in many aspects), stands out as an isolated example of feasible quantification in a few elementary terms.

³A formal treatment of this cost-benefit dilemma, including cross-jurisdictional spillovers, can be found in [13] . More specifically, voting decisions by EU members under partially conflicting preferences are modeled in [10] .

⁴It is noteworthy that both [14] and all the earlier contributions cited therein already take informational losses in hierarchies as an established fact and concentrate effort on the analysis of their sources and mechanisms. This Williamson’s classic paper starts with a citation of a colleague’s speech at an AEA meeting that reminds the audience that “the larger and more authoritarian the organization, the better the chance that its top decision-makers will be operating in purely imaginary worlds”.

⁵The theory of mechanism design, among other things, teaches us that not every objective set by a social planner (social choice rule) can be implemented in a game form under the incentive-compatibility condition. Even among those objectives that can be implemented, many require a mechanism inconsistent with truthful revelation of private information (see [15] for an overview). Examples include the free r id er problem in the provision of public goods and “strategic voting” games. Accordingly, one should not expect the problem of international regulatory cooperation considered here to possess a clear-cut social welfare-maximizing “cheat proof” solution either (this will also be the case in our setting; see particularly Subsections 3.2.3 and 3.2.4). Unfortunately, this circumstance remains largely ignored by the political manifestos underlying the current EU financial regulation reform.

⁶One very topical current example of nation-level regulatory information that has exactly the opposite quantitative implications from the viewpoint of different national interests is provided by the banking sector condition of the EU periphery. It has been recognized by many observers that representatives of the Irish, Spanish, etc., banking sectors have every reason to create an impression of bigger-than-true balance sheet impairments as long as the size of the guarantee and bailout funds intended to help them out grows with negative expectations. On the opposite side, the public finances of the states providing guarantees, i.e., the “northern” EU ones, benefit from downplaying the same problems. A similar situation exists with regard to TARGET 2 imbalances within the Euro system: lowered collateral standards, set by the ECB in reaction to the shut-out of “southern” banks from the interbank market, were a reaction to the adverse conditions, which the “Club Med” members of the ECB’s executive bodies tended to overstate and which the members from the main creditor countries, headed by Germany, tended to understate (see [16] ).

⁷See the proof of Proposition 3 in the Appendix for an example of quantification in this sense.

⁸If the noises were not independent, i.e., there was a correlation caused by a common source of uncertainty, the latter could, thanks to the linear-quadratic set-up chosen, be easily factored out and separated in all analytical solutions analogous to those that we prov id e in the sequel. Qualitatively, the results would not be affected. This is why, for space economy reasons, we do not include any common noise terms.

⁹The difference between harmonization and centralization is important―see the discussion in Section 4.

¹⁰This randomization of signals has been examined in game theory as an attribute of “cheap talk” communication (see below), which is sometimes able to facilitate coordination on a mutually preferable equilibrium outcome. One of the easiest examples is the cheap talk signaling extension of the classical “Battle of the Sexes” game, as discussed in the review [17] . There is also a separate game theoretic literature on stochastic signals―see e.g. [18] . Alternatively, randomized signals emerge as a formal consequence of unobservable player attri- butes that determine the signal value, as covered by, e.g., [19] and [20] .

¹¹In fact, there is virtually no loss of generality compared to the situation of Corollary 1 with N > 2, i.e., with more than one level of signal distortion allowed. As we show in the proof of Corollary 2 in the Appendix, the optimal lie sizes must be equal across all admissible misreporting events. This means that, if the regulator gets to choose the misreporting magnitudes to minimize losses, he chooses the same lie level in all “untruthful” states of the world, effectively clamping down multiple misreporting events to just one.