Modern Economy
Vol.4 No.4(2013), Article ID:30752,8 pages DOI:10.4236/me.2013.44030
How Do Business and Credit Cycles Interact in EMCCA Countries?
Department of Economics, Omar Bongo University, Libreville, Gabon
Email: pamphile.mezui-mbeng@univ-lorraine.fr
Copyright © 2013 Pamphile Mezui-Mbeng. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 22, 2013; revised March 20, 2013; accepted April 12, 2013
Keywords: Credit Cycle; Business Cycle; Pass-Band Filter; Co-Movements; Concordance Indices
ABSTRACT
This article analyzes potential interactions between cyclic fluctuations in credit and activity in countries of the Economic and Monetary Community of Central Africa (EMCCA). Cycles are extracted by using a pass-band filter, then characterized over the period 1960-2008 according to the Bry and Boshan algorithm. Co-movements and concordance analysis establish that credit is procyclical in the EMCCA countries. Cointegration and causality tests specify interactions between the both cycles within countries. Indeed, in Chad credit cycle causes activity cycle; in Gabon and Congo, a feedback effect is observed; in Cameroon and CAR causality seems less obvious. Finally, results reveal specificities in banks behavior towards the financing of activity in EMCCA area.
1. Introduction
The international financial and banking crisis revived the old debate about the interaction between variables of the financial system and those of the real activity. Indeed, economic fluctuations can be amplified during periods of financial crisis as tend to prove, since the 1980s, many theoretical and empirical contributions devoted to the role of bank credit, in the form and amplification of cyclical fluctuations in the economic activity [1-3].
According to the theory of the credit cycle, a contraction of changes in credit supply leads to that of economic activity [4]. Two transmission mechanisms of cyclical movements in credit activity can be highlighted in this regard: the strict channel of credit and the broad channel of credit.
The strict channel of credit refers to the mechanisms associated with macro-financial credit cycle. It establishes a strong correlation between access to finance for borrowers and monetary shocks. In particular, a strict monetary policy leads to a reduction in the credit supply and influence the spending decisions of agents outside the channel of interest [5,6].
The broad channel of credit highlights the impact of imperfections on financial markets. In this regard, the existence of informational asymmetries between lenders and capital applicants, influences the propagation of monetary shocks by promoting an increase in the cost of financing and a lower level of production [7]. Finally, according to [8], the presence of imperfections in the credit market is also pushing banks to overstate the creditworthiness of borrowers during the expansion phase of the business cycle and increase their loans, thus amplifying the cycle.
However, empirically, in particular, all the works do not prove the existence of a link between changes in credit demand and economic activity. Indeed, in case of slowdown in economic growth or even decline in activity, an increase in demand for credit can be observed [9,10].
Ultimately, if the literature is commonly accepted the existence of an interaction between the cycle of financial variables and that of macroeconomic indicators, it seems that its importance depends on the transmission channel through which it passes, on the consumer structure and the financial markets of the countries concerned.
In the case of countries of the Economic and Monetary Community of Central Africa (EMCCA), a six countries Union, 1) the credit channel plays an important role in the transmission of monetary policy to the real activity, given the low development of financial markets and the virtual absence of banking products at variable rates. In addition, the EMCCA zone is characterized by a relatively slow economic growth in recent years [11]; 2) it therefore seems interesting to study the relationship between credit cycle and that of economic activity within EMCCA zone, for at least two reasons:
1) The EMCCA economies are highly open to the outside in terms of trade and financial flows [12]. And as such, they are not immune to the consequences of international financial crises. In this sense, empirical verification of the relationship between business and credit cycles in this area is timely in that it constitutes a contribution to the study of interactions between these variables;
2) Analyzing the relationship between business and credit cycles in EMCCA zone is a further analysis of the effects of monetary policy in this area. This issue is of particular importance for understanding the role and the impact of the banks behavior in financing the economies, on one hand, the strengthening of economic and financial integration in the sub-region, on the other.
To study the relationship between business and credit cycles in EMCCA countries, we first identify them. Then, we analyze interactions between the cyclical components of these two variables.
2. Characterization of Cycles
Like [13], we use a band-pass filter due to [14] to estimate business and credit cycles. Three main reasons guide this choice: 1) it gives the user the possibility to choose the length of cycle frequencies depending on the processed data; 2) it facilitates the identification of cyclical elements as it’s properly removing the volatility of short-term time series; 3) it proposes cycles whose convergence properties are in many ways better than Trend Stationary and stochastic methods.
Concerning historical dating of cycles, several recent studies resort to the nonparametric method of [15] or to the Markov switching regime models. In common with [16,17], we retain the first method. Indeed, Markov models for regime change face the problem of robustness of the estimates related to reliability and quality of data samples in developing countries [18]. In addition, they have imperfections on the rule of identifying turning points in cycles.
2.1. Methodology
The band-pass filter of [14] decomposes a ![]() process in weighted sum of sinusoidal functions
process in weighted sum of sinusoidal functions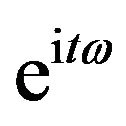 , where
, where ![]() is a frequency whose weight is deduced from the Fourier transform of the process autocorrelogram. This one corresponds to the Yt spectral density value for frequency ω.
is a frequency whose weight is deduced from the Fourier transform of the process autocorrelogram. This one corresponds to the Yt spectral density value for frequency ω.
The method is based on a priori choice of frequencies defining the cycle. According to the authors, a time series cycle generally admits a period included between 6 and 32 quarters. The trend that reflects changes in long-term or low frequency admits a period longer than 32 quarters. The irregular, corresponding to changes in short-term or high frequency, has a period less than six quarters. The cycle extraction consists therefore in applying to Yt process, a band-pass filter that retains these frequencies and cancels the others. Thus, cycle is obtained as difference of two low-pass filters. The ideal low-pass filter associated with the frequency w0 must have a transfer function of the form:
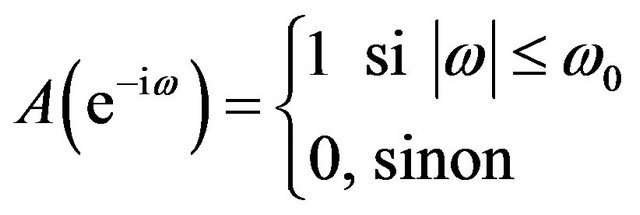 (1)
(1)
Transformation in Fourier series of 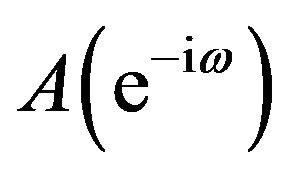 is written:
is written:
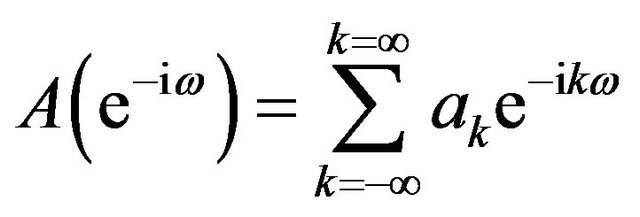 (2)
(2)
where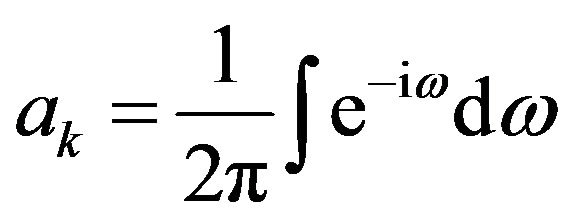 ;
;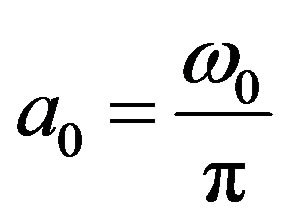 ;
;  and
and
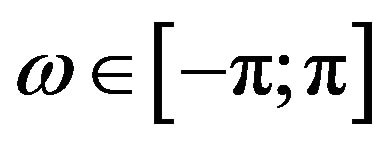
The  series issued from the low-pass filter is provided by the infinite moving average:
series issued from the low-pass filter is provided by the infinite moving average:
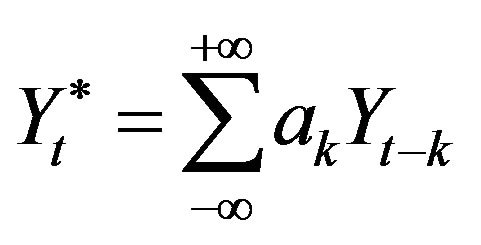 (3)
(3)
In practice, the range of temporal frequencies is specified by the user based on his intuition on the studied cycle periodicity. The contribution of [14] consists in providing a specific band-pass filter to short frequencies that characterize stationary stochastic processes.
Regarding historical dating and characterization of cycles, the Bry and Boshan algorithm which is very used by the National Bureau of Economic Research, allows identification of turning points (peaks and troughs) of a cycle in the tradition of [19]. It can be summarized in three main steps:
1) Determining candidates turning points in an annual series Yt according to the following rule:
- Yt admits a peak in t if: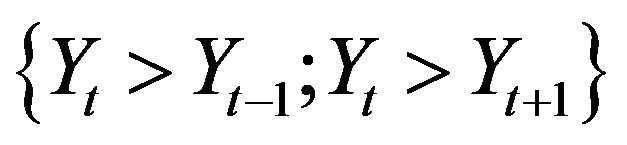 ;
;
- Yt admits a trough in t if: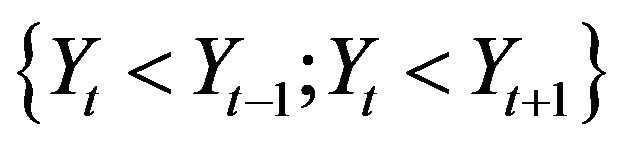 .
.
2) Disqualification of turning points located more or less six months from the beginning or the end of the series.
3) Verification of perfect alternation between the peaks and troughs so that in presence of a double trough, the smallest value is chosen. In presence of a double peak, the highest value is retained.
Once dated, the cyclic component can be characterized based on the calculation of key indicators:
- The depth corresponds to amplitude of recession or expansion and defined by:
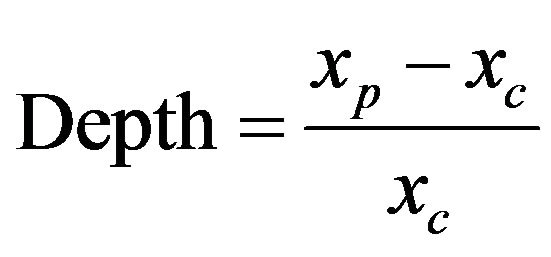 (4)
(4)
where xp and xc are respectively values of the cyclic component at peaks and troughs respectively.
- The severity summarizes information contained in the length and depth, and measures the loss (respectively, the gain) realized by a variable during a contraction phase (an expansion phase, respectively). It is calculated using formula:
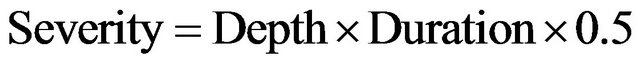 (5)
(5)
2.2. Application to EMCCA Countries
Application of previous methods is performed on GDP and domestic credit of five EMCCA countries (Gabon, Cameroon, Congo, Chad, Central African Republic (CAR)). Equatorial Guinea is excluded due to the lack of data over period 1960-2008. The data used are from the World Development Indicators database. They are all annual frequency and previously transformed into logarithm.
Following [18], regular changes of the main macroeconomic indicators in developing countries and their frequent exposure to economic crises, lead us to retain 2 and 8 years as terminals of the breeding range of credit and business cyclic components of EMCCA countries. These values are commonly used in the literature to estimate the business cycle. They correspond to the range
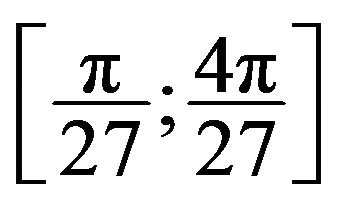 of temporal frequencies of the pass band filter. Therefore, the frequencies below
of temporal frequencies of the pass band filter. Therefore, the frequencies below  correspond to the long term, and those over
correspond to the long term, and those over  to the short term.
to the short term.
Graphical representation of joint credit and GDP cycles extracted using the band pass filter (see Figure 1) is generally shown that credit and GDP cycles are two main periods: one that goes from 1960 to 1988 and the other from 1988 to 2008. For all countries, the first period is characterized by fluctuations of magnitudes substantially identical. However, the last shows fluctuations of larger scale corresponding to effects of the financial liberalization intervened in the 80’s.
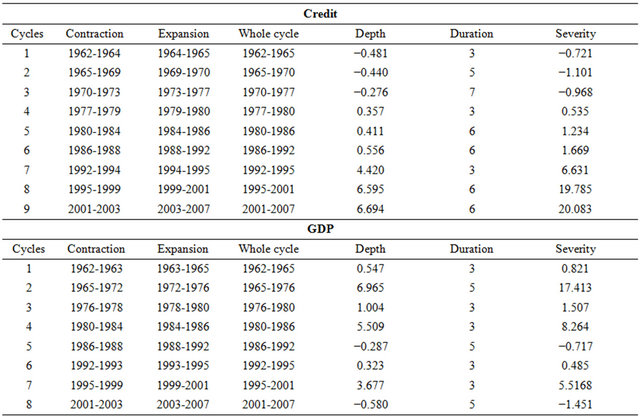
Table 1 provides a chronicle exemple of recessions and expansions of business and credit cycles obtained by using the [15] algorithm. Similarly, on the cycles turning points of each series, a peak (respectively, a trough) corresponds to the end of an expansion period (respectively, to the end of a recession). The following main lessons can be drawn from the EMCCA countries.
1) In average, credit has nine cycles in the EMCCA countries over the period 1960-2008. The average duration of the credit cycle is about six years in CAR and Chad. It is equal to five years in Gabon, Cameroon and Congo. The credit cycle appears inversely proportional to its duration. Justification for this could be that in the case of CAR and Chad, credit ratios/deposits in excess of 100, reflecting a very limited savings and a very low liquidity position from Cameroon and Congo and Gabon [11].
2) Phases of credit expansion are generally for the periods 1973-1981, 1988-1996, 1999-2001 and 2003-2006 for all countries. The first period which knew the first oil shock, has been characterized by a favorable situation in the prices of raw materials exported by the EMCCA countries. The impact has been an increase in bank loans, reflecting a consolidation of banks financial position. The second period of credit expansion is consecutive with increased domestic and external debt in EMCCA countries, which initiated infrastructures funding in previous years. The second and third period may be related firstly to the impact of the new interest rates policy of the Central Bank of Central African States (CBCAS) occurred in late 1990 and which allowed a more flexible management of the rent money. Secondly, it may be related to the Central African States Banking Commission (CASBC) creation impact that promoted harmonization of prudential standards and better banking supervision. The last period of credit expansion corresponds to the effects of CASBC modernization and excess liquidity of banks in the area since 2001, due to an accumulation of excess oil.
The credit contraction phases match for the periods 1966-1973, 1981-1988, 1996-1999, 2001-2003. The second period shows the economic crisis of the mid-80 which profoundly affected the sub-regional banks and was characterized by accumulation of balance for loss and significant bad and irrecoverable debts. The last period coincides with a strengthening of prudential regulation by CASBC. The credit most severe contraction occurred in Congo during the period 1981-1984. The least severe contraction occurred in CAR during the period 1965-1970.
Concerning business cycles, those of the EMCCA countries are similar to credit cycles. However, business cycle is slightly more volatile than the credit one regardless of the country. This suggests a slightly more significant downturns in the real sphere. Moreover, the average GDP cycle is six years in Cameroon, Chad, Congo and CAR. It is equal to four years in Gabon.
Phases of expansion and contraction of GDP correspond almost perfectly with those of the credit cycle. The growth of GDP over the period 1973-1981 corresponds to the effects of the first oil shock, in particular the increase in exports has helped to increase the budgetary resources of states and public investment. Note that the contraction occurred in 1990-1994 prior to the devaluetion of the local currency (CFA Franc). This period coincides with the implementation of structural adjustment programs whose aim was the revival of the economies in the region, strongly marked by the crisis of the mid 1980’s. The failure of these programs has led EMCCA countries to conduct a monetary adjustment in early 1994 to address the economic and financial imbalances re-
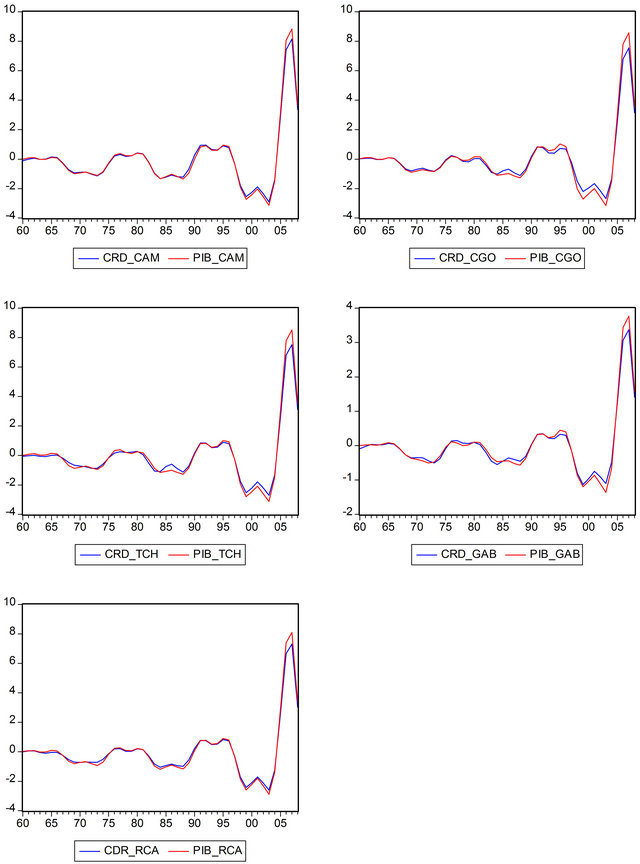
Figure 1. GDP and credit cycles.
corded during the second half of the 1980s. Contraction of GDP in the most severe occurred in Cameroon and Congo during 1965-1969. In contrast, the less severe contraction in GDP occurred in the Congo and the Central African Republic during the period 2001-2003. Disparities between the economies of the EMCCA are attributeable to the degree of opening of EMCCA countries and their greater or lesser dependence on exports of a few
Table 1. Characteristics of cycles in the case of Gabon.
commodities [12].
3. Interactions Analysis
Our approach draws on the work of [17,20], to analyze interactions between the cyclic fluctuations in credit and activity. It begins with a statistical study of co-movements and synchronization. To this end, we first calculate dynamic crossed-correlations of cycles, then concordance indices of both cycles for each country. We complete the interactions analysis by econometric cointegration and causality tests, to identify possible common pathways as well as the nature of interactions within each country.
We begin with a brief presentation of the model before applying to data from the EMCCA countries.
3.1. Modeling Cyclic Interactions
The co-movements analysis of recession and expansion phases is based on calculation of dynamic crossed-correlations  between the cyclic component of credit xt and that of the delayed or advanced activity yt – K (with
between the cyclic component of credit xt and that of the delayed or advanced activity yt – K (with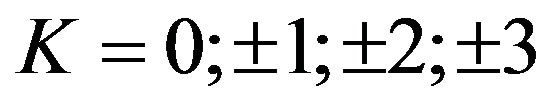 ) and an approximation of the standard deviation of the sample by
) and an approximation of the standard deviation of the sample by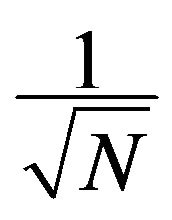 . The approach retains the following criteria:
. The approach retains the following criteria:
- Credit is said to be procyclical if 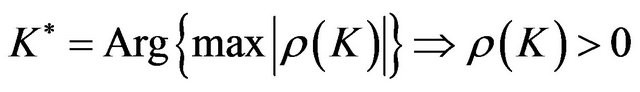
- Credit is said to be acyclical if
- 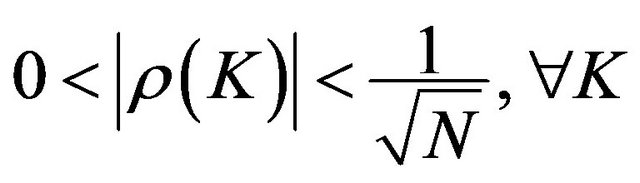
- Credit is said to be contracyclical if 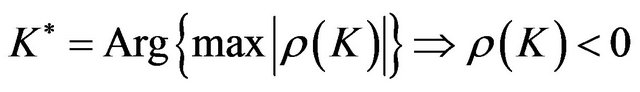
Similarly, the above relations can be classified according to the level of significance. Thus, the relationship between credit and business cycles is:
- Significant at 5% if: 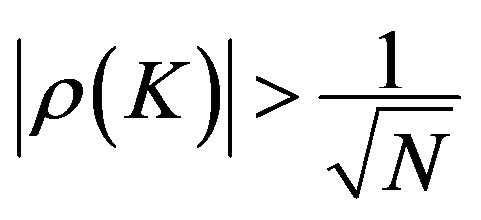 or if
or if 
- Significant at 10% if: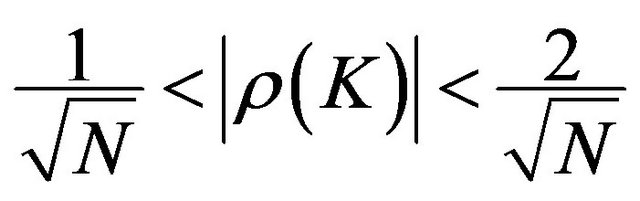 .
.
In addition to analyzing co-movements between the cyclic components is the construction of concordance indices proposed by [21], to assess relationship between recessions and expansions of two series xt and yt. Formally, the concordance index between xt and yt is calculated as follows:
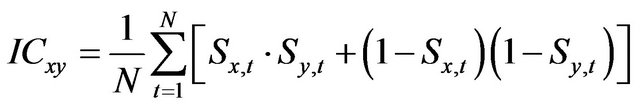 (6)
(6)
where  for a series
for a series ![]() considered.
considered.
So, when ICxy = 1, xt and yt are perfectly in phase. In other words, their expansion and contraction phases are perfectly juxtaposed. When ICxy = 0, series xt and yt are always in opposite phases, and there is perfect anti-concordance between the both cycles.
In general, the concordance index properties are unknown. Also, on the degree of significance [21], show that it corresponds to the degree of significance of ρ coefficient in estimating the following linear model:
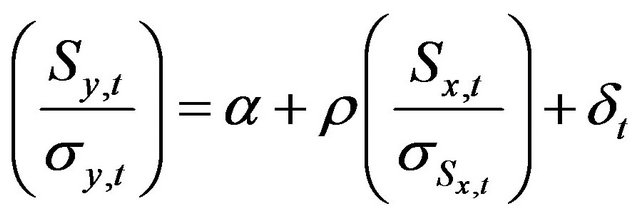 (7)
(7)
where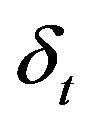 is a white noise.
is a white noise.
Under the null hypothesis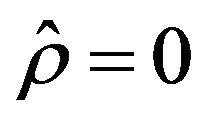 , the serial correlation of errors affects robustness of the model (7) estimation. In this case, the method of least squares plus a HAC procedure to assess significance of the concordance index from the student statistics.
, the serial correlation of errors affects robustness of the model (7) estimation. In this case, the method of least squares plus a HAC procedure to assess significance of the concordance index from the student statistics.
Finally, we use the cointegration test of Engle and Granger and the causality test of Granger causality test. The first test described a two-step procedure: 1) is checked prior that credit and business cycles xt and yt are integrated of order one, which allows to suspect the existence of a cointegrating relationship between these components; 2) it is estimated by OLS Model:
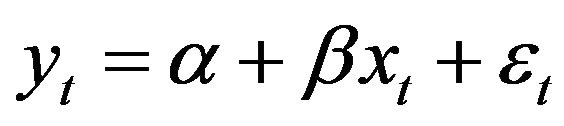 (8)
(8)
When residue of this estimate is stationary, cointegration between cycles is confirmed. It is then possible to estimate an Error Correction Model (ECM) which describes the long-term relationship between xt and yt, which is defined by the equation:
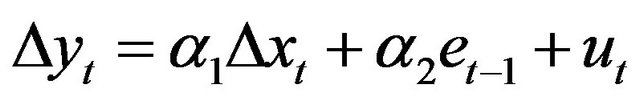 (9)
(9)
Lastly, the Granger causality test examines possibility that there are causal relationships between business and credit cycles of the various countries from a Wald test.
3.2. Empirical Results
Application of previous modeling to GDP and credit cycles of the EMCCA countries leads to the following key lessons:
1) Graphs of joint business and credit cycles (Figure 1) predict that credit is procyclical in the whole EMCCA countries. This intuition is specified by the co-movements analysis and concordance indices within countries.
2) The calculation of dynamic correlation coefficients between cyclic components of credit and activity covering a total of three times delayed and advanced periods of both distributions is provided by Table 2.
Firstly, it shows that the cyclic components of credit and activity of all countries are contemporary, since the maximum value of correlation coefficient is obtained when K = 0. In addition, for K = 0, it appears that 98% of the time, recession and expansion phases of the two cycles are coinciding. Moreover, all the coefficients in column K = 0 are significant as they are all above 0.14 in absolute value. Thus, procyclical nature of credit is confirmed. The positive sign of the correlation coefficients for K = 0 indicates that they are positively related. Thus, we retain that credit is contemporary vis-à-vis the GDP in EMCCA countries, which implies an increase (decrease) in credit coincides with an increase (decrease) of GDP.
Secondly, Table 2 shows the achievement of high correlation coefficients and significant at 5% for all countries when K = ±1. This result suggests that credit is procyclical, with a lag period compared to the activity.
3) Analysis of the concordance degree of business and credit cycles of the EMCCA countries led to calculation of concordance indices contained in Table 3.
The results in Table 3 reveal a perfect concordance between business and credit cycles in Cameroon. In Congo, the concordance index describes synchronization of cyclic phases in nearly 93% of cases. Concordance indices significantly above 80% are also obtained in Gabon, CAR and Chad. The Harding and Pagan criterion
Table 2. Dynamic correlations.

Table 3. Concordance indices.

of significance shows that all concordance indices are significant at 5%. We conclude that the cyclical movements in credit and activity are in phase in EMCCA countries.
4) As cycles obtained from the band-pass filter are stationary, there is a risk of cointegration between business and credit cycles in the EMCCA countries. Moreover, the estimated residuals from Equation (8) are stationary. The existence of a cointegration relationship is confirmed for all countries. It is therefore possible to estimate an error correction model to describe long-run relationship linking the business and credit cycles of EMCCA countries. For each country, it is of the form:
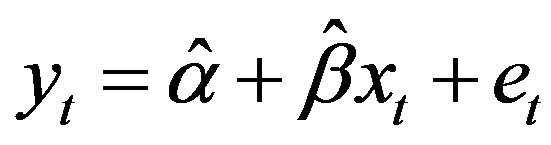 (10)
(10)
Table 4 shows the estimated coefficients in Equations (8) and (9). From this table it appears that the restoring forces estimated through the 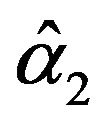 coefficients are significantly negative. The error correction models are validated for each country. The dynamic model (in short term) that links credit cycle to activity cycle in each country is described by the equation:
coefficients are significantly negative. The error correction models are validated for each country. The dynamic model (in short term) that links credit cycle to activity cycle in each country is described by the equation:
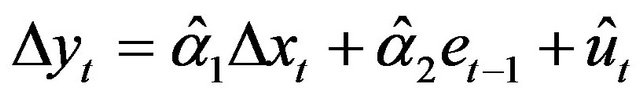 (11)
(11)
5) The Granger causality test carried out for each country reveals the following results:
At 5% threshold, credit cycle causes that of activity in Gabon, Congo and Chad. Thus, the procyclical and contemporary character of credit is confirmed in these three countries with high significance. Therefore, banks policy of offering credit is an important indicator of economic activity. Moreover, as suggested by [8], this result means that during the expansion phases in real activity, the existence of imperfections in the credit market led banks to overstate creditworthiness of borrowers and to proceed to a strong distribution of loans. Two factors may explain this result: 1) a relaxation of criteria for granting credit during the phase of growth; and 2) a decrease in the risk premium during these phases. Meanwhile, it is likely that banks have reduced volume of loans in a recession.
Table 4. Cointegration tests.
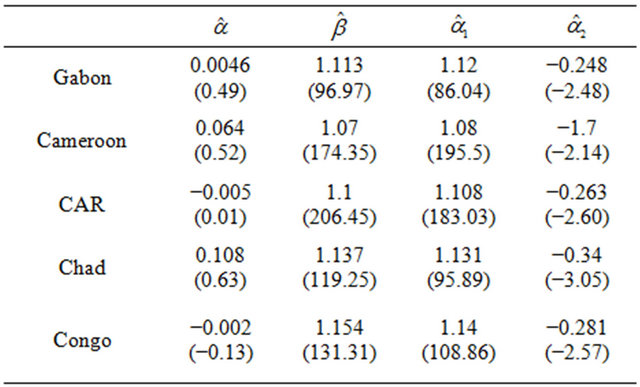
Ultimately, in Gabon, Congo and Chad, the credit distribution has an impact on the economy and amplifies economic cycles by extending expansions and aggravating economic downturns. So in these countries, the prevailing optimism in expansions creates a too generous distribution of funds.
In the specific case of Gabon and Congo, a reciprocal causality (feedback effect) is observed. As business cycle causes credit cycle, it seems that GDP growth increases the household income and easier access to credit. Similarly, this result implies that a decrease in activity leads to closure of the credit market for households.
In Cameroon and CAR, no causal relationship is observed in one way or the other at 5%. However, at 10% credit cycle causes activity cycle in Cameroon, while a feedback effect appears in the case of CAR. These results reveal specificities that may be related to consumption patterns of households, such as massive recourse to a parallel network of funding such as tontine (in the case of Cameroon); and the relatively low weight of credit in the business cycle of these countries, or embryonic nature of the banking system (in the case of CAR).
In general, estimation results show a positive relationship between both cycles, confirming that credit is procyclical within the Union. This behavior corresponds to the fact that in economic expansion periods, banks tend to adopt more risky global strategies to ensure a higher return on capital. Ultimately, this strong link between credit and activity cycles in EMCCA reflects the fact that integration between the real and financial spheres is noticeable through the role of bank credit in the economy, since most of the economy funding comes from the banking system. In addition, our results suggest that credit is an important determinant of the business cycle amplification in EMCCA countries.
4. Conclusions
This article has first allowed proposing a historical dating of business and credit cycles in EMCCA countries. Cycles were obtained using a univariate band-pass filter, and then subjected to the analysis of co-movements and concordance. Our results conclude that cyclical fluctuations of credit and activity interact in the EMCCA countries. However, the econometric analysis shows that the overall behavior has some specificities: in Chad, credit cycle causes the activity, in Gabon and Congo, a feedback effect is observed, in Cameroon and CAR, the highlight of causality is relative.
In short, we hold that at the Union level, credit is procyclical. This means that credit runaway during booms activity, and slowed during contraction phases.
In view of the relatively low ratio of credit/GDP (7% in average), it is likely that the procyclical behavior of credit is favored by macroprudential standards in force in the EMCCA zone, themselves tendentiously procyclical.
Given the potential systemic consequences that this phenomenon exposes the banks of EMCCA, we advocate improvement of banking supervision and establishment of macroprudential regulation rules to reduce procyclicality and to allow stabilization of the banking system in its global dimension.
5. Acknowledgements
1) EMCCA is a set of six countries: Cameroon, Central African Republic (CAR), Congo, Gabon and Chad.
2) For example, the share of banks in total assets held by all financial institutions exceeding 80% in the EMCCA. Thus, banks provide the bulk of credit to the economy and channeling much of the public savings. Financial markets are embryonic. Interbank markets, money and capital are failing. Moreover, the banking system is marked by the presence of foreign banks (63% of total assets, or 10.9% of the EMCCA GDP). Ratios credit/ deposit and deposit/GDP are low. It is a situation of excess liquidity, except in Congo and Chad, where it is low. Pricing of banking products and profitability of banks indices reveal disparities between countries. Finally, the level of bank margins reflects credit risk and operational risk high.
REFERENCES
- S. Gilchrist and E. Zakrajsek, “Linkages between the Financial and Real Sectors: An Overview,” Working Paper, Boston University, 2009.
- P. Aghion, P. Bachetta and A. Banerjee, “Currency Crises and Monetary Policy in an Economy with Credit Constraints,” Working Papers, 2000.
- C. M. Reinhart and K. S. Rogoff, “This Time is Different: Eight Centuries of Financial Folly,” Princeton University Press, Princeton, 2009.
- H. P. Minsky, “Financial Crisis, Financial Systems and the Performance of the Economy,” In: E. Cliffs, Ed., Commission on Money and Credit: Private Capital Market, Prentice-Hall, New Jersey, 1964.
- B. S. Bernanke and A. S. Blinder, “Credit, Money and Aggregate Demand,” American Economic Review, Vol. 78, No. 2, 1988, pp. 435-439.
- F. S. Mishkin, “Les Canaux de Transmission Monétaire : Leçons Pour la Politique Monétaire,” Bulletin de la Banque de France, No. 27, 1996.
- M. Gertler and S. Gilchritst, “Monetary Policy, Business Cycles and the Behaviour of Small Manufacturing Firms,” Quarterly Journal of Economics, Vol. 109, No. 2, 1994, pp. 309-340.
- L. Clerc, “Le Cycle du Crédit, une Revue de la Littérature: Intermédiation, Prime de Financement Externe et Politique Monétaire,” Bulletin de la Banque de France, No. 94, 2001, pp. 43-61.
- B. Friedman and K. Kuttner, “Economic Activity and the Short-Term Credit Markets: An Analysis of Prices and Quantities,” Working Paper Series, Federal Reserve Bank of Chicago, 1993.
- J. Geanokoplos, “The Leverage Cycle,” NBER Macroeconomics Annual, No. 24, 2009, pp. 46-65.
- Y. S. Samer and J. Vacher, “Banking Sector Integration and Competition in EMCCA,” Working paper IMF, 2007.
- C. Eboue, “Nécessité d’une Régulation Macroprudentielle: cas des Pays de la CEMAC,” Actes du Colloque sur la régulation macroprudentielle, 2009.
- D. Corbae and S. Ouliaris, “Extracting Cycles from Nonstationary Data,” In: D. Corbae, S. Durlauf and B. Hansen, Eds., Econometric Theory and Practice: Frontiers of Analysis and Applied Research, Cambridge University Press, New York, 2006.
- L. J. Christiano and T. J. Fitzgerald, “The Band-Pass Filter,” International Economic Review, Vol. 4, 2003, pp. 435-465.
- G. Bry and C. Boshan, “Cyclical Analysis of Time Series: Selected Procedures and Computer Programs,” NBER, Cambridge, 1971.
- D. Aikman, A. G. Haldane and B. Nelson, “Curbing the Credit Cycle,” Working paper for the Columbia University Center on Capitalism and Society Annual Conference Microfoundations for Modern Macroeconomics, New York, 2010.
- S. Avouyi-Dovi, R. Kierzenkowski and C. Lubochinsky, “Are Business and Credit Cycles Converging or Diverging? A Comparison of Poland, Hungary, the Czech and the Euro Area,” NER Banque de France, No. 14, 2006.
- P. R. Agenor, C. J. Mc Dermott and E. S. Prasad, “Macroeconomic Fluctuation in Developing Countries: Some Stylized Facts,” The World Bank Economic Review, Vol. 14, No. 2, 2000, pp. 251-285. doi:10.1093/wber/14.2.251
- A. F. Burns and W. C. Mitchell, “Measuring Business Cycles,” NBER, Cambridge, 1946.
- J. P. Allergret and S. Zantman, “Disentangling Business Cycles and Macroeconomic Policy in Mercusor: A VAR and Unobserved Components Model Approaches,” Document de travail, Observatoire Français de Conjoncture Economique, No. 15, 2006.
- D. Harding and A. Pagan, “Synchronization of Cycles,” Working Paper, Melbourne University, 2002.

