Modern Economy
Vol.3 No.8(2012), Article ID:26148,5 pages DOI:10.4236/me.2012.38116
A Mathematical Proof: Focus during Weekdays Should Be on Supply for the Sabbath a Support for Workable Competition
Ariel University Center of Samaria, Ariel, Israel
Email: garanoff@netvision.net.il
Received November 4, 2012; revised December 5, 2012; accepted December 12, 2012
Keywords: Demand Fluctuations; Consumer Surplus; Business Cycle
ABSTRACT
This paper proves mathematically in a defined model with restrictive assumptions that consumers are better off when they have more food for the Sabbath at the expense of having less food for the other six days of the week! Like the manna that fell from heaven for forty years in the desert—an omer to a person, Sunday through Friday with double portions on Friday—we assume that consumers buy standardized semi-perishable food baskets, one basket per person per day, Sunday through Friday with extra baskets for the Sabbath. We analyze benefits to consumers according to two alternative pricing schemes, whereby consumer expenditures and weekly food consumed are the same. We prove that consumers are better off according to the pricing scheme that allows for more food for the Sabbath day. This agrees with business cycle theories that urge social focus on increasing and prolonging cyclical peaks. This supports John M. Clark’s workable competition thesis and will surprise supporters of SR marginal-cost pricing.
1. Introduction
In economics we work with societal models to better predict and advise on production, consumption, investing, financing and government regulation. In economic models we simplify matters by leaving out factors not relevant to what we are studying.
We first define the model, its terms and assumptions. We define concepts from economics for non-economists to understand. We carry out a geometric demonstration with two states of demand functions. We then vary out a calculus proof with n-states of demand functions.
We developed the thesis of this paper from the work of the economist John M. Clark (1884-1963), who wrote of the importance of retaining old plants and equipment during economic downturns in order to have their capacity available for economic peak times. John M. Clark was a business-cycle economist. He advocated that economists should focus on how business-cycle peaks could run higher and longer as this would increase economic growth and our wellbeing [1].
Using Clark’s theories, we argued elsewhere that, despite high levels of idle capacity, cement capacity in the 1930’s was inadequate, when measuring adequacy of capacity against anticipated peak demand [2]. We learn from this that satisfying peak demand should always be the uppermost consideration, whether business-cycle peaks, seasonal peaks, or Sabbath-day demand.
2. Definition of the Model and Its Terms and Assumptions
There are two groups in our hypothetical society: producers (suppliers) and consumers (households). The households buy standardized semi-perishable food baskets to feed their families. The food baskets have meat, fish, cheese, vegetables, fruits and drinks. Households have no refrigerators and no freezers. They are unable to store food baskets except on Friday for the Sabbath. They are like the Israelites who for forty years in the desert could not save the omer of manna per person from day to day except on Fridays when they could save the extra manna given on Friday for the Sabbath1. Households buy their food baskets in a free market and pay a single market price per food basket for the day. The exception is Friday, when there is the Friday supply price and the Sabbathday supply price.
Households have a fixed budget for food expenditures. They are price sensitive in purchasing food, in the sense that households will purchase more food at a lower market price and less food at a higher market price.
The analysis here leaves out the supplier side. Of course it is more difficult to supply wider variations in output rates. Elsewhere, we have argued that, to the extent that producers and manufacturers become more output flexible, i.e. makes it easier to handle variations in rates of output, this adds to social welfare [3]. For simplification, we assume here that suppliers can handle fluctuations in quantities demanded with infinite ease. We might imagine that suppliers can make long-term contracts for the food at the same cost prices regardless of whether there are wide or narrow differences between weekday and Saturday quantities.
2.1. The Demand Curve, D, and Its Frequency, w
In this model consumers pay a daily market price and obtain daily quantities of food baskets. Consumers pay market price times quantities purchased, 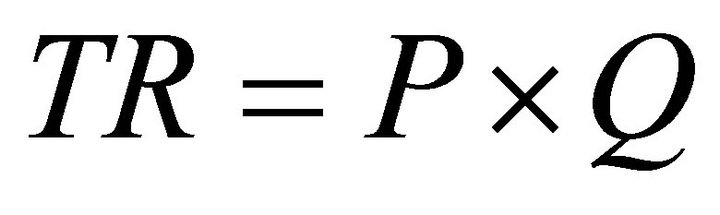 (total revenue to suppliers equals market price times quantities).
(total revenue to suppliers equals market price times quantities).
The demand curve shows the maximum quantities consumers would be willing to purchase at various prices. The area under the demand curve up to the point of quantities of market purchases shows the value to the consumer. It shows theoretically how much consumers would be willing to pay if they were faced with, say, a monopolist who gave each consumer a different price based on each consumer’s maximum willingness to pay.
Figure 1 shows a geometric demonstration with varying pricing (alternative A) versus fixed pricing (alternative B) with fluctuating D functions, weekdays and Sabbath day each with its associated w. Let D1 be consumer demand for baskets of food (such as meat, fish, bread, cheeses, fruits, vegetables, and drinks) during weekdays, Sunday through Friday. This shows a willingness to make a daily payment in the market for daily food on weekdays showing that most consumers would be willing to buy an item daily at daily at varying prices. The assumption is that the demand curve is downward sloping, meaning that consumers would be willing to buy more daily if prices were lower, all else being the same.
Using hypothetical numbers to make the economic concepts clearer, point K could be that, at a market price of $36 per basket of food consumers are willing to buy 35 baskets of food per day. Point H might be that at a market price of $33 per basket of food consumers are willing to buy 37 baskets of food per day.
Let D2 be consumer demand for daily baskets of food on the Sabbath. Assume that Sabbath-day food is actually bought on Friday to be eaten on Saturday. Using hypothetical numbers to illustrate, point D could be that, at a market price of $51.9 per basket of food consumers are willing to buy 42 baskets of food per day. Point J could be that, at a market price of $36 per basket of food consumers are willing to buy 54 baskets of food per day.
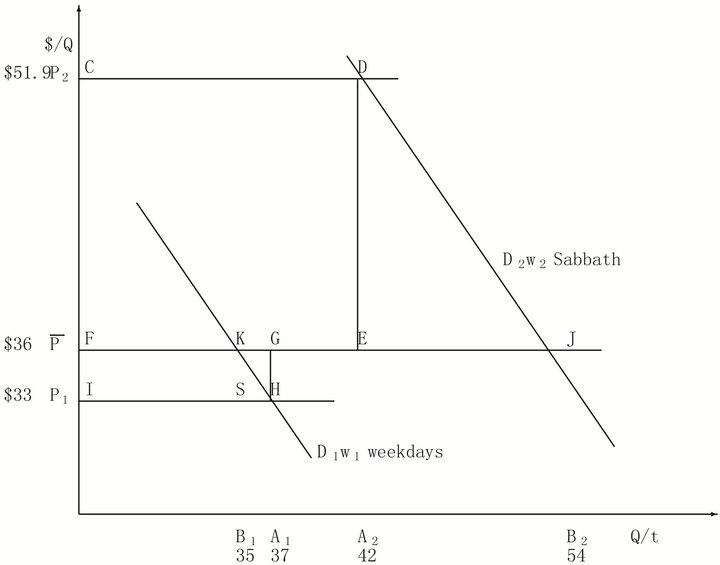
Figure 1. Varying versus fixed pricing with D fluctuations.
The demand curve D1, weekday demand, occurs with frequency, w1, 6/7. The demand curve D2, Sabbath demand, occurs with frequency, w2, 1/7.
2.2. Consumer Surplus, CS
We define consumer surplus as the area under the demand curve and above the price line. Consumer surplus arises because the value to the consumer is greater than what the consumer pays. The consumer pays market price times market purchases and receives in value the whole area under the demand curve until the point of quantities purchased.
2.3. Expected Values, E
When different states of outcomes are possible each with an associated probability, we define expected values, E, as the sum of each outcome times its expected value. Using the illustrated numbers for points H and D, the market equilibrium points for pricing rule A, varying prices, we can calculate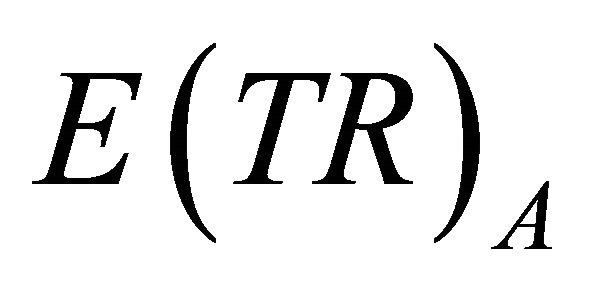 , expected total revenue, and
, expected total revenue, and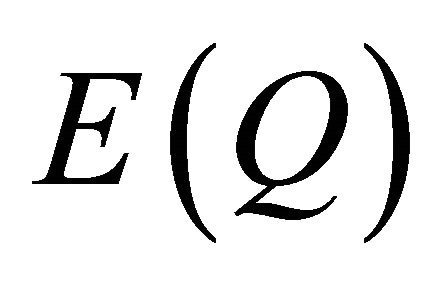 , expected quantities, as follows:
, expected quantities, as follows:
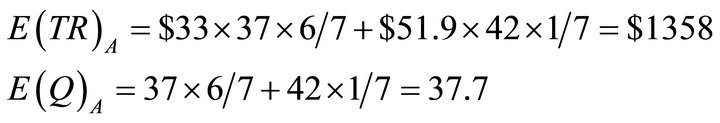
Using the illustrated numbers for points K and J, the market equilibrium points for pricing rule B, fixed prices, we can calculate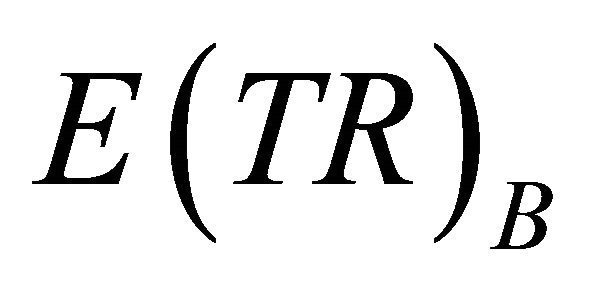 , expected total revenue, and
, expected total revenue, and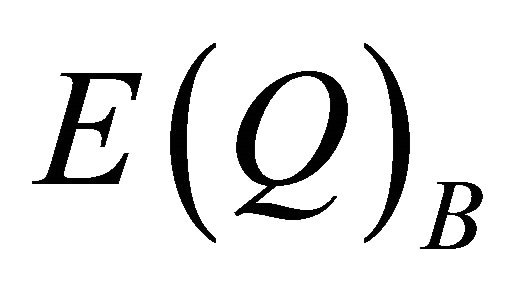 , expected quantities, as follows:
, expected quantities, as follows:
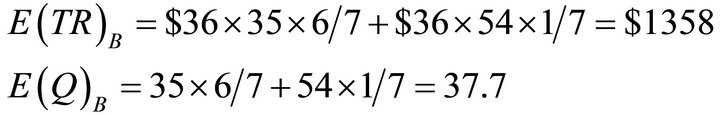
3. Geometric Demonstration with Two States of Demand Functions
Assuming consumers pay the same amount and get the same quantity of food over the week, our proof shows that consumer surplus is necessarily larger in my model in an arrangement whereby more food is available for the Sabbath at the expense of food during the weekdays. We assume that suppliers are willing to sell daily according to two alternative pricing schemes a fixed price,  , at all times, versus
, at all times, versus  for weekdays and
for weekdays and  for the Sabbath. We have two basic assumptions in the model: according to both pricing schemes total payments over the week are the same and total food purchases are the same. Consumers simply allocate their payments and food consumption differently according to two alternative schemes.
for the Sabbath. We have two basic assumptions in the model: according to both pricing schemes total payments over the week are the same and total food purchases are the same. Consumers simply allocate their payments and food consumption differently according to two alternative schemes.
We prove that consumers would prefer the scheme whereby they would have extra or more costly food on the Sabbath. In this way they could enjoy the Sabbath more since they would be spending the day with their families and not at work—knowing that they would have less food on the remaining six days. The gain in consumer surplus on the Sabbath, 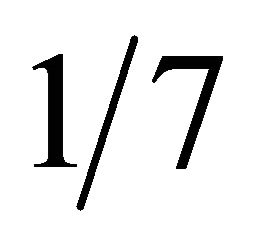 th of the week, with the extra food when demand for food is high, will outweigh the loss in consumer surplus during the rest of the week,
th of the week, with the extra food when demand for food is high, will outweigh the loss in consumer surplus during the rest of the week, 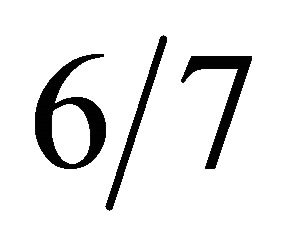 th of the week, when there would be less food when demand for food is lower. This is the prescription in Jewish law—to accentuate, as much as possible, the difference between the Sabbath day and the other days of the week, citing Isaiah 58.13: “... call the Sabbath a delight, the holy day of the Lord honored ....”
th of the week, when there would be less food when demand for food is lower. This is the prescription in Jewish law—to accentuate, as much as possible, the difference between the Sabbath day and the other days of the week, citing Isaiah 58.13: “... call the Sabbath a delight, the holy day of the Lord honored ....”
Proposition 1 A comparison of alternative pricing schemes, A: varying prices, versus B: fixed prices, under conditions of shifting downward-sloping demand curves shows 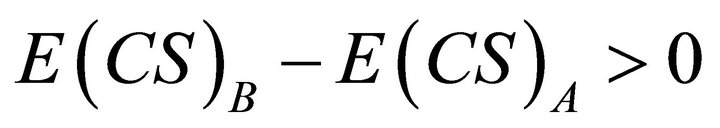 and rises as demand elasticity rises assuming
and rises as demand elasticity rises assuming
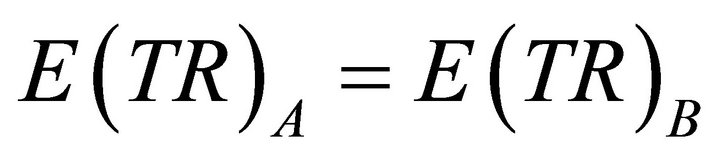 (1)
(1)
and
 (2)
(2)

Proof: By definition of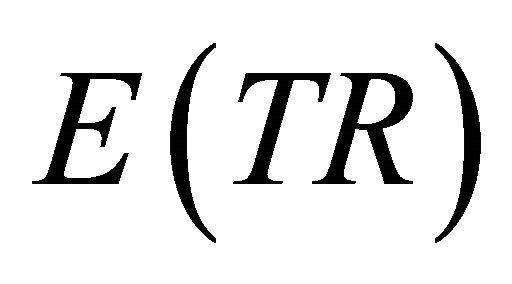 :
:
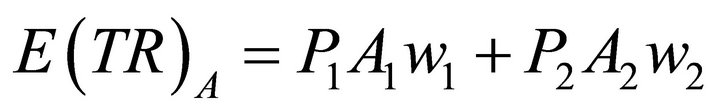 (3)
(3)
and
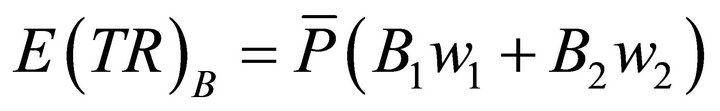 (4)
(4)
By definition of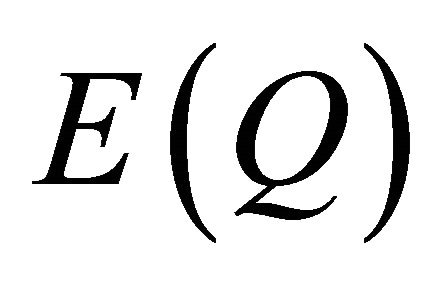 :
:
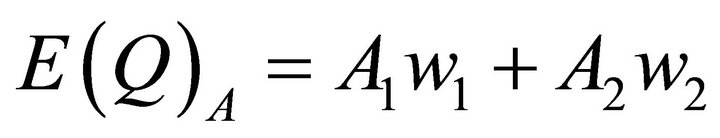 (5)
(5)
and
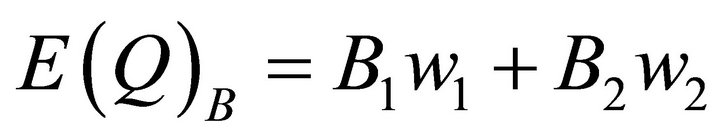 (6)
(6)
By definition of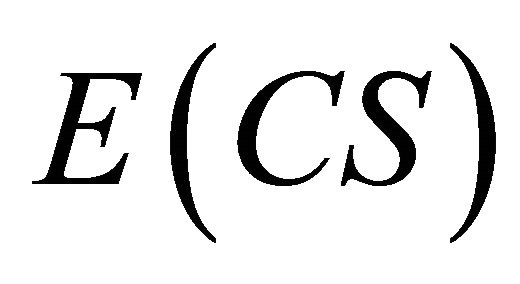 :
:
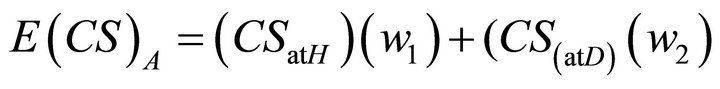 (7)
(7)
and
 (8)
(8)
By assumption (1) we can state:
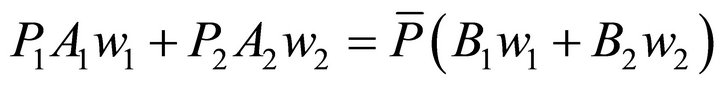 (9)
(9)
By assumption (2) we can state:
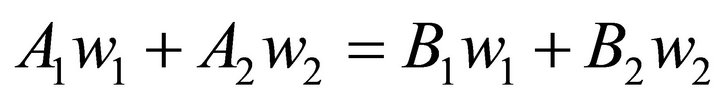 (10)
(10)
Combining assumptions (1) and (2):
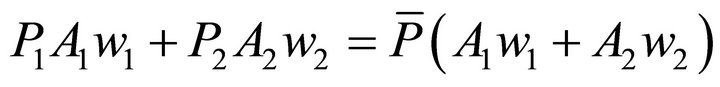 (11)
(11)
Rearranging:
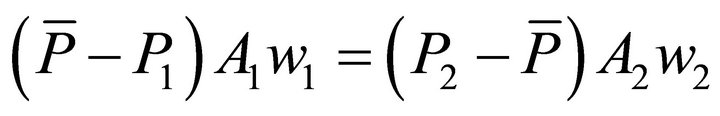 (12)
(12)
Using the letters of the Figure 1:
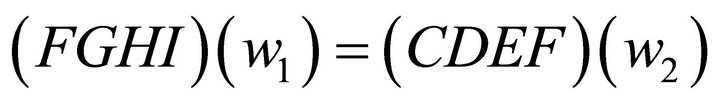 (13)
(13)
we can state:
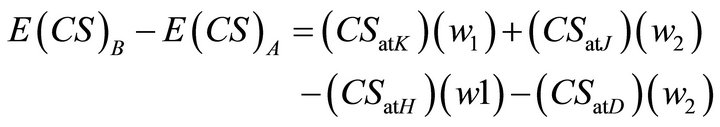 (14)
(14)
Rearranging:
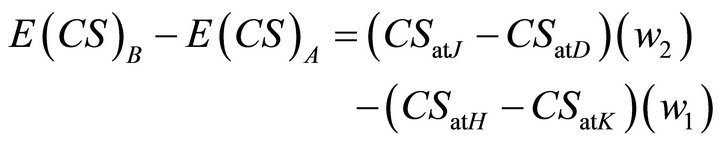 (15)
(15)
we can state:
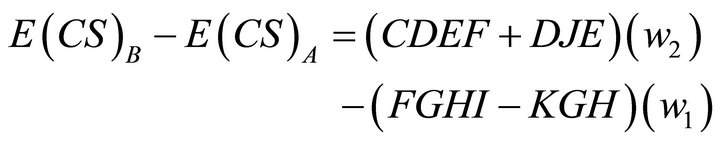 (16)
(16)
Using the results of Equation (13), we can state:
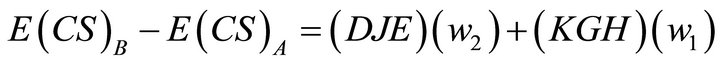 (17)
(17)
Thus,  must be greater than zero, providing that price elasticities of the demand curves are not zero. At zero price elasticity
must be greater than zero, providing that price elasticities of the demand curves are not zero. At zero price elasticity  and
and  and therefore areas
and therefore areas  and
and 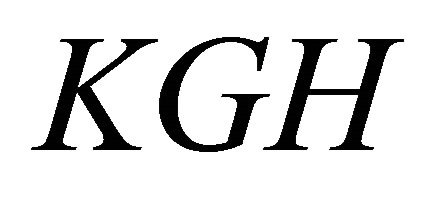 each equals zero.
each equals zero. 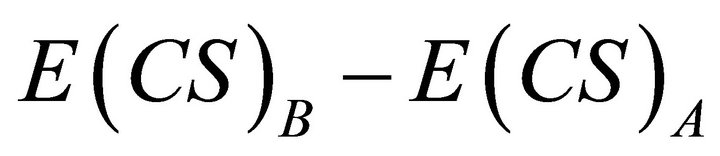 rises as price elasticity rises, since the areas of
rises as price elasticity rises, since the areas of 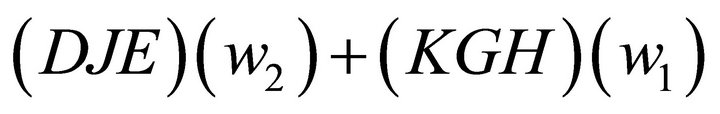 increase with more elastic demand curves.
increase with more elastic demand curves.
4. Proof with n States of Demand Functions
Proposition 2 A comparison of alternative pricing schemes, A: varying prices, versus B: fixed prices, with 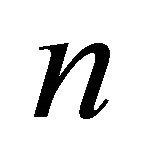 states of demand functions, consumers prefer wider output variability to narrower under demand fluctuations, assuming same expected payments and outputs over the cycle.
states of demand functions, consumers prefer wider output variability to narrower under demand fluctuations, assuming same expected payments and outputs over the cycle.
 and rises as demand elasticity rises where:
and rises as demand elasticity rises where:

Assuming:
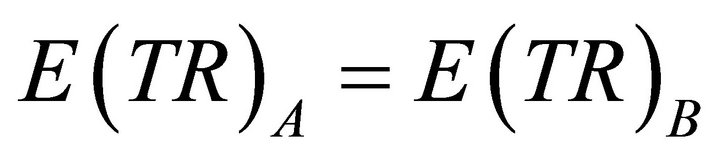 (18)
(18)
and
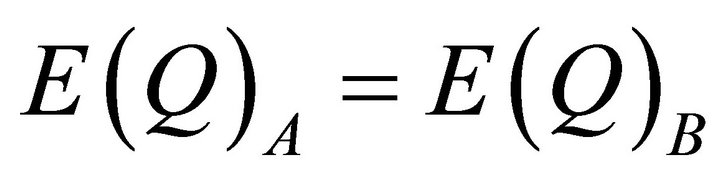 (19)
(19)
Proof: By definition of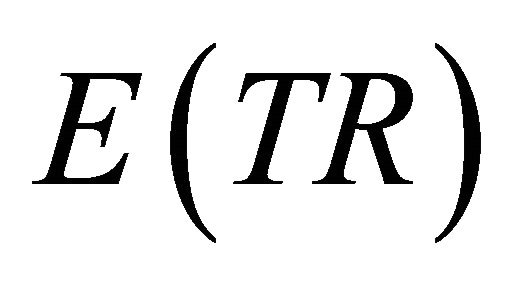 :
:
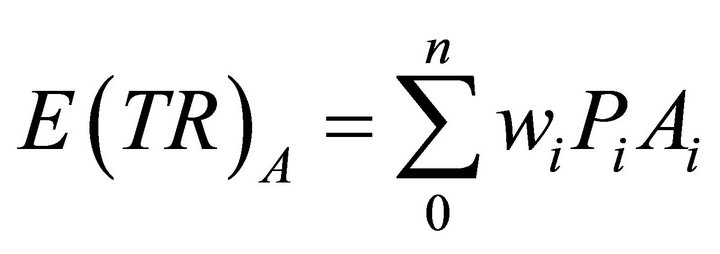 (20)
(20)
By definition of :
:
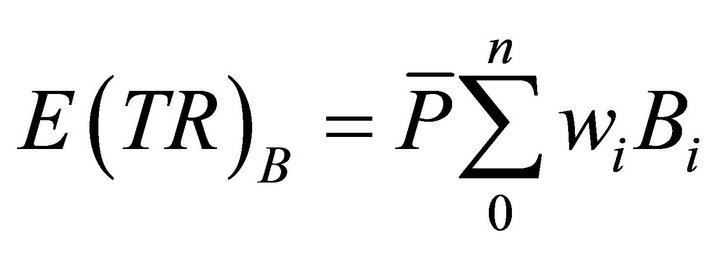 (21)
(21)
By definition of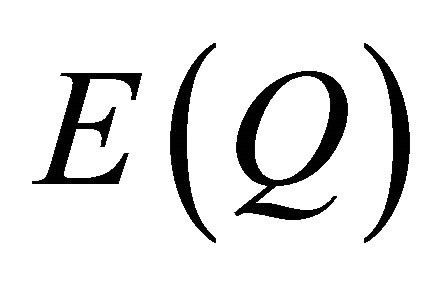 :
:
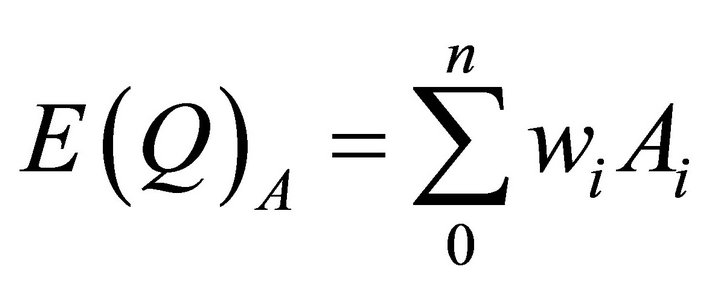 (22)
(22)
By definition of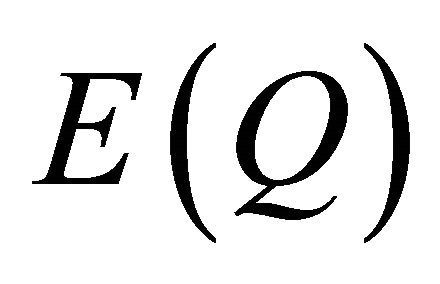 :
:
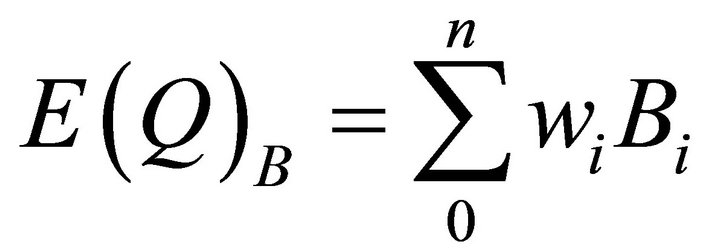 (23)
(23)
By assumption (18) We can state:
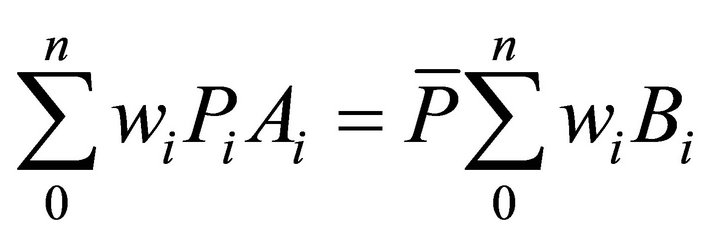 (24)
(24)
By assumption (19) We can state:
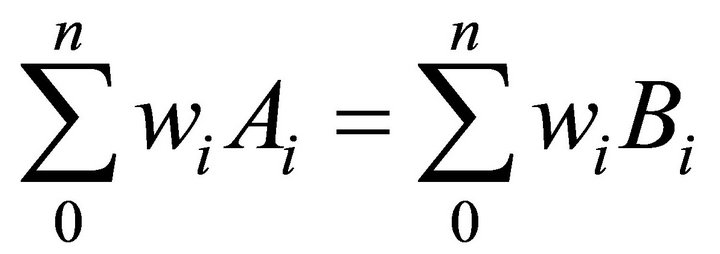 (25)
(25)
Combining assumptions (18) and (19):
 (26)
(26)
For this relationship to hold there must be occasions when 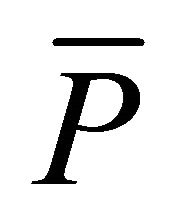 is greater than
is greater than 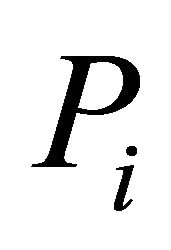 and occasions when
and occasions when 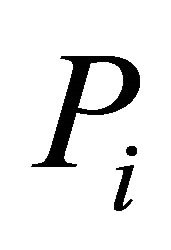 is greater than
is greater than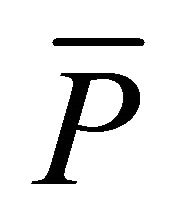 . Dividing the periods to
. Dividing the periods to  through
through 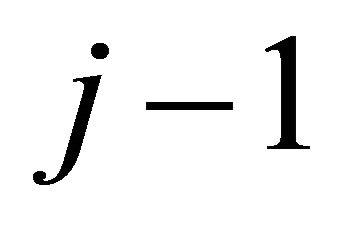 when
when 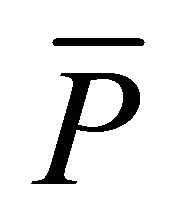 is greater than
is greater than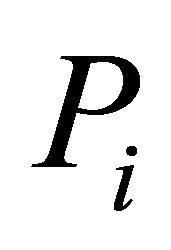 , weekdays, and
, weekdays, and  through
through 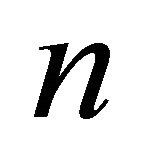 when
when  is greater than
is greater than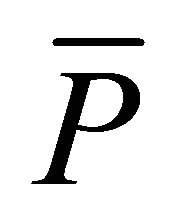 , the Sabbath:
, the Sabbath:
We can write:
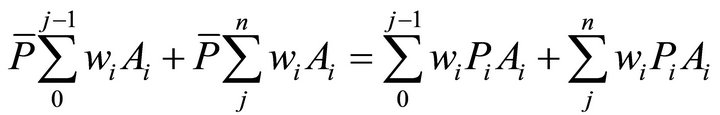 (27)
(27)
Rearranging:
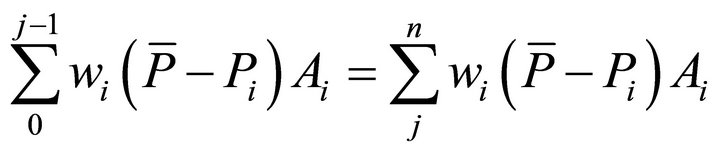 (28)
(28)
In terms of sections in Figure 2:
 (29)
(29)
By definition of consumer surplus:
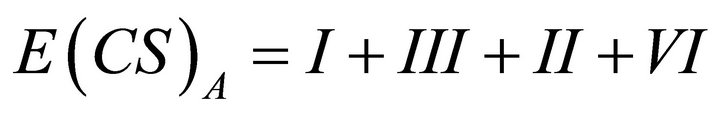 (30)
(30)
 (31)
(31)
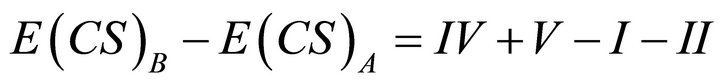 (32)
(32)
Using Equation (29) We can simplify Equation (32):
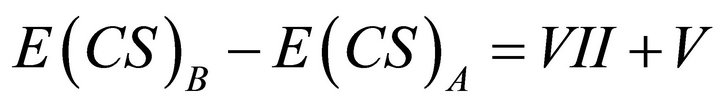 (33)
(33)
We can write:
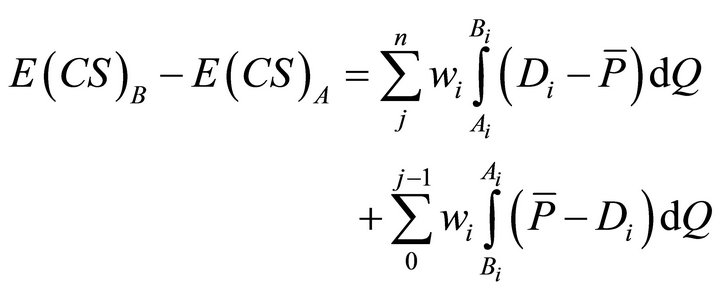 (34)
(34)
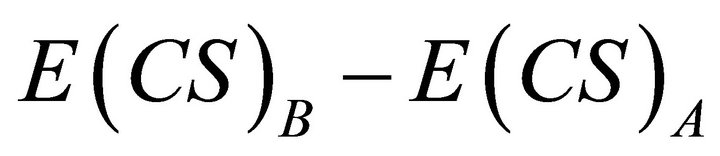 must be greater than zero since in periods
must be greater than zero since in periods  through
through 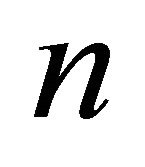 the demand curve lies above the rigid price and in periods
the demand curve lies above the rigid price and in periods  through
through  the demand curve lies below the rigid price.
the demand curve lies below the rigid price. 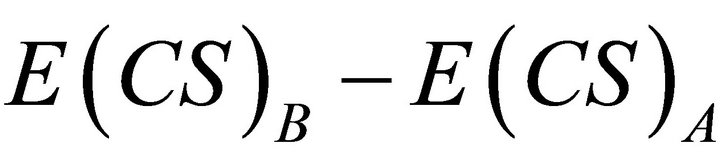 rises as price elasticity rises since with more elastic demand curves the difference of
rises as price elasticity rises since with more elastic demand curves the difference of  increases. At zero elasticity,
increases. At zero elasticity,  and thus
and thus
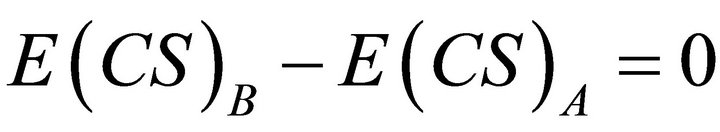 .
.
5. Future Research and Policy
We prove that consumers having fluctuating downwardsloping linear-demand curves, Sabbath versus Weekday, with the Sabbath demand curve to the right of the Weekday demand curve, a pricing scheme that leads to consumers buying less food on Weekdays and more on the Sabbath, will increase consumer surplus. The two basic assumptions are that expected food and expected payments be the same.
An area of future research would be to allow expected food to decline in the alternate pricing scheme while keeping expected payments the same. We could then calculate by how much less expected food would yield
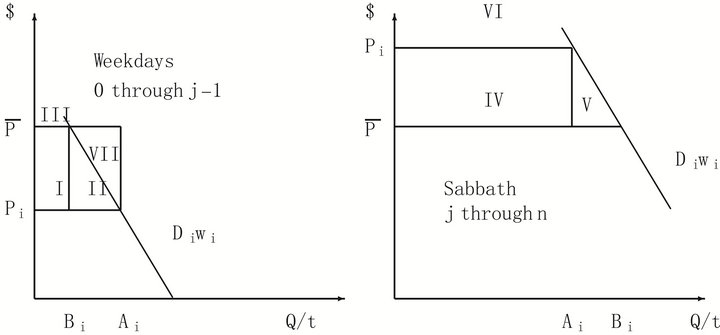
Figure 2. Consumer surplus comparisons.
the same consumer surplus between the two pricing schemes. This would represent a theoretical maximum consumers would be willing to pay suppliers to adopt to the alternate pricing scheme.
This adds realism since to supply a wider range of outputs would cost suppliers more. In our model we assume suppliers have infinite output flexibility, meaning that suppliers could supply wider ranges of outputs at the same costs as narrower range of outputs.
Our policy recommendation is that for economic cycles, focus be on adequacy of supply in high-demand times. Just like the Jewish prescription for saving for the Sabbath improves consumer surplus, so too, economic planning for seasonal and business cycles should focus on adequacy of supply in high-demand times. John M. Clark’s workable competition thesis rejects short-run marginal cost pricing because the required price in highdemand times would be too high to obtain in the real world. In Clark’s view suppliers in an industry of shortrun marginal cost pricing would not provide adequate supply for high-demand times.
6. Conclusions
We demonstrate here that a rigid price in high and low demand periods for a perishable product generates more consumer surplus where consumers pay the same anticipated payments and receive the same anticipated goods over the cycle. The key reason is that the consumer will have more goods for the high-demand periods even at the cost of having less goods in low-demand periods. Though high-demand periods are infrequent, improving supply in high-demand periods will benefit consumers more than the cost to consumers of less supply in lowdemand periods. This has been demonstrated here in a defined model with restrictive assumptions, but we believe that this is widely true for business cycles (such as cement capacity to meet high-demand periods) and for seasonal cycles (such as resort hotels). The Jewish law prescription, that households on a tight budget, should reduce on weekdays to allow more on the Sabbath, adds to consumer surplus.
The lesson is that for all cyclical demand fluctuations, such as business cycles, seasonal cycles, and weekly cycles, focus must be on sufficiency of supply for the high-demand periods.
REFERENCES
- M. J. Clark, “Studies in the Economics of Overhead Costs,” The University of Chicago Press, Chicago, 1923.
- G. Aranoff, “John M. Clark’s Concept of Too Strong Competition and a Possible Case: The US Cement Industry,” Eastern Economic Journal, Vol. 17, No. 1, 1991, pp. 45-60.
- G. Aranoff, “Competitive Manufacturing with Fluctuating Demand and Diverse Technology: Mathematical Proofs and Illuminations on Industry Output-Flexibility,” Economic Modelling, Vol. 28, No. 3, 2011, pp. 1441-1450. doi:10.1016/j.econmod.2011.02.016
NOTES
1Mark that the Lord has given you the Sabbath; therefore He gives you two days’ food on the sixth day. Let everyone remain where he is: let no one leave his place on the seventh day (Exodus 16:29).

