Modern Economy
Vol.4 No.3A(2013), Article ID:29144,4 pages DOI:10.4236/me.2013.43A025
The Evaluation of Dexterity and a Theory of the Growth of a Firm
Institute of Social Science, University of Tokyo, Tokyo, Japan
Email: ohtaki@iss.u-tokyo.ac.jp
Received October 25, 2012; revised November 28, 2012; accepted December 30, 2012
Keywords: Internalization of Dexterity; Penrose Effect as Educational Costs; The Engine for the Growth of a Firm
ABSTRACT
Determining which production resources embody various business skills is a very important issue not only for the investment function theory but for the theory of firm. Uzawa regards these nurtured skills as being entirely attributed to real capital and establishes a microeconomic foundation for Tobin’s [1] q theory. However, it is quite ambiguous how skills are embodied into real capital in Tobin-Uzawa theory, whereas, it seems natural that such skills are acquired by employees both explicitly and implicitly through learning by doing (Arrow [2]) and/or formal education within a firm. Thus, we deal with labor as the quasi-fixed production resource instead of real capital. We set the objective function of a firm as the discounted sum of the surplus from skilled employees, and solve the optimal path of accumulation of intangible skills by deploying an elementary calculus of variation owing to Uzawa [3]. We obtain the following results. First, we obtain human-capital’s q theory of the investment function that emphasizes the importance of internalization of the positive externality from skilled labor force to real capital. We call such an externality “the dexterity of employees”. Second, we consider the case where an employer regards his firm as a standard neoclassical type. The term of standard neoclassical type means that every production resource is marketable and easily substitutable. In such a case, since the contribution of the dexterity is neglected, the employer recognizes his production function is not constant return but decreasing returns to scale. As a result, the equilibrium growth rate of such a firm becomes zero in the long run. This finding implies that it is crucial for sustaining the growth of a firm to evaluate the (non-marketable) dexterity of employees correctly.
1. Introduction
The investment function theory relies heavily on the existence of the adjustment function. Uzawa [3] considers how the quality of installed real capital within a firm utterly differs from the new capital sold in the market. Real capital is assumed to become productive only via the adjustment process. He defines the ability of adjustment as a management skill (Penrose effect).
However, components of adjustment costs are quite ambiguous. Why do automatic changes in the quality of real capital necessarily incur adjustment costs? It would seem natural that the dexterity of employees contributes to increasing the capacity of real capital. The intangible human capital that employees accumulate plays a crucial role in the growth of a firm. In other words, it is a quite important factor for the growth of a firm to internalize a positive externality from skilled labor to capital via the formal/informal education.
Once we admit such a fact, it is plausible to regard labor as the quasi-fixed production factor instead of real capital. The growth of a firm is the equivalent to that of employees’ skills, thus, we should replace the investment function theory with the theory of human capital accumulation.
Such a reconstruction of the investment theory facilitates the economic interpretation of the adjustment cost function. The additional costs necessary for a firm’s growth are the costs of the education that are needed to enhance and/or furnish the human capital held by employees. In addition to reconstruction, we shall establish human-capital’s q theory, corresponding to Tobin’s [1] q theory concerning real-capital accumulation.
Moreover, we shall consider the case that such internalization does not work well. In this case, an employer neglects the existence of the important intangible asset (i.e., the dexterity) and regards his firm as being entirely constructed by marketable and substitutable capitals as elementary neoclassical theory of production assumes.
In such situation, the employer recognizes that his production opportunity faces the diminishing return to scale because the important production factor (i.e., the dexterity) lacks from his perspective. The surplus gained from the dexterity is regards as an autonomous technological progress (a kind of good will) whose return should be attributed to him.
Since the recognized production function is diminishing return to scale and the optimal size of a firm exists, we easily show that the equilibrium growth rate of such a type of firm is zero in the long run. That is, how efficiently to internalize the accumulation of the intangible asset determines whether a firm can continue to grow.
The contents of the article are as follows. In Section 2, we construct a dynamic theory of human-capital accumulation, that is, human-capital’s q theory. Section 3 considers the importance of internalization of employees’ dexterity for promoting the growth of a firm. Section 4 gives brief concluding remarks.
2. The Model
There are employees, who are equally talented, with a fixed continuum density [0,1] at the start of an economy. To avoid the unemployment problem, we assume that full-employment has been attained1. There is also a single perishable good that can not only be consumed but also be used for the formal and/or informal education of employees.
We consider the problem how the correct evaluation of employees’ dexterity contributes to the economic wellbeing. An elementary calculus of variation is deployed for solving such a problem.
The lifetime utility function of each employee 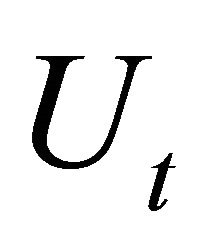 is
is
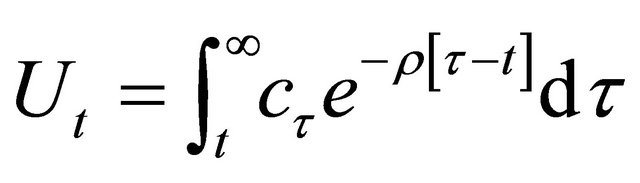 (1)
(1)
where  denotes the consumption level at time
denotes the consumption level at time , and
, and 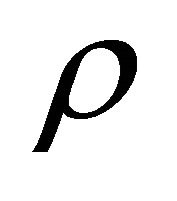 is the time preference rate.
is the time preference rate.
Using Otaki and Yaginuma [5], we specify the production function as follows.
 (2)
(2)
where 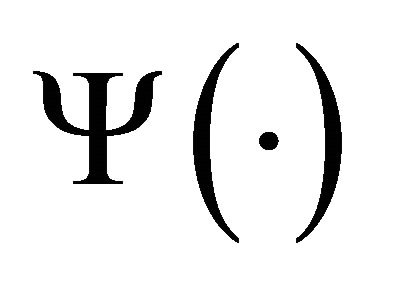 is a linear homogenous function that represents the effective capital input.
is a linear homogenous function that represents the effective capital input. 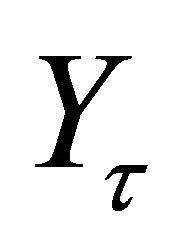 and
and 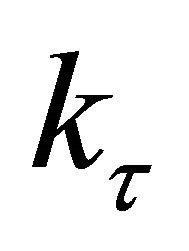 denote the volume of output and the deployed real capital used for it, respectively.
denote the volume of output and the deployed real capital used for it, respectively.  is the labor input in terms of efficiency units. In addition, we assume
is the labor input in terms of efficiency units. In addition, we assume 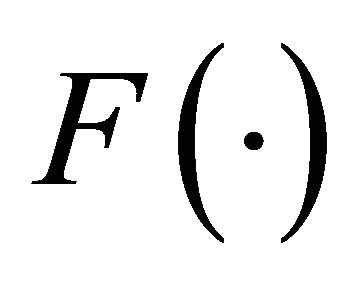 is also linear homogenous.
is also linear homogenous.
The economic meaning of Equation (2) is as follows. As well as the increment in output owing to real capital
 , an improvement of the efficiency unit of the skilled labor force brings about two positive effects. One is direct, in the sense that employees become able to deal with the procedures involved in their jobs more efficiently
, an improvement of the efficiency unit of the skilled labor force brings about two positive effects. One is direct, in the sense that employees become able to deal with the procedures involved in their jobs more efficiently
 . The other is indirect, as real capital works more productively due to the dexterity of a skilled labor force
. The other is indirect, as real capital works more productively due to the dexterity of a skilled labor force
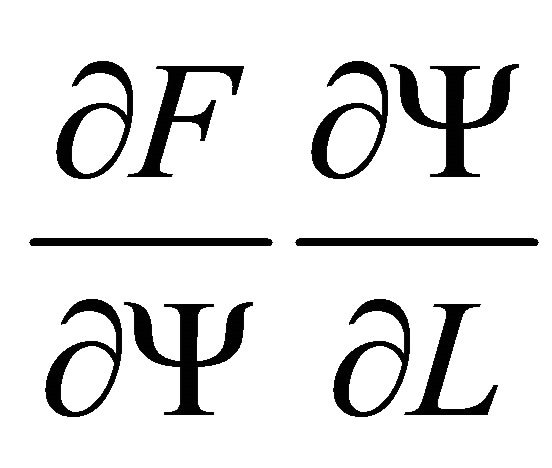 .
.
We regard the internalization of the second effect as meaning that the appropriate enhancement of employees’ dexterity is the raison d’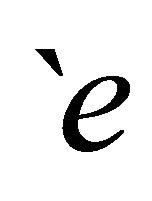 tre of a firm. Elementary economics deploys the linear homogenous production function, and so excludes an externality such as
tre of a firm. Elementary economics deploys the linear homogenous production function, and so excludes an externality such as 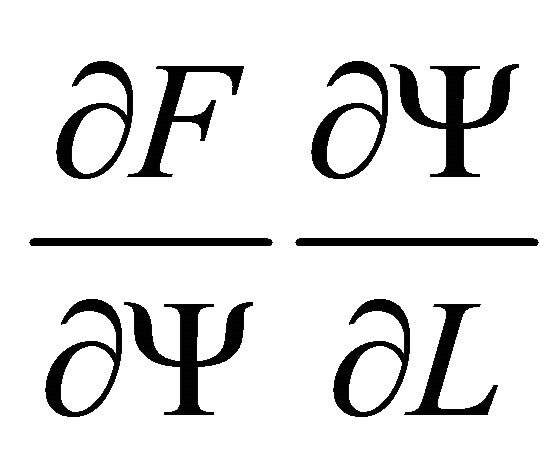
from labor to capital, and thus, a firm can ultimately be decomposed into these two production resources. As Coase [6] suggests, such a firm without the externality, can only be constructed by assembling production resources. Hence, this cannot explain how an organization is differentiated from the market.
Whereas what it is that differentiates a firm from the market is quite ambiguous in Coase-Tobin-Uzawa theory, we emphasize that the substance of a firm is determined by the inseparability of labor and capital originating from employees’ dexterity, namely, the externality from labor to capital.
Net cash flow per employee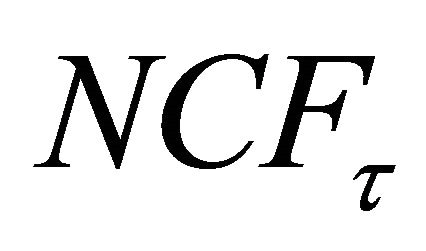 , which in our setting is always equal to current consumption
, which in our setting is always equal to current consumption  can be written as
can be written as
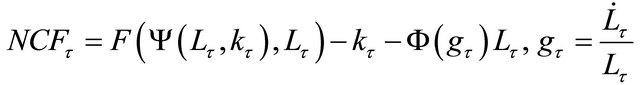 (3)
(3)
where 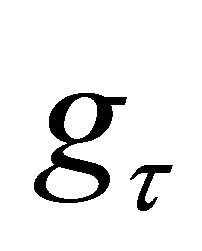 denotes the growth rate of the efficiency of labor.
denotes the growth rate of the efficiency of labor.  is the educational cost function of heightening dexterity; this corresponds to the adjustment cost function (the Penrose function) in Tobin-Uzawa theory.
is the educational cost function of heightening dexterity; this corresponds to the adjustment cost function (the Penrose function) in Tobin-Uzawa theory.
Taking the linear homogeneity of F and  into consideration, from the short-run maximization decision for
into consideration, from the short-run maximization decision for , the Euler theorem transforms Equation (3) into
, the Euler theorem transforms Equation (3) into
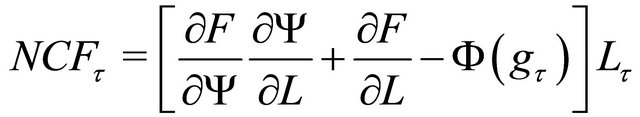 (4)
(4)
From Equations (1) and (4), the objective function of a representative firm becomes
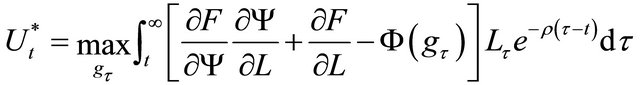 (5)
(5)
It is well-known that under such a linear homogenous environment, the only optimum path of  involves a growth rate
involves a growth rate 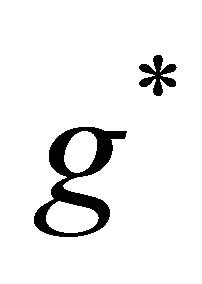 that is constant over time, hence, Equation (5) is rewritten by
that is constant over time, hence, Equation (5) is rewritten by
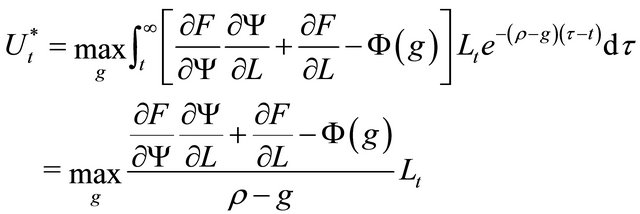 (6)
(6)
Thus, by differentiating Equation (6) with respect to g, we obtain the optimal skill accumulation rate 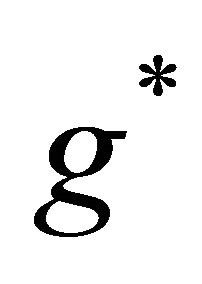 as
as
 (7)
(7)
Similar to Uzawa [3] in the case of real capital accumulation, the right-hand side of Equation (7) expresses human-capital’s q, which corresponds to the shadow price of an employee measured by the efficiency unit, and thus, this equation implicitly defines q theory of the human-capital investment. Hence, it is also clear that the following theorem holds from Equations (5) and (7):
Theorem 1 The equilibrium lifetime utility per capita 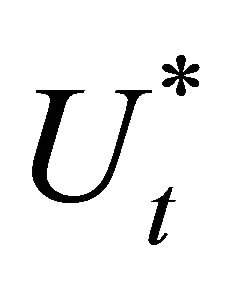 is represented by
is represented by
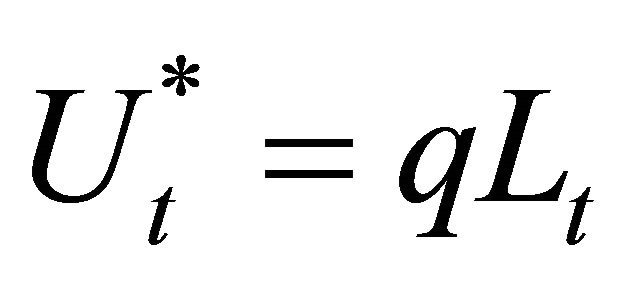 (8)
(8)
Equation (8) succinctly shows that the lifetime utility per employee is equal to the product of his human-capital’s q and accumulated skills .
.
In addition, the equilibrium growth rate of an employee’s skills g* is defined by Equation (7).
3. Dexterity as the Engine for the Growth of a Firm
In above section, we assume that a firm can fully internalize the dexterity of employees. However, such a mechanism works only when the employer can properly evaluate each employee’s performance. It implies that employees are non-anonymous within the firm. This nonanonymity characterizes the difference between the transaction inside and outside firm (i.e., market transaction).
When an employer does not concern with the dexterity of employees and deals with them anonymously as the standard neoclassical-type firm, such internalization is not possible. As the production (2) reveals, the employer fails to count the externality emerging from the dexterity of employees  in such situation. He misinterprets the progress of productivity due to the dexterity as the autonomous progress which is independent of employees’ skills.
in such situation. He misinterprets the progress of productivity due to the dexterity as the autonomous progress which is independent of employees’ skills.
The first-order conditions for maximization problem of such type of firm are
 (9)
(9)
where w denotes the market real wage for unskilled workers. 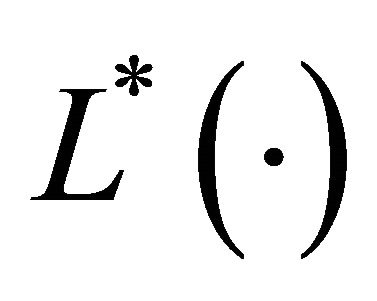 denotes the conditional labor demand function in the sense that the contribution of dexterity is fixed to L*, means the optimal value.
denotes the conditional labor demand function in the sense that the contribution of dexterity is fixed to L*, means the optimal value.
From Euler’s theorem and Equation (9), we obtain
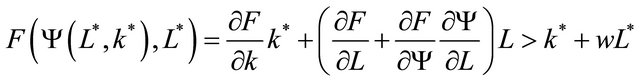
(10)
Equation (10) implies that an employer, who does not evaluate the contribution of dexterity to the production process, recognizes that his production function is diminishing return to scale2. The optimal firm size is determined by Equation (9). This implies that the growth rate of such a firm diminishes into zero in the long run.
Above discussion leads us to the following theorem.
Theorem 2 If an employer does not concern with the development of employees’ dexterity, then, he rationally interprets that his production function is diminishing return to scale. Hence, there is no opportunity of growth for such a firm in the long run. In this sense, whether a firm can continue to grow crucially depends on how efficiently to internalize the dexterity. In other words, the correct evaluation of the dexterity is the engine for the growth of a firm.
4. Concluding Remarks
This article has considered the role of employees’ dexterity in the growth of a firm. The dexterity is represented by a positive externality from skilled labor force to real capital within a firm. The obtained results are as follows: First, when an employer succeeds in internalizing such an externality, he can perceive that his production function is constant return to scale, and thus find the infinite opportunity for the growth of his firm. In relation to this human-capital investment, we have developed the concept of human-capital’s q, replacing Tobin’s q (Tobin [1]), which puts too much importance on a kind of vintage effect concerning real capital (Uzawa [3]).
Second, we have clarified the reason why the adjustment-cost function (Penrose function) exists. While Uzawa’s interpretation is quite ambiguous as he did not expose the mechanism by which real capital is made productive, we suggest that the convex adjustment function expresses the non-negligible informal and/or formal educational costs for nurturing the various skills of employees.
Finally, we have proved that the production function becomes decreasing return to scale and overlooks the opportunity of the growth of a firm whenever an employer fails to internalize the dexterity. Such inefficiency comes from the fact that the employer confuses the surplus derived from the dexterity with the good will of his firm. Although it is an intangible asset, the dexterity is the embedded engine for the growth of a firm.
REFERENCES
- J. Tobin, “A General Equilibrium Approach to Monetary Theory,” Journal of Money Credit and Banking, Vol. 1 No. 1, 1969, pp. 15-29. doi:10.2307/1991374
- K. J. Arrow, “The Economic Implications of Learning by Doing,” Review of Economic Studies, Vol. 29, No. 3, 1962, pp.155-173. doi:10.2307/2295952
- H. Uzawa, “Time Preference and the Penrose Effect in a Two-Class Model of Economic Growth,” Journal of Political Economy, Vol. 77, No. 4, 1969, pp. 628-652. doi:10.1086/259554
- M. Otaki, “A Keynesian Endogenous Growth Model with a Rigorous Microeconomic Foundation,” Theoretical Economics Letters, Vol. 2, No. 3, 2012, pp. 278-282. doi:10.4236/tel.2012.23051
- M. Otaki and H. Yaginuma, “The Growth of the Firm and Accumulation of Human Capital: The Conflict between the Managerial Right and the Growth of the Firm,” DBJ Discussion Paper Series No. 1208, Research Institute of Capital Formation, Development Bank of Japan, 2012.
- R. H. Coase, “The Nature of the Firm,” Economica, Vol. 4, No. 16, 1937, pp. 386-405. doi:10.1111/j.1468-0335.1937.tb00002.x
NOTES
1For example of properties of economic growth under imperfect employment equilibrium, see Otaki [4].
2It is necessary and sufficient condition for a diminishing return to scale production function G that there is a non-negative and strictly increase function Φ such as
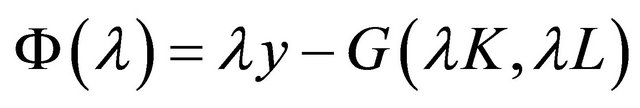
where λ is a non-negative number and y is the output. Function Φ represents the seriousness of diminishing return to scale. Differentiating both sides of above equation with respect to λ and applying the Euler’s theorem, we obtain
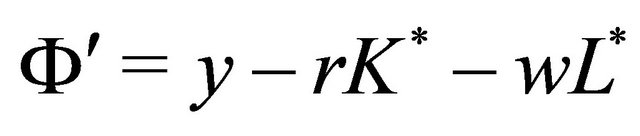
Thus, if the right-hand side of above equation is positive, such a production function is diminishing return to scale.

