Journal of Biophysical Chemistry
Vol.5 No.2(2014), Article ID:45572,10 pages DOI:10.4236/jbpc.2014.52006
Non-Local pH Shifts and Shared Changing Angular Velocity Magnetic Fields: Discrete Energies and the Importance of Point Durations
Nicolas Rouleau, Trevor N. Carniello, Michael A. Persinger
Bioquantum Laboratory, Laurentian University, Sudbury, Canada
Email: mpersinger@laurentian.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 18 March 2014; revised 18 April 2014; accepted 25 April 2014
ABSTRACT
Macroscopic productions of “non-locality” or “excess correlations” of dynamic changes within media between two spaces could be utilized as alternative communication systems. Previous experiments have shown that injections of a weak acid within one of two volumes of spring water sharing the same patterned circular magnetic fields with changing angular accelerations separated by non-traditional (5 m) distances were associated with opposite (basic) shifts in pH within the non-injected, non-local volume. In the present experiments, employing a different technology, pairs of beakers separated by 1 m containing either 25 cc, 50 cc, or 100 cc of spring water were placed within toroids generating weak (30, 300 nT) changing acceleration magnetic fields with 1 ms, 2 ms, or 3 ms point durations or a field whose point durations changed. When a proton source (weak acid) was injected into one beaker (local) pH shifts in the other (non-local) beaker exhibit increased acidity for the 3 ms point duration but increased alkalinity for the 1 ms duration. Neither intermittent point durations nor variable point durations for the same volumes of water placed between the two magnetic field-coupled beakers exhibited significant changes from baseline. Contingent upon the point duration of the applied field, the pH shift was consistent with a fixed quantity of decreased free protons (increased pH) or increased protons (decreased pH) in the non-local beakers. The opposite directions of the pH shifts at 1 ms and 3 ms that correspond to quantitative cosmological solutions for electrons and protons suggest these results may reflect a fundamental physical process.
Keywords:Excess Correlations, pH Shifts, Non-Locality, Novel Communication Systems

1. Introduction
A means by which information could be inexpensively exchanged over large distances without the requirement for classic “transmission” and the escalating expense of equipment would substantially alter the concept and form of communication. The concept of “non-locality” and “excess correlation” has been considered by many as the quintessential property limited to quantum phenomena. As indicated by Hofmann et al. [1] , “observers of two or more entangled particles will find correlations in their measurements that cannot be explained by classical statistics”. Two-photon, three dimensional entanglements may be capable of applied quantum communication [2] . Such quantum energy “teleportation” may not be limited by distance [3] .
Although from some perspectives photons will remain the only means of quantum communication because of the technical requirements [2] , Julsgaard et al. [4] experimentally entangled two macroscopic entities, each containing ~1012 atoms of caesium gas, for which the entanglement was maintained for 0.5 milliseconds. Dotta and Persinger [5] hypothesized that “excess correlation” might be facilitated by exposing two spaces at non-traditional distances (5 m) to the same circularly generated (“rotating”) magnetic fields with intensities of ~1 µT and changing angular velocities. These same intensities when applied strategically produced robust photon emissions from aggregates of cells. Dotta and Persinger [5] demonstrated that if the group and phase velocity of these rotating magnetic fields were dissociated, conspicuous excess correlations in photon emission as measured by photomultiplier tubes were evident. If both loci were exposed to the same computer-generator fields, the simultaneous injections of small aliquots of hydrogen peroxide into hypochlorite solutions at both loci “doubled” the photon emission from one locus. The “excess correlation” was as if both loci were transposed to the same space.
The effect was equivalent to injecting twice the aliquot of peroxide into any one locus without the presence of the field. However, it was only evident for a specific order of presentation of the field configurations and was maintained for about 8 minutes. Considering the numbers of molecules involved with the solutions from which the photons were emitted this duration was consistent with values for a smaller number of molecules reported by Julsgaard et al. [4] and suggested a type of “mass action”. The effect was similar to that observed for pairs of cell cultures or human brains separated by non-traditional distances but exposed to the same magnetic field configurations and parameters [6] [7] .
To test if the effect could be produced in other systems, Dotta et al. [8] measured pH changes in different quantities of spring water separated by 5 m. They shared the same configuration and parameters of magnetic fields which produced the excess correlation of photon emissions. After the required period of exposure injection of a small amount of protons (weak acid) into one beaker which produced a clear shift towards acidic pH, the pH in the other beaker that shared the same patterned, rotating magnetic field exhibited discrete increases towards basic pH. The antithesis of the response, that is the decrease in pH in the active (injected) solution and the increase in pH in the non-local (non-injected) solution, was consistent with the excess correlation associated with “entangled” photons whereby the change in polarity of one photon is associated with a comparable (opposite) shift in the other even at extraordinary distances [9] .
Here we present evidence that the shift in pH with the same patterned magnetic field during the phase associated with excess correlation or entanglement was specific to the point durations of the voltages generated by computer software that produced the field. Unlike previous studies where the changing angular velocities of the magnetic field were generated within circular arrays of solenoids, computer-generated, software driven shifts within toroids were employed. Fixed point durations of 1 ms or 3 ms, solutions from cosmological conditions involving Planck’s lengths [10] , an intermittent value of 2 ms and a field with changing point durations were selected.
2. Experimental Details
2.1. Equipment
The experiment consisted of seventy-two (n = 72) trials separated over several weeks with 6 trials completed per session. Each trial involved four beakers. The four beakers were placed in a row with equal separation along the axis. The two most lateral beakers were separated by 1 m and placed within the center of toroidal coils as described by Burke et al. [11] . The schematic is shown in Figure 1.
Each beaker within the same trial contained either 25 cc, 50 cc, or 100 cc of spring water. The constituents of
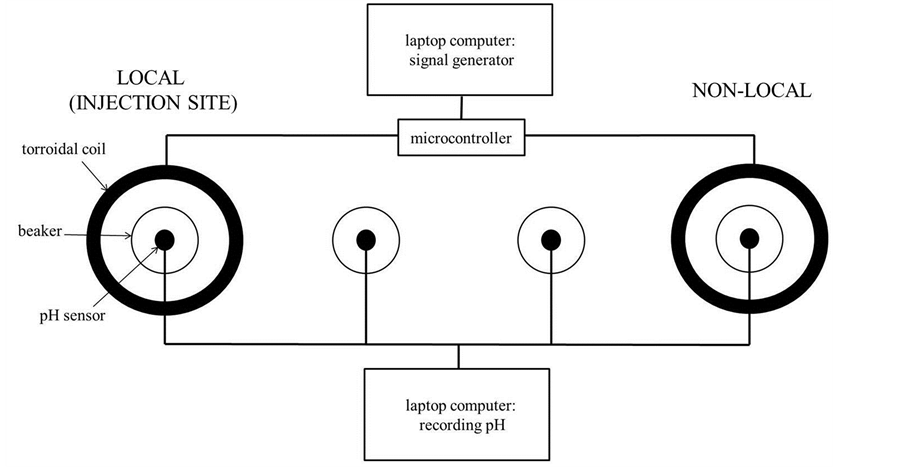
Figure 1. Schematic of the apparatus employed to produce “entanglement” or “excess correlation” in pH shifts within two separate containers of water. The dark circles refer to the toroids that generate the shared fields with changing angular velocities. The two cirlces representing beakers in the center were “controls” to ensure there were no indirect field effects upon pH shifts.
the spring water have been reported elsewhere [8] . Different volumes of water were employed to discern the quantity of potential energy that could be involved, per molecule, from a fixed amount associated with the shared magnetic fields. To verify that the magnetic field intensity was the primary correlate of the energy that mediated the effect of the “entanglement” between the volumes of water, two intensities were generated: 30 nT or 300 nT, within the space occupied by the beakers. These intensities were elected for theoretical [8] [10] reasons and for potential practical applications so that more extensive applications only required the output from conventional laptop computers.
The coils were connected to an electronic breadboard receiving signals from an Arduino UNO microcontroller which generated synchronized, patterned electromagnetic fields (Figure 1).
The shape of the primary pulse, whose durations could be varied experimentally, generated from the Arduino directly and within each toroid is shown in Figure 2. All signals were generated by an Arduino UNO microcontroller receiving uploaded patterns from a Sony Vaio laptop computer running Arduino v1.01 software on a Windows 7 operating system via USB 2.0. Low intensity (30 nT) and high intensity (300 nT) conditions, as measured by an AC MILLIGAUSS METER model UHS by AlphaLab, Inc. (USA), were included. The low intensity was just discernable above the 60 Hz background. The present of the signals and their fidelity were verified by listening to an acoustic amplifier connected to a small solenoid (telephone coupler). Whereas the 5 V output from the USB to the microcontroller defined the low intensity condition, the high intensity condition was achieved by coupling a 9 V (800 mA) Nexxtech power adaptor to the breadboard as an external power source.
2.2. Maintaining the Integrity of the Specifications
The procedure involved exposing a local and non-local beaker to synchronized, counter-clockwise rotating, electromagnetic fields for a total of 18 minutes. A similar procedure using different technologies for generating the fields was described by Dotta et al. [8] . Two field patterns were presented in series, both consisting of looped, 7-point pulses with points lasting 1, 2, or 3 ms in duration.
The first field (the “primer field”), presented from minute 0 to minute 6, was a phase modulated pattern wherein the temporal delay between points (beginning with 20 ms) successively increased by 2 ms as a function of time (i.e. decelerating). The second field (the “excess correlation field”), presented from minute 6 to minute 18, was characterized by a temporal delay between points that successively decreased by 2 ms as a function of time (i.e. accelerating). In both cases, the temporal delay returned to 20 ms after a 7-point pulse, defining the
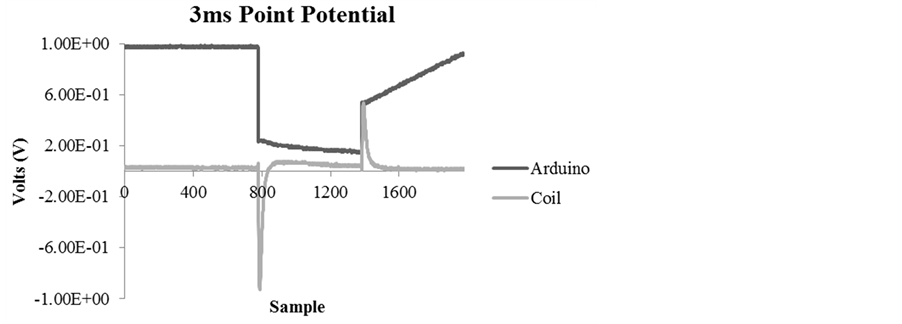
Figure 2. The 2D representation of the 3 ms point durations measured at the level of the Arduino (dark line) and coil (light line) that composed the shape of the field generated within the toroids. The other point durations were similar in shape but were presented for either 1 ms or 2 ms. Here, the x-axis represents samples recorded by an Agilent Technologies MSOX3012A oscilloscope where the time equivalent between peaks is equal to 3 ms.
loop.
The fourth point condition (delta) was an exception to this procedure in that the delays between points remained fixed (100 ms) whereas the points themselves defined the phase modulation. Consequently, cycled through the wave pattern, the point durations started at 20 ms and then either decelerated or accelerated by 2 ms until returning to 20 ms. The rationale was to insure that the critical feature for entanglement was the change in angular velocity of fixed point durations of electromagnetic energy or “quantum wells”.
A proton source (5% acetic acid) was injected into one of the two magnetic fields exposed beakers at fixed intervals throughout the trials. The pH values were recorded for all beakers. Shifts in pH, as measured by probes inserted into the water, relayed information to a Lenovo laptop computer running Pico Technology (UK) via Dr. Daq boards with USB 2.0. The system sampling rate was set to 1 Hz and programmed to terminate recording after 1080 samples. On average, starting pH values ranged from 7.0 to 7.5 which indicated accurate calibration of the instruments.
The two center beakers served as controls; pH shifts were monitored but no injections were administered. At minute 4 of the trial, 68 µL of 5% acetic acid was injected into the local beaker using a micropipette. Subsequent to the switch from the first field to the second, injections were made continuously from minute 7 to minute 15 of the experiment. All conditions were triplicated to ensure reliability of the phenomenon. To reiterate, the local beaker was the only flask to receive a chemical manipulation (i.e. injections of a proton donor).
3. Results
25 cc Volumes
The mean shifts in pH in the 25 cc volumes by the end of the 6th minute of exposure to the decelerating magnetic field are shown in Figure 3. There was a marginally significant shift towards alkalinity for the 1 and 3 ms point (fixed) durations for the 30 nT conditions compared to the same strength magnetic field whose point durations increased while the time between points remained constant.
On the other hand, during the “excess correlation” component, that is when the same magnetic field with fixed point durations was accelerated within the toroid, the mean shift in pH was significantly different for both the 3 ms and 1 ms point durations compared to the delta and 2 ms intervals. The volumes of water exposed to the 3 ms durations shifted towards acidity while the 1 ms point duration-exposed volumes shifted towards alkalinity. The shift in pH in the specific directions exhibited an asymptote at about 2 min after the onset of the accelerating field (see Figure 4).
The mean values for the shifts that demonstrated the “excess correlation” are shown in Figure 5. There was no significant difference between the two intensities of the field applications from baseline for either the same

Figure 3. Means and standard errors of the mean for the shift in pH in the 25 cc volumes as a function of the fixed point durations for the applied decelerating magnetic field configurations for the two intensity conditions. Delta indicates a field with changing point durations but no deceleration.
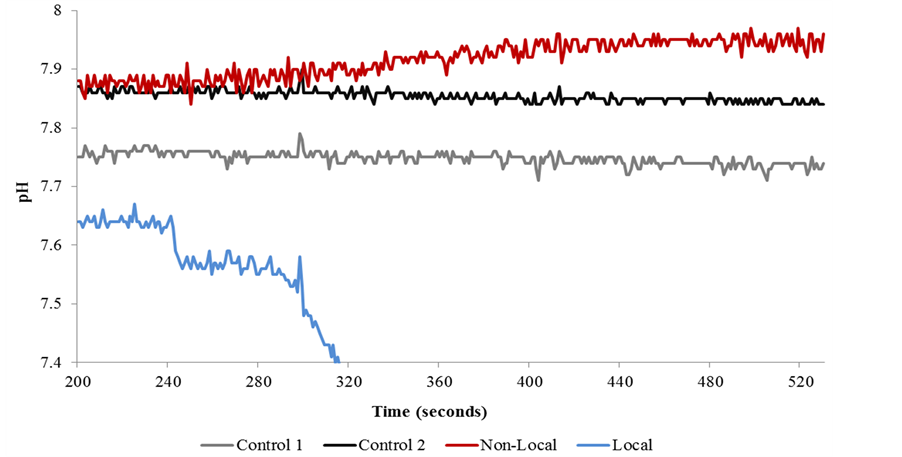
Figure 4. A typical example of non-local and local pH shifts during a trial involving electromagnetic fields composed of 1 ms point durations with an associated intensity of 30 nT. The pH for the control beakers remains static throughout the exposure. Note the first injection of acid at 240 seconds within the local beaker. The non-local shift asymptotes ~100 seconds after the onset of the accelerating field at 360 seconds.
accelerating field with 2 ms point durations or for the field whose point durations cycled by 2 ms from a base of 20 ms to 34 ms throughout the sequence of the field application while the time between points remained fixed at 100 ms. When selecting for only those trials involving beakers containing 25 cc of spring water, significant differences in pH shifts across point duration conditions were observed from the 6th to the 18th minute of the exposure for the non-local beaker, F(3,26) = 5.31, p < 0.01, Ω2 estimate = 0.42. The local as well as the two control beakers did not differ across point duration conditions when considering the same selection criteria (p > 0.05). There was greater inter-experiment variability for the shifts in pH associated with the 300 nT intensities compared to the 30 nT intensities. The effect size of the latter was about 0.82. In other words about 82% of the variance in pH in the volumes exposed to the 30 nT fields at the various point durations could be explained by these temporal features. Post-hoc analysis revealed the major sources of this effect were the marked differences in pH shifts associated with 1 ms (M = 0.04, SE = 0.02) and 3 ms (M = −0.04, SE = 0.01) point conditions, t(4)
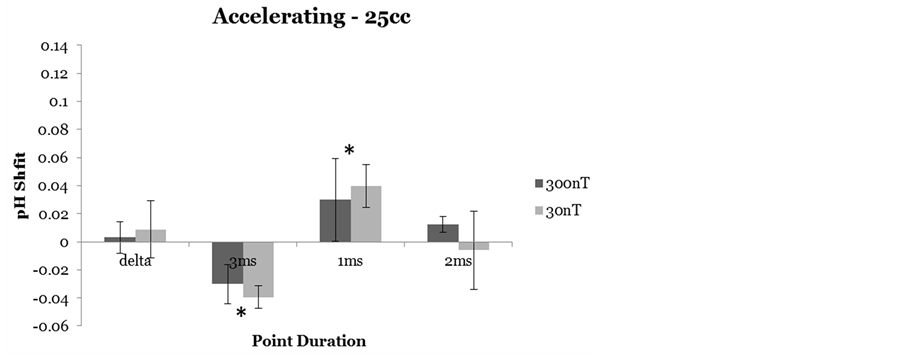
Figure 5. Means and standard errors of the mean (vertical lines) for the mean shift in pH in the 25 cc volumes during the “excess correlation” phase of the experiment as a function of the different fixed point durations. Delta indicates a field with changing point durations but no acceleration. Significant differences across point duration are indicated asterisks.
= −4.59, p = 0.01, r2 = 0.92. Control beakers for these same trials did not differ across point conditions within the 30 nT intensity (p > 0.05).
Within the 50 cc volumes, there were no significant deviations from baseline during the priming (decelerating) phase (Figure 6). During the excess correlation phase there was an increased in alkalinity for both the 1 ms and 3 ms point durations for the 30 nT condition in particular (Figure 7).
Figure 8 and Figure 9 show the results for the 100 cc volumes. Again, there were no significant changes in pH from baseline for any of the experimental conditions during the priming phase. During the presentation of the accelerating field phase, there was a marginally significant increased alkalinity for water exposed to the 1 ms point durations.
4. Discussion
In this experiment, pH values were recorded continuously during EM field exposures. It is reasonable to propose that the digital pH meters were not affected by process of electromagnetic induction. The most compelling result was that the primary effect was associated with the low intensity (30 nT) condition. If an induction effect sufficient to alter the functioning of the pH meters had occurred, the condition expected to express these effects would be the high intensity condition (300 nT). This was not the case. Further, it should be noted that fields composed of delta and 2 ms point durations were not associated with the reported effects. If there had been an inherent confounding variable or artefact that produced these shifts in pH, the delta and 2 ms conditions applied at intensities identical to those conditions which demonstrated an effect should have demonstrated comparable shifts. It should be noted that all of the fields were associated with the same pulsed all-or-none potentials while only the 3 ms and 1 ms conditions demonstrated an effect primarily within a specific volume of water. This suggests that the presence of an EM field of the type described here is not a sufficient condition which would alter the basic function of the pH meters. For these reasons, we are confident that the results presented here were a function of the experimental manipulation.
The results of these experiments are consistent with those reported by Dotta et al. [8] who employed a different technology and distances. They utilized digital-to-analogue (DAC) software generating magnetic fields through discrete shifts in voltages from 256 discrete increments between −5 and +5 V through a circular array of 8 solenoids. Two complex, physiological patterns were generated. The first exhibited a decelerating feature while the second exhibited an accelerating feature.
Here the fields were generated by machine code through toroid arrangements. The pattern was not complex. Instead the time between the fixed point duration (e.g., 1 ms, 2 ms, 3 ms) either increased in 2 ms increments from a base of 20 ms or increased in 2 ms increments. In both studies the movement of the magnetic field

Figure 6. Means and standard errors of the mean for the shift in pH in the 50 cc volumes as a function of the fixed point durations for the applied decelerating magnetic field configurations for the two intensity conditions. Delta indicates a field with changing point durations but no deceleration.
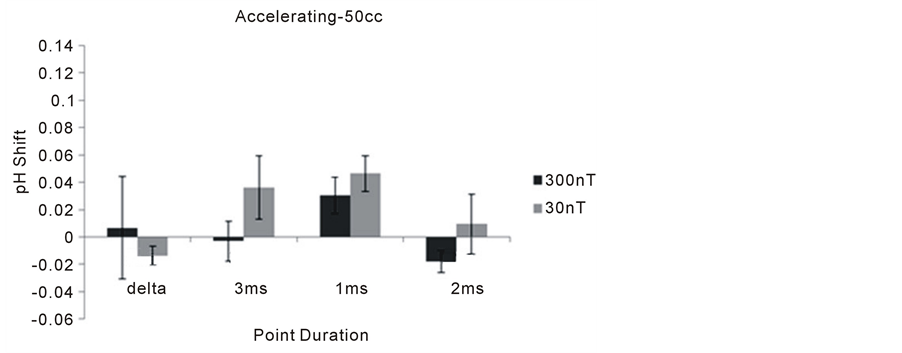
Figure 7. Means and standard errors of the mean (vertical lines) for the mean shift in pH in the 50 cc volumes during the “excess correlation” phase of the experiment as a function of the different fixed point durations. Delta indicates a field with changing point durations but no acceleration.
around the circular geometry displayed the same discrete decreased (the priming phase) and increased (the “excess correlation” phase) angular accelerations.
In the Dotta et al. experiments [8] , the shift in pH in spring water within the non-local volume of water opposite (increased alkalinity) to the acidity in the local volume due to injections of successive small aliquots of acetic acid injection in the local volume occurred only during the “excess correlation” phase as we found here. This increased (alkalinity) pH was maximum in the 25 cc volumes and also involved the 1 ms point duration. The 3 ms point duration was not employed in those studies. The strength of their field was about 1000 nT rather than 300 nT and 30 nT. The results of the Dotta et al. study [8] and the present experiments both exhibited minimum changes in pH during the first phase involving the decelerating angular movement of the field. The conspicuous shifts in pH occurred during the second accelerating phase.
For both experiments the effects were most obvious in 25 cc of water rather than larger volumes. The shift in pH during the excess correlation phase of the Dotta et al. experiments that employed 1000 nT intensities was 0.07, 0.03, and 0.01 units within the 25 cc, 50 cc, and 100 cc volumes, respectively. In the present studies the net values of the changes for the two intensities of the field (30 and 300 nT) and critical point durations (1, 3 ms) were about 0.04 units, 0.03 units, and 0.01 units, respectively. The changes during the priming phase were effec-
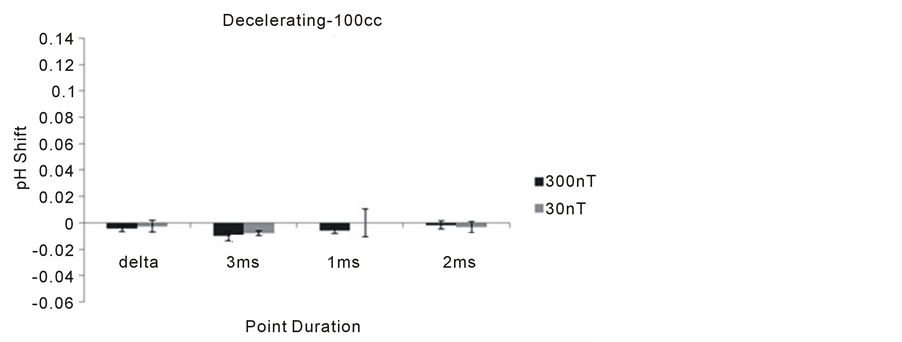
Figure 8. Means and standard errors of the mean for the shift in pH in the 100 cc volumes as a function of the fixed point durations for the applied decelerating magnetic field configurations for the two intensity conditions. Delta indicates a field with changing point durations but no deceleration.
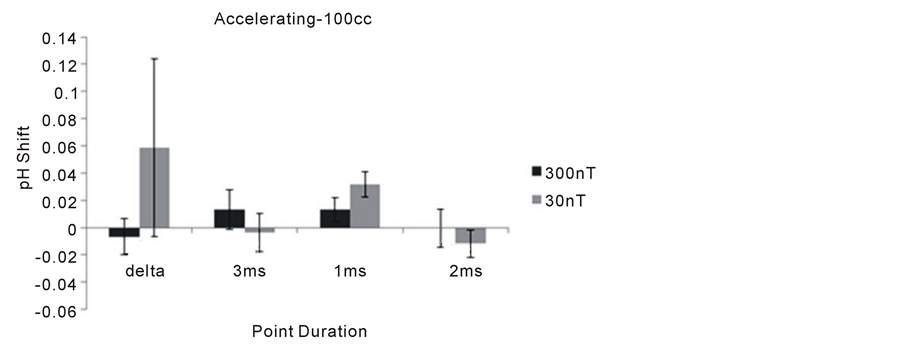
Figure 9. Means and standard errors of the mean (vertical lines) for the mean shift in pH in the 100 cc volumes during the “excess correlation” phase of the experiment as a function of the different fixed point durations. Delta indicates a field with changing point durations but no acceleration.
tively zero. The consistency and maximum magnitude of the effect within the 25 cc volumes compared to larger volumes suggests a discrete amount of energy that is diluted with volume.
The phenomena we measured with this method of generating circular magnetic fields with changing angular velocities was the creation of the opposite effect upon the pH shift depending upon the point duration of the field. When both volumes of water were surrounded by the field with the 1 ms duration, the successive injections of acetic acid produced an increased alkalinity in the non-injected (non-local) volume. This would suggest a decrease in the availability of free protons, or, potentially an increase in free electrons such as OH−. When both volumes of water were surrounded by the field with the 3 ms durations, the successive injections of acetic acid produced increased acidity. This suggests an increased availability of free protons (H+).
One potential source of the energy associated with the excess correlations might be the magnetic field generated by the toroids within the water. This can be estimated by J = B2(2 × 4π × 10−7 N·A−2)−1 V where B is the strength of the magnetic field and V is the volume. For 25 cc of volume, the energy from the 30 nT magnetic field within the volume would be 3 × 10−18 J. Within the 25 cc beaker the shift in pH was associated with a decrease or increase of 0.05. For the 3 ms point durations the shift, which displayed an asymptote after about 2 minutes following activation of the accelerating field, the average pH for 6 different experiments was 7.53. The maximum change levelled at pH = 7.58. Employing the classic H+ = 10−pH, the difference would be 3×10−9 M. Given that 25 cc contains 1.39 M and there are 6.023 × 1023 molecules per Mole, there would be a change (decrease) of ~1014 protons.
This means that there would be (3 × 10−18 J) × (2.5 × 1014 H+)−1 or 1.2 × 10−32 J·H+−1. If there are an average of 0.8 × 1012 H+ (per hydronium ion) s−1 then there would be 1 × 10−20 J·s−1 and over a period of 100 s, the approximate temporal delay observed for the asymptote, the total energy within the system would equal 10−18 J. This value represents an energy equivalent of the total transferred material. According to these calculations, the energy associated with the magnetic field within the 25 cc volume is conserved. However, if the energy were not applied over this temporal interval the total energy involved would equal ~1 × 10−20 J. This range of quantum has been considered to be a fundamental value that exists throughout the fabric if space [12] . It is also within the range of the energy of the second shell hydrogen bonds that diminish and return in the path of proton movements. Obviously, there are other explanations for this quantitative convergence. What is clear is that larger volumes, such as 50 cc or 100 cc, would result in markedly different energy densities with quantitative solutions beyond this range.
The concept of an implicit and cosmological association of the proton with the 3 ms point duration and the electron with the 1 ms duration was developed by Persinger and Koren [10] several years ago while attempting to estimate local values for Hubble’s parameter. Assuming a median value of 2.4 × 10−18 s−1 for Hubble’s expansion parameter H, multiplication by any extent or length produces a term of velocity and when divided by Planck’s length results in a specific duration. For the proton with a classic width of 2.5 × 10−15 m, the duration, is about 3 ms. For the electron, with an estimated length of 4.86 × 10−15 (i.e., twice the classic radius), the value is about 1 ms.
We [10] have interpreted these two intervals as the “time” required for the proton or electron to expand one Planck’s length. Because the total force within the universe when divided by the numbers of Planck voxels results in an energy of 10−20 to 10−19 J when applied over the distance of the neutral hydrogen line [13] , we suggest that if excess correlation is being displayed in a cosmological sense within our experiments, the congruence between the two critical point durations of the accelerating fields, the specific energy available from that field, and the congruence with a fundamental universe quantum, may be required to produce the phenomena. The specific test will be the extent or distance in space for which the “excess correlation” occurs. Some physical experiments with pair photon shifts in polarity have occurred over approximately 100 km [14] .
Acknowledgements
We are grateful to Dr. W. E. Bosarge, Jr., CEO, Capital Technologies, Inc., for his support of new ideas and technologies. Thanks to Professor Ryan Burke for the use of his equipment and to Dr. Blake T. Dotta for his technical advice.
References
- Hoffmann, J., Krug, M., Ortegel, N., et al. (2012) Heralded Entanglement between Widely Separated Atoms. Science, 337, 72-75. http://dx.doi.org/10.1126/science.1221856
- Vaziri, A., Weihs, G. and Zeilinger, A. (2002) Experimental Two-Photon, Three Dimensional Entanglement for Quantum Communication. Physical Review Letters, 89, 240401-1-240401-4.
- Hotta, M., Matsumoto, J. and Yusa, G. (2014) Quantum Energy Teleportation without a Limit of Distance. Physical Review, 89, 012311-1-012311-6.
- Julsgaard, B., Kozhekin, A. and Polzik, E.S. (2001) Experimental Long-Lived Entanglement of Two Macroscopic Objects. Nature, 413, 400-403. http://dx.doi.org/10.1038/35096524
- Dotta, B.T. and Persinger, M.A. (2012) Doubling of Local Photon Emissions from Two Simultaneously Separated, Chemiluminescent Reactions Share the Same Magnetic Field Configurations. Journal of Biophysical Chemistry, 3, 72-80. http://dx.doi.org/10.4236/jbpc.2012.31009
- Dotta, B.T., Buckner, C.A., Lafrenie, R.M., et al. (2011) Photon Emissions from Human Brain and Cell Culture Exposed to Distally Rotating Magnetic Fields Shared by Several Light-Stimulated Brains and Cells. Brain Research, 388, 77-88. http://dx.doi.org/10.1016/j.brainres.2011.03.001
- Dotta, B.T., Mulligan, B., Hunter, M.D., et al. (2009) Evidence of Macroscopic Quantum Entanglement during Double Quantitative Electroencephalographic (QEEG) Measurements of Friends and Strangers. NeuroQuantology, 7, 548-551. http://dx.doi.org/10.14704/nq.2009.7.4.251
- Dotta, B.T., Murugan, N. J., Karbowski, L.M. et al. (2013). Excessive correlated shifts in pH with distal solutions sharing the phase-uncoupled angular accelerating magnetic fields: macro-entanglement and information transfer. International Journal of Physical Sciences, 8, 1783-187.
- Persinger, M.A. and Koren, S.A. (2013) Dimensional Analyses of Geometric Products and the Boundary Conditions of the Universe: Implications for a Quantitative Value for the Latency to Display Entanglement. The Open Astronomy Journal, 6, 10-13. http://dx.doi.org/10.2174/1874381101306010010
- Persinger, M.A. and Koren, S.A. (2007) A Theory of Neurophysics and Quantum Neuroscience: Implications for Brain Function and the Limits of Consciousness. International Journal of Neuroscience, 117, 157-175. http://dx.doi.org/10.1080/00207450500535784
- Burke, R.C., Gauthier, M.Y., Rouleau, N., et al. (2013) Experimental Demonstration of Potential Entanglement of Brain Activity over 300 Km for Pairs of Subjects Sharing the Same Circular Rotating, Angular Accelerating Magnetic Fields: Verification by sLORETA and QEEG Measurements. Journal of Consciousness Exploration and Research, 4, 35-44.
- Persinger, M.A. (2014) Discrepancies between Predicted and Observed Intergalactic Magnetic Field Strengths from the Universe’s Total Energy: Is It Contained within Submatter Spatial Geometry? International Letters of Chemistry, Physics and Astronomy, 11, 18-23.
- Persinger, M.A., Koren, S.A. and Lafreniere, G.F. (2008) A Neuroquantological Approach to How Human Thought Might Affect the Universe. NeuroQuantology, 6, 262-271. http://dx.doi.org/10.14704/nq.2008.6.3.182
- Fedrizzi, A., Ursin, R., Herbst, T., et al. (2009) High-Fidelity Transmission of Entanglement over a High-Loss FreeSpace Channel. Nature Physics, 5, 389-392. http://dx.doi.org/10.1038/nphys1255

